The synergy degree measurement and transformation path of China's traditional manufacturing industry enabled by digital economy

1.   Introduction

In this paper, we use the notation ${\mathbb Z}$ (resp. ${\mathbb N}$ and ${\mathbb R}$) to indicate the set of integers (resp. natural numbers and real numbers). Besides, since we will often use the name "Marcus-Wyse" in this paper, we will take the term $" MW$-" instead of "Marcus-Wyse", if there is no danger of ambiguity. Besides, ${\mathbb Z}_o$ (resp. ${\mathbb N}_e$) means the set of odd integers (resp. even natural numbers) and further, we will use the notation "$\subset$" (resp. $X^\sharp$) to denote a 'proper subset or equal' (resp. the cardinality of the given set $X$). The notation $" : =$" will be used to introduce a new notion or a terminology. In addition, let us denote a simple closed $MW$-curve with $l$ elements by $SC_{\gamma}^l$, $4 \leq l \in {\mathbb N}_e \setminus \{6\}$ (see Definition 2.1(3) in detail).

Indeed, the well-known Jordan curve theorem on the $2$-dimensional real space ^[1] has some limitations of dealing with digital objects on ${\mathbb Z}^2$ from the viewpoints of applied sciences such as digital topology and digital geometry. Thus, in relation to the establishment of several types of Jordan curve theorems in digital topological settings, there are many works including the papers ^{[2,3,4,5,6,7,8,9,10,11,12]}. In the literature, to do this work, digital graph theory ^[7,8,9] and several types of topologies have been used such as Khalimsky, Marcus-Wyse, Alexandroff topology, pretopology, and so on. However, given a certain topological space $({\mathbb Z}^2, T)$, the earlier works did not examine topological features of $J$ and ${\mathbb Z}^2 \setminus J$, where $J$ is a simple closed digital curve in $({\mathbb Z}^2, T)$. Since both $J$ and ${\mathbb Z}^2 \setminus J$ may not be either a closed or an open set in $({\mathbb Z}^2, T)$, we need to intensively study some topological features of both $J$ and ${\mathbb Z}^2 \setminus J$. Furthermore, with a certain topological space $({\mathbb Z}^2, T)$, since the number of the components of ${\mathbb Z}^2 \setminus J$ can be very important from the viewpoint of mathematics, we need to intensively investigate this topic. For instance, on the $MW$-topological plane, i.e., $({\mathbb Z}^2, \gamma)$, the present paper clearly shows that the number of the components of the complement of $SC_{\gamma}^l$ in $({\mathbb Z}^2, \gamma)$ depends on the situation. Besides, we also find that topological features of the sets $SC_{\gamma}^l$ and ${\mathbb Z}^2 \setminus SC_{\gamma}^l$ are so related to the semi-closedness and semi-openness in $({\mathbb Z}^2, \gamma)$. In detail, see ^[13,14] or Section 3 in the present paper. Indeed, there are lots of works studying various properties of semi-closed and semi-open subsets of a topological space ^{[13,14,15,16,17,18,19]}. Based on this approach, the present paper will partially use these works.

The aim of the present paper is initially to propose the semi-Jordan curve theorem on the digital plane with the $MW$-topology (or (${\mathbb Z}^2, \gamma)$) because it has something quite independent from the earlier results in the literature including the papers ^{[3,4,6,8,9,11,12]}. To propose this theorem and support some utilities, we will mainly deal with the following topics.

$\bullet$ Examination of many types of $SC_{\gamma}^l$ with respect to the semi-closedness and semi-openness in $({\mathbb Z}^2, \gamma)$.

$\bullet$ Establishment of a method for making a continuous analog of $SC_{\gamma}^l$ and an investigation of some topological features of $\mathcal{A}(SC_{\gamma}^l)$ with respect to the semi-openness and semi-closedness in $({\mathbb R}^2, \mathcal{U})$, where $({\mathbb R}^2, \mathcal{U})$ is the $2$-dimensional real space with the usual topology.

$\bullet$ Given an $SC_{\gamma}^l$, $l \neq 4$, how to separate $({\mathbb R}^2, \mathcal{U})$ in terms of $\mathcal{A}(SC_{\gamma}^l)$ ?

$\bullet$ Assume the two subspaces $(X, \gamma_X)$ and $(Y, \gamma_Y)$ that are $MW$-homeomorphic to $SC_{\gamma}^l$. Then we will examine if the number of the components of ${\mathbb R}^2\setminus \mathcal{A}(X)$ is equal to that of ${\mathbb R}^2\setminus \mathcal{A}(Y)$. Besides, we strongly need to further compare the number of the components of ${\mathbb Z}^2\setminus X$ and that of ${\mathbb Z}^2\setminus Y$.

$\bullet$ Given an $SC_{\gamma}^l$, we need to examine if the number of the components of ${\mathbb Z}^2 \setminus SC_{\gamma}^l$ is a topological invariant.

$\bullet$ Under what condition, does $SC_{\gamma}^l$ separate $({\mathbb Z}^2, \gamma)$ into exactly two components?

$\bullet$ Development of the semi-Jordan curve theorem on the $MW$-topological plane. Besides, given an $SC_{\gamma}^l$, we investigate how to separate $({\mathbb Z}^2, \gamma)$ with respect to the semi-Jordan curve theorem.

$\bullet$ Investigation of some properties of many kinds of $SC_{\gamma}^l$ relating to the semi-Jordan curve theorem.

After addressing these topics with a success, we can confirm that the semi-Jordan curve theorem has strong advantages and some utilities compared with the earlier works in the literature because it does not have any paradox raised in the Rosenfeld's approach and further, it proceeds with the topological structures, which makes a distinction from the Rosenfeld's approach.

This paper is organized as follows: Section 2 provides some basic notions related to the digital $k$-connectivity on ${\mathbb Z}^2$ and the $MW$-topology. Section 3 studies some tools discriminating between semi-open and semi-closed sets in $({\mathbb Z}^2, \gamma)$ and further, investigates various properties of semi-closed or semi-open subsets in $({\mathbb Z}^2, \gamma)$. In Section 4, after examining if a simple closed $MW$-curve is semi-open and semi-closed in $({\mathbb Z}^2, \gamma)$, we prove the semi-openness of each $SC_{\gamma}^l$ and further, the semi-closedness of it is related to the number of $l$. Section 5 suggests a method for establishing a continuous analog of an $SC_{\gamma}^l$ denoted by $\mathcal{A}(SC_{\gamma}^l)$ by using the local rule in ^[20,21] considered on ${\mathbb R}^2$. Besides, we find some conditions for $\mathcal{A}(SC_{\gamma}^l)$ to separate $({\mathbb R}^2, \mathcal{U})$ into exactly two components, compared to the typical Jordan curve theorem in $({\mathbb R}^2, \mathcal{U})$ that is the $2$-dimensional real plane. Furthermore, we prove that $\mathcal{A}(SC_{\gamma}^l)$ is both a semi-open and a semi-closed subset of $({\mathbb R}^2, \mathcal{U})$. Meanwhile, every semi-closed $SC_{\gamma}^l, l \neq 4$, is proved to separate $({\mathbb Z}^2, \gamma)$ into many semi-open components whose number depends on the number $l$ of $SC_{\gamma}^l$. Section 6 proposes the semi-Jordan curve theorem on the $MW$-topological plane. Besides, a semi-open $SC_{\gamma}^l$ is also proved to separate $({\mathbb Z}^2, \gamma)$ into semi-closed or semi-open components whose number depends on the situation. More precisely, after proving that $SC_{\gamma}^l$ separates $({\mathbb Z}^2, \gamma)$ into many semi-closed or semi-open components depending on the situation, we find a condition for $SC_{\gamma}^l$ to separate $({\mathbb Z}^2, \gamma)$ into exactly two components. Besides, given two simple closed $MW$-curve with $l$ elements $X$ and $Y$, we first prove that the number of components of $X^c$ need not be equal to that of $Y^c$. Section 7 refers to some advantages and utilities of $MW$-topological structure and the semi-Jordan curve theorem on $({\mathbb Z}^2, \gamma)$. Section 8 concludes the paper with summary and a further work.

2.   Preliminaries

To study digital objects in ${\mathbb Z}^2$, many basic notations will be used such as a digital $4$- and $8$-neighborhood of a point $p \in {\mathbb Z}^2$ ^[7,8], as follows:

Based on the digital $4$- and $8$-connectivity in ^[7,8,22], for a point $p = (x, y) \in {\mathbb Z}^2$, the following notations will be often used later ^[7,8].

which is respectively called the $4$-neighborhood and $8$-neighborhood of a point $p$.

Then we recall that distinct points $p, q \in {\mathbb Z}^2$ are $4$-(resp. $8$-)adjacent if and only if $p\in N_4(q)\setminus \{q\}$ (resp. $p\in N_8(q)\setminus \{q\}$) or $q\in N_4(p)\setminus \{p\}$ (resp. $q\in N_8(p)\setminus \{p\}$) ^[7,8].

We now recall an Alexandroff topological structure using the study of some properties of $MW$-topological spaces. More precisely, a topological space $(X, T)$ is called an Alexandroff space if every point $x \in X$ has the smallest open neighborhood in $(X, T)$ ^[24]. As an Alexandroff topological space ^[24,25], the Marcus-Wyse topological space, denoted by $({\mathbb Z}^2, \gamma)$, was established and there are many studies including the papers ^[5,6,26]. Indeed, the $MW$-topology, denoted by $({\mathbb Z}^2, \gamma)$, is generated by the set of all $U(p)$ in (2.2) below, i.e., $\{U(p)\, \vert \, p \in {\mathbb Z}^2\}$, as a base ^[27], where for each point $p = (x, y)\in {\mathbb Z}^2$

In the paper we call a point $p = (x_1, x_2)$ doubly even if $x_1 + x_2$ is an even number such that each $x_i$ is even, $i \in \{1, 2\}$; even if $x_1 + x_2$ is an even number such that each $x_i$ is odd, $i \in \{1, 2\}$; and odd if $x_1 + x_2$ is an odd number ^[12].

In all subspaces of $({\mathbb Z}^2, \gamma)$ of Figures 1–7 the symbols $\lozenge$ and $\bullet$ mean a doubly even point or even point and an odd point, respectively. In view of (2.2), we can obviously obtain the following: Under $({\mathbb Z}^2, \gamma)$, the singleton $\{\lozenge\}$ is a closed set and $\{\bullet\}$ is an open set. Besides, for a subset $X \subset {\mathbb Z}^2$, the subspace induced by $({\mathbb Z}^2, \gamma)$ is obtained, denoted by $(X, \gamma_X)$ and called an $MW$-topological space. Hereinafter, for our purpose, we will use the notations

In terms of this perspective, it turns out that the minimal (open) neighborhood of the point $p: = (p_1, p_2)$ of ${\mathbb Z}^2$, denoted by $SN_{\gamma}(p) \subset {\mathbb Z}^2$, is obtained, as follows ^[26,28]:

Hereinafter, in $(X, \gamma_X)$, for $p \in X$ we use the notation $SN_{\gamma}(p): = SN_{\gamma}(p) \cap X$ for short if there is no danger of ambiguity. Using the smallest open set of (2.4), the notion of an $MW$-adjacency in $({\mathbb Z}^2, \gamma)$ is defined, as follows: For distinct points $p, q$ in $({\mathbb Z}^2, \gamma)$, we say that $p$ is $MW$-adjacent to $q$ ^[26] if

In view of the properties of (2.2) and (2.4), we obviously obtain the following:

Based on the structure of (2.4), for a point $p: = (p_1, p_2)$ of ${\mathbb Z}^2$, the closure of the singleton $\{p\}$ is denoted by $Cl_{\gamma}\{p\}) \subset {\mathbb Z}^2$ as follows ^[26]:

Hereinafter, in relation to the study of $MW$-topological spaces, we will use the term $Cl$ for brevity instead of $Cl_{\gamma}$ if there is no danger of confusion.

Definition 2.1. ^[26] Let $X: = (X, \gamma_X)$ be an $MW$-topological space. Then we define the following:

(1) An $MW$-path from $x$ to $y$ in $X$ is defined as a sequence $(p_i)_{i \in [0, l]_{\mathbb Z}} \subset X, l \in {\mathbb N}$, in $X$ such that $p_0 = x$, $p_l = y$ and each point $p_i$ is $MW$-adjacent to $p_{i+1}$ and $i \in [0, l-1]_{\mathbb Z}$. The number $l$ is the length of this path. In particular, a singleton in $({\mathbb Z}^2, \gamma)$ is assumed to be an $MW$-path.

(2) Distinct points $x, y \in X$ are called $MW$-path connected if there is a finite $MW$-path $(p_i)_{i \in [0, m]_{\mathbb Z}}$ on $X$ with $p_0 = x$ and $p_m = y$. For arbitrary points $x, y \in X$, if there is an $MW$-path $(p_i)_{i \in [0, m]_{\mathbb Z}} \subset X$ such that $p_0 = x$ and $p_m = y$, then we say that $X$ is $MW$-path connected (or $MW$-connected).

(3) A simple closed $MW$-curve (resp. simple $MW$-path) with $l$ elements in $X$ means a finite $MW$-path $(p_i)_{i\in [0, l-1]_{\mathbb Z}}$, $4 \leq l \in {\mathbb N}_e \setminus \{6\}$ in ${\mathbb Z}^2$ such that the points $p_i$ and $p_j$ are $MW$-adjacent if and only if $\vert\, i-j\, \vert = \pm1(mod\, l)$ (resp. $\vert\, i-j\, \vert = 1$). Then we use the notation $SC_{\gamma}^l$ to denote a simple closed $MW$-curve with $l$ elements.

As for some properties of $SC_{\gamma}^l$, it is clear that $SC_{\gamma}^{l_1}$ is $MW$-homeomorphic to $SC_{\gamma}^{l_2}$ if and only if $l_1 = l_2$ ^[26].

3.   Some properties of semi-open and semi-closed sets

This section first recalls the concepts of a semi-open and a semi-closed set. Namely, a subset $A$ of a topological space $(X, T)$ is said to be semi-open if there is an open set $O$ in $(X, T)$ such that $O \subset A \subset Cl(O)$. Besides, we say that a subset $B$ of a topological space $(X, T)$ is semi-closed if the complement of $B$ in $X$, i.e., $B^c$, is semi-open in $(X, T)$. Then it turns out that a subset $A$ of $(X, T)$ is semi-open if and only if $A \subset Cl(Int(A))$ ^[13] and a subset $B$ of $(X, T)$ is semi-closed if and only if $Int(Cl(B))\subset B$ ^[29]. Hence, in $(X, T)$, it is clear that each of the empty set and the total set is both semi-open and semi-closed. Besides, "open" (resp. "closed") is stronger than "semi-open" (resp. "semi-closed"). The notions of semi-openness and semi-closedness enable us to get the following ^[13,19,31]:

$(\star 1)$ The intersection of two semi-open sets need not be semi-open.

$(\star 2)$ The union of two semi-closed sets need not be semi-closed.

$(\star 3)$ The union of two semi-open sets is semi-open.

$(\star 4)$ The intersection of two semi-closed sets is semi-closed.

Remark 3.1. ^[30,31] In $({\mathbb Z}^2, \gamma)$, the following are obtained:

(1) The singleton $\{p\}$ is both semi-closed and semi-open, where $p \in ({\mathbb Z}^2)_o$. Namely, ${\mathbb Z}^2 \setminus \{p\}$ is both semi-closed and semi-open, where $p \in ({\mathbb Z}^2)_o$.

(2) The singleton $\{q\}$ is not semi-open but semi-closed, where $q \in({\mathbb Z}^2)_e$. Namely, ${\mathbb Z}^2 \setminus \{q\}$ is semi-open, where $q \in ({\mathbb Z}^2)_e$.

Let us further establish some techniques to examine if a set in $({\mathbb Z}^2, \gamma)$ is semi-open or semi-closed. In $({\mathbb Z}^2, \gamma)$, for a set $X \subset {\mathbb Z}^2$, we will take the following notation ^[31].

Besides, the topological structure of $({\mathbb Z}^2, \gamma)$ enables us to get the following ^[31]:

Remark 3.2 ^[31] In $({\mathbb Z}^2, \gamma)$, we have the following:

(1) For $x, y\in {\mathbb Z}^2$, $x \in SN_{\gamma}(y)$ if and only if $y \in Cl(x)$, i.e., $y \in Cl_{\gamma}(x)$(see the properties of (2.4) and (2.5) in the present paper).

(2) If $X$ is an open set in $({\mathbb Z}^2, \gamma)$, then there is at least an odd point $x$ in $X$ (see the property of (2.3)).

(3) The set $X_{op}$ of (3.1) is an open set in $({\mathbb Z}^2, \gamma)$.

Given a set $X$ in $({\mathbb Z}^2, \gamma)$, to further examine if the set $X$ is semi-open or semi-closed in $({\mathbb Z}^2, \gamma)$, we now introduce the following two theorems that will be strongly used in discriminating against subsets based on the semi-openness and semi-closedness of the $MW$-topological space.

Theorem 3.3. ^[31] In $({\mathbb Z}^2, \gamma)$, a (non-empty) set $X (\subset {\mathbb Z}^2)$ is semi-open if and only if each $x \in X$, $SN_{\gamma}(x) \cap X_{op} \neq \emptyset$, where $SN_{\gamma}(x)$ is assumed in $({\mathbb Z}^2, \gamma)$.

Since this theorem strongly plays an important role in studying many results in the present paper, to make Theorem 3.3 self-contained, we suggest a proof briefly, as follows: In case $X = \emptyset$, the proof is straightforward. Let us assume that $X$ is not an empty set.

($\Rightarrow$) According to the choice of a point $x \in X$, we can consider the following two cases.

(Case 1) Assume that $x(\in X)$ is an odd point. From the hypothesis, we have $x \in X \subset Cl(Int(X))$ so that we obtain

Since $SN_{\gamma}(x) = \{x\}$, we obtain $x \in Int(X)$ and further, $x\in X_{op}$. Hence, owing to (3.2), we have $SN_{\gamma}(x) \cap X_{op} \neq \emptyset$.

(Case 2) Assume that $x \in X$ is a doubly even or even point. Owing to the hypothesis, we obtain $x \in Cl(Int(X))$ that leads to the following property as mentioned in (3.2).

Since $SN_{\gamma}(x) \cap Int(X)$ is a non-empty open set in $({\mathbb Z}^2, \gamma)$, by Remark 3.2(2), we now take an odd point $z$ in $({\mathbb Z}^2, \gamma)$ such that

By the property of (3.3), since $z \in Int(X) \subset X$, we have $z \in X_{op}$ (see Remark 3.2(2)) so that $z \in SN_{\gamma}(x) \cap X_{op} \neq \emptyset.$ In addition, we see that the point $z$ is indeed $MW$-adjacent to $x$.

($\Leftarrow$) According to the choice of a point $x \in X$, we can consider the following two cases.

(Case 1) For an arbitrary point $x \in X$, assume that $x$ is an odd point in $({\mathbb Z}^2, \gamma)$. Since $\{x\} = SN_{\gamma}(x)$, owing to the hypothesis of $SN_{\gamma}(x) \cap X_{op} \neq \emptyset$, we have $x \in X_{op}$, i.e., $\{x\} \cap X_{op} \neq \emptyset$. Furthermore, owing to the identity $SN_{\gamma}(x) = \{x\}$, by Remark 3.2(3), it is clear that

(Case 2) For an arbitrary point $x \in X$, assume that $x$ is a doubly even or even point in $({\mathbb Z}^2, \gamma)$. Owing to the hypothesis, since $SN_{\gamma}(x) \cap X_{op}\neq \emptyset$, by Remark 3.2(2) and (3), there is an odd point $z$ in $({\mathbb Z}^2, \gamma)$ such that $z \in SN_{\gamma}(x) \cap X_{op}$ because $SN_{\gamma}(x) \cap X_{op}$ is an open set in $({\mathbb Z}^2, \gamma)$. Hence we get $z \in SN_{\gamma}(x)$, by Remark 3.2(1), we have

Owing to both (3.4) and (3.5), we obtain $X \subset Cl(Int(X))$ which prove the assertion.

Owing to the notion of semi-closedness, using Theorem 3.4, we obtain the following:

Theorem 3.4. ^[31] In $({\mathbb Z}^2, \gamma)$, $B (\subset {\mathbb Z}^2)$ is semi-closed if and only if each $x \in {\mathbb Z}^2 \setminus B$, $SN_{\gamma}(x) \cap ({\mathbb Z}^2 \setminus B)_{op} \neq \emptyset$, where $SN_{\gamma}(x)$ is assumed in $({\mathbb Z}^2, \gamma)$.

As examples for Theorems 3.3 and 3.4, see the cases referred to in Remark 3.1(1)–(3).

In view of Theorems 3.3 and 3.4, we have the following:

Remark 3.5. In $({\mathbb Z}^2, \gamma)$, assume a connected subset $X$ with $X^\sharp \geq 2$. Then it is semi-open and it may not be semi-closed.

4.   Classification of simple closed $MW$-curves with respect to the semi-closedness

To classify all types of $SC_{\gamma}^l$ with respect to the semi-openness and semi-closedness, based on the topological features of $SC_{\gamma}^l$, it suffices to consider the only case of $l \in \{2m\, \vert \, m\in {\mathbb N}\setminus \{1, 3\}\}$ because no $SC_{\gamma}^6$ exists. Hereinafter, when studying semi-topological features of a set $X\subset {\mathbb Z}^2$, we assume that the set $X$ is considered in $({\mathbb Z}^2, \gamma)$.

Theorem 4.1. Given an $SC_{\gamma}^l$, $4 \leq l \in {\mathbb N}_e \setminus \{6\}$, the semi-topological features of $SC_{\gamma}^l$ in $({\mathbb Z}^2, \gamma)$ are determined according to the number $l$, as follows:

(1) $SC_{\gamma}^l$ is always semi-open for any $l$, where $l \in \{2m\, \vert \, m \in {\mathbb N}\setminus \{1, 3\}\}$.

(2) $SC_{\gamma}^l$ is always both semi-open and semi-closed whenever $l\in \{4, 10\}$.

Proof: (1) Given an $SC_{\gamma}^l: = (x_i)_{i \in [0, l-1]_{\mathbb Z}}$, take any element $x_i \in SC_{\gamma}^l$. Then $SN_{\gamma}(x_i)$ in $({\mathbb Z}^2, \gamma)$ has the following property,

By Theorem 3.3, we conclude that $SC_{\gamma}^l$ is semi-open in $({\mathbb Z}^2, \gamma)$.

(2) (2-1) In the case of $SC_{\gamma}^4$, let $Y: = {\mathbb Z}^2 \setminus SC_{\gamma}^4$. Then, for any $p \in Y$ we have

which implies that $Y$ is semi-open in $({\mathbb Z}^2, \gamma)$ (see Theorem 3.3). Hence $SC_{\gamma}^4$ is semi-closed in $({\mathbb Z}^2, \gamma)$. Also, using a method similar to the proof of (1), it is clear that $SC_{\gamma}^4$ is semi-open in $({\mathbb Z}^2, \gamma)$.

(2-2) In the case of $SC_{\gamma}^{10}$ (see the objects in Figure 1(3)(a), (b)), let $W: = {\mathbb Z}^2 \setminus SC_{\gamma}^{10}$. Using a method similar to the proof of (2-1) above, by Theorems 3.3 and 3.4, we prove that $SC_{\gamma}^{10}$ is both semi-open and semi-closed in $({\mathbb Z}^2, \gamma)$.

Remark 4.2. In the case of $l\notin\{4, 10\}$, $SC_{\gamma}^l$ may not be semi-closed. The semi-closedness of $SC_{\gamma}^l$ depends on the situation.

Proof: In the case of $SC_{\gamma}^l$, where $l\notin\{4, 10\}$, the semi-closedness of $SC_{\gamma}^l$ depends on the situation. More precisely, given an $SC_{\gamma}^l: = (x_i)_{i \in [0, l-1]_{\mathbb Z}}$, $l \notin \{4, 10\}$, assume that $SC_{\gamma}^l$ does not have the subsequence

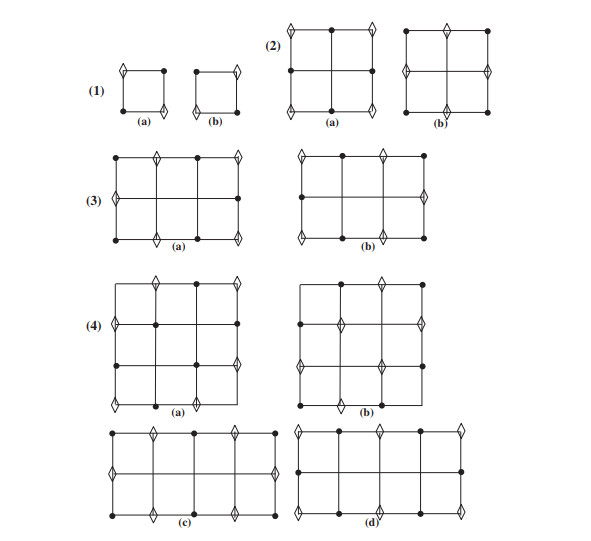
whose each element is an odd point (i.e., $X_1 \subset SC_{\gamma}^l \cap ({\mathbb Z}^2)_o$) and $X_1 \subset N_4(x), x \in {\mathbb Z}^2 \setminus SC_{\gamma}^l$. Then, by Theorem 3.4, $SC_{\gamma}^l$ is semi-closed. For instance, since no $SC_{\gamma}^6$ exists, it suffices to mention that $SC_{\gamma}^l$, $l\notin\{4, 10\}$, is semi-closed depending on the situation. As suggested in Figure 1(2), while the object $SC_{\gamma}^8$ of (a) is not semi-closed (see Theorem 3.4) but semi-open, the object of (b) is both semi-closed and semi-open.

In view of Theorem 4.1, we obtain the following:

Proposition 4.3. There are two types of $SC_{\gamma}^l, l \notin \{4, 10\}$, with respect to the semi-closedness.

Proof: Using Theorems 3.3 and 3.4, we prove the assertion. As mentioned in the proof of Theorem 4.1, we need to consider the following two cases:

(Case 1) Assume an $SC_{\gamma}^l: = (x_i)_{i \in [0, l-1]_{\mathbb Z}}, l \notin \{4, 10\}$, such that $SC_{\gamma}^l$ does not have the subsequence

whose each element is an odd point and $X_1 \subset N_{4}(x), x \in {\mathbb Z}^2 \setminus SC_{\gamma}^l$. Then, by Theorem 3.4, $SC_{\gamma}^l$ is semi-closed.

(Case 2) Assume an $SC_{\gamma}^l: = (x_i)_{i \in [0, l-1]_{\mathbb Z}}, l \notin \{4, 10\}$, in which there is the subsequence $X_1$ of (4.1) whose each element is an odd point and $X_1 \subset N_{4}(x), x \in {\mathbb Z}^2 \setminus SC_{\gamma}^l$. Then, by Theorem 3.4, $SC_{\gamma}^l$ is not semi-closed but only semi-open owing to Theorem 3.3. For instance, since $SC_{\gamma}^{12}$ in Figure 2(a) does not satisfy the condition of Theorem 3.4, it is not semi-closed in $({\mathbb Z}^2, \gamma)$ (see the points $p_1: = (0, 0), p_2: = (1, 1)$ in ${\mathbb Z}^2 \setminus SC_{\gamma}^{12}$ as in Figure 2(b)).

Example 4.1. In Figure 1, some examples for several types of $SC_{\gamma}^l$ are shown for $l \in \{4, 8, 10, 12\}$. In view of Theorems 3.3, 3.4 and 4.1, and Proposition 4.3, we obtain the following:

(1) $SC_{\gamma}^4$ in Figure 1 is both semi-open and semi-closed.

(2) As for the $SC_{\gamma}^8$ in Figure 1(2), the object of (a) is semi-open instead of semi-closed because it satisfies only the condition of Theorem 3.3 instead of that of Theorem 3.4. However, the object of (b) is both semi-open and semi-closed (see also Theorems 3.3 and 3.4).

(3) As for the $SC_{\gamma}^{10}$ in Figure 1(3), each of (a) and (b) is both semi-open and semi-closed (see Theorems 3.3 and 3.4).

(4) As for the $SC_{\gamma}^{12}$ in Figure 1(4), the object of (a) is semi-open instead of semi-closed because it satisfies only the condition of Theorem 3.3 instead of that of Theorem 3.4. To be specific, based on an $SC_{\gamma}^{12}$ in Figure 2(a), consider the object in Figure 2(b). Since the set $Cl(SC_{\gamma}^{12})$ contains the open sets $N_4(p_i) = SN_{\gamma}(p_i), i \in \{1, 2\}$, $p_1 = (0, 0)$ and $p_2 = (1, 1)$, so that $Int(Cl(SC_{\gamma}^{12})) \nsubseteq SC_{\gamma}^{12}$, which implies the non-semi-closedness of $SC_{\gamma}^{12}$ (see the proof of Proposition 4.3). However, the object of Figure 1(4)(b) is both semi-open and semi-closed.

5.   Establishment of a continuous analog of $SC_{\gamma}^l$, $\mathcal{A}(SC_{\gamma}^l)\subset{\mathbb R}^2$, with respect to the $MW$-topology

This section introduces a method for establishing a continuous analog of an object on ${\mathbb Z}^2$ with respect to the $MW$-topology. The local rule introduced in Definition 5.1 below will be used in this work and has been widely used in digitization and digital-based rough set theory ^[20].

Definition 5.1. ^[20] For each point $p: = (p_1, p_2) \in {\mathbb Z}^2$, the continuous analog of the given point $p\in {\mathbb Z}^2$ with respect to the $MW$-topology, denoted by $A_p$, is defined by:

Hereinafter, we assume the set $A_p$ to be a subspace of $({\mathbb R}^2, \mathcal{U})$. Using the local rule around a point $p\in {\mathbb Z}^2$ as in Definition 5.1, we define the following:

Definition 5.2. A continuous analog of $X(\subset {\mathbb Z}^2)$ is defined as

$\mathcal{A}(X) = \bigcup\limits_{p\in X}A_p$ by taking the following way.

Then we assume $\mathcal{A}(X)$ to be $(\mathcal{A}(X), \mathcal{U}_{\mathcal{A}(X)})$ as a subspace of $({\mathbb R}^2, \mathcal{U})$.

In particular, the set $\mathcal{A}({\mathbb Z}^2)$ is defined as $\mathcal{A}({\mathbb Z}^2) = \bigcup\limits_{p\in {\mathbb Z}^2}A_p = {\mathbb R}^2$ by taking the following way.

Then we assume $\mathcal{A}({\mathbb Z}^2)$ to be $(\mathcal{A}({\mathbb Z}^2), \mathcal{U})$, i.e., $(\mathcal{A}({\mathbb Z}^2), \mathcal{U}) = ({\mathbb R}^2, \mathcal{U})$.

Remark 5.3. The operator $\mathcal{A}$ need not preserve an $M$-homeomorphism into a homeomorphism in $({\mathbb R}^2, \mathcal{U})$.

Definitions 5.1 and 5.2 enable us to get the following:

Lemma 5.4. (1) In case $X$ is a connected subset of $({\mathbb Z}^2, \gamma)$, $\mathcal{A}(X)$ is also a connected subset of $({\mathbb R}^2, \mathcal{U})$.

(2) In case $Y$ is a disconnected subset of $({\mathbb Z}^2, \gamma)$, $\mathcal{A}(Y)$ may not be a disconnected subset of $({\mathbb R}^2, \mathcal{U})$. Namely, the connectedness of $\mathcal{A}(Y)$ in $({\mathbb R}^2, \mathcal{U})$ depends on the situation.

Proof: (1) Given a connected subset $X$ of $({\mathbb Z}^2, \gamma)$, we obtain $\mathcal{A}(X) = \bigcup\limits_{p\in X}A_p$ that is a connected subset of $({\mathbb R}^2, \mathcal{U})$ (see Definition 5.1).

(2) As an example, consider the set $\{p, q\}$, where $p, q \in ({\mathbb Z}^2)_e, p\neq q$, and $q \in N_8(p)$. While the set $\{p, q\}$ is a disconnected subset of $({\mathbb Z}^2, \gamma)$, $\mathcal{A}(\{p, q\}) = A_p \cup A_q$ is a connected subset of $({\mathbb R}^2, \mathcal{U})$ (see Definition 5.1). For instance, in Figure 4(1), consider the two points $p: = (0, 0)$ and $q: = (1, -1)$ in $SC_{\gamma}^4$. Then the set $\{p, q\}$ supports the assertion.

Theorem 5.5. Given an $SC_{\gamma}^l$, $\mathcal{A}(SC_{\gamma}^l)$ is both semi-open and semi-closed in $({\mathbb R}^2, \mathcal{U})$.

Proof: Since $\mathcal{A}(SC_{\gamma}^l) \subset Cl(Int(\mathcal{A}(SC_{\gamma}^l)))$, the proof of the semi-openness of $\mathcal{A}(SC_{\gamma}^l)$ is completed.

Besides, since we obtain $Int(Cl(\mathcal{A}(SC_{\gamma}^l)) \subset \mathcal{A}(SC_{\gamma}^l)$, the proof of the semi-closedness of $\mathcal{A}(SC_{\gamma}^l)$ is also completed.

To support Theorem 5.5, we can suggest the following examples. The set $\mathcal{A}(SC_{\gamma}^4)$ is both semi-open and semi-closed in $({\mathbb R}^2, \mathcal{U})$. Similarly, each of the sets $\mathcal{A}(SC_{\gamma}^8)$ and $\mathcal{A}(SC_{\gamma}^{10})$ is also both semi-open and semi-closed in $({\mathbb R}^2, \mathcal{U})$.

Proposition 5.6. Given an $SC_{\gamma}^l$, we obtain the following:

(1) In the case of $SC_{\gamma}^4$, $\mathcal{A}(SC_{\gamma}^4)$ does not separates $({\mathbb R}^2, \mathcal{U})$ into two non-empty components. Namely, ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^4)$ has the only one non-empty component.

(2) In the case of $SC_{\gamma}^l, l \in \{8, 10\}$, $\mathcal{A}(SC_{\gamma}^l)$ separates $({\mathbb R}^2, \mathcal{U})$ into exactly two non-empty components.

(3) For any $l$ of $SC_{\gamma}^l, l \notin \{4, 8, 10\}$, $\mathcal{A}(SC_{\gamma}^l)$ separates $({\mathbb R}^2, \mathcal{U})$ into more than or equal to two non-empty components.

Proof: (1) Given an $SC_{\gamma}^4$, we obtain $\mathcal{A}(SC_{\gamma}^4) = \bigcup\limits_{p\in SC_{\gamma}^4}A_p$ as shown in Figure 4(1)(b) that is a subspace of $({\mathbb R}^2, \mathcal{U})$, where $\mathcal{A}(SC_{\gamma}^4)$ is both semi-open and semi-closed in $({\mathbb R}^2, \mathcal{U})$ (see Figure 4(1)(a), (b)). Then it is clear that $\mathcal{A}(SC_{\gamma}^4)$ does not separate $({\mathbb R}^2, \mathcal{U})$ into two nonempty components.

(2) In the case of $l \in \{8, 10\}$, we obtain $\mathcal{A}(SC_{\gamma}^l)$ as a subspace of $({\mathbb R}^2, \mathcal{U})$ whose complement of $\mathcal{A}(SC_{\gamma}^l)$ in ${\mathbb R}^2$ consists of only two non-empty components. See the process of obtaining $\mathcal{A}(SC_{\gamma}^8)$ in Figure 4(2) from (a) to (b) and (c) to (d).

(3) For any $l$ of $SC_{\gamma}^l, l \notin \{4, 8, 10\}$, $\mathcal{A}(SC_{\gamma}^l)$ separates $({\mathbb R}^2, \mathcal{U})$ to obtain that ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l)$ has more than or equal to two non-empty components. For instance, as shown in each of the objects $SC_{\gamma}^{12}$ in Figure 4(4)(a), (b), we see that ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{12})$ has only two non-empty components.

Meanwhile, as for the $SC_{\gamma}^{12}$ as in Figure 4(c) and $SC_{\gamma}^{18}$ in Figure 5(a), each of ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{12})$ and ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{18})$ has more than two components. To be specific, we need to strongly recognize that the set ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{12})$ of Figure 4(4)(b) has only two components, i.e., we have $C(p_1) = C(p_2)$, where $C(p_i)$ means the component containing the given point $p_i$ in $({\mathbb R}^2, \mathcal{U})$, $i \in \{1, 2\}$. Similarly, ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{18})$ of Figure 5(d) has only two components. However, as shown in Figure 4(4) from (c) to (d), we see that ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{12})$ has three disjoint non-empty components such as

Example 5.1. (1) Given the $SC_{\gamma}^{4}$ in Figure 4(1)(a), $\mathcal{A}(SC_{\gamma}^{4})$ is obtained as in Figure 4(1)(b).

(2) Given the $SC_{\gamma}^{8}$ in Figure 4(2)(a), $\mathcal{A}(SC_{\gamma}^8)$ is obtained as in Figure 4(2)(b) which leads that $\mathcal{A}(SC_{\gamma}^8)$ separates $({\mathbb R}^2, \mathcal{U})$ into two components.

(3) Given the $SC_{\gamma}^{10}$ in Figure 4(3)(a), $\mathcal{A}(SC_{\gamma}^{10})$ is obtained as in Figure 4(3)(b).

(4) Consider the $SC_{\gamma}^{12}$ in Figure 4(4)(a), $\mathcal{A}(SC_{\gamma}^{12})$ is obtained as in Figure 4(4)(b). Note that in Figure 4(4)(b) the set $A_{p_1} \cup A_{p_2}$ is connected in $({\mathbb R}^2, \mathcal{U})$.

However, as for the $SC_{\gamma}^{12}$ in Figure 4(4)(c), we see ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{12})$ has three non-empty components because $C_{q_1}\neq C_{q_2}$ as in Figure 4(4)(c), (d), where $q_1 = (1, 0)$ and $q_2 = (2, 1)$ (see Definition 5.1).

(5) Given the $SC_{\gamma}^{12}$ in Figure 4(5)(a), $\mathcal{A}(SC_{\gamma}^{12})$ is obtained, as in Figure 4(5)(b) to show that $\mathcal{A}(SC_{\gamma}^{12})$ separate $({\mathbb R}^2, \mathcal{U})$ into exactly two disjoint components.

In view of Proposition 5.6, we have the following query.

Under what condition, does ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l)$ have exactly two non-empty components?

Theorem 5.7. Assume an $SC_{\gamma}^l: = (d_i)_{i \in [0, l-1]_{\mathbb Z}}, l \neq 4$, satisfying the following property:

(1) Then $\mathcal{A}(SC_{\gamma}^l)$ separates $({\mathbb R}^2, \mathcal{U})$ into exactly two components in $({\mathbb R}^2, \mathcal{U})$ that are both semi-open and semi-closed.

(2) One of the components of ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l)$ is bounded and the other is unbounded in ${\mathbb R}^2$.

Before proving the assertion, we need to recognize that the hypothesis requires that $SC_{\gamma}^l$ always satisfies the property of (5.2). In particular, we need to focus on the part "$SC_{\gamma}^l\cap ({\mathbb Z}^2)_e$" of (5.2).

Proof: Owing to the hypothesis, assume an $SC_{\gamma}^l: = (d_i)_{i \in [0, l-1]_{\mathbb Z}}, l \neq 4$, that does not contain the subset

having the following property:

where $Con(d_{t_1})$ is the connected maximal subset of $N_8(d_{t_1}) \cap SC_{\gamma}^l$ containing the point $d_{t_1}$. Then, owing to the notion of (5.1) and the features of $SC_{\gamma}^l$, $\mathcal{A}(SC_{\gamma}^l)$ separates $({\mathbb R}^2, \mathcal{U})$ into exactly two both semi-open and semi-closed components in $({\mathbb R}^2, \mathcal{U})$.

For instance, consider the case of $SC_{\gamma}^{12}$ given in Figure 4(4)(a). Then we obtain $\mathcal{A}(SC_{\gamma}^{12})$ to separate $({\mathbb R}^2, \mathcal{U})$ into exactly two both semi-open and semi-closed components in $({\mathbb R}^2, \mathcal{U})$. More precisely, as in Figure 4(4)(a), (b), owing to the property of (5.1), the set $A_{p_1} \cup A_{p_2}$ is a connected subset of $({\mathbb R}^2, \mathcal{U})$.

Meanwhile, without the hypothesis, we can consider the following case. Assume an $SC_{\gamma}^l: = (d_i)_{i \in [0, l-1]_{\mathbb Z}}, l \neq 4$, in which there is a subset $X_1(\subset SC_{\gamma}^l \cap ({\mathbb Z}^2)_e)$ of (5.3) such that $d_{t_2} \in N_8(d_{t_1})$ and $Con(d_{t_1})\cap \{d_{t_2}\} = \emptyset$. To be specific, see the two points $r_1$ and $r_2$ in Figure 5(a). Then, $\mathcal{A}(SC_{\gamma}^l)$ does not separate $({\mathbb R}^2, \mathcal{U})$ into exactly two both semi-open and semi-closed components in $({\mathbb R}^2, \mathcal{U})$. As another example, see the objects in Figure 4(4)(c), (d). To be specific, in Figure 4(4)(c), (d), the set $A_{q_1}$ is not connected with $A_{q_2}$ (see the property of (5.1)).

(2) With the hypothesis, it is clear that one of the components of ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l)$ is bounded and the other is unbounded in ${\mathbb R}^2$.

Example 5.2. Consider the object $SC_{\gamma}^{18}$ in Figure 5(c). Then we observe that the $SC_{\gamma}^{18}$ of Figure 5(c) satisfies the property of (5.2) and $\mathcal{A}(SC_{\gamma}^{18})$ separates $({\mathbb R}^2, \mathcal{U})$ into exactly two components such as

because $C(q_1) = C(q_2) = C(q_3) = C(q_4)$ in ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{18})$ of Figure 5(d).

Theorem 5.8. Assume the subspaces $(X, \gamma_X)$ and $(Y, \gamma_Y)$ that are $MW$-homeomorphic to $SC_{\gamma}^l$. Then the number of the components of ${\mathbb R}^2\setminus \mathcal{A}(X)$ need not be equal to that of ${\mathbb R}^2\setminus \mathcal{A}(Y)$.

Proof: It suffices to prove it by suggesting a counterexample. Given the two types of $SC_{\gamma}^{18}$ as in Figure 5(a), (c), we obtain the corresponding two types of $\mathcal{A}(SC_{\gamma}^{18})$ as in Figure 5(b), (d).

For our purpose, let $A_1$ (resp. $A_2$) be the set ${\mathbb R}^2\setminus \mathcal{A}(SC_{\gamma}^{18})$, where $SC_{\gamma}^{18}$ is the object in Figure 5(a) (resp. Figure 5(c)). Then it is clear that $A_1$ has four components and $A_2$ has the only two components as in Figure 5(b), (d).

Remark 5.9. The number the components of ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l)$ need not be equal to that of ${\mathbb Z}^2 \setminus SC_{\gamma}^l$.

Proof: As a counterexample, see the objects in Figure 5(c), (d). As shown in Figure 5(c), consider the given $SC_{\gamma}^{18}$ in Figure 5(c). While ${\mathbb Z}^2\setminus SC_{\gamma}^{18}$ has four components as in Figure 5(c) in $({\mathbb Z}^2, \gamma)$ such as

the set ${\mathbb R}^2\setminus \mathcal{A}(SC_{\gamma}^{18})$ has exactly two components as in Figure 5(d) because $C(q_1) = C(q_2) = C(q_3)$ as the subspaces of $({\mathbb R}^2, \mathcal{U})$, i.e., $C(q_1)$ is connected with $C(q_2)$ and $C(q_2)$ is also connected with $C(q_3)$. To be specific, see the cases of $SC_{\gamma}^{18}$ in Figure 5(c) and $\mathcal{A}(SC_{\gamma}^{18})$ in Figure 5(d) stated in Example 5.2, which completes the proof.

Lemma 5.10. Assume an $SC_{\gamma}^l: = (d_i)_{i \in [0, l-1]_{\mathbb Z}}, l \in \{4, 8, 10\}$. Then the number of the components of ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l)$ in $({\mathbb R}^2, \mathcal{U})$ is equal to that of ${\mathbb Z}^2 \setminus SC_{\gamma}^l$ in $({\mathbb Z}^2, \gamma)$.

Proof: (Case 1) Consider an $SC_{\gamma}^4: = (d_i)_{i \in [0, 3]_{\mathbb Z}}$. As proved in Proposition 5.6, ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^4)$ in $({\mathbb R}^2, \mathcal{U})$ has one component. Besides, ${\mathbb Z}^2 \setminus SC_{\gamma}^4$ also has one component in $({\mathbb Z}^2, \gamma)$.

(Case 2) Consider an $SC_{\gamma}^8: = (d_i)_{i \in [0, 7]_{\mathbb Z}}$. As proved in Proposition 5.6, ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^8)$ in $({\mathbb R}^2, \mathcal{U})$ has exactly two components. Besides, ${\mathbb Z}^2 \setminus SC_{\gamma}^8$ also has exactly two components in $({\mathbb Z}^2, \gamma)$.

(Case 3) Consider an $SC_{\gamma}^{10}: = (d_i)_{i \in [0, 9]_{\mathbb Z}}$. As proved in Proposition 5.6, ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{10})$ in $({\mathbb R}^2, \mathcal{U})$ has exactly two components. Besides, ${\mathbb Z}^2 \setminus SC_{\gamma}^{10}$ also has exactly two components in $({\mathbb Z}^2, \gamma)$.

Unlike Lemma 5.10, owing to Remark 5.9, let us now find a condition for comparing between the number of the components of ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l)$ in $({\mathbb R}^2, \mathcal{U})$ and that of ${\mathbb Z}^2 \setminus SC_{\gamma}^l$ in $({\mathbb Z}^2, \gamma)$, as follows:

Proposition 5.11. Assume an $SC_{\gamma}^l: = (c_i)_{i \in [0, l-1]_{\mathbb Z}}, l \notin \{4, 8, 10\}$, having the following property:

Then the number of the components of ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l)$ in $({\mathbb R}^2, \mathcal{U})$ is equal to that of ${\mathbb Z}^2 \setminus SC_{\gamma}^l$ in $({\mathbb Z}^2, \gamma)$.

Proof: First of all, without the hypothesis, we need to show that the assertion does not hold. Suppose an $SC_{\gamma}^l: = (c_i)_{i \in [0, l-1]_{\mathbb Z}}, l \notin \{4, 8, 10\}$, that does not satisfy the property of (5.4). For instance, as shown in Figure 5(c), (d), the given $SC_{\gamma}^{18}$ in Figure 5(c) does not satisfy the property of (5.4), i.e., see the two points $s_1$ and $s_2$ in Figure 5(c). Based on the $SC_{\gamma}^{18}$, we find that ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{18})$ has only two components in $({\mathbb R}^2, \mathcal{U})$ (see Example 5.2). Meanwhile, ${\mathbb Z}^2 \setminus SC_{\gamma}^{18}$ has four components in $({\mathbb Z}^2, \gamma)$.

Next, owing to the property of (5.1), the topological feature of ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l)$ in $({\mathbb R}^2, \mathcal{U})$, and that of ${\mathbb Z}^2 \setminus SC_{\gamma}^l$ in $({\mathbb Z}^2, \gamma)$, the proof is completed.

Example 5.3. Let us consider $SC_{\gamma}^{18}$ in Figure 5(a). Then it is clear that it satisfies the property of (5.4) so that we obtain ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{18})$ consisting of four components in $({\mathbb R}^2, \mathcal{U})$ (see Figure 5(b)) and ${\mathbb Z}^2 \setminus SC_{\gamma}^{18}$ is composed of four components in $({\mathbb Z}^2, \gamma)$ (see Figure 5(a)).

6.   Semi-Jordan curve theorem on the $MW$-topological plane

In 1970, Rosenfeld ^[9,10,11] initially considered the digital topological version of the typical Jordan curve theorem (see also ^[22]). Consider $SC_k^{2, l}$ in a binary digital picture $D: = ({\mathbb Z}^2, k, \bar{k}, SC_k^{2, l})$. Then the $\bar{k}$-components are called white components of $D$ and $SC_k^{2, l}$ is said to be a black component (or equivalently, $k$-component) of the digital picture ^[22], where we say that a $k$-component of a non-empty digital image $(X, k)$ is a maximal $k$-connected subset of $(X, k)$ ^[22]. To be precise, given an $SC_8^{2, 4}$ on ${\mathbb Z}^2$, to evade from the so-called "digital connectivity paradox"^[10,11], the papers ^[7,8,9] considered it in a binary digital picture $D: = ({\mathbb Z}^2, 8, 4, SC_8^{2, 4})$ instead of $({\mathbb Z}^2, 8, 8, SC_8^{2, 4})$. In the digital picture $({\mathbb Z}^2, 8, 4, SC_8^{2, 4})$, to avoid the digital connectivity paradox, it turns out that $SC_8^{2, 4}$ should be considered to be an $(8, 4)$-binary digital image in the given digital picture $D$ above. Namely, the part ${\mathbb Z}^2 \setminus SC_8^{2, 4}$ should be considered with $4$-connectivity. Then the given set $SC_8^{2, 4}$ separates ${\mathbb Z}^2$ into the two $4$-components $A$ and $B$ ^[22] such that

Based on this approach, it is clear that one of the sets $A$ and $B$ is finite and the other is infinite. Then we call a finite set $A$ the interior of the given set $B: = SC_8^{2, 4}\cup A$ in the digital picture $({\mathbb Z}^2, 8, 4, B)$. Similarly, as a general case of $SC_8^{2, 4}$, we can consider $SC_k^{2, l}(\neq SC_4^{2, 4})$ in the digital picture $D: = ({\mathbb Z}^2, k, \bar{k}, SC_k^{2, l})$ as mentioned above, where $(k, \bar{k}) \in \{(4, 8), (8, 4)\}$. Then, it also separates ${\mathbb Z}^2$ into two non-empty $\bar{k}$-components $A$ and $B$ such that

Meanwhile, unlike this approach followed from Rosenfeld's work, in the category of $MW$-topological spaces, given an $SC_{\gamma}^l$ in $({\mathbb Z}^2, \gamma)$, we now raise the following queries.

(Q1) How can we propose an $MW$-topological version of the typical Jordan curve theorem?

(Q2) What differences are there between an $MW$-topological version of the well-known Jordan curve theorem and the typical Jordan curve theorem on $({\mathbb R}^2, \mathcal{U})$?

(Q3) What differences are there between the Jordan curve theorem in an $MW$-topological setting and the digital Jordan curve theorem established by Rosenfeld?

The paper ^[12] also studied several types of digital Jordan curve theorems with nine pretopologies on ${\mathbb Z}^2$. Besides, the paper ^[3] also proposed a computational topological version of the curve and surface theorem. In addition, there are some studies on the digital versions of the Jordan curve theorem in digital spaces including the papers ^[6,12,22]. However, to study this topic more intensively from the viewpoint of the $MW$-topology, we strongly need to have an approach using semi-topological structures. To study some properties of the semi-closedness or semi-openness of ${\mathbb Z}^2 \setminus SC_{\gamma}^l$, we first recall that $SC_{\gamma}^4$ does not separate $({\mathbb Z}^2, \gamma)$ into exactly two non-empty components (see Figure 1(1)(a), (b)). Furthermore, we have the following (see Figure 4(1)(a), (2)(a), (3)(a)).

Remark 6.1. ${\mathbb Z}^2 \setminus SC_{\gamma}^4$ has the only one non-empty component that is both semi-open and semi-closed in $({\mathbb Z}^2, \gamma)$.

Lemma 6.2. (1) $SC_{\gamma}^8$ separates $({\mathbb Z}^2, \gamma)$ into exactly two semi-closed components. One of these components need not be semi-open in $({\mathbb Z}^2, \gamma)$.

(2) $SC_{\gamma}^{10}$ separates $({\mathbb Z}^2, \gamma)$ into exactly two components that are both semi-open and semi-closed.

Proof: Based on the $SC_{\gamma}^8$ in Figure 1(2)(a), (b), and $SC_{\gamma}^{10}$ in Figure 1(3)(a), (b), by Theorems 3.3 and 3.4, the proof is clearly completed. In particular, note that the components of ${\mathbb Z}^2\setminus SC_{\gamma}^8$ are obviously semi-closed in $({\mathbb Z}^2, \gamma)$. Indeed, in the case of $SC_{\gamma}^8$ in Figure 1(2)(a), one of them is not semi-open. To be specific, consider $SC_{\gamma}^8$ in Figure 1(2)(a), the finite component of ${\mathbb Z}^2\setminus SC_{\gamma}^8$ is not semi-open. Meanwhile, the components of ${\mathbb Z}^2\setminus SC_{\gamma}^{10}$ are both semi-open and semi-closed in $({\mathbb Z}^2, \gamma)$ (see Theorems 3.3 and 3.4).

Unlike the case of $SC_{\gamma}^l: = (c_i)_{i \in [0, l-1]_{\mathbb Z}}, l \in \{4, 8, 10\}$, motivated by Theorem 5.7 and Proposition 5.11, we obtain the following:

Proposition 6.3. Assume $SC_{\gamma}^l: = (c_i)_{i \in [0, l-1]_{\mathbb Z}}, l\neq 4$, satisfying the following property:

Then $SC_{\gamma}^l$ separates $({\mathbb Z}^2, \gamma)$ into exactly two semi-closed components, e.g., $A$ and $B$. Namely, a partition $\{A, B, SC_{\gamma}^l\}$ of $({\mathbb Z}^2, \gamma)$ exists.

Proof: First of all, we need to strongly point out an importance of the given hypothesis. Without the hypothesis, as shown in Figure 4(4)(a), (c), since the given $SC_{\gamma}^{12}$ in Figure 4(4)(a), (c) do not satisfy the hypothesis of (6.3), they do not separate $({\mathbb Z}^2, \gamma)$ into exactly two components. Besides, some components of ${\mathbb Z}^2 \setminus SC_{\gamma}^{12}$ cannot be semi-open. To be specific, in the $SC_{\gamma}^{12}$ of Figure 4(4)(a), each of $C(p_i) = \{p_i\}, i \in \{1, 2\}$, is not semi-open in $({\mathbb Z}^2, \gamma)$.

As another case, since the given $SC_{\gamma}^{12}$ in Figure 4(4)(c) does not satisfy the property of (6.3) either, it does not separate $({\mathbb Z}^2, \gamma)$ into exactly two components. Besides, note that none of the objects in Figure 5(a), (c), Figure 6, and Figure 7(1), (2) satisfies the property of (6.3) either.

In addition, the condition of (6.3) does not support the semi-openness of the component of ${\mathbb Z}^2 \setminus SC_{\gamma}^l$. For instance, consider $SC_{\gamma}^8$ in Figure 1(2)(a), one component of ${\mathbb Z}^2 \setminus SC_{\gamma}^8$ is not semi-open in $({\mathbb Z}^2, \gamma)$ as mentioned in the proof of Lemma 6.2.

Meanwhile, with the hypothesis of (6.3), owing to the features of $SC_{\gamma}^l$, it is clear that $SC_{\gamma}^l$ separates $({\mathbb Z}^2, \gamma)$ into exactly two components (see Figure 1(4)(c), (d)) which are semi-closed in $({\mathbb Z}^2, \gamma)$.

Owing to Remark 6.1, based on Theorem 5.7, we can define the notions of Definition 6.4 below because given an $SC_{\gamma}^l$ satisfying the hypothesis of (5.2), ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l)$ has exactly two components in $({\mathbb R}^2, \mathcal{U})$ and further, one of them is bounded and the other is unbounded (see the cases of $SC_{\gamma}^{38}$ in Figure 7(1) and $SC_{\gamma}^{28}$ in Figure 7(3)).

Definition 6.4. Assume an $SC_{\gamma}^l$ satisfying the property of (5.2), $l \neq 4$. Then we define the following two notions.

(1) $I(SC_{\gamma}^l): = B({\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l)) \cap {\mathbb Z}^2$, where $B({\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l))$ means the bounded component of ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l)$.

(2) $O(SC_{\gamma}^l): = Ub({\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l)) \cap {\mathbb Z}^2$, where $Ub({\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l))$ stands for the unbounded component of ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l)$.

Comparing the condition of Proposition 6.3 and that of Definition 6.4, we can note that the former is stronger than the latter. Hereinafter, the two notions $I(SC_{\gamma}^l)$ and $O(SC_{\gamma}^l)$ in Definition 6.4 are called "inside" and "outside" of $SC_{\gamma}^l$ in $({\mathbb Z}^2, \gamma)$, respectively. In particular, note that these notions are not related to the notions of interior and exterior of a set of $({\mathbb Z}^2, \gamma)$.

Remark 6.5. (1) In Definition 6.4, the hypothesis of (5.2) is strongly required to establish both $I(SC_{\gamma}^l)$ and $O(SC_{\gamma}^l)$ because it supports the assertion of Theorem 5.7 so that the set ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^l)$ has exactly two components of which one of them is bounded and the other is unbounded.

(2) Without the hypothesis of (5.2), we have some difficulties in establishing the notions of $I(SC_{\gamma}^l)$ and $O(SC_{\gamma}^l)$. For instance, consider the case of $SC_{\gamma}^{42}$ in Figure 6. In particular, see the points $c_2$ and $c_{38}$, and $c_4$ and $c_{36}$. Then, owing to these points, it is clear that this $SC_{\gamma}^{42}$ does not satisfy the property of (5.2). Hence we have some difficulties in establishing $I(SC_{\gamma}^{42})$ because ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{42})$ does not have exactly two components. As another case, consider the case of $SC_{\gamma}^{28}$ in Figure 7(2). In particular, consider the two points $c_{19}$ and $c_{25}$. Then they clearly does not satisfy the property of (5.2) so that ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{28})$ has three components, e.g., two bounded components and one unbounded component. More precisely, since the set $A_{q_2}$ is a bounded component of ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{28})$, $A_{q_2}$ is not related to the set $Ub({\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{28})) \cap {\mathbb Z}^2$ which comes across some difficulties in establishing $O(SC_{\gamma}^{28})$.

(3) As a good example for Definition 6.4, consider the $SC_{\gamma}^{38}$ in Figure 7(1). First, see the two points $d_{29}$ and $d_{35}$ of the $SC_{\gamma}^{38}$ in Figure 7(1). Then they can be admissible to establish $O(SC_{\gamma}^{38})$. Besides, see the two points $d_{11}$ and $d_{17}$ of the $SC_{\gamma}^{38}$ in Figure 7(1). Then they can be admissible to establish the notion of $I(SC_{\gamma}^{38})$ because $A_{q_1}$ is connected with $A_{q_2}$.

Similarly, the $SC_{\gamma}^{28}$ in Figure 7(3) also a good example for Definition 6.4.

Example 6.1. (1) As for the $SC_{\gamma}^{42}$ in Figure 6, it does not satisfy the property of (5.2) (see the points $c_2$ and $c_{38}$, and $c_4$ and $c_{36}$). Hence, as mentioned in Theorem 5.7, $\mathcal{A}(SC_{\gamma}^{42})$ does not separate $({\mathbb R}^2, \mathcal{U})$ into two components. Indeed, ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{42})$ consists of four components as follows: $C(p_i) = A_{p_i}, i \in [1,2]_{\mathbb Z}$, $C(p_3) = C(p_4)$ and $C(q_1) = C(q_2)$.

Furthermore, the set ${\mathbb Z}^2 \setminus SC_{\gamma}^{42}$ has six components such as $C(p_i), i \in [1,4]_{\mathbb Z}$ and $ C(q_j), j \in ^[1,2]_{\mathbb Z} $.

(2) Given the $SC_{\gamma}^{38}$ in Figure 7(1), it satisfies the property of (5.2). Hence the set ${\mathbb R}^2 \setminus \mathcal{A}(SC_{\gamma}^{38})$ consists of the exactly two components. Hence we obtain

$C(q_i)$ is the component of $q_i$ in $({\mathbb Z}^2, \gamma)$ containing the given point $q_i, i \in [1,4]_{\mathbb Z}$.

Meanwhile, the set ${\mathbb Z}^2 \setminus SC_{\gamma}^{38}$ consists of four components in $({\mathbb Z}^2, \gamma)$, e.g., $C(q_i), i \in [1,4]_{\mathbb Z}$.

(3) Given the $SC_{\gamma}^{28}$ in Figure 7(2), it does not satisfy the property of (5.2). Indeed, the set ${\mathbb Z}^2 \setminus SC_{\gamma}^{28}$ consists of three components as follows: $C(q_i), i \in [1,3]_{\mathbb Z}$ and $C(q_1)$ consists of eleven elements as in Figure 7(2). In particular, $C(q_2) = \{q_2\}$ and $(C(q_3))^\sharp = \aleph_0$ that is the cardinal number of the set of natural numbers.

(4) Given the $SC_{\gamma}^{28}$ in Figure 7(3), it is clear that this object satisfies the hypothesis of Definition 6.4. Hence we obtain $I(SC_{\gamma}^{28}) = C(q_1)$ and $O(SC_{\gamma}^{28}) = C(q_2)\cup C(q_3)$.

Owing to Definition 6.4, we have the following:

Theorem 6.6. Assume an $SC_{\gamma}^l$, $l\neq 4$, satisfying the property of (5.2).

Then, a partition $\{I(SC_{\gamma}^l), O(SC_{\gamma}^l), SC_{\gamma}^l\}$ of ${\mathbb Z}^2$ exists.

Proof: Owing to Definition 6.4, the proof is completed.

Remark 6.7. (1) Each of $I(SC_{\gamma}^l)$ and $O(SC_{\gamma}^l)$ need not be connected.

(2) The number of the components of $I(SC_{\gamma}^l)$ depends on the situation.

(3) Each of the sets $I(SC_{\gamma}^l)$ and $O(SC_{\gamma}^l)$ need not be an open set or a closed set in $({\mathbb Z}^2, \gamma)$.

Proof: (1) As an example, consider the $SC_{\gamma}^{38}$ in Figure 7(1). It is clear that the given $SC_{\gamma}^{38}$ satisfies the hypothesis of Definition 6.4. While each of $I(SC_{\gamma}^{38})$ and $O(SC_{\gamma}^{38})$ exists, they are not connected in $({\mathbb Z}^2, \gamma)$. To be specific, it turns out that

such that $C(q_1)\cap C(q_2) = \emptyset$, $C(q_3)\cap C(q_4) = \emptyset$, and each of $C(q_i), i \in [1,4]_{\mathbb Z}$ is not an empty set.

(2) From the above (3) of Example 6.1, it is clear that the number of the components of $I(SC_{\gamma}^l)$ depends on the number $l$.

(3) As an example, consider the $SC_{\gamma}^{8}$ in Figure 4(2)(a). Then $I(SC_{\gamma}^{8})$ is not an open set. Besides, consider the $SC_{\gamma}^{38}$ in Figure 7(1). Then $O(SC_{\gamma}^{38})$ is not an open set.

Let us now investigate the semi-openness or semi-closedness of $I(SC_{\gamma}^l)$ and $O(SC_{\gamma}^l)$.

Example 6.2. Given any $SC_{\gamma}^8$, there is a partition of $({\mathbb Z}^2, \gamma)$, i.e., $\{I(SC_{\gamma}^8), SC_{\gamma}^8, O(SC_{\gamma}^8)\}$ such that each of $I(SC_{\gamma}^8)$ and $O(SC_{\gamma}^8)$ is semi-closed and both of them are connected. Namely, $SC_{\gamma}^8$ separates $({\mathbb Z}^2, \gamma)$ with exactly two components.

Lemma 6.8. $I(SC_{\gamma}^{10})$ is both semi-open and semi-closed in $({\mathbb Z}^2, \gamma)$.

Proof: As shown in Figure 1(4)(c), (d), owing to Theorems 3.3 and 3.4, $I(SC_{\gamma}^8)$ is clearly both semi-open and semi-closed in $({\mathbb Z}^2, \gamma)$.

Remark 6.9. The semi-openness or semi-closedness of $I(SC_{\gamma}^l)$ depends on the situation, $l \notin \{4, 10\}$.

Proof: The semi-topological features of $I(SC_{\gamma}^8)$ is determined according to the two types of $SC_{\gamma}^8$ in Figure 1(2)(a), (b). To be specific, based on the $SC_{\gamma}^8$ in Figure 1(2)(a), we have $I(SC_{\gamma}^8)$ that is only semi-closed instead of semi-open in $({\mathbb Z}^2, \gamma)$. Meanwhile, for the case of $SC_{\gamma}^8$ in Figure 1(2)(b), $I(SC_{\gamma}^8)$ is proved to be both semi-open and semi-closed in $({\mathbb Z}^2, \gamma)$.

Next, let us consider the case $SC_{\gamma}^l$, $12 \leq l \in {\mathbb N}_e$. Then the semi-openness or semi-closedness of $I(SC_{\gamma}^l)$ depends on the situation (see Figure 5(c) and 7(1), (3)). For instance, the $SC_{\gamma}^{18}$ in Figure 5(c) has $I(SC_{\gamma}^{18})$ that is not semi-open but semi-closed.

Corollary 6.10. Let $X$ and $Y$ be simple closed $MW$-curves with $l$ elements in $({\mathbb Z}^2, \gamma)$ and each of them satisfies the property of (6.3). Then the number of the components of $X^c$ is equal to that of $Y^c$.

Proof: By Proposition 6.3, the proof is completed.

Let $E$ be the $SC_{\gamma}^{28}$ in Figure 7(3) and $F$ be the $SC_{\gamma}^{28}$ satisfying the property of (6.3). While $O(E)$ is not connected and $O(F)$ is connected. Thus we obtain the following.

Remark 6.11. Without the condition relating to the property (6.3), each of $I(SC_{\gamma}^l)$ and $O(SC_{\gamma}^l)$ may not be connected.

Theorem 6.12. Assume that the subspaces $(X, \gamma_X)$ and $(Y, \gamma_Y)$ are $MW$-homeomorphic to $SC_{\gamma}^l$.

(1) $(I(X), \gamma_{I(X)})$ need not $MW$-homeomorphic to $(I(Y), \gamma_{I(X)})$.

(2) $(O(X), \gamma_{O(X)})$ need not $MW$-homeomorphic to $(O(Y), \gamma_{O(X)})$.

Proof: To disprove these assertions (1) and (2), we will use some examples.

(1) Consider the two $SC_{\gamma}^{12}$ in Figures 4(4)(a) and 5(a). For our purpose, let $A$ be the $SC_{\gamma}^{12}$ in Figure 4(4)(a) and $B$ be the $SC_{\gamma}^{12}$ in Figure 4(5)(a). While $I(A)$ is not connected and $I(B)$ is connected, which completes the proof.

(2) For our purpose, let $C$ be the $SC_{\gamma}^{28}$ in Figure 7(3) and $D$ be the $SC_{\gamma}^{28}$ satisfying the property of (6.3). While $O(C)$ is not connected and $O(D)$ is connected, which completes the proof.

Corollary 6.13. (1) $O(SC_{\gamma}^l)$ need not be semi-open.

(2) The number of the components of $O(SC_{\gamma}^l)$ need not depend on the number $l$.

Proof: To disprove these assertions (1) and (2), we will use some examples.

(1) Let us consider the $SC_{\gamma}^{28}$ in Figure 7(3). Then it is clear that $O(SC_{\gamma}^{28})$ is not semi-open.

(2) In view of the $SC_{\gamma}^{28}$ in Figure 7(3), the proof is completed. To be specific, let $A$ be the $SC_{\gamma}^{28}$ in Figure 7(3) and $B$ be the $SC_{\gamma}^{28}$ satisfying the property of (6.3). Then $O(A)$ has two components and $O(B)$ has the only one component.

Unlike Theorem 6.6, let us find a condition to separate $({\mathbb Z}^2, \gamma)$ into exactly two components, as follows:

Theorem 6.14. Let $SC_{\gamma}^l$ satisfy the property of (6.3), $l\neq 4$. Under $({\mathbb Z}^2, \gamma)$, we obtain the following:

(1) There is a partition $\{I(SC_{\gamma}^l), O(SC_{\gamma}^l), SC_{\gamma}^l\}$ such that each of $I(SC_{\gamma}^l)$ and $O(SC_{\gamma}^l)$ is connected.

(2) Each of $I(SC_{\gamma}^l)$ and $O(SC_{\gamma}^l)$ is semi-closed. While $O(SC_{\gamma}^l)$ is semi-open, $I(SC_{\gamma}^l)$ need not be semi-open.

Proof: (1) It suffices to prove the connectedness of both $I(SC_{\gamma}^l)$ and $O(SC_{\gamma}^l)$. Owing to the hypothesis of the property of (6.3), each of $I(SC_{\gamma}^l)$ and $O(SC_{\gamma}^l)$ is proved to be connected because there are not two points

Indeed, this property of (6.4) supports the connectedness of both $I(SC_{\gamma}^l)$ and $O(SC_{\gamma}^l)$.

(2) With the hypothesis, using Theorems 3.3 and 3.4, we prove that both $I(SC_{\gamma}^l)$ and $O(SC_{\gamma}^l)$ are semi-closed. To be specific, for any point $x \in {\mathbb Z}^2 \setminus I(SC_{\gamma}^l)$, owing to the hypothesis, we always obtain

which implies the semi-closedness of $I(SC_{\gamma}^l)$.

Similarly, for any point $x \in {\mathbb Z}^2 \setminus O(SC_{\gamma}^l)$, owing to the hypothesis, we also obtain

which implies the semi-closedness of $O(SC_{\gamma}^l)$.

Besides, by Theorem 3.3, owing to the hypothesis, $O(SC_{\gamma}^l)$ is proved to be semi-open. However, $I(SC_{\gamma}^l)$ need not be semi-open. For instance, for the $SC_{\gamma}^8$ in Figure 4(2)(a). Then $I(SC_{\gamma}^8)$ is not a semi-open in $({\mathbb Z}^2, \gamma)$.

7.   Advantages and utilities of $MW$-topological structure and the semi-Jordan curve theorem on $({\mathbb Z}^2, \gamma)$

When studying digital objects $X$ in ${\mathbb Z}^2$, the properties of (2.4) and (2.5) enable us to get the following utilities of the $MW$-topological structure of $X$.

Remark 7.1. (Utilities of the $MW$-topological structure)

(1) When studying a self-homeomorphism of $({\mathbb Z}^2, \gamma)$, we should consider the following map ^[31]

Since the modern electronic devices are usually operated on the finite digital planes with more than ten million pixels to support the high-level display resolution, the mapping of (7.1) can be very admissible. At the moment, note that the following map $g$ cannot be a homeomorphism, where

(2) Since the $MW$-topological structure is one of the fundamental frames, motivated by this structure, some more generalized topological structures on ${\mathbb Z}^n$ can be established.

(3) Based on the $MW$-topological structure of ${\mathbb Z}^2$, we can obtain the $4$-digital adjacency induced by the given topological structure ^[26]. In detail, for distinct elements $x, y \in ({\mathbb Z}^2, \gamma)$, they are $MW$-adjacent if $x \in SN_{\gamma}(y)$ or $y \in SN_{\gamma}(x)$ ^[26]. Namely, the $MW$-adjacency is equivalent to the $4$-adjacency of ${\mathbb Z}^2$ as in (2.2).

Example 7.1. The map $g:({\mathbb Z}^2, \gamma) \to ({\mathbb Z}^2, \gamma)$ defined by $g(x_1, x_2) = (x_1+2m_1+1, x_2+2m_2), m_1, m_2 \in {\mathbb Z}$ cannot be a homeomorphism. Meanwhile, it is clear that the map $h:({\mathbb Z}^2, \gamma) \to ({\mathbb Z}^2, \gamma)$ defined by $h(x_1, x_2) = (x_1+2m_1+1, x_2+2m_2+1)$ or $(x_1+2m_1, x_2+2m_2)$, $m_1, m_2 \in {\mathbb Z}$, is a homeomorphism.

Remark 7.2. (Advantages of the semi-Jordan curve theorem)

(1) Unlike the typical Jordan curve theorem in a digital topological setting estabsihed by Rosenfeld ^[22], no paradox exists in the semi-Jordan curve theorem in the $MW$-topological structure.

(2) Based on the semi-Jordan curve theorem in the $MW$-topological structure, we can consider a digital topological version of the typical Jordan curve theorem in terms of a simple closed $4$-curve in the digital plane $({\mathbb Z}^2, 4, 8)$.

(3) When digitizing a set $X$ in the $2$-dimensional real space with respect to the $MW$-topological structure, we can use a local rule in ^[20] to obtain a digitized set $D_{\gamma}(X) \subset {\mathbb Z}^2$ from $X$ which is used in the fields of mathematical morphology, rough set theory, digital geometry, and so on ^[20,21].

8.   Concluding remark and further work

After developing the semi-Jordan curve theorem in the $MW$-topological setting, we have studied various properties of it. In particular, we have found a condition for $SC_{\gamma}^l$ to separate $({\mathbb Z}^2, \gamma)$ with exactly two components, Furthermore, we studied many semi-topological properties of both $I(SC_{\gamma}^l)$ and $O(SC_{\gamma}^l)$. As a further work, we can compare among several kinds of digital versions of the typical Jordan curve theorem and the combinatorial version of the Jordan curve theorem in ^[3]. Besides, based on the digital-topological group structure in ^[32], we can further examine a topological group structure of $SC_{\gamma}^l$. In addition, based on the established structure in ^[33], we can study covering spaces in the category of $MW$-topological spaces.

Acknowledgments

The author was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2019R1I1A3A03059103). Besides, this work was supported under the framework of international cooperation program managed by the National Research Foundation of Korea (2021K2A9A2A06039864).

Conflict of interest

The author declares no conflict of interest.