Numerical simulation for cutoff draft of sea ice ridge keels based on a novel optimal modeling with nonlinear-statistical constraints

1.   Introduction

As a major component of the polar environment, sea ice cover affects the exchange of heat, energy, mass, and momentum between the atmosphere and the ocean in the polar regions ^[1,2,3,4]. Morphology of polar sea ice changes continuously under the influences of external driving forces, e.g., wind, ocean current and waves. The surface and bottom topographies of ridged sea ice differ greatly from that of other sea-ice types, and the most important morphological features of ridged sea ice are the ridge sails on surface and keels on bottom formed by the dynamic deformation, except for other roughness features ^[5,6]. The ridge sails/keels have major effects on the optimization of the ice thickness remote sensing algorithm based on sea ice roughness parameters and sea ice thermodynamics numerical simulation parameterization scheme, and the analysis of the relationship between polar sea ice and climate variations ^[7,8].

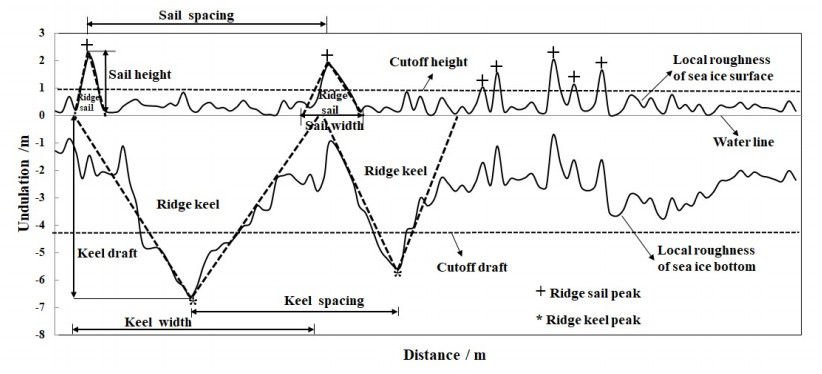
In general, the ridge sails/keels can be separated from sea ice surface/bottom undulations by a key parameter, namely, a cutoff height/draft: where any peaks lower than the cutoff height/draft are classified as non-ridged ice surface/bottom fluctuations, whereas other peaks exceeding the cutoff height/draft are defined as ridge sails/keels ^[9]. The sea ice morphology is shown in Figure 1 by approximating the ridge sail/keel cross-sections as the isoceles triangle, and a field photograph of sea ice ridge sails in Antarctic is shown in Figure 2. This height/draft affects estimations of the sea ice mass and thickness, and plays an important role in the establishment of large-scale sea ice dynamic models ^{[10,11,12,13,14]}. Therefore, the determination of the cutoff height/draft is an essential and significant stage for the analysis of the ridge morphologies and the improvement of sea ice thermodynamics numerical models. The Rayleigh criterion and in-situ measurement experience were always combined as a staple method to determine this cutoff height/draft ^[15,16]. However, the cutoff height/draft used in many previous studies were always arbitrary and empirical, resulting in confusions when comparing results from different observations, owing to no-upper limitation defined by the Rayleigh criterion. The cutoff height and morphology of the ice ridge sails were analyzed in our previous study ^[17]. So, a novel optimal modeling and method for the determination of the ridge keel cutoff draft are the main contribution of this research.

To seek an effective method for determining the keel cutoff draft and analyzing the pressure ridge morphology, data measured by a helicopter-borne electromagnetic-induction (EM) bird in northwestern Weddell Sea of Antarctic during the ANT-XXIII/7 cruise carried out by Alfred Wegener Institute for Polar and Marine Research were collected ^[10]. The length, diameter, and weight of the EM instrument were 3.5 m, 0.35 m, and 105 kg, and the sampling frequency was 10 Hz. During the cruise, total accumulated distance of measurement was nearly 3000 km, and EM survey flights were segmented into 94 profiles for the avoidance of open water in the survey areas. Different ice types and ice regimes in northwestern Weddell Sea were perfectly covered.

EM induction determines sea ice thickness remotely and has high precision and reliability based on the difference between the electrical properties of sea ice and sea water ^[11]. The observations provide ground validations to satellite remote sensing and numerical simulations ^[20], thus have been extensively employed in sea ice investigations ^{[11,18,19,20,21,22,23,24]}. Generally, sea ice thickness derived by EM induction are consistently reliable over undeformed ice, and usually within 10% of that by drilling ^[21]. While over rough and deformed ice, the estimations are possibly affected by the water within the porous keels and 3D structure of keels, which may lead to underestimation of the maximum keel draft ^[20]. However, the EM fields can penetrate through the water and are also sensitive to ice bottom further below. Thus, EM measurements can distinguish between thinner and deeper keels, and the rationality and validity of the EM data had been discussed by numerous researchers ^{[11,18,20,22]}. The detailed description of EM ice thickness measurement and data processing can refer to Haas et al. ^[10,11].

The accuracy of EM measurements was better than 0.1m over level ice, becoming lower for rough and deformed ice. For a helicopter flight speed varying between 80 and 90 knots, the spatial sampling distances of EM ranged from 3 to 4 m, respectively. The bottom draft is relative to the local level ice surface.

A novel optimal model with nonlinear-statistical constraints is proposed to find out a reasonable and effective value for the cutoff draft. The performance function consists of the relative deviation between the numerical results and the measured data of the keel draft, and that between the numerical results and the measured data of the keel spacing, and the cutoff draft is taken as the identified parameter. Then, the properties of the model and the existence of the optimal parameter are discussed. The optimal value of the cutoff draft is identified by a numerical algorithm and employed to separate the ridge keels from undeformed sea ice bottom. Finally, the correlation between the keel draft and frequency (number of ridge keels per km) is analyzed and discussed.

This paper is organized as follows. In Section 2, a novel optimal model with nonlinear-statistical constraints for the determination of the cutoff draft is established, based on the traditional models of the keel draft and spacing, the properties of the proposed model and the existence of the optimal parameter are proved. Moreover, the optimal cutoff draft is identified using a numerical algorithm and applied to separate the ridge keels from undeformed sea ice bottom in Section 3. Section 4 discusses the correlation between the keel draft and frequency in detail. Conclusions and some discussions are given in the final section.

2.   Optimal modeling of the ridge keel cutoff draft

To find out the optimal value of the cutoff draft and separate effectively ridge keels from other sea ice bottom morphology, a novel optimal model with nonlinear-statistical constrains is formulated, the properties and the existence of the optimal parameter are proved in this section.

The probability functions of the traditional keel spatial distributions are introduced firstly in the following.

2.1.   Traditional spatial distributions of ridge keel

2.1.1.   Draft distribution of ridge keel

Let the function ${f_{kd}}{\text{ = }}\; {f_{kd}}(d; {d_{k{\text{ - }}c}}, {\Phi _k})$ denote the theoretical density for the ridge keel draft, which is Lipchitz continuous, where $d \in {D_k}$ is the keel draft with the set ${D_k}: = [{d_{k- c}}, \; \; {d_{k - \max }}]$, ${d_{k - c}}$ is the cutoff draft, ${d_{k - \max }} \in {R^ + }$ is the maximum keel draft and it is a limited constant (${d_{k - c}} < \; {d_{k - \max }}$), ${\Phi _k}$ is a parameter set related to the cutoff draft ${d_{k - c}}$.

There are two traditional theoretical functions of the ice ridge keel draft distribution. One was presented by Hibler et al. ^[26] as follows.

where

and ${\lambda _1}$ is the distribution shape parameter in set ${\Phi _k}$, and related to the mean keel draft $\mathop d\limits^\_ \;$ by the following equation.

The other was advanced by Wadhams ^[27], who showed that the keel draft distribution can be fitted well by the following exponential function.

where ${\lambda _2}$ is the distribution shape parameter in set ${\Phi _k}$ determined by

2.1.2.   Spacing distribution of ridge keel

Set the function ${f_{ks}}{\text{ = }}{f_{ks}}(s; {d_{k{\text{ - }}c}}, {\Psi _k})$ as the theoretical density for the ridge keel spacing, which is also Lipchitz continuous, where $s \in {S_k}$ is the keel spacing, and the set ${S_k}$ is defined as ${S_k}: = [{s_{k- \min }}, \; \; {s_{k - \max }}]$, ${s_{k - \min }}, \; \; {s_{k - \max }} \in {R^ + }$ are the minimum and maximum keel spacings (${s_{k - \min }} < \; {s_{k - \max }}$), respectively, and they are both limited constants, ${\Psi _k}$ is a parameter set related to the cutoff draft ${d_{k - c}}$.

One traditional function of the keel spacing distribution was presented by Hibler et al. ^[26] as the following exponential form.

where ${\lambda _3} \in {\Phi _k}$ related to the mean keel spacing $\; \mathop s\limits^\_ \;$ by the following equation.

Following, a lognormal distribution density function was proposed and showed fitted better the keel spacing by the by Wadhams and Davy ^[28].

where ${\theta _k}$ is the shift parameter, ${\mu _k}$ and ${\sigma _k}$ are the mean and standard error of ${\text{ln(}}s{\text{ - }}{\theta _k}{\text{)}}$, respectively, and determined by the following equation.

2.2.   Novel optimization for the cutoff draft

To find out the optimal value of the cutoff draft and separate accurately the ridge keels from the local roughness of sea ice bottom, a novel optimal model with nonlinear-statistical constrains is formulated, in which, the deviation between the numerical results and the measured data of the keel draft and that between the numerical results and the measured data of the spacing are combined as the performance criterion, and the cutoff draft ${d_{k - c}}$ is the identified parameter. Then, the properties of the proposed model and the existence of the optimal parameter are discussed in this section.

2.2.1.   Novel optimal modeling

Let ${E_{kd}}({d_{k - c}})$ and ${E_{ks}}({d_{k - c}})$ be the relative deviation between the theoretical function and the measured keel draft distribution and that between the theoretical function and the measured keel spacing distribution, respectively, and described by the following equations.

where ${d_i}$ and ${s_j}$ are the measured keel draft and spacing corresponding to the cutoff draft ${d_{k - c}}$, respectively, ${f_{kd, i}}$ and ${f_{ks, j}}$ are the probability densities of the measured ridge keel draft ${d_i}$ and spacing ${s_j}$, and $i = 1, 2, \cdots, n$ and $j = 1, 2, \cdots, m$.

Let ${d_{k - c}} \in {U_{ad}}({d_{k - c}})$ be the identified parameter, where ${U_{ad}}({d_{k - c}})$ is the admissible parameter set limited by the Rayleigh criterion and cover a sufficient range of the measured ridge keel drafts.

Obviously, the admissible parameter set ${U_{ad}}(\cdot)$ is a nonempty, bounded, closed, and convex.

For simplicity, Eq (1) is referred to as Hibler'72 function and Eq (4) as Wadhams'80 function in the following study. The initial cutoff draft of ${d_{k - c, 0}}{\text{ = }}\; 3.58$ m and step increment of $\Delta {d_{k - c}}{\text{ = }}\; 0.1$ m are employed to search for the best fits to the measured ridge keel draft and spacing distributions. The results in Figure 3 indicate that for any cutoff draft in the parameter set ${U_{ad}}(\cdot)$, the Wadhams'80 and lognormal functions yield the best fits to the measured keel draft and spacing distributions, respectively.

Effects of the ridge sail and spacing on the sail intensity (the ratio of the sail height to spacing) were very different, and the contribution of sail spacing is much larger than that of sail height in general ^[17]. To comprehensively evaluate the effects of the cutoff draft on both the measured keel draft and spacing distributions, the following performance criterion $J(\cdot)$ is defined by considering the different effects of the keel draft and spacing on the keel intensity (the ratio of the keel draft to spacing).

with

where $J({d_{k - c}})$ is the performance function, ${E_{kd - w}}({d_{k - c}})$ is the relative deviation between the Wadhams'80 function and the measured keel draft distribution, ${E_{ks - l}}({d_{k - c}})$ is the relative deviation between the lognormal function and the measured keel spacing distribution, ${f_{kd - w}}({d_i}, {d_{k - c}}; {\lambda _2})$ is the probability density function of the Wadhams'80 distribution for the keel draft [refer to Eq (4)], and ${f_{ks - l}}({s_j}, {d_{k{\text{ - }}c}}; {\theta _k}, {\mu _k}, {\sigma _k})$ is the probability density function of the lognormal distribution for the keel spacing [refer to Eq (8)], $i = 1, 2, \cdots, n$ and $j = 1, 2, \cdots, m$. A novel optimal model with nonlinear-statistical constraints (NOPM-NS) is then established as follows.

2.2.2.   Properties of the model (NOPM-NS) and existence of the optimal parameter

For the strictness of the above model (NOPM-NS), namely, the existence of the optimal cutoff draft, we set

and

Then,

Set

and

Then,

Define the feasible region set of the model (NOPM-NS) as

Theorem 1. The feasible region set $X(\cdot)$ defined by Eq (23) of the model (NOPM-NS) is compact.

Proof: Let ${R^{1{\text{ + }}}}$ be the set of positive real numbers. Obviously, the admissible parameter set ${U_{ad}}(\cdot) \subset {R^{1{\text{ + }}}}$, and ${U_{ad}}(\cdot)$ is nonempty, bounded and closed, namely, it is compact. The probability density function ${f_{kd - w}}({d_i}, {d_{k - c}}; {\lambda _2})$ is continuous on the parameter ${d_{k - c}} \in {U_{ad}}({d_{k - c}})$, so, the set $M({f_{kd - w}})$ is compact.

Additionally, ${\lambda _2}^{ - 1}$ is continuous on the parameter ${d_{k - c}} \in {U_{ad}}({d_{k - c}})$ based on the definition of Eq (5), it is clear that the set $N({\lambda _2})$ is also compact. Therefore, the set $K({U_{ad}}(\cdot))$ is obviously compact based on Eq (19).

Similarly, we can also prove that the set ${K^{'}}({U_{ad}}(\cdot))$ defined by Eq (22) is compact. Therefore, the feasible region set $X(\cdot)$ in Eq (23) is compact, namely, the feasible region set of the novel optimal model (NOPM-NS) is compact.

Theorem 2. The performance function $J(\cdot)$ of the model (NOPM-NS) is continuous in the feasible region set $X(\cdot)$.

Proof: The admissible parameter set ${U_{ad}}(\cdot) \subset {R^{1{\text{ + }}}}$ is nonempty, bounded, closed and convex, and the function ${f_{kd - w}}({d_i}, {d_{k - c}}; {\lambda _2})$ is continuous on the parameter ${d_{k - c}} \in {U_{ad}}({d_{k - c}})$, so, the relative deviation function ${E_{kd - w}}({d_{k - c}})$ is continuous on the parameter ${d_{k - c}} \in {U_{ad}}({d_{k - c}})$ according to its definition [refer to Eq (14)].

Similarly, the relative deviation function ${E_{ks - l}}({d_{k - c}})$ is continuous on the parameter ${d_{k - c}} \in {U_{ad}}({d_{k - c}})$ according to its definition [refer to Eq (15)].

Therefore, combining with the definition [refer to Eq (13)], the performance function $J(\cdot)$ of the novel model (NOPM-NS) is continuous in the feasible region set $X(\cdot)$.

From the above two theorems, we can obtain the following theorem easily.

Theorem 3. $\exists {d_{k - c}}^* \in {U_{ad}}(\cdot)$, such that $\forall {d_{k - c}} \in {U_{ad}}(\cdot)$, $J({d_{k - c}}^*) < J({d_{k - c}})$ holds. Namely, the optimal solution of the model (NOPM-NS) exists.

3.   Numerical algorithm and result for the novel model (NOPM-NS)

It is known that the optimal solution of the optimal model (NOPM-NS) exists from Theorem 3. A numerical algorithm is developed for the determination of the optimal cutoff draft and result is analyzed in this section.

3.1.   Numerical algorithm for the model (NOPM-NS)

The linear search method is applied to make the performance function $J(\cdot)$ of the novel optimal model (NPM-NS) attain its minimum, and the numerical algorithm is described as follows.

Step 1. Initialize: ${d_{k - c, 0}}$ (cutoff draft), $\Delta {d_{k - c}}$ (step increment), and ${d_{k - c, \max }}$(maximum of the cutoff draft). Set $p\; {\text{ = }}\; 1$.

Step 2. Import: measured keel draft ${d_i}$($i = 1, 2, \cdots, n$) and spacing ${s_j}$($j = 1, 2, \cdots, m$), mean keel draft $\mathop d\limits^\_$ and spacing $\mathop s\limits^\_$.

Step 3. Identify: the parameters ${\lambda _2}$, ${\theta _k}$, ${\mu _k}$ and ${\sigma _k}$ by Eqs (5) and (9), respectively.

Step 4. Calculate:${f_{kd - w}}({d_i}, {d_{k - c}}; {\lambda _2})$, ${f_{ks - l}}({s_j}, {d_{k{\text{ - }}c}}; {\theta _k}, {\mu _k}, {\sigma _k})$ and $J(\cdot)$ by Eqs (4), (8) and (16) (model NOPM-NS), respectively.

Step 5. Set ${d_{k - c, p}}{\text{ = }}{d_{k - c, 0}} + p \times \Delta {d_{k - c}}$, if ${d_{k - c, p}} < {d_{k - c, \max }}$, go to Step 2. Else, Set

Step 6. If $J({d_{k - c, p}}) < J({d_{k - c, p{\text{ - }}1}})$, set ${d_{k - c, p}}^* = {d_{k - c, p}}$, stop. Else, set $p = p + 1$, go to Step 5.

3.2.   Result of the numerical algorithm

Set the initial cutoff draft ${d_{k - c, 0}}{\text{ = }}\; 3.58\; {\text{m}}$, step increment $\Delta {d_{k - c}}{\text{ = }}0.1\; {\text{m}}$, and maximum of the cutoff draft ${d_{k - c, \max }}{\text{ = 4}}{\text{.18}}\; {\text{m}}$. The result of the above numerical algorithm shows that the optimal cutoff draft of the ridge keels is ${d_{k - c, p}}^* = 3.78$ m. The variations in the relative deviations ${E_{kd - w}}({d_{k - c}})$ and ${E_{ks - l}}({d_{k - c}})$, and the performance function $J({d_{k - c}})$ of the novel optimal model (NOPM-NS) as the cutoff draft increase are all shown in Figure 4. It is obvious that ${E_{kd - w}}({d_{k - c}})$ and ${E_{ks - l}}({d_{k - c}})$, and $J({d_{k - c}})$ all reach their minima at the cutoff draft of 3.78 m. According to novel optimal model (NOPM-NS), ${d_{k - c}}^* = 3.78$ m should be taken as the optimal cutoff draft.

Granberg and Leppäranta ^[29] proposed that the cutoff height should be much larger than the standard deviation of the ice surface elevation or larger than twice this value. In the present study, the same method is applied to assess the keel cutoff draft. The standard deviation of the ice bottom draft is ${e_{k - s}} = 0.52$ m and it is obvious that the optimal cutoff draft ${d_{k - c}}^* = 3.78$ m is much larger than twice of the standard deviation ${e_{k - s}}$. So, this optimal cutoff draft is taken on as the lower limit of the keel peak and the deepest point of a ridge keel is defined as its peak (Figure 5). Davis and Wadhams ^[30] set the cutoff draft as 5 m to analyze the Arctic ridge keel morphology. Ekeberg et al. ^[15] also obtained a cutoff draft of 5 m by the Rayleigh criterion based the upward looking sonar data in the Fram Strait. Obert and Brown ^[31] analyzed the morphologies of 3199 ridge keels in Northumberland Strait of Arctic with a cutoff draft of 2 m. The different cutoff draft results of the present and previous studies are likely caused by a combination of the following reasons: 1) the physical properties of the ice/ridge are directly related to the seasonal and interannual variations. 2) Different dynamical processes might lead to differences in the dominant formation mechanisms of the ridges in different regions. 3) Differences in the methods of determining the cutoff draft.

4.   Discussion on the relationship between the keel draft and frequency

The draft and frequency (numbers of keels per km) denote the vertical and level features of ridge keels, respectively. To accurately describe the keel morphology and spatial distribution, it is necessary to analyze the relationship between the mean keel draft and frequency, as shown in Figure 6. There was scatter but the obvious logarithmic relationship yielded a correlation coefficient of 0.7 between the mean keel draft and frequency with reasonable confidence. This logarithmic function showed that the mean keel draft increased logarithmically, while the ratio of the increments in the keel draft and frequency decreased as the corresponding frequency increased. Moreover, according to the measured data shown in Figure 6, for a given increase in ridge frequency, the increases in the keel spacing and draft were both greater in the lower ridging intensity regime than the larger regime. In addition, the logarithmic function showed that the mean ridge keel varied much less than the mean spacing, reflect well the real observation. Therefore, the proposed logarithmic function is a suitable relationship for describing the ridge keel morphology.

5.   Conclusions and discussion

Based on helicopter-borne EM data collected in northwestern Weddell Sea, we determine the best fit to measured ridge keel draft distribution which is represented by the Wadhams'80 function (refer to Eq (4)), and the spacing is achieved by a lognormal function(refer to Eq (8)).

We propose a novel optimal model with nonlinear-statistical constraints (NOPM-NS) to determine the optimal cutoff draft for ridge keel, by minimizing the deviations of the theoretical and measured ridge keel draft and spacing distributions, and the cutoff draft is taken as the identified variable. The properties of the novel model (NOPM-NS) and the existence of the optimal parameter are proved, and the optimal value of cutoff draft is identified by a developed numerical algorithm as ${d_{k - c}}^* = 3.78$ m, which is employed to separate the ridge keels from undeformed sea ice bottom.

We obtain a logarithmic relationship yielded a correlation coefficient of 0.70 between the mean keel draft and frequency in the present study, with a 95% confidence degree. This relationship indicates that there is a general increase in the mean keel draft as the mean keel frequency increases, whereas the ratios of the increments in the keel draft and frequency decrease as the ridge frequency increases.

Due to climate change, sea ice in the polar region subject to significant deformation because of thinner ice thickness and smaller ice concentration. Ice ridge parameterization is getting more attention and become more important in sea ice dynamic modeling. Therefore, the present novel optimal model (NOPM-NS) for determining the cutoff draft has the potential to be applied for the separation of ridge keels from other ice bottom undulations in any sea-ice region, and we believe that it is a promising approach worthy of further studies under different environmental conditions in the polar regions. We expect this study can provide more accurate standard as analyzing data of sea ice thickness, benefiting to a comprehensive understand on ice mass balance.

It must be noted that the present optimal model (NOPM-NS) and method of analyses are proposed for helicopter-borne EM data. We focus on the mathematical theoretic method in data analyses, and the possible inaccuracies of EM for deformed ice is somewhat beyond the scope of this study. However, more validations to the universality and effectivity of EM data especially on deformed ice, are still necessary by using other instruments, e.g., upword looking sonar or radar, and will be conducted in our future work.

Acknowledgments

We would like to thank Dr. Christian Haas and Dr. Marcel Nicolaus from the Alfred Wegener Institute for Polar and Marine Research (AWI) for providing the valuable EM data, Dr. Qingkai Wang for providing the field photograph of sea ice ridge sails during the 36^th Antarctic scientific expedition of china. The Arctic and Antarctic Administration is also thanked for supporting the participation of Zhijun Li in the expedition organized by AWI. This work was supported by the National Nature Science Foundation of China (Nos. 41876219, 41922045, 42074094), the Key Science Foundation for Universities of Henan Province (No. 22A110017), and the project of Nanyang Normal University (STP2017023, 2022STP014).

Conflict of interest

The authors declare there is no conflict of interest.