Near-resonances and detuning in classical and quantum mechanics

1.   Introduction

Stochastic age-dependent population system has an increasingly important status in biomathematics, being the main research direction in biology and ecology in recent years. Especially, one of the most striking and meaningful problems in the study of stochastic age-dependent population system is its numerical scheme because of its nonlinear structure and non-existent explicit solutions. In ^[1], Li et al. first introduced Poisson jumps into stochastic age-dependent population system and proposed the following model:

where $T > 0$, $A$ is the maximal age of the population species and $A > 0$, $Q = (0, T) \times (0, A)$. $d_{t}P_{t}$ is the differential of $P_{t}$ relative to $t$, i.e., $d_{t}P_{t} = \frac{\partial P_{t}}{\partial t}dt$. $P_{t} = P(t, a)$ denotes the population density of age $a$ at time $t$, $\mu(t, a)$ denotes the mortality rate of age $a$ at time $t$, $\beta(t, a)$ denotes the fertility rate of females of $a$ at time $t$, $f(t, P_{t})$ denotes effects of external environment for population system, $g_1(t, P_{t})$ is a diffusion coefficient, $h(t, P_{t})$ is a jump coefficient (it represents the size of the population systems increases or decreases drastically because brusque variations from earthquakes, floods, immigrants and so on), $B_{t}$ is a Brownian motion, $N_{t}$ is a Poisson process with intensity $\lambda > 0$. Then, they investigated the convergence of Euler method for model (1.1). Since then, an increasing number of authors have analyzed stochastic age-dependent population models with Poisson jumps, and many significant results have been obtained (see e.g., ^{[2,3,4,5,6,7,8,9,10,11]}). For example, Wang and Wang ^[3] established the semi-implicit Euler method for stochastic age-dependent population models with Poisson jumps and discussed the convergence order of numerical solutions. Tan et al. ^[5] presented a split-step $\theta$ ($SS\theta$) method of stochastic age-dependent population models with Poisson jumps, and the exponential stability of the model was established. Pei et al. ^[8] constructed two types of numerical methods for stochastic age-dependent population models with Poisson jumps, which are compensated and non-compensated. Then the asymptotic mean-square boundedness is discussed for numerical scheme.

In the above-mentioned model (1.1), we can easily see that the effects of randomly environmental variations of parameter $\mu$ are described as a linear function of Gaussian white noise ^[12,13], that is $\mu dt\rightarrow \mu dt+\sigma dB_{t}$ (where $\sigma^2$ represents the intensity of $B_{t}$). Obviously, it is unreasonable to use linear function of Gaussian white noise to simulate parameters perturbation in a randomly varying environment. In ^[14], Duffie proposed to use a mean-reverting Ornstein-Uhlenbeck process to describe parameters which fluctuate around an average value. Up until now, the mean-reverting OU process have been extensively discussed in ^{[15,16,17,18]}. Zhao et al. ^[16] analyzed stationary distribution for stochastic competitive model incorporating the OU process. Wang et al. ^[17] introduced the OU process into the Susceptible-Infected-Susceptible (SIS) epidemic model and investigated its threshold. However, to the authors' knowledge, there is no literature to consider the OU process into the stochastic age-dependent population system with Poisson jumps. On the other hand, we find that the influence of time delay are not considered in the above papers ^{[1,2,3,4,5,6,7,8,9,11]}. There are very few papers in the literature that take time delay into account in the stochastic age-dependent population system so far (see e.g., ^[19,20]). Therefore, based on the above analysis, studying stochastic age-dependent delay population jumps equations, coupled with mean-reverting OU process have more practical significance.

Obviously, the age-dependent stochastic delay population equations with mean-reverting OU process and Poisson jumps have no explicit solution. Thus, numerical approximation schemes should be developed as a essential and powerful tool to explore its properties. The numerical schemes of stochastic age-dependent population system have been extensively researched by many scholars, for example, ^{[1,3,4,5,8,9,19,21,22,23]}. However, due to the fact that the coefficients $f$, $g_1$ and $h$ of model (1.1) are particularly complex functions, so using the existing numerical methods to approximate the age-dependent stochastic delay population equations with mean-reverting OU process and Poisson jumps will result in slow convergence and very high computational cost. Recently, Jankovic and Ilic ^[24] introduced a Taylor approximation method for stochastic differential equations and proved that its convergence rate and computational cost is better than other numerical methods such as the Euler method, the semi-implicit Euler method and $SS\theta$ method mentioned in ^{[1,2,3,4,5,6,7,8,9,11]}. Motivated by Jankovic et al., we construct a Taylor approximation scheme for the age-dependent stochastic delay population equations with mean-reverting OU process and Poisson jumps in this paper. Furthermore, the convergence between the exact solutions and numerical solutions is investigated.

The highlights of the present paper are summarized as follows:

● Age-dependent stochastic delay population equations with mean-reverting OU process and Poisson jumps are given.

● To improve the convergence speed and reduce cost, the Taylor approximation scheme for the age-dependent stochastic delay population equations with mean-reverting OU process and Poisson jumps is developed.

● The convergence and convergence order of Taylor approximation scheme are discussed.

The arrangement of this paper is as follows. In section 2, we establish the age-dependent stochastic delay population equations with mean-reverting OU process and Poisson jumps, as well as introduce some notations and preliminaries. Then, the $pth$ moments boundedness of exact solutions for age-dependent stochastic delay population equations with mean-reverting OU process and Poisson jumps are presented. In section 3, we propose a Taylor approximation scheme for a age-dependent stochastic delay population equations with mean-reverting OU process and Poisson jumps, and the convergence theory for the numerical method is proved. In section 4, we present some numerical simulations to demonstrate our theoretical results. Section 5 presents the conclusions of our research.

2.   Model formulation and preliminaries

2.1.   Model formulation

In the above model (1.1), the authors took advantage of a traditional parameter perturbation method to reflect the effect of environmental noise, $(-\mu(t, a) P_{t} + f(t, P_{t}))dt$ when it is stochastically perturbed with $(-\mu(t, a) P_{t} + f(t, P_{t}))dt+g_1(t, P_{t})dB_{t}$. It is worth mentioning that Cai et al. ^[18] pointed out that due to environmental continuous fluctuations, the mortality rate $\mu(t, a)$ can not be described by a linear function of Gaussian white noise. In order to model the randomly varying environmental fluctuations in $\mu(t, a)$, we introduce the following mean-reverting Ornstein-Uhlenbeck process for $\mu(t, a)$ inspired by ^[16]:

where we assume that $\mu_{1}(t)$ represents the mortality rate at time $t$ and $\mu_{2}(a)$ represents the mortality rate at age $a$. All parameters $\eta$, $\mu_{e}$ and $\xi$ are positive constants. $\eta$ is the reversion rate, $\mu_{e}$ is the mean reversion level or long-run equilibrium of growth rate $\mu_{1}(t)$, $\xi$ is the intensity of volatility.

For (2.1), applying the stochastic integral format, we obtain the explicit form of the solution as:

where $(\mu_{1}^{0} : = \mu_{1}(0))$. It is not difficult to see that the expected value of $\mu_{1}(t)$ is

and variance value of $\mu_{1}(t)$ is

Combining (2.2), (2.3) and (2.4), we easily have that the term $\xi \int_{0}^{t}e^{-\eta (t-s)} dB_t$ satisfies the normal distribution $\mathbb{E}\Big(0, \frac{\xi^2}{2\eta}\big(1-e^{-2\eta t}\big) \Big)$. Then we obtain $\xi \int_{0}^{t}e^{-\eta (t-s)} dB(t)$ being equal to $\frac{\xi}{\sqrt{2\eta}}\sqrt{1-e^{-2\eta t}}\frac{dB_{t}}{dt}$ a.e..

Therefore, we can rewrite (2.2) in the following form ^[17,18]

where $\sigma(t) = \frac{\xi}{\sqrt{2\eta}}\sqrt{1-e^{-2\eta t}}$. A conceptual problem immediately occurs in that $\frac{dB_{t}}{dt}$ is not defined except in a generalized sense.

Replacing $\mu(t, a)$ in model (1.1) with (2.2) and (2.5) and rearranging leads to the following stochastic age-dependent population equation:

where $g(t, P_{t}) dB_{t}$ contains $g_{1}(t, P_{t})dB_{t}$ and $-\sigma(t)\mu_{2}(a) P_{t}dB_{t}$.

On the other hand, due to the time delay is unavoidable in a real world. Motivated by ^[19] and ^[25], we derive the following system:

where $P_{t} = P(t, a)$ denotes the population density of age $a$ at time $t$, $P_{t-\tau} = P(t-\tau, a)$ denotes the population density of age $a$ at time $t-\tau$, $\tau$ is time delay and $\tau > 0$. $f(t, P_{t}, P_{t-\tau})$ denotes the effects of external environment for the population system, $g(t, P_{t}, P_{t-\tau})$ is a diffusion coefficient, $h(t, P_{t}, P_{t-\tau})$ is a jump coefficient, $\phi_{t} = \phi(t, a)$ denotes the histories of the population density of age $a$ at time $t$, $\beta$(t, a) denotes the fertility rate of females of age $a$ at time $t$. $A$ is the maximal age of the population species, so $P(t, a) = 0, \forall a \geq A$. $N_{t}$ is a Poisson process with intensity $\lambda > 0$. The explanation of the other symbols was given under Eq (2.1). In the following section, we concentrate on studying model (2.7).

2.2.   Preliminary results

Let $V = D^{1}([0, A])\equiv \{\varphi| \varphi \in L^{2}([0, A]), \text{where}\ \frac{\partial \varphi}{\partial a}\ \text{represent the generalized partial derivatives}\}$, $V$ be a Sobolev space. $D = L^2[0, A]$ such that $V\hookrightarrow D\equiv D' \hookrightarrow V'.$ $V'$ is the dual space of $V$. We denote by $\|\cdot\|, \mid\cdot\mid$ and $\|\cdot\|_{*}$ the norms in $V, D$ and $V'$ respectively; by $\langle \cdot, \cdot \rangle$ the duality product between $V$ and $V'$, and by $(\cdot, \cdot)$ the scalar product in $D$.

For simplicity, we introduce some notations. Throughout this paper, unless otherwise, let $(\Omega, \mathcal{F}, \mathbb{P})$ be a complete probability space with filtration $\{\mathcal{F}_{t}\}_{t\geq 0}$ satisfying the usual conditions (i.e. it is increasing and right continuous while $\mathcal{F}_{0}$ contains all $\mathbb{P}$-null sets), and let $\mathbb{E}$ signify the expectation corresponding to $\mathbb{P}$. For an operator $H \in L(M, D)$ on the space of all bounded linear operators from $M$ into $D$, we denote by $\|H\|_{2}$ the Hilbert-Schmidt norm, i.e., $\|B\|_{2} = tr(HWH)^{T}$.

Let $\tau > 0$ and $C = C ([-\tau, 0]; D)$ be the space of all continuous function from [0, T] into $H$ with sup-norm $\|\psi\|_{C} = \sup\limits_{-\tau \leq s\leq 0}|\psi(s)|$, $L_{V}^{P} = L^{P}([0, T];V)$ and $L_{D}^{P} = L^{P}([0, T];D)$. Moreover, let $\mathcal{F}_{0}$-measurable, $C_{\mathcal{F}_{0}}^{b}([-\tau, 0]; D)$ denote the family of all almost surely bounded, $F_{0}$-measurable $C = C ([-\tau, 0]; D)$ -value random variables. For a pair of real numbers $a$ and $b$, we use $a \vee b = \max(a, b)$. If $G$ is a set, its indicator function by $1_{G}$, namely $1_{G}(x)$ = 1 if $x \in G$ and 0 otherwise.

The integer version of Eq (2.7) is given by

For the existence and uniqueness of the solution, we assume that the following assumptions are satisfied:

$(A1)$ $\mu(t, a)$ and $\beta(t, a)$ are nonnegative measurable, such that

$(A2)$ $f(t, 0, 0) = g(t, 0, 0) = h(t, 0, 0) = 0$.

$(A3)$ The Lipschitz and linear growth conditions: there exists a positive constant $K$ such that

$|f(t, x_{1}, y_{1})-f(t, x_{2}, y_{2})|\vee\|g(t, x_{1}, y_{1})-g(t, x_{2}, y_{2})\|_{2}\vee|h(t, x_{1}, y_{1})-h(t, x_{2}, y_{2})|$

$\leq K(\|x_{1}-x_{2}\|_{C}+\|y_{1}-y_{2}\|_{C})$,

$|f(t, x, y)|^{2}\vee \|g(t, x, y)\|_{2}^{2}\vee|h(t, x, y)|^{2}\leq 2K^{2}(\|x\|_{C}^{2}+\|y\|_{C}^{2})$

for $\forall x, y, x_{1}, x_{2}, y_{1}, y_{2}\in C$.

$(A4)$ There exists constants $\tilde{K}, \bar{K} > 0$ and $\gamma \in (0, 1]$ such that for $-\tau \leq s \leq 0$, $0 \leq a \leq A$ and $r \geq 2$

$\mathbb{E} |\phi_{t}-\phi_{s}|^{r}\leq \tilde{K}(t-s)^{\gamma}$.

Consequently,

$\mathbb{E} |\phi_{t}|^{r} < \infty$.

$(A5)$ $f$, $g$ and $h$ have Taylor approximations in the second argument, up to $\alpha_{1}th$, $\alpha_{2}th$ and $\alpha_{3}th$ derivatives, denoted as $f_{x}^{(\alpha_{1})}(t, x, y)$, $g_{x}^{(\alpha_{2})}(t, x, y)$ and $h_{x}^{(\alpha_{3})}(t, x, y)$, respectively.

$(A6)$ $f_{P_{t}}^{(\alpha_{1}+1)}(t, P_{t}, P_{t-\tau})$, $g_{P_{t}}^{(\alpha_{2}+1)}(t, P_{t}, P_{t-\tau})$ and $h_{P_{t}}^{(\alpha_{3}+1)}(t, P_{t}, P_{t-\tau})$ are uniformly bounded, i.e. there exist positive constants $K_{1}$, $K_{2}$ and $K_{3}$ satisfying

Throughout the following analysis, for the purpose of simplicity, we will use $C, C_{1}, C_{2}, \cdots$ to stand for generic constants that depend upon $K$ and $T$, but not upon $\Delta$. The precise value of these constants may be determined via the proof. Our first theorem shows the existence and uniqueness of the strong solution for the model (2.7).

Theorem 2.1. Under the assumptions $(A1)-(A4)$, for $t \in [0, T]$, Eq (2.7) has a unique strong solution.

Proof. The proof of this theorem is standard (see Zhang et al. ^[26]) and hence is omitted.

Moreover, the $pth$ moment boundedness of the true solution $P_t$ of the model (2.7) is proved in the following theorem.

Theorem 2.2. Under the assumptions $(A1)-(A4)$, for each $q \geq 2$, there exists a constant $C$ such that

Proof. Form (2.8), applying Itô's formula ^[25] to $|P_t|^q$ yields

where $\bar{N}_s = N_s-\lambda s$ is a compensated Poisson process.

Since

by the assumptions $(A1)$-$(A3)$, we get that

Note that for any $t\in[0, T]$,

Hence, we have

where $C_1 = q\Big[(\frac{\bar{\beta}^2A^2}{2}+\mu_{1}^{0}\bar{\mu})+2K+2(q-1)K^2 +2K\lambda+2\lambda K^2 (q-1)\Big]$.

Using the Burkholder-Davis-Gundy's inequality, we derive that

Similarly, we can obtain that

and

Substituting (2.15), (2.16) and (2.17) into (2.14) yields

Thus, the well-known Gronwall inequality obviously implies the desired equality (2.9).

3.   Taylor approximation scheme and convergence

In this section, we will establish the Taylor approximation scheme for the stochastic age-dependent population Eq (2.7) and investigate the strong convergence between the true solutions and the numerical solutions derived from the Taylor approximation scheme.

3.1.   Taylor approximation

Let $\tau_{j}$ denote the $jth$ jump of $N_{s}$ occurrence time. For example, assume that jumps arrive at distinct, ordered times $\tau_{1} < \tau_{2} < \cdots$, let $t_{1}, t_{2}, \cdots, t_{m}$ be the deterministic grid points of $[0, T]$. We establish approximate solutions to (2.7) at a discrete set of times $\{\tau_{j}\} (j = 1, 2, \cdots)$. This set is the superposition of the random jump times of the Poisson process on $[0, T]$ and a deterministic grid $t_{1}, t_{2}, \cdots, t_{m}$ and satisfy $\max\{|\tau_{i+1}-\tau_{i}|\} < \Delta t$ (for the sake of simplicity, we denote $\Delta t$ as $\Delta$). It is quite clear that the random Poisson jump times can be computed without any knowledge of the realized path of (2.7).

Next, we propose a Taylor approximation of the solutions of Eq (2.7). Without loss of any generality, given a step size $\Delta \in (0, 1)$, we let $t_k = k\Delta$ for $k = 0, 1, 2, 3, \cdots, [\frac{\tau}{\Delta}]$, here $[\frac{\tau}{\Delta}]$ is the integer part of $\frac{\tau}{\Delta}$. The continuous time Taylor approximate solution $Q_{t} = Q(t, a)$ to the stochastic age-dependent population Eq (2.7) can be defined by setting $Q_{0} = P_{0}(a) = \phi(0, a)$ and $Q(t, 0) = \int_{0}^{A}\beta(t, a)Q_{t}da$ and forming

where $Z_{1t} = Z_{1}(t, a) = \sum_{k = 0}^{[\frac{\tau}{\Delta}]}Q_{t_{k}}1_{[t_k, t_{k+1})}(t)$ and $Z_{2t} = Z_{2}(t, a) = \sum_{k = 0}^{[\frac{\tau}{\Delta}]}Q_{t_{k}-\tau}1_{[t_k, t_{k+1})}(t)$ are step processes. That is, $Z_{1t} = Q_{t_{k}}$ and $Z_{2t} = Q_{t_{k}-\tau}$ for $t\in[t_k, t_{k+1})$ when k = 0, 1, 2, 3, $\cdots$, $[\frac{\tau}{\Delta}]$.

3.2.   Convergence of the Taylor approximate solutions

In this subsection, let us investigate the convergence of the Taylor approximate solutions of the stochastic age-dependent population Eq (2.7).

In the following three lemmas we will show that $Q_{t}$ and $Q_{t-\tau}$ are close to $Z_{1t}$ and $Z_{2t}$ based on $L^{r}$, respectively.

Lemma 3.1. For any $q \geq 2$, there exists a positive constant $K_{4}$ such that

where $\alpha = \max\{\alpha_{1}, \alpha_{2}, \alpha_{3}\}$.

Proof. This proof is completed in Appendix A.

Remark 3.1. If $\alpha_{1} = \alpha_{2} = \alpha_{3} = 0$, then $(A3)$ shows that the Taylor approximation solutions $Q_t$ admit finite moments (see, ^[27,28]).

Lemma 3.2. Under the assumptions $(A1), (A3), (A5)$, $(A6)$, Lemma 3.1 and $\mathbb{E}\Big|\frac{\partial Q_{s}}{\partial a}\Big|^{r} < K_{5}$ hold, $K_{5}$ is a positive constant. For $2 \leq r \leq (\alpha+1)q$, we have

Proof. For any $t \geq 0$, there exists an integer $k \geq 0$ such that $t \in[t_{k}, t_{k+1})$, we have

where

By the elementary inequality, we further have

Applying the Hölder inequality and moment inequality, we obtain

For the jump integer, by virtue of the elementary inequality and Doob's inequality, we derive

Moreover, by the well-known mean value theorem, we observe that there exists a $\theta \in (0, 1)$ such that

Then, by the assumptions $(A1), (A3), (A5)$, $(A6)$ and Lemma 3.1, we obtain

In the same way as (3.6) was derived, we can show that

and

Substituting (3.5), (3.6), (3.7) and (3.8) into (3.4) yields

which is the required inequality (3.3).

Lemma 3.3. Under the assumptions $(A1)$-$(A6)$, Lemma 3.1 and $\mathbb{E}\Big|\frac{\partial Q_{s}}{\partial a}\Big|^{r} < K_{5}$ holds. For $2 \leq r \leq (\alpha+1)q$, there exists a $\gamma \in (0, 1]$ such that

Proof. For any $t \geq 0$, there exists an integer $k \geq 0$ such that $t \in[t_{k}, t_{k+1})$. We divide the whole proof into the following three cases.

● If $-\tau \leq t_{k}-\tau \leq t-\tau \leq 0$. Then, by the assumption $(A4)$, we have

● If $0 \leq t_{k}-\tau \leq t-\tau$. Then, by Lemma 3.2, we have

● If $-\tau \leq t_{k}-\tau \leq 0\leq t-\tau$. Then, we have

Then together with (3.10) and (3.11), we have the following results immediately,

Summarizing the above three cases, we therefore derive that

for $2 \leq r \leq (\alpha+1)q$ and $\gamma \in (0, 1]$, which is the desired inequality (3.9).

We can now begin to prove the following theorem which reveals the convergence of the Taylor approximate solutions to the true solutions.

Theorem 3.1. , Let the assumptions $(A_{1})-(A_{6})$ and Lemma 3.1 hold. Then for any $q \geq 2$ and $\gamma \in (0, 1]$,

Consequently

Proof. By the (2.2) and (3.1), it is not difficult to show that

We write

for simplicity. For all $t\in[0, T]$, using Itô's formula to $|e(t)|^q$ and copying the analysis of (2.11) to (2.13), we have

The Young inequality yields

for $\forall a, b \in R$ and $\forall c, d, \varepsilon > 0$. We hence have

where $K_{6} = \frac{(q\bar{\beta}^2A^2+2\mu_{1}^{0}\bar{\mu}q)}{2}$, $K_{7} = \frac{1}{q}\Big[\frac{q-1}{\varepsilon q}\Big]^{q-1}$ and $K_{8} = \frac{2}{q}\Big[\frac{q-2}{\varepsilon q}\Big]^{\frac{q-2}{2}}$.

Applying the Burkholder-Davis-Gundy's inequality ^[29] and Young inequality, we obtain that

Continuing this approach, we have

and

where $K_{9} = \frac{4}{q}\Big[\frac{q-4}{\varepsilon q}\Big]^{\frac{q-4}{4}}$.

Next, under the assumptions $(A_{3})$, $(A_{6})$, Lemma 3.2 and Lemma 3.3, we then compute

Moreover, we can similarly compute

and

Substituting (3.18) to (3.23) into (3.17) we obtain that

and the required result (3.14) and (3.15) follows from the Gronwall inequality.

4.   Numerical simulation

In this section, we present some numerical experiments to demonstrate the theoretical result. Let us consider the following age-dependent stochastic delay population equations with OU process and Poisson jumps:

where $A = 1$, $T = 1$, $\tau = 1$, $\mu_{e}$ = 0.65, $\mu_{1}^{0}$ = 0.5, $\eta$ = 0.75, $\mu_{2}(a) = \frac{1}{1-a}$, $B_{t}$ is a scalar Brownian motion, $N_{t}$ is a Poisson process with intensity $\lambda = 1$, $\phi(t, a) = \exp(\frac{-1}{1-a})$ and $\beta(t, a) = \frac{1}{(1-a)^2}$.

Now, we employ MATLAB for numerical simulations. First, we compare the convergence speed of the Taylor approximation scheme and backward Euler methods (BEM) mentioned in ^[30]. Let $T = 1$, $\Delta t = 5 \times 10^{-4}$ and $\Delta a = 0.05$. For $f$, $g$ and $h$ of model (4.1), we choose three different groups of functions as examples. Obviously, it is easy to verify that assumptions $(A1)-(A6)$ are satisfied. By averaging over all of the 500 samples, on the computer running at Intel Core i5-4570 CPU 3.20 GHz, the runtimes of the Taylor approximation scheme (where $f$, $g$ and $h$ are approximated up to the 5th order) and the backward Euler methods for model (4.1) are given in Table 1.

Form the fist group $f$, $g$ and $h$ functions in Table 1, we observe that the runtime of the Taylor approximation scheme (3.1) is about 17.561282 seconds while the runtime of backward Euler method is about 29.227642 seconds on the same computer, and conclude that the convergence speed of the Taylor approximation scheme is 1.664 times faster than that of the backward Euler methods. As the theoretical results, Table 1 reveals that the rate of convergence for the Taylor approximation scheme is faster than the backward Euler methods.

Next, we explore the convergence of the Taylor approximation scheme (3.1). By Theorem 3.1, we obtain that the numerical solution of the Taylor approximation scheme will converge to the exact solution with $\frac{\gamma}{q}$, where $\gamma \in (0, 1]$ and $q \geq 2$. Since the age-dependent stochastic delay population equations with OU process and Poisson jumps (4.1) cannot be solved analytically, we use more precise numerical solutions to obtain the exact solution. We take $T = 1$, $\Delta t = 0.005$, $\Delta a = 0.05$, $f(t, P_{t}, P_{t-\tau}) = \sin2 P_{t}+\frac{1}{4}\sin4 P_{t-1}$, $g(t, P_{t}, P_{t-\tau}) = \sqrt{P^2_{t}+1}+P_{t-1}$ and $h(t, P_{t}, P_{t-\tau}) = \sin P_{t}-P_{t-1}$. Based on ^[5], the "explicit solutions" $P(t, a)$ to model (4.1) can be given by the numerical solution of the $SS\theta$ method with $\theta = 0.2$.

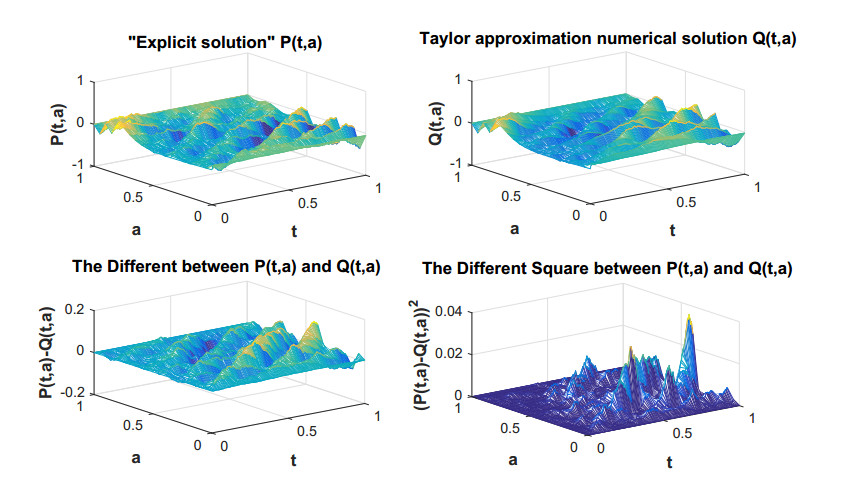
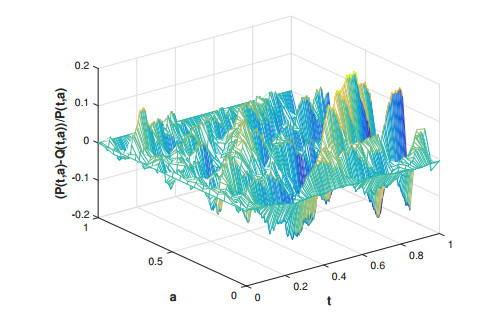
In Figure 1, we show the paths of the "explicit solutions" $P(t, a)$, the numerical solution $Q(t, a)$ of the Taylor approximation scheme (where $f$, $g$ and $h$ approximated up to the 10th order) and error simulations between them. In Figure 2, the relative difference between "explicit solutions" P(t, a) and numerical solutions $Q(t, a)$ is presented. Moreover, we can see that the maximum value of the error square is less than 0.04 from Figure 1 and the maximum value of the the relative difference is less than 0.2 from Figure 2. Clearly the numerical solution $Q(t, a)$ converge to exact solution in the mean sense.

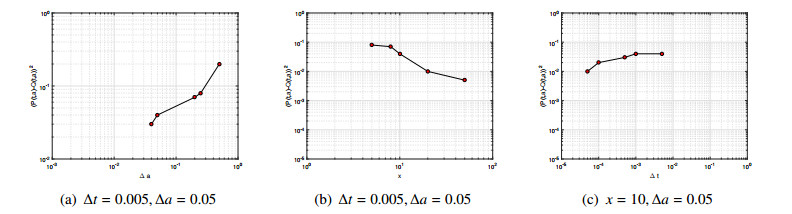
To further demonstrate the convergence of the Taylor approximation scheme, we show the errors between the "explicit solutions" $P(t, a)$ and numerical solutions $Q(t, a)$ at different values of time step $\Delta t$, expansion order $x$ and age step $\Delta a$ in Table 2. Table 2(a) shows that for fixed expansion order $x = 10$ and time step $\Delta t = 0.005$, the corresponding value of $(P(t, a)-Q(t, a))^{2}$ when $\Delta a$ take 0.04, 0.05, 0.2, 0.25 and 0.5, separately. In Table 2(b), for Taylor approximations of the coefficients $f$, $g$ and $h$, we choose the expansion order to take 5, 8, 10, 15 and 20, separately. Then the values of $(P(t, a)-Q(t, a))^{2}$ are given. In Table 2(c), for fixed expansion order $x = 10$ and age step $\Delta a = 0.05$, we give the corresponding value of $(P(t, a)-Q(t, a))^{2}$ when $\Delta t$ take 0.005, 0.001, 0.0005, 0.0001 and 0.00005, separately. To illustrate our results more succinctly and forcefully, we use log-log plot Figure 3(a)–(c) to simulate the data of Table 2(a)–(c), respectively. In Figure 3(b), when expansion order $x = 10$ and time step $\Delta t = 0.005$, as the value of age step $\Delta a$ increases, the value of $(P(t, a)-Q(t, a))^{2}$ increases. In Figure 3(b), as one would expect, as the expansion order increases, the value of $(P(t, a)-Q(t, a))^{2}$ is getting smaller with time step $\Delta t = 0.005$, age step $\Delta a = 0.05$. From Figure 3(c), it clearly reveals the fact that for fixed expansion order $x = 10$ and age step $\Delta a = 0.05$, the value of $(P(t, a)-Q(t, a))^{2}$ will tend to decrease when the increments of time $\Delta t$ smaller. Thus, based on the above numerical analysis, we conclude that the Taylor approximation scheme is a simple and efficient numerical method for the age-dependent stochastic delay population equations with OU process and Poisson jumps.

5.   Concluding remarks

This paper discuss a Taylor approximation scheme for a class of stochastic age-dependent population equations. In order to obtain a more realistic and improved model compared to those in the literature ^{[1,2,3,4,5,6,7,8,9,11]}, we introduce the mean-reverting Ornstein-Uhlenbeck (OU) process, time delay and Poisson jumps into equation and form a new system (2.7). We investigate the $pth$ moments boundedness of exact solutions of age-dependent stochastic delay population equations with mean-reverting OU process and Poisson jumps (2.7). When the drift and diffusion coefficients satisfies Taylor approximations, we construct a Taylor approximation scheme for Eq (2.7) and reveal that the Taylor approximation solutions converge to the exact solutions for the equations. Furthermore, we estimate the order of the convergence. We also utilize a numerical example to confirm our theoretical results. In our future work, we will consider the effect of variable delay for stochastic age-dependent population equations and investigate the convergence of numerical methods for stochastic age-dependent population equations with OU process and variable delay.

Acknowledgements

The authors are very grateful to the anonymous reviewers for their insightful comments and helpful suggestions. This research was funded by the "Major Innovation Projects for Building First-class Universities in China's Western Region" (ZKZD2017009).

Conflict of interest

All authors declare no conflicts of interest in this paper.

Appendix A

Proof of Lemma 3.1. For the purpose of simplification, let $l = (\alpha+1)^{2}q$. Applying Itô's formula to $|Q_{t}|^l$, we have

where $\bar{N}_s = N_s-\lambda s$ is a compensated Poisson process. Since

by the assumptions $(A1)$-$(A3)$, we get that

Using the well-known mean value theorem, we derive that there exists a $\theta \in (0, 1)$ such that

Denotes

Therefore, we obtain that

where $\bar{\alpha} = \min\{\alpha_{1}, \alpha_{2}, \alpha_{3}\}$.

By the Burkholder-Davis-Gundy's inequality, we then have

Note that for any $t\in[0, T]$,

Combining (5.4), (5.5) and (5.6), we can show that

Finally, by Generalization of the Bellman lemma ^[31], we obtain the desired result (3.2).