On the classical Gauss sums and their some new identities

1.   Introduction

Climate change is arguably one of the greatest challenges of our time. Although shipping is regarded as an environmentally efficient mode of transportation, it generates tremendous air emissions that have harmful effects on the global environment. Carbon dioxide (${\mathrm{C}\mathrm{O}}_{2}$) accounts for the vast majority of greenhouse gas emissions from the transportation sector ^[1]. Moreover, United Kingdom broker Simpson Spence Young estimated that ${\mathrm{C}\mathrm{O}}_{2}$ emissions from global shipping in 2021 increased 4.9% from 2020 and surpassed 2019 levels ^[2]. Unless serious actions are taken soon, ${\mathrm{C}\mathrm{O}}_{2}$ emissions from global shipping may increase by between 50 and 250% by 2050 ^[3], which undoubtedly will contribute to global warming.

Maritime decarbonization in particular is necessary to achieve the long-term goal of the Paris Agreement adopted at the Paris climate conference (COP21) in 2015 ^[4], that is, to limit the increase in the average global temperature to well below 2 ℃, preferably to 1.5 ℃, above pre-industrial levels. For this reason, many emission limits and regulations are promulgated to reduce ${\mathrm{C}\mathrm{O}}_{2}$ emissions and stop global warming. For example, the International Maritime Organization (IMO), which is the United Nations specialized agency for international shipping, has set strategies to reduce carbon emissions per unit of transport work by at least 40% by 2030 and reduce the total annual greenhouse gas emissions from international shipping by at least 50% by 2050, with 2008 as a baseline ^[5]. Despite the intensifying regulatory environment, international shipping released 833 million tons of ${\mathrm{C}\mathrm{O}}_{2}$ in 2021, an increase of 4.9% from 2020 ^[6]. Hence, it is urgent for liner companies to consider how to reduce carbon emissions when scheduling shipping activities to meet international requirements.

The carbon emissions per unit of transport work can be referred to as the carbon intensity, and one of the carbon intensity indicators is the EEOI, which was introduced by the IMO in 2009 and enforced in 2011 to measure the energy efficiency level of each operating ship ^[7]. The EEOI value of a ship over a year reflects the energy efficiency of the ship and may help liner companies to schedule ship fleets when considering the maritime decarbonization target. The EEOI value of a ship can be calculated by dividing annual carbon emissions of the ship (g) by actual ton-miles carried by the ship (the amount of transported cargo times total travel distance) in the year ^[8]. Therefore, the EEOI value of a ship is directly influenced by the type of used fuel, cargo load and total distance traveled. The lower the EEOI value is, the better the energy efficiency performance. From an operational perspective, several operation decisions, such as voyage planning and speed optimization, which further influences fleet deployment, can be jointly optimized to reduce the EEOI because these decisions directly affect fuel consumption. Moreover, displacement (tons), i.e., the total weight of the ship itself, cargo, ballast water and bunker, also influences fuel consumption ^[9]. Hence, seeking the optimal fleet deployment, voyage planning and speed to achieve liner operations management optimization is an efficient way to reduce EEOI, achieve energy savings and reduce emissions.

This study is motivated by the abovementioned real-world challenge in green shipping, and it may contribute to liner operations management by proposing a nonlinear mixed-integer programming (MIP) model and a tailored exact algorithm. Two assumptions are considered in this study: 1) Ships are homogenous on each route in terms of the cost structure, which is consistent with the assumptions considered in Zhen et al. ^[10]; 2) ships' dwell time at all ports of call on a ship route is given, which is in line with the assumptions considered in Zhen et al. ^[11]. This study provides liner companies with scientific methods to optimize fleet deployment, voyage planning and speed to reduce both the total weekly cost and the average EEOI value of all deployed ships on all routes with the consideration of the influences of sailing speed, displacement and voyage option on fuel consumption. Eleven sets of numerical experiments with different route compositions were first conducted to evaluate the performance of the proposed algorithm. Moreover, sensitivity analyses with crucial parameters, including the weighting factor, unit price of fuel, Suez Canal toll fee per ship, weekly fixed operating cost and cargo load in each leg, are carried out to show the influence of these aspects on the results to look for managerial insights.

The remainder of this study is organized as follows. Related works are reviewed in Section 2. Section 3 elaborates on the problem background and proposes a nonlinear MIP model for the integrated problem. A tailored exact algorithm is designed in Section 4. Section 5 reports the computational experiments, including basic experiments to evaluate the efficiency of the proposed algorithm and sensitivity analyses to seek managerial insights. Conclusions are outlined in the last section.

2.   Literature review and discussion

The core part of this study is related to the widely-studied fleet deployment problem. Readers interested in overviews of the above problem can refer to Meng et al. ^[12], Wang and Meng ^[13] and Christiansen et al. ^[14]. This study focuses on an integrated optimization problem of fleet deployment, voyage planning and speed optimization to minimize both the total weekly cost and the average EEOI value of all deployed ships on all routes. Thus, this section reviews the streams of related literature from the following two perspectives: the fleet deployment problem and studies related to EEOI.

The first research stream is concerned with the fleet deployment problem. As an important concern for liner companies, the fleet deployment problem determines the number of ships to be deployed on various ship routes to maximize the total profit or to minimize the total cost. Lai et al. ^[15] formulated a two-stage model for a fleet deployment problem with shipping revenue management under demand uncertainty whose randomness is represented by probability-free uncertain sets. They also developed a column-and-constraint generation based exact algorithm to solve the model. In recent years, sustainable development is the main development direction of the shipping industry ^[16]. One of the most important green shipping factors in the fleet deployment problem is reducing emissions from ships, such as ${\mathrm{C}\mathrm{O}}_{2}$, sulfur oxides (${\mathrm{S}\mathrm{O}}_{\mathrm{X}}$) and nitrogen oxides (${\mathrm{N}\mathrm{O}}_{\mathrm{X}}$). Zhu et al. ^[17] investigated the influence of a maritime emissions trading system on fleet deployment and mitigation of ${\mathrm{C}\mathrm{O}}_{2}$ emissions. They proposed a stochastic integer programming model to determine fleet deployment and ${\mathrm{C}\mathrm{O}}_{2}$ emissions with different ${\mathrm{C}\mathrm{O}}_{2}$ prices. Considering sulfur emission control areas, Wang et al. ^[18] studied an integrated problem of schedule design, fleet deployment, sailing optimization and path selection, and they proposed a nesting algorithmic framework to solve the problem. Pasha et al. ^[19] designed a decomposition-based heuristic algorithm to solve an integrated problem of service frequency determination, fleet deployment, speed optimization and ship schedule design considering emissions released by ships with the aim of maximizing the total turnaround profit. Zhao et al. ^[20] formulated a two-stage stochastic linear model for a fleet renewal problem considering three sulfur reduction technologies and uncertain markets. With the consideration of sulfur emission limits, Chen et al. ^[21] built an ellipsoidal uncertainty set to describe demand uncertainties and developed a robust optimization model for an alliance fleet deployment problem with slot exchange. Moreover, Zhao et al. ^[22] investigated how to reduce ${\mathrm{S}\mathrm{O}}_{\mathrm{X}}$ and ${\mathrm{N}\mathrm{O}}_{\mathrm{X}}$ emissions in shipping economically by determining the optimal technology choice.

The second topic considered in the related works is EEOI. Operational data, such as speed and deadweight, are usually used to analyze EEOI. Existing papers on EEOI mainly focus on two aspects, namely, estimation of EEOI values and scheduling based on EEOI values. In terms of the estimation of EEOI values, Acomi and Acomi ^[23] used commercial software to estimate the value of EEOI before a voyage, and they compared estimated values and true values according to speeds, days on anchor and waiting days. In terms of scheduling based on EEOI values, Hou et al. ^[24] formulated a sailing speed optimization model with consideration of uncertain ice loads to minimize the EEOI value of each ship in ice areas. Sun et al. ^[25] developed a dynamic optimization model for sailing speeds of ships to improve fuel efficiency as well as reduce EEOI. They used a neural network to predict fuel consumption rate and ship speed, and they applied a genetic algorithm to optimize engine revolution and seek the minimum EEOI. Considering the uncertainty in ice loads as well as water velocity, Ichsan et al. ^[26] studied a decided route on the sea tollway of Indonesia and optimized the rate of EEOI of ships deployed on the route. With the aim of minimizing EEOI values of seven types of specialized ships, Prill et al. ^[27] assumed that the EEOI of each ship is related to the deadweight of the ship, the type and amount of consumed fuel and the voyage distance traveled by the ship, and they proposed a new method of determining the EEOI of each ship by optimizing sailing speeds of ships and the realization time of each exploitation task. Hou et al. ^[28] developed a ship speed optimization model which brought a 15% reduction in EEOI in the computational experiment.

In summary, the prevailing trend in the fleet deployment problem is studying how to reduce emissions from the shipping industry because of the increasing public concern about environmental protection. However, few works focus on an integrated optimization problem of fleet deployment, voyage planning and speed optimization to minimize both the total weekly cost and the average EEOI value of all deployed ships on all routes. Therefore, this paper studies an integrated optimization problem of fleet deployment, voyage planning and speed optimization with consideration of the influences of sailing speed, displacement and voyage option on fuel consumption. Moreover, some other frequently ignored operating limits, such as Suez Canal toll fee, are considered in this paper. This study proposes a nonlinear MIP model to minimize two objectives, i.e., the total weekly cost and the average EEOI value of all deployed ships on all routes, by determining the optimal fleet deployment, voyage planning and speed.

3.   Problem description and model formulation

This study is oriented toward an integrated optimization problem of fleet deployment, voyage planning and speed optimization with consideration of the influences of sailing speed, displacement and voyage option on fuel consumption. This section first elaborates on the detailed background of the problem in Section 3.1, explains the objective function of the problem in Section 3.2 and presents the mathematical model in Section 3.3.

3.1.   Problem background

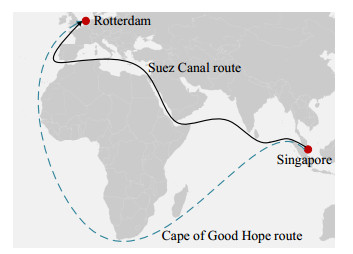
We consider a liner company operating on a network containing a set $R$ of container ship routes (services). The liner company has already determined the optimal service plan including fleet deployment, sailing speed and voyage selection. However, in the context of the Carbon Intensity Indicator (CII) introduced by the IMO, especially considering EEOI, the liner company may need to reoptimize their service plan including fleet deployment, sailing speed and voyage options such as the Cape of Good Hope route or the Suez Canal route ^[29] in Figure 1.

Some ship routes, e.g., $r$ ($r\in R$), operated by the liner company may contain the voyage between Asian ports and European ports. We assume that the liner company originally selects the Suez Canal route for these voyages because sailing through the Suez Canal saves a lot of time. In this case, let ${I}_{r}$ and ${I}_{r}^{'}$ represent the set of legs that do not cross Asian and European ports on ship route $r$ and the set of legs across Asian and European ports on ship route $r$, respectively. For example, Table 1 summarizes the sets of ${I}_{r}$ and ${I}_{r}^{'}$ of route $r$ whose port rotation is Qingdao-Shanghai-Ningbo-Yantian-Rotterdam-Hamburg-Antwerp-Singapore-Qingdao. We then let ${\gamma }_{ri}$ denote a binary variable which equals 1 if and only if the voyage option of leg $i$, $i\in {I}_{r}^{'}$, on ship route $r$ selects the Suez Canal voyage and equals 0 if selecting the Cape of Good Hope voyage. In addition, sailing speeds of deployed ships during each leg should be between $\underset{\_}{v}$ and $\overline{v}$, where $\underset{\_}{v}$ and $\overline{v}$ represent the minimum and maximum speeds of ships on ship routes, respectively. Let $V$ represent a set of all possible sailing speeds indexed by $v$, and $V = \{\underset{\_}{v}, \underset{\_}{v}+0.1, \dots, \overline{v}-0.1, \overline{v}\}$.

In terms of fleet deployment and speed optimization, EEOI values of all deployed ships on all ship routes should be regarded as an important consideration because when stricter ${\mathrm{C}\mathrm{O}}_{2}$ emission reduction regulations issued by international organizations take effect, liner companies have to find ways to reduce their deployed ships' EEOI values. The incorporation of EEOI may result in higher costs for liner companies in practice; however, companies certainly aim to minimize their total cost while complying with EEOI regulations. Therefore, this study considers the influences of sailing speed, displacement and voyage option on fuel consumption. Bi-objective programming has been widely applied before when minimizing carbon emissions and maximizing profit of liner companies, such as in Zhao et al. ^[30]. From the perspective of the liner company, this study develops a bi-objective model to balance the total weekly cost, including the weekly fixed operating cost, weekly Suez Canal toll fee and weekly fuel cost, and the average EEOI value of all deployed ships on all ship routes by determining fleet deployment, voyage planning and sailing speed of all deployed ships. The above strategic-level problem involves many intertwined decisions, so a scientific decision-making methodology is needed for this problem.

3.2.   Objective function

This problem is formulated as a bi-objective programming model. These two objective functions are the total weekly cost and the average EEOI value of all deployed ships on all routes. In the following paragraphs, we first explain separately how to formulate these two objective functions and then introduce how to deal with the bi-objective programming.

The first objective function focuses on the total weekly cost, which contains three parts: the weekly fixed operating cost, weekly Suez Canal toll fee and weekly fuel cost. Specifically, the first part is the weekly fixed operating cost of deployed ships. Because a fleet of homogeneous ships is deployed on each route to maintain a weekly service frequency, the total fixed operating cost for all deployed ships on all routes during one week can be calculated as ${\sum }_{r\in R}o{\beta }_{r}$, where $o$ and ${\beta }_{r}$ denote the weekly operating cost for deploying one ship on ship routes and the number of ships deployed on route $r$, respectively. Next is the weekly Suez Canal toll fee faced by the liner company. Let ${q}_{r}$ denote the Suez Canal toll fee of each ship deployed on route $r$ (USD/ship). Hence, we can calculate the weekly Suez Canal toll fee by ${\sum }_{r\in R}{\sum }_{i\in {I}_{r}^{'}}{q}_{r}{\gamma }_{ri}$.

The last part of the total weekly cost is the fuel cost, which depends on fuel consumption. Each ship contains a main engine, which provides propulsion power for the ship, and an auxiliary engine, which provides power for uses other than propulsion. Specifically, in terms of fuel consumption of the main engine, most of the existing fuel consumption models in the literature ^[11,31,32] agreed that a ship's unit fuel consumption significantly depends on its sailing speed and calculated the unit fuel consumption function by $\dot{c}{v}^{\ddot{c}}$ to conduct liner shipping network analyses, where $v$ is sailing speed (knots), and $\dot{c}$ and $\ddot{c}$ are positive coefficients. However, apart from sailing speed, several other factors also influence fuel consumption. The first one is displacement (tons), i.e., the total weight of the ship itself, cargo, ballast water and bunker. Meng et al. ^[9] investigated the relationship between the fuel consumption rate of a container ship and several factors, including sailing speed, displacement and weather/sea conditions. However, it is extremely difficult to record the precise weather/sea conditions because the effects of waves, wind and currents are interwoven in practice. Hence, the influence of weather/sea conditions on fuel consumption is not considered in this study. Also, this study formulates the unit fuel consumption function as ${c}_{1}{v}^{{c}_{2}}{d}^{{c}_{3}}$ (tons/hour), which is given by Meng et al. (2016) ^[9], where ${c}_{1}$, ${c}_{2}$ and ${c}_{3}$ are positive coefficients, and $v$ and $d$ represent the actual sailing speed (knots) and displacement (tons) of the ship during one leg, respectively. Finally, in terms of fuel consumption of the auxiliary engine, we assume the auxiliary engine of a ship deployed on ship route $r$ consumes an amount ${e}_{r}$ of fuel per day. In summary, the total amount of fuel consumed by a ship's main engine on ship route $r$, denoted by ${\varepsilon }_{r}$, can be calculated by ${\varepsilon }_{r} = {\sum }_{i\in {I}_{r}}{\sum }_{v\in V}{c}_{1}{v}^{{c}_{2}}{\alpha }_{riv}{{d}_{ri}}^{{c}_{3}}\frac{{l}_{ri}}{v}+{\sum }_{i\in {I}_{r}^{'}}{\sum }_{v\in V}{c}_{1}{v}^{{c}_{2}}{\alpha }_{riv}{{d}_{ri}}^{{c}_{3}}\frac{{l}_{ri}{\gamma }_{ri}+{l}_{ri}^{'}(1-{\gamma }_{ri})}{v}$, where ${\alpha }_{riv}$, ${d}_{ri}$, ${l}_{ri}$ and ${l}_{ri}^{'}$ represent, respectively, a binary variable which equals 1 if and only if the speed of the ship sailing during leg $i$ on route $r$ is $v$ and 0 otherwise, actual displacement (tons) of the ship during leg $i$ on ship route $r$, length (n mile) of the $i$th leg if $i\in {I}_{r}$ or length of the $i$th leg taking the Suez Canal route if $i\in {I}_{r}^{'}$ on ship route $r$ and length (n mile) of the $i$th ($i\in {I}_{r}^{'}$) leg taking the Cape of Good Hope route on ship route $r$. Weekly fuel consumption of auxiliary engines of all deployed ships on route $r$ is $7{e}_{r}{\beta }_{r}$ because the total time for a ship completing travel along route $r$ including dwell time and sailing time is $7{\beta }_{r}$ days to maintain a weekly container shipping service frequency. In summary, the total weekly fuel cost of all deployed ships on all routes is ${\sum }_{r\in R}({a}_{1}{\varepsilon }_{r}+7{a}_{2}{e}_{r}{\beta }_{r})$, where ${a}_{1}$ and ${a}_{2}$ are the unit prices of fuels consumed by the main and auxiliary engines, respectively (USD/ton). Therefore, the total weekly cost can be calculated by ${\sum }_{r\in R}[o{\beta }_{r}+{\sum }_{i\in {I}_{r}^{'}}{q}_{r}{\gamma }_{ri}+{a}_{1}{\varepsilon }_{r}+7{a}_{2}{e}_{r}{\beta }_{r}]$.

The second objective is the average EEOI value of all deployed ships on all routes. According to the IMO ^[8], the EEOI of a ship is described by the ratio of the total amount of ${\mathrm{C}\mathrm{O}}_{2}$ emissions released by the ship over a year to the product of the ship's cargo transported and total distance over a year, and it is related to fuel consumption, sailing speed, load tonnage and mileage of voyage. The calculation formula of EEOI is Eq (1), which is given by the IMO ^[8].

Here, notice that the EEOI of a ship is also equal to the ratio of the total amount of ${\mathrm{C}\mathrm{O}}_{2}$ emissions released by the ship over a week to the product of the ship's cargo transported and total distance over a week because of the weekly service frequency. In addition, we assume that the ships owned by the liner company generate $g$ tons of ${\mathrm{C}\mathrm{O}}_{2}$ when burning one ton of fuel, and let ${m}_{ri}$ denote the volume of cargo load in the ship during leg $i$, $i\in {I}_{r}\cup {I}_{r}^{'}$. Also, since we calculate the amount of ${\mathrm{C}\mathrm{O}}_{2}$ emissions in tons, but the amount of ${\mathrm{C}\mathrm{O}}_{2}$ emissions in the EEOI calculation formula is in grams, we need to multiply the amount of ${\mathrm{C}\mathrm{O}}_{2}$ emissions by ${10}^{6}$ when calculating the EEOI value of each operating ship. Therefore, the average EEOI value of all ships deployed on all routes is ${\sum }_{r\in R}\frac{{10}^{6}({\varepsilon }_{r}+7{e}_{r}{\beta }_{r})g}{{\sum }_{i\in {I}_{r}}{m}_{ri}{l}_{ri}+{\sum }_{i\in {I}_{r}^{'}}{m}_{ri}[{l}_{ri}{\gamma }_{ri}+{l}_{ri}^{'}\left(1-{\gamma }_{ri}\right)]}/{\sum }_{r\in R}{\beta }_{r}$.

Since this study aims to minimize both of the above objectives, i.e., the total weekly cost and the average EEOI value of all deployed ships on all routes, this study applies a typical way to solve the problem, which is the weighted sum method. We use $\lambda$ as a weighting factor for the bi-objective programming which reveals the relative importance between the above two objective functions. Hence, the objective function of this problem is formulated as $\lambda \left[{\sum }_{r\in R}(o{\beta }_{r}+{\sum }_{i\in {I}_{r}^{'}}{q}_{r}{\gamma }_{ri}+{a}_{1}{\varepsilon }_{r}+7{a}_{2}{e}_{r}{\beta }_{r})\right]$$+(1-\lambda)\left({\sum }_{r\in R}\frac{{10}^{6}\left({\varepsilon }_{r}+7{e}_{r}{\beta }_{r}\right)g}{{\sum }_{i\in {I}_{r}}{m}_{ri}{l}_{ri}+{\sum }_{i\in {I}_{r}^{'}}{m}_{ri}\left[{l}_{ri}{\gamma }_{ri}+{l}_{ri}^{'}\left(1-{\gamma }_{ri}\right)\right]}/{\sum }_{r\in R}{\beta }_{r}\right)$.

3.3.   Model formulation

Based on the above analysis of the objective function, this study formulates a nonlinear MIP model in this section. Before formulating the mathematical model for this problem, we list the notations used in this paper as follows.

Indices and sets:

$R$: set of all ship routes, $r\in R$.

${I}_{r}$: set of all legs that do not cross Asian and European ports on ship route $r$, $i\in {I}_{r}$.

${I}_{r}^{'}$: set of all legs across Asian and European ports on ship route $r$, $i\in {I}_{r}^{'}$.

$V$: set of all possible sailing speeds, $v\in V$, $V = \{\underset{\_}{v}, \underset{\_}{v}+0.1, \dots, \overline{v}-0.1, \overline{v}\}$, where $\underset{\_}{v}$ and $\overline{v}$ represent the minimum and maximum speeds of ships on ship routes, respectively.

${Z}_{+}$: set of all non-negative integers.

Parameters:

${a}_{1}, {a}_{2}$: unit prices of fuels consumed by the main and auxiliary engines, respectively (USD/ton).

${c}_{1}, {c}_{2}, {c}_{3}$: coefficients to calculate the unit fuel consumption for traveling per hour, which mainly depends on sailing speed and displacement (tons/hour).

${d}_{ri}$: actual displacement of the ship during leg $i$ on ship route $r$ (tons).

${e}_{r}$: amount of fuel consumed by the auxiliary engine of a ship deployed on ship route $r$ per day (tons/day).

$g$ : amount of ${\mathrm{C}\mathrm{O}}_{2}$ released by a ship when burning one ton of fuel (tons).

${l}_{ri}$: length of the $i$th leg if $i\in {I}_{r}$ or length of the $i$th leg taking the Suez Canal route if $i\in {I}_{r}^{'}$ on ship route $r$ (n mile).

${l}_{ri}^{'}$: length of the $i$th ($i\in {I}_{r}^{'}$) leg taking the Cape of Good Hope route on ship route $r$ (n mile).

${m}_{ri}$: cargo load in leg $i$, $i\in {I}_{r}\cup {I}_{r}^{'}$, on ship route $r$ (tons).

$o$: weekly operating cost of one ship deployed on ship routes (USD).

${q}_{r}$: Suez Canal toll fee for a ship deployed on route $r$ (USD/ship).

${s}_{r}$: maximum number of ships that can be deployed on ship route $r$.

${t}_{r}$: total duration a ship dwells at all ports of call on ship route $r$ (hours).

$\lambda$: weighting factor for the bi-objective programming.

Variables:

${\alpha }_{riv}$: binary, equals 1 if and only if the speed of the ship sailing during leg $i$ on ship route $r$ is $v$; 0 otherwise.

${\gamma }_{ri}$: binary, equals 1 if and only if the voyage option of leg $i$, $i\in {I}_{r}^{'}$, on ship route $r$ selects Suez Canal route; 0 if Cape of Good Hope route.

${\beta }_{r}$: integer, number of ships deployed on ship route $r$.

${\varepsilon }_{r}$: continuous, weekly fuel consumption of the main engine of all deployed ships on ship route $r$ (tons).

Mathematical model

Based on the above definitions of parameters and variables, a nonlinear MIP model is formulated as follows.

$[{\bf{M1}}] \ \ \mathrm{Min}\lambda \left[{\sum }_{r\in R}(o{\beta }_{r}+{\sum }_{i\in {I}_{r}^{'}}{q}_{r}{\gamma }_{ri}+{a}_{1}{\varepsilon }_{r}+7{a}_{2}{e}_{r}{\beta }_{r})\right]$

subject to

Objective (2) minimizes the weighted sum of two objectives considered in this study. Constraint (3) guarantees that at least one ship and at most ${\mathrm{s}}_{\mathrm{r}}$ ships should be deployed on each route. Constraint (4) ensures that the total number of hours for a ship completing its travel on a route is the number of ships deployed on the route times 168, because all services follow the weekly arrival pattern, and one week has 168 hours. Constraint (5) calculates the weekly fuel consumption of the main engine of all deployed ships on ship route $\mathrm{r}$. Constraint (6) ensures that sailing speeds of deployed ships during each leg on all ship routes satisfy the feasible speed range of ships. Constraints (7)–(10) state the ranges of the defined decision variables.

4.   Algorithm design

It is challenging to solve the nonlinear model [M1], which contains multiple nonlinear parts, including objective function (2) and constraints (4) and (5). By reviewing several algorithms and their features in some existing fleet deployment studies, we find that specially tailored solution methods are usually designed for their models because these fleet deployment studies contain specific characteristics. For example, Zhen et al. ^[10] proposed a tailored dynamic linearization algorithm to solve a mixed-integer second-order cone programming model. In addition, considering specific characteristics of our problem, we find that nonlinear parts in model [M1] can be replaced by enumerating the possible values, and the model after the above transformation can be solved directly and effectively by Gurobi. Since the number of possible values of the nonlinear parts in model [M1] is small, this study designs an efficient exact algorithm based on the enumeration method to solve the model [M1]. Due to the efficiency and accuracy of the proposed algorithm, the proposed algorithm can quickly find the optimal solution of the model in a very short time.

Before introducing our algorithm, one transformation of constraint (4) is first introduced. Since sailing speed is discretized, the feasibility of constraint (4), which contains the equality symbol, might be affected. Hence, constraint (4) is replaced with constraint (11). Here, notice that the equality symbol in constraint (4) is replaced with the less than or equal to symbol in constraint (11).

As a result, the final version of model [M1] becomes the following:

[M2] objective (2) subject to constraints (3), (5)–(11).

Finally, we design the following exact algorithm, whose framework is introduced in Algorithm 1 to solve the model [M2]. The main difficulty in solving the model [M2] is the nonlinear part in objective (2). Two key techniques are applied to this nonlinear part. Specifically, the first one focuses on ${\sum }_{r\in R}{\beta }_{r}$ in the denominator. According to constraint (11), the number of ships deployed on route $r$, denoted by ${\beta }_{r}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, is at least ${\beta }_{r}^{\mathrm{m}\mathrm{i}\mathrm{n}} = ⌈({\sum }_{i\in {I}_{r}}\frac{{l}_{ri}}{\overline{v}}+{\sum }_{i\in {I}_{r}^{'}}\frac{\mathrm{m}\mathrm{i}\mathrm{n}({l}_{ri}, {l}_{ri}^{'})}{\overline{v}}+{t}_{r})/168⌉$ (recall that $\overline{v}$ represents the maximum speed of ships on ship routes). Because constraint (3) guarantees that at most ${s}_{r}$ ships could be deployed on route $r$, the value of ${\sum }_{r\in R}{\beta }_{r}$ ranges from ${\sum }_{r\in R}{\beta }_{r}^{\mathrm{m}\mathrm{i}\mathrm{n}}$ to ${\sum }_{r\in R}{s}_{r}$, which means we can directly enumerate the number of ships deployed on all ship routes. The other one is ${\sum }_{i\in {I}_{r}^{'}}{m}_{ri}\left[{l}_{ri}{\gamma }_{ri}+{l}_{ri}^{'}\left(1-{\gamma }_{ri}\right)\right]$. In most cases, not all routes need to be reoptimized in terms of voyage option because these routes do not contain voyages across Asia and Europe. Even if all routes need to be reoptimized in terms of voyage option, the total number of voyage options on a single route is $\left|{I}_{r}^{'}\right|$, which means there are ${2}^{\left|{I}_{r}^{'}\right|}$ permutations of the values of ${\gamma }_{ri}$ ($\forall r\in R, i\in {I}_{r}^{'})$ for route $r$. Moreover, the value of $\left|{I}_{r}^{'}\right|$ is either 0 or 2 because in real life, a liner route is either for a certain continent, or it only crosses Asian and European ports twice. Hence, the number of permutations is significantly small, and we can directly enumerate all permutations.

5.   Computational experiments

In order to evaluate the efficiency of the proposed algorithm, we performed a large number of computational experiments on a PC (4 CPU cores, 1.6 GHz, Memory 8 GB). The mathematical models and algorithms proposed in this study are implemented in Gurobi 9.0.1 (Anaconda, Python). This section first summarizes the setting of our parameters in Section 5.1, validates the proposed algorithm in Section 5.2 and describes sensitivity analyses to seek managerial insights in Section 5.3.

5.1.   Experimental setting

Sailing distance data, including ${l}_{ri}$ and ${l}_{ri}^{'}$, used in this study were obtained from the standard instances of LINER-LIB ^[33]. The value of the weekly fixed operating cost, i.e., $o$, is set to 180,000 USD, which is in line with the setting used in previous studies ^[11,34]. In real life, main and auxiliary engines of a ship may use the same type of fuel, such as liquefied natural gas (LNG). Therefore, this study assumes that main and auxiliary engines use the same type of fuel when calculating fuel costs of the main and auxiliary engines for the sake of simplicity in the computational experiments. Therefore, unit prices of fuels (i.e., ${a}_{1}$ and ${a}_{2}$) are set to 544.5 USD/ton because the average price of very low sulfur fuel oil (VLSFO) in global 20 ports in 2021 is 544.5 USD/ton ^[35]. For the sake of simplicity, a ship can only adjust its speeds by at least one knot in this study. The minimum and maximum values of sailing speed (i.e., $\underset{\_}{v}$ and $\overline{v}$) are set to 8 and 22 knots, respectively, which are also consistent with the settings used in related works ^[36,37]. The values of ${c}_{1}$, ${c}_{2}$ and ${c}_{3}$ are set to 0.00022, 2.5506 and 0.2072, respectively, which are consistent with the settings in related studies ^[9,36]. The value of the total duration, i.e., ${t}_{r}$, that a ship dwells at all ports of call on ship route $r$ is randomly selected from $[24\times \left(\left|{I}_{r}\right|+\left|{I}_{r}^{'}\right|\right), \ 48\times \left(\left|{I}_{r}\right|+\left|{I}_{r}^{'}\right|\right)]$. The value of ${s}_{r}$ (i.e., the maximum number of ships that can be deployed on ship route $r$) depends on the length of one cycle time, and it is set to 4 for regional ship routes or 10 for intercontinental shipping routes. The amount of ${\mathrm{C}\mathrm{O}}_{2}$ released by a ship when burning one ton of VLSFO, i.e., $g$, is set to 3.15 tons, which is in line with the realistic data from Lloyd's List ^[38]. Some parameters are generated by sampling from some normal distributions. Specifically, values of Suez Canal toll fee (i.e., ${q}_{r}$) of a ship on all routes are uniformly distributed over (400,000,700,000) (USD/ship), which is in line with actual Suez Canal toll fees ^[39]. The average value of daily fuel consumption for the auxiliary engines (${e}_{r}$) on all routes is set to 3 tons per day (normal distribution with standard deviation 0.5). The average value of cargo load (${m}_{ri}$) on all legs is set to 180,000 tons (normal distribution with standard deviation 3000), and the value of actual displacement (${d}_{ri}$) on all legs is set to ${m}_{ri}+\mathrm{20,000}$ tons.

5.2.   Performance of the algorithm

We used the proposed exact algorithm to solve the model [M2] and conducted 11 sets of numerical experiments with different route compositions, which are summarized in Table 2. We first fixed $\lambda = 0.5$ and recorded computational results, including objective function value (${\mathrm{O}\mathrm{B}\mathrm{J}}_{\mathrm{T}}$), CPU running time (Time) and selected voyage option (Voyage option) in Table 3. Since the difference between the two objective function values in our model is very large, we normalize these two objective functions by dividing them by their respective maximum values. To obtain the maximum values, we set $\lambda$ (i.e., the weighting factor for the bi-objective programming) to 0 and solve all computational experiments of the model [M2] to get the maximum objective function value ${\mathrm{O}\mathrm{B}\mathrm{J}}_{1} = \ 15148529.7881$. Similarly, we set $\lambda$ to 1 and solve all computational experiments of the model [M2] to get the maximum objective function value ${\mathrm{O}\mathrm{B}\mathrm{J}}_{2} = \ 0.3384$. From Table 3, we can see that the computing time increases with more routes, which is intuitive because more routes will bring more decision variables and constraints. Since the computing time of 6 routes is quick enough, case 10 is used for the following numerical experiments. The Suez Canal route was chosen in all experiments. This may be due to the fact that the Suez Canal route is more popular on trips because it saves more sailing time. Our algorithm has good performance because it can solve the numerical experiment with 7 ship routes and 32 legs in four minutes, which means our algorithm can be applied well to real problems and quickly provides optimal solutions for liner companies.

5.3.   Sensitivity analyses

The impact of $\lambda$ on the bi-objective programming is first described in this section. The value of $\lambda$ ranged from 0 to 1. In Table 4, we show the normalized objective function value of model [M2] (${\mathrm{O}\mathrm{B}\mathrm{J}}_{\mathrm{T}}$), the total weekly cost value (${\mathrm{O}\mathrm{B}\mathrm{J}}_{1}$), the average EEOI value of all deployed ships on all routes (${\mathrm{O}\mathrm{B}\mathrm{J}}_{2}$), the total number of deployed ships (${\sum }_{r\in R}{\beta }_{r}$), the selected voyage option (Voyage option) and the computing time (Time). It is obvious that ${\mathrm{O}\mathrm{B}\mathrm{J}}_{1}$ decreases with increasing $\lambda$, which is reasonable because a larger $\lambda$ indicates a larger weight on ${\mathrm{O}\mathrm{B}\mathrm{J}}_{1}$. However, ${\mathrm{O}\mathrm{B}\mathrm{J}}_{2}$ stays the same at the beginning, then goes down and finally goes up. In addition, the total number of deployed ships decreases as the value of $\lambda$ increases. Finally, the change of the value of $\lambda$ does not affect the voyage option, and the change of the value of $\lambda$ has no obvious effect on the solution time. Therefore, with increasing $\lambda$ (i.e., larger weight on the minimization of the total weekly cost), fewer ships are needed, which means that each deployed ship sails at a higher speed and releases more ${\mathrm{C}\mathrm{O}}_{2}$ (i.e., higher EEOI value). However, since the average EEOI value of all deployed ships on all routes is relatively small, the increase in the $\lambda$ value in the early stage has no proportional effect on the second objective function value, i.e., ${\mathrm{O}\mathrm{B}\mathrm{J}}_{2}$.

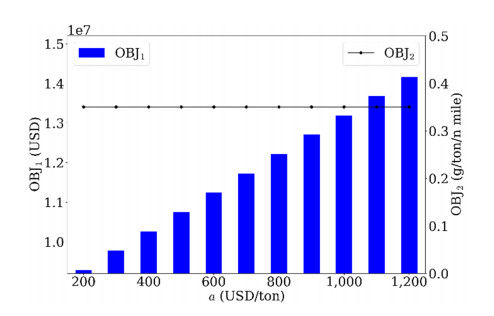
We next studied the impact of unit price of fuel on the operation decisions. According to S & B ^[35], the lowest and highest prices of VLSFO in global 20 ports from January 01, 2020, to July 14, 2022, were 211.25 USD/ton, and 1120.50 USD/ton, respectively. Hence, we set the value of $a$ from 200 to 1200 USD/ton to investigate its influence. Relevant results, including ${\mathrm{O}\mathrm{B}\mathrm{J}}_{\mathrm{T}}$, ${\mathrm{O}\mathrm{B}\mathrm{J}}_{1}$, ${\mathrm{O}\mathrm{B}\mathrm{J}}_{2}$, ${\sum }_{r\in R}{\beta }_{r}$ and Voyage option, are presented in Table 5. In order to make the result more intuitive, we also give Figure 2, whose abscissa is the fuel price, and the primary and secondary ordinate axes are ${\mathrm{O}\mathrm{B}\mathrm{J}}_{1}$ and ${\mathrm{O}\mathrm{B}\mathrm{J}}_{2}$, respectively. When the unit price of fuel increases, both ${\mathrm{O}\mathrm{B}\mathrm{J}}_{\mathrm{T}}$ and ${\mathrm{O}\mathrm{B}\mathrm{J}}_{1}$ increase because the weekly fuel cost increases, but ${\mathrm{O}\mathrm{B}\mathrm{J}}_{2}$ is not influenced by fuel price. In addition, changes in the fuel price do not affect fleet deployment and voyage option decisions. The above observations are reasonable because changes in the unit price of fuel do not cause changes in fleet deployment strategies and sailing speeds, resulting in no changes in ${\mathrm{C}\mathrm{O}}_{2}$ emissions and no changes in the value of the second objective function. However, the continuous increase in the unit price of fuel leads to an increase in the weekly fuel consumption cost, which eventually leads to an increase in the value of the first objective function.

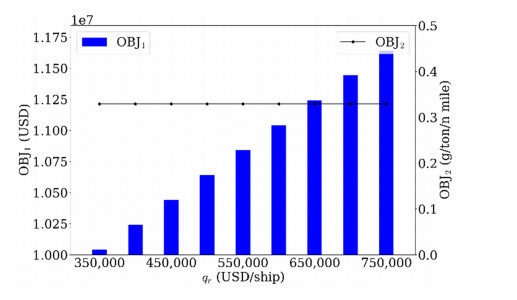
Next, we discuss the impact of Suez Canal toll fee per ship on the operation decisions. According to HKTDC ^[39], Suez Canal toll fees for a ship range from 400,000 to 700,000 USD. Hence, we set the Suez Canal toll fee for a ship from 350,000 to 750,000 USD/ship to investigate its influence. Relevant results, including ${\mathrm{O}\mathrm{B}\mathrm{J}}_{\mathrm{T}}$, ${\mathrm{O}\mathrm{B}\mathrm{J}}_{1}$, ${\mathrm{O}\mathrm{B}\mathrm{J}}_{2}$, ${\sum }_{r\in R}{\beta }_{r}$ and Voyage option, are given in Table 6. In order to make the result more intuitive, we also give Figure 3, whose abscissa is the Suez Canal toll fee per ship, and the primary and secondary ordinate axes are ${\mathrm{O}\mathrm{B}\mathrm{J}}_{1}$ and ${\mathrm{O}\mathrm{B}\mathrm{J}}_{2}$, respectively. When the Suez Canal toll fee per ship increases, both ${\mathrm{O}\mathrm{B}\mathrm{J}}_{\mathrm{T}}$ and ${\mathrm{O}\mathrm{B}\mathrm{J}}_{1}$ increase, but ${\mathrm{O}\mathrm{B}\mathrm{J}}_{2}$ does not change with increasing ${q}_{r}$. In addition, changes in the Suez Canal toll fee per ship do not affect fleet deployment and voyage option decisions, which further makes the EEOI of each ship unchanged, as the ship's ${\mathrm{C}\mathrm{O}}_{2}$ emissions and mileage do not change. The above observations are reasonable because the weekly Suez Canal toll fee is small compared to the weekly fuel consumption and operating costs of deployed ships. Therefore, the increase in the Suez Canal toll fee per ship does not lead to changes in fleet deployment, sailing speeds and voyage planning.

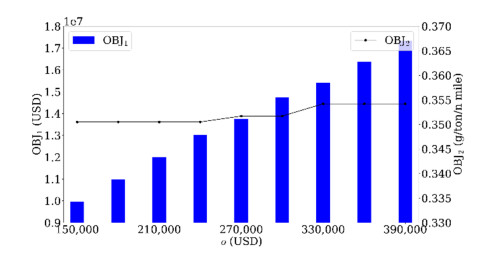
In the basic experiment, the value of the weekly fixed operating cost ($o$) was set to 180,000 USD. However, weekly operating costs may double several times due to outbreaks and other reasons. To analyze the impact of weekly fixed operating cost on the operation decisions, we set the value of $o$ from 150,000 USD to 390,000 USD. Relevant results, including ${\mathrm{O}\mathrm{B}\mathrm{J}}_{\mathrm{T}}$, ${\mathrm{O}\mathrm{B}\mathrm{J}}_{1}$, ${\mathrm{O}\mathrm{B}\mathrm{J}}_{2}$ ${\sum }_{r\in R}{\beta }_{r}$ and Voyage option are given in Table 7. In order to make the result more intuitive, we also give Figure 4, whose abscissa is the weekly operating cost, and the primary and secondary ordinate axes are ${\mathrm{O}\mathrm{B}\mathrm{J}}_{1}$ and ${\mathrm{O}\mathrm{B}\mathrm{J}}_{2}$, respectively. When the weekly operating cost increases, all of ${\mathrm{O}\mathrm{B}\mathrm{J}}_{\mathrm{T}}$, ${\mathrm{O}\mathrm{B}\mathrm{J}}_{1}$ and ${\mathrm{O}\mathrm{B}\mathrm{J}}_{2}$ increase, but ${\mathrm{O}\mathrm{B}\mathrm{J}}_{2}$ remains unchanged in the three intervals [150,000, 240,000], [270,000, 300,000] and [330,000, 390,000]. In addition, changes in the weekly fixed operating cost directly influence fleet deployment but do not affect voyage option decision. The above observations are reasonable because the weekly fixed operating cost accounts for a large proportion of the total weekly cost. The continuous increase in the weekly fixed operating cost causes liner companies to reduce the number of deployed ships, which causes ships to sail at higher speeds to maintain the weekly arrival pattern. Moreover, high speeds of deployed ships cause more ${\mathrm{C}\mathrm{O}}_{2}$ emissions.

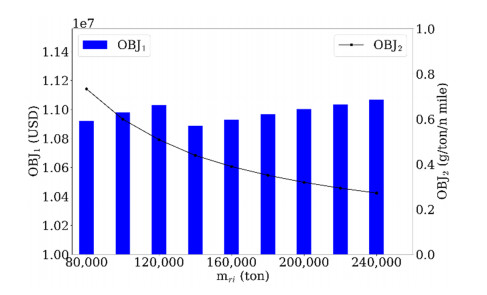
Finally, we investigated the impact of cargo load on the operation decisions. In the basic experiment, the average value of cargo load (${m}_{ri}$) was set to 180,000 tons (normal distribution with standard deviation 3000). Hence, we set the average value of cargo load in each leg from 80,000 to 240,000 (normal distribution with standard deviation 3000) to investigate its influence. Relevant results, including ${\mathrm{O}\mathrm{B}\mathrm{J}}_{\mathrm{T}}$, ${\mathrm{O}\mathrm{B}\mathrm{J}}_{1}$, ${\mathrm{O}\mathrm{B}\mathrm{J}}_{2}$, ${\sum }_{r\in R}{\beta }_{r}$ and Voyage option, are given in Table 8. In order to make the result more intuitive, we also give Figure 5, whose abscissa is the cargo load in each leg, and the primary and secondary ordinate axes are ${\mathrm{O}\mathrm{B}\mathrm{J}}_{1}$ and ${\mathrm{O}\mathrm{B}\mathrm{J}}_{2}$, respectively. When the cargo load in each leg increases, ${\mathrm{O}\mathrm{B}\mathrm{J}}_{\mathrm{T}}$ and ${\mathrm{O}\mathrm{B}\mathrm{J}}_{1}$ increase, but ${\mathrm{O}\mathrm{B}\mathrm{J}}_{2}$ and the number of deployed ships decrease. However, voyage option decision is not influenced by changes in the cargo load. The above observations are reasonable because, with the increase in the cargo load, the product of the ship's cargo transported and the total distance over a week becomes larger. Although the ship sails at a higher speed due to the fewer deployed ships, the increase in the product of the ship's cargo transported and total distance over a week has a more significant impact on the expected EEOI value of all deployed ships than the increase in sailing speeds. Therefore, the average EEOI value of all deployed ships increases significantly with the increase in cargo load.

In summary, this study investigated the impact of $\lambda$ on the bi-objective programming and the impacts of unit price of fuel, Suez Canal toll fee per ship, weekly fixed operating cost and cargo load on the operation decisions. Specifically, with increasing $\lambda$ (larger weight on the minimization of the total weekly cost), fewer ships are needed, which means that each deployed ship sails at a higher speed and releases more ${\mathrm{C}\mathrm{O}}_{2}$ (i.e., higher EEOI value). In addition, the increase in the $\lambda$ value in the early stage has no significant effect on the second objective function value. For the impact of unit price of fuel on the operation decisions, if changes in the unit price of fuel do not cause changes in fleet deployment strategies and sailing speeds, the amount of ${\mathrm{C}\mathrm{O}}_{2}$ emissions and the expected EEOI value of all deployed ships will stay the same. However, the continuous increase in the unit price of fuel leads to an increase in the weekly fuel consumption cost, which eventually leads to an increase in the total weekly cost. For the impact of Suez Canal toll fee per ship on the operation decisions, since the weekly Suez Canal toll fee is less than the weekly fuel consumption and operating costs of deployed ships, the increase in the Suez Canal toll fee per ship does not lead to changes in fleet deployment, sailing speeds and voyage options. However, for the impact of the weekly fixed operating cost on the operation decisions, since the weekly fixed operating cost accounts for a large proportion of the total weekly cost, the continuous increase in the weekly fixed operating cost causes liner companies to reduce the number of deployed ships and causes ships to sail at higher speeds. Finally, for the impact of cargo load on the operation decisions, with the increase in the cargo load, the increase in the product of the ship's cargo transported and total distance over a week has a more significant impact on the expected EEOI value of all deployed ships than the increase in sailing speeds. Therefore, the average EEOI value of all deployed ships increases significantly with the increase in cargo load.

6.   Conclusions

The existing literature lacks research on the integrated optimization problem of fleet deployment, voyage planning and speed optimization with consideration of the influences of sailing speed, displacement and voyage option on fuel consumption. To fill this research gap, this study formulates a nonlinear MIP model capturing all these elements and designs a tailored exact algorithm for the model. Contributions of this paper are summarized from the following three aspects.

1) A nonlinear MIP model is proposed for this problem with the aim of minimizing both the total weekly cost and the average EEOI value of all deployed ships on all routes by determining the optimal sailing speed during each leg, the voyage option between the Suez Canal route and Cape of Good Hope route and the number of ships deployed on each ship route. 2) To deal with the challenge of solving a nonlinear MIP model, a tailored exact algorithm is proposed by considering specific characteristics of our problem. Efficiency of the proposed algorithm for computational instances of different sizes is verified. 3) Sensitivity analyses with crucial parameters, including the weighting factor, unit price of fuel, Suez Canal toll fee per ship, weekly fixed operating cost and cargo load in each leg, are carried out to show the influences of these factors on the results to obtain managerial insights. For example, with increasing $\lambda$ (i.e., larger weight on the minimization of the total weekly cost), fewer ships are needed, which means that each deployed ship needs to sail at a higher speed and releases more ${\mathrm{C}\mathrm{O}}_{2}$ (i.e., higher EEOI value).

In the future, uncertain shipping transportation in demand can be incorporated in the problem because shipping transportation demands change dramatically from time to time, and uncertainty affects the performance of transportation systems under different conditions ^{[40,41,42,43]}. In addition, container terminal planning ^{[44,45,46,47]} can be integrated into the fleet deployment problem. Additionally, fleet deployment with the consideration of subsidy design ^[48,49] can also be studied. Finally, several new techniques can be incorporated into the fleet deployment problem, such as computer vision algorithms ^[50], deep learning ^[51], blockchain technology ^[52], autonomous driving ^[53], cooling system management ^[54,55], combined prediction and optimization ^[56,57] and supply chain management ^[58].

Conflict of interest

The authors declare there are no conflict of interest.