Dynamical properties of a novel one dimensional chaotic map

1.   Introduction

In the middle of the 20th century, the chaotic behaviors were frequently observed in social and natural sciences, which engrossed wide attention from several fields ^[1,2]. Chaos theory describes the behavior of non-linear dynamical systems that exhibits sensitive dependence on the initial conditions. The term "chaos" is engaged to illustrate the time evaluation behavior of nonlinear dynamical systems when their behavior becomes aperiodic and seems as unpredictable or noisy ^[3]. The whole chaos theory is based on the developments made by Lorenz ^[4] and May ^[5]. According to Barnsley ^[6], a continuous interval map $f:I\to I$ is called a dynamical system, where $I$ is a non-degenerate compact interval, and is denoted by $(I, f)$. Further, the infinite sequence $\{f^n (x)\}_{n\ge0}$ is known as the trajectory of $x\in I$.

The chaotic systems have potential applications in various fields such as synchronization control ^[7,8], finance ^[9], particle swarm optimization ^[10], image encryption ^[11,12], secure communication ^[13], pseudo-random number generation ^[14,15], network evolution ^[16], neural network model ^[17], traffic control model ^[18] and population biology, physics, chemistry and engineering ^[19] and so on.

The chaos theory can be better studied through high-dimensional chaotic maps in comparison with one-dimensional chaotic maps. However, the complicated nature of high dimensional maps makes it difficult to use them for practical purposes. Therefore, one-dimensional chaotic maps can be easily implemented practically due to their simple structure and good chaotic properties.

Lorenz, the father of chaos theory, investigated first chaotic map in ^[4]. Many one dimensional chaotic maps have been introduced, for example, Logistic map ^[5], Tent map ^[20], Henon Map ^[21], coupled map lattices ^[22], Lorenz-like system ^[23], and some new other chaotic maps ^{[24,25,26,27]}. Among these maps, the most popular map of discrete nonlinear dynamical systems is the logistic map which has been proved as a milestone to study the nonlinear dynamical systems. It was primarily introduced by Verhulst in ^[28] as a population growth model defined by:

where $\mu > 0$ is a nonlinear population growth parameter, and $x_{n}\in[0, 1]$ represents the value of $x$ after $n$ iterations. The logistic map has been widely used practically to study every nonlinear phenomenon since it exhibits stable behavior for larger value of control parameter $\mu$, i.e., for $0 < \mu < 3.56995$ and shows chaotic behavior for $3.56995 < \mu\leq 4$ ^[20,28,29]. Moreover, if we examine its behavior for $\mu > 4$, the map can not be defined for all $x_{n}\in [0, 1]$ since there exists atleast one $x_{n}$ which does not belong to $[0, 1]$ (see, Figure 12(a)). Various methods or iteration procedures were used to increase this range of stability so that the dynamical system can be made stable and predictable for a higher value of control parameter (see ^{[18,30,31,32,33,34,35]} and references therein).

The wide applications of logistic map motivate us to introduce a novel one-dimensional chaotic map $K$ which has excellent ergodicity, more complex chaotic behavior, and better stability performance than existing one dimensional chaotic maps. We analyze the stability and chaotic performance of this map theoretically and graphically by adopting various dynamical techniques. We show that this new chaotic map remains stable for a high value of control parameter $\mu$, i.e, for $0 < \mu\leq 5.21$ which is very large than that of classical logistic map. Due to its wider range of stability, this map might be applied in real life nonlinear phenomena where stability is essential, for example, to control population, traffic on the roads etc. Moreover, its higher range of chaos (i.e., $5.21 < \mu\leq 5.8284$) makes it more secure against cyber attacks than the logistic map. Therefore, these advantages of the new chaotic map $K$ will encourage authors to apply the new chaotic map to get better outputs in cryptography, image encryption, signal processing, bio-engineering, and secure communication systems.

The rest of the paper is organized as follows: Section 2 deals with the basic definitions that are used in the discrete dynamical systems. In Section 3, we examine the dynamical properties of the proposed chaotic map including fixed points, period orbits, stability, chaos and visualize these properties through various plots like cobweb plot, time series analysis, bifurcation diagram, and maximal Lyapunov exponent. In Section 4, we compute the entropy and probability distribution of our chaotic map and the comparison shows that the proposed chaotic map is more uniformly distributed, i.e., more chaotic than the classical logistic map. In Section 5, we prove the superiority of our map $K$ by comparing bifurcation diagrams. A brief description of advantages of the proposed map is given in Section 6. In Section 7, we conclude the findings of our paper.

2.   Essential preliminaries

Some basic definitions, facts and notations are recollected in this section that are acting as fundamentals for further study.

Definition 2.1. ^[20,29] The function iteration process (also called Picard iteration) is represented as

It is known that Picard iteration process is a one-step feedback iteration method because it requires one number as input to return a new number as an output, which acts as an input number for the next step.

Definition 2.2. ^[20,29] A point $x\in I$ is said to be a periodic point of period $p$, if $p$ is the smallest positive integer such that $f^{p} (x) = x$ and the orbit of $x$ is called periodic orbit of period $p$. In addition, the orbit $O_{f} (x)$ of a periodic point of period $p$ is a finite set of $p$ distinct points, i.e.,

If $p = 1$, i.e., $f(x) = x$, then $x$ is called a fixed point.

Further, the fixed point $x$ is said to be:

(i) attracting (stable) fixed point or sink if $|f'(x)| < 1$.

(ii) repelling (unstable) fixed point or source if $|f'(x)| > 1$.

(iii) neutral (indifferent) fixed point if $|f'(x)| = 1$.

where $f'(x)$ is the first order derivative of map $f$.

Definition 2.3. (Maximal Lyapunov exponent) ^[36,37]. Consider a differentiable map $f\colon \mathbb{R}\to \mathbb{R}$. The maximal Lyapunov exponent (MLE) of $f$ for an orbit $\{x_{n}\}$ is defined by

provided this limit exists.

Remark 2.4. The system is stable if the value of maximal Lyapunov exponent is negative, i.e., $\sigma < 0$. Further, the positive value of maximal Lyapunov exponent indicates that chaos occurs in the system. Also, if the value of maximal Lyapunov exponent is zero, i.e., $\sigma = 0$, system remains neutral. Hence, the maximal Lyapunov exponent is used to examine the stability and unstability of the system.

3.   Formation of the one dimensional chaotic map $K$

We introduce a novel one dimensional chaotic map $K:[0, 1]\to [0, 1]$ and the corresponding nonlinear dynamical system is estimated as

where $\mu > 0$ $n = 0, 1, 2, \ldots,$ represents the number of iterations, $x_{n} \in [0, 1]$. The parameter $\mu$ alters the dynamical behavior and control the intensity level of the nonlinear map given by Eq (3.1), therefore, $\mu$ is known as control parameter.

We examine its dynamical behaviors such as fixed points, periodic points with different periods, visualize the iterations using cobweb plot, demonstrate bifurcation diagram, its key-points and time series diagrams, and maximum Lyapunov exponent in the following subsections.

3.1.   Fixed Points, attracting points and repelling points of the map $K$

Since the map defined by Eq (3.1) is an irreducible rational function. The fixed points of this map are calculated by solving the equation $K(x) = x$, which is a quadratic equation and therefore, it has two fixed points, i.e., the fixed points are as $x = 0 \ \rm{and} \ x = \frac{\mu-1}{\mu+1}, \; \mu > 0$.

Now, we consider the following cases:

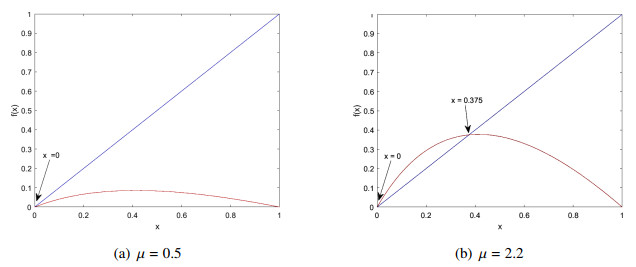
Case 1: It is clear that the map $K$ has only one fixed point for $\mu\in (0, 1]$. Figure 1(a) displays this graphically for $\mu = 0.5$. Indeed, the graph of $K$ intersects the line $y = x$ once at $x = 0$, so the map has only one fixed point that is $0$.

Case 2: $(\mu > 1)$. There are two fixed points of $K(x)$, $x = 0$ and $x = \frac{\mu -1}{\mu + 1}$. Figure 1(b) displays the graph of the map $K$ that intersects the line $y = x$ at $x = 0$ and $x = 0.375$ for $\mu = 2.2$.

Now, we find the condition on $\mu$ for which the fixed points are attracting and repelling. In view of ^[20], it is clear that the fixed-point $x$ is attracting if $|K'(x)| < 1$ and repelling if $|K'(x)| > 1$. Clearly, the derivative of $K$ is

a) For the fixed point $x = 0$, Eq (3.2) implies that $|K'(x)| = |\mu|$, i.e., the behavior of the fixed point $x$ is attracting if $\mu < 1$, neutral for $\mu = 1$ and repelling for $\mu > 1$.

b) The fixed point $x = \frac{\mu - 1}{\mu + 1}$ is attracting for $1 < \mu \le 2+\sqrt{5}$, i.e., $|K'(x)| < 1$. And the behavior of $x$ is repelling for $\mu > 2+\sqrt{5}$. Further, $x$ moves from 0 to $\frac{1+\sqrt{5}}{2}$ as an attracting fixed point as $\mu$ increases from 1 to $2+\sqrt{5}$.

3.2.   Cobweb and time series representation of the map $K$

In this subsection, we are going to show the graphical representation of the iteration process through the cobweb and time series plots which demonstrate the dynamical properties of proposed chaotic map $K$. Each figure is composed of two panels, one being the cobweb and second the corresponding time series plot so that behavior of orbits can be interpreted immediately. In cobweb plots, one may construct the iteration sequence by using the graphs of the mapping $K$ and the line $y = x$. In time series plots, we count first 100 points of the orbit for initial point $x_{0}$. Here, we start with the initial point $x_{0}$ and show its iteration sequence graphically for some particular values of $\mu$ by considering the following possible cases:

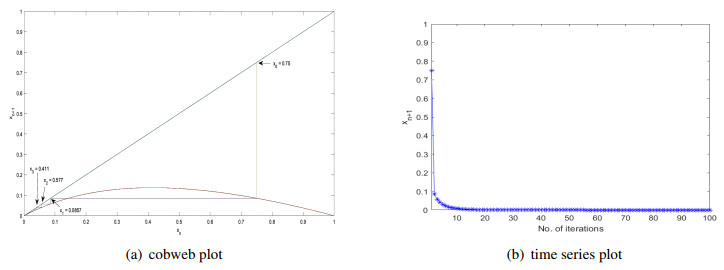
Case 1 $(0 < \mu < 1)$: For this range of control parameter $\mu$, the proposed map $K$ shows convergent behavior converging to the fixed point $x = 0$. Figure 2, exhibits this convergent behavior by plotting cobweb and time series diagrams for $x_0 = 0.75$ at $\mu = 0.8$. In Figure 2(a), the iteration sequence for $x_0 = 0.75$ at $\mu = 0.8$ is depicted by cobweb plot. The orbit of $x_0 = 0.75$ is $x_1 = 0.0857$, $x_2 = 0.0577$, $x_3 = 0.0411, \ldots, x_n = 0$. Also, Figure 2(b) displays the time series presentation of the orbit $x_{0} = 0.75$ at $\mu = 0.8$. It is clear that after fifteen iterations, the orbit of $x_{0} = 0.75$ converges to zero.

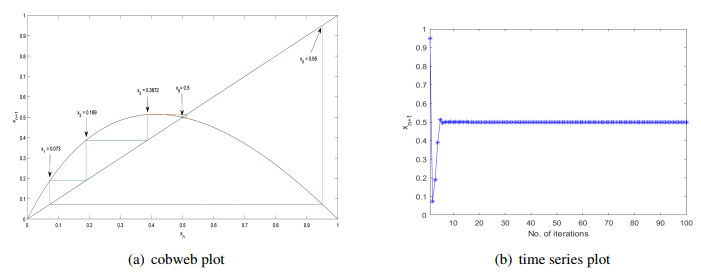
Case 2 $(1 < \mu \le 4.236)$: The chaotic map $K$ shows convergent behavior converging to a fixed point other than zero for $1 < \mu \le 4.236$. In Figure 3, we represent this behavior for $\mu = 3$. Figure 3(a) displays the orbit of the initial point $x_{0} = 0.95$ for $\mu = 3$ through cobweb plot. The sequence of the iteration of $x_0 = 0.95$ is $x_1 = 0.073, x_2 = 0.189, x_3 = 0.3872, \ldots, x_8 = 0.5, \ldots, x_n = 0.5$, for all $n\ge 8$. Further, for $\mu = 3$, $|K'(0.5)| < 1$ shows that $x = 0.5$ is attracting. Also, the time-series plot shows that the orbit of $x_{0} = 0.95$ for $\mu = 3$ is convergent to the fixed point $x = 0.5$ (see Figure 3(b)).

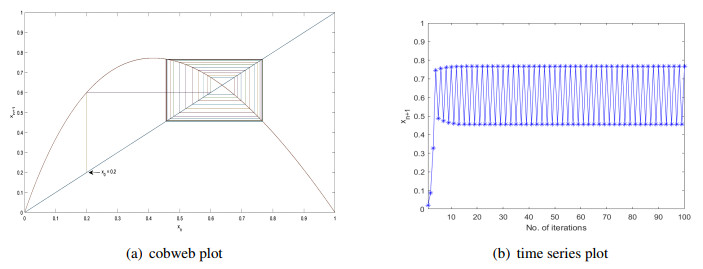
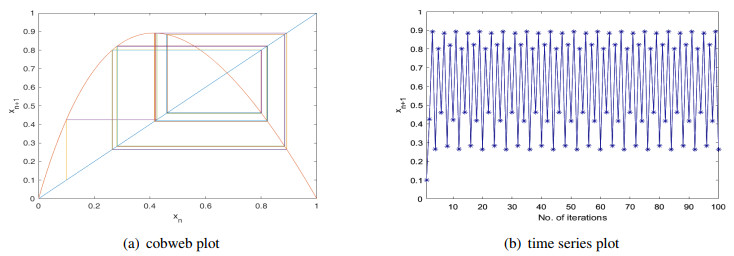
Case 3 $(4.237\le \mu \le 5.033)$: For this range of control parameter $\mu$, the chaotic map $K$ remains periodic with period two. Figure 4(a) shows that the orbit of the point $x_{0} = 0.02$ for $\mu = 4.5$ is not converging to a fixed point but it is periodic of period two. Similarly, the Figure 4(b) displays the time-series plot for $x_{0} = 0.02$ at $\mu = 4.5$ which shows same behavior of the orbit.

Case 4 $(5.033 < \mu \le 5.21)$: The map $K$ exhibits periodic behavior of periods more than $2$. We present some examples of period $4$ and $8$ with the help of cobweb and time series plots. For $\mu = 5.1$ at $x_{0} = 0.5$, the behavior of the map is periodic with period $4$ (see Figure 5). Moreover, for $\mu = 5.2$, the behavior of the map is again periodic with period 8, we demonstrate this behaviors in Figure 6.

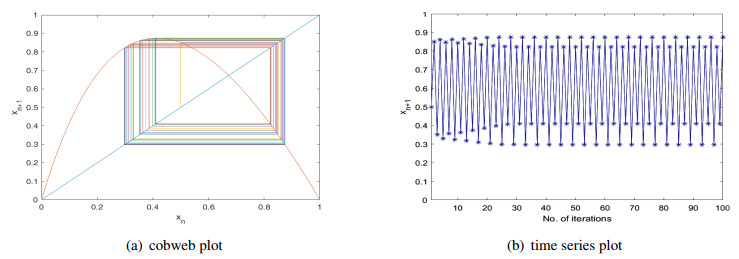
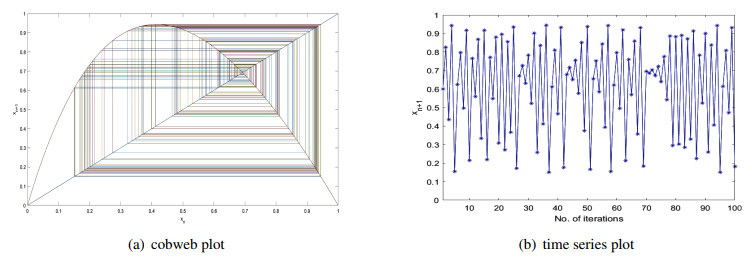
Case 5 $(\mu > 5.21)$: For this range of $\mu$, the orbit of the initial point $x_0\in (0, 1)$ is unstable. Figure 7 exhibits that the orbit of the point $x_0 = 0.6$ at $\mu = 5.5$ is unstable which is clear from cobweb and time series diagrams. The map $K$ shows chaotic behavior for all $\mu > 5.21$.

3.3.   Bifurcation analysis of the map $K$

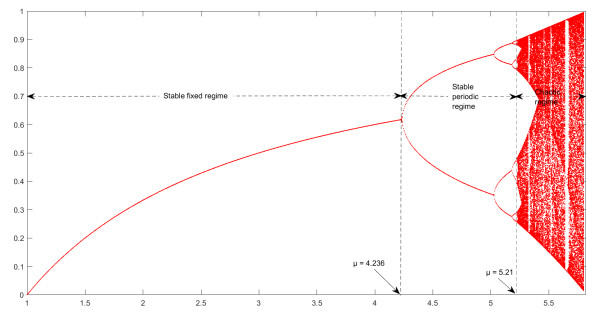
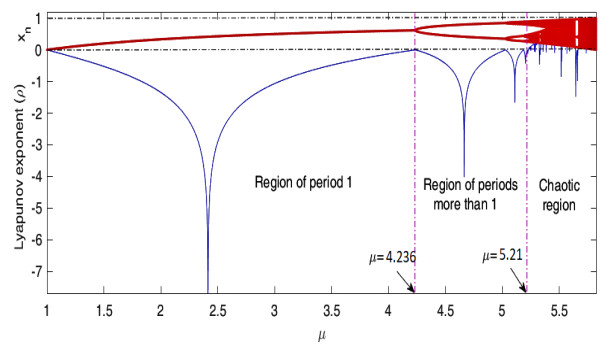
Bifurcation means there is a change in stability of a dynamical system when the control parameters of the system are changed. A bifurcation diagram summarizes the long-term dynamics (be it chaotic or regular) of the map when the governing parameter is varied ^[20]. To plot bifurcation diagram, we take the parameter $\mu$ along the horizontal axis, although the vertical axis shows all the possible values of the variable $x$ (see Figure 8). From the figure, we conclude that the behavior of the map is convergent for $0 < \mu \le 2+\sqrt{5}$, i.e. $0 < \mu \le 4.236$, for $4.236 < \mu \le 5.21$ the orbits of map are periodic which are also convergent, just to a per-n orbit (after skipping transients) and for $\mu > 5.21$ it becomes unstable.

3.4.   Mathematical and experimental approach of the map $K$ via maximal Lyapunov exponent

The maximal Lyapunov exponent (MLE) provides a powerful tool that characterizes the rate of separation of two close trajectories. MLE plays a key role in recognition of the dynamical behavior and the chaotic degree of the strange attractors. Predominantly, one positive MLE is sufficient to signalize the chaos of the dynamical system ^[36,37]. By using Eq (2.2), the MLE of new model $K(x)$ is given by

We draw the following results about the dynamical behavior of $K$:

a) The MLE $\sigma$, can be used to predict how much the dynamical system Eq (3.1) depends on initial conditions. For $\sigma > 0$, the system exhibits extreme sensitive dependence on initial conditions and for $\sigma < 0$, the system remains dissipative (stable).

b) For the periodic orbit with any period $p$, $\sigma$ takes the form

For $p = 1$ in particular, the MLE reduces to

Remark 3.1. For the orbit which is neither fixed nor periodic, MLE is evaluated by considering infinite number of iterations which is impracticable, therefore, the MLE has been estimated only for finite number of iterations.

Example 3.2. The dynamical behavior of the map $K_{\mu}(x) = (\mu x(1-x))/(1+x)$; $x\in [0, 1]$ is evaluated by plotting MLE for $0 \le \mu \le 5.8284$. Further, the behavior of fixed and periodic orbit is examined by calculating MLE for $\mu = 3$ and $\mu = 4.5$.

As we have shown in Subsection 3.3, that the orbit for each $x_{0}\in[0, 1]$ of the map $K$ is convergent to a fixed point for $0 < \mu \le 4.236$. The MLE is calculated for the fixed point 0.5 at $\mu = 3$ by solving Eq (3.5). Putting $\mu = 3$ and $x = 0.5$ in Eq (3.2), we obtain

Substituting this value in Eq (3.5), we get

Thus, the estimated value of MLE is $-0.477121255$, which is less than zero. Therefore, the orbit of $x = 0.5$ is stable and becomes stable attractor for the map $K_{3} (0.5)$.

For the range $4.236 < \mu < 5.02$, the behavior of the map $K$ is periodic of period two for all $x$ in $(0, 1)$. And the periodic points are evaluated as $x_1 = 0.355$ and $x_2 = 0.845$ for $\mu = 5$. The MLE is calculated by solving Eq (3.4) for $p = 2$. By using Eq (3.2), we have

and

Using Eqs (3.6) and (3.7) in Eq (3.4), we get

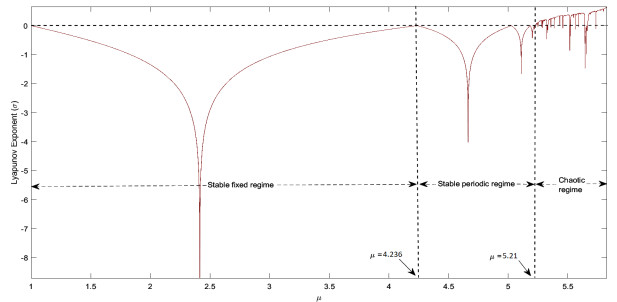
Therefore, the calculated value of MLE is $-0.808843451$, i.e., Lyapunov exponent is negative. As a result, the periodic points $x_1$ and $x_2$ are the stable attractors for the map $K$. Figure 9 shows the MLE diagram for the map $K$, where we observe that the behavior of the map is stable for $0 < \mu < 5.21$ and becomes chaotic as $\mu$ exceeds the value 5.21.

Further, we combine the bifurcation diagram and MLE to examine the accurate value of control parameter $\mu$ obtained in previous subsections at which the map $K$ alters its behavior. We have divided the dynamical map $K$ into different regions separated by a magenta dotted line as shown in Figure 10. This figure shows the combined graphical representation of bifurcation and MLE for $1\le\mu\le 5.8284$. The system possesses two regimes, stable periodic regime and chaotic regime, separated by a magenta dotted line at $\mu = 5.21$, which is the maximum value of $\mu$ for the map to be stable, thereafter, chaos occurs in the system.

4.   Entropy

Dynamical systems are characterized by the loss of memory of the previous state ^[38]. Classification of nonlinear dynamical systems is a challenging task, as there are insystematic approaches to tackle them. Entropy can be used to quantify the degree of nonlinearity of dynamical systems ^[38,39,40]. As the entropy increases, the degree of nonlinearity increases while for linear systems the value of entropy is zero. Here, we compute the entropy for the new proposed map $K$. For the sake of comparison, we also provide the probability distribution and entropy of the logistic map.

Consider a set of $N$ items. These $N$ items fall into $m$ categories, $m_1$ has label 1, $m_2$ has label 2, $\ldots$, $m_k$ has label $k$ whose probabilities of occurrence are $p_1, p_2, \ldots, p_k$, respectively. The entropy of our set is given by the formula:

Lower entropies are achieved by the samples that have higher probabilities to be closer to the mean value. On the other hand, the uniform distribution of samples represents the least predictable dynamical system, i.e., more chaotic behavior ^[7,41].

There is an interesting connection between chaos and cryptography. According to this relation, a more irregular system gives more secure privacy against different types of attacks. Several chaos-based cryptosystems have been put forward since 1990 ^[42,43,44]. The logistic map is one of the most commonly used chaotic map in cryptography as it is one of the simplest and most studied nonlinear systems. Further, it has been widely used in block ciphers, stream ciphers and hash functions ^[45].

Here, we look into the entropy of the classical logistic map and our new proposed map. We consider 1000 cycles and 20 partitions of the interval $[0, 1]$. As we know that the range of the parameter $\mu$ is $[0, 4]$ for the logistic map while for our new map it is $[0, 5.8284]$. We compute the entropy at $\mu = 4$ for the logistic map and at $\mu = 5.8284$ for the proposed map $K$. We find that the entropy of the logistic map is $E = 1.24116601$ (see Table 1) and for our new model it is $E = 1.254500592$ (see Table 2) which proves that our map is more uniformly distributed than the logistic map. Thus the proposed map is more chaotic in nature than the logistic map. To know more about the relation between chaos and entropy, one can refer to ^[46,47] and references therein.

5.   Superiority of the map $K$

To prove the excellence and superiority of the map $K$, we compare its stability and chaos performance with existing one dimensional maps in terms of bifurcation plots.

5.1.   Stability performance of the map $K$

In order to facilitate comparison, we compare the stability performance of the map $K$ with existing one dimensional logistic map.

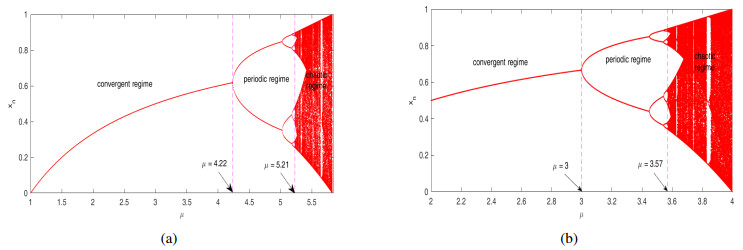
From Figure 11, we observe that $K$ remains stable for $0 < \mu\leq 5.21$ while the logistic map is stable for $0 < \mu\leq 3.57$. Hence, the map $K$ has largest range of stability which is very higher than the existing one dimensional chaotic maps.

5.2.   Chaos performance of the map $K$

The chaos performance of a chaotic map is very significant tool for image encryption. The properties of chaotic maps such as: extreme sensitivity on initial conditions, ergodicity and unpredictable behavior are very suitable for image encryption. In 1997, the chaos based image encryption was firstly introduced by Fridrich ^[48]. Here, we also evaluate the chaos performance of the map $K$ so that it can be used in image encryption.

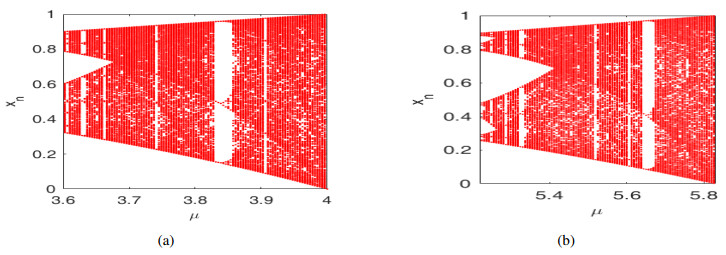
In Figure 12, we evaluate the chaos performance of logistic map, and the map $K$ by magnifying the chaotic regimes of their respective bifurcation diagrams represented in Figure 11. From the figure, we notice that the logistic map remains chaotic for $3.58\leq \mu \leq 4$. The map $K$ shows chaotic behavior for $5.22\leq \mu \leq 5.83$. Therefore, the proposed map $K$ has a wider chaotic range and therefore, more complex chaotic behavior than the logistic map.

6.   Advantages of the map $K$

In the above sections, we have shown that the stability and chaos performance of the proposed map $K$ is wider than that of logistic map. Due to its wider range of stability, this map might be applied in real life nonlinear phenomena where stability is essential, for example, to control traffic on the roads ^[18,30]. Moreover, higher entropy of this model proves that the degree of nonlinearity of it is high that indicates a more uniform distribution ^[38,39]. As a result, our new model is more chaotic, makes it more secure against cyber attacks than the logistic map. Therefore, our new approach is more credible for cryptography, random number generation, image encryption, and end-to-end encryption, among other applications (see ^{[26,47,49,50]} and references therein).

7.   Conclusions

In this paper, a new one dimensional nonlinear chaotic map $K(x) = \frac{\mu x(1-x)}{1+x}$, $x \in[0, 1]$, $\mu > 0$ is proposed. The dynamical behavior of the map is examined by using various techniques such as cobweb plots, bifurcation diagrams, time series plots and maximal Lyapunov exponent. Moreover, MLEs are computed. Further, it turns out that the proposed map has more chaotic behavior than the classical logistic map as entropy of the proposed map is higher than the entropy of the logistic map. Moreover, comparison shows that our map is superior to logistic map due to its wider range of stability and chaos. We conclude the main characteristics of the map as follows:

$\bullet$ The map has only one fixed point $x = 0$ for $0 < \mu < 1$ which is attracting.

$\bullet$ There are two fixed points $x = 0$ (repelling) and $\frac{\mu - 1}{\mu + 1}$(attracting) for $1 < \mu\le4.236.$

$\bullet$ The proposed map remains periodic for $4.236 < \mu\le 5.21$.

$\bullet$ For $5.21 < \mu\leq 5.8284$, the dynamical system becomes unstable/chaotic.

We believe that the results obtained in this paper are of great significance for relative community. As the new map is more stable and chaotic than the classical logistic map (see, Section 5), therefore, it has potential applications in every field where logistic map has been applied so far. In our future research, we will apply this map in real life, specially, in image encryption.

Acknowledgments

The authors are thankful to the reviewers for their valuable and insightful comments/suggestions that improve the quality of the paper. J. Alzabut would like to thank Prince Sultan University and OSTİM Technical University for supporting this research.

Conflict of interest

The authors declare there is no conflict of interest.