Analysis of a finite difference scheme for a nonlinear Caputo fractional differential equation on an adaptive grid

1.   Introduction

In this paper, we consider the following nonlinear Caputo fractional initial value problem:

where $\alpha\in (0, 1)$, $D_0^{\alpha}$ is a caputo fractional order derivative operator, which is defined by

and $f(t, u(t))\in C^1\left(\Omega\times \mathbb{R}\right)$ is a known function. Furthermore, throughout this paper we shall assume that there exist two positive constants $\beta_i(i = 1, 2)$ such that

It is well known that fractional-order differential equations (FDEs) have widely been applied in many fields like bio-engineering^[1], food science^[2], electrical engineering^[3], Biomedicine^[4,5,6], epidemiology^[7], etc. Due to the importance of these problems, there has been tremendous interest in developing numerical methods for FDEs, such as finite difference method ^[8,9,10,11], finite element method ^[12], collocation method ^[13,14,15] and spectral method^[16,17]. However, many of these methods are based on local operations and the authors don't consider the weak singularities. For this reason, Stynes and Gracia ^[18,19] first considered a two point boundary value problem with a Caputo derivative of order $\delta\in (1, 2)$, and analyzed the bounds for the derivatives of exact solution $u(x)$. Then they constructed finite difference methods on a uniform mesh to solve this problem and gave the corresponding convergence analysis.

As far as we known, there is great current interest in the use of some numerical methods on a graded grid for time fractional diffusion equations with a Caputo derivative (see, e.g., ^{[20,21,22,23]}). In these literature, the authors derived the bounds for the time derivatives of $u(x, t)$, and constructed a finite difference scheme on a graded grid. Recently, for a two-point boundary value problem with a Riemann-Liouville fractional derivative, Cen, et.al., ^[24] developed an adaptive grid method based on an a posteriori error estimation. Furthermore, Liu, et.al., ^[25] and Huang, et.al., ^[26] proposed an adaptive grid method based on a priori error estimation and obtained a first-order and a second-order convergence results, respectively. Inspired by literature ^[24,25,26], the authors in ^[27] also developed an adaptive grid method by using a backward Euler formula to approximate the first-order derivative of problem (1.1) and obtained an a posteriori error estimation for the presented discretization scheme. Liu and Chen ^[28] derived a new a posteriori error estimation and gave the corresponding adaptive strategy for problem (1.1).

In this paper, similar to literature ^[25,26], we {first} transform problem (1.1) into a Volterra integro equation by using the Riemann-Liouville fractional integral transformation. Then a right rectangle formula on an arbitrary nonuniform mesh is used to approximate this integro equation. Furthermore, a convergence analysis based on a priori error estimation is carried out by using the mesh equidistribution principle. It is shown that there exists a grid that gives the optimal first-order convergence for the presented method. Besides, we also derive an a posteriori error estimation for the presented discretization scheme and design an adaptive grid generation algorithm. Finally, some numerical results are provided to validate the theoretical results.

Notation. Throughout the paper, $C$ will denote a generic positive constant that is independent of the mesh parameter $N$ and $\alpha$. To simplify the notation we set $g_i = g(t_i)$ for any function $g$ defined on the interval $[0, 1]$. We define the maximum norm by $\|\cdot\|_{\infty}$.

2.   Preliminary results

In Section 2.1, we first convert problem (1.1) into an equivalent Volterra integral equation and give the bounds for the exact solution $u(t)$ and its derivatives. Then for the transformed Volterra integral equation, a finite difference scheme and the corresponding stability result are given in Section 2.2.

2.1.   Reformulation the initial value problem

Let

be the Riemann-Liouville fractional integral of order $\alpha\in (0, 1)$ (see ^[29]), which satisfies the following property

Then, the above problem (1.1) can be written into the following Volterra integral equation

Similar to the argument of Lemma 2.1 of ^[24], we derive the following results for the exact solution $u(t)$ and its derivatives.

Lemma 2.1. Let $u(t)$ be the continuous solution of problem (2.2). Then exists a constant $C$ such that

Proof. By using the Taylor series expansion to $f(t, u(t))$, problem (2.2) can be changed into the following linear formal

where $a(s) = f_u(s, \lambda u(s))$ with $0 < \lambda < 1.$ Then, the proof of (2.3) can be followed from (2.5) and Lemma 2.1 of ^[24].

For the proof of (2.4), we may refer to the Theorem 2.1 in ^[20].

2.2.   Discretization scheme

For our numerical scheme we consider an arbitrary nonuniform mesh

where $N$ is a positive integer. For $i = 1, \cdots, N$, let $\tau_i = t_i-t_{i-1}$ be the local mesh step. Then, by using the right rectangle formula to approximate the integral given in (2.2), we obtain

where $u_i^N$ is the approximation solution of $u(t)$ at point $t = t_i$, $i = 0, 1, \cdots, N$.

Next, the following lemma gives the stability for the discretization scheme (2.6).

Lemma 2.2. Under the assumption $f(t, u(t))\in C^1\left(\Omega\times \mathbb{R}\right)$, the solution $\left\{ u_i^N \right\}_{i = 0}^N$ of the scheme (2.6) on an arbitrary mesh $\bar{\Omega}^N$ satisfies

Proof. Similar to (2.5), the numerical scheme (2.6) can be written into the following formula

where $\xi\in (0, 1)$.

Furthermore, we have

where

For $1\leq i\leq N$ with sufficiently large $N$, we have

Then, for each $i$, it follows from the proof of Lemma 3.3 given in ^[30] that

Furthermore, we have

Finally, by using the modified Grönwall inequality given in [30, Lemma 3.3], we can obtain the desirable result (2.7).

3.   A priori error analysis

Let $e_i^N = u(t_i)-u_i^N$ be the error at $t_i$ in the computed solution, $i = 0, 1, \cdots, N$. Then it follows from (2.2) and (2.6) that we can obtain the following error equation

where

is the truncation error at $t = t_i$.

Lemma 3.1. Let $u(t)$ be the exact solution of (2.2) and $\left\{ u_i^N \right\}_{i = 0}^N$ be the discrete solution of (2.6) on an adaptive grid. Then

Proof. For each $i$, it follows from (3.2) that

Thus, the desired result can be followed from (3.1) and Lemma 2.2.

Corollary 3.1. Assume that there exists a grid $\left\{t_i\right\}_{i = 0}^N$ such that

for $k = 1, \cdots, N$. Then

Proof. It follows form (1.3) and Lemma 2.1 that

Thus, the desired result can be obtained by using Lemma 3.1, (3.3) and (3.5).

Remark 3.1. It is shown from Corollary 1 that there exists a mesh that gives the optimal first-order convergence of the presented discretization scheme (2.6). However, it is difficult to construct this mesh $\left\{t_i\right\}_{i = 0}^N$ based on (3.3) since this requires the exact solution $u(t)$.

4.   A posteriori error analysis

In this section, we will derive an a posteriori error estimation for the numerical solution $u_i^N$, $i = 0, 1, \cdots, N$.

Theorem 4.1. Let $u(t)$ be the exact solution of (1.1), $u_i^N$ be the solution of (2.6) and $u^{N}(t)$ be the piecewise linear interpolation function through knots $\left(t_i, u_i^N\right)$, $i = 0, 1, \cdots, N$. Then we have

Proof. For $\forall t\in [t_{i-1}, t_i]$, it follows from (2.2) and (2.6) that

where

For $p$, we have

It follows from the assumption of $f(t, u(t))$ that

Thus, from (4.2), (4.3) and (4.7)-(4.9), we obtain

where we have used the bound of $u_i^N$ and the condition (1.3). Finally, the desired result can be followed by applying the generalized Grönwall's inequality[31, Corollary 2] to the above inequality.

Corollary 4.1. Under the assumption of $f(t, u(t))\in C^1\left(\Omega\times \mathbb{R}\right)$, we have

Proof. For $\forall t\in [t_{i-1}, t_i]$

which completes the proof by virtue of the above Theorem 4.1.

5.   Numerical experiments and discussion

In Section 5.1, we describe an adaptive grid generation algorithm by equidistributing a monitor function. Then, numerical experiments are presented in Section 5.2 to demonstrate the validity and efficiency of the presented adaptive grid method.

5.1.   An adaptive algorithm

As is stated in Remark 3.1 that it is hard to obtain a grid $\left\{t_i\right\}_{i = 0}^N$ satisfying (3.3). Therefore, in practical computation, the key problem is to find a grid $\left\{t_i\right\}_{i = 0}^N$ and the corresponding numerical solution $u_i^N$ such that

where $\widetilde{M}(s, u_i^N)$ is a monitor function which is a function about $u_i^N$. For a given monitor function $\widetilde{M}$, the adaptive grid generation algorithm based on (5.1) aims to construct a mesh that equidistributes $\widetilde{M}$. Thus, it is very important to choose a suitable monitor function $\widetilde{M}$. Here, in this paper, by using the a posteriori error estimation given in Theorem 4.1, we construct the monitor function as follows:

In order to compute the equidistributed mesh $\left\{t_i\right\}_{i = 0}^N$ and corresponding numerical solution $u_i^N$, an adaptive grid algorithm is given as follows:

Step 1. Let $\bar{\Omega}_N^{(0)} = \left\{t_i^{(0)}\right\}_{i = 0}^N$ be an initial uniform mesh with mesh size $\frac{1}{N}$.

Step 2. For a given mesh $\bar{\Omega}_N^{(k)} = \left\{t_i^{(k)}\right\}_{i = 0}^N$, $k = 0, 1, \cdots,$ solve the solution $\left\{u_i^{(k), N}\right\}_{i = 0}^N$ of scheme (2.6) on this mesh. For each $i$, set $\tau_i^{(k)} = t_i^{(k)}-t_{i-1}^{(k)}$, $L_0^{(k)} = 0$ and $L_i^{(k)} = \sum\limits_{j = 1}^i \widetilde{M}_j^{(k)}$, where $\widetilde{M}_j^{(k)}$ is the value of the monitor function (5.2) computed at the current mesh and corresponding numerical solution.

Step 3. Define

For a given constant $\gamma^* > 1$, if $\gamma^{(k)}\leq \gamma^*$, go to Step 5. Otherwise, continue to Step 4.

Step 4. Let $Y_i^{(k)} = iL_N^{(k)}/N$ and $\phi^{(k)}(t)$ be a piecewise linear interpolation function through knots $\left(L_i^{(k)}, t_i^{(k)}\right)$, $i = 0, 1, \cdots, N$. Generate a new mesh $\left\{t_i^{(k+1)}\right\}$ by computing the value of function $\phi^{(k)}(t)$ at $t = Y_i^{(k)}$ for $i = 0, \cdots, N$. Let $k = k+1$ and return to Step 2.

Step 5. Take $\left\{t_i^{(k)}\right\}_{i = 0}^N$ as the final computed mesh and $\left\{u_i^{(k), N}\right\}_{i = 0}^N$ as the corresponding computed solution. Then stop iteration process.

5.2.   Two test examples

Here, we give some numerical experiments to illustrate the validity of our presented adaptive grid method. The test problem follows ^[27] by taking (1.1) with

where $s(t)$ is chosen such that the exact solution is

The initial value condition is $u(0) = 1$.

Since the analytic solution of this problem is given, the maximum point-wise error $E^N$ and the order of convergence $r^N$ are calculated as follows:

For different values of $N$ and $\alpha$, we use our presented adaptive grid algorithm to solve this test problem. The maximum errors $E^N$, the orders of convergence $r^N$ and the number of iterations $K$ of the above grid generation algorithm are listed in Table 1. One can see from the numerical results in Table 1 that our presented adaptive grid method is first-order convergent. which is robust with respect to the order of fractional derivative $\alpha$. Meanwhile, to illustrate the advantage of our presented adaptive grid method, we also use the presented discretization scheme (2.6) on a uniform mesh to solve this test problem, see Table 2.

It is shown from these numerical results that the maximum errors calculated on an adaptive grid are much lower than that computed on a uniform mesh with the increase of $N$. Besides, the order of convergence obtained on an adaptive grid is more higher than that obtained on a uniform mesh.

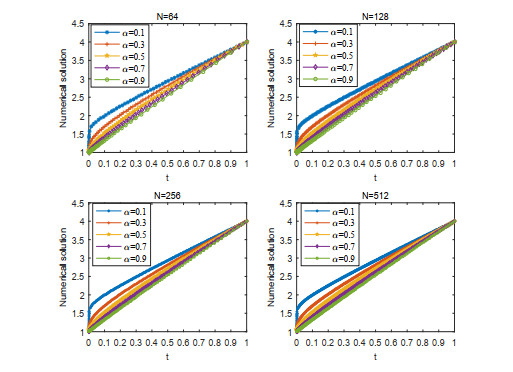
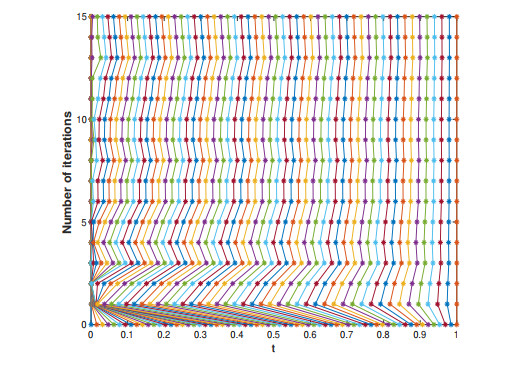
Furthermore, in order to verify the relationship between numerical solution $u_i^N$ and the order of fractional derivative $\alpha$, Figure 1 represents some graphs of numerical solution for different values of $N$ and $\alpha$. Obviously, the solution of this test problem has a boundary layer at $t = 0$ with the decrease of $\alpha$. When $\alpha = 0.1$, the Figure 2 shows how a mesh with $N = 64$ intervals evolves through successive iterations of the above grid generation algorithm.

Finally, for $\alpha = 0.2, 0.4, 0.6, 0.8$ and the same $N$ given in Table 1, Table 3 gives the numerical results calculated by using our presented adaptive grid method, while we also list the results obtained by the method in ^[28]. Obviously, it is shown from Table 3 that our presented method produces better results than that produced by method in ^[28].

6.   Conclusions

This work mainly discusses a nonlinear value problem whose the differential operator is a Caputo derivative of order $\alpha$ with $0 < \alpha < 1$. By using the Riemann-Liouville integral operator, the problem (1.1) can be changed into a Volterra integral equation, which is approximated by using the integral discrete formula. A priori error estimation and convergence analysis have been given on an adaptive grid. Meanwhile, an a posterior error estimation has been obtained by using the polynomial interpolation technique and the corresponding adaptive grid generation algorithm is constructed. It should be pointed out that the presented adaptive grid method can be extended to the other time fractional differential equations.

Acknowledgments

This work is supported by the National Science Foundation of China (11761015), the Natural Science Foundation of Guangxi Province (2020GXNSFAA159010, 2018GXNSFAA294079) and the projects of Excellent Young Talents Fund in Universities of Anhui Province (gxyq2017105).

Conflict of interest

The authors declare there is no conflict of interest.