Genetic polymorphisms in eostrogen and progesterone receptor genes in Papio anubis induced with endometriosis during early stage of the disease

1.   Introduction

In many industrial applications, due to the ubiquity of stochastic noise and nonlinear ^[1,2], real systems are often modelled by stochastic differential equations, which attracts researchers to pay more and more attention to the control of stochastic systems. Using the state-feedback, a closed-loop pole can be arbitrarily configured to improve the performance of the control systems. Therefore, some scholars research the problem of state-feedback stabilization for stochastic systems, e.g., reference ^[3] focuses on the cooperative control problem of multiple nonlinear systems perturbed by second-order moment processes in a directed topology. Reference ^[4] considers the case where the diffusion term and the drift term are unknown parameters for stochastic systems with strict feedback. Reference ^[5] studies stochastic higher-order systems with state constraints and ^[6] discusses output constrained stochastic systems with low-order and high-order nonlinear and stochastic inverse dynamics. However, it is often difficult to obtain all the state variables of the system directly, it is unsuitable for direct measurement or the measurement equipment is limited in economy and practicality, so the physical implementation of state-feedback is difficult. One of the solutions to this difficulty is to reconstruct the state of the system. At this time, scholars use an observer to investigate the output-feedback stabilization, e.g., reference ^[7] investigates the prescribed-time stability problem of stochastic nonlinear strict-feedback systems. Reference ^[8] focuses on stochastic strict feedback systems with sensor uncertainties. In addition, based on output-feedback, for nonlinear multiagent systems, a distributed output-feedback tracking controller is proposed in ^[9].

It should be noted that all of the above results ^[7,8,9], Markovian switching is not considered in the design of output-feedback controller. However, as demonstrated by ^[10], switching system is a complex hybrid system, which consists of a series of subsystems and switching rules that coordinate the order of each subsystem. In real life, due to the aging of internal components, high temperature, sudden disturbance of external environment, operator error and other inevitable factors, the structure of many systems changes suddenly. Such systems can be reasonably modelled as differential equation with Markovian switching, see ^[11,12]. Recently, references ^[13] and ^[14] discuss the adaptive tracking problem and output tracking problem with Markovian switching respectively. Besides, as shown in ^[15], the power of the system changes because of factors such as the aging of the springs inside the boiler-turbine unit. Therefore, the research on the stability of stochastic nonlinear systems with time-varying powers has important practical significance. Reference ^[16] investigates the optimality and stability of high-order stochastic systems with time-varying powers. However, these results do not address the output-feedback stabilization for higher-order stochastic systems with both Markovian switching and time-varying powers.

Based on these discussions, we aim to resolve the output-feedback stabilization for higher-order stochastic nonlinear systems with both Markovian switching and time-varying powers. The main contributions and characteristics of this paper are two-fold:

1) The system model we take into account is more applicable than the existing results ^[7,8,9] and ^[12,13,14]. Different from the previous results ^[7,8,9], the stochastic system with Markovian switching is studied in this paper. Unlike previous studies in ^[12,13,14], we investigate the power is time-varying. The simultaneous existence of the Markov process and time-varying order makes the controller design process more complicated and difficult. More advanced stochastic analysis techniques are needed.

2) We propose a new observer. The existence of Markovian switching and nondifferentiable time-varying power makes the observer constructed in ^[7,8,9] invalid. We use the time-varying power's bounds to construct a new observer, which can effectively observe the unmeasurable state and can deal with the nonlinear growth rate, while the existing observer can only deal with constant growth rate.

The rest of this paper is listed as follows. The problem is formulated in Section 2. In Section 3, an output-feedback controller is designed. Section 4 is the stability analysis. A simulation is given in Section 5. The conclusions are collected in Section 6.

Notations: $\mathrm{R}^2$ denotes the 2-dimensional space and the set of nonnegative real numbers is represented by $\mathrm{R}^+$. $X$ denotes the matrix or vector, its transpose is represented by $X^T$. $|X|$ denotes the Euclidean norm of a vector $X$. When $X$ is square, $\mathrm{Tr}\{X\}$ denotes its trace. The set of all functions with continuous $i$th partial derivatives is represented by $C^i$. Let $C^{2, 1}(\mathrm{R}^2\times\mathrm{R}^+\times S; \mathrm{R}^+)$ represent all nonnegative functions $V$ on $\mathrm{R}^2\times\mathrm{R}^+\times S$ which are $C^2$ in $x$ and $C^1$ in $t$.

2.   Problem formulation

This paper studies the output-feedback stabilization for stochastic nonlinear systems with both Markovian switching and time-varying powers described by:

where $\zeta = \bar{\zeta}_2 = (\zeta_1, \zeta_2)^T\in \mathrm{R}^2$, $y\in \mathrm{R}$ and $u\in \mathrm{R}$ are the system state, control output and the input, respectively. The state $\zeta_2$ is unmeasurable. The function $m(t): \mathrm{R}^+\rightarrow \mathrm{R}^+$ is continuous and bounded, which satisfies $1\leq\underline{m}\leq m(t)\leq\bar{m}$ with $\underline{m}$ and $\bar{m}$ being constants. The powers sign function $[\cdot]^\alpha$ is defined as $[\cdot]^\alpha: = \mathrm{sign}(\cdot)|\cdot|^\alpha$ with $\alpha\in(0, +\infty)$. The functions $f_{\gamma(t)}$ is assumed to be smooth, and for all $t\geq0$, the locally Lipschitz continuous in $x$ uniformly. $f_{\gamma(t)}(t, 0) = 0$. $\omega$ is an $r-$dimensional standard Wiener process, which is defined on the complete probability space $(\Omega, \mathcal{F}, \mathcal{F}_t, P)$ with the filtration $\mathcal{F}_t$ satisfying the general conditions. $\gamma(t)$ is a homogeneous Markov process on the probability space taking values in a space $S = \{1, 2, ..., N\}$, which the generator $\Gamma = (\lambda_{ij})_{N\times N}$ given by

where $\lambda_{ij} > 0$ is the transition rate from $i$ to $j$ if $i\neq j$ while $\lambda_{ii} = -\Sigma^N_{j = 1, i\neq j}\lambda_{ij}$ for any $s, t\geq0$. Suppose the Markov process $\gamma(t)$ is irrelevant to the $\omega(t)$.

To implement the controller design, we need the following assumption.

Assumption 2.1. There exists a non-negative smooth function $\tilde{f}(\zeta_1)$ such that

Remark 2.1. As we know, the existing results for stochastic systems with time-varying powers (e.g., ^[16]), neither the state-feedback control nor the output-feedback control, has considered Markovian switching. However, the structure of many physical systems in the actual system often mutates, which makes it necessary to study systems with both Markovain switching and time-varying powers. Therefore, compared with ^[16], the model we consider is more practical and more general.

Remark 2.2. In Assumption $2.1$, we can see that the power $m(t)$ is time-varying and the growth rate $\tilde{f}(\zeta_1)$ is a nonlinear function. When $m(t) = 1$ and $\tilde{f}(\zeta_1)$ is a constant, Assumption $2.1$ is a linear growth condition. However, we consider that $\tilde{f}(\zeta_1)$ is a nonlinear function, which includes the constant case as a special case. The growth condition of Assumption $2.1$ is broader than the linear growth condition. The time-varying power $m(t)$ makes the design in ^[7,8,9] for time-invariant power invalid. In addition, the nonlinear growth rate $\tilde{f}(\zeta_1)$ makes the design in ^{[7,8,9,17,18]} for constant growth rate fail. A new design scheme should be proposed.

3.   Controller design

In this section, we develop an output-feedback controller design for system (2.1). The process is divided into two steps:

$\bullet$ Firstly, we assume that all states are measurable and develop a state-feedback controller using backstepping technique.

$\bullet$ Secondly, we construct a reduced-order observer with a dynamic gain, and design an output-feedback controller.

3.1.   State-feedback controller design

In this part, under Assumption $2.1$, our objective is to develop a state-feedback controller design for the system (2.1).

Step 1. Introducing the coordinate transformation $\xi_1 = \zeta_1$ and choosing $V_1 = \frac{1}{4}\xi_1^4$, by using the infinitesimal generator defined in section 1.8 of ^[11], we have

If we choose $\zeta_2^*$ as

we get

where $\alpha_1 = c_1^{1/\underline{m}}\geq1$ is a constant with $c_1\geq1$ being a design parameter.

Substituting (3.3) into (3.1) yields

Step 2. Introducing the coordinate transformation $\xi_2 = \zeta_2-\zeta_2^*$, and using Itô's differentiation rule, we get

Choose $V_2 = V_1+\frac{1}{4}\xi_2^4$. From (3.4) and (3.5), we obtain

By (3.2) and using Lemma 1 in ^[19], we have

By using Lemma 2.1 in ^[20], we get

where

Substituting (3.8) into (3.7) yields

where $\beta_{21} = \beta_{211}+\beta_{212}$ is a positive constant.

By (3.2) and using Lemma 5 in ^[21], we get

which means that

where $\varphi_1 = 2^{\bar{m}-1}\alpha_1^{\bar{m}}+1\geq0$ is a constant.

By (3.11) and using Lemma 1 in ^[19], we have

By using Lemma 2.1 in ^[20], we get

where

Substituting (3.14) into (3.13) yields

where $\beta_{22}(\zeta_1) = 2^{\bar{m}-1}\alpha_1^{\bar{m}}|\frac{\partial \zeta_2^*}{\partial \zeta_1}|+\beta_{221}(\zeta_1)$ is a smooth function irrelevant to $m(t)$.

By (3.12), using Assumption $2.1$ and Lemma 1 in ^[19], we get

where $\varphi_2 = 2^{\bar{m}}\alpha_1^{\bar{m}+1}+1\geq0$ is a constant.

From Lemma 2.1 in ^[20], we obtain

where

Substituting (3.18) into (3.17) yields

where $\beta_{23}(\zeta_1) = 3\tilde{f}^2(\zeta_1)\varphi_2+\beta_{231}(\zeta_1)\geq0$ is a smooth function irrelevant to $m(t)$.

By using (3.6), (3.10), (3.16) and (3.20), we obtain

where $\beta_{2}(\zeta_1) = \beta_{21}(\zeta_1)+\beta_{22}(\zeta_1)+\beta_{23}(\zeta_1)$ is a smooth function irrelevant to $m(t)$.

Constructing the virtual controller as

we have

where $c_2 > 0$ is a constant and $\alpha_2(\zeta_1)\geq0$ is a smooth function irrelevant to $m(t)$.

Substituting (3.23) into (3.21) yields

3.2.   Output-feedback controller design

In this part, we first design a reduced-order observer with a dynamic gain, then we design an output-feedback controller.

Since $\zeta_2$ are unmeasurable, we construct the following observer

where $L(\zeta_1)$ is a smooth function, and $\frac{\partial L(\zeta_1)}{\partial \zeta_1} > 0$ is irrelevant to $m(t)$.

Defining $e = \zeta_2-L(\zeta_1)-\eta$ and by the construction of the observer, we have

Choose $U = \frac{1}{4}e^4$. From (3.26), we get

By definition of $e$ and lemma 2.2 in ^[22], we have

From (3.12), (3.17) and Assumption $2.1$, we get

By using Lemma 2.1 in ^[20], we have

where

Substituting (3.30) into (3.29) yields

where $\beta_{3}(\zeta_1) = \beta_{31}(\zeta_1)+\beta_{32}(\zeta_1)\geq0$ is a smooth function irrelevant to $m(t)$.

Substituting (3.28), (3.32) into (3.27) yields

Since $\zeta_2$ is unmeasurable, replace $\zeta_2$ in virtual controller $x_3^*$ with $\eta+L(\zeta_1)$, and we can get the controller as follows

By (3.22), (3.24) and (3.34), we obtain

By using Lemma 1 in ^[19], we have

By using Lemma 2.1 in ^[20], we get

where

Substituting (3.37) into (3.36) yields

where $\beta_{4}(\zeta_1) = \beta_{41}(\zeta_1)+\beta_{42}(\zeta_1)\geq0$ is a smooth function irrelevant to $m(t)$.

By using (3.39) and (3.35), we have

Choosing $V(\xi_1, \xi_2, e) = V_2(\xi_1, \xi_2)+U(e)$, by (3.33) and (3.40), we obtain

Let

and the controller as

where $c_3 > 0$ is a design parameter.

By using (3.41) and (3.42), we can obtain

Remark 3.1. If $m(t)$ is time-invariant and the growth rate is a constant rather than a smooth function, such as those in ^[7,8,9], from (3.32) and (3.39), $\beta_3$ and $\beta_4$ are constants irrelevant to $\zeta_1$. Then, the dynamic gain $L(\zeta)$ is a linear function of $\zeta_1$. We can design $L(\zeta_1) = c\; \zeta_1$ by choosing the right parameter $c$ to make $\mathcal{L}V$ in (3.41) negative definite. However, in this paper, the growth rate $\tilde{f}(\zeta_1)$ is a nonnegative smooth function and the $m(t)$ is time-varying and non-differentiable, which makes the deducing of the dynamic gain much more difficult. To solve this problem, we introduce two constants $\underline{m}$ and $\bar{m}$, which are reasonably used in the design process, see (3.7) and (3.11). In this way, the dynamic gain (3.42) can be designed irrelevant to $m(t)$, which is crucial to assure the effectiveness of the observer and controller. This is one of the main innovations of this paper.

4.   Stability analysis

In this section, for the closed-loop system (2.1), (3.25) and (3.43), we first give a lemma, which is useful to prove the system has a unique solution. Then, we present the main results of the stability analysis.

Lemma 4.1. For $\zeta\in \mathrm{R}$, the function $g(\zeta) = [\zeta]^{m(t)}$ satisfies the locally Lipschitz condition.

Proof. If $\zeta = 0$, we can get

Then, we have

thus, $h(\zeta)$ is differentiable function in $\zeta = 0$ and so meets the locally Lipschitz condition in $\zeta = 0$.

As $\zeta > 0$, we get

For $m(t)\geq1$, $h(\zeta)$ is differentiable function in $\zeta > 0$, so meets the locally Lipschitz condition in $\zeta > 0$. Similarly, as $\zeta < 0$, the conclusion is valid.

Therefore, the conclusion holds for $\zeta\in \mathrm{R}$.

Next, we give the stability results.

Theorem 4.1. Under Assumption $2.1$, for the system (2.1), using the observer (3.25) and controller (3.43) with

we can get

1) For each $\zeta(t_0) = \zeta_0\in \mathrm{R}^2$ and $\gamma(t_0) = i_0\in S$, the closed-loop system has an almost surely unique solution on $[0, +\infty)$;

2) For any $\zeta_0\in \mathrm{R}^2$ and $i_0\in S$, the closed-loop system is almost surely regulated to the equilibrium at the origin.

Proof. By (2.1), (3.25), (3.43) and using Lemma $4.1$, we can conclude that the closed-loop system satisfies the locally Lipschitz condition. By (3.2), (3.22), (3.25) and (3.42), we can get that $\xi_1, \xi_2, \eta$ are bounded, which implies that $\zeta_1$ is bounded, which means that

Through the verification of the controller development process, we choose appropriate design parameters $c_i$ to satisfy (4.4), and we can get $IIV = 0$. For each $l > 0$, the first exit time is defined as

When $t\geq t_0$, choose $t_l = \min\{\sigma_l, t\}$. We can obtain that bounded $|\zeta(t)|$ on interval $[t_0, t_l]$ a.s., which means that $V(\zeta)$ is bounded in the interval $[t_0, t_l]$ a.s. By using (3.44), we can get that $\mathcal{L}V$ is bounded in the interval $[t_0, t_l]$ a.s. By using Lemma 1.9 in ^[11], (3.44) and (4.4), we can obtain

By (4.5), (4.7) and using Lemma 1 in ^[23], we can obtain conclusion (1).

From (3.44), (4.5), by using Theorem 2.1 in ^[24], we can prove conclusion (2).

5.   A simulation example

In this section, a simulation example is given to show the availability of the control method.

Study the stabilization for system with two modes. The Markov process $\gamma(t)$ belongs to the space $S = \{1, 2\}$ with generator $\Gamma = (\lambda_{ij})_{2\times2}$ given by $\lambda_{11} = 2, \lambda_{12} = -2, \lambda_{21} = -1$ and $\lambda_{22} = 1$. We have $\pi_1 = \frac{1}{3}, \pi_2 = \frac{2}{3}$. When $\gamma(t) = 1$, the systems can be written as

where $m(t) = \frac{3}{2}+\frac{1}{2}\sin t, \underline{m} = 1, \bar{m} = 2$. When $\gamma(t) = 2$, the systems are described by

where $m(t) = 2+\sin t, \underline{m} = 1, \bar{m} = 3$. Clearly, system (5.1) and (5.2) satisfy Assumption $2.1$.

According to the above design process, when $\gamma(t) = 1$, the observer is constructed as

and the control is

where $L(\zeta_1) = \frac{1}{2}(c_3\zeta_1+6\zeta_1^2)$.

When $\gamma(t) = 2$, the observer is constructed as

and the control is

where $L(\zeta_1) = \frac{1}{4}(c_3\zeta_1+20\zeta_1+4\zeta_1^2)$.

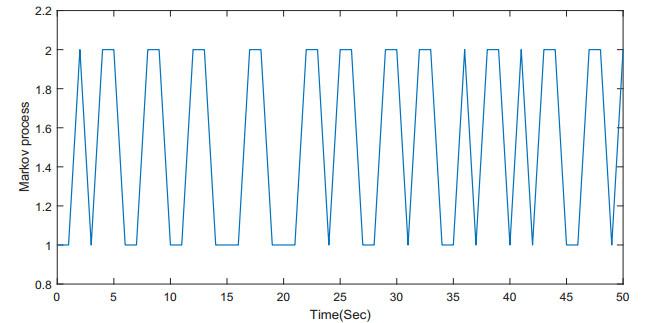
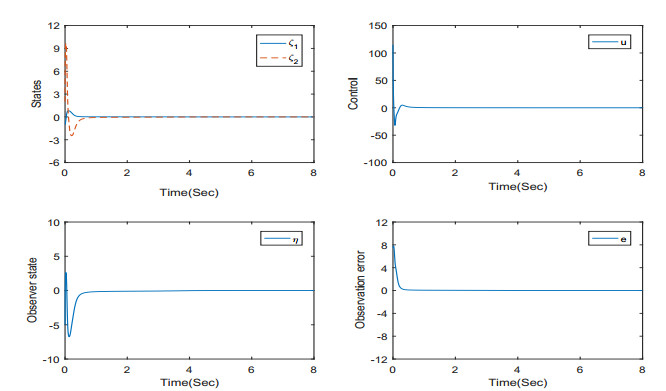
For simulation, we select $c_1 = 6, c_2 = 6, c_3 = 5$, and the initial conditions as $\zeta_1(0) = -1, \zeta_2(0) = 2, \eta(0) = -5$. We can obtain Figure 1, which illustrates that the signals of the closed-loop system $(\zeta_1, \zeta_2, u, \eta, e)$ converge to zero. Specifically, the states and controller of the closed-loop system converge to zero. The observation error also converges to zero, which means that our constructed observer and controller are efficient. Figure 2 illustrates the jump of Markov process $\gamma(t)$ in 1 and 2.

Remark 5.1. It can be observed from the example that there are time-varying powers and Markovian switching in systems (5.1) and (5.2). For the output-feedback control of the system (5.1) and (5.2), the method in ^[7,8,9] fails since they can only deal with time-invariant powers without Markovian switching. To solve the difficulties caused by time-varying powers, we introduce constants 1, 2, and 1, 3 so that the design of the observer and controller is irrelevant to the power. This is one of the characteristics of our controller and observer design scheme (5.3)–(5.6).

6.   Concluding remarks

We investigate the output-feedback stabilization for stochastic nonlinear systems with both Markovian switching and time-varying powers in this paper. Compared with existing work, the system model considered in this paper is more general because it studies the time-varying power and Markovian switching, simultaneously. To achieve stabilization, we first design a state observer with a dynamic gain and an output-feedback controller, then use advanced stochastic analysis techniques to prove that the closed-loop system has an almost surely unique solution and the states are regulated to the origin almost surely. Even though there is no Markovian switching, the results in this paper are also new in the sense that we consider nonlinear growth rate, which is much more general than constant growth rate cases in ^[7,8,9].

There are many related problems to be considered, such as how to extend the result to impulsive systems ^[25,26,27] and systems with arbitrary order.

Acknowledgments

This work is funded by Shandong Province Higher Educational Excellent Youth Innovation team, China (No. 2019KJN017), and Shandong Provincial Natural Science Foundation for Distinguished Young Scholars, China (No. ZR2019JQ22).

Conflict of interest

The authors declare there is no conflict of interest.