Evaluation of c-Kit (CD117) expression in patients with squamous cell carcinoma (SCC) and basal cell carcinoma (BCC) of the skin

Abbreviation: SFF: spacecraft formation flying; ETS: event triggered strategy; DETS: dynamic event triggered transmission strategy; ESO: extended state observer; FTSM: fast terminal sliding mode

1.   Introduction

In advanced space technologies, spacecraft formation flying (SFF) technology has attracted considerable attention due to its evident advantages over traditional single spacecraft technology, such as low cost, high reliability, and greater flexibility. The applications of SFF technology have covered a wide range of space missions, including Earth observation, deep space exploration, on-orbit servicing and gravitational-wave detection ^[1,2,3]. For the SFF system, one of the main characteristics is that the spacecraft in the system should coordinate with each other to perform the specified mission, and thus it is crucial to design an efficient coordinated control strategy ^[4,5]. In general, the existing coordinated control strategies can be classified into centralized control strategies and decentralized control strategies, in which decentralized strategies have high reliability and strong robustness ^[6,7,8,9]. Therefore, for SFF system, the development of decentralized coordinated control strategies with distinguished potential in practical applications have received a great deal of research attention ^{[10,11,12,13,14]}.

In traditional decentralized coordinated control methods, each spacecraft is required to continuously broadcast its own real-time state and receive the real-time global state through the wireless communication network, which consumes significant communication resources and contains a large amount of redundant communication. However, restricted by current launch capability and wireless communication technology, the on-board communication modules are generally small in size and narrow in bandwidth, and a flood of unnecessary communication may cause congestion and packet loss. It is therefore essential to investigate coordinated control strategies with less communication bandwidth occupancy. In light of this, some recent investigations on SFF systems adopt an intermittent communication transmission strategy, called event triggered strategy (ETS), to schedule inter-spacecraft data transmission ^{[15,16,17,18,19]}. In ETS, the communication is only carried out when a pre-defined triggering condition is met, which significantly avoids the unnecessary communication waste caused by continuous communication transmission or periodic communication transmission ^[20,21]. More recently, a dynamic event triggered transmission strategy (DETS) that can further reduce the communication frequency has gained growing research interest ^[22]. By introducing an auxiliary dynamic variable, the average inter-event interval of DETS can be larger than that of the traditional static ETS, thereby reducing the communication consumption. However, there has been little work on DETS-based distributed coordinated control strategies for SFF systems.

It should be pointed out that, a majority of the existing studies on SFF systems have been concerned with the asymptotical stability of the coordinated control strategy. However, the corresponding investigations on finite-time control strategy have attracted little research attention, not to mention the case where unmeasured velocity and event triggered transmission are taken into account. In fact, finite-time convergence performance is a very concerned indicator in engineering ^[23,24]. When performing real-time and emergency space missions, it is more desirable to achieve finite-time coordination of the SFF systems. It is, therefore, of essential practical significance to design an event-based velocity-free coordinated control strategy that can provide finite-time relative position coordination for SFF, which motivates this current study.

In this paper, a finite-time velocity-free relative position coordinated control strategy based on DETS is proposed for SFF systems under an undirected communication graph. The entire design process of this control strategy is divided into the following four steps: First, considering the situation where the velocities of the spacecraft cannot be accurately measured, a finite-time extended state observer (ESO) is constructed to estimate the velocity information and the effects of non-linearity and disturbance of each spacecraft. Second, a DETS among spacecraft is designed to reduce communication burden. Further, on the basis of the proposed observer and ETS, a fast terminal sliding mode (FTSM) coordinated control law is developed to achieve finite-time coordination of the overall spacecraft formation. Finally, a numerical simulation is performed to demonstrate the effectiveness of the control law.

The main contributions of this paper lie in the following folds:

$1)$ In this paper, a finite-time ESO is constructed to estimate the velocity information and the effects of non-linearity and disturbance of each spacecraft, which lays the foundation for the subsequent design of the finite-time controller.

$2)$ Different from the traditional static ETS employed in coordinated control for SFF, in this design, a DETS is introduced into the SFF system, which can reduce the communication burden among spacecraft more effectively than the static ETS.

$3)$ In this paper, we have make the first attempt to investigate the coordinated control law design problem for SFF systems where finite-time coordination, unmeasured velocity and the limited communication bandwidth among spacecraft are considered simultaneously.

The arrangement of this paper is as follows. Preliminaries along with the problem formulation are exhibited in Section 2. The main results of the ESO based FTSM coordinated control law under DETS are presented in Section 3. The numerical simulation result is given in Section 4, to demonstrate the performance of the proposed control strategies. Conclusions are provided in Section 5.

2.   Preliminaries

2.1.   Some definitions of graph theory

In fact, an SFF system is a typical kind of distributed network system in the aerospace area, and it realizes coordinated flight on the basis of information exchange between spacecraft. On the other hand, graph theory is a useful tool both in the description of information topology and in coordinated control design ^[25]. Therefore, similar to most existing spacecraft formation coordinated control strategies ^{[15,16,17,18,19]}, in this paper, we employ the graph tool to describe the information transmission among spacecraft and to cope with the problem of coordinated control law design. In this subsection, we will introduce some basic definitions of graph.

A graph $\mathit{\boldsymbol{\Lambda}} = (\mathit{\boldsymbol{\upsilon, \varsigma, G}})$ consists of a node set (limited and non-empty) $\mathit{\boldsymbol{\upsilon}} = \left\{ {{\upsilon }_{1}}, \cdots, \left. {{\upsilon }_{n}} \right\} \right.$, an edge set (composed by ordered pairs of nodes) $\mathit{\boldsymbol{\varsigma}}\subseteq \mathit{\boldsymbol{\upsilon}}\times \mathit{\boldsymbol{\upsilon}}$ and a weight adjacency matrix $\mathit{\boldsymbol{G}} = \left[ {{g}_{ij}} \right]\in {{\bf{R}}^{n\times n}}$. If all edges in a graph have no direction, the graph is classified as an undirected graph; otherwise, the graph is classified as a directed graph. For the weight adjacency matrix, the default value of ${{g}_{ii}}$ is $0$. If node ${{\upsilon }_{j}}$ can transmit information to node ${{\upsilon }_{i}}$, namely $({{\upsilon }_{i}}, {{\upsilon }_{j}})\in \mathit{\boldsymbol{\varsigma}}$, the corresponding weighted adjacency coefficient ${{g}_{ij}} > 0$. Obviously, when it comes to undirected graphs, there is ${{g}_{ij}} = {{g}_{ji}} > 0$, once ${{\upsilon }_{i}}$ and ${{\upsilon }_{j}}$ are connected.

2.2.   The relative dynamic model

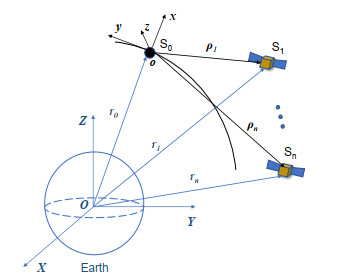
The nonlinear dynamic model of SFF based on the relative position vector and relative velocity vector is established in this paper. The schematic diagram of the relative motion of SFF is shown in Figure 1, where $\; {{S}_{0}}$ denotes the leading spacecraft while ${{S}_{i}}\left(i = 1, 2, \ldots n \right)$ denotes the $i\rm{th}$ follower. Two coordinate frames are introduced to describe the absolute motion and relative motion: the geocentric inertial coordinate frame $C-OXYZ$ and the orbit coordinate frame of the leading spacecraft $C-oxyz$. It should be noted that $\; {{S}_{0}}$ does not have to be a real spacecraft, and it could be a virtual leader for a distributed SFF system, flying on an ideal Kepler orbit with its motion state known to all followers. Since we are not going to discuss issues related to spacecraft attitude, to simplify the analysis below, a spacecraft is considered as a particle. Then, the nonlinear relative position dynamic model of the $i\rm{th}$ spacecraft represented in the orbital coordinate frame of the virtual leader can be written as follows ^[1]:

where ${{\mathit{\boldsymbol{r}}}_{i}}(t)\left(i = 0, 1, 2, \ldots n \right)$ denotes the position vector in the geocentric inertial coordinate frame, ${{\mathit{\boldsymbol{\rho}}}_{i}(t)} = {{\mathit{\boldsymbol{r}}}_{i}(t)}-{{\mathit{\boldsymbol{r}}}_{0}}\left(i = 1, 2, \ldots n \right)$ denotes the relative position vector in the orbit coordinate frame, $\mu$ represents the gravitational coefficient of the earth, the angular velocity of the virtual leading spacecraft is denoted by ${\boldsymbol{\theta}}(t)$, ${{\mathit{\boldsymbol{f}}}_{di}(t)}$ represents the external disturbance force, the control force of the $i\rm{th}$ spacecraft is denoted by ${{\mathit{\boldsymbol{f}}}_{ai}(t)}$, and the mass of each spacecraft is denoted by ${{m}_{i}}$.

For an SFF mission, there will be a predesigned configuration, which provides the expected position $\mathit{\boldsymbol{\rho}}_{i}^{d}(t)$ and the expected velocity $\mathit{\boldsymbol{v}}_{i}^{d}(t) = \mathit{\boldsymbol{\dot{\rho }}}_{i}^{d}(t)$ of each spacecraft. Subtracting the expected value from the real value, we obtain the position tracking error ${{\mathit{\boldsymbol{e}}}_{\rho i}(t)} = {{\mathit{\boldsymbol{\rho}}}_{i}(t)}-\mathit{\boldsymbol{\rho}}_{i}^{d}(t)$ and velocity tracking error ${{\mathit{\boldsymbol{e}}}_{vi}(t)} = {{\mathit{\boldsymbol{v}}}_{i}(t)}-\mathit{\boldsymbol{v}}_{i}^{d}(t)$ of the $i\rm{th}$ spacecraft. Furthermore, the relative error dynamic model can be derived.

Considering the relative position keeping problem for distributed SFF without velocity information over limited communication bandwidth, this paper attempts to propose a finite-time coordinated control law based on a state observer and ETS. That means that by applying the control law we would like to make sure $\left|{{\mathit{\boldsymbol{e}}}_{\rho i}(t)}-{{\mathit{\boldsymbol{e}}}_{\rho j}(t)}\right|\le {\Delta}_\rho$, $\left|{{\mathit{\boldsymbol{e}}}_{vi}(t)}-{{\mathit{\boldsymbol{e}}}_{vj}(t)}\right|\le {\Delta}_v$, and ${{\mathit{\boldsymbol{e}}}_{\rho i}(t)}\to {{\mathit{\boldsymbol{0}}}^{{p}}}$, ${{\mathit{\boldsymbol{e}}}_{vi}(t)}\to {{\mathit{\boldsymbol{0}}}^{{p}}}$ in finite time, where ${\Delta}_\rho$ and ${\Delta}_v$ are small constants.

2.3.   Assumptions and Lemmas

$\bf{Assumption}$ 1. In the following derivation, we assumed that the communication topology among spacecraft is undirected and connected.

$\bf{Assumption}$ 2. The external disturbance considered in this paper is assumed to be bounded, meaning that $\left\| {{\mathit{\boldsymbol{f}}}_{di}(t)} \right\|\le {{d}_{i}}$ holds, and the constant ${{d}_{i}}\ge 0$.

$\bf{Lemma}$ 1^[26] : For positive constants ${{x}_{i}} (i = 1, 2, \ldots, n)$ and $q\in (0, 1)$, there are the following relations

$\bf{Lemma}$ 2^[26] : Suppose the dynamic model of the system is $\dot {\mathit{\boldsymbol{s}}} = f(\mathit{\boldsymbol{s}})$, $\mathit{\boldsymbol{s}} \in {\mathit{\boldsymbol{U}}} \subseteq {\bf R}^p$, where ${\mathit{\boldsymbol{U}}}$ is an open neighbor of the origin. If the Lyapunov function ${V}(\mathit{\boldsymbol{s}}) = \frac{1}{2}{{\mathit{\boldsymbol{s}}}^{T}{\mathit{\boldsymbol{s}}}}$ satisfies the inequality

$\mathit{\boldsymbol{s}}$ will converge to $\mathit{\boldsymbol{s}} = {{\mathit{\boldsymbol{0}}}^{p}}$ in finite time, where constants ${{v}_{1}}, {{v}_{2}} > 0$, $0 < \gamma < 1$. The settling time can be given by

$\bf{Lemma}$ 3^[26] : For a system with dynamic $\dot {\mathit{\boldsymbol{s}}} = f(\mathit{\boldsymbol{s}})$, $\mathit{\boldsymbol{s}} \in {\mathit{\boldsymbol{U}}} \subseteq {\bf R}^p$, where ${\mathit{\boldsymbol{U}}}$ is an open neighbor of the origin, if the Lyapunov function $V(\mathit{\boldsymbol{s}}) = \frac{1}{2}{{\mathit{\boldsymbol{s}}}^{T}{\mathit{\boldsymbol{s}}}}$ satisfies the inequality

$\mathit{\boldsymbol{s}}$ will converge to $\mathit{\boldsymbol{s}} = {{\mathit{\boldsymbol{0}}}^{p}}$ in finite time, where ${{v}_{1}} > 0$, $0 < \gamma < 1$. The settling time can be given by

3.   Main results

In this section, the ESO-based finite-time relative position coordinated control law for distributed SFF system under DETS will be investigated. A finite-time ESO method is developed first to obtain the estimates of system states, based on which an FTSM control approach is proposed based on the DETS to achieve the coordinated control objective.

3.1.   Finite-time ESO

In practical engineering, due to cost and technology limitations, the velocity of a spacecraft may be unavailable for precise measurement. An ESO has been recognized as an effective approach to simultaneously compensate the system states and disturbances/uncertainty. Therefore, in this paper, a modified ESO is proposed to generate finite-time observations of both the velocity information and the effects of non-linearity and disturbance of each spacecraft. Transform the dynamic (1) into the following form:

where, ${\mathit{\boldsymbol{f(}}}{{\mathit{\boldsymbol{\rho}}}_i(t)}{\bf{, }}{\mathit{\boldsymbol{v}}_i(t)}{\bf{)}}{\rm{ = }}{{\mathit{\boldsymbol{C}}}_i}{\mathit{\boldsymbol{v}}_i(t)} + {{\mathit{\boldsymbol{D}}}_i}{{\mathit{\boldsymbol{\rho}}}_i(t)}$, ${{\mathit{\boldsymbol{G}}}_i(t)}{\mathit{\boldsymbol{ = (}}}{{\mathit{\boldsymbol{u}}}_{di}(t)}{\bf{ + }}{{\mathit{\boldsymbol{N}}}_i(t)})$, ${{\mathit{\boldsymbol{u}}}_{ai}(t)} = \frac{{\mathit{\boldsymbol{f}}}_{ai}}{m_i}$ and ${{\mathit{\boldsymbol{u}}}_{di}(t)} = \frac{{\mathit{\boldsymbol{f}}}_{di}}{m_i}$. Let the observed position and the observed velocity be ${{\mathit{\boldsymbol{\hat \rho}}}_i(t)}$, ${{\mathit{\boldsymbol{\hat v}}}_i(t)}$. Then, define position observation error and velocity observation error as ${{\mathit{\boldsymbol{\tilde \rho}}}_i(t)} = {{\mathit{\boldsymbol{\hat \rho}}}_i(t)} - {{\mathit{\boldsymbol{\rho}}}_i(t)}$ and ${{\mathit{\boldsymbol{\tilde v}}}_i(t)} = {{\mathit{\boldsymbol{\hat v}}}_i(t)} - {\mathit{\boldsymbol{v}}_i(t)}$, respectively.

Then, the finite-time ESO is designed as follows:

where ${{\mathit{\boldsymbol{z}}}_{i1}(t)} = \alpha_1 {\mathop{\rm sgn}} ({{\mathit{\boldsymbol{\tilde \rho}}}_{{i}}(t)})$, ${{\mathit{\boldsymbol{z}}}_{i2}(t)} = \alpha_2 {\mathop{\rm sgn}} ({{\mathit{\boldsymbol{z}}}_{i1}(t)}) + \alpha_3 {{\mathit{\boldsymbol{z}}}_{i1}}^{q}(t)+ \alpha_4 {{\mathit{\boldsymbol{z}}}_{i1}(t)}$, ${{\mathit{\boldsymbol{z}}}_{i3}(t)} = \alpha_5 {\mathop{\rm sgn}} ({{\mathit{\boldsymbol{z}}}_{i2}(t)}) + \alpha_6 {{\mathit{\boldsymbol{z}}}_{i2}(t)}$, $\alpha_1, \alpha_2, \alpha_3, \alpha_4, \alpha_5, \alpha_6$ are parameters to be designed, and matrix ${{\mathit{\boldsymbol{L}}}_{i1}} = {\mathop{\rm diag}\nolimits} \left\{ {{l_{ij}}} \right\}$, ${l_{ij}}$ $(j = 1, 2, 3)$ is a constant, and $q$ is a fraction that satisfies $q < 1$ where the numerator and denominator are odd numbers. By subtracting Eq (3) from Eq (4), the following error system is constructed:

The convergence of the observer will be stated in Theorem 1.

Before giving Theorem 1, we make some assumptions from a practical point of view. The position, velocity, non-linearity term and disturbance of a spacecraft cannot be infinite in actual systems; thus, it is reasonable to assume that there exists an upper bound for the observation state. In other words, we can always find positive constants $M_0$ and $G_0$ that make $\left\| {{{{\mathit{\boldsymbol{\tilde v}}}}_i(t)}} \right\| \le M_0$ and $\left\| {{{{\mathit{\boldsymbol{\tilde G}}}}_i}(t)} \right\| \le {G_{0}}$ hold. Also, there exists a positive constant $C_0$, such that $\left\| {{{{\mathit{\boldsymbol{C}}}}_i(t)}} \right\| \le C_0$ holds. Moreover, external disturbances are also bounded according to Assumption 2. It follows that there exists a positive constant ${G_{1}} > 0$ such that $\left\| {{{{\mathit{\boldsymbol{G}}}}_i}(t)} \right\| \le {G_{1}}$ holds.

Theorem 1. For system (3), if the observer (4) is applied, and the design parameters satisfy:

then ${\boldsymbol{ \rho} }_i(t)$, ${{\mathit{\boldsymbol{v}}} }_i(t)$ and ${{\mathit{\boldsymbol{G}}} }_i(t)$ can be accurately estimated by the designed observer in a finite time.

Proof. First, we analyze the convergence of ${\mathit{\boldsymbol{\tilde {\rho }}}_i(t)}$. Propose such a Lyapunov candidate:

Taking the derivative of ${V}_0(t)$, we have

Note that $\alpha_1 > M_0$, and the finite-time convergence of $\left\| {{{{\mathit{\boldsymbol{\tilde \rho}}}}_i(t)}} \right\|$ can be proved according to Lemma 3, where

Next, we perform the convergence analysis on $\mathit{\boldsymbol{\tilde v}}_i(t)$. Suppose that $\left\| {{{{\mathit{\boldsymbol{\tilde \rho}}}}_i(t)}} \right\| = {0}, t \ge T_0$ also represents $\left\| {{\mathit{\boldsymbol{\dot{\tilde\rho}}}}_i(t)} \right\| = {{{\mathit{\boldsymbol{\tilde v}}}}_i(t)} - {{\mathit{\boldsymbol{z}}}_{i1}(t)} = {0}, t \ge T_0$. In other words, there is ${{{\mathit{\boldsymbol{\tilde v}}}}_i(t)} = {{\mathit{\boldsymbol{z}}}_{i1}(t)},$ and $t \ge T_0$. Propose a new Lyapunov candidate

Taking the time derivative of ${V}_1(t)$ yields

Note that $\alpha_2 > G_{0}$, $\alpha_3 > 0$, and $\alpha_4 > {{C}}_0$, and thus the finite-time convergence of $\left\| {{{{\mathit{\boldsymbol{\tilde v}}}}_i}(t)} \right\|$ is proved according to Lemma 2. That means there exists a time instant $T_1 > T_0$, such that $\left\| {{{{\mathit{\boldsymbol{\tilde \rho}}}}_i}(t)} \right\| = 0$ and $\left\| {{{{\mathit{\boldsymbol{\tilde v}}}}_i}(t)} \right\| = {{\mathit{\boldsymbol{\tilde G}}}_i(t)}- {{\mathit{\boldsymbol{z}}}_{i2}(t)} = 0$ hold, when $t > T_1$, where

Finally, the finite-time convergence analysis of $\left\| {{{{\mathit{\boldsymbol{\tilde G}}}}_i(t)}} \right\|$ is given as follows. Another new Lyapunov candidate is proposed:

Taking the derivative of ${V}_2(t)$ yields

Similarly, by substituting $\alpha_5 > G_{1}$, $\alpha_6 > 0$, $\left\| {{{{\mathit{\boldsymbol{\tilde G}}}}_i(t)}} \right\|$ will converge to the origin in a finite time according to Lemma 3. That means that there exists a time instant $T_2 > T_1$, such that $\left\| {{{{\mathit{\boldsymbol{\tilde G}}}}_i(t)}} \right\| = 0$ holds, when $t > T_2$, where

We thus complete the proof.

3.2.   Finite-time relative position coordinated control strategy

In this subsection, based on the estimates ${{\mathit{\boldsymbol{\hat v}}}_i(t)}$ and ${{\mathit{\boldsymbol{{\hat G}}}}_i(t)},$ we will propose an event-based FTSM control law for SFF systems (1). First, a fast terminal sliding surface is given as follows:

where $\mathop{\rm sig^\beta}({\mathit{\boldsymbol{x}}}) = \rm {diag} (|x_i|^\beta)\mathop{\rm sgn}({\mathit{\boldsymbol{x}}}) = \left[|x_1|^\beta\mathop{\rm sgn}(x_1)\; \; |x_2|^\beta\mathop{\rm sgn}(x_2)\; \; \cdots\; \; |x_n|^\beta\mathop{\rm sgn}(x_n)\right ]^T$, ${{\mathit{\boldsymbol{e}}}_{\hat v_i}(t)}{\rm{ = }}{{\mathit{\boldsymbol{\hat v}}}_i(t)} - {\mathit{\boldsymbol{v}}}_i^d(t) = {{\mathit{\boldsymbol{\hat v}}}_i(t)} - {{\mathit{\boldsymbol{v}}}_i(t)} + {{\mathit{\boldsymbol{v}}}_i(t)} - {\mathit{\boldsymbol{v}}}_i^d(t) = {{\mathit{\boldsymbol{\tilde v}}}_i(t)} + {{\mathit{\boldsymbol{e}}}_{v_i}(t)}$, and $\gamma, \kappa\in {\bf R^+}$are parameters to be designed.

For the convenience of later derivation, we define

In order to reduce communication frequency, an improved DETS is introduced in this paper. To better understand DETS, we first define a traditional static triggering condition as follows

where $\zeta, {\mathcal L }\in {\bf R^+}$are parameters to be designed. Next, a dynamic variable $H_i(t)$ is introduced:

where constant $\beta \in (0, 1)$ and $\lambda \in {\bf R^+}$. It will be proved later that the dynamic variable ${{H}_i(t)}$ remains positive throughout the process. Then, the dynamic triggering condition can be defined as

where $\theta\in{\bf R^+}$. From the triggering condition, during each interval $\left[ {t_{k_i}^i, t_{k_i + 1}^i} \right)$, we have

Substituting (13) into (11) yields

By applying the differential equation theorem and the comparison lemma, it follows that

This completes the construction of the DETS. From the above DETS, the trigger state will only be updated and broadcasted when the trigger condition (12) is met.

Further, a DETS based finite-time coordinate control law is proposed as

where $\zeta, {w}, {\varsigma }, k_i \in {\bf R^+}$ are control parameters to be designed. The performance of the proposed control law (16) is stated in Theorem 2.

Theorem 2. For distributed SFF systems (1) with the DETS based control law (16), suppose Assumptions 1 and 2 hold, and the following inequalities hold

where ${{\rm{\tilde\Delta}}_{max}}$ will be defined later in Eq (33). Then, the relative position coordination problem that states in Section 2 can be achieved in a finite time.

Proof. The proof of Theorem 2 is divided into the following two parts.

(i) First, we should prove that spacecraft in a formation system can achieve consensus in a finite time. Since it has been proved that the observation velocity can converge to a real velocity in finite time ${T_2}$, we set the initial moment when we start to exert control actions to ${t_0} \ge {T_2}$. Then, it is available to use real velocity to replace the observed one in the following proof. By substituting the control law (16) into the error dynamic model (2), we have

It follows from (9) that

Since the communication topology is undirected and connected, we have ${g_{ij}} = {g_{ji}}$, and obviously

can be obtained. It follows that

Considering the following Lyapunov candidate:

where ${V_{31}(t)} = {\frac{1}{2}{\mathit{\boldsymbol{\eta}}}^T(t)}{\mathit{\boldsymbol{\eta (t)}}}$, and ${V_{32}(t)} = \sum\limits_{i = 1}^n{{\mathit{\boldsymbol{H}}}_i(t)}$. Taking the time derivative of $V_{31}(t)$, it is shown that

For the first term in ${\dot{V}}_{31}(t)$, we have

For the second term in ${\dot{V}_{31}(t)}$, it is derived that

When it comes to the last term in ${\dot{V}_{31}(t)}$, we can obtain

By using the Cauchy-Schwarz inequality and Lemma 1, from $\dot{V}_{31}(t)$ it can be further derived that

According to the dynamic function (11), during each interval $\left[ {t_{k_i}^i, t_{k_i + 1}^i} \right)$, we rewrite the second term of ${\dot{V}}_{3}(t)$ into the following version:

Since $\zeta\le \frac{1}{2}{w}$ and ${\mathcal L \ge {w}}$, it follows that

Obviously, based on Lyapunov stability analysis theory, the asymptotical consensus of system (2) can be achieved under the control law (16). Next, the finite-time consensus will be further proved.

For the dynamic variable $H_i(t)$, it can be easily calculated that $\sum\limits_{i = 1}^nH_i(t)\ge \sum\limits_{i = 1}^nH_i^ \frac{1+\beta}{2}(t)-n$. One can thus obtain

where $\Delta _0 = \lambda n$. On the one hand, it can be obtained that

On the other hand, it can be deduced that

Furthermore, in view of practical engineering and ETS, the following inequality holds during each trigger interval $\left[ {t_{k_i}^i, t_{k_i + 1}^i} \right)$:

where $\kappa_i$ and $\Delta_i$ are positive constants. That leads to

where $\phi_i = \kappa_{min}(\frac{1}{2}-\zeta{w})$ and $\Delta = \sum\limits_{i = 1}^n\Delta_i$. Moreover, we have

In combination of Eqs (26), (30) and (31), it can be concluded that

where $\tilde\Delta = \Delta+\Delta_0$, ${\phi _2} = min\{\phi_1 n^{1+\beta}, \lambda\}$. According to Lemma 3 and bounded theory, it can be proved that the consensus error will converge to a small bound in a finite time $T_3$, where

(ii) Second, we should prove that the states of each spacecraft can converge to the expected values in a finite time. Another Lyapunov candidate is proposed as

Taking the derivative of $V_4(t)$, one can obtain that

where $\phi_3 = 2\kappa_{min}$, $\phi_4 = \sqrt 2 ({\varsigma }{\rm{ - }}{{\rm{\tilde\Delta}}_{max}})$, ${{\rm{\tilde\Delta}}_{i} = \Delta_i+\Delta_0}$, and ${{\rm{\tilde\Delta}}_{max}} =$ max $\{{{\rm{\tilde\Delta}}_{i}, i = 1, 2, ..., n}\}$. According to Lemma 2, the finite-time convergence of each spacecraft is proved, and the convergence time $T_4$ satisfies

Hence, the proof of Theorem 2 is finished.

3.3.   Zeno behavior analysis

For an event triggered control system, not only the stability of the controller should be analyzed, but also the Zeno behavior in the system should be further analyzed. In this subsection, we would like to exclude the Zeno behavior by proving that the trigger interval cannot be infinitely small.

Theorem 3. For an SFF system (1) under the proposed control law (16) and the triggering function (12), there exists a lower bound for the time interval between any two triggers. In other words, there will be no Zeno behaviour during the whole process.

Proof. During each trigger interval $\left[ {t_{k_i}^i, t_{k_i + 1}^i} \right)$, it is easy to obtain that

By substituting Eq (17) into (34), we have

Since $||{\mathit{\boldsymbol{s}}}_i(t)||$ and $\left\| { {\mathop{\rm sig}\nolimits}^{{\beta }} {{({{\mathit{\boldsymbol{s}}}_i}(t_{k_i}^i) - {{\mathit{\boldsymbol{s}}}_j}(t_{k_j}^j))}}} \right\|$ are bounded, it can be obtained that

where ${M_{si}}$, ${M_{hi}}$ represent the upper bounds of $||{\mathit{\boldsymbol{s}}}_i||$ and $\left\| { {\mathop{\rm sig}\nolimits}^{{\beta }} {{({{\mathit{\boldsymbol{s}}}_i}(t_{k_i}^i) - {{\mathit{\boldsymbol{s}}}_j}(t_{k_j}^j))}}} \right\|$ respectively. Recalling the trigger condition (12), and thus we have

It follows from Eqs (36) and (37) that

Notice that it has been proved that $H_i(t) > 0$; in each interval $\left[ {t_{k_i}^i, t_{k_i + 1}^i} \right)$, there must exist a lower bound ${\mathcal H}_{(i, k)} > 0$ for $H_i(t)$. It follows that

Based on the above deduction, we proved that the interval between two triggers of spacecraft is strictly greater than a positive constant, which means that Zeno behavior is avoided in the DETS. This completes the proof for Theorem 3.

4.   Simulation results

This section takes the three-spacecraft distributed formation system as an example to verify the effectiveness of ESO (4), DETS (12) and the FTSM control law (16) through simulation. The simulation scenario and parameter settings are as follows.

Assuming that the spacecraft in the formation are of equal mass, and ${{m}_{i}} = 100$ Kg $(i = 1, 2, 3)$. The external disturbance in the simulation is taken as ${{\mathit{\boldsymbol{f}}}_{di}(t)} = 0.0001\times \left[\rm{ sin}(3t), \rm{ cos}(4t), \rm {sin}(5t) \right]^\rm{T}$ N. Assume that the three spacecraft are slightly deviated from the pre-designed relative orbit at the initial time. The initial relative position errors and the initial velocity errors are set as ${{\mathit{\boldsymbol{e}}}_{\rho 1}(0)} = \left[ 14, 11, -5 \right]^\rm{T}$ m, ${{\mathit{\boldsymbol{e}}}_{\rho 2}(0)} = \left[ 17, 12, 18 \right]^\rm{T}$ m, ${{\mathit{\boldsymbol{e}}}_{\rho 3}(0)} = \left[ -8, 13, 6 \right]^\rm{T}$ m, ${{\mathit{\boldsymbol{e}}}_{vi}(0)} = \left[ 0, 0, 0 \right]^\rm{T}$ m/s, $(i = 1, 2, 3)$. For the communication topology, the weighted adjacency is set as

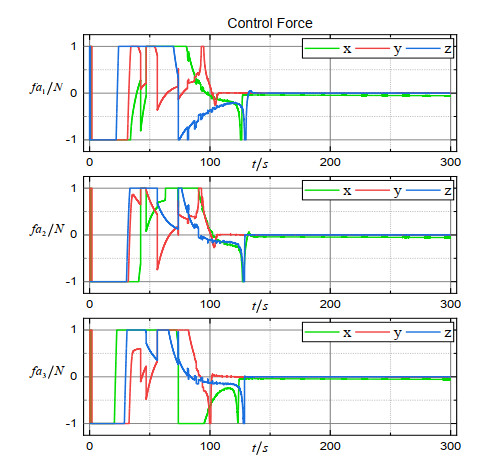
The parameters of the ESO are chosen as ${{{l}}_{ij}} = 5, (i, j = 1, 2, 3)$, ${{\alpha }_{1}} = 1$, ${{\alpha }_{2}} = 0.1$, ${{\alpha }_{3}} = 4$, ${{\alpha }_{4}} = 5$, ${{\alpha }_{5}} = 0.01$, ${{\alpha }_{6}} = 0.01$ and $q = \frac{1}{5}$. We select the parameters of the FTSM control law as $w = 1$, $k_1 = k_2 = k_3 = 3$, ${{\gamma }} = 0.1$, ${{\varsigma }} = 0.2$, ${{\kappa }} = 0.1$, $p = \frac{1}{7}$. In addition, since the control force in practical engineering cannot be infinite, we limit the control force to 1N in the simulation. Simulation results under the above parameter settings are provided in Figures 2–12.

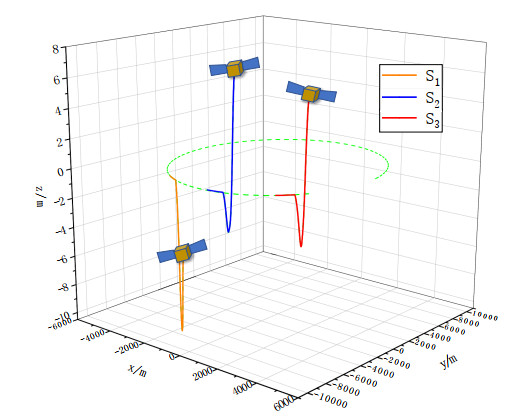
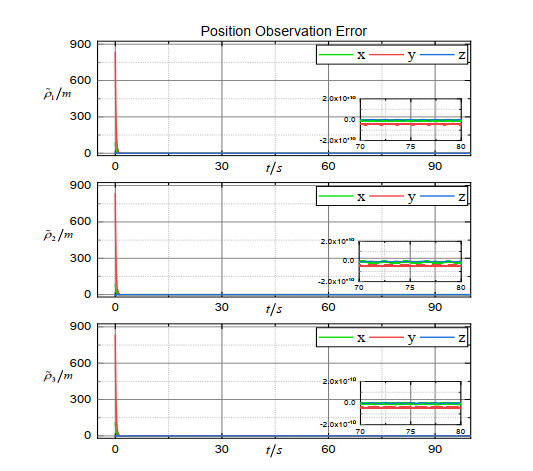
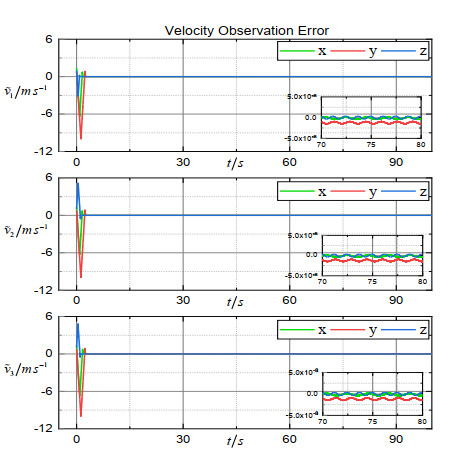
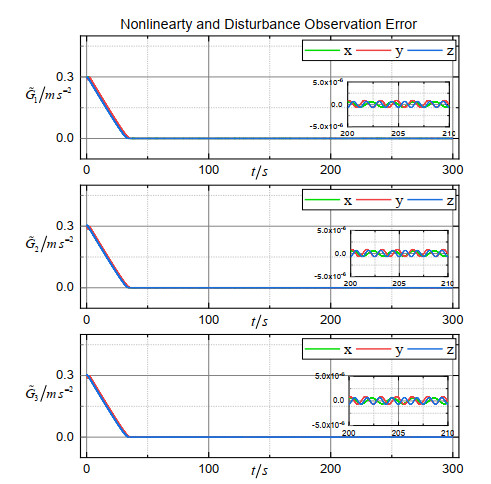
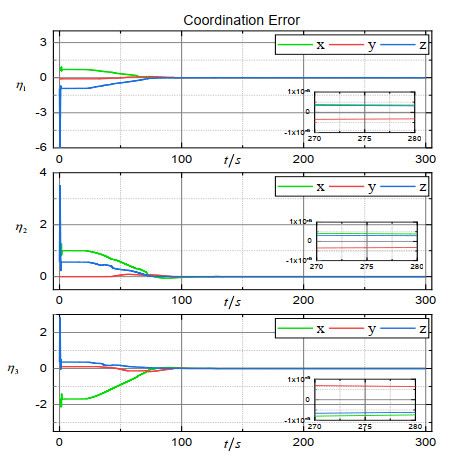
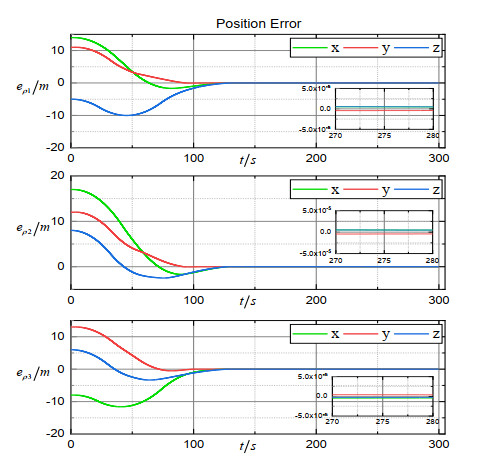
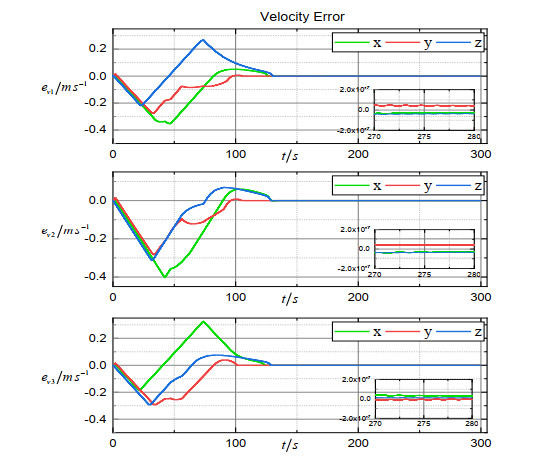
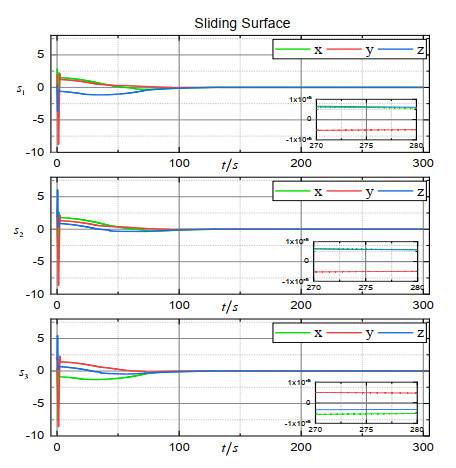
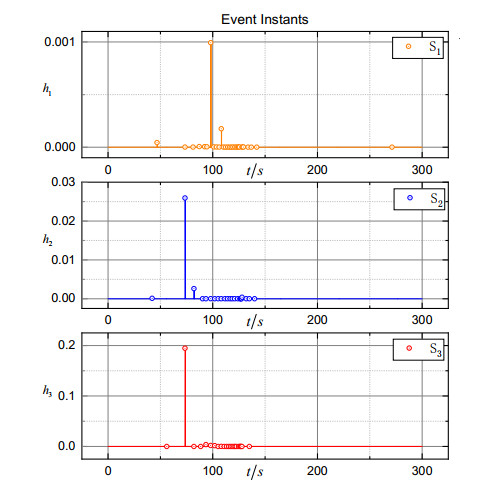
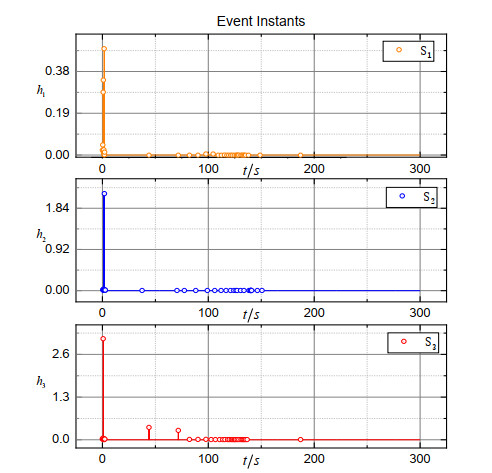
Figure 2 shows the 3D trajectory of the formation, from which we can see that the spacecraft converged to the expected orbit. The trajectories of the estimation error vectors are shown in Figures 3–5. Obviously, the position observation error, the velocity observation error and the merging observation error of non-linearity and disturbance quickly converge to the origin. Figure 6 shows the trajectory of the coordination vector. Figures 7–9 show, respectively, the trajectory of the relative position error vector, the trajectory of the relative velocity error vector and the trajectory of the sliding surface vector of the simulation system. The trajectory of the control force vector is shown in Figure 10. It can be seen that states of three spacecraft converge at around 150 s in a coordinated manner under control law (16). The coordination accuracy is within $1\times {{10}^{-5}}$ m, the relative position accuracy is within $5\times {{10}^{-5}}$ m, and the relative velocity accuracy is within $2\times {{10}^{-7}}$ m. Finally, the trigger instants for each spacecraft are exhibited in Figure 11 (according to the dynamic trigger condition (12), once $h_i\ge 0$, an event is triggered). It can be noticed that under the DETS, the communication frequency is significantly reduced, and the Zeno behaviour is successfully avoided. In order to further illustrate the effectiveness of DETS (12), we added a comparative simulation by replacing DETS (12) with traditional static ETS (10), and the trigger instants under static ETS are exhibited in Figure 12. From the simulation figures, it can be seen that under the same working conditions, the amount of trigger instants for DETS is less than that of the static ETS, which shows the superiority of the method proposed in this paper.

Through the above simulation results, we know that the finite-time relative position coordination can be achieved under the proposed FTSM control law in the presence of lacking velocity information and limited communication. The finite-time ESO can accurately and rapidly generate observations of position, velocity and the merging of non-linearity and disturbance. Also, the DETS can effectively reduce the communication frequency while ensuring the accuracy of the coordination.

5.   Conclusions

In this paper, we made the first attempt to investigate the coordinated control law for SFF systems that simultaneously considers finite-time coordination, unmeasured velocity and limited communication bandwidth. An ESO based FTSM control law under DETS was proposed. Lyapunov based theoretical stability analysis and numerical simulation have been carried out to verify the effectiveness of the control law. The result shows that finite-time relative position coordination of a distributed spacecraft formation without velocity information over limited communication bandwidth can be achieved by applying the proposed control law. Future work will focus on the optimization of the controller parameters using artificial intelligence technology.

Acknowledgments

This work was supported by the Science Center Program of the National Natural Science Foundation of China (62188101), the National Natural Science Foundation of China (61833009, 61690212, 51875119), the Heilongjiang Touyan Team, and the Guangdong Major Project of Basic and Applied Basic Research (2019B030302001).

Conflict of interest

The authors declare that they have no conflict of interest.