1. Introduction

Cell-based in vitro assays [27] are efficient methods to study the effect of industrial chemicals on environment or human health. Our work is based on the cytotoxicity profiling project carried by Alberta Centre for Toxicology in which initially 63 chemicals were investigated using the xCELLigence Real-Time Cell Analysis High Troughput (RTCA HT) Assay [26]. We consider a mathematical model represented by stochastic differential equations to study cytotoxicity, i.e. the effect of toxicants on human cells, such as the killing of cells or cellular pathological changes.

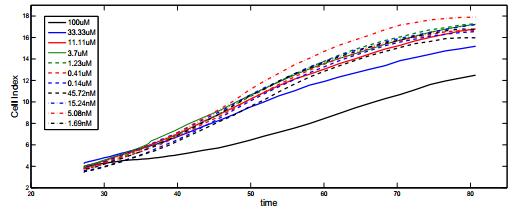
The cells were seeded into wells of micro-electronic plates (E-Plates), and the test substances with 11 concentrations (1:3 serial dilution from the stock solution) were dissolved in the cell culture medium [20]. The microelectrode electronic impedance value was converted by a software to Cell Index ($n$), which closely reflects not only cell growth and cell death, but also cell morphology. The time-dependent concentration response curves (TCRCs) for each test substance in each cell line were generated [26] and based on these curves the toxicants in the present study were divided in 10 groups [30]. In Fig. 1 we display the TCRCs for the toxicant monastrol.

The success of clustering and classification methods depends on providing TCRCs that illustrates the cell population evolution from persistence to extinction. In [1] we consider a model represented by a system of ordinary differential equations to determine an appropriate range for the initial concentration of the toxicant. The model's parameters were estimated based on the data included in the TCRCs [1].

Let $n(t)$ be the cell index, which closely reflects the cell population, $C_o(t)$ be the concentration of internal toxicants per cell, and $C_e(t)$ be the concentration of toxicants outside the cells at time $t$. We suppose that the toxicants do not exist in the cells before experiments, so $C_o(0 ) = 0$, and that $C_e(0 )$ is equal to the concentration of toxicant used in the experiments. We assume that the death rate of cells is linearly dependent on the concentration $C_o$ of internal toxicants and we consider linear kinetic, so we get the following deterministic model [1]:

$\begin{align} \frac{dn(t)}{dt} & = \beta n(t)-\gamma n^2(t)- \alpha C_o(t) n(t), \label{model1}\end{align}$

(1)

$\begin{align} \frac{dC_o(t)}{dt} & = \lambda_1^2 C_e(t) -\eta_1^2C_o(t), \end{align}$

(2)

$\begin{align} \frac{dC_e(t)}{dt} & = \lambda_2^2C_o(t)n(t) -\eta_2^2C_e(t)n(t) \label{model3} \end{align}$

(3)

Here $\beta>0$ denotes the cell growth rate, $\gamma = \frac{\beta}{K}$, where $K>0$ is the capacity volume, $\alpha>0$ is the cell death rate, $\lambda_1^2$ represents the uptake rate of the toxicant from environment, $\eta_1^2$ is the toxicant input rate to the environment, $\lambda_2^2$ is the toxicant uptake rate from cells, and $\eta_2^2$ represents the losses rate of toxicants absorbed by cells.

The deterministic model (1)-(3) is a special case of the class of models proposed in [5], and it is related to the models considered in [7, 11, 15]. However, since we consider an acute dose of toxicant instead of a chronic one, the analysis of the survival/death of the cell population is different from the one done in the previously mentioned papers.

We have noticed that, for the toxicants considered here, the estimated values of the parameters $\eta_1$, $\eta_2$, $\lambda_1$, and $\lambda_2$ verify $\eta_1^2\eta_2^2-\lambda_1^2\lambda_2^2>0$ [1]. In this case we have $0<C_e(t)\le C_e(0)$, $0\le C_o(t)\le \frac{\lambda_1^2C_e(0)}{\eta_1^2}$, and $n(t)>0$, for all $t\ge 0.$ (see Lemma 3.1 in [1]). Moreover from Theorem 3.2 in [1] we know that $\lim_{t\rightarrow \infty} C_e(t)$ exists and its value determines the asymptotic behavior of the system:

1. If $\lim_{t\rightarrow \infty} C_e(t)<\frac{\beta\eta_1^2}{\alpha\lambda_1^2}$ then the population is uniformly persistent:

$\lim\limits_{t\rightarrow\infty} n(t) = K, ~~~~\lim\limits_{t\rightarrow\infty} C_o(t) = \lim\limits_{t\rightarrow\infty} C_e(t) = 0.$

2. If $\lim_{t\rightarrow \infty} C_e(t)>\frac{\beta\eta_1^2}{\alpha\lambda_1^2}$ then $|n|_1 = \int_0^\infty n(t)dt<\infty$ and the population goes to local extinction:

$\lim\limits_{t\rightarrow\infty} n(t) = 0, ~~~ \lim\limits_{t\rightarrow\infty} C_o(t) = C_e^*\frac{\lambda_1^2}{\eta_1^2}, ~~~ \lim\limits_{t\rightarrow\infty} C_e(t) = C_e^*>\frac{\beta\eta_1^2}{\alpha\lambda_1^2},$

In practice we usually estimate a parameter by an average value plus an error term. To keep the stochastic model as simple as possible, we ignore the relationship between the parameters $\beta$ and $\gamma$, and we replace them by the random variables

$\tilde{\beta} = \beta+\text{error}_1~~~~, \tilde{\gamma} = \gamma+\text{error}_2$

(4)

By the central limit theorem, the error terms may be approximated by a normal distribution with zero mean. Thus we replace equation (1) by a stochastic differential equation and, together with equations (2) and (3), we get the stochastic model

$\begin{align} &dn(t) = n(t)\left(\beta -\gamma n(t)- \alpha C_o(t)\right)dt+\sigma_1 n(t) dB_1(t)-\sigma_2 n^2(t) dB_2(t), \label{sm1} \end{align}$

(5)

$\begin{align} &dC_o(t) = (\lambda_1^2 C_e(t) -\eta_1^2C_o(t))dt, \label{sm2} \end{align}$

(6)

$\begin{align} &dC_e(t) = (\lambda_2^2C_o(t)n(t) -\eta_2^2C_e(t)n(t))dt, \label{sm3} \end{align}$

(7)

Here $\sigma_i\ge 0$, $i = 1, 2$ are the noise intensities. $(\Omega, \mathcal{F}, \{\mathcal{F}_t\}_{t\ge 0}, \mathbb{P})$ is a complete probability space with an increasing, right continuous filtration $\{\mathcal{F}_t\}_{t\ge 0}$ such that $\mathcal{F}_0$ contains all $\mathbb{P}$-null sets, and $B_i$, $i = 1, 2$ are independent standard Brownian motions defined on the above probability space.

Several versions of a stochastic logistic equation similar with (5) were considered in [18], [19], [8], [9], [10] and [21]. The system of stochastic differential equations (5)-(7) is closely related with the stochastic models in a polluted environment considered in [15], [16], and [24]. However, for the models considered in these papers, instead of the equations (6) and (7), $C_o(t)$ and $C_e(t)$ obey two linear equations without any terms involving $n(t)$. Moreover, instead of a combination of linear and quadratic terms as in (5), in [15] only a linear stochastic term is considered, and in [16] two stochastic competitive models are considered including exclusively either linear stochastic terms or quadratic stochastic terms.

In this paper we extend the methods applied in [15] and [16] to find conditions for extinction, weakly persistence, and weakly stochastically permanence for the model (5)-(7). In addition to this we focus on the ergodic properties when the cell population is strongly persistent. The main contribution of this paper is the proof that $n(t)$ converges weakly to the unique stationary distribution. If only one of the noise variances $\sigma_1^2$, $\sigma_2^2$ is non-zero, we also determine the density of the stationary distribution. For the study of the ergodic properties we apply techniques used for stochastic epidemic models in [4], [28], [29] and [23], and for a stochastic population model with partial pollution tolerance in a polluted environment in [25].

In the next section we prove that there is a unique non-negative solution of system (5)-(7) for any non-negative initial value. In section 3 we investigate the asymptotic behavior, and in section 4 we study the weak convergence of $n(t)$ to the unique stationary distribution using Lyapunov functions. Numerical simulations that illustrate our results are presented in section 5. The last section of the paper contains a short summary and conclusions.

---

2. Existence and uniqueness of a positive solution

We have to show that system (5)-(7) has a unique global positive solution in order for the stochastic model to be appropriate. Let $\mathbb{R}_+ = \left\{x\in\mathbb{R}:x\ge 0\right\}$, and $\mathbb{R}_+^* = \left\{x\in\mathbb{R}:x> 0\right\}$.

Since equations (6) and (7) are linear in $C_o$ and $C_e$ we have

$\begin{align} C_o(t)& = C_o(0)e^{-\eta_1^2 t}+\lambda_1^2 e^{-\eta_1^2 t}\int_0^t C_e(s) e^{\eta_1^2 s} ds \end{align}$

(8)

$\begin{align} C_e(t)& = C_e(0)\exp{\left(-\eta_2 ^2\int_0^t n(s)ds\right)}+\lambda_2^2\exp{\left(-\eta_2 ^2\int_0^t n(s)ds\right)}\notag\\ &\int_0^t C_o(s) n(s)\exp{\left(\eta_2 ^2\int_0^s n(l)dl\right )}ds, ~~~t\ge 0. \end{align}$

(9)

Let's define the differential operator $L$ associated with the system (5)-(7) by

$\begin{align} L& = \frac{\partial}{\partial t}+\left(\beta n-\gamma n^2- \alpha C_o n\right)\frac{\partial}{\partial n}+(\lambda_1^2 C_e -\eta_1^2C_o)\frac{\partial}{\partial C_o}+(\lambda_2^2C_o n \notag\\ &-\eta_2^2C_en)\frac{\partial}{\partial C_e}+\frac{1}{2}\biggl((\sigma_1^2 n^2+ \sigma_2^2 n^4)\frac{\partial^2}{\partial^2 n}\biggl)\notag \end{align}$

For any function $V\in C^{2, 1}\left(\mathbb{R}^3 \times (0, \infty);\mathbb{R}\right)$, by Itô's formula ([17]) we have

$dV(x(t), t) = LV(x(t), t)dt+\frac{\partial V(x(t), t)}{\partial n}\left(\sigma_1 n(t)dB_1(t)-\sigma_2 n^2(t) dB_2(t)\right), \label{ito1}$

(10)

where $x(t) = (n(t), C_o(t), C_e(t))'$, $t\ge 0$.

Theorem 2.1. Let $D = \mathbb{R}_+^*\times \mathbb{R}_+\times \mathbb{R}_+^*$. For any given initial value $x(0)\in D$ the system (5)-(7) has a unique global positive solution almost sure (a.s.), i.e. $\mathbb{P}\{x(t)\in D, t\ge 0\} = 1$.

Proof. The proof is similar with the proof of theorem 3.1 in [29]. Since the coefficients are locally Lipschitz continuous functions, there exists a unique solution on $[0, \tau_e)$, where $\tau_e$ is the explosion time ([3]). To prove that the solution is in $D$ and $\tau_e = \infty$ we define the stopping time

$\begin{align} &\tau_m = \inf \{t\in [0, \tau_e): \min\{n(t), C_e(t)\}\le m^{-1} \text{ or } \max\{n(t), C_o(t), \notag\\&C_e(t)\}\ge m\}, \label{infi} \end{align}$

(11)

where $m>m_0$ and $m_0> 0$ is a positive integer sufficiently large such that $n(0)\in [1/m_0, m_0]$, $0\le C_o(0)\le m_0$, and $C_e(0)\in [1/m_0, m_0]$. Here we set $\inf \emptyset = \infty$. Obviously $\{\tau_m\}$ is increasing and let $\tau_\infty = \lim_{n\rightarrow \infty}\tau_m$, where $0\le \tau_\infty\le \tau_e$ a.s.. From formula (8) it is easy to see that $C_o(t)\ge 0$ for any $t< \tau_\infty$.

We show that $\tau_\infty = \infty$ a.s., so $\tau_e = \infty$ a.s. and the solution is in $D$ for any $t\ge 0$ a.s. Assume that there exists $T>0$, and $\epsilon>0$ such that $P(\tau_\infty\le T)>\epsilon$. Thus there exists an integer $m_1\ge m_0$ such that $P(\Theta_m)\ge\epsilon$ for any $m\ge m_1$, where $\Theta_m = \{\tau_m\le T\}$.

We define the $C^3-$ function $V:D\rightarrow R_+^*$ as follows

$V(x) = C_o+\frac{\alpha}{4\lambda_2^2}(C_e-\log C_e-1)+\frac{\alpha C_e}{4\lambda_2^2}+\left(\sqrt{n}-\log\sqrt{n}-1\right)+n.$

We get

$\begin{align} &LV(x) = (\lambda_1^2 C_e -\eta_1^2C_o)+\frac{\alpha}{4\lambda_2^2}\left(1-\frac{1}{C_e}\right)(\lambda_2^2C_on -\eta_2^2C_en)\notag\\ &+\frac{\alpha}{4\lambda_2^2}(\lambda_2^2C_on -\eta_2^2C_en)+\left(\beta n-\gamma n^2- \alpha C_o n\right)\left(\frac{1}{2\sqrt{n}}-\frac{1}{2n}\right)+\frac{1}{2}(\sigma_1^2 n^2\notag \\&+ \sigma_2^2 n^4)\left(-\frac{1}{4n\sqrt{n}}+\frac{1}{2n^2}\right)+\left(\beta n-\gamma n^2- \alpha C_o n\right)\notag \end{align}$

Omitting some of the negative terms, for any $x\in D$ we have

$\begin{align} LV(x)&\le \lambda_1^2 C_e+\frac{\alpha C_on}{4}+\frac{\alpha C_on}{4}+\frac{\alpha C_o}{2}-\alpha C_o n+f(n), \notag \\ &\le \lambda_1^2 C_e+\frac{\alpha C_o}{2}+f(n), \notag \end{align}$

where

$\begin{align} &f(n) = -\frac{\sigma_2^2n^2\sqrt{n}}{8}+\frac{\alpha}{4\lambda_1^2}\eta_2^2n+\frac{\beta\sqrt{n}}{2}+\frac{\gamma n}{2}+\frac{\sigma_1^2}{4}+\frac{\sigma_2^2 n^2}{4}+\beta n\notag \end{align}$

Since $f$ is continuous on $(0, \infty)$ and $\lim_{n\rightarrow \infty}f(n) = -\infty$ it can easily be shown that $LV(x)\le C V(x)+C$, where the constant $C>0$ and $x\in D$.

Let's define $\tilde{V}(t, x) = e^{-Ct}(1+V(x))$. We have

$L\tilde{V}(x, t) = -Ce^{-Ct}(1+V(x))+e^{-Ct}LV(x)\le 0.$

Using Itô's formula (10) for $\tilde{V}$ and taking expectation we have for any $m\ge m_1$:

$\begin{align} E\left[\tilde{V}(x(t\wedge \tau_m), t\wedge \tau_m)\right]& = \tilde{V}(x(0), 0)+E\left[\int_0^{t\wedge \tau_m} L\tilde{V}(x(u\wedge \tau_m), u\wedge \tau_m)du\right]\notag\\ &\le \tilde{V}(x(0), 0).\notag \end{align}$

Notice that for any $\omega\in \Theta_m$, $m\ge m_1$ we have $V(x(\tau_m, \omega))\ge b_m = \min \{ V(y) | y = (y_1, y_2, y_3)'\text{ has the components } y_1 \text{ or } y_3 \text{ equal with } m^{-1}\text{ or } m,$ $\text{ or } y_2 = m\}$. Hence

$E\left[V(x(\tau_m, \omega))I_{\Theta_m}(\omega)\right]\ge P(\Theta_m)b_m\ge\epsilon b_m\rightarrow \infty$

as $m\rightarrow \infty$. But $E\left[V(x(\tau_m, \omega))I_{\Theta_m}(\omega)\right]\le e^{CT}\tilde{V}(x(0), 0))<\infty$, for any $m\ge m_1$. Thus we have proved by contradiction that $\tau_\infty = \infty$.

Here we focus on the case when $n(0)>0$, we have only an acute dose of toxicant $C_e(0)>0$, $C_o(0) = 0$, and the external concentration of toxicant $C_e(t)$ is never larger than $C_e(0)$. For this we have to impose some conditions on the parameters. Similarly with the deterministic case we obtain the following results (for completion the proofs are included in Appendix A and Appendix B).

Lemma 2.2. If $\eta_1^2\eta_2^2-\lambda_1^2\lambda_2^2>0$, $n(0)>0$, $C_e(0)>0$, and $C_o(0) = 0$ then almost surely we have $0<C_e(t)\le C_e(0)$, $0\le C_o(t)\le \frac{\lambda_1^2C_e(0)}{\eta_1^2}$ for all $t\ge 0.$

Theorem 2.3. If $\eta_1^2\eta_2^2-\lambda_1^2\lambda_2^2>0$, $n(0)>0$, $C_e(0)>0$, and $C_o(0) = 0$, then almost surely $\lim_{t\rightarrow\infty}C_o(t)$ and $\lim_{t\rightarrow\infty}C_e(t)$ exist and

$\lim\limits_{t\rightarrow\infty}C_o(t) = \frac{\lambda_1^2}{\eta_1^2}\lim\limits_{t\rightarrow\infty}C_e(t).$

---

3. Survival analysis

In this section we assume that $n(0)>0, C_o(0) = 0, C_e(0)>0$. We have the following definitions ([16]).

Definition 3.1. The population $n(t)$ is said to go to extinction a.s. if $\lim_{t\rightarrow\infty}n(t) = 0$ a.s..

Definition 3.2. The population $n(t)$ is weakly persistent a.s. if $\limsup_{t\rightarrow\infty}n(t)>0$ a.s..

Definition 3.3. The population $n(t)$ is said to be strongly persistent a.s. if $\liminf_{t\rightarrow\infty}n(t)>0$ a.s..

Definition 3.4. The population $n(t)$ is said to be stochastically permanent if for any $\epsilon>0$ there exist the positive constants $c_1(\epsilon)$ and $c_2(\epsilon)$ such that $\liminf\limits_{t\rightarrow\infty}P\biggl(n(t)$ $\le c_1(\epsilon)\biggl)\ge 1-\epsilon$ and $\liminf\limits_{t\rightarrow\infty}P\left(n(t)\ge c_2(\epsilon)\right)\ge 1-\epsilon$.

Theorem 3.5. a. If $\beta -\frac{\sigma_1^2}{2}-\alpha\liminf\limits_{t\rightarrow\infty}\frac{\int_0^t C_o(s)ds}{t}<0$ a.s. then the population $n(t)$ goes exponentially to extinction a.s..

b. If $\beta -\frac{\sigma_1^2}{2}-\alpha\liminf\limits_{t\rightarrow\infty}\frac{\int_0^t C_o(s)ds}{t}>0$ a.s. then the population $n(t)$ is weakly persistent a.s.

Proof. The proof is similar with the proof of Theorem 6 in [16]. We start with some preliminary results. By Itô's formula in (5) we have

$d \ln n(t) = \left(\beta -\gamma n(t)- \alpha C_o(t)-\frac{\sigma_1^2+\sigma_2^2 n^2(t)}{2}\right)dt+\sigma_1 dB_1(t)-\sigma_2 n(t) dB_2(t).\notag$

This means that we have

$\begin{split} \ln n(t)-\ln n(0) & = \left(\beta-\frac{\sigma_1^2}{2}\right)t -\gamma \int_0^t n(s)ds- \alpha \int _0^t C_o(s)ds\\ &-\frac{\sigma_2^2 }{2}\int_0^t n^2(s)ds+\sigma_1 B_1(t)-\sigma_2 \int_0^t n(s) dB_2(s), \end{split}\label{eqex}$

(12)

Notice that the quadratic variation [17] of $M(t) = -\sigma_2 \int_0^t n(s) dB_2(s)$ is

$\langle M(t), M(t)\rangle = \sigma_2^2\int_0^t n^2(s) ds.\notag$

Now we do the proof for part a. Using the exponential martingale inequality (Theorem 7.4 [17]) and Borel-Cantelli lemma ([22], pp. 102), and proceeding as in the proof of Theorem 6 in [16] we can show that for almost all $\omega$ there exists a random integer $n_0 = n_0(\omega)$ such that for all $n\ge n_0$ we have

$\sup\limits_{0\le t\le n}\left(M(t)-\frac{1}{2}\langle M(t), M(t)\rangle \right)\le 2 \ln n.\notag$

Hence, for all $n\ge n_0$ and all $0\le t\le n$ we have

$-\frac{\sigma_2^2 }{2}\int_0^t n^2(s)ds-\sigma_2 \int_0^t n(s) dB_2(s)\le 2 \ln n \text{ a.s.}.\notag$

Substituting the above inequality in (12) we get

$\frac{\ln n(t)-\ln n(0)}{t} \le \beta-\frac{\sigma_1^2}{2} - \alpha \frac{\int _0^t C_o(s)ds}{t}+\sigma_1\frac{B_1(t)}{t}+2\frac{\ln n}{n-1} \text{ a.s.}, \notag$

for all $n\ge n_0$, and any $0<n-1\le t\le n$. Since $\lim_{t\rightarrow \infty}\frac{B(t)}{t} = 0$ a.s. (see Theorem 3.4 in [17]) we get

$\limsup\limits _{t\rightarrow \infty}\frac{\ln n(t)}{t}\le \beta-\frac{\sigma_1^2}{2} - \alpha \liminf\limits_{t\rightarrow \infty}\frac{\int _0^t C_o(s)ds}{t}<0\text{ a.s.}.$

Next we prove part b. Suppose that $P(\Omega)>0$ where $\Omega = \{\lim\sup _{t\rightarrow \infty} n(t)\le 0\}$. From Theorem 2.1 we know that $n(t)> 0$, $t\ge 0$ a.s., so $P(\Omega_1)>0$ where $\Omega_1 = \{\lim_{t\rightarrow \infty} n(t) = 0\}$, and $\Omega_1\subseteq \Omega$. Thus, for any $\omega \in \Omega_1$ we have

$\limsup\limits _{t\rightarrow \infty} \frac{\ln n(t, \omega)}{t}\le 0\label{contre1}$

(13)

Moreover, from the law of large numbers for local martingales (Theorem 3.4 in [17]) there exists a set $\Omega_2\subseteq \Omega_1$ with $P(\Omega_2)>0$ such that for any $\omega\in \Omega_2$ we have

$\lim\limits_{t\rightarrow \infty}\frac{M(t, \omega)}{t} = \lim\limits_{t\rightarrow \infty}\frac{ B_1(t, \omega)}{t} = 0.\notag$

From (12) we get:

$\begin{align}&\frac{\ln(n(t))}{t} = \frac{\ln (n(0))}{t}+\left(\beta-\frac{\sigma_1^2}{2}\right) - \alpha \frac{\int _0^t C_o(s)ds}{t}\notag\\ &- \frac{\int_0^t \left(\gamma n(s)+\frac{\sigma_2^2 }{2} n^2(s)\right)ds}{t}+\sigma_1\frac{ B_1(t)}{t}+\frac{M(t, \omega)}{t}\notag \end{align}$

Hence, for any $\omega\in \Omega_2$ we have

$\limsup\limits_{t\rightarrow \infty} \frac{\ln n(t, \omega)}{t} = \left(\beta-\frac{\sigma_1^2}{2}\right) - \alpha \liminf \limits_{t\rightarrow \infty}\frac{\int _0^t C_o(s, \omega)ds}{t}\notag$

Since we know that $\beta -\frac{\sigma_1^2}{2}-\alpha\liminf\limits_{t\rightarrow\infty}\frac{\int_0^t C_o(s, \omega)ds}{t}>0$ a.s., we have a contradiction with (13), so $\limsup_{t\rightarrow\infty}n(t)>0$ a.s.

We have the following result regarding the expectation of $n(t)$.

Lemma 3.6. There exists a constant $K_1>0$ such that $\sup_{t\ge 0}E[n(t)]\le K_1$.

Proof. Using Itô's formula in (5) we get:

$\begin{align} &d(e^tn(t)) = n(t)e^t\biggl(1+\beta-\alpha C_o(t)-\gamma n(t)\biggl)dt+\sigma_1n(t)e^t dB_1(t)-\sigma_2n^{2}(t)\notag\\ &e^t dB_2(t)\le n(t)e^t\left(1+\beta-\gamma n(t)\right)dt+\sigma_1n(t)e^t dB_1(t)-\sigma_2n^{2}(t)e^t dB_2(t)\notag\\ &\le e^t \frac{(1+\beta)^2}{4\gamma}dt+\sigma_1n(t)e^t dB_1(t)-\sigma_2n^{2}(t)e^t dB_2(t) \label{eqa} \end{align}$

(14)

Let

$\eta_m = \inf\{t\ge 0: n(t)\notin(1/m, m)\}, \label{infi2}$

(15)

for any $m>m_0$, where $m_0>0$ was defined in the proof of Theorem 2.1. Obviously $\eta_m\ge\tau_m$, $m>m_0$, where $\tau_m$ is given in (11). In Theorem 2.1 we have proved that $\lim_{m\rightarrow\infty}\tau_m = \infty$ a.s., so we also have $\lim_{m\rightarrow\infty}\eta_m = \infty$ a.s.. Taking expectation in (14) we get:

$E\left[e^{t\wedge \tau_m} n(t\wedge \tau_m)\right]\le n(0)+E\left[\int_0^{t\wedge \tau_m} e^s\frac{(1+\beta)^2}{4\gamma} ds\right]\le n(0)+\frac{(1+\beta)^2}{4\gamma}(e^t-1).\notag$

Letting $m\rightarrow \infty$ we get

$E\left[n(t)\right]\le \frac{n(0)}{e^t }+\frac{(1+\beta)^2}{4\gamma}(1-e^{-t}).$

Thus, there exists a constant $K_1>0$ such that $\sup_{t\ge 0}E[n(t)]\le K_1$.

Corollary 1. For any $\epsilon>0$ there exists $c_1(\epsilon)$ such that $\lim\inf _{t\rightarrow\infty}\mathbb{P}(n(t)\le c_1(\epsilon))\ge 1-\epsilon$.

Proof. For any $\epsilon>0$, set $c_1(\epsilon) = K_1/\epsilon$, where the constant $K_1>0$ is given in the previous lemma. From the Markov's inequality [22] we obtain

$P\left(n(t)>c_1(\epsilon)\right)\le \frac{E[n(t)]}{c_1(\epsilon)}.$

Hence, from Lemma 3.6 we get

$\limsup\limits_{t\rightarrow \infty}P\left(n(t)>c_1(\epsilon)\right)\le \limsup\limits_{t\rightarrow \infty}\frac{E[n(t)]}{c_1(\epsilon)}\le \epsilon.$

Theorem 3.7. If $\eta_1^2\eta_2^2-\lambda_1^2\lambda_2^2>0$ and $\beta -\sigma_1^2-\alpha\frac{\lambda_1^2C_e(0)}{\eta_1^2}>0$, then the cell population is stochastically permanent.

Proof. First we show that $\lim\sup_{t\rightarrow \infty}E[1/n(t)]\le M_2$, where $M_2$ is a positive constant.

By Itô's formula in (5) we get for any real constant c:

$\begin{align} &d\left(\frac{e^{ct}}{n(t)}\right) = e^{ct}\biggl(\frac{1}{n(t)}\left(c-\beta+\sigma_1^2+\alpha C_o(t)\right)+\gamma +\sigma_2^2n(t)\biggl)dt\notag\\ &-\frac{\sigma_1e^{ct}}{n(t)}dB_1(t)+\sigma_2 e^{ct}dB_2(t)\notag \end{align}$

Since $\eta_1^2\eta_2^2-\lambda_1^2\lambda_2^2>0$, from Lemma 2.2 we know that $0\le C_o(t)\le \frac{\lambda_1^2C_e(0)}{\eta_1^2}$ for all $t\ge 0$ a.s.. We choose any $0<c<\beta -\sigma_1^2-\alpha \frac{\lambda_1^2C_e(0)}{\eta_1^2}$, and we get:

$d\left(\frac{e^{ct}}{n(t)}\right)\le e^{ct}\biggl(\gamma +\sigma_2^2n(t)\biggl)dt-\frac{\sigma_1e^{ct}}{n(t)}dB_1(t)+\sigma_2 e^{ct}dB_2(t)\label{eqa2}$

(16)

Taking expectation in (16) and using Lemma 3.6 we get:

$\begin{align} &E\left[\frac{e^{c (t\wedge \eta_m)}}{n(t\wedge \eta_m)}\right]\le \frac{1}{n(0)}+E\left[\int_0^{t\wedge \eta_m} e^{cs}\left(\gamma+\sigma_2^2n(s)\right) ds\right]\notag\\ &\le \frac{1}{n(0)}+\left(\gamma+\sigma_2^2 K_1\right)\frac{(e^{ct}-1)}{c}, \notag \end{align}$

where $\eta_m$ was defined in (15). Letting $m\rightarrow \infty$ we get

$E\left[\frac{1}{n(t)}\right]\le \frac{1}{n(0)e^{ct} }+\frac{\left(\gamma+\sigma_2^2 K_1\right)}{c}(1-e^{-ct}),$

so $\limsup\limits_{t\rightarrow \infty}E[1/n(t)]\le M_2$, where $0<M_2 = (\gamma+\sigma_2^2 K_1)/c$.

Next we show that for any $\epsilon>0$ there exists $c_2(\epsilon)$ such that $\liminf\limits _{t\rightarrow\infty}\mathbb{P}(n(t)\ge c_2(\epsilon))\ge 1-\epsilon$.

For any $\epsilon>0$ set $c_2(\epsilon) = \epsilon/M_2$. From Markov's inequality we have

$\mathbb{P}(n(t)< c_2(\epsilon)) = \mathbb{P}\left(\frac{1}{n(t)}>\frac{1}{c_2(\epsilon)}\right)\le c_2(\epsilon)E\left[\frac{1}{n(t)}\right]$

Hence

$\limsup\limits_{t\rightarrow\infty}\mathbb{P}\left(n(t)< c_2(\epsilon)\right)\le \epsilon\limsup\limits_{n\rightarrow \infty}E[1/n(t)]/M_2\le\epsilon.$

Thus $\liminf_{t\rightarrow\infty}\mathbb{P}(n(t)\ge c_2(\epsilon))\ge 1-\epsilon$, and this inequality and Corollary 1 implies that $n(t)$ is stochastically permanent.

---

4. Stationary distributions

The deterministic system (1)-(3) has a maximum capacity equilibrium point $(K, 0, 0)^{'}$, where $K$ is the capacity volume ([1]). For the stochastic system (5)-(7), $(K, 0, 0)^{'}$ is not a fixed point, and, when the cell population is persistent, we no longer have $\lim_{t\rightarrow\infty} n(t) = K$. In this section we study the asymptotic behavior of $n(t)$ when $\lim_{t\rightarrow \infty} C_o(t) = 0$ a.s..

For stochastic differential equations, invariant and stationary distributions play the same role as fixed points for deterministic differential equations. In general, let $X(t)$ be the temporally homogeneous Markov process in $E\subseteq \mathbb{R}^l$ representing the solution of the stochastic differential equation

$dX(t) = b(X(t))dt+\sum\limits_{r = 1}^d \sigma_r(X(t))dB_r(t), \label{eqerg1}$

(17)

where $B_r(t)$, $r = 1, \ldots, d$ are standard Brownian motions. We define the operator $L$ associated with equation (17):

$L = \sum\limits_{i = 1}^l b_i(x)\frac{\partial}{\partial x_i}+\frac{1}{2}\sum\limits_{i, j = 1}^l A_{i, j}(x)\frac{\partial^2}{\partial x_i\partial x_j}, ~~~ A_{i, j}(x) = \sum\limits_{r = 1}^d \sigma_{r, i}(x)\sigma_{r, j}(x).\notag$

Let $P(t, x, \cdot)$ denote the probability measure induced by $X(t)$ with initial value $X(0) = x\in E$: $P(t, x, A) = P(X(t)\in A|X(0) = x)$, $A\in \mathcal{B}(E)$, where $\mathcal{B}(E)$ is the $\sigma-$algebra of all the Borel sets $A\subseteq E$.

Definition 4.1. A stationary distribution [6] for $X(t)$ is a probability measure $\mu$ for which we have

$\int_E P(t, x, A)\mu(dx) = \mu(A), \text{ for any }t\ge 0, \text{ and any }A\in \mathcal{B}(E).\notag$

Definition 4.2. The Markov process $X(t)$ is stable in distribution if the transition distribution $P(t, x, \cdot)$ converges weakly to some probability measure $\mu(\cdot)$ for any $x\in E$.

It is clear that the stability in distribution implies the existence of a unique stationary measure, but the converse is not always true [2]. We have the following result (see lemma 2.2 in [29] and the references therein).

Lemma 4.3. Suppose that there exists a bounded domain $U\subseteq E$ with regular boundary, and a non-negative $C^2-function$ $V$ such that $A(x) = (A_{i, j}(x))_{1\le i, j\le l}$ is uniformly elliptical in $U$ and for any $x\in E \setminus U$ we have $LV(x)\le -C$, for some $C>0$. Then the Markov process $X(t)$ has a unique stationary distribution $\mu(\cdot)$ with density in $E$ such that for any Borel set $B\subseteq E$

$\begin{align} &\lim\limits_{t\rightarrow \infty}P(t, x, B) = \mu(B)\notag\\ &P_x\left\{\lim\limits_{T\rightarrow\infty}\frac{1}{T}\int_0^T f(X(t))dt = \int_E f(x)\mu(dx)\right\} = 1, \notag \end{align}$

for all $x\in E$ and $f$ being a function integrable with respect to the probability measure $\mu$.

We now study the stochastic system (5)-(7) when $\lim_{t\rightarrow \infty}C_o(t) = 0$ a.s.. We introduce two new stochastic process $X(t)$ and $X_{\epsilon}(t)$ which are defined by the initial conditions $X(0) = X_\epsilon (0) = n(0)\in \mathbb{R}_+^*$ and the stochastic differential equations

$\begin{align} dX(t) & = \left(\beta X(t)-\gamma X^2(t)\right)dt+\sigma_1 X(t) dB_1(t)-\sigma_2 X^2(t) dB_2(t), \label{eqx}\end{align}$

(18)

$\begin{align}dX_\epsilon (t) & = \left(\beta X_\epsilon(t)-\gamma X_\epsilon^2(t)-\alpha \epsilon X_\epsilon(t) \right)dt+\sigma_1 X_\epsilon(t) dB_1(t)\notag\\ &-\sigma_2 X_\epsilon^2(t) dB_2(t), \label{eqxe} \end{align}$

(19)

Lemma 4.4. a. For any given initial value $X(0)>0$, the equation (18) has a unique global solution $X(t)$ such that $\mathbb{P}\left\{ X(t)>0, t\ge 0\right\} = 1$.

b. For any $\epsilon>0$ and any given initial value $X_\epsilon(0)>0$, the equation (19) has a unique global solution $X_\epsilon(t)$ such that $\mathbb{P}\left\{ X_\epsilon(t)>0, t\ge 0\right\} = 1$.

c. There exists a constant $C_1>0$ such that $\sup_{t\ge 0} E[X(t)]\le C_1$ and, for any $\epsilon>0$, $\sup_{t\ge 0} E[X_\epsilon(t)]\le C_1$.

Proof. The proofs for a. and b. can be done similarly with the proof of Theorem 2.1, using the $C^2$-function $V:\mathbb{R}_+^*\rightarrow \mathbb{R}_+$, $V(x) = \sqrt{x}-\log\sqrt{x}-1$. The proof of c. is analogous with the proof of Lemma 3.6.

Let $P_{X}(t, x, \cdot)$ denote the probability measure induced by $X(t)$ with initial value $X(0) = x\in \mathbb{R}_+^*$, $t\ge 0$. In the following theorem, using Lemma 4.3, we show that the Markov process $X(t)$ is stable in distribution.

Theorem 4.5. If $\sigma_1^2<2\beta$ then the Markov process $X(t)$ has a unique stationary distribution $\mu_1(\cdot)$ with density in $\mathbb{R}_+^*$ such that for any Borel set $B\subseteq \mathbb{R}_+^*$

$\begin{align} &\lim\limits_{t\rightarrow \infty}P_X(t, x, B) = \mu_1(B)\notag\\ &P_x\left\{\lim\limits_{T\rightarrow\infty}\frac{1}{T}\int_0^T f(X(t))dt = \int_E f(x)\mu_1(dx)\right\} = 1, \notag \end{align}$

for all $x\in \mathbb{R}_+^*$ and $f$ being a function integrable with respect to the probability measure $\mu_1$.

Proof. We consider the $C^2$-function $V:\mathbb{R}_+^*\rightarrow \mathbb{R}_+$, $V(x) = \sqrt{x}-\log\sqrt{x}-1$. Simple calculations show that

$LV(x) = -\frac{\sigma_2^2}{8}x^{5/2}+\frac{\sigma_2^2}{4}x^2-\frac{\gamma}{2}x^{3/2}+\frac{\gamma}{2}x+\left(\frac{\beta}{2}-\frac{\sigma_1^2}{8}\right)x^{1/2} +\left(\frac{\sigma_1^2}{4}-\frac{\beta}{2}\right).$

Since $LV(\cdot)$ is a continuous function on $\mathbb{R}_+^*$ and $LV(0) = \frac{\sigma_1^2}{4}-\frac{\beta}{2}<0$, there exists a constant $A_1>0$ such that $LV(x)<-C_1$ for any $x\in (0, A_1]$, for some $C_1>0$. We also have $\lim_{x\rightarrow\infty}LV(x) = -\infty$. Thus, there exists a constant $A_2>A_1>0$ such that $LV(x)<-C_2$ for any $x\in [A_2, \infty)$, for some $C_2>0$.

Let $U = (A_1, A_2)\subset \mathbb{R}_+^*$. Then $U$ is a bounded domain, and $LV(x)<-C$ for any $x\in \mathbb{R}_+^*\setminus U$, where $C>0$ is the minimum between $C_1$ and $C_2$. Notice that $A(x) = \sigma_1^2x^2+\sigma_2^2x^4$ is uniformly elliptical on $U$, so the assumptions of Lemma 4.3 are met. Therefore, the Markov process $X(t)$ has a unique stationary distribution $\mu_1(\cdot)$ and it is ergodic.

Let define the processes $N(t) = 1/n(t)$ a.s., $Y(t) = 1/X(t)$ a.s., $Y_\epsilon(t) = 1/X_\epsilon(t)$ a.s., $t\ge 0$, with $N(0) = Y(0) = Y_\epsilon(0) = 1/n(0)>0$. Then from Lemma 4.4 and Theorem 2.1 we have $\mathbb{P}\{ N(t)>0, Y(t)>0, Y_\epsilon(t)>0, t\ge 0\} = 1$. Applying Itô's formula in equations (5), (18) and (19) we get

$\begin{align} dN(t)& = \left(N(t)(\sigma_1^2-\beta)+\alpha N(t) C_o(t)+\gamma+\frac{\sigma_2^2}{N(t)}\right)dt-\sigma_1N(t)dB_1(t)\notag\\ &+\sigma_2dB_2(t)\text{ a.s.}, \label{eqi1}\end{align}$

(20)

$\begin{align} dY(t)& = \left(Y(t)(\sigma_1^2-\beta)+\gamma+\frac{\sigma_2^2}{Y(t)}\right)dt-\sigma_1Y(t)dB_1(t)\notag\\ &+\sigma_2dB_2(t)\text{ a.s.}, \label{eqi2} \end{align}$

(21)

$\begin{align} dY_\epsilon(t)& = \left(Y_\epsilon(t)(\sigma_1^2-\beta+\alpha\epsilon)+\gamma+\frac{\sigma_2^2}{Y_\epsilon(t)}\right)dt-\sigma_1Y_\epsilon(t)dB_1(t)\notag\\ &+\sigma_2dB_2(t)\text{ a.s.}.\label{eqi3} \end{align}$

(22)

From the proof of Theorem 3.7 we know that if $\eta_1^2\eta_2^2-\lambda_1^2\lambda_2^2>0$ and $\beta-\sigma_1^2-\alpha\frac{\lambda_1^2C_e(0)}{\eta_1^2}>0$ then there exist a constant $K_2>0$ such that $\sup_{t\ge 0} E[N(t)]\le K_2$. We have similar results for the processes $Y(t)$ and $Y_\epsilon(t)$.

Lemma 4.6. If $\sigma_1^2<\beta$ then $\sup_{t\ge 0} E[Y(t)]< \infty$ and $\sup_{t\ge 0} E[Y_\epsilon(t)]< \infty$, for any $0<\epsilon<\frac{\beta-\sigma_1^2}{\alpha}$.

Proof. The proof is based on the results in Lemma 4.4 and it is similar with the first part of the proof of Theorem 3.7. For completeness we have included it in Appendix C.

We use the processes $N(t)$, $Y(t)$, $Y_\epsilon(t)$ to prove the main result of this section.

Theorem 4.7. Let $(n(t), C_o(t), C_e(t))$ be the solution of the system (5)-(7) with any initial value $(n(0), C_o(0), C_e(0))'\in D = \mathbb{R}_+^*\times \mathbb{R}_+\times \mathbb{R}_+^*$. If $\lim_{t\rightarrow \infty} C_o(t) = 0$ a.s. and $\beta -\sigma_1^2>0$ then $n(t)\overset{w}{\underset{t\rightarrow \infty}{\rightarrow}} \mu_1$, where $\overset{w}{\rightarrow}$ means convergence in distribution (weak convergence [22]) and $\mu_1$ is the probability measure on $\mathbb{R_+^*}$ given in Theorem 4.5.

Proof. We follow the same idea as in the proof of Theorem 2.4 in [28]. From theorem 4.5 we know that $X(t)\overset{w}{\underset{t\rightarrow \infty}{\rightarrow}} \mu_1$, where $\mu_1$ is a probability measure on $\mathbb{R_+^*}$. By the Continuous Mapping Theorem [22], $Y(t) = 1/X(t)$ also converges weakly to a probability measure $\nu_1$ on $\mathbb{R_+^*}$, the reciprocal of $\mu_1$. We will show that $N(t) = 1/n(t)\overset{w}{\underset{t\rightarrow \infty}{\rightarrow}} \nu_1$.

Firstly, let's notice that

$Y(t)\le N(t) \text{ and } Y(t)\le Y_\epsilon(t) \text{ for any } t\ge 0 \text{ a.s..} \label{fact1}$

(23)

Indeed, if we denote $\xi(t) = N(t)-Y(t)$, then $\xi(0) = 0$ and from equations (20) and (21) we get

$d\xi(t) = \left(\xi(t)\left(\sigma_1^2-\beta-\frac{\sigma_2^2}{N(t)Y(t)}\right)+\alpha N(t) C_o(t)\right)dt-\sigma_1\xi(t)dB_1(t)\text{ a.s.}.$

The solution of the previous linear equation is given by (see chapter 3, [17])

$\xi(t) = \Phi(t)\int_0^t \frac{\alpha N(s) C_o(s)}{\Phi(s)}ds\text{ a.s.},$

where

$\Phi(t) = \exp\left\{ -t\left(\beta-\frac{\sigma_1^2}{2}\right)-\int_0^t\frac{\sigma_2^2}{N(s)Y(s)}ds-\sigma_1 B_1(t) \right\}>0$

Obviously $\xi(t)\ge 0$, $t\ge 0$, a.s., and this means that we have $Y(t)\le N(t)$ for any $t\ge 0$ a.s. Similarly, using equations (21) and (22), we can show that $Y(t)\le Y_\epsilon(t)$ for any $t\ge 0$ a.s..

Secondly we show that for any $0<\epsilon<\frac{2\beta-\sigma_1^2}{2\alpha}$

${\lim\inf}_{t\rightarrow\infty}(Y_\epsilon(t)-N(t))\ge 0\text{ a.s.}.\label{fact2}$

(24)

From equations (20) and (22) we get

$\begin{align} &d(Y_\epsilon(t)-N(t)) = \biggl((Y_\epsilon(t)-N(t))\left(\sigma_1^2+\alpha\epsilon-\beta-\frac{\sigma_2^2}{N(t)Y_\epsilon(t)}\right)\notag\\ &+\alpha N(t) (\epsilon-C_o(t))\biggl)dt-\sigma_1(Y_\epsilon(t)-N(t))dB_1(t)\text{ a.s.}.\notag \end{align}$

The solution of the linear equation is given by

$Y_\epsilon(t)-N(t) = \Phi_1(t)\int_0^t \frac{\alpha N(s) \left(\epsilon-C_o(s)\right)}{\Phi_1(s)}ds\text{ a.s.},$

where

$\begin{align} 0<\Phi_1(t)& = \exp\left\{ -t\left(\beta-\alpha\epsilon-\frac{\sigma_1^2}{2}\right)-\int_0^t\frac{\sigma_2^2}{N(s)Y_\epsilon(s)}ds-\sigma_1 B_1(t) \right\}\notag\\ &\le \exp\left\{ -t\left(\beta-\alpha\epsilon-\frac{\sigma_1^2}{2}+\sigma_1 \frac{B_1(t)}{t}\right) \right\}\notag \end{align}$

Since $\lim_{t\rightarrow \infty} B_1(t)/t = 0$ a.s., for any $0<\epsilon<\frac{2\beta-\sigma_1^2}{2\alpha}$ we get $\lim_{t\rightarrow \infty}\Phi_1(t) = 0$ a.s.. Moreover, because $\lim_{t\rightarrow \infty}C_o(t) = 0$ a.s., for almost any $\omega$ there exist $0<T = T(\omega)$ such that $\epsilon-C_o(t, \omega)>0$ for any $t>T(\omega)$. Thus for almost any $\omega$ and any $t>T$,

$\begin{align} Y_\epsilon(t)-N(t)& = \Phi_1(t)\left(\int_0^T \frac{\alpha N(s) \left(\epsilon-C_o(s)\right)}{\Phi_1(s)}ds+\int_T^t \frac{\alpha N(s) \left(\epsilon-C_o(s)\right)}{\Phi_1(s)}ds\right)\notag\\ &\ge \Phi_1(t)\int_0^T \frac{\alpha N(s) \left(\epsilon-C_o(s)\right)}{\Phi_1(s)}ds\notag \end{align}$

Therefore for any $0<\epsilon<\frac{2\beta-\sigma_1^2}{2\alpha}$ we have

$\liminf\limits_{t\rightarrow\infty}(Y_\epsilon(t)-N(t))\ge \lim\limits_{t\rightarrow\infty} \Phi_1(t)\int_0^T \frac{\alpha N(s) \left(\epsilon-C_o(s)\right)}{\Phi_1(s)}ds = 0 ~~~a.s..$

Thirdly we prove that

$\lim\limits_{\epsilon\rightarrow 0}\lim\limits_{t\rightarrow\infty}E[Y_\epsilon(t)-Y(t)] = 0.\label{fact3}$

(25)

We know from (23) that $Y_\epsilon(t)-Y(t)\ge 0$, $t\ge 0$ a.s. Using equations (21) and (22) we get

$\begin{align} &d(Y_\epsilon(t)-Y(t)) = \biggl((Y_\epsilon(t)-Y(t))\left(\sigma_1^2+\alpha\epsilon-\beta-\frac{\sigma_2^2}{Y(t)Y_\epsilon(t)}\right)\notag \\&+\alpha \epsilon Y(t)\biggl)dt-\sigma_1(Y_\epsilon(t)-Y(t))dB_1(t)\notag\\ &\le \biggl((Y_\epsilon(t)-Y(t))\left(\sigma_1^2+\alpha\epsilon-\beta\right)+\alpha \epsilon Y(t)\biggl)dt-\sigma_1(Y_\epsilon(t)-Y(t))dB_1(t)\text{ a.s.}.\notag \end{align}$

From Lemma 4.6 we know that $\sup_{t\ge 0} E[Y(t)]<\infty$, so taking expectations in the previous inequality we have

$\begin{align} &E[Y_\epsilon(t)-Y(t)]\le \int_0^t E[Y_\epsilon(s)-Y(s)]\left(\sigma_1^2+\alpha\epsilon-\beta\right)+\alpha \epsilon E[Y(s)]ds\notag\\ &\le \int_0^t E[Y_\epsilon(s)-Y(s)]\left(\sigma_1^2+\alpha\epsilon-\beta\right)ds+t\alpha \epsilon\sup\limits_{t\ge 0}E[Y(t)]\text{ a.s.}.\notag \end{align}$

For any $0<\epsilon< (\beta-\sigma_1^2)/\alpha$, by the comparison theorem (see theorem 1.4.1 in [14]) we get

$0\le E[Y_\epsilon(t)-Y(t)]\le\frac{\alpha\epsilon \sup\limits_{t\ge 0}E[Y(t)] }{\beta-\sigma_1^2-\alpha\epsilon}\left(1-\exp(-t(\beta-\sigma_1^2-\alpha\epsilon))\right)$

Taking limits in the previous inequality we get equation (25).

Finally, using (23), (24), and (25) we obtain that $\lim_{t\rightarrow \infty}(N(t)-Y(t)) = 0$, in probability. But it has been shown that $Y(t)\overset{w}{\underset{t\rightarrow \infty}{\rightarrow}} \nu_1$, where $\nu_1$ is a probability measure on $\mathbb{R_+^*}$. Thus, from Slutsky's theorem [22], $N(t)\overset{w}{\underset{t\rightarrow \infty}{\rightarrow}} \nu_1$, and, by the Continuous Mapping Theorem, $n(t) = 1/N(t)\overset{w}{\underset{t\rightarrow \infty}{\rightarrow}} \mu_1$.

Corollary 2. Let $(n(t), C_o(t), C_e(t))$ be the solution of the system (5)-(7) with any initial value $(n(0), C_o(0), C_e(0))'\in D$, and such that $\lim_{t\rightarrow \infty} C_o(t) = 0$ a.s..

a. If $\sigma_1 = 0$ then $n(t)\overset{w}{\underset{t\rightarrow \infty}{\rightarrow}} \mu_1$ where $\mu_1$ is the probability measure on $\mathbb{R_+^*}$ with density

$\begin{align} &p(x) = \frac{1}{G_1 x^4}\exp\left(-\frac{\beta}{\sigma_2^2}\left(\frac{1}{x}-\frac{\gamma}{\beta}\right)^2\right), x>0\label{dens1} \end{align}$

(26)

$\begin{align} &G_1 = \frac{\sigma_2}{2\beta^{5/2}}\left(\Psi\left(\frac{\gamma\sqrt{2\beta}}{\beta\sigma_2}\right)\sqrt{\pi}(\sigma_2^2\beta+2\gamma^2)+ \gamma\sigma_2\beta^{1/2}\exp\left(-\frac{\gamma^2}{\sigma_2^2 \beta}\right)\right)\label{dens2} \end{align}$

(27)

where $\Psi(x) = \mathbb{P}(Z\le x)$ is the distribution function for the standard normal distribution $Z\sim N(0, 1)$.

b. If $\sigma_1^2<\beta$ and $\sigma_2 = 0$ then $n(t)\overset{w}{\underset{t\rightarrow \infty}{\rightarrow}} \mu_1$ where $\mu_1$ is a gamma distribution with shape parameter $\frac{2(\beta-\sigma_1^2)}{\sigma_1^2}+1$ and scale parameter $\frac{\sigma_1^2}{2\gamma}$.

Proof. We know that $Y(t)\overset{w}{\underset{t\rightarrow \infty}{\rightarrow}} \nu_1$, where $\nu_1$ is a probability measure on $\mathbb{R_+^*}$. When $\sigma_1 = 0$ or $\sigma_2 = 0$ we can prove the ergodicity of $Y(t)$ directly using Theorem 1.16 in [13].

a. If $\sigma_1 = 0$ the equation (21) become

$dY(t) = \left(-Y(t)\beta+\gamma+\frac{\sigma_2^2}{Y(t)}\right)dt+\sigma_2dB_2(t)\text{ a.s.}, \label{eqi2new}$

(28)

Let define

$\begin{align} q(y)& = \exp\left(-\frac{2}{\sigma_2^2}\int_1^y\left( -\beta u+\frac{\sigma_2^2}{u}+\gamma\right) du\right) = \frac{1}{y^2}\exp\left(-\frac{\beta}{\sigma_2^2}\left(1-\frac{\gamma}{\beta}\right)^2\right)\notag\\ &\exp\left(\frac{\beta}{\sigma_2^2}\left(y-\frac{\gamma}{\beta}\right)^2\right)\notag \end{align}$

It can be easily shown that

$\int_0^1 q(y)dy = \infty, ~~ \int_1^\infty q(y)dy = \infty, ~~\int_0^\infty\frac{1}{\sigma_2^2 q(y)}dy = \frac{G_1}{\sigma_2^2}\exp\left(\frac{\beta}{\sigma_2^2}\left(1-\frac{\gamma}{\beta}\right)^2\right), \notag$

where $G_1$ is given in (27). So, by Theorem 1.16 in [13], $Y(t)$ is ergodic and with respect to the Lebesgue measure its stationary measure $\nu_1$ has density

$p_1(x) = \frac{1}{\sigma_2^2q(x)\int_0^\infty\frac{1}{\sigma_2^2 q(y)}dy} = \frac{x^2\exp\left(-\frac{\beta}{\sigma_2^2}\left(x-\frac{\gamma}{\beta}\right)^2\right)}{G_1}$

Thus, by Theorem 4.5, $X(t) = 1/Y(t)$ is ergodic and its stationary measure $\mu_1$ is the reciprocal of the measure $\nu_1$, so with respect to the Lebesgue measure has density $p(x) = p_1(1/x)/x^2$ given in equation (26). Notice that we also have

$\begin{align} &\lim\limits_{t\rightarrow \infty}\frac{1}{t}\int_0^tX(u)du = \int_0^\infty xp(x)dx = \frac{\sigma_2}{2\beta^{3/2} G_1}\left( \sigma_2\sqrt{\beta}\exp\biggl(-\frac{\gamma^2}{\sigma_2^2 \beta}\right)\notag\\ &+2\gamma \sqrt{\pi}\Psi\left(\frac{\gamma\sqrt{2\beta}}{\beta\sigma_2}\right)\biggl)\text{ a.s..}\notag \end{align}$

b. If $\sigma_2 = 0$, then the equation (21) becomes

$dY(t) = \left(\gamma-Y(t)(\beta-\sigma_1^2)\right)dt-\sigma_1Y(t)dB_1(t)\text{ a.s.}.$

Proceeding similarly as for a. we can show that $\nu_1$ is the reciprocal gamma distribution with shape parameter $\frac{2(\beta-\sigma_1^2)}{\sigma_1^2}+1$ and scale parameter $\frac{\sigma_1^2}{2\gamma}$ (see also the proof of Theorem 4.5 in [29]). Thus, by Theorem 4.5, $X(t) = 1/Y(t)$ is ergodic and its stationary measure $\mu_1$ is the gamma distribution with shape parameter $\frac{2(\beta-\sigma_1^2)}{\sigma_1^2}+1$ and scale parameter $\frac{\sigma_1^2}{2\gamma}$. Since the mean for this gamma distribution is $\left(\frac{2(\beta-\sigma_1^2)}{\sigma_1^2}+1\right)\frac{\sigma_1^2}{2\gamma}$, we also have

$\lim\limits_{t\rightarrow \infty}\frac{1}{t}\int_0^tX(u)du = \left(\frac{2(\beta-\sigma_1^2)}{\sigma_1^2}+1\right)\frac{\sigma_1^2}{2\gamma}\text{ a.s..}$

Notice that if $\sigma_1^2>2\beta -2\alpha\lim\inf_{t\rightarrow\infty}\frac{\int_0^t C_o(s)ds}{t}$ a.s. then, according to Theorem 3.5, $\lim_{t\rightarrow \infty}n(t) = 0$, so $n(t)\overset{w}{\underset{t\rightarrow \infty}{\rightarrow}} \delta_0$, where $\delta_0$ is the Dirac distribution centered in $0$.

On the other hand, if $\sigma_1^2<\beta$, $\eta_1^2\eta_2^2-\lambda_1^2\lambda_2^2>0$, and $\lim\inf_{t\rightarrow \infty}n(t)>0$ a.s., then according to Theorem 4.7 $n(t)\overset{w}{\underset{t\rightarrow \infty}{\rightarrow}} \mu_1$. Indeed, since $\lim\inf_{t\rightarrow \infty}n(t)>0$ a.s., then $\int_0^\infty n(t)dt = \infty$ a.s., and from the proof of Theorem 2.3 we know that $\lim_{t\rightarrow \infty}C_o(t) = \lim_{t\rightarrow \infty}C_e(t) = 0$, so the assumptions of Theorem 4.7 are satisfied.

---

5. Numerical simulations

First we illustrate numerically the results obtained in section 3 regarding survival analysis.We consider a cell population exposed to the toxicant monastrol as in the experiments described in [1]. The parameters' values for this toxicant are estimated in [1]: $\beta = 0.074$, $K = 18.17$, $\eta_1 = 0.209$, $\lambda_1 = 0.177$, $\lambda_2 = 0.204$, $\eta_2 = 0.5$, and $\alpha = 0.016$. Notice that for this toxicant we have $\eta_1^2\eta_2^2-\lambda_1^2\lambda_2^2>0$. We solve numerically the system (5)-(7) using an order 2 strong Taylor numerical scheme [12].

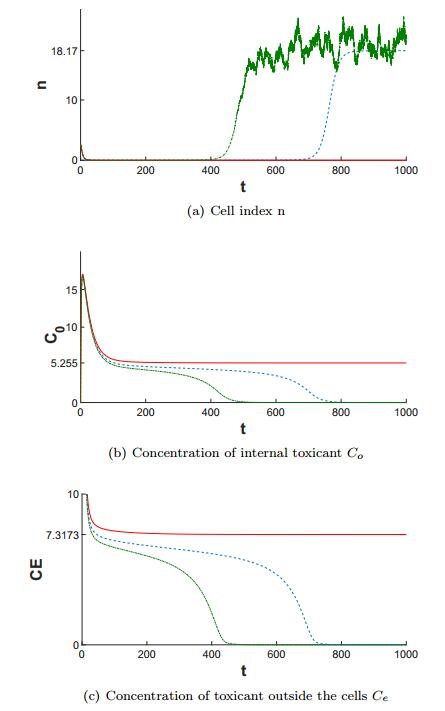
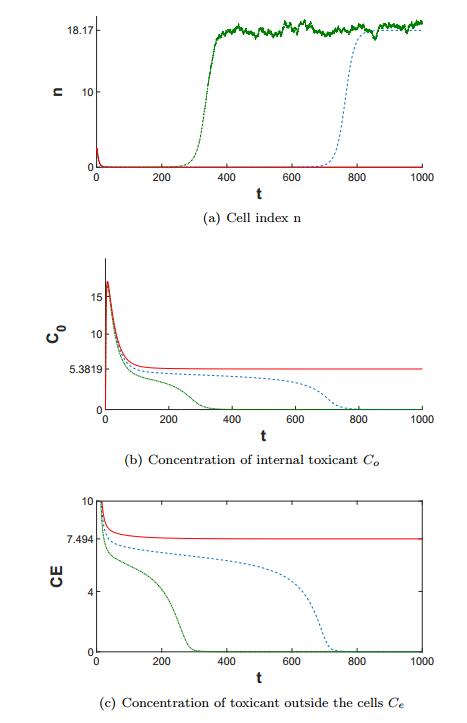
One of the applications of the mathematical model is for finding the threshold value for $C_e(0)$ at which the population becomes extinct. This value depends on the initial value $n(0)$ and for the deterministic model (1)-(3) can be found numerically (see also Fig. 3 in [1]). From Theorem 3.5 we can see that large values of the noise variance $\sigma_1^2$ result in population extinction, so we expect that the presence of noise will lower the values of the threshold.

We illustrate this for the model with initial values $n(0) = 2.5$ and $C_o(0) = 0$. In the deterministic case the threshold value where the population goes extinct can be found numerically, and it is approximately $C_e^{det}(0) = 382.2$. We can see in Fig. 2 (a) that for the stochastic model with $\sigma_1 = 0.01$, $\sigma_2 = 0$ and initial value $C_e(0) = 380$ the population goes to extinction, while in the deterministic case ($\sigma_1 = \sigma_2 = 0$) the population is persistent for these initial values. According to Fig. 2 (a), in the stochastic case the threshold value for this simulation is $C_e^{stoch}(0)\in(375, 380)$. Similar results are obtained for the stochastic model with $\sigma_1 = 0$, $\sigma_2 = 0.001$ and are presented in Fig. 3 (a). For this simulation the threshold value in the stochastic case is $C_e^{stoch}(0)\in(379, 380)$.

Notice also that the results displayed in Figs. 2 and 3 agree with the conclusion of Theorem 2.3. For the stochastic model with $C_e(0) = 380$, for the simulations presented in Figs. 2 and 3 we have $\lim_{t\rightarrow \infty}n(t, \omega) = 0$ (the trajectories plotted with red plain lines). For $\sigma_1 = 0.01$ and $\sigma_2 = 0$ we can see that $\lim_{t\rightarrow \infty}C_o(t, \omega) = 5.3819$ and $\lim_{t\rightarrow \infty}C_e(t, \omega) = 7.494$ (the trajectories plotted with red plain lines in Fig. 2 (b), (c)). For $\sigma_1 = 0$ and $\sigma_2 = 0.002$ from Fig. 3 (b), (c) we can notice that $\lim_{t\rightarrow \infty}C_o(t, \omega) = 5.255$ and $\lim_{t\rightarrow \infty}C_e(t, \omega) = 7.3173$. For both simulation we have $\lim_{t\rightarrow\infty} C_o(t) = \frac{\lambda_1^2}{\eta_1^2}\lim_{t\rightarrow\infty} C_e(t)$, as given in Theorem 2.3. Moreover, for the stochastic model with $C_e(0) = 375$, $\sigma_1 = 0.01$ and $\sigma_2 = 0$ (the green dot -dashed lines in Fig. 2) and the model with $C_e(0) = 379$, $\sigma_1 = 0$ and $\sigma_2 = 0.002$ (the green dot -dashed lines in Fig. 3), we have

$\liminf\limits_{t\rightarrow\infty} n(t, \omega)>0, \lim\limits_{t\rightarrow \infty}C_o(t, \omega) = \lim\limits_{t\rightarrow \infty}C_e(t, \omega) = 0$

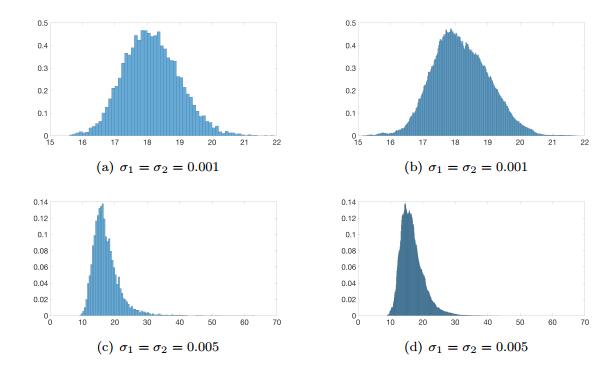
Next we use the same parameters values as stated at the beginning of this section and the initial values $n(0) = 2.5$, $C_o(0) = 0$, $C_e(0) = 1.8$ to illustrate the stability in distribution of the process $n(t)$. For both $\sigma_1 = \sigma_2 = 0.001$ and $\sigma_1 = \sigma_2 = 0.005$ the assumptions of Theorem 4.7 are met. In Figs. 4 (a) and (c) we show the histograms of the result of running 10 000 simulations of the path $n(t)$ for a long run of 5 000 0000 iterations, but storing only the last of these $n(t)$ values. For comparison Figs. 4 (b) and (d) show the histograms of the last 4 000 000 samples from a single run of 5 000 000 iterations. For both sets of values for $\sigma_1$ and $\sigma_2$ the corresponding histograms are similar. Because of this similarity and of the huge number of iterations considered, we may assume that the probability distribution of $n(t)$ has more or less reached the distribution $\mu_1$ given in Theorem 4.7.

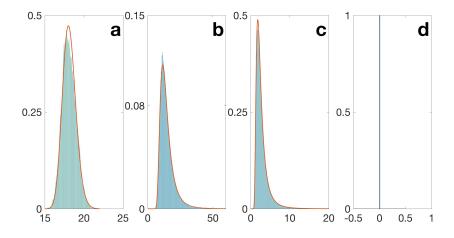
When $\sigma_2 = 0$ or $\sigma_1 = 0$, the density of the probability distribution $\mu_1$ is given in Corollary 2 (a) and (b), respectively. To illustrate these results we use the same parameter values as stated at the beginning of this section and the initial values $n(0) = 2.5$, $C_o(0) = 0$, $C_e(0) = 180$. For $\sigma_1 = 0$ and several values of $\sigma_2$ we display the histograms for the last 4 000 000 samples of a single run of 5 000 000 iterations (shaded areas in Fig. 5) and the graph of the corresponding density given in Corollary 2 (a). In Fig. 6 we do similar plots for $\sigma_2 = 0$, several values of $\sigma_1$, and the density of the corresponding Gamma distribution in Corollary 2 (b). We can notice that the histograms give very accurate approximations for the densities in Corollary 2. Also, in both Fig. 5 and Fig. 6, when the values of $\sigma_1$ or $\sigma_2$ increase, the histograms become right skewed. Moreover, for large values of $\sigma_1$ or $\sigma_2$ the population becomes extinct and $\mu_1 = \delta_0$ (see also Theorem 3.5).

---

6. Conclusions

We present a stochastic model to study the effect of toxicants on human cells. To account for parameter uncertainties, the model is expressed as a system of coupled ordinary stochastic differential equations. The variables are the cell index $n(t)$, which closely reflects the cell population, the concentration $C_o(t)$ of internal toxicants per cell, and the concentration $C_e(t)$ of toxicants outside the cells at time $t$. There are a few papers that consider similar stochastic models for population dynamics, but they mainly study conditions for extinction and persistence. Here we focus on the ergodic properties when the population is persistent.

We first prove the positivity of the solutions. Then we investigate the influence of noise on the cell population survival. When the noise variances $\sigma_1^2$ or $\sigma_2^2$ are sufficiently large, the population goes to extinction. Numerical simulations show that, for the stochastic model, the population goes to extinction at threshold values $C_e^{stoch}(0)$ below the deterministic threshold value $C_e^{det}(0)$. Furthermore, increasing the noise variances $\sigma_1^2$ or $\sigma_2^2$ results in a lower value $C_e^{stoch}(0)$ at which the population becomes extinct.

Moreover, we prove that when the noise variance $\sigma_1^2$ is sufficiently small and the population is strongly persistent, then the cell index converges weakly to the unique stationary probability distribution. Increasing the noise intensity causes a right skewness of the stationary distribution.

Here we illustrate our results for the toxicant monastrol. We have also considered other toxicants from the experiments described in [1] classified in various clusters [30]. We have noticed that the cluster type does not change the type of stationary distribution, nor has an effect on the behavior of the distributions in response to increased noise variances.

---

Appendix A. Proof of Lemma 2.2

Proof. The proof is similar with the proof of Lemma 3.1 in [1]. We define the stopping time $\tau = \inf \{t\ge 0: C_e(t)> C_e(0)\}$. We show that $\tau = \infty$ a.s.. Assume that there exists $T>0$, and $\epsilon>0$ such that $P(\tau\le T)>\epsilon$ and let $\Omega$ be the set where the solution $(n(t), C_o(t), C_e(t))'$ of the system (5)-(7) is continuous. Hence $P(\Omega) = 1$ ([3]), and $P(\Omega_1)>0$, where $\Omega_1 = \Omega\cap \{\tau\le T\}$.

From (8) with $C_o(0) = 0$ we get for any $\omega\in \Omega_1$ and any $0<t<\tau(\omega)$

$\begin{align} &0\le C_o(t, \omega) = \lambda_1^2 e^{-\eta_2^2 t}\int_0^t C_e(s, \omega) e^{\eta_1^2 s} ds\le \lambda_1^2 e^{-\eta_2^2 t}C_e(0)\int_0^t e^{\eta_1^2 s} ds\notag\\ & = \frac{\lambda_1^2 C_e(0)}{\eta_1^2}\left(1-e ^{-\eta_1^2t}\right)\le \frac{\lambda_1^2 C_e(0)}{\eta_1^2}\notag \end{align}$

Moreover, on $\Omega_1$ we have $C_e(\tau) = C_e(0)$, and then from equation (7) we obtain

$\begin{align} \frac{dC_e}{dt}\biggl |_{t = \tau}& = \lambda_2^2C_o(\tau)n(\tau)-\eta_2^2 C_e(\tau)n(\tau)\notag\\ &\le C_e(0) n(\tau)\left(\frac{\lambda_1^2 \lambda_2^2}{\eta_1^2}-\eta_2^2\right)<0\notag \end{align}$

Thus we have a contradiction with the definition of $\tau$.

---

Appendix B. Proof of Theorem 2.3

Proof. The proof is similar with the proof of Theorem 3.2 in [1]. Let $\Omega$ be the set where the solution $(n(t), C_o(t), C_e(t))'$ of the system (5)-(7) is continuous and $n(t)>0$, $0<C_e(t)\le C_e(0)$, $0\le C_o(t)\le\lambda_1^2C_e(0)/\eta_1^2$ for any $t\ge 0$. From Theorem 2.1 and Lemma 2.2 we know that $P(\Omega) = 1$. Let $\Omega_1 = \{\omega\in \Omega: |n|_1(\omega)<\infty\}$ and $\Omega_2 = \{\omega\in \Omega: |n|_1(\omega) = \infty\}$, where $|n|_1(\omega) = \int_0^\infty n(t, \omega)dt$.

If $P(\Omega_1)>0$, then for any $\omega\in\Omega_1$ and any $t\ge 0$, we have

$\int_0^t C_o(s, \omega) n(s, \omega)\exp{\left(\eta_2 ^2\int_0^s n(l, \omega)dl\right )}ds\le \frac{\lambda_1^2 C_e(0)}{\eta_1^2}\exp{\left(\eta_2 ^2|n|_1(\omega)\right )}|n|_1(\omega).$

Thus $0\le M(\omega): = \int_0^\infty C_o(s, \omega) n(s, \omega)\exp{\left(\eta_2 ^2\int_0^s n(l, \omega)dl\right )}ds<\infty$, and from (9) we get

$\lim\limits_{t\rightarrow\infty} C_e(t, \omega) = C_e(0)\exp(-\eta_2^2|n|_1(\omega))+\lambda_2^2 M(\omega)\exp(-\eta_2^2|n|_1(\omega))<\infty.$

Consequently, there exists $T_1(\omega)>0$ such that for any $t>T_1(\omega)$ we have $C_e(t, \omega)>C_e(0)\exp(-\eta_2^2|n|_1(\omega))/2$. This implies that $\int_0^\infty C_e(s, \omega) e^{\eta_1^2s}ds = \infty$ because for any $t> T_1(\omega)$ we have

$\begin{align} &\int_0^t C_e(s, \omega) e^{\eta_1^2s}ds\ge \int_{T_1(\omega)}^t C_e(s, \omega) e^{\eta_1^2s}ds\notag\\ &\ge C_e(0)\exp(-\eta_2^2|n|_1(\omega))/2\int_{T_1(\omega)}^t e^{\eta_1^2s}ds.\notag \end{align}$

So we can apply L'Hospital's rule in (8), and we get

$\lim\limits_{t\rightarrow\infty} C_o(t, \omega) = \frac{\lambda_1^2}{\eta_1^2}\lim\limits_{t\rightarrow\infty} C_e(t, \omega)>0.$

Thus, on $\Omega_1$, $\lim_{t\rightarrow\infty} C_e(t)$ and $\lim_{t\rightarrow\infty} C_o(t)$ exist and they are related by the previous equation.

Next, if $P(\Omega_2)>0$ we consider any $\omega\in \Omega_2$. If $0\le\int_0^\infty C_o(s, \omega) n(s, \omega)$ $\exp \bigl(\eta_2 ^2$ $\int_0^s n(l, \omega)dl\bigl)ds<\infty$, from (9) we get $\lim_{t\rightarrow\infty} C_e(t, \omega) = 0$. On the other hand, if $\int_0^\infty C_o(s, \omega) n(s, \omega)\exp{\left(\eta_2 ^2\int_0^s n(l, \omega)dl\right )}ds = \infty$, from L'Hospital's rule in (9) we have

$0\le \frac{\lambda_2^2}{\eta_2^2}\liminf\limits_{t\rightarrow\infty}C_o(t, \omega)\le \liminf\limits_{t\rightarrow\infty}C_e(t, \omega)\le \limsup\limits_{t\rightarrow\infty}C_e(t, \omega)\le \frac{\lambda_2^2}{\eta_2^2}\limsup\limits_{t\rightarrow\infty}C_o(t, \omega)$

Similarly, from (8) we either get that $\lim_{t\rightarrow\infty} C_o(t, \omega) = 0$ (if $\int_0^\infty C_e(s, \omega) e^{\eta_1^2s}ds<\infty$), or we have

$0\le \frac{\lambda_1^2}{\eta_1^2}\liminf\limits_{t\rightarrow\infty}C_e(t, \omega)\le \liminf\limits_{t\rightarrow\infty}C_o(t, \omega)\le \limsup\limits_{t\rightarrow\infty}C_o(t, \omega)\le \frac{\lambda_1^2}{\eta_1^2}\limsup\limits_{t\rightarrow\infty}C_e(t, \omega),$

(if $\int_0^\infty C_e(s, \omega) e^{\eta_1^2s}ds = \infty$). All these possible cases give

$\lim\limits_{t\rightarrow\infty}C_o(t, \omega) = \lim\limits_{t\rightarrow\infty}C_e(t, \omega) = 0,$

because $\eta_1^2\eta_2^2-\lambda_1^2\lambda_2^2>0$. Thus, on $\Omega_2$, $\lim_{t\rightarrow\infty} C_e(t)$ and $\lim_{t\rightarrow\infty} C_o(t)$ exist and they are equal with zero.

In conclusion, on $\Omega = \Omega_1\cup \Omega_2$ we have shown that $\lim_{t\rightarrow\infty} C_e(t)$ and $\lim_{t\rightarrow\infty} C_o(t)$ exist, and we have $\lim_{t\rightarrow\infty} C_o(t) = \frac{\lambda_1^2}{\eta_1^2}\lim_{t\rightarrow\infty} C_e(t)$.

---

Appendix C. Proof of Lemma 4.6

Proof. We choose any $0<c<\beta-\sigma_1^2$. Using Itô's formula in (21) we get:

$\begin{align} &d(e^{ct}Y(t)) = e^{ct}\biggl(Y(t)(c+\sigma_1^2-\beta)+\gamma +\sigma_2^2 X(t)\biggl)dt-\sigma_1e^{ct}Y(t)dB_1(t)\notag\\ &+\sigma_2e^{ct}dB_2(t)\le e^{ct}\biggl(\gamma +\sigma_2^2 X(t)\biggl)dt-\sigma_1e^{ct}Y(t)dB_1(t)+\sigma_2e^{ct}dB_2(t) \label{eqa1} \end{align}$

(29)

Let $\tau_m = \inf\{t\ge 0: Y(t)\notin(1/m, m)\}$, for any $m>m_0$, where $m_0>0$ is sufficiently large such that $n(0)\in(1/m_0, m_0)$. Obviously $\lim_{m\rightarrow\infty}\tau_m = \infty$ a.s.. Taking expectation in (29) and using Lemma 4.4 we get:

$\begin{align} &E\left[e^{c (t\wedge \tau_m)} Y(t\wedge \tau_m)\right]\le \frac{1}{n(0)}+E\left[\int_0^{t\wedge \tau_m} e^{cs}\left(\gamma+\sigma_2^2X(s)\right) ds\right]\notag\\ &\le \frac{1}{n(0)}+\left(\gamma+\sigma_2^2 C_1\right)\frac{(e^{ct}-1)}{c}.\notag \end{align}$

Letting $m\rightarrow \infty$ we get

$E\left[Y(t)\right]\le \frac{1}{n(0)e^{ct} }+\frac{\left(\gamma+\sigma_2^2 C_1\right)}{c}(1-e^{-ct}).$

Thus, there exists a constant $C_2>0$ such that $\sup_{t\ge 0}E[Y(t)]\le C_2$. The proof that $\sup_{t\ge 0} E[Y_\epsilon(t)]< \infty$, for any $0<\epsilon<\frac{\beta-\sigma_1^2}{\alpha}$, is similar.

---