Modified salp swarm algorithm based multilevel thresholding for color image segmentation

1.   Introduction

Image segmentation has always been an important research object of image processing. The purpose of image segmentation is to better segment the desired target area. So far, there are many kinds of image segmentation methods, such as thresholding, feature clustering, pixel segmentation and artificial neural network. Among image segmentation methods, the threshold segmentation has the characteristics of simplicity and rapidity and is widely used. The color image segmentation method is divided into bi-level segmentation and multi-threshold segmentation. The image is divided into two parts: Foreground and background, which is called bi-level segmentation method. In order to divide more regions, it is necessary to select multiple thresholds for the image flavor multi-region, which is called multi-threshold segmentation. Therefore, the multi-threshold color image segmentation becomes the main research problem, and the main segmentation method is between-class variance, maximum entropy, Renyi entropy, etc. Applying multi-threshold segmentation to color image segmentation can obtain a more accurate segmentation image, which is very important in image segmentation.

A color pixel embeds dissimilar color constituents, and the concoction of them in color images enhanced the massive integral computational complexities in the context of segmentation ^[1,2,3]. In order to improve the segmentation precision of multi-threshold image segmentation method, optimization algorithm is used to optimize the multi-threshold image segmentation method ^[4,5,6,7]. Meta-heuristics algorithms handled the optimization problems by mimicking physical or biological phenomena ^[8]. In the last couple of years, few works have been accomplished in favor of multilevel segmentation of colored images due to the exponentially increasing complexities involved in the computation of threshold values ^[9]. Evolutionary techniques such as ACO ^[10]. ACO imitated ants to find the shortest path social behavior, PSO algorithm ^{[11,12,13,14,15]} simulated the behavior of birds in navigation and hunting. Other group optimization algorithms were: Artificial Bee Colony Algorithm proposed by Karaboga in 2015 ^[16,17,18] which can be optimized by imitating the behavior of bees to collect nectar, which can adapt to the transformation of the environment; the Firefly Algorithm ^{[18,19,20,21,22]} was proposed by Xin-she Yang. By imitating the phototaxis of fireflies, it can be optimized by moving the light source. Bat Algorithm ^{[23,24,25,26,27]} was an efficient global search method. The algorithm searches for the optimal solution by approximating the optimal solution in iteration; Whale optimization algorithm ^[28,29,30] proposed stimulating humpback whales to hunt. The algorithm has strong ability of global search and local optimization. Although there are differences between evolutionary optimization and population optimization, the common point is that the optimal value of a restricted domain can be found ^[31]. Although each algorithm has its own advantages, no-free lunch ^[32] has proved that no one algorithm can solve all optimization problems. The above algorithm was able to have the best optimization ability, but the slap swarm algorithm has better global searching ability ^[33,34], it imitated the behavior of the slap swarm, can effective to hunt prey. It has two advantages: (1) SSA is swarmed based optimization technique. The entry wise product shows similarity with PSO, but the parameter is very efficient in determining the search space due to its longer step size in the lengthy execution; (2) SSA has excellent searching ability, local optimization is more accurate. At the same time, the number of parameters tuned is lesser as compared to PSO, FPA and WOA. This makes SSA more suitable for a variety of optimization procedures. However, SSA algorithm has problems in different problems, so many scholars improve SSA algorithm to improve its optimization ability through improvement strategies. Sayed G.I. proposed a novel chaotic salp swarm algorithm that can solve the stagnation in local optima and low convergence rate of SSA ^[35]. The experiment result can significantly boost the performance of original SSA. Mohammed H.Q. proposed an enhanced salp swarm algorithm ^[36]. The algorithm can be improved the inadequate results of the SSA. So, in order to better solve practical problems, the strategy method is used to improve the traditional algorithm, which can better improve the optimization ability.

Threshold segmentation based on histogram is a simple and most popular image segmentation technology ^[37]. Threshold technology can be roughly divided into local threshold technology and global threshold technology. The global threshold selection technique is most popular for its simplicity and efficiency. Among the global threshold technologies, Kapur ^[38] and Otsu ^[39] are the most popular. Otsu method maximizes the inter-class variance function, while Kapur method maximizes the posterior entropy of the segmented class to find the optimal threshold ^[40,41]. Since exhaustive search is used to find thresholds, the computational complexity of Kapur and Otsu methods increases exponentially with the increase of thresholds ^[42]. Kapur's entropy, between-class variance and Renyi's entropy techniques were often used in thresholding segmentation and can be easily extended to multilevel thresholding. They are very efficient for bi-level thresholding, but are very time consuming when the number of thresholds grows exponentially. So many swarm intelligence algorithms based on Kapur's entropy, between-class variance and Renyi's cross are used for multilevel thresholding problem. In 2011, Tan and Khang Siang presented a novel histogram thresholding-fuzzy C-means hybrid (HTFCM) approach that could find different application in pattern recognition as well as in computer vision ^[43]. After that, in 2013, two swarm intelligence algorithms, particle swarm optimization (PSO) and artificial bee colony (ABC), have been used for multilevel thresholding. Kapur's entropy and between-class variance have been investigated as objective functions ^[44]. In 2016, Bhandari, Ashish Kumar, et al. introduced the comparative performance study of different objective functions using quick search and other optimization algorithms to solve the color image segmentation problem via multilevel thresholding ^[45]. Recently, S. Pare et al. presented new multilevel thresholding methods using Tsallis's entropy, which were based on cuckoo search (CS) algorithm and Gray-Level Co-occurrence Matrix ^[46]. For Kapu's entropy, Bhandari, Ashish Kumar, et al. proposed two successful swarm-intelligence-based global optimization algorithms, cuckoo search (CS) algorithm and wind driven optimization (WDO) for multilevel thresholding using Kapur's entropy has been employed ^[47]. After that Khairuzzaman proposed a new approach of multilevel thresholding based on Grey Wolf Optimizer using Kapur's entropy ^[48]. Liang Hongnan proposed a Tsallis entropy image segmentation based modified grasshopper optimization algorithm ^[49]. The proposed segmentation approach has a fewer iterations and a higher segmentation accuracy. He Lifang proposed a modified firefly algorithm (MFA) to find the optimal multilevel threshold values for color image ^[50]. This method improved the precision of image segmentation by using optimization algorithm. S. Pare proposed gray-level co-occurrence matrix (GLCM) based color image Segmentation ^[51]. This method used the optimization algorithm to optimize multi-threshold GLCM, which has good image segmentation accuracy and simple structure. Zhikai Xing proposed an improved salp swarm algorithm to solve the threshold selection problem of multi-threshold GLCM ^[52]. This algorithm effectively improves the image segmentation accuracy of GLCM algorithm. Recently, Mishra proposed optimal threshold values have been calculated using bat algorithm and maximizing different objective function values based on Kapur's entropy ^[53].

Although there is no perfect optimization algorithm, the optimization algorithm can be improved to make it more suitable for solving engineering problems. The strategies commonly used by scholars are as follows Levy-flight. Levy flight (LF) was a random walk strategy whose step length obeyed the Levy distribution ^[54]. Rongyu L proposed the Lévy particle swarm optimization ^[55]. The proposed method solved the problem that the particle swarm optimization (PSO) has some demerits, such as relapsing into local extremum, slow convergence velocity and low convergence precision in the late evolutionary. Mesa A used Levy flight improve the cuckoo search ^[56]. Results showed that applying CS-LF yielded better facility locations compared to particle swarm optimization and other existing algorithms. Mousavirad S. J. proposed a simple but efficient population-based metaheuristic algorithm called Human Mental Search (HMS) ^[57]. The mental search of HMS that explored the region around each solution based on Levy flight.

Now, many optimization algorithms are applied to the more threshold image segmentation problem ^[58]. This paper presents a new method of multilevel thresholding based on a slap swarm optimization algorithm (SSA). The proposed method selects the optimal set of thresholds using Otsu's between class variance, Kapur's entropy function or Renyi's entropy method. The main contributions of this paper are: (1) the application of MSSA for optimal multilevel thresholding using Otsu, Kapur methods and Renyi. The result of experimentation suggests that MSSA gives better result compared to SSA, WOA and FPA based methods, and (2) the computational complexity of multilevel thresholding is greatly reduced.

The remainder of this article is organized as follows. Section 2 describes the multilevel thresholding problem. It also describes Kapur's entropy, Otsu's between class variance and Renyi's enropy thresholding problem. Section 3 gives an overview of MSSA followed by its mathematical model. Section 4 describes the experimental environment of the proposed method and demonstrates the effectiveness of the proposed method by experimental results. Finally, the conclusions are provided in section 5.

2.   Problem assessment of multilevel thresholding

An efficient way of performing the image analysis for image segmentation is provided by the multilevel thresholding that the pixels of grayscale image or the colored image into distinct classes depending on their intensity values. Appropriate classes of an image can be selected by choosing the optimal threshold value ${T^ * }$ by bi-level thresholding as followed by:

The problem can be extended to multi-level threshold segmentation with multiple thresholds and the original image can be divided into multiple classes:

where ${N_i}$ is the ith class, n is the number of threshold values, and ${t_i}(i = 1, \cdots, n)$ is the ith threshold value.

2.1.   Kapur's entropy method

Kapoor's entropy method is based on information theory, which seeks the optimal threshold by maximizing the entropy or entropy sum of each characteristic class. Due to its superior performance, kapoor entropy method has attracted many researchers' attention and been widely used in image segmentation.

Let there be N pixels and L gray levels in a given image, then the probability of each gray level i is the relative occurrence frequency of the gray level i, normalized by the total number of gray levels:

where $h(i)$ is the number of pixels with gray level i.

For bi-level threshold may be described by Eq (4):

where ${H_0}{\rm{ = - }}\sum\limits_{i = 0}^{t - 1} {\frac{{{p_i}}}{{{\varpi _0}}}} \ln \frac{{{p_i}}}{{{\varpi _0}}}, \begin{array}{*{20}{c}} {} & {{\varpi _0}} \end{array} = \sum\limits_{i = 0}^{t - 1} {{p_i}}$ and ${H_1}{\rm{ = - }}\sum\limits_{i = t}^{L - 1} {\frac{{{p_i}}}{{{\varpi _0}}}} \ln \frac{{{p_i}}}{{{\varpi _0}}}, \begin{array}{*{20}{c}} {} & {{\varpi _1}} \end{array} = \sum\limits_{i = t}^{L - 1} {{p_i}}$. The optimal threshold value ${t^ * }$ can be found by maximizing Eq (5):

Further, Kapur's entropy can be easily extended for the multilevel thresholding problem as given by ^[41,42]:

In order to search m optimal threshold values $[{t_1}, {t_2}, \cdots, {t_m}]$ for a given image, we try to maximize the objective function:

2.2.   Between-class variance method (Otsu's method)

In order to search m optimal threshold values $[{t_1}, {t_2}, \cdots, {t_m}]$ for a given image, we try to maximize the objective function.

The Otsu based between-class variance method was used to determine the optimal threshold. Otsu's method can be described as follows: Suppose an image can be represented by L gray levels (1, 2..., L), and there are N pixels. The number of pixels at level i is denoted by ${f_1}$, then $N = {f_1} + {f_2} + \cdots {f_i}$. Then, the occurrence probability of gray level i is defined as:

In bi-level thresholding, the optimum threshold t divides the image into two classes, and the cumulative probabilities of each class can be described as follows:

The mean levels of two classes can be defined as follows:

Let ${\mu _T}$ be the mean levels of the whole image and is defined by

The between-class variance of whole classes can be represented by

where ${\sigma _0}{\rm{ = }}{\varpi _0}{({\mu _0} - {\mu _T})^2}$ and ${\sigma _1}{\rm{ = }}{\varpi _1}{({\mu _1} - {\mu _T})^2}$. For bi-level thresholding, the Otsu's method finds an optimal threshold ${t^ * }$ by maximizing the between-class variance, that is

The Otsu's method can be also extended to multi-level thresholding. Assuming that there are m thresholds, which divide the image into m + 1 classes. The extended between-class variance is calculated by

The sigma terms are determined using Eq (15) and the mean levels are calculated by Eq (16):

The optimum thresholds M are found by maximizing the between-class variance by Eq (17):

2.3.   Renyi's entropy method

Renyi's entropy calculates the entropy absolute value and entropy difference between the target region and the background region, and obtains the threshold value of the larger region. The Renyi entropy of the entire class can be expressed as

where

where the parameter q is a real number not equal to one associated with the extensibility of the system, and it is dependent. The threshold value ${t^ * }$ can be found by maximizing:

Further, Renyi's entropy can be easily extended for the multi-level thresholding problem as given by:

In order to search M optimal threshold values $[{t_1}, {t_2}, \cdots, {t_M}]$ for a given image, we try to maximize the objective function:

3.   Modified slap swarm algorithm

Salps belong to the family of Salpidae and have transparent barrel-shaped body. Their tissues are highly similar to jelly fishes ^[59]. They also move very similar to jelly fish, in which the water is pumped through body as propulsion to move forward. In the deep oceans, shapes often form a swarm called shop chain. This chain is illustrated in Figure 1. The main reason for this behavior is not very clear yet, but some researchers believe that this is done for achieving better locomotion using rapid coordinated changes and foraging.

3.1.   The mathematical model of slap

In order to establish the mathematical model of salp chain, the population is first divided into two groups: leaders and followers. The leader is the shape at the front of the chain, while the rest of the salps are seen as followers. As the names of these salps suggest, leaders lead the swarm and followers follow each other.

The position of salps is defined in the dimensional search space, where n is the number of variables for a given problem. Therefore, all salp positions are stored in a two-dimensional matrix x, and it is assumed that there is a food source F in the search space as the target of the group.

To update the position of the leader the following equation is proposed:

where $X_{\rm{j}}^1$ shows the position of the first salp (leader) in the jth dimension, ${F_j}$ is the position of the food source in the jth dimension, $u{b_j}$ indicates the upper bound of jth dimension, $l{b_j}$ indicates the lower bound of jth dimension, ${c_1}$, ${c_2}$ and ${c_3}$ are random numbers. Equation (23) shows that the leader only updates its position with respect to the food source. The coefficient ${c_1}$ is the most important parameter in SSA because it balances exploration and exploitation defined as follows:

where l is the current iteration and L is the maximum number of iterations.

The parameter ${c_2}$ and ${c_3}$ are random numbers uniformly generated in the interval of [0, 1]. In fact, they dictate if the next position in jth dimension should be towards positive infinity or negative infinity as well as the step size.

To update the position of the followers, the following equations utilized:

where ${\rm{i}} \geqslant 2$, $x_j^i$ shows the position of ith follower slap in jth dimension, t is time, ${v_0}$ is the initial speed, and ${\rm{a = }}\frac{{{{\rm{v}}_{{\rm{final}}}}}}{{{{\rm{v}}_0}}}$ final ${\rm{v = }}\frac{{{\rm{x - }}{{\rm{x}}_0}}}{{\rm{t}}}$.

Because the time in optimization is iteration, the discrepancy between iterations is equal to 1, and considering ${v_0}{\rm{ = }}0$, this equation can be expressed as follows:

With Eqs (23) and (26), the slap chains can be simulated.

3.2.   Levy flight trajectory

Levy's flight was first proposed by levy and then detailed by Benoit Mandelbrot. In fact, Levy flight is a random step that describes the Levy distribution ^[60]. Many studies have shown that the behavior of many animals and insects is a classic feature of levy's flight. Levy flight is a special random step length method, as shown in Figure 2, which is the simulation of Levy flight trajectory. It always has a small step size, but occasionally has a large pulse ^[61].

The formula for levy flight is as follows:

The formula for generating Levy random step proposed by Mantegna is as follows:

where parameter $\beta {\rm{ = }}1.5$, $\mu {\rm{ = N(0, }}\sigma _\mu ^2{\rm{)}}$ and ${\rm{v = N(0, }}\sigma _\mu ^2{\rm{)}}$ are gamma functions.

The variance of the parameters as follows:

3.3.   Modified slap swarm algorithm

The slap swarm optimization algorithm can solve the problem of low dimensional single mode optimization with simple and efficient solution. However, when dealing with high dimensional and complex image processing problems, traditional SSA is not very satisfactory. In order to improve the global search capability of SSA, an improved optimization algorithm of SSA is proposed in this paper ^[62]. Levy flight can maximize the diversity of search domains, so that the algorithm can efficiently search the location of food sources and achieve local optimization. The levy flight can help SSA get better optimization results, therefore to slap leader position update formula optimization, can be used to express the following mathematical formula:

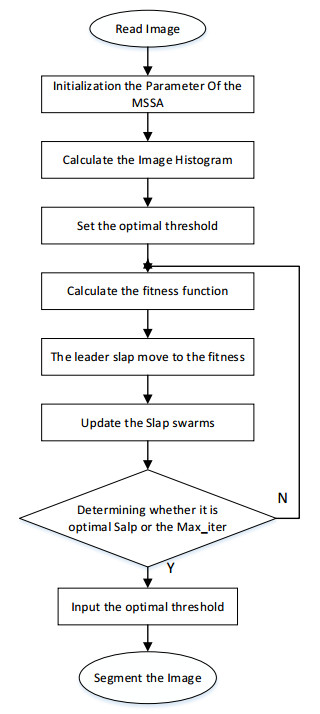
The SSA algorithm has a simple structure, but it is prone to fall into local optimization when dealing with practical engineering problems. Therefore, we choose levy flight strategy to improve it, increase the jumping ability of salp individuals, and improve their optimization ability. Levy flight can significantly improve SSA's global search capability and avoid falling into a local optimal value. This method not only improves the search intensity of SSA, but also improves the diversity of algorithm. The optimization algorithm ensures that the algorithm can find the optimal value and avoid falling into the local optimal value. By increasing diversity, the algorithm has better global search ability ^[63]. The framework of the proposed algorithm is given in Table 1. The flowchart of the modified slap swarm algorithm can be seen from Figure 3.

The computational complexity of the proposed method MSSA-Kapur depends on the number of each combination (L), the number of threshold (K), the number of generations (g), the population number (n) and the parameters dimensions (d). Therefore, the overall computational complexity is O (Kapur, MSSA) = g × (O (Updating the position of all search agents) + O (Evaluate the fitness of all agents) + O (Calculate the oppositional position of all search agents and evaluate its fitness) + O (Sort searchagents in population and oppositional population). As we all know, Kapur's computational complexity on L combination is $O({L^K})$. The computational complexity of updating the position of all search agents is O (n*d). Evaluating the fitness of all agents is $O(n \times {L^K})$. Calculating the oppositional position of all search agents and evaluate its fitness is C. Sorting search agents in population and oppositional population is $O(2n \times \log 2n)$. Therefore, the final computational complexity of the proposed method is as follow:

4.   Experiments and results

4.1.   Experiment setup

When applied to solve a specific problem, because of the different search strategies and mathematical formula, different nature inspired algorithm has optimal performance. In other words, optimization is the method to calculate the value of a function and find the optimal result by maximizing and minimizing an objective function in a given domain. Therefore, the objective function plays an important role in the optimization problem. Therefore, in this paper, the algorithm with the SSA, WOA, different optimization algorithms such as FPA has carried on the comparative study. In addition, in order to assess the effectiveness and robustness of the proposed approach, this paper also studied the recently proposed method variance between (Otsu method) and multilevel threshold based on Renyi entropy function technique. The image has three basic color components: Red, green and blue, so we need to search for the optimal threshold of each component. The comparison algorithm is representative of multilevel threshold algorithm, as shown in Table 2.

In this section, Kapur entropy, inter-class variance method and Renyi entropy are used to conduct a large number of experimental evaluations on the performance of MSSA algorithm. The experiment used six standard test color images from the Berkeley image database. The test image and its corresponding histogram are shown in Figure 4. All images are 481 × 321 in size. All algorithms are developed using MATLAB Release 2016. In order to eliminate random errors, each color image is compared with each algorithm 30 times. It is well known that the parameter has important influence on the performance of swarm intelligence algorithm. For this reason, a large number of experimental studies have been carried out in this paper, and appropriate parameter values have been found. In all algorithms, the population size is set to 25 and the maximum iteration quantity is 500.

In order to judge the image segmentation results, we choose peak signal to noise ratio (PSNR) and feature similarity (FSIM) to measure the performance of the segmentation results. PSNR is used to calculate the PSNR of the original image and the segmented image. PSNR index can be calculated by:

where

where M, N is the size of the color image, I is the original color image, and $\hat I$ is the segmented color image.

The Feature similarity (FSIM) is used to estimate the structural similarity of the original image and the segmented image. We define FSIM as:

where Ω represent the entire color image, and ${S_L}(x)$ indicates the similarity between the segmented color image obtained through multilevel thresholding task and input color image. The FSIM parameter of color RGB image is defined as:

where ${x^O}$ and ${y^O}$ represent oth channel of the original image and segmented image respectively, o is the channel number.

4.2.   Experiment 1: Levy parameter selection

In order to observe the influence of parameters on the optimization algorithm, Tables 3–6 show the PSNR of Levy variants against the original optimizers at rational values for β parameter. We use the Kapur entropy as the fitness function. We can see that performance is unclear which can be explained by the fact that output random steps under the circumstances become either very small leading to expense of optimization iterations without attaining the optimum or very large that makes the optimizer oscillate. At the same time, it can be seen obviously that the values of MSSA are superior to the traditional optimization algorithm. It shows that levy flight can effectively improve the segmentation accuracy of image segmentation algorithm. When the parameter β = 0.8, the values of MSSA are the best among all comparison algorithms. Therefore, in the subsequent experiments, the parameter of MSSA is set to β = 0.8.

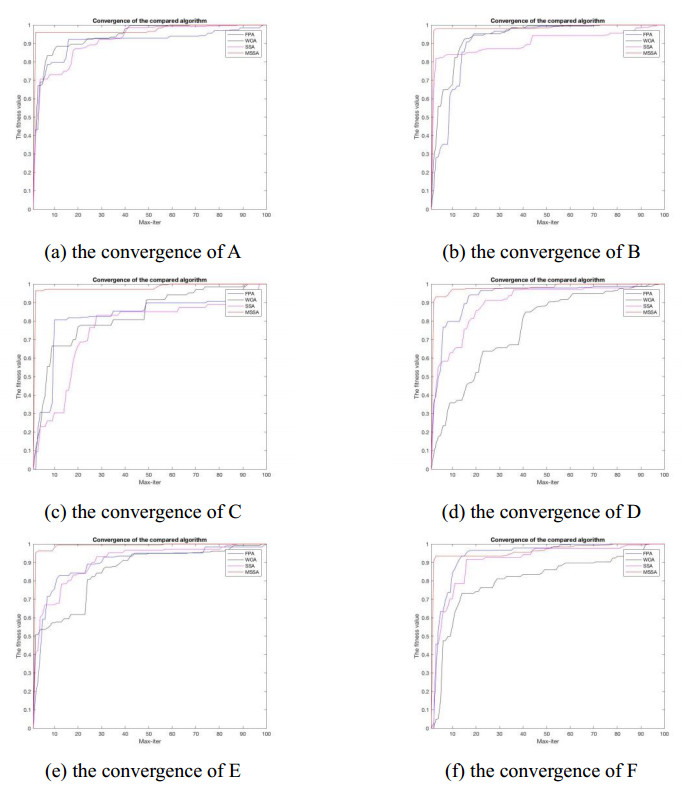
4.3.   Experiment 2: Convergence of the algorithm

The convergence of the six images depicted in Figure 5. In order to facilitate observation, we normalize the convergence data of each algorithm, and set the maximum iteration number to 100. It can be detected from the figure that the proposed MSSA has fast convergence compared with other algorithms. It can be seen from a, b and f that the search ability of MSSA algorithm is similar to that of other algorithms at the beginning, but with the exploration of space, the ability of MSSA is reflected, and the optimal value is superior to other comparison algorithms. It can be seen from c, d and e that MSSA has a faster convergence rate, and MSSA still explores the search domain to find a better solution when other algorithms have found the optimal value.

4.4.   Experiment 3:Mmaximizing Kapur's entropy

In this experiment, the results obtained by SSA, WOA, FPA and MSSA algorithm based on Kapur's entropy are analyzed at different threshold levels (k = 4, 5, 6, 7) for the test images. The optimal threshold values for each of the color components (R), (G), and (B) of SSA, WOA, FPA and MSSA algorithm and objective function values are shown in Tables S1 and S2. For a RGB color image, the peak signal to noise ratio (PSNR) value is equal to the average of PSNR values of three basic components. Table S3 compares the PSNR and FSIM values of the segmented results. Higher values of PSNR and FSIM signify better and accurate segmentation. For a visual qualitative analysis, the performance of the proposed technique at different segmentation levels is represented in Figures S1–S6 for color natural images.

As can be seen from the values in the Table S3, when K = 4, the FSIM and PSNR values of each algorithm are small, while PSNR and FSIM are gradually increasing with the increase of the number of threshold values, indicating that the increase of the number of threshold values can effectively improve the segmentation accuracy. As shown in Table S3, the higher threshold value makes FSIM approximate to the original image, and the segmentation result is better. Therefore, the MSSA algorithm can solve the optimization problem of the number of high thresholds, which means that the image segmentation accuracy is improved.

4.5.   Experiment 4: Maximizing between-class variance method

In this experiment, to show the merits of the proposed MSSA technique, the results are compared with SSA, WOA and FPA use maximizing between-class variance method. Tables S4 and S5 present the optimal thresholds and objective values of segmentation result of SSA, WOA, FPA and MSSA algorithm over the six test images. Table S6 indicates the PSNR and FSIM values obtained through different approaches for all the color images. From Figures S7–S12, the visual results show that this method achieves good segmentation effect in color image segmentation by accurately identifying complex objects and backgrounds at each level of segmentation.

From Tables S4 and S5, it can be observed that the threshold K of each algorithm is basically the same as the low threshold value, indicating that the calculation amount is small, and each algorithm can find the optimal threshold effectively. It can be seen from the results in Table S6 that, for all test images, MSSA's search results are obviously better and more reliable than SSA, WOA and FPA because of its accurate search ability, especially at the high threshold level (K). WOA and FPA's solution renewal strategy may have led to poor results.

4.6.   Experiment 5: Mmaximizing entropy method

In this experiment, in order to further demonstrate the advantages of the proposed MSSA algorithm, we compared it with other multi-level segmentation methods by using the maximum Renyi entropy function. Tables S7 and S8 show the number and optimal thresholds of the comparison algorithm. The PSNR and FSIM obtained are shown in Table S9, from which it can be seen that MSSA has better values than SSA, WOA and FPA due to its precise search capability, especially at high threshold level (K). The segmentation image obtained through the algorithm of inter-class variance objective function is shown in Figures S13–S18.

From Tables S7 and S8, it can be seen that the optimal threshold value is superior to other algorithms when the algorithm is a high threshold. As can be seen from Table S9, in image segmentation, the results obtained with the MSSA-based optimization algorithm are mostly slightly better than those obtained with the Renyi's entropy method, such as SSA, WOA and FPA.

5.   Comparisons and results

5.1.   Comparison of MSSA with other algorithm

Tables S1, S2, S4, S5, S7 and S8 are the target function values of SSA, WOA, FPA and MSSA algorithms based on Kapur entropy, minimum cross entropy and inter-class variance. As can be seen from Tables S3, S6 and S9 when K = 4, the fitness function values of each algorithm are basically the same. When K = 6 and 7, the fitness function values of MSSA algorithm are obviously better than the comparison algorithm. Tables S3, S6 and S9 are FSIM and PSNR values of each algorithm. As can be seen from Tables S3, S6 and S9, FSIM and PSNR values of the MSSA algorithm are the best, indicating that the segmentation results are the most similar to the original image and have a good segmentation effect. However, FPA has a poor segmentation effect, and data analysis shows that it fails to segment images well. Therefore, MSSA algorithm has a good segmentation capability.

It can be seen from the image results that for all natural images at K = 4, the results obtained by the method proposed in this paper are almost the same as those obtained by other algorithms. However, when the number of thresholds increases, the segmentation ability of MSSA algorithm is reflected, and its segmentation effect is better than other comparison algorithms. It can be observed from the image, MSSA of image segmentation effect is best, not present segmentation area error, color rendering there appeared deviation, show that the algorithm not only on the numerical value is higher, at the same time, after the color image segmentation of rendering the same.

5.2.   Comparison between Kapur's entropy, between-class variance and Renyi's entropy

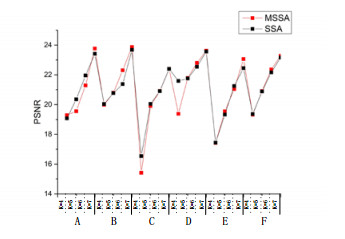
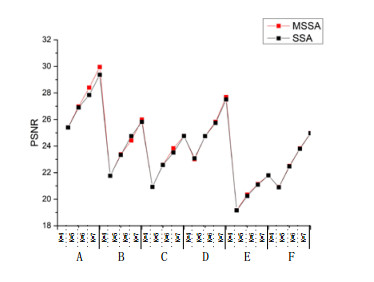
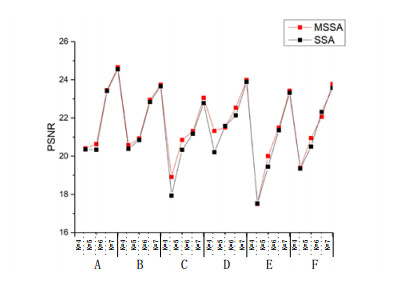
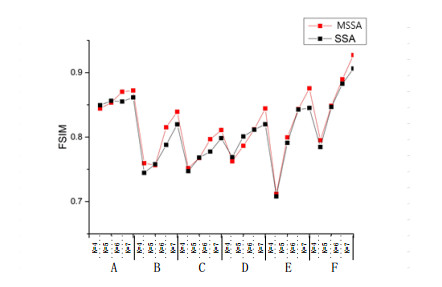
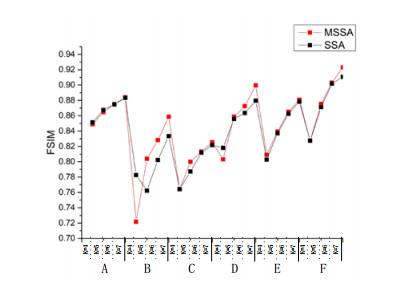
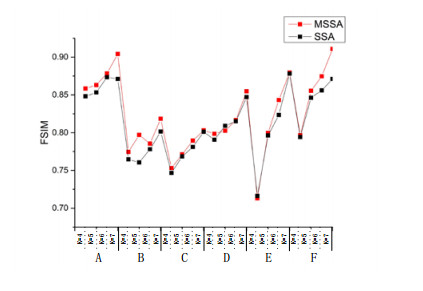
In order to compare the segmented performance of MSSA algorithm based on Kapur's entropy, between-class variance and Renyi's entropy. The curves of PSNR and FSIM values of the algorithm are shown in the Figures 6–11. From Figures 6–11, it is clear that the PSNR and SSIM values of MSSA algorithm based on Kapur's entropy are higher than those obtained by between-class variance and Renyi's entropy method. Through the above analysis, it shows that MSSA algorithm using Kapur's entropy has better segmented performance than MSSA algorithm using between-class variance and Renyi's entropy.

We use an extensive comparative study on test images by using performance metrics like Probability Rand Index (PRI), Variation of Information (VoI), Global Consistency Error (GCE), and Boundary Displacement Error (BDE) ^[64]. Table 7 shows the average results of PRI, BDE, GCE, VoI and CPU time of ground truth results of the test images. The results displayed in Table 7, that the proposed technique outperforms all other compared algorithms. The MSSA technique has obtained results close to the ground truth images. Higher values of PRI indicate better segmentation performance. While lower values of BDE, GCE, and VoI show better segmentation. It can be seen from the table that the numerical value of MSSA algorithm is the best, indicating that its segmentation result is the closest to groundtruth and the segmentation effect is the best. The results of FPA algorithm are poor, and the results of WOA and SSA algorithm are basically the same. MSSA algorithm not only improves the optimization ability of SSA algorithm, but also is better than other comparison algorithms. Kapur's results are better than those of Otsu and Renyi, indicating that Kapur, as a fitness function, can improve segmentation accuracy. So, Kapur-MSSA algorithm can well solve the problem of multi-threshold image segmentation. It can be seen from CPU time, the time of Kapur algorithm is significantly less than that of Otsu and Renyi algorithm. Kapur-MSSA algorithm takes the least time and reduces operator time while ensuring segmentation accuracy.

5.3.   Statistical analysis

Wilcoxon signature rank test ^[65] was used to test the statistical significance between kapur-based MSSA method and SSA, WOA, FPA and other inspired methods. The significance value alpha was 0.05 and the sample space was 30. Tables S10–S12 gives the Wilcoxon test results with p values for evaluation. As can be seen from Tables S10–S12, MSSA is superior to other methods, because p values are statistically significant in all cases. In most cases MSSA based Kapur multilevel thresholding algorithm performs better than the other algorithms.

6.   Conclusion

In this paper, a new multi-threshold Kapur's entropy segmentation algorithm based on MSSA is proposed, which can effectively solve the problem of image segmentation. The proposed SSA simulates the salp swarm behavior to select the optimum thresholds for multilevel thresholding. We proposed SSA based on levy flight to better solve the balance between the exploration and exploitation. In order to verify the good performance of the proposed algorithm, more heuristic algorithms are adopted to find the best threshold segmentation algorithm, and the excellent performance in image segmentation is evaluated by PSNR and FSIM. Experimental results illustrate that MSSA is superior to other comparison algorithms. And then we compared MSSA and SSA for Kapur's entropy, between-class variance and Renyi's entropy optimization optimal values of the segmentation algorithm. As a result, from the experiment we can find the Kapur's entropy segmentation algorithm obtained FSIM and PSNR value superior to other algorithms.

As a scope of further research, Multi-threshold Kapur entropy based on MSSA algorithm has a good segmentation ability for Berkeley image library. When processing images with complex backgrounds, the improved algorithm is prone to fall into the local optimum and cannot obtain a better threshold. In order to solve this problem, on the basis of MSSA, we continue to study different improvement strategies to improve SSA, so as to improve the optimization ability of SSA algorithm and better solve the problem of multi-threshold image segmentation. In the future, this image segmentation method will be applied to solve practical image segmentation problems, such as medical images, satellite images and plant phenotype images.

Acknowledgments

This work is partially supported by the National Natural Science Foundation of China (51279039). The authors would like to thank the anonymous reviewers for their constructive comments and suggestions.

Conflicts of Interest

The authors declare no conflict of interest.