Dynamics of an edge-based SEIR model for sexually transmitted diseases

Hai-Feng Huo; Qian Yang; Hong Xiang; Hai-Feng Huo; Qian Yang; Hong Xiang

doi:10.3934/mbe.2020035

Mathematical Biosciences and Engineering

2020, Volume 17, Issue 1: 669-699. doi: 10.3934/mbe.2020035

Previous Article Next Article

Research article Special Issues

Dynamics of an edge-based SEIR model for sexually transmitted diseases

Department of Applied Mathematics, Lanzhou University of Technology, Lanzhou, Gansu, 730050, China

Received: 16 August 2019 Accepted: 26 September 2019 Published: 22 October 2019

A new edge-based sexually transmitted SEIR model on the contact network is introduced in this paper. The contact infection between the opposite sex and no infectivity during the latent period on bipartite networks are included. The basic reproduction number and the equations of the final size of epidemic are derived. The dynamics of our model with arbitrary initial conditions are further studied. Sensitivity analysis on several parameters and numerical results of the model are derived. We show that the length of the latent period has an effect on arrival time and size of disease peak, but does not affect the final epidemic size and the basic reproduction number of the disease.

Keywords:

sexually transmitted disease,
SEIR epidemic model,
bipartite networks,
initial value and basic reproduction number

Citation: Hai-Feng Huo, Qian Yang, Hong Xiang. Dynamics of an edge-based SEIR model for sexually transmitted diseases[J]. Mathematical Biosciences and Engineering, 2020, 17(1): 669-699. doi: 10.3934/mbe.2020035

Related Papers:

[1]	Deepalakshmi Sarkarai, Kalyani Desikan . QSPR/QSAR analysis of some eccentricity based topological descriptors of antiviral drugs used in COVID-19 treatment via $\mathscr{D}\varepsilon$ - polynomials. Mathematical Biosciences and Engineering, 2023, 20(9): 17272-17295. doi: 10.3934/mbe.2023769
[2]	Saylé C. Sigarreta, Saylí M. Sigarreta, Hugo Cruz-Suárez . On degree–based topological indices of random polyomino chains. Mathematical Biosciences and Engineering, 2022, 19(9): 8760-8773. doi: 10.3934/mbe.2022406
[3]	Cheng-Peng Li, Cheng Zhonglin, Mobeen Munir, Kalsoom Yasmin, Jia-bao Liu . M-polynomials and topological indices of linear chains of benzene, napthalene and anthracene. Mathematical Biosciences and Engineering, 2020, 17(3): 2384-2398. doi: 10.3934/mbe.2020127
[4]	Edil D. Molina, Paul Bosch, José M. Sigarreta, Eva Tourís . On the variable inverse sum deg index. Mathematical Biosciences and Engineering, 2023, 20(5): 8800-8813. doi: 10.3934/mbe.2023387
[5]	José M. Sigarreta . Extremal problems on exponential vertex-degree-based topological indices. Mathematical Biosciences and Engineering, 2022, 19(7): 6985-6995. doi: 10.3934/mbe.2022329
[6]	Fengwei Li, Qingfang Ye, Juan Rada . Extremal values of VDB topological indices over F-benzenoids with equal number of edges. Mathematical Biosciences and Engineering, 2023, 20(3): 5169-5193. doi: 10.3934/mbe.2023240
[7]	Wanlin Zhu, Minglei Fang, Xianya Geng . Enumeration of the Gutman and Schultz indices in the random polygonal chains. Mathematical Biosciences and Engineering, 2022, 19(11): 10826-10845. doi: 10.3934/mbe.2022506
[8]	Bo Sun, Ming Wei, Wei Wu, Binbin Jing . A novel group decision making method for airport operational risk management. Mathematical Biosciences and Engineering, 2020, 17(3): 2402-2417. doi: 10.3934/mbe.2020130
[9]	Qingqun Huang, Muhammad Labba, Muhammad Azeem, Muhammad Kamran Jamil, Ricai Luo . Tetrahedral sheets of clay minerals and their edge valency-based entropy measures. Mathematical Biosciences and Engineering, 2023, 20(5): 8068-8084. doi: 10.3934/mbe.2023350
[10]	Yi Liu, Xuan Zhao, Feng Mao . The synergy degree measurement and transformation path of China's traditional manufacturing industry enabled by digital economy. Mathematical Biosciences and Engineering, 2022, 19(6): 5738-5753. doi: 10.3934/mbe.2022268

Abstract

1. Introduction

One of the life-threatening diseases world-wide is Malaria caused by the bite of female anopheles’ mosquitoes. There are 5 such parasite species that affect humans of which 2 of these viz., P. falciparum and P. vivax are the greatest threats. These two deadliest parasites are prevalent in African continent and Saharan Africa. It is an acute febrile illness which causes rapid onset of fever with headache and chills only after 10 to 15 days after the mosquito bite. If the symptoms are not treated immediately, it will lead to fatal in just one day ^[1].

In the year 2020, there was a high risk for nearly half the world population of contracting malaria. Some population groups with high risk include infants, and young children, pregnant women, and people with low immunity.

A considerable number of mortality and complications of morbidity is caused by malaria that has become a major health problem globally. As the resistant parasite strains emerge, the therapeutic options are limited which has led to the large spread of malaria. This can be prevented by potential public health emergency in designing new drugs, providing single dose cures and by introducing some novel mechanism of action. New excipients may be included in the medicine that could be effective in fighting the new variants of the strain. Using the available genomic techniques, advancement of the study of biology of the parasites can be developed for the new therapy.

In recent years, various advanced drug interventions have been revealed. This focusses on the discovery of antimalarial agents using the latest scientific and technological advances. There are many antimalarial targets that include proteins such as proteases, plasmodium sugar, farnesyltransferase inhibitor and DNA replication. World malaria report shows an increase of cases from 2019 to 2020 and an increase of almost 69,000 deaths in 2020 compared to 2019 ^[2].

To test the molecular properties in a laboratory consumes more time and money. This inconvenience can be avoided using quantitative structure activity relationship models to forecast different properties of various chemical compounds using topological descriptors. Topological indices find significant applications in various areas of mathematical chemistry ^[3,4] such as isomer discrimination, chirality, molecular complexity, drug design, selection of database, QSAR/QSPR/QSTR studies in the recent years ^[5].

The main objectives of this study are:

● QSPR analysis of the properties of the topological indices using regression models for the nine anti-malaria drugs.

● Computation of topological indices for the considered drugs.

● Comparison of topological indices with correlation coefficients of few physical properties and statistical parameters.

Identifying drug-like from non-drug-like molecules is very much necessary to reduce the cost and time with failed drug development. There are various approaches that screen chemical databases against biological targets in the progress of new potential leads. QSAR modelling is a significant approach in the discovery of drug that correlates the structure of the molecule with biological activities. There are different methods like 2D (topological indices) and 3D (structure-based) of which 2D requires less calculation time and hence used for the preliminary screening of the drug development. Academia, industry, and research institutions across the globe, widely use 2D approach.

The principal step involves the selection of the right descriptor for various reasons. Only few descriptorsgive a better understanding of the results and their interpretability, can reduce the risk of overfitting from redundant descriptors, and provides speedy and cost-effective models.

Topological index represents translations of molecular structures into structural descriptors that are expressed as numerical indices. These topological indices find their applications in drug design where the QSAR/QSPR/QSTR studies are involved. The QSAR/QSPR methods are based on the assumption that the activity or the property, such as a drug binding to DNA or toxic effect, of a certain chemical compound related to its structure through a certain mathematical algorithm.

For the chemical compound under the study, a series of parameters, called chemical descriptors are computed. Then, an algorithm that provides a quite accurate value, similar to theoretical experimental value is found. The final step is to check if the obtained algorithm is capable of predicting the activity/property values.

QSAR/QSPR/QSTR models are used to predict the association between the molecular structure and its activity/property/toxicity. Over the years many algorithms have been proposed and applied in QSAR/QSPR studies. The model framework includes molecular structure (graph) representation, calculation of molecular descriptors (graph invariants) and multiple linear regression method. The model will be validated through statistical parameters (r and r2). The same approach is employed in this work and the statistical parameters have shown significant results.

Recently, Adnan et. al. made a study on the QSPR analysis of anti tuberculosis drugs in which 15 drugs were considered for the regression analysis of 6 physico chemical properties. Eleven topological indices were computed for which the correlation analysis showed a high positive good correlation with all the 6 physico chemical properties. Shanmukha et.al. studied 21 breast cancer drugs for which QSPR analysis were carried out. Eleven topological indices were studied in the study and linear models for each index were carried out. In 2020, Sigarreta ^[6,7] provided new tools that obtained a unified way inequalities involving many different topological indices. Joseobtained new optimal bounds on the variable Zagreb indices, the variable sum-connectivity index, the variable geometric-arithmetic index and the variable inverse sum indeg index. Recently, Jose computed new lower and upper optimal bounds for general (exponential) indices of a graph. In the same direction, new inequalities involving some well-known topological indices like the generalized atom-bound connectivity index and the generalized second Zagreb index were shown. Some extremal problems for their corresponding exponential indices were computed.

The numerical representation of the arrangement of a molecule of a compound refers to topological index. Wiener index was one of the first topological indices proposed by Harold Wiener in 1947 which proved that his index correlated well with the boiling points of alkanes. At present, there are various indices introduced by various researchers which are divided into three categories, namely, degree-based, neighborhood degree-based and distance based topological indices ^[8,9,10]. Sixty years ago, QSAR was introduced that included modelling of biological activities of molecules which was extended to modelling of few physicochemical properties of molecules leading to QSPR studies. Initially, it was chemical interpretation of topological indices ^[11,12] which has now extended to modelling of structural characteristics of molecules with their biological activity leading to complex modelling of compounds in QSAR/QSPR/QSTR studies ^{[13,14,15,16,17,18,19,20,21,22,23,24,25]}.

This model does not require any lab equipment to perform the analysis. It saves a lot of time and money and the results obtained using the QSPR model are compared with the actual values for further analysis.

A graph G(V, E) with vertex set V(G) and edge set E(G) is connected if there exists an edge between every pair of vertices in G.

The graphs used in this work are simple graphs and have no loops and multiple edges. The number of edges incident to vertex v is the degree of the vertex v, denoted by d_v. For graph terminologies and notations refer ^[26,27].

Some of the topological descriptors which are used in this work are given below.

The earliest set of topological indices are the first and the second version of Zagreb indices. They have been found impressive in finding the total π-electron energy of molecules. Gutman and Polansky ^[28] introduced these indices in the year 1986 and are defined as follows

${M}_{1}\left(G\right) = \sum _{vw\in E\left(G\right)}({d}_{v}+{d}_{w})$

(1)

${M}_{2}\left(G\right) = \sum _{vw\in E\left(G\right)}({d}_{v}\times {d}_{w})$

(2)

Harmonic index is proposed and defined by Fatjlowicz ^[29] as

$H\left(G\right) = \sum _{vw\in E\left(G\right)}\frac{2}{({d}_{v}+{d}_{w})}$

(3)

Forgotten index was first defined by Furtula and Gutman ^[30] in 2015. It became popular as its performance in prediction of the index analogues to that of the original Zagreb index and is defined as

$F\left(G\right) = \sum _{vw\in E\left(G\right)}{\left({d}_{v}\right)}^{2}+{\left({d}_{w}\right)}^{2}$

(4)

A novel graph invariant called the SS index of a graph is proposed by Zhao et al. ^[31] and is stated as

$SS\left(G\right) = \sum _{vw\in E\left(G\right)}\sqrt{\frac{{d}_{v}\times {d}_{w}}{{d}_{v}+{d}_{w}}}$

(5)

Ranjini et al. ^[32] introduced redefined version of the second and third Zagreb indices and are defined as

$Re{ZG}_{2}\left(G\right) = \sum _{vw\in E\left(G\right)}\frac{{d}_{v}\times {d}_{w}}{{d}_{v}+{d}_{w}}$

(6)

$Re{ZG}_{3}\left(G\right) = \sum _{vw\in E\left(G\right)}\left({d}_{v}\times {d}_{w}\right)({d}_{v}+{d}_{w})$

(7)

2. Materials and methods

In this study, anti-malaria drugs are modelled by simple graphs. To compute the TIs of the considered drug's structure, the employed methods are vertex partitioning, edge partitioning, neighbourhood vertex partitioning and computational techniques. For depicting the results in terms of graphs and verification of computed results, the work is equipped with SPSS17 version.

3. Results and discussion

In this work, degree-based topological indices are computed for the drugs used in the treatment of malaria. The QSPR analysis of the computed indices are discussed, and it is observed that these indices are highly correlated with the physico chemical properties of the drugs that are used in the treatment of malaria.

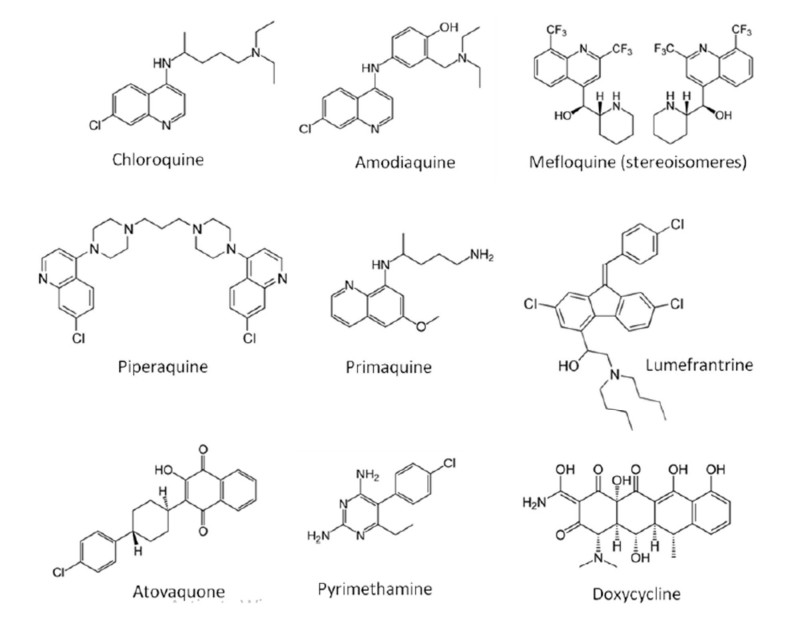
The nine drugs viz., Chloroquine, Amodiaquine, Mefloquine, Piperaquine, Primaquine, Lumefrantrine, Atovaquone, Pyrimethamine and Doxycycline used in the malaria treatment are considered for the analysis. The molecular structures of these drugs are shown in Figure 1. It is modelled as a graph where the atoms are referred to as vertices while the bonds by its edges which is represented in Figure 2.

Figure 1. Molecular structures of drugs.

DownLoad: Full-Size Img PowerPoint

Figure 2. Molecular graphs.

DownLoad: Full-Size Img PowerPoint

3.1. Regression models

The six physical properties of the drugs viz., boiling point, enthalpy, flash point, molar refraction, molar volume and polarizability for the 9 drugs are studied. A linear regression model used in this work is given below.

$\mathrm{P} = \mathrm{A}+\mathrm{B}\left[\mathrm{T}\mathrm{I}\right]$

(8)

where $P\to$ Physical property of the drug, $A, B\to$ constants, $TI\to$ topological descriptor.

Using the linear regression equation discussed, the regression model for the above considered topological indices are defined.

The physical properties of anti-malaria drugs are considered as dependent variables and the topological indices for molecular graphs of 9 drugs are considered as independent variables. A linear regression model is fitted using SPSS software where the constants A and B in the regression equation (8) are calculated by using the training set in Tables 1 and 2.

Table 1. Physical properties of drugs used for the tratment of Malaria.

Drugs	BP (℃ at 760 mmHg)	Enthalpy (kj/mol)	Flash point (℃)	Molar refraction	Molar volume (cm³)	Polarizability
Chloroquine	460.6	72.1	232.23	97.4	287.9	38.6
Amodiaquine	478	77	242.9	105.5	282.8	41.8
Mefloquine	415.7	70.5	205.2	83	273.4	32.9
Piperoquine	721.1	105.3	389.9	153.7	414.2	60.9
Primaquine	451.1	71	226.6	80.5	230.3	31.9
Lumefrantrine	642.5	99.6	342.3	151	422.3	59.9
Atovaquine	535	85.4	277.3	99.5	271.8	39.5
Pyrimethamine	368.4	61.5	176.6	67.1	180.2	26.6
Doxycycline	762.6	116.5	415	109	271.1	43.2

| Show Table

DownLoad: CSV

Table 2. The values of the topological indices of the drugs.

Drugs	M₁(G)	M₂(G)	H(G)	F(G)	SS(G)	ReZG2(G)	ReZG3(G)
Chloroquine	106	120	10.3	262	23.9599	25.2333	584
Amodiaquine	128	149	11.7333	324	28.5664	30.5333	742
Mefloquine	114	137	9.5857	306	24.5829	26.631	728
Piperoquine	202	240	17.8	510	45.1804	48.9	1200
Primaquine	92	105	9	226	20.903	22.0833	512
Lumefrantrine	182	213	16.3666	466	40.3883	43.4333	1090
Atovaquine	158	194	12.6047	446	33.4116	36.5619	1064
Pyrimethamine	86	100	7.7667	222	18.9478	20.2167	506
Doxycycline	200	264	14.4164	608	40.4521	45.55	1594

| Show Table

DownLoad: CSV

Using the linear regression equation discussed, the regression model for the above considered topological indices are defined.

3.1.1. Regression models for first Zagreb index ${M}_{1}\left(G\right)$

$Boilingpoint = 124.096+2.932\left[{M}_{1}\left(G\right)\right]$

$Enthalpy = 49.292+0.228\left[{M}_{1}\left(G\right)\right]$

$Flashpoint = 28.813+1.773\left[{M}_{1}\left(G\right)\right]$

$MolarRefraction = 28.194+0.546\left[{M}_{1}\left(G\right)\right]$

$MolarVolume = 114.389+1.265\left[{M}_{1}\left(G\right)\right]$

$Polarizability = 11.164+0.217\left[{M}_{1}\left(G\right)\right]$

3.1.2. Regression models for second Zagreb index ${M}_{2}\left(G\right)$

$Boilingpoint = 161.996+2.219 \left[{M}_{2}\left(G\right)\right]$

$Enthalpy = 33.198+0.302 \left[{M}_{2}\left(G\right)\right]$

$Flashpoint = 51.729+1.342 \left[{M}_{2}\left(G\right)\right]$

$MolarRefraction = 41.872+0.374 \left[{M}_{2}\left(G\right)\right]$

$MolarVolume = 150.949+0.838 \left[{M}_{2}\left(G\right)\right]$

$Polarizability = 16.589+0.148 \left[{M}_{2}\left(G\right)\right]$

3.1.3. Regression models for first Harmonic index $H\left(G\right)$

$Boilingpoint = 87.905+36.905 \left[H\right(G\left)\right]$

$Enthalpy = 25.031+4.870 \left[H\right(G\left)\right]$

$Flashpoint = 6.939+22.319 \left[H\right(G\left)\right]$

$MolarRefraction = 3.348+8.365 \left[H\right(G\left)\right]$

$MolarVolume = 44.044+20.421 \left[H\right(G\left)\right]$

$Polarizability = 1.318+3.317 \left[H\right(G\left)\right]$

3.1.4. Regression models for first Forgotton index $F\left(G\right)$

$Boilingpoint = 177.821+0.960 \left[F\right(G\left)\right]$

$Enthalpy = 34.961+0.132 \left[F\right(G\left)\right]$

$Flashpoint = 61.301+0.581 \left[F\right(G\left)\right]$

$MolarRefraction = 48.115+0.152 \left[F\right(G\left)\right]$

$MolarVolume = 167.744+0.334 \left[F\right(G\left)\right]$

$Polarizability = 19.061+0.060 \left[F\right(G\left)\right]$

3.1.5. Regression models for first Sum connectivity index $SS\left(G\right)$

$Boilingpoint = 111.354+13.867 \left[SS\right(G\left)\right]$

$Enthalpy = 27.343+1.855 \left[SS\right(G\left)\right]$

$Flashpoint = 21.110+8.387 \left[SS\right(G\left)\right]$

$MolarRefraction = 18.858+2.811 \left[SS\right(G\left)\right]$

$MolarVolume = 87.819+6.670 \left[SS\right(G\left)\right]$

$Polarizability = 7.465+1.115 \left[SS\right(G\left)\right]$

3.1.6. Regression models for redefined second Zagreb index $ReZ{G}_{2}\left(G\right)$

$Boilingpoint = 123.738+12.440\left[Rez{G}_{2}\right(G\left)\right]$

$Enthalpy = 28.782+1.671\left[Rez{G}_{2}\right(G\left)\right]$

$Flashpoint = 28.597+7.524\left[Rez{G}_{2}\right(G\left)\right]$

$MolarRefraction = 24.545+2.426\left[Rez{G}_{2}\right(G\left)\right]$

$MolarVolume = 103.449+5.693\left[Rez{G}_{2}\right(G\left)\right]$

$Polarizability = 9.720+0.962\left[Rez{G}_{2}\right(G\left)\right]$

3.1.7. Regression models for redefined third Zagreb index $ReZ{G}_{3}\left(G\right)$

$Boilingpoint = 223.151+0.352\left[Rez{G}_{3}\right(G\left)\right]$

$Enthalpy = 40.942+0.049\left[Rez{G}_{3}\right(G\left)\right]$

$Flashpoint = 88.713+0.213\left[Rez{G}_{3}\right(G\left)\right]$

$MolarRefraction = 59.754+0.051\left[Rez{G}_{3}\right(G\left)\right]$

$MolarVolume = 196.894+0.107\left[Rez{G}_{3}\right(G\left)\right]$

$Polarizability = 23.678+0.020\left[Rez{G}_{3}\right(G\left)\right]$

3.2. Comparison of topological indices with correlation coefficients of few physical properties and statistical parameters

In Table 1, six physical properties of the anti-malaria drugs considered in the study are presented. Various degree-based topological indices mentioned above are computed and tabulated in Table 2. The correlation of the indices in this study against all the six physical properties are tabulated in . It is observed that the indices and their corresponding physical properties are highly correlated for most of the properties and the correlation coefficient of second Zagreb index with enthalpy being the highest value of correlation (0.978). The correlation coefficients of the discussed topological indices with physical properties and graphically presented in . The statistical parameters viz., the sample size (N), constant (A), slope (b), correlation coefficient (r), the percentage of the dependent variable ${r}^{2}$ , and p-value for the QSPR study for all the above seven topological indices are studied. The null hypothesis is tested for p-value of each term is where the coefficient equals zero while the higher the p-value infers those changes in predictor are not related to changes in response. In this case, all the regression coefficients of a null hypothesis are zero while testing gives rise to F value. In such a case, the model does not have predictive capability. Using this test, one can compare their model with zero predictor variables to decide their coefficients improve the model.

Table 3. Correlation coefficients of physical properties of drugs.

Drugs	BP	Enthalpy	Flash point	Molar refraction	Molar volume	Polarizability
M₁(G)	0.961	0.968	0.961	0.838	0.735	0.838
M₂(G)	0.962	0.978	0.963	0.76	0.645	0.76
H(G)	0.908	0.894	0.908	0.963	0.891	0.964
F(G)	0.947	0.969	0.947	0.704	0.584	0.704
SS(G)	0.948	0.945	0.948	0.899	0.809	0.899
ReZG₂(G)	0.957	0.958	0.957	0.873	0.776	0.873
ReZG₃(G)	0.934	0.962	0.934	0.632	0.505	0.633

| Show Table

DownLoad: CSV

Figure 3. Correlation between physical properties of drugs and Topological indices.

DownLoad: Full-Size Img PowerPoint

Tables 4–10 represent the statistical parameters such as number of drugs considered, constant, regression coefficient, correlation coefficient, Fisher’s statistic, significant value, and standard error denoted by N, A, b, r, r2, F and p respectively, for all the considered topological indices and physical properties. Table 11 denotes the standard error of estimate for physical properties of drugs. Tables 12–17 denote the comparison of actual and computed values of all physical properties of anti-malaria drugs. Figure 3 depicts the graphical representation of physical properties and the topological indices.

Table 4. Statistical parameters for the linear QSPR model for M₁(G).

Phy. Pro,	N	A	b	r	r²	F	p	Indicator
BP	9	124.096	2.932	0.961	0.923	83.956	0	Significant
EN	9	28.483	0.396	0.968	0.937	104.502	0	Significant
FP	9	29.813	1.773	0.961	0.923	83.973	0	Significant
MR	9	28.194	0.546	0.838	0.702	16.501	0.05	Significant
MV	9	114.389	1.265	0.735	0.541	8.244	0.02	Significant
PO	9	11.164	0.217	0.838	0.702	16.529	0	Significant

| Show Table

DownLoad: CSV

Table 5. Statistical parameters for the linear QSPR model for M₂(G).

Phy. Pro,	N	A	b	r	r²	F	p	Indicator
BP	9	161.996	2.219	0.962	0.926	88.088	0	Significant
EN	9	33.198	0.302	0.978	0.956	151.468	0	Significant
FP	9	51.729	1.342	0.963	0.926	88.162	0	Significant
MR	9	41.872	0.374	0.76	0.578	9.575	0.01	Significant
MV	9	150.949	0.838	0.645	0.416	4.982	0.06	Significant
PO	9	16.589	0.148	0.76	0.578	9.588	0.01	Significant

| Show Table

DownLoad: CSV

Table 6. Statistical parameters for the linear QSPR model for H(G).

Phy. Pro,	N	A	b	r	r²	F	p	Indicator
BP	9	87.905	36.905	0.908	0.825	33.003	0.01	Significant
EN	9	25.031	4.87	0.894	0.798	27.731	0	Significant
FP	9	60939	22.319	0.908	0.825	32.986	0	Significant
MR	9	3.348	8.365	0.963	0.928	90.501	0	Significant
MV	9	44.044	20.421	0.891	0.795	27.106	0	Significant
PO	9	1.318	3.317	0.964	0.928	90.704	0	Significant

| Show Table

DownLoad: CSV

Table 7. Statistical parameters for the linear QSPR model for F(G).

Phy. Pro,	N	A	b	r	r²	F	p	Indicator
BP	9	177.821	0.96	0.947	0.897	60.643	0	Significant
EN	9	34.961	0.132	0.969	0.94	109.495	0	Significant
FP	9	61.301	0.581	0.947	0.897	60.678	0	Significant
MR	9	48.115	0.152	0.704	0.495	6.865	0.03	Significant
MV	9	167.744	0.334	0.584	0.341	3.619	0.09	Significant
PO	9	19.061	0.06	0.704	0.496	6.877	0.03	Significant

| Show Table

DownLoad: CSV

Table 8. Statistical parameters for the linear QSPR model for SS(G).

Phy. Pro,	N	A	b	r	r²	F	p	Indicator
BP	9	111.354	13.867	0.948	0.898	61.748	0	Significant
EN	9	27.343	1.855	0.945	0.894	58.818	0	Significant
FP	9	21.11	8.387	0.948	0.898	61.739	0	Significant
MR	9	18.858	2.811	0.899	0.808	29.522	0	Significant
MV	9	87.819	6.67	0.809	0.654	13.222	0	Significant
PO	9	7.465	1.115	0.899	0.809	29.572	0	Significant

| Show Table

DownLoad: CSV

Table 9. Statistical parameters for the linear QSPR model for ReZG₂(G).

Phy. Pro,	N	A	b	r	r²	F	p	Indicator
BP	9	123.738	12.44	0.957	0.915	75.323	0	Significant
EN	9	28.782	1.671	0.958	0.918	77.887	0	Significant
FP	9	28.597	7.524	0.957	0.915	75.331	0	Significant
MR	9	24.545	2.426	0.873	0.762	22.437	0	Significant
MV	9	103.449	5.693	0.776	0.603	10.626	0.01	Significant
PO	9	9.72	0.962	0.873	0.762	22.47	0	Significant

| Show Table

DownLoad: CSV

Table 10. Statistical parameters for the linear QSPR model for ReZG₃(G).

Phy. Pro,	N	A	b	r	r²	F	p	Indicator
BP	9	223.151	0.352	0.934	0.873	47.933	0	Significant
EN	9	40.942	0.049	0.962	0.925	86.586	0	Significant
FP	9	88.713	0.213	0.934	0.873	47.97	0	Significant
MR	9	59.754	0.051	0.632	0.4	4.665	0.05	Significant
MV	9	196.894	0.107	0.505	0.255	2.4	0.05	Significant
PO	9	23.678	0.02	0.633	0.4	4.671	0.05	Significant

| Show Table

DownLoad: CSV

Table 11. Standard error of estimate for physical properties of drugs.

Drugs	BP	Enthalpy	Flash point	Molar refraction	Molar volume	Polarizability
M₁(G)	41.3818	5.0133	25.0251	17.3965	56.9863	6.8934
M₂(G)	40.4727	402053	24.4681	20.7148	64.279	8.21
H(G)	62.3993	8.9827	32.985	8.5408	38.0989	3.3828
F(G)	47.9859	4.9047	29.014	22.6488	68.2796	8.9761
SS(G)	47.5989	6.6252	28.7891	13.955	49.478	5.5292
ReZG₂(G)	43.4975	5.7457	26.3056	15.5439	52.9971	6.1595
ReZG₃(G)	53.2487	5.4722	32.1935	24.6926	72.5723	9.7875

| Show Table

DownLoad: CSV

Table 12. Comparision of actual and computed values for boiling point from regression models of TI.

Drug	Boiling point ℃ (at 760 mmHg)	M1(G)	M2(G)	H(G)	F(G))	SS(G)	ReZG₂(G)	ReZG₃(G)
Chloroquine	460.6 ± 40.0	434.88	428.27	468.02	429.341	443.60	437.64	428.71
Amodiaquine	478.0 ± 45.0	499.39	492.62	520.92	488.861	507.48	503.57	484.33
Mefloquine	415.7 ± 40.0	458.34	465.99	441.66	471.581	452.24	455.02	479.40
Piperoquine	721.1 ± 60.0	716.36	694.55	744.81	667.421	737.87	732.05	645.55
Primaquine	451.1 ± 45.0	393.84	394.99	420.05	394.781	401.21	398.45	403.37
Lumefrantrine	642.5 ± 55.0	657.72	634.64	691.91	625.181	671.41	664.04	606.83
Atovaquine	535.0 ± 50.0	587.35	592.48	553.08	605.981	574.67	578.56	597.67
Pyrimethamine	368.4 ± 52.0	376.24	383.89	374.53	390.941	374.10	375.23	401.26
Doxycycline	762.6 ± 60.0	710.49	747.81	619.94	761.501	672.30	690.38	784.23

| Show Table

DownLoad: CSV

Table 13. Comparison of actual and computed values for enthalpy from regression models of TI.

Drug	Flash point (℃)	M1(G)	M2(G)	H(G)	F(G))	SS(G)	ReZG₂(G)	ReZG₃(G)
Chloroquine	232.23 ± 27.3	216.75	212.76	236.82	213.52	222.06	218.45	213.10
Amodiaquine	242.9 ± 28.7	255.75	251.68	268.81	249.54	260.69	258.32	246.75
Mefloquine	205.2 ± 27.3	230.93	235.58	220.88	239.08	227.28	228.96	243.77
Piperoquine	389.9 ± 32.9	386.95	373.80	404.21	357.61	400.03	396.52	344.31
Primaquine	226.6 ± 28.7	191.92	192.63	207.81	192.60	196.42	194.75	197.76
Lumefrantrine	342.3 ± 31.5	351.49	337.57	372.22	332.04	359.84	355.38	320.88
Atovaquine	277.3 ± 30.1	308.94	312.07	288.26	320.42	301.33	303.68	315.34
Pyrimethamine	176.6 ± 30.7	181.29	185.92	180.28	190.28	180.02	180.70	196.49
Doxycycline	415.0 ± 32.9	383.41	406.01	328.69	414.54	360.38	371.31	428.23

| Show Table

DownLoad: CSV

Table 14. Comparison of actual and computed values for flash point from regression models of TI.

Drug	Enthalpy (kj/mol)	M1(G)	M2(G)	H(G)	F(G))	SS(G)	ReZG₂(G)	ReZG₃(G)
Chloroquine	72.1 ± 3.0	73.46	69.438	75.19	69.545	71.78	70.94	69.55
Amodiaquine	77.0 ± 3.0	78.476	78.19	82.17	77.72	80.33	79.80	77.3
Mefloquine	70.5 ± 3.0	75.28	74.57	71.71	75.35	72.94	73.28	76.61
Piperoquine	105.3 ± 3.0	95.34	105.67	111.71	102.28	111.15	110.49	99.74
Primaquine	71.0 ± 3.0	70.268	64.90	68.86	64.79	66.11	65.68	66.03
Lumefrantrine	99.6 ± 3.0	90.788	97.52	104.73	96.47	102.26	101.35	94.35
Atovaquine	85.4 ± 3.0	85.316	91.78	86.41	93.83	89.31	89.87	93.07
Pyrimethamine	61.5 ± 3.0	68.9	63.39	62.85	64.26	62.48	62.56	65.73
Doxycycline	116.5 ± 3.0	94.892	112.92	95.23	115.21	102.37	104.89	119.04

| Show Table

DownLoad: CSV

Table 15. Comparison of actual and computed values for molar refraction from regression models of TI.

Drug	Molar refraction (cm³)	M1(G)	M2(G)	H(G)	F(G))	SS(G)	ReZG₂(G)	ReZG₃(G)
Chloroquine	97.4 ± 0.3	86.07	86.75	89.50	87.93	86.20	85.76	89.53
Amodiaquine	105.5 ± 0.3	98.08	97.59	101.49	97.36	99.15	98.61	97.59
Mefloquine	83.0 ± 0.3	90.43	93.11	83.53	94.62	87.96	89.15	96.88
Piperoquine	153.7 ± 0.3	138.48	131.63	152.24	125.63	145.86	143.17	120.95
Primaquine	80.5 ± 0.3	78.42	81.14	78.63	82.46	77.61	78.11	85.86
Lumefrantrine	151.0 ± 0.3	127.56	121.53	140.25	118.94	132.38	129.91	115.34
Atovaquine	99.5 ± 0.3	114.46	114.42	108.78	115.90	112.77	113.24	114.01
Pyrimethamine	67.1 ± 0.5	75.15	79.27	68.31	81.85	72.12	73.59	85.56
Doxycycline	109 ± 0.4	137.39	140.60	123.94	140.53	132.56	135.04	141.04

| Show Table

DownLoad: CSV

Table 16. Comparison of actual and computed values for molar volume from regression models of TI.

Drug	Molar volume (cm³)	M1(G)	M2(G)	H(G)	F(G))	SS(G)	ReZG₂(G)	ReZzG₃(G)
Chloroquine	287.9 ± 3.0	248.47	251.509	254.38	255.25	247.63	247.10	259.38
Amodiaquine	282.8 ± 3.0	276.30	275.811	283.64	275.96	278.35	277.27	276.28
Mefloquine	273.4 ± 3.0	258.59	265.755	239.79	269.94	251.78	255.05	274.79
Piperoquine	414.2 ± 3.0	369.91	352.069	407.53	338.08	389.17	381.83	325.29
Primaquine	230.3 ± 3.0	230.76	238.939	227.83	243.22	227.24	229.16	251.67
Lumefrantrine	422.3 ± 3.0	344.61	329.443	378.26	323.38	357.20	350.71	313.52
Atovaquine	271.8 ± 3.0	314.25	313.521	301.44	316.70	310.67	311.59	310.74
Pyrimethamine	180.2 ± 7.0	223.17	234.749	202.64	241.89	214.20	218.54	251.03
Doxycycline	271.1 ± 5.0	367.38	372.181	338.44	370.81	357.63	362.76	367.45

| Show Table

DownLoad: CSV

Table 17. Comparison of actual and computed values for polarizability from regression models of TI.

Drug	Polarizability (10^-24 cm³)	M1(G)	M2(G)	H(G)	F(G))	SS(G)	ReZG₂(G)	ReZG₃(G)
Chloroquine	38.6 ± 0.5	34.16	34.34	35.48	34.78	34.18	33.99	35.35
Amodiaquine	41.8 ± 0.5	38.94	38.64	40.23	38.50	39.31	39.09	38.51
Mefloquine	32.9 ± 0.5	35.90	36.86	33.11	37.42	34.87	35.33	38.23
Piperoquine	60.9 ± 0.5	54.99	52.10	60.36	49.66	57.84	56.76	47.67
Primaquine	31.9 ± 0.5	31.12	32.12	31.17	32.62	30.77	30.96	33.91
Lumefrantrine	59.9 ± 0.5	50.65	48.11	55.60	47.02	52.49	51.50	45.47
Atovaquine	39.5 ± 0.5	45.45	45.30	43.12	45.82	44.71	44.89	44.95
Pyrimethamine	26.6 ± 0.5	29.82	31.38	27.08	32.38	28.59	29.16	33.79
Doxycycline	43.2 ± 0.5	54.56	55.66	49.13	55.54	52.56	53.53	55.55

| Show Table

DownLoad: CSV

4. Conclusions

In this study, seven degree-based topological indices are computed for nine anti-malaria drugs which is presented in Table 2. The coefficient of correlation for the said indices against six physical properties are computed and tabulated in Table 3. It is observed from Table 3 that every topological index shows good correlation with its corresponding physical properties in which, considering second Zagreb index row wise, the correlation coefficient is high with that of enthalpy for M2(G). The first Zagreb index has a high correlation with enthalpy of 0.963. The Harmonic index shows good correlation with polarizability, Forgotten index with enthalpy having r = 0.969, SS index has highest correlation with boiling point and flash point, both being 0.948, while the redefined Zagreb indices with enthalpy having 0.947, 0.958 and 0.962 respectively for the three indices.

This work focusses on the drugs used for the treatment of malaria which is caused by mosquitoes. The analysis done in this paper may help the chemists and pharmaceutical industry researchers to design novel drugs using various excipients by the values of indices computed here. They may constitute different drugs for various ailments based on the available topological indices in the article. The correlation coefficients of various drugs help the chemists to choose the right composition based on the high correlation value to form a new drug for novel ailments. New tools to obtain a unified way of involving inequalities of various topological indices may be carried out. The extremal values for the considered indices may be computed for exponential version of the indices.

Conflict of interest

The author declare that they have no conflict of interest.

References

[1]	National Library of Medicine, Sexually Transmitted Diseases, 2019. Available from: https://medlineplus.gov/sexuallytransmitteddiseases.html.
[2]	M. J. Keeling and P. Rohani, Modeling infectious diseases in humans and animals, Clin. Infect. Dis., 2008.
[3]	P. Manfredi and A. D'Onofrio, Modeling the interplay between human behavior and the spread of infectious diseases, Springer, 2013.
[4]	L. Zhao, L. Zhang and H. F. Huo, Traveling wave solutions of a diffusive seir epidemic model with nonlinear incidence rate, Taiwan J. Math., 23 (2019), 951-980.
[5]	H. F. Huo, P. Yang and H. Xiang, Dynamics for an sirs epidemic model with infection age and relapse on a scale-free network, J. Franklin I., 356 (2019), 7411-7443.
[6]	H. Xiang, M. X. Zou and H. F. Huo, Modeling the effects of health education and early therapy on tuberculosis transmission dynamics, Int. J. Nonlin. Sci. Num., 20 (2019), 243-255.
[7]	Z. P. Ma, Spatiotemporal dynamics of a diffusive leslie-gower prey-predator model with strong alee effect, Nonlinear Anal-Real., 50 (2019), 651-674.
[8]	Q. Shi and S. Wang, Klein-gordon-zakharov system in energy space: Blow-up profile and subsonic limit, Math. Method Appl. Sci., 42 (2019), 3211-3221.
[9]	Y. L. Cai, J. Jiao, Z. Gui, et al., Environmental variability in a stochastic epidemic model, Appl. Math. Comput., 329 (2018), 210-226.
[10]	Z. Du and Z. Feng, Existence and asymptotic behaviors of traveling waves of a modified vectordisease model, Commun. Pur. Appl. Anal., 17 (2018), 1899-1920.
[11]	L. Zhang and Y. F. Xing, Extremal solutions for nonlinear first-order impulsive integro-differential dynamic equations, Math. Notes, 105 (2019), 124-132.
[12]	X. Y. Meng, N. N. Qin and H. F. Huo, Dynamics analysis of a predator-prey system with harvesting prey and disease in prey species, J. Biol. Dynam., 12 (2018), 342-374.
[13]	X. Y. Meng and Y. Q. Wu, Bifurcation and control in a singular phytoplankton-zooplankton-fish model with nonlinear fish harvesting and taxation, Int. J. Bifurcat. Chaos, 28 (2018), 1850042.
[14]	X. B. Zhang, Q. H. Shi, S. H. Ma, et al., Dynamic behavior of a stochastic SIQS epidemic model with levy jumps, Nonlinear Dyn., 93 (2018), 1481-1493.
[15]	X. Bao, W. T. Li and Z. C. Wang, Uniqueness and stability of time-periodic pyramidal fronts for a periodic competition-diffusion system, Commun. Pur. Appl. Anal., 19 (2020), 253-277.
[16]	X. Bao and W. T. Li, Propagation phenomena for partially degenerate nonlocal dispersal models in time and space periodic habitats, Nomlinear Anal-Real., 51 (2020), 102975.
[17]	S. Huang and Q. Tian, Marcinkiewicz estimates for solution to fractional elliptic laplacian equation, Comput. Math. Appl., 78 (2019), 1732-1738.
[18]	H. F. Huo, S. L. Jing, X. Y. Wang, et al., Modelling and analysis of an alcoholism model with treatment and effect of twitter, Math. Biosci. Eng., 16 (2019), 3595-3622.
[19]	Y. D. Zhang, H. F. Huo and H. Xiang, Dynamics of tuberculosis with fast and slow progression and media coverage, Math. Biosci. Eng., 16 (2019), 1150-1170.
[20]	Z. K. Guo, H. F. Huo and H. Xiang, Global dynamics of an age-structured malaria model with prevention, Math. Biosci. Eng., 16 (2019), 1625-1653.
[21]	A. L. Barábasi and R. Albert, Emergence of scaling in random networks, Science, 286 (1999), 509-512.
[22]	S. Moghadas, Two core group models for sexual transmission of disease, Ecol. Model., 148 (2002), 15-26.
[23]	J. Gómez-Gardeñes, V. Latora, Y. Moreno, et al., Spreading of sexually transmitted diseases in heterosexual populations, P. Natl. Acad. Sci. USA, 105 (2008), 1399-1404.
[24]	Y. Moreno, R. Pastor-Satorras and A. Vespignani, Epidemic outbreaks in complex heterogeneous networks, Eur. Phys. J. B., 26 (2001), 521-529.
[25]	J. Lindquist, J. Ma, P. V. D. Driessche, et al., Effective degree network disease models, J. Math. Biol., 62 (2011), 143-164.
[26]	H. F. Huo, F. F. Cui and H. Xiang, Dynamics of an SAITS alcoholism model on unweighted and weighted networks, Physica. A., 496 (2018), 249-262.
[27]	H. F. Huo, H. N. Xue and H. Xiang, Dynamics of an alcoholism model on complex networks with community structure and voluntary drinking, Physica. A., 505 (2018), 880-890.
[28]	H. Xiang, Y. Y. Wang and H. F. Huo, Analysis of the binge drinking models with demographics and nonlinear infectivity on networks, J. Appl. Anal. Comput., 8 (2018), 1535-1554.
[29]	J. C. Miller, A. C. Slim and E. M. Volz, Edge-based compartmental modelling for infectious disease spread, J. R. Soc. Interface, 9 (2012), 890-906.
[30]	J. C. Miller and E. M. Volz, Incorporating disease and population structure into models of SIR disease in contact networks, PLOS ONE, 8 (2013), e69162.
[31]	J. C. Miller, Model hierarchies in edge-based compartmental modeling for infectious disease spread, J. Math. Biol., 67 (2013), 869-899.
[32]	J. C. Miller, Epidemics on networks with large initial conditions or changing structure, PLOS ONE, 9 (2014), e101421.
[33]	S. Yan, Y. Zhang, J. Ma, et al., An edge-based SIR model for sexually transmitted diseases on the contact network, J. Theor. Biol., 439 (2018), 216-225.
[34]	M. E. Newman, S. H. Strogatz and D. J. Watts, Random graphs with arbitrary degree distributions and their applications, Phys. Rev. E, 64 (2001), 026118.
[35]	M. Molloy and B. Reed, A Critical Point for Random Graphs with a Given Degree Sequence, Random. Struct. Algor., 6 (2010), 161-180.
[36]	J. C. Miller, A note on the derivation of epidemic final sizes, B. Math. Biol., 74 (2012), 2125-2141.
[37]	P. V. D. Driessche and J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Math. Biosci., 180 (2002), 29-48.
[38]	M. E. J. Newman, Spread of epidemic disease on networks, Phys. Rev. E., 66 (2002), 016128.

This article has been cited by:

1.	Rongbing Huang, Abid Mahboob, Muhammad Waheed Rasheed, Sajid Mahboob Alam, Muhammad Kamran Siddiqui, On molecular modeling and QSPR analysis of lyme disease medicines via topological indices, 2023, 138, 2190-5444, 10.1140/epjp/s13360-023-03867-9
2.	Muhammad Waheed Rasheed, Abid Mahboob, Iqra Hanif, An Estimation of the Physicochemical Properties of Heart Attack Treatment Medicines by Using Molecular Descriptors, 2023, 10269185, 10.1016/j.sajce.2023.04.003
3.	Xiujun Zhang, Muhammad Jawwad Saif, Nazeran Idrees, Salma Kanwal, Saima Parveen, Fatima Saeed, QSPR Analysis of Drugs for Treatment of Schizophrenia Using Topological Indices, 2023, 8, 2470-1343, 41417, 10.1021/acsomega.3c05000
4.	Dongming Zhao, Muhammad Farhan Hanif, Hasan Mahmood, Muhammad Kamran Siddiqui, Mazhar Hussain, Nazir Hussain, Topological analysis of entropy measure using regression models for silver iodide, 2023, 138, 2190-5444, 10.1140/epjp/s13360-023-04432-0
5.	Mazhar Hussain, Muhammad Kamran Siddiqui, Muhammad Farhan Hanif, Hasan Mahmood, Zohaib Saddique, Samuel Asefa Fufa, On K-Banhatti indices and entropy measure for rhodium (III) chloride via linear regression models, 2023, 9, 24058440, e20935, 10.1016/j.heliyon.2023.e20935
6.	Ali N. A. Koam, Muhammad Faisal Nadeem, Ali Ahmad, Hassan A. Eshaq, Weighted Asymmetry Index: A New Graph-Theoretic Measure for Network Analysis and Optimization, 2024, 12, 2227-7390, 3397, 10.3390/math12213397
7.	Muhammad Waheed Rasheed, Abid Mahboob, Iqra Hanif, Uses of degree-based topological indices in QSPR analysis of alkaloids with poisonous and healthful nature, 2024, 12, 2296-424X, 10.3389/fphy.2024.1381887
8.	Micheal Arockiaraj, J. Celin Fiona, Arul Jeya Shalini, Comparative Study of Entropies in Silicate and Oxide Frameworks, 2024, 16, 1876-990X, 3205, 10.1007/s12633-024-02892-2
9.	Asad Ullah, Safina Jabeen, Shahid Zaman, Anila Hamraz, Summeira Meherban, Predictive potential of K‐Banhatti and Zagreb type molecular descriptors in structure–property relationship analysis of some novel drug molecules, 2024, 71, 0009-4536, 250, 10.1002/jccs.202300450
10.	Tahreem Ashraf, Nazeran Idrees, Topological indices based VIKOR assisted multi-criteria decision technique for lung disorders, 2024, 12, 2296-2646, 10.3389/fchem.2024.1407911
11.	Abid Mahboob, Muhammad Waheed Rasheed, Iqra Hanif, Laiba Amin, Abdu Alameri, Role of molecular descriptors in quantitative structure‐property relationship analysis of kidney cancer therapeutics, 2024, 124, 0020-7608, 10.1002/qua.27241
12.	B. Vijayakumar, B. Karthikeyan, A. Nelson, K. Arputha Christy, Synthesis, characterisation and topological indices approach of hydrazone derivatives of disubstituted-2,6-diaryl piperidin-4-one, catalysed by CdO-SnO2 nanocatalyst, 2024, 1306, 00222860, 137843, 10.1016/j.molstruc.2024.137843
13.	Abdul Hakeem, Nek Muhammad Katbar, Fazal Muhammad, Nisar Ahmed, On the molecular structure modelling of gamma graphyne and armchair graphyne nanoribbon via reverse degree-based topological indices, 2024, 122, 0026-8976, 10.1080/00268976.2023.2259510
14.	Deepa Balasubramaniyan, Natarajan Chidambaram, Vignesh Ravi, Muhammad Kamran Siddiqui, QSPR analysis of anti‐asthmatic drugs using some new distance‐based topological indices: A comparative study, 2024, 124, 0020-7608, 10.1002/qua.27372
15.	Ali Raza, Muhammad Mobeen Munir, Exploring spectrum-based descriptors in pharmacological traits through quantitative structure property (QSPR) analysis, 2024, 12, 2296-424X, 10.3389/fphy.2024.1348407
16.	Muhammad Waheed Rasheed, Abid Mahboob, Iqra Hanif, On QSAR modeling with novel degree-based indices and thermodynamics properties of eye infection therapeutics, 2024, 12, 2296-2646, 10.3389/fchem.2024.1383206
17.	Asma Jabeen, Shahzad Ahmad, Shahid Zaman, The study of regression model based on CoM-polynomial in blood cancer drug properties, 2024, 9, 26668181, 100648, 10.1016/j.padiff.2024.100648
18.	Deepa Balasubramaniyan, Natarajan Chidambaram, On some neighbourhood degree-based topological indices with QSPR analysis of asthma drugs, 2023, 138, 2190-5444, 10.1140/epjp/s13360-023-04439-7
19.	Abid Mahboob, Muhammad Waheed Rasheed, Aya Mohammed Dhiaa, Iqra Hanif, Laiba Amin, On quantitative structure-property relationship (QSPR) analysis of physicochemical properties and anti-hepatitis prescription drugs using a linear regression model, 2024, 10, 24058440, e25908, 10.1016/j.heliyon.2024.e25908
20.	Deepalakshmi Sarkarai, Vignesh Ravi, Kalyani Desikan, 2024, 3180, 0094-243X, 020014, 10.1063/5.0224422
21.	Esra Öztürk Sözen, Elif Eryaşar, Şükriye Çakmak, Szeged-like topological descriptors and COM -polynomials for graphs of some Alzheimer’s agents , 2024, 122, 0026-8976, 10.1080/00268976.2024.2305853
22.	Xiujun Zhang, Shamaila Yousaf, Anisa Naeem, Ferdous M. Tawfiq, Adnan Aslam, Analyzing topological descriptors of guar gum and its derivatives for predicting physical properties in carbohydrates, 2024, 253, 01697439, 105203, 10.1016/j.chemolab.2024.105203
23.	Gayathri K. B, S. Roy, Quantitative structure property relationship study of postpartum depression medications using topological indices and regression models, 2024, 20904479, 103194, 10.1016/j.asej.2024.103194
24.	Fatima Saeed, Nazeran Idrees, Integrating Structural Modeling and Decision-Making for Anti-psychotic Drugs through Topological Indices, 2025, 15, 2191-1630, 10.1007/s12668-024-01732-2
25.	Deepa Balasubramaniyan, Natarajan Chidambaram, Vignesh Ravi, 2024, Chapter 29, 978-3-031-69145-4, 380, 10.1007/978-3-031-69146-1_29
26.	W. Tamilarasi, B. J. Balamurugan, New reverse sum Revan indices for physicochemical and pharmacokinetic properties of anti-filovirus drugs, 2024, 12, 2296-2646, 10.3389/fchem.2024.1486933
27.	Muneeba Mansha, Sarfraz Ahmad, Zahid Raza, Eccentric indices based QSPR evaluation of drugs for schizophrenia treatment, 2025, 11, 24058440, e42222, 10.1016/j.heliyon.2025.e42222
28.	Micheal Arockiaraj, J. J. Jeni Godlin, S. Radha, Comparative study of degree and neighborhood degree sum-based topological indices for predicting physicochemical properties of skin cancer drug structures, 2025, 0217-9849, 10.1142/S0217984925501064
29.	Adnan Asghar, QSPR analysis of anti-hepatitis prescription drugs using degree based topological indices through M-polynomial and NM-polynomial, 2025, 12, 2411-1414, 10.15826/chimtech.2025.12.2.06
30.	S. Gayathri, K. Dhanalakshmi, Ebenezer Bonyah, QSPR analysis of vitiligo treatment of some drugs using reverse degree-based topological indices, 2025, 24682276, e02636, 10.1016/j.sciaf.2025.e02636

Reader Comments

Your name:*

Email:*
© 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)