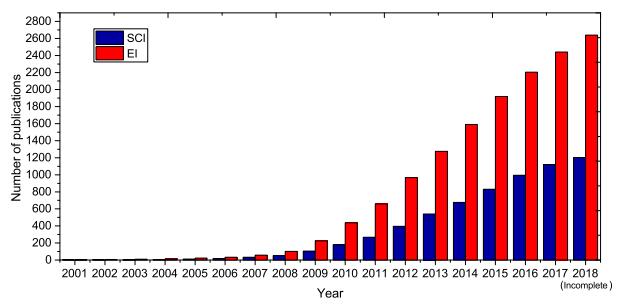
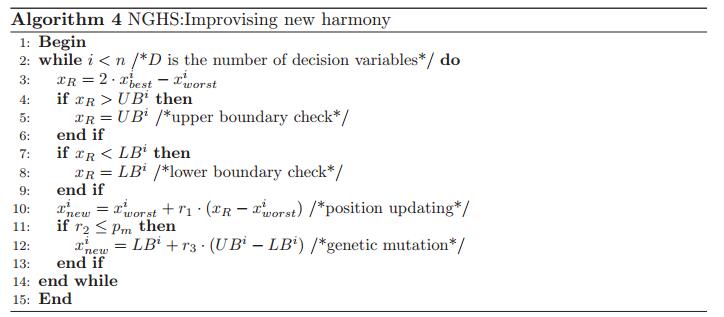
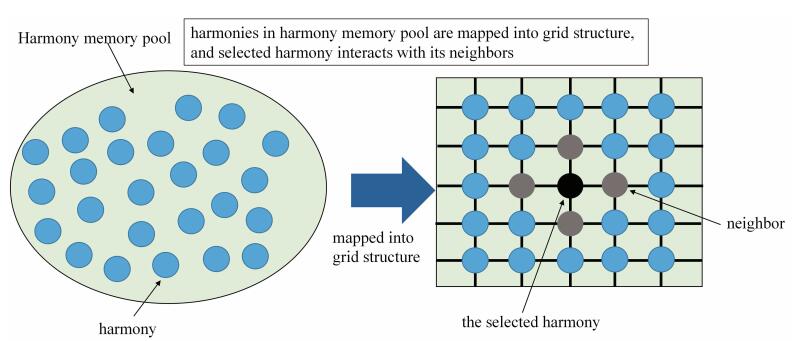
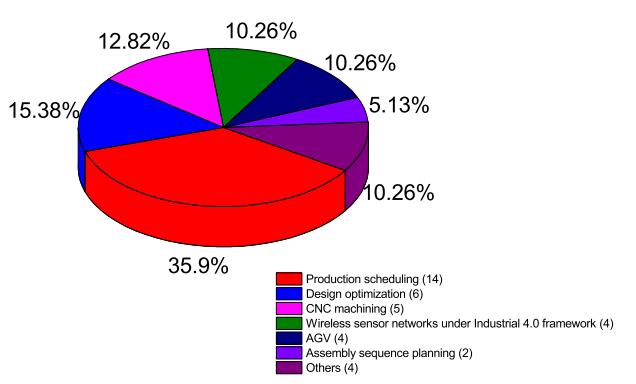
The harmony search (HS) algorithm is one of the most popular meta-heuristic algorithms. The basic idea of HS was inspired by the music improvisation process in which the musicians continuously adjust the pitch of their instruments to generate wonderful harmony. Since its inception in 2001, HS has attracted the attention of many researchers from all over the world, resulting in a lot of improved variants and successful applications. Even for today, the research on improved HS variants design and innovative applications are still hot topics. This paper provides a detailed review of the basic concept of HS and a survey of its latest variants for function optimization. It also provides a survey of the innovative applications of HS in the field of intelligent manufacturing based on about 40 recently published articles. Some potential future research directions for both HS and its applications to intelligent manufacturing are also analyzed and summarized in this paper.
Abbreviations
5-FU: 5-fluorouracil; ACh: acetylcholine; AChE: Acetylcholinesterase; ACI: adoptive cellular immunotherapy; ACT: adoptive cell transfer; ADCC: immune effector cells; ADME: absorption, distribution, metabolism and excretion; AI: Artificial Intelligence; AIDS: immune deficiency syndrome; ANS: autonomic nervous system; AODNs: dendrimers conjugated with oligo anti-sense; ARTs: antiretroviral therapies; AuNC: Au-nanocages; AuNPs: Gold nanoparticles; AuNR: Au-nanorods; AuNS: Au-nanoshells; BCRP: breast cancer resistance protein; CBD: cannabidiol; CDC: cascade complement activation; ChAT: acetylcholine; CNTs: Carbon nanotubes; CpG: non-methylated guanosine deoxynucleotides; CPT: camptothecin; Cu: copper; CuS NP: copper sulfide nanoparticles; DDFT: dynamic density functional theory; Deff: effective diffusion coefficient; DHF: dihydrofolate; DHFR: dihydrofolate reductase; DOX: doxorubicin; DRG: dorsal root ganglia; DS: Disulfiram; DTI: drug-target interaction; E. coli: Escherichia coli; EGFR: epidermal growth factor receptor; EPR: enhaced permeability and retention; EPR: penetration and retention effects; ER: endoplasmic reticulum; ER: estrogen receptor; ERK: kinase regulated by the extracellular signal; FDA: Food and Drug Administration; FISH: fluorescence in situ hybridization; Foxp3: forkhead box P3; GEM: modified mouse models; GIP: Gaussian interaction profile; GM-CSF: granulocyte-macrophages colony-stimulating factor; GMS: glycerine monostearate; GSH: glutathione; GSK3: glycogen synthase kinase-3; HA: hyaluronic acid; HDL: high density lipoprotein; HDR: homologous directed repair; HER2: Human epidermal growth factor 2 receptor; HIV-1: human immunodeficiency virus type 1; HK: hexokinase; HPA: hypothalamus-hypophysis axis; HRH: receptor neuron gene histamine 1; HRH2: histamine receptor 2; HSA: serum albumin; Hyal: hyaluronidase; ICB: immunological checkpoint blocking; ICG: indocyanine green agent; ICZ: Itraconazole; IFN: interferons; Ig: specific tumor antigen; IL: interleukins; IP3: inositol 1, 4, 5-triphosphate; K+: Potassium; LD: liposomal doxorubicin; LIT: Laser immunotherapy; LPNs: hybrid lipid-polymer nanoparticles; mAb: monoclonal antibody; mAbs: monoclonal antibodies; mAChRs: muscarinic acetylcholine receptors; MAMA2: mammaglobin A2; MAMB1: mammaglobin B1; MAOA: monoamine oxidase A; MBZ: Mebendazole; MCF-10A: normal breast tissue cells; MDSCs: myeloid-derived suppressive cells; Met: Metformin; MMP-9: matrix metallopeptidases 9; MMPs: matrix metalloproteinases; MNPs: Magnetic nanoparticles; MRI: magnetic resonance imaging; mTORC1: inhibitor of rapamycin complex 1 signaling; MTX: methotrexate; nAChRs: nicotinic acetylcholine receptors; NDDS: nanosized drug delivery system; NE: norepinephrine; NIR: near-infrared; NIRF: near-infrared fluorescence; NK: natural killer cell; NLCs: nanostructured lipid carriers; NLD: Lonidamine; NNRTI: non-nucleoside reverse transcriptase inhibitor; NO: nitric oxide; NOS1: nitric oxide synthase 1; NOS3: nitric oxide synthase 3; NP: nanoparticles; NPY: neuropeptide Y; NSCLC: non-small cell lung cancer; OAT1: organic anion carrier 1; OAT3: organic anion carrier 3; OCT2: organic cation carrier limb 2; ODE: ordinary differential equations; PAI: photoacoustic imaging; PCL: poly(caprolactone); PED: partial equations; PEI: polyethyleneimine; PFK-1: phosphofructokinase-1; PK: pharmacokinetic; PLC: phospholipase C; PLD: pegylated liposomal doxorubicin; PLGF2: placental growth factor 2; PPI: protein-protein interaction; PR: progesterone receptor; PVA: polyvinyl alcohol; RH: hormonal receptors; RLS: regularised least squares; ROS: reactive oxygen species; SEA: similarity ensemble approach; SIPNs: pluronic copolymer; siRNA: small interfering RNA; SLNB: sentinel lymph node biopsy; SLNs: solid lipid nanoparticles; SMA: styrene-co-maleic acid; SMILES: Simplified Molecular Line Entry System; SNS: sympathetic nervous system; SP: substance P; SPC: soy phosphatidylcholine; SPIO: superparamagnetic iron oxide; STING: stimulate interferon genes; TAs: tumor-associated antigens; THC: Δ9-tetrahydrocannabinol; THF: tetrahydrofolate; TME: tumor microenvironment; TNBC: triple-negative breast cancer; TNF α: tumor necrosis factor; TS: thymidylate synthase; VEGF: vascular endothelial growth factor; VEGF-A: endothelial growth factor A; VLPs: Virus-like particles; ZnO NPs: Zinc oxide nanoparticles; βAR1: type 1 receptor agonist β-adrenergic; βAR2: type 2 receptors β-adrenergic
1.
Introduction
Today, one of the most common cancers is undeniably breast cancer, which mainly affects women at any time in their lives and its incidence has continued to rise throughout the world. It can also appear in men, although with a much lower incidence [1]. In 2012, 1.7 million new cases were diagnosed worldwide representing 25% of all cancers observed in women [2], and in 2016,249,000 new cases were registered, leading to 40,890 deaths, most of them caused by metastases rather than primary cancer [3]. In 2017, in the United States alone, an estimated 252,710 new cases of invasive breast cancer were reported and about 63,410 new cases of breast carcinoma in situ, leading to 40,610 deaths that year [4]. In 2018, the number of breast cancers worldwide stood at 2,088,849 new cases and represented 11.6% of all cancers diagnosed. In the same year, 626,679 patients died of cancer, 6.6% of which were breast cancer, making it the second most common cause of death in the world after lung cancer. In the USA alone, incidence and mortality were estimated at 268,670 and 62,330 cases respectively, with an increase in incidence continuing in 2019, with an estimated 271,270 cases, but with a significant decrease in mortality, which fell to 42,260. In the UK the incidence was around 55,200 with 11,400 recorded deaths [5]. Overall, the incidence of cancer has been steadily increasing worldwide and estimates suggest that 21 million people will have been affected by 2030 and this pathology is expected to cause about 13 million deaths [6]. Western nations have a higher incidence rate but a lower mortality rate, unlike the least developed countries where the mortality rate is very high. This is probably justified because, in the various age groups, women in the least developed countries, like most African countries, are the ones diagnosed at a more advanced or late-stage for poor medical care leading to a higher mortality rate than any other racial/ethnic group in the world. However, these differences can also be explained by intrinsic biological pathways, with different evolution in metastases, lymph nodes, distance metastases, or the prevalence of triple-negative tumors in different racial/ethnic groups. Triple-negative tumors are those which do not express hormonal receptors (RH) or super-express human epidermal growth factor 2 receptor (HER2) on the surface of breast cancer cells [5].
2.
Types of breast cancer
Breast cancer is a heterogeneous disease, as it is composed of several different entities, with different biological characteristics and clinical behaviours [1,7]. It is divided into distinct subtypes (Luminal A [ER + / PR + / HER2-, grade 1 or grade 2] [8,9], Luminal B [ER + / PR + / HER2 +, or ER + / PR + / HER2-grade 3] [8,9], HER2 overexpression [ER-/ PR-/ HER2 +] and triple negative breast cancer [TNBC, ER-/ PR-/ HER2-]) [10], which, because they have different clinical manifestations, determine the pathophysiological ambiguity of the disease [11,12,13]. In addition, inflammatory breast cancer has to be considered.
2.1. Cancer: first moment
Early breast cancer includes stage I which is divided into IA and IB. Stage I is defined by the size of the tumor (≤ 20 mm) and negative lymph nodes. Stage IB is defined by the size of the tumor (≤ 20 mm) and the micrometastasis to lymph nodes of Level I and II ipsilateral mobile axillary tumors or, if there is no evidence of a primary breast tumor, present micrometastasis to ipsilateral mobile axillary lymph nodes of Level I and II. Studies show that about 99.1% of patients with stage IA and IB breast cancer have a disease-specific survival of about 5 years [14]. Other studies have shown that about 30% of all patients with early-stage disease have metastases [15] and that about 20-50% of women develop incurable metastatic breast cancer [16]. The five-year survival rate in breast cancer patients with metastasis at a distance can be as high as 26% although they have a shorter disease-free interval and have worse outcomes [17].
2.2. Advanced Breast Cancer
When the results of tests performed to detect the presence of breast cancer already show metastases, it is considered to be of the advanced type [18]. In this type of cancer, the patient's survival is related to the presence of HER2. It can be said to be inoperable [9,18,19], but treatable with various therapies that are already available and in use and with others that are still in the experimental phase [18,20].
2.3. Triple-Negative Breast Cancer (TNBC)
Breast tumors are characterized in immunohistochemistry by lack of expression of the estrogen receptor (ER), progesterone receptor (PR), and HER2 (also defined by lack of amplification of HER2 by fluorescence in situ hybridization (FISH), are classified as highly aggressive triple-negative breast cancer (TNBC). It has an early onset, greater metastatic potential, and has worse clinical pictures because there are more relapses and lower survival rates [21,22,23,24]. The molecular mechanisms involved in the recurrence of triple-negative breast cancer are not yet well understood [21].
2.4. Inflammatory breast cancer
Inflammatory breast cancer is a unique and rare entity, with more aggressive behavior and worse prognosis than non-inflammatory or locally advanced breast cancer. It is characterized by diffuse erythema and edema (peau d'orange), no palpable mass, early age at diagnosis, low nuclear grade, negative hormone receptor status, and poor survival outcomes [25]. Inflammatory breast cancer is classified as a high-risk disease because it has a high rate of metastasis at a distance (approximately 30–40%) at first diagnosis and approximately 80% at stage III and with the involvement of lymph nodes [26].
3.
Immunotherapy
Immunotherapy was developed by the knowledge of tumor leakage [27]. It involves the stimulation of the immune system to selectively attack cancer cells with fewer off-target adverse effects [28,29]. This stimulation aims to recognize and reactivate the anti-tumor mechanisms and to inhibit the mechanisms of tumor leakage [27]. Tumor immunotherapy aims to induce effective immune responses against malignant tumors, but induction and elimination may be hampered by the existence of several targets, which does not facilitate their recognition and therefore the elimination of tumor cells by immune cells may not be as effective [30]. Immunotherapy is currently effective against hematological tumors, but in solid tumors, its effectiveness has not been as expected, due to the great heterogeneity within tumors and differences in the external microenvironment of each [29]. It is essential to understand the mechanisms that tumor cells use to 'escape' the immune system, but also to understand the interactions between the tumor and that system. It was recently discovered that the immune system could alter the progression of the tumor by surviving the most suitable tumor cells and by altering the microenvironment of the tumor, causing it to develop. This process has been called cancer immune-editing, as the immune system can act either as a tumor stimulus or as a tumor suppressor [31,32]. In patients with a high tumor burden, immunotherapy is less effective due to the supposed correlation of immune suppression with tumor burden. Immune responses take time to translate and in the case of patients with advanced disease, it is not possible to wait for such responses [33]. Current anti-cancer immunotherapies consist of different strategies that include the systemic use of monoclonal antibodies, which target co-regulatory pathways, small molecules, antitumor vaccines, cytokines, cell therapies, and bacterial toxins (such as Coley's toxin). The mechanisms used by immunological therapies at the cellular level are the interruption of the direct signaling of the receptor-ligand, the suppression of the dominant tolerogenic pathways present in the tumor, and the direct stimulation of the immune cells [34].
3.1. Antibodies
Tumor-specific immunity can be stimulated by the production of tumor-associated antigens (TAs), either within the tumor cells themselves or in other cells, or by opsonization of tumor cells or by antibodies produced by viral vectors [35]. Passive cancer immunotherapy based on antibodies establishes the relationship between the binding of tumor-associated antigens and the individual (native) immune system, where a specific tumor antigen (Ig) has been discovered, immunoglobulins have two crystallized fragments (Fc) and it is in this region where interaction with the surface receptors of effector cells, immune proteins and other antibodies of the host immune system occurs. When antibodies are passively administered, they have biological effects, such as agglutination, neutralization of signaling proteins, or blocking of the binding sites of the receptors. When monoclonal antibodies (mAbs) are used to block growth factor molecules in their receptors, they will prevent growth stimulation in cancer cells. Trastuzumab (Herceptin) is a non-conjugated monoclonal antibody (mAb), which is used against advanced breast cancer because it functions similarly to the above. Trastuzumab targets the HER-2/neu antigen and is the first humanized antibody approved for the treatment of metastatic positive breast cancer for HER2. The Herceptin is designed to target and block the over-expression function of the HER2 protein. Another mechanism of action for the antibodies can be described, which involves marking cancer cells so that they are recognized by the immune system and subsequently destroyed by antibody-mediated effector functions such as cascade complement activation (CDC) and immune effector cells (ADCC). Antibodies can be used as vehicles to supply a cytotoxic agent covalently bound to tumor sites [36]. In a study with injectable polyvinyl alcohol (PVA) hydrogel nets, these were designed to respond to reactive oxygen species, which are present at high levels in the tumor microenvironment. After injection into a murine model of low immunogenicity breast cancer, the hydrogel degraded and first released the chemotherapeutic gemcitabine which killed cancer cells and promoted an immunogenic tumor phenotype. It then released an anti-PD-L1 antibody to stimulate antitumor immunity [37].
3.2. Cytokines
The three types of cytokines developed were interferons (IFN), interleukins (IL), and granulocyte-macrophages colony-stimulating factor (GM-CSF), and these are used in cancer immunotherapy. The second generation of drugs is being developed from cytokines consisting of known molecules with mechanisms to alter their action, new targets, and fusion proteins that increase their shelf life and activity [28]. Imiquimod is a cytokine and interferon inducer and has been shown to increase the antigenic presentation and maturation of Langerhans cells through the tumor necrosis factor (TNF α) and INF α, acting on the Toll-like 7-agonist receptor belonging to the imidazoquinoline family, which has as a key characteristic the improvement of skin adaptive responses and innate immune response. The treatment of imiquimod can suffer interference with the increase of natural killer cells (NK), which leads to spontaneous regression and IFN-α-induced regression in breast cancer cells. Recently the topical application of imiquimod cream (as a single agent) has increased the response of T cells and increased the survival of rats with breast carcinoma. The addition of imiquimod in combination with radiation resulted in inhibition of tumor growth in rats with breast cancer and when a low dose of cyclophosphamide was given before starting treatment, it further improved tumor inhibition and reduced tumor recurrence [28].
3.3. Anti-tumor vaccines
Antitumor vaccines aim to evoke tumor-specific immunity and be able to eradicate established tumors and maintain immunological memory [35]. They belong to a class of biological response modifiers that usually contain a tumor-associated antigen-like agent or a specific marker protein of a tumor-causing microorganism. Either of these agents stimulates the body's immune system and causes it to recognize and fight tumor cells. Vaccines, to be successful, must either be able to stimulate the immune system by targeting viable tumor cells or target the tumor antigen that plays an important role in the process of tumorigenesis and metastasis. In breast cancer, antigen-specific vaccines are being used, namely HER2-derived and MUC1-derived vaccines, as well as cell-based vaccines that will be described below [12].
3.3.1. Antigen-specific Vaccines
HER2 and MUC1 antigen-specific vaccines, already well studied in breast cancer, can amplify the adaptive immune system to a beneficial therapeutic level, since the levels of HER2 or MUC1-specific T cells and antibodies are very low in most patients with this cancer [12].
3.3.2. HER2-derived vaccines
HER2-derived vaccines are administered as adjuvants. In a phase I/II trial, a HER2-derived E75 MHC class I peptide was used with granulocyte-macrophage colony-stimulating factor (GM-CSF) and involved 195 patients with HER2+ breast cancer. The trial results showed an improvement in 5-year disease-free survival compared to the control group, and systemic effects were milder. The University of Washington Tumor Vaccine Group found that combination therapy with trastuzumab (HER2 inhibitor antibody) and HER2 vaccine increases levels of HER2-specific immune responses, in patients with HER2+ metastatic breast cancer, compared to those treated with trastuzumab alone. This combination therapy was well tolerated. As was the HER2 vaccine used in combination with lapatinib (a tyrosine kinase inhibitor that disrupts the HER2 and epidermal growth factor receptor (EGFR) pathways) was also well tolerated. These investigations have shown that HER2-derived vaccines are promising in breast cancer research and treatment, especially when they are combined with HER2 adjuvants or monoclonal antibodies and the kinase inhibitor. These have mild toxicity and show good clinical responses [12].
3.3.3. MUC1-derived Vaccines
Mucin 1 (MUC1) belongs to the mucoprotein family that is abnormally expressed in the various epithelial cells of malignant tumors. MUC1 is overexpressed in tumor cells, which contributes to carcinoma formation of epithelial cells where breast cancer is included by promoting cell adhesion, blocking the apoptosis pathway, and regulating intracellular growth signals. It is a biomarker in the early diagnosis of breast cancer. Theratope (STn-KLH) is a therapeutic cancer vaccine consisting of a synthetic antigen including MUC1. It was used in a phase III trial involving 1208 patients with metastatic breast cancer treated with concomitant endocrine theratope and it was observed that the time to progression and survival were significantly longer than in the control group and this advantage was more pronounced in patients who had a robust antibody response to theratope. The 12 breast cancer patients received monthly PANVAC vaccines, which is a poxviral vaccine that contains transgenes for MUC1, carcinoembryonic antigen (CEA), and 3 T-cell co-stimulatory molecules. They had mild side effects such as slight injection site reactions. 33% of patients had stable disease and 8% had a complete response. Patients who had a limited tumor burden obtained a better CD4 response or increased numbers of CEA-specific T cells demonstrating the benefits of the vaccine. L-BLP25 is a MUC1 antigen-specific vaccine, consisting of a combination with letrozole which can induce an antigen-specific immune response and increase survival. This was tested in the breast cancer mouse model expressing MUC1. The PEGuylated gold nanoparticle (AuNP)-based vaccine immobilizes chimeric peptides consisting of a glycopeptide sequence derived from MUC1 and the T cell P30 epitope sequence, and can induce MHC-II-mediated immune responses in mice. AuNP-labeled mouse antisera can recognize human MCF-7 breast cancer cells. With future studies, it is expected that the therapeutic effects of the MUC1-derived vaccine in breast cancer will be evaluated [12].
3.3.4. Cell-based vaccines
These vaccines present tumor antigens and activate tumor immunity directly or indirectly via dendritic cells. Lapuleucel-T (APC8024) was prepared using peripheral blood mononuclear cells and HER-2 sequences bound to granulocyte-macrophage colony-stimulating factor (GM-CSF). In a clinical trial involving 18 lapuleucel-T-treated patients with HER2 + metastatic breast cancer, it was well tolerated and no grade 3 or 4 adverse events were observed. There was also significant HER2-specific T-cell proliferation, where 5.5% showed a partial response and 16.6% had stable disease lasting longer than one year. p53 acts as a favorable immune target, as most breast cancer patients have high p53 expression and can initiate a p53-specific IFN response. In a phase II study to the p53 DC vaccine involving 26 individuals with progressive breast cancer, they found that 19 of the patients continued treatment after 6 weeks of vaccination and that 42% of them achieved stable disease which indicates the efficacy of p53-specific immunotherapy [12].
3.4. Oncolytic virus
The oncolytic virus is defined as a genetically modified or naturally occurring virus that can selectively replicate and kill cancer cells without harming normal tissues [38,39,40,41]. These viruses infect and express lytic genes in cancer cells, resulting in cell death and subsequent spread of offspring from cell to cell [42]. Oncolytic viruses have been preconceived to infect and spread selectively within the tumor cell population, leading to the death of cancer cells due to a variety of mechanisms, including direct cell lysis, cell to cell fusion, expression of therapeutic genes or enzymes, which lead to the activation of toxic molecules and stimulation of the immune system, with a breakdown of immunological tolerance [34,43,44]. Oncolytic virus therapy uses the virus itself as the active ingredient of the drug [38]. Successful tumor therapy with oncolytic viruses is based on the principle that the virus can access the tumor and selectively proliferate there within the population of tumor cells, leading to its destruction. The results obtained in animal models and human studies have been variable [43]. The virus has no difficulty replicating within the cancer cells. What becomes complicated is that it does not replicate within normal cells, maintaining the ability to replicate within the cancer cells. Attempts to obtain specific replication in cancer cells have been made by selecting a virus that was not itself virulent in humans or by engineering the virus genome [38]. Oncolytic viruses that safely eliminate tumor cell line populations in vitro show variable results in vivo when the same cells are used to generate tumor xenografts. It is essential to understand the dynamics of the virus within the tumor to understand the outcome of therapy and optimize the use of these new therapeutic agents [43]. The therapeutic activity of oncolytic viruses is not only limited to their tumoral oncolytic activity, but also the interactions within the cells of the tumor microenvironment (TME), as well as the vascular and immunological system of the patients [42,45]. Oncolytic viruses are already approved for head and neck cancer and malignant melanoma therapy, but soon others will also be approved for other types of cancer [43]. Two of the genetically modified cancer viruses have been approved for marketing as drugs. One is Oncorine, which is an adenovirus excluded by E1B, approved in China in 2005 for head and neck cancer and oesophageal cancer, and the other is T-Vec (talimogene laherparepvec, IMLYGIC, formerly OncoVEXGMCSF), which was approved for advanced melanoma by the Food and Drug Administration (FDA) in the US in October 2015 and subsequently approved in Europe in January 2016 and Australia in May 2016 [34,38,40,45,46]. The oncotropic viruses, which include canine parvovirus, baculovirus, and canarypox virus, are all being developed as vectors to target cancer, but none of them exhibit intrinsic oncological capacity [35]. Many viruses evoke a strong immune response and can function as adjuvants, and therefore oncolysis can be considered a dual strategy, in which cancer cells are destroyed on the one hand by the direct action of viral replication, and on the other hand, become targets for recognition by the immune system [34,35]. Another approach involves increasing the recognition of tumor cells by T-cells or dendritic cells that have been transduced with viruses encoding immunostimulating cytokines [35]. Although many of these oncotropic viruses never reach clinics, they can contribute to virotherapy research in other ways and can act as models and provide information on oncolysis mechanisms. Onchotropic viruses are absorbed by human cells, but their genes are not expressed [35]. Some of the oncholic viruses used in studies for breast cancer therapy are reoviruses [35], vesicular stomatitis virus (VSV; gender: vesiculovirus) [35], T-VEC which is a herpes simplex oncolytic virus [41,46], and measles virus (MeV; family of Paramyxoviridae) [47], although their efficacy is not yet well proven for solid tumors due to large heterogeneity and differences in the tumor microenvironment [47].
3.5. Cellular Therapies
In cancer immunotherapy one of the most successful strategies used so far is T-cell-based therapies, specifically immunological checkpoint blocking (ICB) and adoptive cell transfer (ACT). Inhibitors of mitochondrial reactive oxygen species (ROS), such as ME-344 which are inhibitors of mitochondrial complex I, are currently being evaluated in a clinical trial with breast cancer patients (ClinicalTrials.gov ID NCT02806817). ROS play an important role and it is, therefore, necessary to control them in T-cells to allow the metabolic remodeling necessary to establish the functions and memory of the effector T-cells. Regulatory T-cells are more resistant to oxidative stress compared to effector T-cells containing high glutathione (GSH) and their functionality also depends on their redox state. The genetic ablation of GSH synthesis increases the metabolic activity of the regulating T cells, which decreases the expression of forkhead box P3 (Foxp3) and impairs its suppressive activity. The removal of this ROS defense mechanism in the regulating T-cells significantly increases the anti-tumor immunity. However, in effector T-cells, the extraction or inhibition of ROS can improve the expansion and proliferation of these cells in TME, which would be beneficial in existing T-cell-based immunotherapies such as ICB [48]. CB-839 is a glutaminase inhibitor that is currently being evaluated in clinical trials for several solid tumors (ClinicalTrials.gov ID: NCT02071862 and NCT02861300). CB-839 inhibits the use of glutamine by tumors, blocking the production of energy. Furthermore, by increasing the availability of glutamine, CB-839 can increase mTOR and c-Myc signaling in natural killer cells (NK) and hence their cytotoxic capacity. Another approach uses glycogen synthase kinase-3 (GSK3), which inhibits Myc degradation, to sustain NK effector functions [48]. In a study by Zheng and colleagues [49], they showed that with ICB treatment on a mouse model with breast cancer, the infiltration of eosinophils into the TME increased. It was again associated with the normalization of blood vessels and increased infiltration of T cells. The presence of eosinophils correlated with the positive outcome of therapy in a pre-clinical model showed that activated eosinophils within TME can normalize vasculature and thus increase the infiltration of CD8+ T cells, promoting tumor rejection [50]. Besides, this group of researchers showed that the ACT of eosinophils and T cells exert changes in the TME vasculature and induce polarization of macrophages towards an anti-inflammatory phenotype [48]. Checkpoint inhibitors have been linked to a peptide derived from placental growth factor 2 (PLGF2), which has an exceptionally high affinity for multiple matrix proteins, which use a water-soluble reticulator, amine for sulfhydryl. After peritumoral administration, these conjugates remained located, mainly in the extracellular matrix, closer to the tumor tissue than the non-modified inhibitors. This location slowed the growth of the tumor and prolonged survival in genetically modified mouse models (GEM) of melanoma and breast cancer. Also, these conjugates have induced antitumor immunity and reduced treatment-related toxicities that are commonly associated with systemic administration of checkpoint inhibitors [37].
3.6. Bacterial Toxins
Candice R. Gurbatri et al. [51] reported a probiotic bacteria system to simultaneously deliver PD-L1 and CTLA-4 nanobodies into the tumor. The probiotic bacteria system is designed to control the production and continuous delivery of target PD-L1 and CTLA-4 immunomodulating nanocorps, respectively, through synchronized and optimized lysis which promotes superior anti-tumor immunity [52].
3.7. Laser Immunotherapy (LIT)
Laser immunotherapy (LIT) was first mentioned in 1997 for the treatment of metastatic cancers in rats. The therapy includes three components: a near-infrared laser, an absorbent alloy dye, and an immuno-adjuvant whose importance was observed in a pre-clinical study. The LIT has been evaluated in clinical trials of end-stage and metastatic breast cancer, and long-term systemic effects have shown to be a promising route for patients in the advanced stages of the disease [28].
3.8. Genomics
In metastatic mouse tumors, epigenetic modulation plus ICB has proven effective in suppressing myeloid-derived suppressive cells (MDSCs). The use of azathidin (methyltransferase inhibitor of DNA) and entinostat (deacetylase histone inhibitor) in combination with anti-PD-1 and anti-CTLA4 antibodies has shown pre-clinical benefits and is under clinical testing (ClinicalTrials.gov ID NCT01928576). This epigenetic modulation is thought to influence the metabolic status of MDSCs. Further research is needed to address the metabolic properties of MDSCs to counter their suppressive effect on anti-tumor immunity [48]. Nucleic acid therapy has emerged as a promising candidate for cancer treatment, including immunotherapy. Nucleic acid therapy is a diverse class of DNA or RNA such as plasmids, mRNA, ASO, small interfering RNA (siRNA), miRNA, low activation RNA, aptamers, gender editing gRNA as well as immunomodulating DNA/RNA. Nucleic acid therapy is versatile to functions ranging from changing the regulation (up or down) of gene expression to modulating immune responses. Since 1995 immunomodulating nucleic acids have been investigated, and since then an increasing number of potential immunomodulating nucleic acids have been discovered and tested for immunotherapy. Nucleic acid regulatory drugs such as siRNA and ASO can regulate post-translational gene expression and silence target genes, further regulating the intracellular signaling pathway involved in cancer progression. Nucleic acid immunostimulants such as non-methylated guanosine deoxynucleotides (CpG), poly I: C, 5′-triphosphate RNA, as well as di-cyclic nucleotides that actively stimulate interferon genes (STING), which induce or increase anti-cancer immune activation [53]. Rajagopalan et al. [54] used a 4-1 BB-targeting aptamer conjugated to siRNA against CD25 (IL-2 receptor) to deregulate IL-2 signaling in CD8+ T-cells. The results showed that the aptamer-siRNA conjugate could activate circulating T-cells, increase differentiation to memory T-cells, and further suppress tumor growth in a breast carcinoma model [53]. Genome editing nucleases include zinc-finger nuclease, nuclease (TALEN) or effect type transcription activator and, regularly grouped, short palindrome repeating nuclease or CRISPR associated protein system (CRISPR/Cas). Since its first application in mammalian cells (2013), the CRISPR/Cas system, based on a nuclease guided by RNA, has revolutionized precise genome manipulations [53]. Gene editing has been used in T-cell engineering, for immunotherapy of diseases such as acquired immune deficiency syndrome (AIDS) and cancers, but also as large-scale genetic screening, used to dissect genetic functions and biological pathways associated with human diseases [30,53]. CRISPR/Cas9 is currently one of the most widely studied tools due to its simple utility, programmability, cost-effectiveness, and most importantly, the highly efficient capacity in multiplex genome engineering [30]. With the use of CRISPR-Cas9 libraries in humans or mouse cells, several groups have been able to discover targets for the drugs that have therefore been developed and applied in the search for targets for cancer treatment [30]. A variety of targets have been discovered, related to survival, proliferation, metastasis, and resistance to tumor cell drugs. The use of CRISPR in combination with immunotherapy can lead to the emergence of new immuno-oncological targets [30], such as the CRISPR/Cas9 system which contains two critical components, the Cas9 nuclease, and a gRNA, the latter of which is a fusion of a crRNA and a constant tracrRNA. Recently, a CRISPR class II system based on the Cas12a, also called Cpf1, was developed, which is a single RNA-guided endonuclease without tracrRNA [53]. The Cas12a cleaves the DNA, opening the DNA in a staggered manner and the sticky-end mediated DNA repair facilitates genetic modifications in non-divided cells, in which homologous directed repair (HDR) is difficult to achieve. The genomic edition has expanded the landscape of oncology immunotherapy approaches, such as adoptive T cell engineering and therapy [53].
3.9. Neurotransmitters
Neurotransmitters are involved in the development of cancer through the tumor microenvironment and the progression of cancer. They are therefore potential targets in the fight against cancer but can also be associated with the pain that cancer patients may experience.
3.9.1. β-adrenergic receptors
Catecholamines such as dopamine, norepinephrine, epinephrine, and serotonin modulate pain transmission in the Peripheral and Central Nervous Systems. Changes in these neurotransmitters are implicated in the development of persistent pain syndromes. The sympathetic nervous system (SNS) is part of the autonomic nervous system (ANS) and plays an important role in stress response, leading to the release of catecholaminergic neurotransmitters into the nerve fibers of the SNS [55]. Prolonged stress is known to have deleterious effects on various tissues, through the release of norepinephrine (NE) at nerve endings, which then bind to the β-adrenergic receptors (βAR) in target cells, including bone-forming cells [56]. Several studies have shown that activation of the hypothalamus-hypophysis axis (HPA) and SNS are marks of chronic stress and can boost the progression of prostate, ovarian, and breast cancer, accelerating the appearance of metastases in vivo models of rats with various types of cancer [56,57,58]. This discovery makes it possible to direct therapy towards stress-responsive signaling and this can slow the progression of cancer and the metastatic spread being a further hypothesis for its treatment [57]. The catecholamine neurotransmitters activate βARs. Several cells that express βARs are present in the tumor microenvironment and are therefore able to respond to stress pathway signaling. The cells that are involved in the progression of cancer are the cells of the immune system and the endothelial cells. In the stress response, stromal cells contribute to the formation of metastases and alter the architecture of cancer in such a way as to favor the spread of cancer cells. Macrophages are recruited into the primary tumor, which causes vascular remodeling by increasing blood and lymphatic vessel pathways and promoting the spread of cancer cells. One strategy is to avoid macrophage recruitment or not to allow vascular remodeling by blocking stress-enhanced metastasis formation. Regulation of the tumor stroma plays an important role in the effects of stress on the progression of cancer. It has been proven in vitro tests and explant cultures that tumor cells that also express βARs and the activation of their signaling increase the ability of cancer cells to invade [57]. Recent studies have shown that breast cancer tissue expresses type 2 receptors β-adrenergic (βAR2) [59]. Formoterol, which is a selective agonist βAR2, induces the formation of invadopods in breast cancer cells, but shamoterol, which is a type 1 receptor agonist β-adrenergic (βAR1), did not have this effect [57]. In vivo the role of invasion regulated by βAR2 is unclear. It is not yet known whether the signposting of β2ARs on tumor cells is necessary for the early stages of the metastatic cascade, including tumor cell invasion and primary tumor escape [57]. Primary breast tumors are infiltrated by sympathetic axons and the sympathetic nervous system can induce a metastatic change in breast cancer. Macrophage infiltration of the tumor is induced by sympathetic activation mediated by β-adrenergic receptors and contributes to metastases [56,60,61]. In one study MDA-MB-231HM cells, a human breast cancer cell line, which shows a high response to signaling βAR, were used and investigated the effect of the tumor cell knockdown βAR2 on the metastasis of a primary orthotopic breast tumor. In previous pharmacological studies they found that genetic modulation of MDA-MB-231HM, βAR2 reduced cell invasion and prevented a shift to mesenchymal cell morphology. However, the positive regulation of expression of βAR2 in MCF-7 tumor cells with low endogenous expression of βAR2 increased the formation of invadopodia, thus proving the role of βAR2 in regulating the invasion of cancer cells. The modulation of βAR2 in MDA-MB-231HM tumor cells has also been shown to attenuate stress-induced metastases in primary breast tumors [57,61] and the role of the invasion of cancer cells induced by βAR2 and the achievements of stress in metastases has been proven [57]. In another study of orthotopic breast cancer in BALB/c mice, with the administration of propranolol, an antagonist to βAR, they were able to demonstrate the decrease in metastases in breast cancer [58,61]. The role of dopamine in the development of metastases in cancer is not yet known [61]. In a study of transgenic and orthotopic breast cancer mice, chronic chemical sympathectomy with 6OHDA reduces intratumoral noradrenaline and inhibits tumour growth [58]. Enzymes such as monoamine oxidase A (MAOA) that degrade catecholamines and serotonin can also play an important role in the influence of cancer metastases. MAOA inhibition stimulates malignant behaviour in MDA-MB-231 breast cancer cells, but several studies have shown controversial results [61].
β-blockers are used in heart disease, hypertension and anxiety and act by inhibiting β-adrenergic receptors by blocking communication between sympathetic nerves and target cells. Numerous in vitro studies have shown that β-blockers can interrupt migratory activity and inhibit angiogenesis of cancer cells [56,59]. Similarly, the use of β-blockers in breast cancer patients inhibits metastases and recurrence of the disease and improves patient survival [61,62].
3.9.2. Cholinergic receptors
In cancer studies, crosstalk between neuronal cells and tumor cells has been highlighted in co-culture trials, which causes a stimulation of neuronal growth by the cancer cells and an induction of the aggressiveness of the cancer cells by the neuronal cells. This discovery has shown interest in the role of acetylcholine and its receptors, in tissue regeneration and also in tumor progression [60]. The involvement of cholinergic receptors in prostate and gastric cancer, both in tumor growth and metastases, has recently been described. Neurotransmitters that are released by nerves into the microenvironment stimulate regenerative and cancer cells [60]. Muscarinic acetylcholine receptors (mAChRs) are expressed in some of the tumors derived from epithelial and endothelial cells, but some tumors can express nicotinic acetylcholine receptors (nAChRs). Tumors can also release acetylcholine (ACh) which can induce their growth and promote the proliferation of tumor cells. Acetylcholinesterase (AChE) and acetylcholine (ChAT) manifest and are active in malignant tissues and continuously regulate ACh levels. The expression levels of mAChRs may vary between the tumor tissue and normal tissue. The activation of odd receptors (M1, M3, and M5) coupled with Gq proteins increases cell viability. The expression of M3 receptors in different origins of tumors is involved in tumor growth/invasion during malignant progression through different metabolic signaling pathways. Previously it had been documented that the expression of mAChRs in cell lines of breast adenocarcinoma, designated as LM2 and LM3, appear spontaneously in BALB /c mice through different techniques and it was confirmed that the subtype of M2 receptor is predominant in both cell lines. In one experiment they performed the activation of mAChRs with carbachol for short periods, which led to increased proliferation in cell lines LM2 and LM3. In the LM3 tumor, the proliferation stimulated by carbachol activated the M3 receptor and led to the production of inositol 1, 4, 5-triphosphate (IP3) and nitric oxide (NO). They stimulated the LM2 cells with carbachol which led to the activation of the M2 and M1 receptors, causing a release of prostaglandin E2 and the activation of arginase. They verified the increased proliferation of tumor cells through these actions. Another binding experiment performed on cellular lysates indicated that mAChRs are highly regulated in M3 cells, derived from an M3 tumor metastasis indicating the invasive role of mAChRs when present in high concentrations [63]. The MCF-7 cell line, derived from a human adenocarcinoma of the breast (estrogen-dependent), expresses mAChRs. The subtypes of M3 and M4 receptors in these cells were identified by Western blot, but in normal breast tissue cells (MCF-10A) mAChRs were absent. In the trials, MCF-7 cells were treated with carbachol for short periods, which promoted their proliferation mainly by the M3 receptor, causing activation of nitric oxide synthase 1 (NOS1) and nitric oxide synthase 3 (NOS3) calcium / PLC / PKC dependent. It is necessary to understand whether the muscle stimulation in MCF-7 cells induces malignant angiogenesis through the positive regulation of vascular endothelial growth factor A (VEGF-A) and the number of tumor blood vessels. Carbachol has also been effective in increasing invasive capacity, expression, and activity of matrix metallopeptidases 9 (MMP-9) [63]. Taking into account that for the treatment of cancer drugs must be administered in effective doses to kill tumor cells with minimal side effects on normal tissues, paclitaxel was associated with carbachol in subliminal-doses. This combination induced cytotoxicity in the tumor cells of cell lines LM2 and LM3 without affecting the viability of normal breast cells but also caused a potentiation of tumor cell death by apoptosis. The same results were observed in the human MCF-7 cell line derived from a luminal adenocarcinoma. They analyzed the same combination of drugs in the MDA-MB231 cell line, derived from a triple-negative adenocarcinoma where they observed that the expression of mAChRs makes them sensitive to low doses of paclitaxel with carbachol, leading to a significant decrease in cell viability, but less potently than in MCF-7 cells [63]. The pre-treatment of cells with nicotine stimulates the activation of the sub-unit α9-nAChR, which intervenes in the migration of breast cancer cells MCF-7 and MDA-MB-231, through the expression of epithelial-mesenchymal transition markers. Both mAChRs and nAChRs thus play a functional role in cell proliferation, differentiation and apoptosis [61].
3.9.3. μ-Opioid receptors
The μ-opioid receptor is over-expressed in several human cancers where breast cancer is included and promotes tumor growth and metastasis. In medical practice, tramadol is a centrally acting analgesic agent, used to treat moderate to intense pain. The mechanism of action of tramadol is the activation of the receptors μ-opioid which leads to the inhibition of the recaptation of monoamines released from the nerve endings, such as norepinephrine and serotonin. Tramadol can activate the serotoninergic system and can have a positive effect on the immune system, causing an increase in lymphocyte proliferation and NK activity. Tramadol has a lower affinity for the μ-opioid receptors than morphine, although they have the same mechanism of action. A recent study showed that tramadol inhibits proliferation, migration, and invasion of breast cancer cells by inactivating the α-adrenergic receptor signal. It is necessary to continue the studies to demonstrate the anti-tumor activity of tramadol [64].
3.9.4. GABA receptors
It plays a role in the metastasis of cancer through the activation of ionotropic (GABAA) and methotropic (GABAB) receptors. In breast cancer patients the activation of GABAA receptors positively regulates brain metastasis. The expression of the GABAA receptor subunit, Gabra3, which is not normally present in breast epithelial cells, is increased in human metastatic breast cancer and therefore linked to the patients' worst survival. The overexpression of Gabra3 promotes the migration and metastasis of breast cancer cells through the activation of the serine/threonine kinase or protein kinase B (Akt) signaling pathway as demonstrated in the orthotopic mouse model, induced by breast cancer cell lines MCF7 and MDA-MB-436. Activation of the AKT signaling pathway increases metastasis via molecules such as focal adhesion kinase and matrix metalloproteinases (MMPs). Cells (MCF7) and human breast cancer tissues express the GABAB receptor [61].
3.9.5. Cannabinoid receptors
The Δ9-tetrahydrocannabinol (THC) has been subjected to several studies where it has been shown to have a therapeutic effect against cancer. Another phytocannabinoid, cannabidiol (CBD), also inhibits the functions of cancer cells. Synthetic agonists of cannabinoid receptors, WIN55,212-2, and JWH-133, have also been shown to have a dose-dependent antiproliferative effect on breast cancer cells. Many studies have been carried out on different models of breast cancer where cannabinoids have been used to stimulate proliferation and metastasis. WIN-55 and 212-2 mediated activation of CB1 and/or CB2 receptors in triple-negative breast cancer xenografts have been shown to significantly decrease growth and metastasis of the tumor. In two separate studies, CBD and THC were shown to prevent growth and metastasis of the tumor in xenografts of triple-negative breast cancer and type 2 (HER2) positive human epidermal growth factor receptors in MMTV-neu mice, as well as in mice with xenografts, respectively. Studies on the activation of CB2 receptors, through the agonist JWH-015 in cellular lines of luminal breast cancer A and MCF-7, have shown that they prevent migration and invasion. HER2 tumors that do not respond well to conventional therapy showed higher levels of CB2 expression. In basal cell lines and triple-negative breast cancer cells, MDA-MB-231 and xenograft-based model, cannabinoid treatment was directed at CB1 and showed to inhibit cell proliferation. In another study, antiproliferative actions that prevent cell invasion of CBD in the metastatic MDA-MB436 cell line were shown. THC has been shown to inhibit cell cycle advancement by stopping at the G2-M stage when mediated by CB2 in breast cancer cell lines. Studies advocate the induction of autophagy and inhibition of cell cycle progression in breast tumors after cannabinoid treatment [65].
3.9.6. Receptors for neuropeptides
Some studies have shown that the nervous system facilitates the development of tumor metastases by modulating metastatic cascades through the release of neural factors from nerve endings such as neurotrophins, neurotransmitters, and neuropeptides [61]. There are nerve endings within some types of cancers and cancer cells express receptors for neuropeptides and neurotransmitters that stimulate migration and promote tumor growth, which affects the response of chemotherapy [61,66]. Several neurotransmitters and neuropeptides involved in tumor metastasis have already been identified. Several cancer cells express receptors for several neuropeptides and neurotransmitters, such as norepinephrine, epinephrine, dopamine, GABA, acetylcholine, substance P (SP), and neuropeptide Y (NPY), which have stimulating effects on the migration of cancer cells [61]. NPY increases the expression of vascular endothelial growth factor (VEGF) and its secretion, promoting angiogenesis and the progression of breast cancer [61]. The working group of Fernández-Nogueira and colleagues demonstrated that the nervous system and nerve factors can play an important role in the progression and spread of cancer [66]. Two pioneering studies on prostate and gastric cancer showed that peripheral nerves are an important component of the tumor microenvironment and regulate the progression and metastasis of cancer [61,66]. In another study, several neurogenic were identified which are expressed differently among the subtypes of breast cancer and whose expression is correlated with prognosis. One of the neurogenic found is the receptor neuron gene histamine 1 (HRH1) which is positively regulated in basal tumor samples and enriched with HER2. Other authors have reported over-expression of HRH1 in cancer. In experimental breast carcinomas, histamine has become an autocrine growth factor that regulates cell proliferation via HRH1 and histamine receptor 2 (HRH2) and is considered the initial events responsible for the onset of malignant transformation. In vivo treatments with HRH2 antagonists produced complete remission in about 70% of experimental tumors. The role of HRH1 in the progression of basal breast cancer and resistance to targeted therapies has not yet been studied. HRH1 measures the functional effects of histamine on different cell types by activating the heterotrimeric G protein Gaq/11 and its effector, phospholipase C (PLC). The PLC will break down phosphatidylinositol 4, 5-bisphosphate into inositol 1, 4, 5-triphosphate (IP3) and 1, 2-diacylglycerol. IP3 will act on specific membrane retorts of the endoplasmic reticulum (ER) and will mobilize the Ca2+ of the ER reserves, which will activate certain proteins where the kinase regulated by the extracellular signal (ERK), which is involved in cell proliferation and survival, is included [66].
3.9.7. Potassium channels
Potassium (K+) channels are selective ionic channels for the conduction of potassium ions (K+), which are widely distributed in a variety of tissues and cells including excitable cells, non-excitable cells, and cancer cells, allowing the passive transport of K+ through cell membranes. These channels are important in participating in the control of the K+ homeostasis, in the regulation of cell volume, in the configuration of resting membrane potentials, in the release of neurotransmitters, in hormonal secretion and excitability of neurons and muscles, and also participate in cell processes such as proliferation, migration, apoptosis and cell adhesion. Studies have shown that genetically blocking or suppressing potassium channels, impair the growth of tumors. In this study potassium channels are now considered as new targets in oncology. One of these is the two-pore potassium channel of the TASK-3 domain (TWIK-related acid-sensitive K+ channel 3) which has become a target of great interest mainly for its involvement in carcinogenesis and tumor progression. TASK-3 belongs to the K2P channel subfamily and is composed of TASK-1, TASK-3, and TASK-5, which exhibit external K+ rectifying currents that do not depend on membrane strain. The currents mediated by TASK-1- and TASK 3 are highly sensitive to extracellular pH, while TASK-5 has no functional expression. TASK-1 and TASK-3 are expressed in various tissues of the peripheral and central nervous system, including dorsal root ganglia (DRG). TASK-3 is expressed mainly in central nervous system tissues, including the cerebellum, and different types of neurons. The activity of TASK-3 is involved in maintaining resting membrane potential and regulating action potential. The TASK-3 gene is expressed in KCNK9, located in the chromosome region 8q24.3, which is increased 10-44% in human breast tumors and 35% in lung tumors. In the studies performed it was shown that the over-expression of the KCNK9 gene is associated with the acquisition of malignant characteristics and resistance to hypoxia, with these changes' cancer cells can survive in areas of low oxygen tumors which is common in fast-growing solid tumors. The effect of TASK-3 depends on the function of the potassium channel. Several studies have consistently shown that a monoclonal (Y4) antibody against the cap domain of TASK-3 inhibits the growth of human lung cancer xenografts and breast cancer metastases in mice. Other studies have shown that the knockdown of the TASK-3 gene in breast cancer cells is associated with induction of cell senescence and interruption of the cell cycle [67].
4.
Nanoparticles
Nanoparticles loaded with drugs with a diameter of 1 to 1000 nm, can be used to selectively bring cytotoxic agents to tumors, thus increasing the effectiveness of therapy and minimizing systemic adverse reactions. To improve the effectiveness of nanoparticles in therapy, several strategies have been developed, such as active targeting, tumor-responsive nano-systems, together with optimization of the physicochemical parameters of nanoparticles [27]. Recently, nano-formulations such as liposomes, hybrid nanoparticles (NP), and exosomes have attracted interest due to their biocompatibility, tumor specificity, and high transfection efficiency. Vectors less than 200 nm in diameter are designed with favorable properties to prolong their blood circulation and allow their passive accumulation in tumor tissues through the effect of enhanced permeability and retention (EPR) [68,69]. The nano-vectors can be modified so that they are actively targeted at the specific receptors of the tumor and have reduced toxicity and reduced immunogenic problems in normal tissues. Cationic polymers, such as polyethyleneimine (PEI), can condense the gene and promote endosomal leakage capacity through the 'proton sponge' effect, resulting in efficient gene transfection. In some tumor-specific environments, such as lower pH, higher levels of GSH, and higher levels of ROS, they can be used to trigger gene release in the cytoplasm [68]. Su and colleagues [70] designed a nanoaeron of variable-sized graphene quantum dots for increased penetration and distribution of doxorubicin (DOX) deep into tumor tissue, which was triggered by pathological pH [69]. The nanosized drug delivery system (NDDS) is a promising strategy to increase the accumulation of drugs in the tumor because of its higher penetration and retention effects (EPR) and to minimize side effects [71].
4.1. Nanosized Drug Delivery System (NDDS)
The use of the light-witchable system incorporated with an NDDS system seems to be an ideal strategy for tumor treatment. The combination of the LightOn gene expression system and the nanoparticle carrier gene showed effective inhibition of the 4T1 tumor (breast cancer mouse model) with negligible toxicity, resulting in a promising platform for delivery of genes targeted for breast cancer therapy [68]. To further improve the therapeutic efficacy of cancer treatments, a combination therapy based on NDDS has been developed, which includes chemo/photodynamic or Immuno/photothermic combinations [71]. Photothermal therapy (PTT) uses photothermal agents such as gold nanoparticles, carbon nanoparticles, conjugated polymers, and green indocyanine-containing carriers to transform near-infrared (NIR) laser beams into rapid localized warming to cause irreversible damage and ablation of cancer cells [69]. The use of photothermic therapy (PTT) mediated by Near-Infrared Laser (NIR) (650-900 nm) in cancer therapy has recently gained more attention [71]. Sun and colleagues [71] designed a new NDDS, combining the anti-metastasis drug (silybinine) and PTT agent to prevent the growth of tumor cells and metastases simultaneously in vitro. The NDDS was assembled with silybinine and the indocyanine green agent (ICG) was self-assembled into the poly(caprolactone) (PCL) lipid nanoparticles (NPs) prepared by PCL, soy phosphatidylcholine (SPC), and F68 pluronic copolymer (SIPNs) [71]. Chen and colleagues [69], encouraged by the excellent properties of gelatine, have built a dual-response photothermal /MMP-2 nano-system to achieve drug release and synergistic therapeutic efficacy. The gelatine nanoparticles (GNP-DOX / ICG) were designed to co-encapsulate a photothermal (ICG) and chemotherapeutic agent (DOX). A commonly used reticulator, glutaraldehyde (GA), has been added to provide superior mechanical properties and improved stability. After laser irradiation, GNP-DOX/ICG swelled, remained at the tumor sites, and released its charges of ICG and DOX. GNP-DOX/ICG was then degraded by metalloproteinase-2 (MMP-2) and released DOX and ICG to further penetrate the tumors [69]. Sun and colleagues [72] developed a multi-functional nanoparticle PPy @ CPTHA-IRDye800CW (abbreviated as "P @ CH") that was highly efficient and targeted for breast tumors. For targeted chemo-photothermic therapy they used near-infrared fluorescence (NIRF) and photoacoustic imaging (PAI) to follow the tumor and observe the effects of the nanoparticle in vivo. IRDye800CW is one of the most commonly used near-infrared fluorescent dyes and has been FDA approved and can be detected by fluorescence imaging. Sun's group and colleagues have raised the hypothesis that hyaluronic acid (HA) can increase the distribution of the nanoparticle directed at the breast tumor. The covalent conjugation of camptothecin (CPT) in HA can prevent the premature release of the drug during circulation and allow the targeted release at the tumor site by hyaluronidase (Hyal) degradation of HA [72].
4.2. Metallic nanoparticles
The various metallic nanoparticles, including silver (Ag), gold (Au), platinum (Pt), zinc (ZnO), titanium dioxide (TiO2), and selenium, were analyzed to inhibit the growth of breast cancer cells [73,74]. Other nanoparticles such as copper (CuO NP), iron oxide (Fe2O3), silica, cerium oxide, and titanium oxide are also being explored and used in the diagnosis and treatment of breast cancer [74]. Nanoparticles can offer ample opportunity for therapeutic and diagnostic testing due to their magnetic, optical, thermal, and electrical properties. Different metallic nanoparticles use different molecular mechanisms such as the production of ROS intracellular, increasing oxidative stress, and tumor-specific cell death by apoptosis. The nanoparticles of the metal transition class induce hyperthermia (non-invasive method), to heat the cells, thus killing the tumor cells by converting electromagnetic radiation into heat. Few metallic nanoparticles have inherent potent anti-cancer activity due to their unique physical and chemical properties [74]. Gold nanoparticles (AuNPs) are extensively investigated for drug distribution and imaging and cancer diagnosis [75]. AuNPs have been designed and synthesized in different forms and configurations such as Au-nanoshells (AuNS), Au-nanorods (AuNR), and Au-nanocages (AuNC) that are emerging as versatile nano vehicles for cancer therapy. The AuNP is coated with PEG, in addition to ionizing radiation, has provided a higher survival rate in models of mice with breast cancer. Serum-coated AuNR has inherited the ability to negatively regulate the expression of genes related to energy generation and as there is a reduction in energy, migration, and invasion of cancer cells are inhibited, both in vitro and in vivo. Andey and colleagues have shown the inhibition/suppression of triple-negative cancer and metastasis using the combination of cisplatin-loaded AuNR and NIR laser [74]. AuNPs can serve as sensitizers to increase the effects of ionizing radiation (IR) through the photoelectric effect. AuNPs can increase the effects of radiation by producing secondary electrons and ROS, increasing DNA breaks. Radiosensitization using AuNPs has achieved high specificity and efficiency in breast cancer cells, targeting specific molecules [75]. The metal nanoparticles are densely compacted and selectively spread and/or absorb high-energy gamma/X-ray radiation [76]. Liu and colleagues [77] observed promising results in the treatment of glioma using AgNPs followed by radiotherapy. These nanoparticles inhibit VEGF in cancer cells, thus limiting metastasis. Zinc oxide nanoparticles (ZnO NPs) function as genotoxic drugs in the treatment of cancer. ZnO NPs form micronuclei within the tumor cell that increase cell death by mitotic and interphase apoptosis. ZnO NPs carry asparaginase and its stability and specificity increase further when administered in combination with paclitaxel and daunorubicin. ZnO NPs used in combination with paclitaxel and cisplatin showed reduced toxicity and increased efficacy in breast cancer cells [74]. Dual modal therapy using photodermal and radiotherapy with copper sulfide nanoparticles (CuS NP) marked with Cu-64 showed suppression of tumor growth in the BT474 subcutaneous breast cancer model and prolonged the survival of orthotopic 4T1 breast tumors [74]. Metal cerium oxide nanoparticles have unique properties that are advantageous compared to other nanoparticles. They have a crystalline network consisting of a cerium nucleus surrounded by an oxygen network and can coexist in Ce3+ and Ce4+ ions with the ability to have oxygen vacancies on their surface, allowing the modulation of free radicals according to redox chemistry. Several studies demonstrate a protective effect of these nanoparticles (nano cerium) concerning free radical-induced damage and others have shown an increase in the induction of oxidative stress. These results may have to do with environmental conditions such as pH. Nanocerials used in cancer cells have shown comprehensive effects, ranging from anti-invasive properties to simultaneous radio sensitisation and radioprotection [78].
4.3. Magnetic nanoparticles
Magnetic nanoparticles (MNPs) have unique properties, making them highly attractive for medical applications. These properties are their surface-to-volume ratio, their ability to transport other compounds due to their small size, and their quantum properties. MNPs with a hydrodynamic diameter of less than 5 nm extend rapidly through the endothelium and have short blood circulation times. NPMs smaller than 6 nm in size undergo glomerular filtration and renal clearance. NPMs above 8 nm are those with specific surface properties such as load and hydrophobicity and are phagocytized by the Kupffer cells of the liver and undergo elimination through the bile system. Some small MNPs may escape opsonization by the reticuloendothelial system and may be large enough to be retained in the systemic circulation. These features, together with the effect of improved retention and permeability (EPR), can lead to longer periods of these particles in the body. NPMs are also being developed for breast cancer therapies, namely, molecular imaging with magnetic resonance imaging (MRI) directed contrast agents; new techniques for sentinel lymph node biopsy (SLNB); magnetic hyperthermia, and magnetic drug delivery systems. These therapies are being used as potential cutting-edge clinical applications relevant to the field of breast cancer surgery [79]. Oghabian and colleagues [80] used the superparamagnetic iron oxide (SPIO) nanoparticles (30 nm), characterized as superparamagnetic, in properties and conjugated with HER2 Ab, as an MRI contrast agent in a model of xenograft of induced breast cancer cell BT474 in naked female mice. Artemov and colleagues [81] used SPIO conjugated with Herceptin to visualize breast cancer cell lines (MCF-7, MDA-MB-231, and AU-565). Prashant and colleagues [82] used SPIO loaded into a poly(lactic acid) copolymer (PLA) and D-alpha tocopherol polyethylene glycol 1000 (TPGS) succinate as a contrast agent for MRI. These PLA-TPGS loaded with SPIO (SPIO-PNPs) were subjected to qualitative cell-capture research in MCF-7 breast cancer cells by TEM viewing. In vivo mouse xenograft models demonstrated SPIO-PNPs internalization by tumor cells, 5 hours after SPIO-PNP administration. Kievit and colleagues [83] used SPIO coated with a chitosan copolymer and PEG (NP) (which aids in anchoring drugs, imaging agents, and provides increased steric colloidal stability and decreased immune recognition) with neu antibody (HER2 Ab) to target metastatic breast cancer. Magnetic resonance imaging studies in transgenic mice have shown that directed NP-neu significantly shortened T2 relaxation time, making it suitable as a magnetic resonance contrast agent for disease detection or monitoring drug distribution [79]. NPMs provide an opportunity to develop drug delivery systems that are specifically designed for their target. Current chemotherapy regimens suffer from non-specific toxicity that limits their therapeutic potential. Jain and colleagues [84] have developed a new formulation of magnetic iron oxide nanoparticles coated with water-dispersible oleic acid, (OA-) Pluronic, which was loaded with high doses of solutes of chemotherapeutic drugs in water. This group demonstrated the internalization of DOX-charged nanoparticles into MCF-7 cells, with sustained intracellular retention and dose-dependent antiproliferative activity, in cancer cells. Kohler and colleagues [85] have developed conjugate drug-nanoparticle insert methotrexate (MTX) into the iron oxide nanoparticle. Khohler's group modified the surface of the MNP conjugate using a peptide bond, preventing MTX from being released from the surface of the nanoparticles under intravenous conditions. Amide binding cleavage occurs in the lysosomal compartment. NPMs have been used to locate non-touchable lesions in various ways for imaging, drug administration, and magnetic hyperthermic [79].
4.4. Polymeric nanoparticles
Polymeric nanoparticles have a diameter between 50 nm-10 μm and if they are larger than 10 microns they can no longer be considered as nanoparticles, which have the additional advantage of encapsulating drugs and proteins without chemical modifications. These nanoparticles can be prepared from natural or synthetic polymers [74]. Polymers derived from natural sources are also being explored as drug delivery systems due to their biochemical similarity to extracellular matrix components, ease of isolation and chemical modifications, and biocompatibility after enzymatic and hydrolytic degradation in the body [86]. Nanoparticles including polymeric micelles, capsules, colloids, and dendrimers are core-shell structures that self-assemble in an aqueous solution by amphiphilic and biodegradable polymers such as poly (D, L-lactic acid), poly (D, L-lactic-co-glycolic acid), poly (ε caprolactone), and copolymers with PEG, which is typically used to prevent particle agglomeration. The molecule of the drug can be efficiently encapsulated by the method of nanoprecipitation, electro-pulverization, and emulsification [74,87]. Drug formulations by polymeric nanoparticles have proven promising for the treatment of cancer because they improve therapeutic efficacy and reduce systemic toxicity [86,88]. These can be formulated to improve the solubility of hydrophobic drugs and hormone regulators such as taxanes, camptothecin, cisplatin, and tamoxifen because they make their half-life longer and increase the concentration of the drug in the target tumor as a result of improved permeability and retention (EPR) [86,87]. Poly (lactic acid-co-glycolic; PLGA) is an FDA-approved biodegradable synthetic polymer and has been more widely used in the formation of nanoparticles [89]. PLGA loaded with cisplatin is shown to be efficiently absorbed by prostate cancer cells, LNCaP, resulting in a higher cytotoxic effect compared to free cisplatin. Encapsulation with dextranocytosan sulfate and tyrosine kinase inhibitor (lapatinib) is more effective against BT474 HER2-positive breast cancer cells than free cisplatin [86]. GenexolⓇ-PM, poly (D-acid, L-lactic), combined with paclitaxel is a polymeric nanoparticle, which is being used in clinical trials for the treatment of breast cancer [87]. The untargeted distribution of the mitaplatin Pt (IV) drug using PLGA-PEG, i.e., poly D, L- lactic acid - polyethylene glycol block nanoparticle, showed increased tumor inhibition in naked mouse models with MDA MB 468 cells in vivo. Although polymeric nanoparticles are effective in transporting hydrophobic chemotherapy or hormone regulators, they still have deficiencies. One of the main concerns is their stability under adverse conditions, such as high temperature and radiation during sterilization, an important step in their production, but also the presence of residual toxic solvents introduced during polymer production and exocytosis caused by undissolved polymeric structures cannot be ignored [87].
4.5. Liposomes
Liposomes are spherical vesicle molecules (400 nm) with a central aqueous nucleus surrounded by lipidic bilayers. The possibility of encapsulating the drug both on the lipid membrane and inside the aqueous nucleus makes the liposomes more versatile nanotransporters and with a better distribution of the drug whose release can be easily modulated by applying an appropriate stimulus (e.g. temperature, pH, etc.) [74,90]. Liposomal nanoparticles are developed by different methods, such as extrusion (production process of nanoparticles of fixed cross-section area), solvent injection (method of precipitation of lipids, from a lipid dissolved in solution), and reverse-phase evaporation [74]. Lipid-based nanoparticles include solid lipid nanoparticles (SLNs), nanostructured lipid carriers (NLCs), and hybrid lipid-polymer nanoparticles (LPNs). The most commonly used lipid materials in nanoparticles include soy lecithin, cholesterol, glycerine monostearate (GMS), oleic acid, linoleic acid, stearic acid, and others [90]. Dai and colleagues [91] directed the over-expression of integrin-α3, in models of triple-negative breast cancer, with cyclic octapeptide LXY (Cys-Asp-Gly-Phe (3.5-DiF) -Gly-Hyp-Asn-Cys) linked to liposomes containing double drugs, doxorubicin, and rapamycin. This approach to the dual combination of drugs showed better efficacy compared to free drugs [74]. Feng and colleagues [92] observed the binding of CK3 peptide (Cys-Leu-Lys-Ala-asp-Lys-Cys) to NRP-1 trans-membrane protein (neuropilin-1) by NIR fluorescence imaging in triple-negative cancer mouse models. The modified iron oxide (Fe2O3) nanoparticles linked to the cyclic RGD peptide are more targeted and more efficient for integrin receptors αvβ3. The liposomal nanoparticle which is bonded to the double binder (P-selectin and RGD-peptide) can be captured at different sites of the tumor by the expression of its receptors in breast cancer cells [74]. Until now, liposomal doxorubicin (LD) and pegylated liposomal doxorubicin (PLD) have entered phase II and III clinical trials and the FDA has approved their clinical use in breast cancer [90]. DoxilⓇ, PEGuilated liposomes, which encapsulate doxorubicin, was the first nanoparticle approved by the FDA. Doxorubicin interacts with the base pairs of the DNA chains, inhibiting DNA synthesis and transcription, and Doxil was used to treat Kaposi's sarcoma, refractory breast cancer, and ovarian cancer [87]. Nanoparticles, based on liposomes for breast cancer, are well developed, but there are still limitations, such as physical and chemical instability. Physical instability can be caused by aggregation or fusion of vesicles due to the poor stability of the colloid, with larger particles than when formed being rapidly eliminated. Chemical instability can be caused by oxidation of unsaturated lipid chains and/or hydrolysis of the ester bonds, which causes the liposomes to run off and in turn the drugs to be released before the liposomes can reach the cancerous tissues. Liposomes have a low efficiency in encapsulating hydrophobic drugs (paclitaxel) due to their low affinity for the lipid layer [87].
4.6. Dendrimers
Dendrimers are synthetic macromolecules (10 nm to 100 nm), prepared by the divergent or convergent synthesis of branched monomer. They have a spherical shape enriched by a cavity with a hydrophobic core and hydrophilic periphery, which makes them exclusive vehicles for the delivery of siRNA. Wang and colleagues [93] have demonstrated the reduction of tumor vascularisation in a rat model with triple-negative breast cancer xenograft using poly (amidoamine) dendrimers conjugated with oligo anti-sense (AODNs). This therapeutic approach is directed towards the highest expression of VEGF, such as AODNs receptors. In another targeted therapy, where they use the poly (amidoamine) dendrimer, conjugated with siRNA, Finlay, and colleagues [94] showed the negative regulation of the transcriptor factor TWISTI which is a promising target in triple-negative breast cancer. Zhang and colleagues [74] tried to evaluate the dendrimer as a targeted diagnostic module in the rat model with triple-negative breast cancer. A new G4PAMAM dendrimer, combined with GdDOTA (MRI contrast) and DL680 (NIR dye), was prepared and injected subcutaneously into mice as a dual model for imaging and drug administration. Scanning magnetic resonance imaging and near-infrared (NIR) fluorescence imaging revealed a dendrimeric homing and a higher fluorescence signal in triple-negative breast cancer, thus showing the role of the small-sized dendrimeric agent 42-G4PAMAM-DL680 (GdDOTA) in the application of the targeted diagnosis for triple-negative breast cancer [74].
4.7. Micelles
The micelles are colloidal particles (5-100 nm) with a hydrophobic core formed from Van-der Waals bonds and stabilized by a hydrophilic shell. The micelle can provide hydrophobic and water-soluble drugs for cancer therapy. Taurin and colleagues [95] have synthesized a micellar system, where they used styrene-co-maleic acid (SMA) to deliver a hydrophobic derivative of curcumin, i.e. RL71, for the treatment of triple-negative breast cancer. This system has been shown to have greater toxicity to cancer cells due to increased cell absorption mediated by endocytosis and a slow-release profile. Although this system has increased the absorption of the drug, it needs specificity, which is a serious challenge in the treatment of metastatic breast cancer. Kutty, Feng, and colleagues [96] have developed micelles of vitamin E D-conjugated with cetuximab and alpha-tocopheryl polyethylene glycol succinate for targeted distribution of the drug docetaxel. Muthu and colleagues [97] developed a TPGS micelle, conjugated with the transferrin binder, which mediated the co-delivery of docetaxel and used the nanoclusterAuNc (imaging diagnosis) for the simultaneous detection of treatment and transferrin receptor, which was expressed in the breast cancer model MDA-MB-231-Luc in vitro. The system described above showed real-time imaging and tumor inhibition in the xenograft model. Sun and colleagues [98] developed Poli (acrylic acid)-g-PEG, i.e. copolymeric PAA-g-PEG micelles, which carry DOX (50% by weight/weight) where it showed an efficient reduction of lung metastases and reduction of breast tumor growth in 4T1 mice. The only micelle that entered the phase II clinical trials in triple-negative breast cancer patients was SN-38 (irinotecan), which contains poly (ethylene glycol) -poly (glutamic acid) PEG-PGlu, so the micelle NK012 needs to be validated in other phases of clinical trials [74].
4.8. DNA nanoparticles
DNA nanoparticles use Watson-Crick complementary nucleic acid pairing to design nanoparticles with different shapes, such as tetrahedral, bipyramids, cages, and cubes with the desired shapes, sizes, and configurations. DNA nanoparticles can incorporate binders and/or small functional compounds for site-specific fixation and/or bioimaging. Kutty and colleagues [99] have created a self-assembled DNA nano pyramid, marked with gold nanoparameters, protected by red emissive glutathione (GSH-Au NCs) at the base and actinomycin incorporated in the smallest DNA groove. This DPAu/AMD teranose has been developed so far for the detection and elimination of Escherichia coli (E. coli) but also guarantees evaluation and modification in other diseases where cancer is included. The same group has developed another nanoparticle, the tetrahedral DNA (TH), for the delivery of the drug directed and mediated by antibodies. The tetrahedron of the DNA self-assembles to form four vertices. The TH is conjugated with cetuximab (THC3) and the drug doxorubicin (DOX) is interspersed in them (THDC3) preferably killing the cancer cells MDA-MB-468. This is due to the cetuximab that targets the cancer cells that over-express the epidermal growth factor receptor (EGFR). Another modified formulation, loaded with one Cy3 probe and three cetuximab, i.e. Cy3-THC3, showed a high-intensity signal due to the increased uptake of Cy3-THC3 in MDA-MB-68 cells. The slight modifications (THDC3 and Cy3-THC3) in the TH showed a direction towards the cancer cells, killing them, which can be an excellent strategy for cancer diagnosis and treatment especially for triple-negative breast cancer [74].
4.9. Aptamers
Aptamers are short segments of single-chain DNA/RNA oligonucleotides. Through a 3D assay, it has been confirmed that the aptamer binds specifically to the target molecule with high affinity and strength. The use of aptamers presents a single limitation, which is that it is degraded by nucleases, but its stability is good for the development of molecular probes. Li and colleagues [100], in a preliminary study, specifically target a triple-negative breast cancer cell membrane surface protein by the LXL-1 aptamer, recently identified by the SELEX cell method. Huang and colleagues [74] used the PDGF-aptamer, in combination with gold nanoparticles, to detect the differential overexpression of platelet-derived growth factor (PDGF) receptor in the triple-negative breast cancer cell line. Breast cancer cells MCF7 and MDA-MB 415 are known to over-express mammaglobin A2 (MAMA2) and mammaglobin B1 (MAMB1). Hassann and colleagues [74] used aptamers in metastatic breast cancer to detect MAMA2 and MAMB1 by chemical terahertz (THz) microscopy, which is highly sensitive using THz radiation. Another DNA aptamer, rich in G 26-mer, specifically targets the nucleolin receptor in some breast cancer cells. The use of aptamers for cancer diagnosis and treatment still needs to be improved and combined with drug administration [74].
4.10. Carbon nanotubes (CNTs)
Carbon nanotubes (CNTs) are flat sheets knitted with benzene rings, folded to form cylindrical structures with single and/or multiple walls. With a slight chemical modification, they can have various functions with enormous possibilities in cancer therapy. Single-walled CNTs (1 nm-2 nm in diameter) can penetrate inside the cells showing a prolonged distribution and localized effects. The oxidized multi-walled CNTs (o-MWNTs) present a breakthrough in cancer therapy as they reduce macrophages and vessel density in the tumor. Burke and colleagues theorized that by hyperthermia, nanotubes can promote cell membrane permeability, destroying the tumor mass. They proposed induced photothermic ablation, using the multi-walled nanotubes for triple-negative breast cancer therapy [74].
4.11. Virus-like particles (VLPs)
Virus-like particles (VLPs) are self-assembled (0.1-100 nm) multimeric nano-structures produced by the expression of viral structural genes in heterologous systems. The VLP is free of any viral genetic material which makes them versatile for drug delivery. Because the VLPs are small in size, they move easily into the bloodstream and the functional viral proteins they have on their surface facilitate their entry/penetration into the cell. VLP's can encapsulate small molecules/ drugs, which allows them to be applied in cancer treatment by targeting, entering the specific tumor cells by receptor-mediated endocytosis, wasting energy, and releasing the encapsulated drug inside the cancer cell. The VLPs have a surprising ability to escape the endosomes, before the liposomal degradation, which favors the availability of the drug, protecting it in the blood plasma. One of the disadvantages of using VLP as a drug delivery system is that they induce an innate immune response due to the viral protein particle and are readily absorbed by dendritic cells, but even so when classic chemotherapy fails, it can be a solution for the treatment of triple-negative breast cancer [74].
4.12. Artificial Intelligence (AI) guide nano-robot
The Artificial Intelligence (AI) guided nano-robot is evolved and made of biocompatible and biodegradable material (carrageenin/coating capsule) that can transport the drugs specifically to the target site, cancer. They must also have a tracking sensor, self-detonating property, to be eliminated from the body after the required purpose. Shortly, AI will be used in nanoparticles not only to diagnose and treat cancer but also to apply to other diseases [74].
5.
Drugs repurposing
There is much research on anti-cancer therapy, although many of the major anti-cancer compounds are at various stages of pre-clinical or clinical research, but only 5% of them enter Phase I clinical trials and are eventually approved [101]. One promising strategy is the repurposing of drugs. The drugs repurposing is the process of finding new therapeutic indications for existing and approved drugs [6,101,102] and is considered (ⅰ) a faster and more economical strategy than synthesizing a new drug [6,101,102,103,104], (ⅱ) a low-risk strategy, as they have already been tested for pharmacokinetics, pharmacodynamics, and human toxicity and have overcome regulatory obstacles [6,101,102,103,104], (ⅲ) an efficient strategy to expand alternative therapy options for various medical conditions, including cancer [103]. Many pharmacological classes are repurposed and used in cancer treatment, based on their anti-cancer activity. These classes include psychopharmaceuticals, antibiotics, antirheumatics, antimalarials, antihypertensives, and antivirals [6]. In cancer therapy, particularly in breast cancer, strategies for the reuse of drugs and/or combinations of drugs are widely used [105]. The repurposing of drugs that may be or are already used in the treatment of breast cancer is those described in the table below.
5.1. Zoledronic acid
Zoledronic acid is a biphosphonate used in the treatment of osteoporosis [6]. It prevents bone loss associated with aromatase inhibitors in postmenopausal women and premenopausal women with early breast cancer [106]. New evidence has emerged that zoledronic acid also has antitumor and antimetastatic properties, which include inhibition of angiogenesis, invasion of tumor cells and adhesion to the bone, induction of apoptosis, antitumoral synergy with chemotherapy and immunomodulatory effects through T cell induction γ / δ [106]. It has therefore been approved for the treatment of metastatic bone disease, in which case higher doses than those required for the treatment of postmenopausal osteoporosis are recommended [6].
5.2. Atorvastatin
Atorvastatin (ATO) is a statin that inhibits the function of the 3-hydroxy-3-methylglutaryl-CoA (HMG-CoA) reductase limiting enzyme. ATO has been widely used to lower lipid levels and reduce cardiovascular risk. Several animal studies have shown that ATO also effectively inhibits the growth of breast, prostate, pancreas, and liver cancer [107]. ATO shows antiproliferative effects on different cancer cells, including breast cancer cells. It inhibits p-AKT expression level and positively regulates RhoB expression level, increases PTEN expression level, inhibits PI3K / AKT route, and exerts breast cancer inhibitory effect. ATO also promotes autophagy and apoptosis in the cells of this cancer and reveals antitumor activity in MCF-7 cells by inhibiting their proliferation [107,108]. Breast cancer cells, with treatment with ATO, showed immunoreactivity for Beclin-1 and LC3B that can be induced by stress [108].
5.3. Chloroquine
Chloroquine is an old antimalarial drug that is being investigated in clinical trials for potential use in anticancer therapy in advanced-stage tumors. Its anticancer mechanisms are mediated by reducing tumor cell autophagy and promoting tumor vessel normalization. Chloroquine exerts its anticancer effect by its immunoregulatory function on tumor-associated macrophages but also utilizes T-cell immunity. Chloroquine redefines macrophages from tumor-promoting M2 to tumor-inhibiting M1 in the tumor microenvironment. This has been considered a tumor immunotherapeutic agent. Chloroquine promotes the polarization of M1 macrophages and thus interferes with phagocytosis, which causes an increase in lysosomal pH. For macrophages to reconvert from the M2 phenotype to the M1 phenotype, lysosomal calcium release is required [109]. Phase I studies with chloroquine have shown very promising results in breast cancer cell lines both used alone and in combination with other drugs. When the results of the studies were analyzed they showed that chloroquine was more effective in reducing cell viability than other drugs and drug combinations [105].
5.4. Clotrimazole
Clotrimazole is an antifungal. This drug can also affect glycolytic enzymes by decreasing the binding of hexokinase (HK) to the external mitochondrial membrane and by highlighting phosphofructokinase-1 (PFK-1) and aldolase from the cytoskeleton. Clotrimazole can trigger apoptosis which is related to its ability to displace HK from the mitochondria and PFK-1 and aldolase from the cytoskeleton. The results obtained in several studies showed the same pattern as MCF-7 and MDA-MB-231 cells concerning sensitivity and increased concentration of clotrimazole, which, when introduced into the metastatic cell line of breast cancer, shows increased inhibition of glycolysis [110].
5.5. Disulfiram
Disulfiram (DS) is a commercially available antialcoholism drug that shows both in vitro and in vivo anticancer activity and also enhances cyclophosphamide, cisplatin, and in vitro radiation and protects normal kidney, intestine, and bone marrow cells in vivo while increasing the therapeutic rate of cytotoxic drugs. Studies have shown that the DS increases 5-fluorouracil (5-FU) -induced apoptosis in cell lines of colon cancer and breast cancer. The anti-cancer activity of the DS is copper (Cu) dependent. Copper plays an important role in redox reactions and triggers the generation of ROS in human cells. The DS/Cu is a strong ROS inducer and inhibitor of the proteasome-NF-kB pathway. The combination of DS and Cu can target cancer cells and combat both ROS and NFkB [111,112]. The DS can also penetrate cancer cells to form Cu 2 (deDTC) with intracellular Cu. Normal tissues and the carcinogenic tissues of many cancers, including the breast, have higher levels of Cu (two to three times), which may allow the DS to enter the cancer cells selectively [111].
5.6. Doravirine
Doravirine (MK-1439) is a highly potent non-nucleoside reverse transcriptase inhibitor (NNRTI) administered once a day and used for the treatment of infection with human immunodeficiency virus type 1 (HIV-1) in combination with existing antiretroviral therapies (ARTs). Clinical studies have shown that doravirine does not perpetuate clinically significant drug interactions with substrates for CYP3A4, breast cancer resistance protein (BCRP), organic cation carrier limb 2 (OCT2), organic anion carrier 1 (OAT1), and organic anion carrier 3 (OAT3). Doravirine inhibits BCRP and increases the level of exposure to atorvastatin [113].
5.7. Flubendazole
Flubendazole is an FDA-approved anthelmintic drug that inhibits the proliferation of cancer cells in vitro and in vivo at clinically tolerable concentrations. Flubendazole targets the stem cells of breast cancer, where it interrupts the progression of the cell cycle but also suppresses cell migration, inducing cell differentiation and increasing conventional chemotherapy efficiency in breast cancer cells. In one study, Hou and colleagues [114] demonstrated that flubendazole, as an anti-stem cell agent in breast cancer therapy, had several effects such as inhibiting the proliferation of cancer cells in vitro and suppressing tumor growth in vivo. The reduction of breast cancer stem cells was evidenced by the loss of the CD44high / CD24low population, the reduction of mammals, and the suppressed expression of genes related to c-myc, oct4, sox2, Nanog, and ciclinD1 stem cells. Flubendazole induces monopolar spindle formation by inhibiting tubulin polymerization, which causes cell cycle block in the G2/M phase of breast cancer cells [114].
5.8. Gemcitabine
Gemcitabine is an antiviral drug that after some preclinical trials demonstrated anticancer activity against leukemic cells in vitro and after further studies were performed the FDA approved its use in the treatment of pancreatic cancer (1996) non-small cell lung cancer (1998) and metastatic breast cancer (2004) [6]. Gemcitabine kills breast cancer stem cell-like cells by reducing levels of the truncated biomarker p95HER2, phospho-HER2, phospho-HER3, and phospho-Akt, but also by reducing the expression of genes associated with self-renewal where c-myc, oct-4, sox-2, nanog, and cyclin D1 are included [103].
5.9. Itraconazole (ICZ)
Itraconazole (ICZ) is a broad-spectrum antifungal that inhibits lanosterol 14-methylase and is used in the treatment of fungal infections and prophylaxis of immunosuppressive diseases. Studies show that this drug has an antineoplastic activity and also a synergistic action when associated with chemotherapeutic agents. Its anti-cancer activity is promising in several types of cancer, but its mechanism is not yet defined, as it is also known to act on several mechanisms to prevent tumor growth which include inhibition of the Hedgehog pathway, prevention of angiogenesis, decrease in endothelial cell proliferation and stopping the cell cycle [105]. In vitro studies have confirmed that ICZ inhibits glycoprotein P, thus reversing the resistance conferred by this efflux pump [105,115]. In another study, ICZ inhibited the proliferation of MCF-7, MDA-MB-231, and SKBR-3 cells by inducing cell death and interrupting the cell cycle in the G0/G1 phase [105,116]. This drug may also induce autophagy in medulloblastoma and breast cancer cells [115].
5.10. Ivermectin
Ivermectin is an antiparasitic and can be a potential anti-cancer agent in colon cancer, ovarian cancer, melanoma, and leukemia [117,118]. It prevents the closure of chloride ion channels blocked by glutamate, which causes hyperpolarisation of the plasma membrane, which paralyzes the parasite's pharyngeal and somatic muscles, leading to its death [119]. Ivermectin also has a promising anti-cancer effect on breast cancer. This has been shown, after 24-hour treatments, by inhibiting growth in a variety of breast cancer cell lines, without causing obvious effects on human non-tumor cells. Ivermectin inhibits expression of the PAK1 gene (p21 [RAC1] kinase 1 activated) in breast cancer cells by inactivating the AKT MTOR signaling pathway, which is a key negative modulator of autophagy induction [117,118]. A recent study has shown that ivermectin can relieve multidrug resistance in breast cancer and increase the cytotoxicity of doxorubicin and paclitaxel [118]. Another study showed that ivermectin had synergy with docetaxel, tamoxifen, and cyclophosphamide [119]. This may also be linked to the stopping of the cell cycle. ivermectin can be used in the treatment of breast cancer [118].
5.11. Levofloxacin
Levofloxacin is a second-generation synthetically derived fluoroquinolone and is an antibiotic that kills bacteria by inhibiting topoisomerase enzymes, thus avoiding DNA replication. Many antibiotics act on protein synthesis or DNA replication in bacteria and are effective against tumor cells by inhibiting mitochondrial biogenesis. The role of levofloxacin in cancer is unknown. In one study, levofloxacin has been shown to selectively inhibit cell proliferation and induce apoptosis of a panel of breast cancer cells. Levofloxacin acts synergistically with the conventional chemotherapeutic drug 5-FU ACh in inhibiting breast tumor growth. This drug targets breast cancer cells by inhibiting mitochondrial biogenesis. It has been shown that inhibition of mitochondrial biogenesis leads to the deactivation of the PI3K/Akt/mTOR and MAPK/ERK pathways in the cells of this cancer [120].
5.12. Lonidamine
Lonidamine (NLD) is a derivative of indazole which was introduced as an anti-spermatogenic agent in 1979. Studies have proven that NLD has an antitumor activity because it interferes with the energetic metabolism mainly in the action of the mitochondria of tumor cells. Nowadays, NLD can be used in the treatment of non-small cell lung cancer (NSCLC), breast cancer, colon cancer, astrocytoma, squamous cell carcinoma, and human glioma, among others. In a study with breast cell carcinoma MCF-7, the cytotoxicity of cisplatin was increased approximately 100 times after exposure to NLD, within 24 hours of pre-treatment and 12 hours of post-treatment. Madrid and colleagues demonstrated that the combination of NLD with cisplatin was more effective in inhibiting the growth of breast cancer MX-1 and ovarian cancer A2780 than cisplatin used alone [121].
5.13. Mebendazole
Mebendazole (MBZ) is a broad-spectrum anthelmintic drug and, taken orally, has been used in clinical practice worldwide since 1971 [102,104]. Some authors argue that benzimidazole derivatives can inhibit the polymerization of tubulins, which causes microtubular damage to parasitic cells. Tubulin plays a key role in cell division and is, therefore, an important target for chemotherapeutic drugs such as colchicine, paclitaxel, and vincristine. MBZ has been recognized as a potential antitumor agent and its mechanism of action is described as having the selective ability to bring cancer cells to a standstill in the G2/M phase by binding to the colchicine dominance in tubulin causing cell apoptosis [104]. Limited pre-clinical studies have been carried out to investigate the anti-cancer efficacy of MBZ in breast cancer cells. In one of these studies it was found that, after radiotherapy, the MBZ caused a mitotic catastrophe with DNA breaks and subsequent cell apoptosis of breast cancer cells. MBZ is a good candidate for drug reutilization [103].
5.14. Metformin
Metformin (Met) is a hypoglycemic drug that can reduce the incidence of various types of cancer in diabetic patients [114,122,123]. Met has suppressed tumor growth in xenoglycemics because it inhibits nuclear translocation of NF-κB and phosphorylation of STAT3 in cancer stem cells [114]. Cancers that increase in tissues and/or organs rich in white fat, such as the digestive tract, breast, and prostate, seem to benefit most from the administration of Met that targets these white fat progenitor cells in both in vitro and in vivo trials [123]. Currie and colleagues [124] and Landman and colleagues [125] reported that female diabetic patients receiving neoadjuvant chemotherapy for breast cancer had a higher complete pathological response rate if they also used Met compared to those who did not. Anisimov and colleagues [126] showed that the Met increased the life span and decreased the development of spontaneous breast cancers in HER-2/neu transgenic mice. Further studies on breast cancer cells showed that Met acts as a growth inhibitor and this inhibition was mediated by over-regulation of the activity of the protein kinase, which was activated by AMPK. Several studies suggest that Met exerts the direct antitumour activity that passes through the activation of AMPK which causes interference with the metabolism of cancer cells [122].
5.15. Methotrexate
Methotrexate (MTX) is the most widely used antifolate that interferes with thymine synthesis. The main target of MTX is dihydrofolate reductase (DHFR), which is responsible for reducing dihydrofolate (DHF) to tetrahydrofolate (THF) and is also a thymidylate synthase (TS) inhibitor, which catalyzes uracil methylation in thymine [127]. MTX is analogous to folic acid indicated for the treatment of leukemia, where it has shown its anti-cancer efficacy against some malignancies. The FDA has approved its use for the treatment of osteosarcoma, breast cancer, acute lymphoblastic leukemia, and Hodgkin's lymphoma [6].
5.16. Niclosamide
Niclosamide is an ancient anthelmintic drug used to kill worms in animals and humans. It is known to decouple mitochondrial oxidative phosphorylation during tapeworm death. Niclosamide also induces specific stem cell toxicity in breast cancer. A study of autophagic modulators revealed that niclosamide was a new inhibitor of rapamycin complex 1 signaling (mTORC1). The study by Wang and colleagues [128] showed that treatment of niclosamide resulted in the negative regulation of the target genes involved in the self-renewal of breast cancer stem cells [128].
5.17. Pimozide, Olanzapine and Trifluoperazine
All antipsychotic drugs (pimozide, olanzapine, and trifluoperazine) that may have chemically diverse structures and distinct affinity profiles to the recipient interfere with dopaminergic transmission, which is believed to underlie their effects in reducing the "positive" symptoms (e.g. delusions and hallucinations) of schizophrenia. The pharmacological actions measuring the cytotoxicity of antipsychotics have remained unclear. Most authors concluded that cytotoxicity is not related to the binding actions of antipsychotics to dopaminergic and serotonergic receptors because the concentrations of the drugs are often above those needed to saturate these receptors to induce cytotoxicity. Some studies show that sigma receptor antagonism can play an important role in cytotoxicity. The mechanisms involved in antipsychotic cytotoxicity may not only be changes in cholesterol metabolism but may also include effects on calcium homeostasis. Antipsychotics have a potent antagonistic action of calmodulin, which correlates with their cytotoxic potential. In antipsychotics used in combination with conventional chemotherapy, dosing regimens have to be different, as antipsychotics inhibit the resistance of multiple drugs as well as breast cancer resistance protein efflux pumps [129].
5.18. Tamoxifen
Tamoxifen is a modulator of selective estrogen receptors. Its effects are due to its anti-estrogenic activity, which is mediated by the competitive inhibition of estrogen binding to its receptors. Tamoxifen also inhibits the expression of estrogen-regulated genes, also prevents the cell cycle from advancing from the G1 phase, decreases cell proliferation, and can even cause programmed cell death [130]. Prospective chemoprevention studies have shown that tamoxifen and raloxifene modelers, which are aromatase inhibitors, can reduce the risk of breast cancer by 30α–65% [103].
5.19. Verapamil
Verapamil is a calcium channel blocker, mainly L-type, which inhibits the transmembrane flow of calcium ions and is used in the treatment of cardiac arrhythmias, angina, and cardiomyopathy. The ionic channels of specialized excitable cells play a role in the pathophysiology of cancers, through various mechanisms that control the proliferation of cancer cells by regulating various survival signaling pathways and membrane potential. Verapamil is also a first-generation inhibitor of glycoprotein P. Several studies have reported beneficial effects of verapamil which has an antiproliferative effect on the mouse model with breast cancer. Another study showed that verapamil potentiated the activity of tamoxifen in the MCF-7 cell line of this cancer. In any case, the studies are still contradictory as to the anti-cancer properties of verapamil [105].
6.
Mathematical models for cancer treatment
Currently, mathematical models have greater applications to investigate the phenomena related to specific cancers such as leukemia, glioma, breast and prostate cancers. Many mathematical oncology studies seek to integrate and calibrate the interdisciplinary models with the goal of validating them. The main function of mathematical oncology is to create models of the various cancer treatments, such as surgery, radiation therapy, chemotherapy, antiangiogenic therapy, virotherapy, immunotherapy, as well as their numerous combinations. When temporal data are available, ordinary differential equations (ODE) are sufficient. When spatio-temporal resolved data are present or the temporal dynamics are not sufficient to clarify the observed biomarker dynamics, partial equations (PED) are used and the number of variables and model parameters must be carefully determined and limited based on the available data [131].
6.1. Model to explore immunotherapy treatment alone or in combination
Although the empirical knowledge of cancer is an essential aspect of modelling cancer systems, the knowledge of exponential or Malthusian growth laws tumor cells is also necessary. In this context, Ordinary Differential Equation (ODE) models are applied in different contexts of oncology, whether at the theoretical or practical level. [132]. In this study Kirschner and Panetta [133] reviewed the literature and found that Kuznetsov and colleagues [134] had defined an ordinary differential equation (ODE) model for two main populations of cells: effectors and tumor cells. According to Kuznetsov and colleagues [134] it is possible to predict a threshold above which there is uncontrollable tumor growth and below which the disease is attenuated, with periodic exacerbations occurring every 3–4 months. These authors also presented a model of stable spirals, but this model is contrary to the Dulac-Bendixson criterion that focuses exactly on the planar system where the measure of initial conditions always shrinks with time, i.e., dynamical systems with vector fields whose divergence is always negative (or always positive). Other authors such as DeLisi and Rescigno [135] and Adam [136] have also considered ODE for immune and tumor cell populations and have shown that survival increases if the immune system is stimulated. In some cases, there is still an increase in effector cells that can lead to an increase in tumor survival. They were also able to reach the limit of uncontrolled tumor growth. In a study, Nani and Oguztoreli [137] developed a model of ACI (adoptive cellular immunotherapy) based on the work of Rosenberg and colleagues [138], whose stochasticity model was based on the immune interactions of the tumor. The results presented by this model were that treatment success depends on the initial tumor burden. Simulation of the treatment of aggressive tumors with immunotherapy indicated that ACI dominates. The authors did not take into account the sensitivity, bifurcation or stability analyses of the model. The model come up with by DeBoer and colleagues [139] is more detailed as it has ten or more differential equations along with three to five algebraic equations that describe most of characteristic involved in cancer progression or tumor immune dynamics. They showed tumor regression (in a highly antigenic tumor) and uncontrolled tumor growth (in a low antigenic tumor). Kirschner and Panetta [133] aimed to use the best ideas of the systems while keeping the model as simple as possible, incorporating the most important concepts of the dynamics of tumor immunology and IL-2 dynamics [133,140,141]. They defined three populations where effector cells, cytotoxic T cells and macrophages and NK cells that are cytotoxic to cancer cells are included. This model is applied to the single tumor site compartment and describes the interactions between effector cells, tumor cells and the cytokine (IL-2). This method, despite that, needs improvements. For this, we can consider a profile which is more mechanistic bases, utilize the time-dependent portion, role of other cytokines such as Interferon-c, IL-10, IL-12. Then include the combined effects of immunotherapy with chemo- and/or radiotherapy [133]. Arciero and colleagues [140] used the aggressive tumor model which in addition to describing the temporal changes in effector cells and IL-2 also incorporates the immunosuppressive and stimulatory effects of TGF-β. They also used another siRNA Treatment Model where they demonstrated an alternative immunotherapy approach where they used siRNA strands to suppress TGF-β production, thus getting traditional immunotherapy treatment to work again. They created a mathematical model where they included siRNA treatment that directly blocks TGF-β expression in tumor cells [142].
6.2. Radioimmunotherapy models
Radioimmunotherapy is more challenging to implement in cancer treatment. Given that several biological, physical and other complex factors interrelated, one needs to consider these factors in designing a successful protocol [142]. Mathematical models are used that integrate antibody pharmacokinetics in plasma, extravasation, interstitial transport, and antibody-antigen interaction. Fujimori and colleagues [143] and van Osdol and colleagues [144] investigated the connection between a variety of antibody-specific parameters, microscopic distribution and absorbed dose within the tumor. O'Donoghue and colleagues [145] devised a mathematical model of uniform tumor dosimetry that compared single and fractionated dose radioimmunotherapy over a time interval. Kumar [146] suggested a model for radioimmunotherapy, where he developed the radiotherapy dose distributions with respect to optimizing the probability of tumor cure and where the rate of its distribution was found to be high enough to stop instantaneously. The numerical results showed that tumor cell density and dose distribution are not sensitive to other functional forms of tumor parameters and immune response plays a critical role during cancer treatment [142]. Flux and colleagues [147] reported a 3-D dosimetry model where they quantified the amount of absorbed dose as a result of administration of a radiolabeled monoclonal antibody, showing the distribution of spatial and temporal heterogeneity. This model was tested using a recorded dataset of patients, where dose profiles and histograms of their volume were produced. Flux and colleagues [147] demonstrated that the 3-D dose distribution was not uniform [142]. Serre and colleagues [148] proposed a discrete-time mathematical pharmacodynamic model of the amalgamation of radiotherapy and immune checkpoint inhibitors, such as PD1-PDL1 and CTLA4. The model reveals how a growing tumor triggers and inhibits its immune responses and describes the effects of irradiation. This model is able to predict pharmacodynamic endpoints when analyzing data obtained from experimental studies using the combination of radiotherapy and immune checkpoint inhibitors. In silico studies should be compared by simulating Kaplan-Meier curves and mathematical tools and these can be used to partially automate the optimized protocols [142].
6.3. Immunovirotherapy models
Lai and Friedman [149] used a combination therapy with one drug as a vaccine to activate dendritic cells to stimulate more T cells to invade the tumor, while using another drug as a checkpoint inhibitor to suppress the cancer cells [142]. These authors developed a mathematical model using partial differential equations to examine whether the combination of treating two drugs given at certain levels or treating one drug with almost double the dose was better [142]. The model specifies the interaction of dendritic cells cancer cells, cytokines IL-I2 and IL-2 and introduces the concept of synergy between the developed drugs and a synergy map that suggests the proportion in which drugs should be administered in order to achieve the maximum tumor volume to be reduced under the constraint of a maximum tolerated dose. Mahasa and colleagues [150] described a mathematical model that explains the interactions between oncolytic viruses, tumor cells, normal cells, and the antitumor and antiviral immune responses. This model consists of the differential lag equations, with a discrete lag indicating the time required to trigger a tumor-specific immune response [142].
6.4. Radiovirotherapy models
Radiation therapy is most effective when used synergistically with oncolytic virotherapy. Tao and Guo [151] devised a partial differential equation model where they described cancer radiovirotherapy as a generalization of existing ODE models [142].
6.5. Mathematical models of targeted therapies
Abbott and Michor [152] did a comprehensive review on mathematical models for targeted therapy. Sun and colleagues [153] presented a stochastic model that uses a set of differntial stochastic equations to ascertain the dynamics of drug-sensitive cells, drug-resistant cells, and new metastatic cells. Owen and colleagues [154] created a spatio-temporal mathematical model, to stipulate the outcome of combining macrophage-based hypoxia targeted gene therapy with chemotherapy. The simulation results indicated that the combination of conventional drugs and macrophage-based targeted therapies worked synergistically and resulted in better anticancer effects than the individual effects of each of the therapies [142].
7.
Mathematical models used in chemotherapy alone or in combination
Mathematical models can be used to recognize potential cellular mechanisms from which synergy can be derived. Efforts have been made to find mechanistic models aimed at the synergy of anticancer therapeutics, where signaling networks with kinetic models and partial differential equation are considered, based on agents and various models. The models used are ordinary differential equations (ODE), which are described as the number of tumor cells changing as a function of time and drug concentration [155].
7.1. Chemoimmunotherapy models
There are a variety of mathematical models that have been designed to try to understand tumor-immune interactions and determine the elements of the immune system that play a critical role in the response to immunotherapy. Modern methods of cancer treatment utilize the ability to trigger the immune response. These models have played an important role in clinically observed phenomena such as tumor dormancy, uncontrolled tumor growth and oscillations in tumor size [142]. The first model that attempted to demonstrate immunotherapy-related effects using ordinary differential equations (ODEs) was given by Kirschner and Panetta [133]. Their study examined interleukin (IL-2) with adaptive immunotherapy developed through the dynamic equations and in it they explain the external influx of IL-2 and immune cells [142]. Chappell and colleagues [156] presented a mathematical model where they explore the interactions of immune cells and tumor cells by combining immunotherapeutic agents with chemotherapy and radiotherapy. Similar data presented by Deng and colleagues [157] were tested on the model through numerical simulations. The numerical results showed that the best combination was that of radiotherapy and immunotherapy, as it significantly reduced the tumor mass. This combination of radiotherapy and immunotherapy leads to an increase in the number of T cells that are activated compared to single therapies. Another mathematical model using ODEs highlighted the interaction between T, NK and CD8+ cells in different tumor cell lines [142].
7.2. Chemovirotherapy models
The use of viruses as targeted cancer therapy began in the early 20th century with several viruses already tested in humans and animals. There is a great diversity of mathematical models that attempt to understand and characterize viral dynamics. Currently there are few mathematical models created and studied to investigate the combination of chemotherapeutic drugs and viruses [142]. Malinzi and colleagues [158] developed and analyzed a nonlinear parabolic partial differential equations model to study the spatio-temporal dynamics of tumor cells under chemo-virotherapy treatment. This model used compartments of different densities of tumor cells infected and uninfected by a free virus and a chemotherapeutic agent. Numerical simulations confirmed that the combination of chemotherapeutic drugs with oncolytic viruses were more effective compared to any monotherapy [142]. Malinzi and colleagues [159] proposed a mathematical model using ODE and an optimal control for chemo-virotherapy. This model specified the interactions between tumor cells, immune response and treatment by combining virotherapy and chemotherapy. The combined effects of virotherapy and chemotherapy were examined using sensitivity analysis of model parameters and optimal control simulations showed that half of the maximum tolerated doses for chemotherapy and virotherapy optimized treatment outcomes. Malinzi [160] designed a mathematical model for chemivirotherapy where he used infusion methods of three drugs. The author compares his work efficacy with that of others, performed a mathematical analysis to predict the outcomes of oncolytic viruses in combination with chemotherapy, and compared the efficacy of each individual treatment modality [142].
7.3. Chemoradiotherapy models
The main advantages of using chemoradiotherapy, considering that there is no interaction between the two, are the use of cytotoxic drugs to combat the disease by irradiating the sites of seclusion, outside the radiation field. A study by Goldie and Coldman [161] used the stochastic model for alternating radiation and chemotherapy. This model was based on the first approaches for combination therapy and three compartments, stem cells, differentiation and end cells were used in the tumor growth model. This model integrated chemotherapy resistant, radiotherapy resistant and extra parameters to measure cells with joint resistance [142]. In another study developed by Beil and Wein [162] the mathematical model was designed to determine how best to sequence the three: standard therapies for cancer treatment: chemotherapy, radiation therapy and surgery. Differential equations were used to reproduce the growth of tumors and their metastases given that the behavior of primary and metastatic tumors is similar. The combination that showed the highest curative probability was surgery followed by chemotherapy and radiation therapy [142]. Ergun and colleagues [163] used a similar approach to find the optimal schedule, the doses of angiogenic inhibitors and radiotherapy that increase the clearance of the primary tumor. The mathematical model used two compartments of tumor cells and vascular endothelial cells and the radiation damage was reproduced with the linear quadratic widely determined by the fractionation schemes in the radiobiology society. This model did not consider the fact that radiation can cause vascular endothelial growth factor (VEGF) expression that attenuates endothelial cell destruction by radiation therapy. Ghaffari and colleagues [164] designed an ODE model where they considered chemotherapy and radiation therapy for metastatic cancer. This model examined the interaction between immune cells and cancer cells with chemotherapy [142].
7.4. Algorithms used in cancer treatment
Tang and colleagues [165] developed a new model called (Target Inhibition Inference using Maximization and Minimization Averaging) and aims to show its feasibility in systematically investigating the predictions of the model where they used experimental single and pairwise siRNA silencing studies. The model used functional data on drugs to construct the predictions of target matching. This model was used in studies of MCF-7 and MDA-MB-231 breast cancer cells and BxPC-3 pancreatic cancer cells and it was confirmed that the kinase targets predicted by TIMMA are important for cell survival individually or in combination. The construction of this algorithm indicated better predictive accuracy and computational efficiency than an existing algorithmic solution. In another study by Tang and colleagues [166] they ran a network pharmacology model to predict synergistic drug combinations. They used a stochastic simulation algorithm (SSA) to highlight the signaling pathways and implement and understand the mechanisms of action of the identified target interactions. The signaling network of the human breast adenocarcinoma cell line the model was built using this dynamic model to simulate the effect of perturbation of genes of interest on cell viability [142].
8.
Mathematical models used in the treatment of cancer with nanoparticles
Dogra and colleagues [167] reviewed various techniques of mathematical models that are useful for the field of cancer nanoparticles and answer questions related to nanoparticle interactions in providing information about the problem of low tumor delivery capacity of NPs. To describe the process of NPs when they reach the capillary walls and extravasate into the extravascular space, a discrete model is used. Pharmacokinetic models are used to describe the whole-body distribution and elimination of the NPs. Hybrid models describe the delivery capability of the nanoparticles into the tumor. Pharmacodynamic models describe the efficacy and toxicity of the NPs [167].
8.1. Kinetics model
Dell'Orco and colleagues [168] created a mathematical model to describe the kinetics of the competitive interaction of serum albumin (HSA), high density lipoprotein (HDL) and fibrinogen for binding with a 70 nm copolymer NP. This model is based on the law of mass action and consists of a system of three first-order linear differential equations that describe the interaction of each protein with the NPs [167]. The model is also used to simulate the evolution of the nanoparticle composition that depends on the constants of the rate of association and dissociation of the proteins that take time to reach steady state. The Vroman effect was demonstrated by the lower affinity of HSA for NPs. The model was modified to study the effect of the formation of the NPs on the target cell surface receptors, taking into account the kinetic, stoichiometric and geometric variables of the system. Using this model, they found that the most successful binding of the NP receptor depends more on the size of the NP than the number and size of peptides bound to the NP surface. Sahneh and colleagues [169], meanwhile, produced improvements to the model using population balance equations to derive the ordinary differential equations for the successive binding of HSA, HDL, and the fibrinogen to NPs, demonstrating the binding of a protein when the NP is covered with different proteins. This model presents a more realistic physiological scenario [167]. Zhdanov and Cho [170] to improve the model incorporated irreversible protein reconfiguration (denaturation) into the kinetic equations for adsorption and desorption of proteins on the NP surface. With this model they also studied the role of protein diffusion during the adsorption process, as the diffusion rate constant decreases at the solution-solid interface compared to mass. Zhdanov and Cho [170] also revealed that the rate limitations imposed by protein diffusion were negligible. Angioletti-Uberti and colleagues [171] developed a model based on dynamic density functional theory (DDFT) where they described the density evolution of systems subjected to Brownian dynamics that include the effects of particle interactions on protein adsorption kinetics. This model was used to learn about the temporal evolution of the protein density profile with respect to the NP-solution interface and the adsorption of proteins on the NP surface [167].
8.2. Continuum Models
Decuzzi and Ferrari [172] studied the longitudinal transport of nanotransporters in permeable and non-permeable capillaries using the Taylor-Aris theory of shear scattering. The model uses a convection diffusion equation. This equation states that NPs in blood are transported under the influence of blood flow driven by the pressure gradient (advection) and inherent Brownian motion (diffusion) [167]. Taylor (Taylor 1953) and Aris (Aris 1956) change the model as they introduced the concept of the effective diffusion coefficient (Deff) as a solution to the cross-section equation of a cylindrical tube of radius and the mean fluid velocity, and combined the contribution of convection and diffusion in the longitudinal dispersion of NPs and used Peclet's number. With this model they found that increasing hematocrit or vessel permeability causes a reduction in the effective diffusion coefficient of NPs and highlighted the implications for intravascular transport of NPs [167]. Tsoi and colleagues [173] performed a minimal model of the hepatic sinusoid in order to establish the clearance mechanism of hard nanomaterials by the liver, where they described the role of flow dynamics and physicochemical properties of NPs in the sequestration of NPs in the sinusoids. The model was expressed by the partial differential equation that defines the temporal evolution of NP density along the length of the channel. The equation is solved by the probability of NP sequestration in the channel [167].
8.3. Discrete models
Discrete models are used to study the margining of NPs in blood vessels. Decuzzi and colleagues [174] created a mathematical model of a spherical NP with a radius freely circulating in blood at a distance from the endothelial wall. This model also considered buoyancy, hemodynamics, van der Walls, electrostatics, and steric force interactions acting on the NP and was presented in a nonlinear differential equation [167]. The model determined the trajectory of the NP in the bloodstream and its velocity from marginalization and the time required to contact the endothelium. One of the limitations of the model was that it did not take into account the presence of the erythrocytes but it obtained interesting results. Decuzzi and Lee [175] explored NP marginalization using a computational model of erythrocyte and NP transport in blood capillaries using the immersed finite element method. Furlani and Ng [176], meanwhile, originated an analytical model specifically for magnetic NPs, where they studied their microvascular transport and capture under the influence of an external magnetic field. The model takes into account the magnetic and viscous forces that acted on the particles and solved the trajectory of the NPs in the microvessels, when they inserted the magnetic force (obtained by the Beffective dipolar moment method) and the fluidic force (obtained from Stoke's law) into Newton's second law of motion [167].
8.4. Hybrid models
The hybridized hydrodynamics model was based on NPs and blood cells where it demonstrated valuable information about the dynamics of NP movement within capillary flow and further disclosed new information about how NPs could be designed to increase extravasation [167]. This model was described using Navier-Stokes of the blood plasma flow within the capillary and was solved numerically to obtain the flow dynamics around different blood cells and NPs. Lee and colleagues [175] demonstrated that NPs ≤100 nm in diameter remained circulating with blood volume and reduced incidence and adhesion to the vasculature wall, while NPs 500 to 1000nm in diameter were more likely to move through the red blood cells towards the vasculature wall (margins) [167]. In an experiment, Müller and colleagues observed the similar feats of NPs size on the radial distribution of NP within the capillary and further demonstrated that particle shape, hematocrit and capillary diameter play important roles in the distribution and dynamics of NP within the capillary as well as NP extravasation [167]. The model showed that spherical NPs margin better, contrary to the observations of Lee and colleagues [175], Tan and colleagues [177] showed that rod-shaped nanoparticles have a higher binding capacity than spherical ones due to reduced drag and larger contact area. Decuzzi and Ferrari and colleagues used mathematical models to demonstrate the adhesion of NPs with the endothelium during the flow of NPs through the microvasculature. They explored the binding of spherical and non-spherical nanoparticles under the influence of hemodynamic displacement forces and non-specific and non-specific adhesive interactions of the NP-endothelial cell interface [167].
8.5. Pharmacokinetic models
The pharmacokinetic (PK) model occurs in organs and involves a set of phenomena called ADME (absorption, distribution, metabolism and excretion) of NPs. The classic PK approach deconstructs the body into a system of compartments that usually contain a central compartment that may be linked to others through constants[167]. ODEs are used to describe various PK processes, which have been fitted to the concentration-time data of NPs in plasma, urine or other tissues, where the numerical coefficient estimates and the relevant PK parameters such as half-life, clearance, distribution volume and mean residence time are obtained. This model is utilized, for example, for dosing regimen design, but its predictive ability is limited since it has no underlying physiological and mechanistic references. The two-compartment model is used to describe the systemic disposition of NPs. Classical PK approaches have been used to study NP delivery in solid tumors. Sykes and colleagues [178] modified the mathematical model developed by Schmidt and Dane Wittrup (2009) [179] for antibodies. This was used to predict the delivery efficiency of gold NPs [167].
8.6. Pharmacodynamic models
The pharmacodynamic model has been used to investigate the efficacy of NPs against cancer. This model is based on the hypothesis that the rate of cell death is a function of the total amount of drug ingested by the cells over time. The predictions of this model were validated with in vitro cell viability assays and where they demonstrated a superiority of drug delivery using NPs over free drug delivery, it was proven that the cell death rate was increased because drug delivery through NPs was more efficient. This model was also modified to incorporate the effect of spatial heterogeneities of diffusion and perfusion in solid tumors [167].
9.
Mathematical models to support the repurposing of pharmaceuticals
The efficient development of drug repurposing is a process of exchange of purposes, methods, and available information and, for its better understanding, computational mathematical models are used, of which the blind search or screening methods stand out, based on the target, knowledge, signature, pathway or network and the mechanism to which it is directed [180,181]. Currently, in silico models, it is still not known which is the best option for drug repurposing, and therefore various computational approaches can be used, such as those based on structure, transcriptional signatures, biological networks, and data mining [181]. Computational reuse of drugs has recently gained increasing interest in modern pharmacogenomic studies. Numerical computational approaches have been developed, taking full advantage of these high-throughput resources, for in silico prediction of disease-drug connectivity and drug-drug connectivity. CMap has demonstrated positive results for discovering new drugs reused to treat different types of diseases where they include obesity, neurodegenerative diseases, gastrointestinal and liver diseases, stroke, sepsis, and cancers [182].
9.1. Blinded search or screening methods
These drug repurposing methods do not include pharmaceutical or biological information and do not help to elucidate any mechanism of action of these drugs and their identification occurs fortuitously, through tests that target specific diseases and drugs. The advantage of these methods is that they include their use outside the initial FDA indication and phenotypic screening, which presents high flexibility for application to a large number of drugs and diseases. Through the phenotypic screening method, the FDA discovered 28 out of 75 small molecules and biologics between 1999 and 2008 [180].
9.2. Target-based methods
Target-based drug repurposing methods comprise high throughput and/or high content screening (HTS / HCS), both in vitro and in vivo, for a protein or biomarker of interest, in silico screening in drug or compound libraries, and also ligand-based screening or docking. Compared to the previous method this significantly improves drug discovery as most targets are directly linked to the disease mechanism. The integration of target information into the drug repurposing process allows researchers to screen almost any drug or compound with known chemical structure information, such as the Simplified Molecular Line Entry System (SMILES). Pharmaceutical companies, including Genentech and Melior, have used this method to find new indications for drugs [180].
9.3. Knowledge-based methods
Knowledge-based drug repurposing methods are those that apply bioinformatics and chemoinformatics approaches, where available information from these drugs, drug-target networks, chemical structures of targets and drugs, information from clinical trials (adverse effects), FDA approval, signaling or metabolic pathways, among others, are included. These knowledge-based methods, as they incorporate known information, can also help predict unknown mechanisms, unknown targets for drugs, and unknown similarities between drugs and novel biomarkers for disease. The advantage of these methods is that it includes a wide variety of known information in the process of drug repurposing to improve its prediction accuracy. These methods have been applied for the reuse of known drugs for pediatric hematological oncology [180]. Su et al. [183] described a method for drug reuse that uses a public database, ClinicalTrials.gov (HTTPS://clinicaltrials.gov/), and two text search tools I2E (Linguamatics) and PolyAnalyst (Megaputer). This method consists in the extraction of serious adverse events data, which allow identifying drugs that have fewer of these events in the test arm than in the control arm and also allow the classification of these drugs, thus enabling the discovery of potential drug candidates for diseases different from those of the test conditions [181].
9.4. Methods based on transcriptional signatures
Signature-based drug repurposing is also known as connectivity mapping, a concept first introduced with the creation of the Connectivity Map (CMap) database, which comprises a genome-wide dataset of transcriptional expression responses of human cell lines to perturbagens, e.g. chemical treatments or genetic perturbations [181]. Signature-based drug repurposing methods use gene signatures derived from omics data from disease with and without treatments to discover unknown targets or unknown disease mechanisms. The advancement of microarray and next-generation sequencing techniques generates a large amount of genomic data that is pertinent to the study of drug repurposing. Several genomic databases are publicly available such as Gene Expression Omnibus NCBI-GEO (http://www.ncbi.nlm.nih.gov/geo/), SRA Sequence Read Archive (http://www.ncbi.nlm.nih.gov/Traces/sra/), CMAP Connectivity Map, CCLE Cancer Cell Line Encyclopedia, Ensembl (www.ensembl.org/) and The Cancer Genome Atlas (TCGA; https://portal.gdc.cancer.gov/), [180,181]. The advantage of signature-based methods is useful in discovering unknown mechanisms of action of molecules and drugs. This method involves the mechanisms at the cellular level, such as the significantly altered genes using computational approaches [180]. Transcriptional signatures related to a disease or transcriptional responses associated with a specific treatment can be used for drug repurposing. Candidates can be identified by negatively correlating the gene expression profile of a disease with the transcriptional signature induced by a small compound, to find a drug that can reverse the disease state to the normal state. The positive correlation can be used to identify small compounds that have similar transcriptional signatures to a genetically or chemically induced perturbation to induce similar gene expression [181].
9.5. Route-based or network-based methods
Biological networks are data representations used to model biological interactions of any kind, where the "nodes" represent various biological components, such as genes or proteins, while the "edges" represent the associations between them. Some interesting examples are protein-protein interaction (PPI) networks and drug-target interaction (DTI) networks, [181]. Pathway- or network-based drug repositioning methods use disease data through available signaling or metabolic pathways and protein interaction networks to reconstruct disease-specific pathways that provide key targets for repurposed drugs [180,181]. The advantage of these methods is their utility in constraining the general signaling networks of a large number of proteins until a specific network with a few proteins (or targets) is reached [180]. PPI analysis can be performed with the PRISM (Protein Interactions by Structural Matching; http://gordion.hpc.eng.ku.edu.tr/prism) server or OmicsNet (https://omicsnet.ca/). DTIs are considered bipartite networks in which the "nodes" represent both drugs and targets. Several tools exist to predict potential DTIs such as DT-web (https://alpha.dmi.unict.it/dtweb/) or STITCH (http://stitch.embl.de/). Systems biology often combines different network models with quantitative mathematical network models to infer the dynamics of biological systems and thus provide a more complete perspective for drug reuse. Complex biological networks are found in the Causal Biological Networks database (CBN, http://causalbionet.com/) and complex biological pathways are found in the KEGG database (www.kegg.jp/) [181]. A drug repurposing study based on the network method addressed the signaling mechanism of distinct metastatic breast cancer subtypes [180].
9.6. Targeted mechanism-based methods
Mechanism-directed drug repurposing methods integrate data from treatment omics techniques, information from available signaling pathways, and protein interaction networks to delineate the unknown mechanisms of drug action. Drug reuse still needs to be studied to improve precision medicine. Drug resistance remains an unresolved issue in cancer therapy. Initially, patients respond well to therapy, but after some time (months), they eventually acquire resistance to these drugs. For drug treatment to be successful, more information is needed about their mechanisms of action to find better targets. The systems biology approach is promising in its approach to these challenges. The advantage of these methods is that their goals are not only to discover the mechanisms related to disease and drugs but also to identify those that are directly related to the treatment of specific diseases. There is some difficulty in deriving effective computational models, but there are also studies that have developed such models, managing to predict the effect of drugs and the target pathways that are related to them [180].
9.7. An example of bringing together the different methods used in cancer drug repurposing
The pathways or mechanisms responsible for breast cancer metastasis to the brain, bone, and lung are still unclear, which creates a challenge for drug repurposing for "this cancer subtype. Knowledge-based methods alone are not enough to solve this problem as they only provide general information or canonical pathways of breast cancer signaling, rather than those that are specific to various types of metastasis. In one study they combined the knowledge-based and network-based methods to reconstruct the signaling networks of metastatic breast cancer subtypes so that drug repurposing for each cancer subtype was feasible to implement. The knowledge-based method inserted known signaling network elements that are called cancer signaling bridges, to identify general known signaling information for breast cancer, while the network-based method used mathematical models to address the specific signaling networks for metastatic breast cancer subtypes. Through this study, they were able to identify two drugs, sunitinib, and dasatinib, and the efficacy of sunitinib for brain metastases from breast cancer was tested in phase II clinical trial (ClinicalTrials.gov ID: NCT00570908). Example: distinct breast cancer metastases + knowledge-based methods + network or pathway-based methods + drug libraries + in vitro and in vivo validations + clinical trials - sunitinib for brain metastasis [180].
9.8. Use of algorithms in the repurposing of drugs
Current algorithms are classified into four categories, such as 3D structure-based, similarity-based, network inference-based, and ML-based methods. Furthermore, drug reuse methods are characterized by three generic properties, such as the level at which interactions between compounds are considered, the type of computational approach used (stochastic or deterministic), and whether the method is network-based or not, this being dependent on the explicit use of topology properties to obtain additional information about the interactions. To improve the efficiency of these methods it is necessary to combine the different algorithms which lead to the implementation of more complex hybrid methods. All these algorithms rely on simple assumptions to define similar measures that are used as quantitative metrics to identify candidates and alternative targets. Usually, these algorithms provide a list of candidates that match a set of predefined criteria [184].
9.8.1. 3D structure-based methods
The 3D structure-based methods make the predictions of interactions by exploration, such as the chemical-protein interactome. These methods use the chemical structure files of the compounds to calculate docking scores and several molecular docking programs exist, such as Glide (www.schrodinger.com/glide), GOLD (www.ccdc.cam.ac.uk/solutions/csd-discovery/components/gold/), UCSF DOCK (http://dock.compbio.ucsf.edu/), AutoDock Vina (http://vina.scripps.edu/) or Ledock software [181]. A docking program was used to calculate the binding energy between a charged molecule and other drugs in the library. A second algorithm used was based on docking scores to calculate the association scores between the charged molecule and each drug in the library. An advantage of these methods is that the interaction can be analyzed for structural properties. Docking algorithms are computationally extensive and rely on structural files, which are not readily available [184].
9.8.2. Similarity-based methods
Many similarity measures have been implemented using biological, chemical, or topological properties of targets, drugs, and known interactions. Performance and predictive power vary according to the similarities used, and generally, the accuracy of similarity-based methods improves with the amount of data available. The results showed that not all similarity measures are equal to the type of information they had access to. Similarities based on topology or network do not provide information about the mechanism of action of the drug [184]. Algorithms that combine different similarity measures are more advantageous but require the use of different types of data. In one study where they used the disease-disease, drug-drug, and disease-drug network, this was set up to combine the molecular profiles of disease and drug expression. Two methods were used to calculate the similarity for pairs of genomic profiles [184]. The first was based on the similarity of the profile-profile correlations by calculating the Pearson correlation, using the values of the cyver-T statistic, of the two profiles. The second method was based on the concept of enrichment [185]. The combination of the two similarity measures was implemented by using the chemical similarity measure based on the relationships between the drug-related terms that were annotated with distinct but closely related terms and a phenotypic adverse effect similarity using the observation that there is a correlation between adverse effect similarity and the probability that two drugs share a target protein. The similarities are applied to infer a common target between the two drugs. The results of this study showed that the two methods combined are more sensitive than when applied separately. The similarity ensemble approach (SEA) relies on the chemical similarities between the drugs and the targets defined by their ligands to compare the targets by the similarity of the ligands that bind to them. The novel targets are considered biologically relevant if they meet at least three criteria such as the novel targets contribute to the primary activity of the drug, mediate the adverse effects of the drugs, and are unrelated by sequence, structure, and function of the canonical targets [184]. The network-based method is a new proximity measure that combines six different topological measures and uses topological structures called 'disease modules'. The disease module is formed by genes associated with a particular disease. The authors proposed the hypothesis that the drug is effective against disease if it has target proteins in the vicinity of the related disease module. The proximity measure performs better than six of the most common similarities. The proximity method is able to account for the high number of target interactions and is not biased as to the number of targets a drug may possess and their degrees, but access to disease genes and drug targets is required [184].
9.8.3. Inference-based methods
Inference-based methods use a priori knowledge about known interactions, referred to as the 'training set', to predict new interactions and suggest new targets for re-use. Two inference methods based exclusively on topology measures have been applied to predict associations between drugs and diseases [184]. In a work by Zhou et al. [186] the problem formulated was disease recommendation for a drug, exploiting already known data on the properties of a bipartite drug-disease network on experimentally verified drug-disease associations. Three methods based on different similarity measures were implemented [184]. The first used network-based similarity, the second used a drug-based approach, where the assumption is used that if a drug interacts with a target, then other drugs similar to that target will be recommended for that target. The third used a target-based approach, considering that if a drug interacts with the target then that drug is recommended for other targets with similar sequences [184]. The results demonstrated an advantage in using the network similarity-based algorithm. A Bayesian factor analysis was developed, based on the protein complex that modeled the chemical-genetic profiles, using these protein complexes to infer, by Bayesian inference, the mechanism of action of the drugs in the protein complexes. The hybrid DT algorithm improved Cheng's method [187] that uses a similarity matrix to directly connect the domain-dependent biological knowledge in the model. The similarity matrix was obtained by linearly combining a structure similarity matrix with a target similarity matrix. This method has a better performance in predicting significant biological interactions and outperforms other methods in retrieving deleted links. Although biological knowledge increases its performance and improves its numerical accuracy, the parameters introduced in the similarity matrix can lead to practical complications because its optimal value depends on the characteristics of the datasets and prior analysis is required for its selection [184].
9.8.4. ML-based algorithms
ML-based algorithms exploit similarity measures to create classification features and subsequent learning of a classification rule that distinguishes true and false "node" associations. Several ML methods have been published and their performance and predictive power have been improved by integrating additional algorithmic approaches to address the three challenges. There is another category of complex algorithms, whose configuration varies and depends on the datasets used. Novel targets are predicted [188] using multi-category Bayesian models trained on chemogenomic databases, while in [189], the authors used another ML method to investigate the extent to which the chemical characteristics of small molecules could be reliably associated with significant changes in gene expression [184]. A review of network-based ML models and their use for predicting compound-target interactions in both target-based and phenotype-based drug discovery applications has been published elsewhere. PREDICT is an example of an ML-based method for predicting new associations between drugs and diseases. Using a set of known drug-disease associations constructed through various sources as a training set, the algorithm classifies additional drug-disease associations based on their similarity to the known associations. Five drug-disease similarity measures and two types of disease-drug similarity measures were constructed in this step. Association scores were calculated in pairs of these similarity measures and were used by a logistic regression algorithm to construct classification features and subsequent learning of a rule that helps identify new associations between drugs and diseases [184]. This method can be applied to new molecules with information from the indication of use. To move forward, negative drug-disease associations had to be experimentally verified. Yamanishi et al. [190] investigated new interactions for four different classes of target drugs using the Kernel Regression Method (KRM) [184]. In this supervised learning method, biological information was integrated within a "pharmacological space", which combines chemical (drugs) and genomic (targets) spaces. A drug-target interaction network was then constructed for each protein class using a bipartite graphical representation. A regression model was also developed between the combined chemical structure, amino acid sequence-based similarity spaces, and the pharmacological space. The putative drugs and targets were mapped in the pharmacological space using this regression model and predictions of new interactions were made by binding drugs and targets closer to the threshold in the pharmacological space [184]. Dai et al. [191] suggested a matrix factoring model taking advantage of the richness of interaction data to detect potential drug-dissociation rather than following like others, the usual computational approach in matching a drug to disease profiles [184]. This method works in two steps. First, a gene interaction network was constructed and topology information was extracted from this genomic space by computing a gene proximity metric. Using this information, the low-ranked feature vectors were retrieved from the gene interaction network using eigenvalue decomposition. The drug and disease feature vectors were obtained from the gene-drug and gene-disease interactions, respectively. The matrix factoring model was then generated and used to approximate known associations between drugs and diseases. This model provided an estimate of the possibility of an association between a given drug and the disease. After the training phase, the model was used to predict new drug indications [184]. The integration of topology information allowed this method to perform better than others. When drug or disease association information is rare it may remain limited by the availability of gene-drug interactions and gene-disease interactions, necessary for accurate measurement of feature vectors. A specific class of methods, called local bipartite models (BLMs), has been developed [192] using similarity measures in the form of kernels. The advantage of these methods is that they allow the incorporation of multiple sources of information in making predictions [184]. The BLM was constructed from the detection of drug-target interactions through training that comprised two classes: all targets known in the drug search except the target of interest and targets for which no drug interaction was known. A support vector machine (SVM) was then constructed that discriminated between the two classes, using the genomic kernel available for the targets. This model was used to predict the target identification and determine the drug-target pair, considering that they share an interaction. Using the chemical structure kernel, the procedure was applied with the roles of the drugs and targets reversed, combining the two results [184]. BLM was also investigated by van Laarhoven et al. [193] but its implementation is different as the Gaussian kernel was constructed to be exclusively used with the topology information and regularized least squares (RLS) classifiers instead of SVM [184]. The method works from the known target drug-drug interactions used to generate interaction profiles from which a Gaussian interaction profile (GIP) kernel was constructed. The predictive power was improved by combining the GIP kernel with a kernel representation of chemical structure similarity between compounds and sequence similarity between proteins. These interaction profiles were used as feature vectors for two types of RLS classifiers [184]. They concluded that the method provides more accurate results when the GIP kernel is combined with chemical and genomic kernels, especially for small datasets. They noted that sequence similarity for targets was more informative than chemical similarity for drugs. Despite the promising results the authors pointed out that the method was sensitive to inherent biases contained in the training data and that it can only be applied to detect new interactions for a target or drug for which at least one interaction is already known. Mei and colleagues have launched a method called BLM-NII [192], which combines a BLM with a procedure called 'neighbour-based interaction profile inference' (NII), and is designed to work with the inability to provide predictions for drugs and target those that are new. This technical problem is known as the 'new candidate problem' of BLM [184]. The NII procedure made the classifier capable of incorporating new information and 'learning from its neighbour' into the original BLM method. Comparisons with previous methods demonstrate the ability of BLM-NII to predict interactions between new drug candidates and new target candidates with high reliability [184].
10.
Optimal control analysis of a mathematical model of breast cancer
Mathematical models have over time been used in the optimal choice of a combination therapy or to improve the delivery of antitumor drugs. These have become an important tool in understanding breast cancer dynamics and making decisions about medical intervention. Oke and colleagues [194] used a four-dimensional deterministic compartmental model that was designed and used to track breast cancer dynamics. Optimal control analysis of the model performed and optimal disease control conditions to control tumor cell metastasis [194,195,196] that used deterministic continuous-time models of tumor growth and treatment are obtained using Pontryagin's maximum principle. In addition, the authors applied classical optimal control theory to determine enhanced chemotherapy administration regimens. Also, we can consider that the principal model was developed from combining some valuable features of existing models and exhibits qualitative behavior that reproduces the "Jeffs phenomenon" and tumor dormancy. The Jeffs phenomenon is a clinically observed temporal oscillation in tumor size that is not synchronized with chemotherapy administration. The chemotherapy protocol was formulated as optimal control with constraints, through the fixed time interval, to find those points at which the drug should be administered so that the number of tumor cells is minimized and the number of healthy cells is kept above the threshold. The optimal control theory is derived from the Hamiltonian for the optimal control problem. The optimal control protocol allowed the tumor size to oscillate with a larger amplitude, resulting in a smaller tumor mass, in the final time of the prescribed treatment [195]. Mathematical models based on ordinary differential equations, delay differential equations and partial differential equations prove to be useful tools in analyzing and understanding the interactions of the immune system with viral, bacterial and cancer cell infections. Rihan [196] used a mathematical model through the interactions of the tumor with the immune system in the presence of chemotherapy treatment and optimal control variables. These variables were incorporated to justify the best treatment strategy and decrease the side effects of external treatment by decreasing the production of new tumor cells and maintaining the number of normal cells above their capacity limit. They also used numerical approximations of the optimal control problem using Euler methods [196].
11.
Conclusions
We can therefore say that breast cancer is a complex disease that may involve a wide variety of pathways and molecules, which makes its treatment a constant challenge, the target of many and varied studies [105]. To achieve promising results in the treatment of this cancer, it is necessary to use the different approaches that are emerging from these studies, alone or in combination, such as immunotherapy, virotherapy, the use of nanoparticles targeted at this cancer, and the reuse of different drugs and the combination of these drugs [42]. There are still no targeted therapies for the specific treatment of TNBC, which, of course, will be reflected in a decrease in patient survival time and a worse quality of survival. To make cancer treatment faster and more effective, one of the main approaches suggested is the use of reused drugs, since the development of new drugs and their testing is a long and costly process. Drug repurposing currently includes different computational methods, mathematical models, and in-silico studies. These methods, even though they are already being applied, still require many studies to make them more accurate, so that they can be validated and standardized, thus achieving better reuse in a medicine directed to the patient [181]. Recently, the possibility of applying CRISPR techniques has been studied to more effectively treat metastatic breast cancer, which is considered one of the most difficult cancers to treat [30]. It is concluded, therefore, that breast cancer still requires many studies and new techniques, including those of artificial intelligence, mathematical models, and computer algorithms, among others that may be improved, always aiming for shorter and more effective treatments, with cost reduction.
Acknowledgments
This work was financed by FEDER - Fundo Europeu de Desenvolimento Regional through the COMPETE 2020 - Operational Programme for Competitiveness and Internationalization (POCI), Portugal 2020, and by Portuguese funds through FCT - Fundação para a Ciência e a Tecnologia, in a framework of the projects in CINTESIS, R & D Unit (reference UIDB/4255/2020. N.V. also thanks support from FCT and FEDER (European Union) award number IF/00092/2014/CP1255/CT0004.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: