A genetic regulatory network based method for multi-objective sequencing problem in mixed-model assembly lines

1.   Introduction

Mixed-model assembly line (MMAL) is one of the most popular production systems in manufacturing industry because it can assemble various product models in an intermixed sequence while reducing setup times ^[1,2,3]. In MMAL, a well arranged model sequence brings considerable economic benefits to enterprises and thus attracts a lot of research efforts ^[4,5,6]. This sequencing problem generally has two fundamental goals, i.e. leveling the load on each station and keeping a constant rate of usage of every part ^[7]. In addition, the goal of minimizing setup times is also crucial in some MMALs because the stations might spend a long time on model changeovers. Based on above facts, this paper deals with the multi-objective sequencing problem in MMALs.

For MMAL sequencing problems, mixed-model sequencing, car sequencing and level scheduling are three alternative approaches that have been initially proposed to realize single objective ^[8]. Car sequencing achieves workload balancing in an implicit manner by formulating some general rules ^[9,10], whereas mixed-model sequencing and level scheduling generate a detailed problem solution to realize workload balancing and stable part usage, respectively ^{[11,12,13,14]}. Of these approaches, car sequencing has been mainly applied to MMAL sequencing problems in the automobile industry. As part of the famous ''Toyota Production System'', level scheduling and mixed-model sequencing have attracted wide attention in research and practical applications. Because of their similar mathematical model, these approaches also deal with multiple objectives by developing enhanced algorithms for some more comprehensive mathematical models ^[17,18]. For instance, Mansouri ^[15] developed a genetic algorithm to minimize both the variation of production rates and the number of setups. This problem was also investigated by using simulated annealing algorithm, Kohonen self-organizing map and ant colony optimization ^{[16,17,18,19]}. Hyun et al. ^[20] proposed a genetic evaluation and selection mechanism to realize three objectives: (1) minimizing total utility work, (2) keeping a constant rate of part usage, and (3) minimizing total setups. On this basis, Tavakkoli-Moghaddam and Rahimi-Vahed ^[21] proposed a memetic algorithm to minimize the weighted sum of these objectives, whereas Chutima and Naruemitwong ^[22] employed Pareto biogeography-based optimization with a learning effect to deal with these objectives. In general, sequencing rules are rarely employed because they can hardly be coordinated for an integrated optimization of multiple objectives, whereas metaheuristic algorithms are widely-used because their general computing procedure realizes more comprehensive consideration of each objective. However, when solving large-scale problems, metaheuristic algorithms could hardly obtain high-quality solutions without a great deal of computational efforts.

Since various networked systems have been employed to deal with complicated practical problems, for instance, networked control systems that deal with actuator saturations and stochastic cyber-attacks ^[23,24], supply networks for retailing and power industry ^[25,26], this paper attempts to solve multi-objective sequencing problems by modelling and optimization of a proper networked system. Inspired by genetic regulatory network (GRN) that originates from the biological area to describe the complicated regulation mechanism in cells, a GRN-based sequencing method is proposed to realize a good balance between solution quality and computational efforts. Its main contribution is the innovative use of gene regulations to describe compound sequencing rules for multiple objectives. This description enables effective minimization of weighted sum of these objectives through regulatory parameter optimization in the GRN. The remainder of this paper is organized as follows. The mathematical model of multi-objective sequencing problems is presented in Section 2. The GRN-based sequencing method is given in Section 3. Section 4 contains experimental results and discussions. Conclusions and future research directions are discussed in Section 5.

2.   Problem description

Following assumptions are taken into consideration in the sequencing problem:

(1) The assembly line is a "moving line" in which the conveyor moves at a constant speed;

(2) The workers move downstream with the conveyor while operating on a product;

(3) The length of a station is a fixed one (measured by a product's passing time), and neighboring stations do not overlap;

(4) The stations are all closed stations in which workers cannot walk across station boundaries;

(5) Products are equi-spaced on the line by launching each other after a constant time interval, which is known as the cycle time;

(6) The operation processing times of each station are not longer than the station length;

(7) The impacts of unfinished works on succeeding stations are not taken into consideration;

(8) The workers return with infinite velocity to subsequent products.

The notations listed in Table 1 are used in the mathematical model.

Table 1.  Problem's notations.

Notations	Definitions
Sets
{1, …, t, …, T}	Set of products in a Minimum Part Set (MPS) production
{1, …, k, …, K}	Set of stations
{1, …, m, …, M}	Set of models
Parameters
lk	Length of station k (time unit)
pmk	Operation processing time of model m at station k (pmk≤lk)
dm	Demand for products of model m in a MPS production, $\sum\nolimits_{m = 1}^M {{d_m}} = T$
Cmps	Total processing time required in a MPS production, ${C_{mps}} = \sum\nolimits_{m = 1}^M {{d_m}} \sum\nolimits_{k = 1}^K {{p_{mk}}}$
c	Cycle time (standard time assigned to a station to process any product), $c = {C_{mps}}/\left({T \times K} \right)$
wk	Utility work cost per unit time at station k
vtm	Production rate variation cost of model m when assembling the tth product in model sequence
ukmr	Setup cost at station k when the product changes from model m to model r
Variables
stk	Starting time for assembling the tth product in a model sequence at station k
etk	Extra operation processing time for the tth product in a model sequence at station k (utility work)
xtm	Binary decision variable: 1, if the tth product in a model sequence belongs to model m; 0, otherwise

---

 | Show Table

DownLoad: CSV

The mathematical model takes the following form:

If the workers fail to finish the operation tasks of a product before reaching the down-stream station border, a work overload situation occurs. The unfinished operation part, also called utility work, is typically handled by utility operators at the expense of increased labor cost. Eq 7 evaluates the total utility work costs. The assembly line should also achieve a constant production rate of each model to decrease the inventory cost of different product components. Based on this requirement, Eq 8 evaluates the total production rate variation costs. Moreover, some stations might require a setup operation when two consecutive products belong to different models. Thereupon, the objective value in Eq 9 evaluates the total setup costs. In Eq 1, these objectives are combined in a weighted sum function by using parameters ${\lambda _1}$, ${\lambda _2}$ and ${\lambda _3}$ ($0 \le {\lambda _1}, {\lambda _2}, {\lambda _3} \le 1$).

Apart from these objective functions, Eq 2 ensures the model sequence to satisfy the demanded quantity for each product model. Eq 3 makes sure that exactly one product is assigned to each position of the model sequence. Eq 4 defines the initial state of stations. Eq 5 describes the station state during MMAL production. Eq 6 gives the utility work of the tth product of the model sequence at station k.

3.   Genetic regulatory network-based sequencing method

GRN is a representational structure that describes the complicated interaction between gene expression in cells ^[27,28]. It has been widely applied by biologists to investigate the dynamic change of cell morphologies, and has become a hot topic in the past few years. A GRN has at least three elements in common: genes, gene regulations and gene expression procedure. Each gene has two alternative states, i.e. the expressed state and the unexpressed state. If a gene is in the expressed state, it has regulatory effects on the states of other ones, which is the primary form of gene regulations. Such regulations enable gene expression procedure to convert some unexpressed genes into the expressed state if the regulatory effects on them are positive enough. Based on components (e.g. mRNAs and proteins) copied from expressed genes, gene expression procedure finally determines cell morphologies. Various formalisms have been developed to describe a GRN, including Bayesian networks, directed graphs, partial differential equations, Boolean networks, qualitative differential equations, stochastic equations, and rule-based formalisms ^[29].

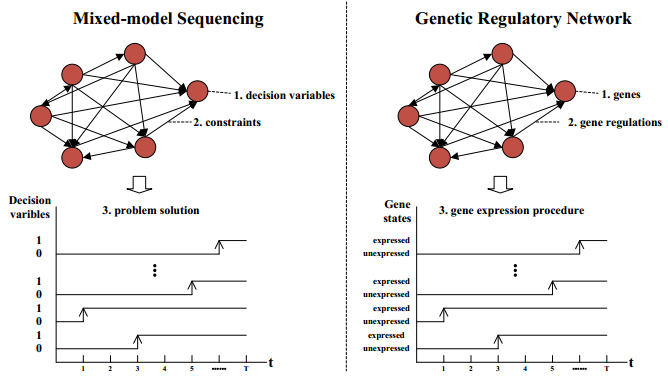
GRN has several similarities with the mathematical model of sequencing problems. Gene states and decision variable values are both binary. Gene regulations describe the interconnection between genes, whereas the constraints define the interconnection between decision variables. Gene expression procedure determines cell morphology based on gene regulations, while the model sequence determines MMAL performance based on constraints and some sequencing rules. These similarities enable the development of a GRN based on the mapping relation illustrated by Figure 1, in which a differential equation is specially used to give the gene regulations in a quantitative form.

Figure 1.  Mapping relationship between mathematical model and GRN.

DownLoad: Full-Size Img PowerPoint

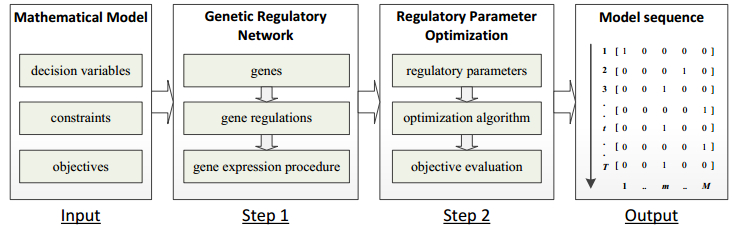
In this GRN, gene expression procedure generates a good solution if the differential equation describes all the constraints and appropriate sequencing rules. Moreover, this equation realizes reasonable integration of sequencing rules if its regulatory parameter optimization can minimize the weighted sum of production costs. Consequently, the GRN-based sequencing method contains two major steps, as shown in Figure 2.

Figure 2.  Outline of GRN-based sequencing method.

DownLoad: Full-Size Img PowerPoint

Step 1: Constructs the GRN:

Step 1.1: Generates a set of genes, each of which represents a decision variable;

Step 1.2: Designs a gene regulation equation to describe all the constraints and some sequencing rules;

Step 1.3: Designs a gene expression procedure that determines decision variable values based on the gene regulation equation.

Step 2: Optimizes the GRN:

Step 2.1: Designs a regulatory parameter optimization mechanism for the gene regulation equation;

Step 2.2: Generates some solutions determined by varied regulatory parameter values;

Step 2.3: Outputs the solution with minimum weighted sum of production costs.

3.1.   Genetic regulatory network

3.1.1.   Genes

Based on decision variables in the mathematical model, genes $\{ {\psi _{tm}}|t = 1, \cdots, T;m = 1, \cdots, M\}$ are defined in the GRN. Each gene ${\psi _{tm}}$ denotes that a product of model $m$ is assigned to the $t$th position of a model sequence.

3.1.2.   Gene regulation

Based on Eqs 2 and 3, gene regulations first describe following constraints for each position of the model sequence: (ⅰ) a model cannot be selected if other models have been selected yet; (ⅱ) a model cannot be selected if the demand quantity for this model has already been satisfied at former positions. Moreover, some sequencing rules generalized from the study of Cano et al. ^[30] are also included: (ⅲ) a model can be selected if it causes the least work overload at stations; (ⅳ) a model can be selected if it leads to the least idle time at stations; (ⅴ) a model can be selected if its current production ratio best matches its demand ratio in the MPS; (ⅵ) a model can be selected if it results in the least setup costs at stations. No model sequence could satisfy all these rules completely, and each unsatisfied case might increase the production costs. Following regulation equation is thus developed:

Where ${\theta _{tm}}$ represents the inhibition coefficient of converting gene ${\psi _{tm}}$ to the expressed state, ${x_{tm}}$ is a binary variable that is equal to 1 if gene ${\psi _{tm}}$ is in the expressed state, otherwise, it is equal to 0, $H(x)$ is a step function satisfying $H(x) = 0{\text{ }}(x \leqslant 0)$ and $H(x) = {\text{ + }}\infty {\text{ }}(x > 0)$, $\phi (x)$ is a piecewise function satisfying $\phi (x) = 0{\text{ }}(x < 0)$ and $\phi (x) = x{\text{ }}(x \geqslant 0)$. The first two terms of the right side of Eq 10 indicate regulation segments resulted from constraints (ⅰ) and (ⅱ), respectively. The last four terms of the right side of Eq 10 describe rules (ⅲ) to (ⅵ), respectively. ${\varepsilon _1}$, ${\varepsilon _2}$, ${\varepsilon _3}$ and ${\varepsilon _4}$ are regulatory parameters weighting different regulation segments.

3.1.3.   Gene expression procedure

Based on Eq 10, gene expression procedure determines the product model at each position of the model sequence iteratively. At each discrete time $t \in \{ 1, 2, \cdots, T\}$, ${\theta _{tm}}$ is calculated for genes $\{ {\psi _{tm}}|m = 1, \cdots, M\}$, and the gene ${\psi _{t\ddot m}}$ with minimum ${\theta _{tm}}$ is converted to the expressed state (i.e. ${x_{t\ddot m}} = 1$). When $t > T$, the model sequence is obtained based on gene states $\{ {x_{tm}}|t = 1, \cdots, T;m = 1, \cdots, M\}$. Table 2 presents the pseudo codes of gene expression procedure of ${\psi _{tm}}$.

Table 2.  The expression procedure of gene ψ_tm.

//initialization for t←1 to T do for m←1 to M do     xtm←0                // all the genes are initialized in the unexpressed state next; next; //gene expression circulation for k←1 to K do   s1k←0                // initialization of stations next; for t←1 to T do                //discrete time m0←1, θ0←+∞                 //index of the gene with minimum θtm     for m←1 to M do         calculate θtm in Eq 10         if θtm < θ0 then             m0←m                //update index             θ0←θtm                //update the minimum θtm         end if;     next;     xtm0←1                // convert the gene with minimum θtm to the expressed state     for k←1 to K do         calculate s(t+1)k in Eq 5                //update station status next; next;

---

 | Show Table

DownLoad: CSV

3.2.   Regulatory parameter optimization

Based on this established GRN, regulatory parameters ${\varepsilon _1}$, ${\varepsilon _2}$, ${\varepsilon _3}$ and ${\varepsilon _4}$ determine a feasible solution to the sequencing problem. A real-coded genetic algorithm (RCGA) is further designed to optimize these parameters, as illustrated in Figure 3.

Figure 3.  Real-coded genetic algorithm for regulatory parameter optimization.

DownLoad: Full-Size Img PowerPoint

First, the initial population of $N$ individuals is generated randomly. Each individual has its chromosome composed of regulatory parameter values (i.e. ${\varepsilon _1}$, ${\varepsilon _2}$, ${\varepsilon _3}$ and ${\varepsilon _4}$). These values determine a specific model sequence (i.e. $\{ {x_{tm}}|t = 1, \cdots, T;m = 1, \cdots, M\}$) based on the established GRN, and evaluate the chromosome fitness with related production cost. Assuming that the current generation is $r$ and the current population is represented by $P(r)$, then individuals from $P(r)$ are selected in accordance with their fitness. These selected individuals will be placed into a mating pool where the genetic operations of crossover and mutation are performed. During these operations, each individual has a specific possibility (denoted by PMutation) to reinitialize the value of a randomized position in its chromosome, and has a possibility (denoted by PCrossover) to change the values of first two positions of its chromosomes with another random individual. All these newly generated individuals are then collected to form the population $P(r + 1)$ for next generation $r + 1$. If the best fitness value in current generation is not better than that in the previous generation, then the iteration is terminated.

4.   Comparative experiments

To validate the proposed method, comparative experiments are constructed based on following assumptions:

(1) The objectives have the same importance weights, i.e. ${\lambda _1}{\text{ = }}{\lambda _2}{\text{ = }}{\lambda _3}{\text{ = }}1$.

(2) The utility work cost per unit time is equal to 1 at each station, i.e. ${w_k}{\text{ = }}1$ for $k = 1, 2, \cdots, K$.

(3) The production rate variation costs are equal to 1, i.e. ${v_{tm}}{\text{ = }}1$ for $t = 1, 2, \cdots, T$ and $m = 1, 2, \cdots, M$.

(4) Setup costs are taken into account only at the first station, i.e.${u_{kmr}} = 0$ for $k = 2, 3, \cdots, K$, $m = 1, 2, \cdots, M$ and $r = 1, 2, \cdots, M$.

An Intel(R) Core(TM) i7-2720QM CPU @ 2.20GHz, and 8.00 GB RAM based notebook computer is used to run the experiments. Table 3 lists the minimum part sets (MPSs) of a series of problems collected from reference instances ^[26] (Block I and Block Ⅱ) as well as industrial instances (Block Ⅲ). For each problem, the number of feasible solutions is calculated:

Table 3.  MPSs of different problems.

Block	Problem	MPS	Nf
Ⅰ	1	(4, 3, 2)	1260
	2	(3, 5, 1)	504
	3	(5, 3, 2)	2520
	4	(4, 4, 2)	3150
	5	(4, 3, 3)	4200
	6	(4, 6, 1)	2310
	7	(6, 3, 2)	4620
	8	(5, 3, 3)	9240
	9	(6, 4, 2)	13860
Ⅱ	1	(4, 4, 4, 5, 3)	2.44 × 1011
	2	(5, 3, 3, 4, 5)	1.95 × 1011
	3	(6, 2, 2, 5, 5)	5.87 × 1010
	4	(6, 6, 6, 7, 5)	1.18 × 1018
	5	(7, 6, 4, 6, 7)	8.39 × 1017
	6	(8, 9, 8, 7, 8)	6.80 × 1024
	7	(9, 9, 7, 7, 8)	6.05 × 1024
Ⅲ	1	(6, 3, 4, 3, 9, 7, 9, 3, 8, 8)	4.84 × 1052
	2	(6, 8, 7, 7, 4, 5, 9, 3, 8, 3)	1.34 × 1052
	3	(5, 8, 5, 6, 8, 9, 2, 6, 8, 3)	2.56 × 1052
	4	(8, 5, 5, 8, 7, 5, 7, 3, 3, 9)	1.12 × 1052
	5	(10, 4, 3, 6, 7, 6, 7, 5, 7, 5)	6.00 × 1053
	6	(3, 5, 8, 5, 8, 7, 3, 8, 6, 7)	7.47 × 1053
	7	(3, 8, 4, 3, 6, 3, 9, 4, 10, 10)	2.07 × 1051

---

 | Show Table

DownLoad: CSV

Where ${d_m}$ is the demand for model $m$ in the MPS. Two well-known sequencing methods, i.e. memetic algorithm (MA) ^[26] and ant colony optimization (ACO) ^[31], are used to provide benchmark results.

4.1.   Reference instances

Based on N_f, reference instances are classified into small-sized problems in Block Ⅰ and large-sized problems in Block Ⅱ.

4.1.1.   Small-sized problems

Small-sized problems are based on a MMAL composed of four stations. Table 4 lists the processing times of three product models (A, B, C) at these stations (s₁, s₂, s₃, s₄) and their station lengths. Table 5 gives setup costs at the first station. To solve these problems, the GRN-based method sets RCGA parameters as N = 50, r ≤ 50, Pmutation = 0.1 and Pcrossover = 0.8 after a parameter analysis, whereas MA parameters and ACO parameters are obtained from references ^[26,31]. Table 6 presents the minimum value ("Min" column), the maximum value ("Max" column), the average value ("Ave" column) and the standard deviation ("STD" column) of weighted production costs (adimensional) obtained by these methods over 20 replications.

Table 4.  Processing times and station lengths.

Station	Model			Station length
	1	2	3
1	4	8	7	12
2	6	9	4	14
3	8	6	6	12
4	4	7	5	11

---

 | Show Table

DownLoad: CSV

Table 5.  Setup costs at the first station.

Model	Model
	1	2	3
1	0	1	2
2	3	0	1
3	2	3	0

---

 | Show Table

DownLoad: CSV

Table 6.  Comparison of solution quality for small-sized problems.

Problem	GRN-based method				Memetic algorithm				Ant colony optimization
	Min	Max	Ave	STD	Min	Max	Ave	STD	Min	Max	Ave	STD
1	19.4	19.4	19.4	0	19.4	19.4	19.4	0	19.4	23.97	22.4	1.23
2	21.42	22.27	22.18	0.34	21.07	21.42	21.32	0.13	21.07	22.64	21.56	0.59
3	23.39	23.79	23.51	0.19	23.39	24.32	23.67	0.47	23.39	26.24	24.52	0.84
4	22.01	22.01	22.01	0	22.01	22.66	22.48	0.15	22.01	24.86	23.17	1.09
5	21.05	21.05	21.05	0	21.05	21.42	21.15	0.23	21.05	24.03	22.75	0.76
6	25.1	25.1	25.1	0	23.91	24.1	23.97	0.11	24.93	26.36	25.85	0.46
7	27.9	27.9	27.9	0	27.9	28.14	27.97	0.08	27.9	31.44	29.44	0.99
8	25.78	25.99	25.89	0.11	24.5	25.48	24.6	0.4	25.48	30.14	26.97	1.49
9	27.64	27.64	27.64	0	26.84	27.05	26.92	0.22	27.05	33.51	30.18	2.06

---

 | Show Table

DownLoad: CSV

As shown in the "Min" column, the GRN-based method achieves the same objective function value with MA in some problems, but fails in other ones. These results reveal that the GRN-based method cannot generate the optimal solution for some instances owing to its predetermined sequencing rules, while MA is a kind of global searching algorithm that can find out the optimal solution from a small number of feasible solutions. ACO also fails to realize the minimum objective value in some problems because its constructive procedure might trap in the local optimum when the number of ants is not adequate. In addition, the results in the "STD" columns demonstrate that the stability of the GRN-based method is better than that of MA and ACO in most problems. This is because the predetermined sequencing rules enable regulatory parameter optimization to search among good solutions, rather than all the feasible ones in other methods.

4.1.2.   Large-sized problems

Large-sized problems are based on a MMAL consisting of 10 stations and assembling five product models (A, B, C, D, E) ^[26]. Assembly times (p_mk), station lengths (l_k) and setup costs (u_kmr) are generated from uniform distributions U(4, 9), U(12, 15), and U(1, 3), respectively. To solve these problems, the GRN-based method sets RCGA parameters as N = 100, r ≤ 50, Pmutation = 0.2 and Pcrossover = 0.8. MA parameters and ACO parameters are obtained from references ^[26,31]. Table 7 presents experimental results obtained by these methods over 20 replications.

Table 7.  Comparison of solution quality for large-sized problems.

Problem	GRN-based method				Memetic algorithm				Ant colony optimization
	Min	Max	Ave	STD	Min	Max	Ave	STD	Min	Max	Ave	STD
1	93.72	94.68	94.12	0.32	93.87	97.59	95.64	0.68	93.02	100.33	96.23	2.01
2	94.24	94.9	94.45	0.17	94.28	98.9	96.21	1.25	99.08	101.7	99.96	0.79
3	93.14	95.02	94.63	0.34	93.19	96.78	95.27	1.38	95.79	99.4	97.57	1.3
4	129.36	132.7	130	1.3	135.05	142.17	137.85	2.37	137.51	142.86	139.77	1.85
5	131.35	133.19	132.23	0.49	137.38	144.24	141.32	2.07	140.6	146.98	143.09	1.83
6	159.46	161.95	159.81	0.79	172.58	181.28	177.18	2.57	173.97	185.98	182.34	4.23
7	165.53	166.48	166.11	0.49	176.58	184.97	182.27	3.06	177.32	185.81	181.61	2.64

---

 | Show Table

DownLoad: CSV

As shown in the "Min" column, the GRN-based method achieves the best results for problems 3, 4, 5 and 7, whereas MA and ACO achieve the minimum objective value in other problems. These results reveal that the global searching procedure in MA and the constructive procedure in ACO cannot ensure the optimal solution when the number of feasible solutions is increased. In contrast, the GRN-based method realizes each objective to a certain level by using sequencing rules and makes reasonable tradeoff between these objectives through regulatory parameter optimization. Although this procedure might not find out the optimal solution, it can obtain near-optimal solutions that are in some cases even better than those obtained by MA and ACO. In addition, the "Ave" column and the "STD" column demonstrate that the GRN-based method has better stability than MA and ACO during different replications. This is useful for real cases because the GRN-based method can ensure enough good solutions when it can be run only once. Consequently, the GRN-based method is validated to be an effective means to solve multi-objective sequencing problems in reference instances, especially for large-sized ones.

4.2.   Industrial instances

Industrial instances are collected from a diesel engine assembly line composed of 26 stations (s₁, s₂, …, s₂₆). This line assembles 10 models of four series (A, B, C of the 1^st series; D, E of the 2^nd series; F, G, H, I of the 3^rd series; D of the 4^th series). Table 8 presents processing times of these models at each station and station lengths. Table 9 gives setup costs at the first station. The GRN-based method, MA and ACO use the same algorithm parameters with those employed in large-sized problems to deal with these instances. Table 10 lists experimental results.

Table 8.  Processing times and station lengths at the diesel engine assembly line.

Model	A	B	C	D	E	F	G	H	I	J	Station length
s1	100	100	100	132	132	97	97	97	97	139	180
s2	156	156	151	92	92	91	91	91	91	156	180
s3	151	151	151	103	103	91	95	95	95	111	180
s4	139	154	154	98	98	94	95	100	103	136	180
s5	116	116	111	152	154	139	122	139	139	91	180
s6	101	101	101	151	139	123	123	134	123	95	180
s7	143	158	158	97	97	109	109	109	109	149	180
s8	125	125	111	96	95	144	144	124	164	122	180
s9	129	129	129	117	117	112	112	112	112	134	180
s10	151	139	151	116	116	114	100	105	107	91	180
s11	115	114	114	146	146	100	95	100	100	123	180
s12	100	100	100	144	144	98	98	98	98	144	180
s13	115	115	115	112	112	153	142	153	153	116	180
s14	110	110	110	136	167	97	97	97	97	111	180
s15	128	128	128	124	124	140	140	140	140	108	180
s16	119	119	124	109	109	137	137	145	137	153	180
s17	77	98	98	113	108	101	114	114	131	146	180
s18	153	133	133	130	130	96	96	96	96	117	180
s19	102	113	102	144	144	111	111	111	111	97	180
s20	107	107	113	138	138	104	104	92	95	135	180
s21	95	105	95	96	96	131	131	149	130	145	180
s22	94	101	94	128	132	113	99	99	111	94	180
s23	156	158	158	97	94	114	114	114	114	123	180
s24	104	104	104	116	116	132	132	145	132	132	180
s25	136	136	125	156	134	95	95	95	95	100	180
s26	93	93	93	155	155	131	132	131	131	85	180

---

 | Show Table

DownLoad: CSV

Table 9.  Setup time at the first station in industrial references.

Model	A	B	C	D	E	F	G	H	I	J
A	2	5	5	11	11	13	12	10	12	12
B	7	2	8	13	11	9	10	9	12	11
C	7	6	3	10	9	10	11	13	11	10
D	13	11	11	3	7	13	10	9	12	9
E	9	9	10	8	4	10	12	13	13	10
F	11	13	13	13	13	3	7	9	7	11
G	9	10	12	13	10	9	2	5	9	12
H	9	11	11	13	11	7	9	2	8	9
I	11	12	10	13	9	6	8	6	3	10
J	12	9	11	13	10	9	13	13	9	3

---

 | Show Table

DownLoad: CSV

Table 10.  Comparison of solution quality for industrial instances.

Problem	GRN-based method				Memetic algorithm				Ant colony optimization
	Min	Max	Ave	STD	Min	Max	Ave	STD	Min	Max	Ave	STD
1	3928.8	3952.2	3938.2	8.2	3971	4131.9	4054.5	43.6	4165.4	4711.3	4417.3	147
2	4174.4	4197.8	4191.3	7.3	4219.9	4376.5	4284.7	49.6	4411.5	4850.4	4623.9	131
3	4123.9	4158.7	4136.9	12.5	4161.6	4453.6	4307.3	95.4	4476.7	4841.8	4608.1	120.6
4	3448.9	3504.6	3488.9	15.7	3526.3	3938.5	3724.1	126.5	3989.3	4447.9	4265.5	150
5	3872.6	3904	3884.6	11.3	3910.3	4130.3	4021.2	57.3	4088.9	4613.6	4389.3	158.2
6	3883.5	3926.6	3908.9	13.2	3977.3	4194.3	4058.9	76.1	4118.3	4547.9	4380.3	114.8
7	4349.3	4381.1	4364.1	10.7	4365.8	4493.9	4428.5	38.8	4535.9	4807.5	4669.6	84.2

---

 | Show Table

DownLoad: CSV

As shown in Table 10, the GRN-based method achieves the best results for these instances. Owing to the enlarged solution space composed of more than 10⁵⁰ feasible solutions, the superiority of integrating reasonable sequencing rules over random searching procedure and construction heuristic is highlighted. Rather than searching among a huge number of feasible solutions in MA and ACO, the GRN-based method chooses among good solutions generated by diversified sequencing rules. This enables regulatory parameter optimization to obtain near-optimal solutions, whereas MA and ACO can hardly find out these solutions. Thereupon, the GRN-based method is validated to be more effective than MA and ACO for industrial instances.

5.   Conclusion

A GRN-based sequencing method is proposed to minimize total utility work cost, total production rate variation cost and total setup cost in MMALs. A series of comparative experiments are constructed to validate the effectiveness of this method. The experimental results demonstrate that the GRN-based method outperforms MA and ACO for large-sized problems in reference instances and practical problems collected from industrial instances. The main contribution is the development of a GRN to describe mathematical model of sequencing problems and some validated sequencing rules for single objective, which enables a reasonable tradeoff between multiple objectives through regulatory parameter optimization. Such GRN-based concept has potential interests for other kinds of multi-criteria optimization problems, e.g. scheduling problem in flexible manufacturing systems. Thereupon, we will develop other GRN-based optimization methods in our future work. In addition, we will further investigate new regulatory parameter optimization mechanisms to improve the efficiency of GRN-based sequencing methods.

Acknowledgments

The work described in this paper was supported by China Postdoctoral Science Foundation (No. 2018M641890), Shanghai Sailing Program (No. 18YF1400800), the Fundamental Research Funds for the Central Universities (No. 2232018D3-28) and the National Natural Science Foundation of China (No. 51435009).

Conflict of interest

The authors have declared that no conflict of interest in this paper.