1. Introduction
Modern oncology provides a wide array of alternative cancer treatment options. With 1.6 million cases in the U.S. in 2014 and only 600,000 deaths, treatment capabilities are improving [29]. Treatment regimes are usually designed to balance the expedited removal/reduction of cancer cells with the quality of life and long term health of the patient.
One common form of cancer treatment is external beam radiotherapy, often referred to as just radiation therapy. In radiation therapy beams of x-rays (high energy photons), gamma rays, or other charged particles are fired into the body of a patient at a specifically targeted point. As the beam passes through tissue the DNA of cells are damaged, typically resulting in cell death. Note that the cell death does not occur instantaneously as the radiation is applied. Depending on the type of cell, it may take several hours or even days before the damaged cells begin to die. By firing the beam multiple times from different angles, referred to as conformal radiation therapy, radiation oncologists can cause significant damage to cancer cells [27]. Though damage is done to both cancer cells and surrounding healthy cells, the aim of radiation therapy is to kill cancer cells while minimizing damage to healthy cells [27,22,20].
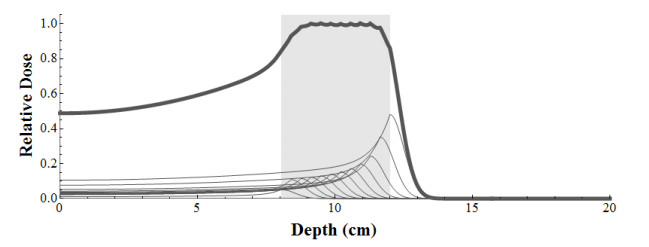
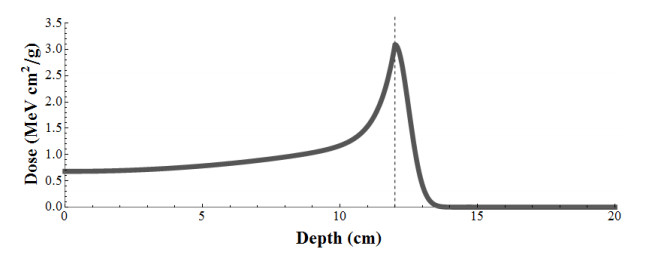
Proton therapy is a form of radiation that uses a particle accelerator to form a beam of high energy protons that are fired into the patient to irradiate cancer cells. The advantage of proton therapy is that it provides more localized treatment and allows for higher dose treatments for patients than radiation therapy using photons. As shown in Figure 1 and first observed by Bragg and Kleenman [10], charged particle beams of proton mass deliver the majority of their dose (energy per unit mass) at a depth near the end of their range and over a narrow depth range (about 0.5-1.0 cm) known as the Bragg peak region [20,35,22,2]. For a single Bragg peak curve, the depth at which the maximum dosage is received, called the target depth, can be controlled by altering the initial energy generated by the particle accelerator forming the proton beam. Note that the amount of dosage received at tissue depths greater than the target depth quickly fall off to zero.
The narrowness of the Bragg peak, and the relatively low dose outside the Bragg peak region prompted Wilson in 1946 [37] to suggest the use of protons for radiation therapy as a means of minimizing damage to tissue surrounding a tumor site, and the first patient treated with proton therapy was in 1954 at the Lawrence Berkeley Laboratory [27,2]. Since then it has been observed that proton therapy results in a higher probability of tumor control and patient tolerance (i.e., less negative side-effects) than treatment with photon therapy [27]. Due to the ability of proton therapy to target a narrow region, the use of proton therapy has been of particular interest in treating tumors growing in close proximity to what are called serially organized tissues in which damage to a small portion of this type of tissue will have secondary effects on adjacent tissue such that normal function may cease [21,27], for example the spinal chord. Proton therapy has been used to treat tumors located in a variety of locations, including the paranasal sinus [31], the prostate [16,30], the brain [18], the base of the skull [34], and the liver [11].
Since the mass of a typical tumor targeted with proton therapy is wider than the Bragg peak region of a single proton beam, to treat the entire tumor a proton beam is modulated to create a spread out Bragg peak (SOBP) [22]. Modulation is achieved through a sequence of absorbers, each creating a single Bragg peak curve with the sequential set of Bragg peaks occurring at decreasing depths and with decreasing relative dosage [27]. Figure 2 shows a SOBP which is the sum of the sequence of Bragg peak curves shown. A typical treatment session involves the firing of one or more modulated proton beams [27]. If multiple modulated beams are fired, each beam targets the tumor from a different angle in a treatment method known as conformal proton therapy.
Due to the fact that the relative dose of a proton therapy treatment is heterogeneously delivered over a range of depths, we have developed a spatially explicit model to examine the effects of proton therapy upon a tumor mass and surrounding tissue. Specifically, we have formulated a discrete difference equation patch model with discrete diffusion to simulate tumor growth over one-dimensional space and with discrete bursts of applied proton therapy. Using this model we examine the effects of applying proton therapy multiple times over a period of several weeks (a single treatment course). The development of our model builds off of existing models of linear cancer networks [36,23] which are briefly described in Section 2. A detailed description of our proposed model and assumptions are given in Section 3. In Section 4 we describe how the model is parameterized using data from in vitro and clinical studies. As an example, we parameterize the model for the treatment of Hepatocellular carcinoma, a common form of liver cancer. In Section 5 we describe and compare the results of simulations. We examine one treatment course of non-conformal proton therapy and two different conformal proton therapy treatment courses. Finally, in Section 6 we consider the implication and impact of our results, discuss the potential drawbacks of our proposed model, and consider some future extensions to the proposed model.
2. Linear cancer networks
In 2011, Werner proposed a general theoretical framework describing all possible cancer networks [36]. Werner's new paradigm presents many open research problems, and much work remains to be done in translating these abstract networks into descriptive implementations such as differential equation or descrete difference equation models in order to simulate and quantify the impact of radiation and other therapies. Linear cancer networks, one of the conceptual frameworks of tumor growth developed by Werner [36], allows for a simplified approach to modeling tumor development. A tumor is assumed to begin with cancer stem cells (denoted as A cells) which differentiate to produce non-proliferating cancer cells (denoted as B cells). It is assumed the B cells amass to form the bulk of the tumor. A single A cell, however, will continue differentiating, producing more and more B cells.
Let A(t) be the number of A cells at time t, and B(t) be the number of B cells at time t. The initial model of a linear cancer network proposed by Werner [36] assumed the number of A cells remained constant, while the growth rate of B cells increased linearly with respect to the number of A cells (hence the name linear cancer networks). This simple model is described by dA/dt=0 and dB/dt=kAA, where kA is the differentiation rate for the B cells. Manley [23] expanded on the model proposed by Werner by adding the cells of healthy tissue, H(t), to the model, and allowing logistic growth of the cancer cells which is justified by previous research on tumor growth rates (see [32] for details). This expanded model is described by
|
dBdt=kAA(AMA)(1−BMB)−δB−rB
|
(1b)
|
where MA, MB, and MH represent the carrying capacities of the A, B, and H cells in a given tissue volume, respectively; kA and kH are the intrinsic growth rates of the cancer and healthy cells, respectively; δ is the natural death rate of tumor cells; and rA, rB, and rH are constant death rates due to radiation therapy. Manley uses the model to explore the effects of both photon and proton radiation therapy, but the assumption of a continuous application of the therapy and a spatially homogeneous dosage is unrealistic. Thus, we propose a spatial explicit model where the application of proton therapy is applied in discrete bursts.
3. Model description & assumptions
The model we propose builds on the Werner-Manley model given in System (1). However, our model is discrete in time and space (using discrete difference equations), uses diffusion to simulate tumor growth, and allows for the repeated application of proton radiation in discrete bursts. Our model uses a depth-range targeted SOBP to simulate the application of proton radiation and assumes cell death over time due to a single application of proton radiation is modeled by a Gaussian distribution function.
Let Ait, Bit, and Hit be the densities of A, B, and H cells respectively at time t and depth i, where t,i∈N. Each time step t represents 1 hour, and each depth i represents a layer of tissue 1 mm thick. Let Pit be the relative dose of proton therapy at time t and depth i. We assume that cancer stem cells and healthy cells will diffuse from tissue depths of high concentration to tissue depths of low concentration, and use the formulation for discrete diffusion described in [15]. Since the Werner-Manley model of the linear cancer networks assumes the amassing of B cells, we consider the diffusion of B cells to be negligible. Our model is given by
|
Ait+1=Ait+kAAit(1−AitMA)−AitPit+dAn∑j=0(Ajt−Ait)e−(j−i)2/μA
|
(2a)
|
|
Bit+1=Bit+kAAit(AitMA)(1−BitMB)−BitPit
|
(2b)
|
|
Hit+1=Hit+kHHit(1−Hit1−Ait−Bit)−HitPit+dHn∑j=0(Hjt−Hit)e−(j−i)2/μH,
|
(2c)
|
where MA, MB represent the relative carrying capacities of the A and B cells respectively, and kA and kH are the intrinsic growth rates of the cancer and healthy cells, respectively. Note that for any given tissue depth i, Ait+Bti+Hit≤1, and thus the maximum density at tissue depth i is 1 cell per unit area. The effective rates of diffusion for A and H cells are given by parameters μA and μH, respectively, and the diffusion coefficients dA and dH are defined as
|
dA=(n∑i=0n∑j=0(e−(j−i)2/μA))−1 and dH=(n∑i=0n∑j=0(e−(j−i)2/μH))−1.
|
For a given time t, let τ be the set of previous times at which proton therapy has been applied. Then
|
Pit=α∑t∗∈τ[Dit∗e−β(t−t∗−δ)2],
|
(2d)
|
where α is the maximum cell death rate at tissue depth i due to a single proton treatment, Dit∗ is the relative dose at depth i and time t∗ due to the treatment applied at time t∗, δ is the number of hours after t∗ at which the cell death rate is maximized due to treatment applied at t∗, and β determines the time range over which the majority of cell death occurs. The relative dose D over all tissue depths is defined by a clinical approximation of the solution to the Bethe-Block Equation which simulates a Bragg-Peak curve (see Section 3.1). Note that the formulation of Pti allows for the delayed effect of proton therapy treatment applied at a previous time step to combine with the effect of treatment applied at a later time step thus accounting for the delayed effect of a proton therapy treatment on cell death.
3.1. Bethe-Bloch equation
High energy particles such as protons and photons damage tissue through which they travel in distinct patterns defined by their stopping power. As a particle travels through a given material, it may collide with the molecules or cells of that material, releasing a portion of its energy. The stopping power of a charged particle, S(z), is defined to be the amount of energy at depth z a given material will receive when high energy particles pass through it [10,33]. The Bethe-Bloch formula, explained in detail in [38], gives the stopping power of a given system of excited particles through a given material. However, in a clinical setting, the stopping power, and the dose at each depth, is determined from an approximate solution to the Bethe-Bloch equation, which we will refer to as a clinical solution.
3.1.1. A clinical solution for the Bethe-Bloch equation
We use the clinical solution of the Bethe-Bloch equation developed by Ulmer and Schaffner [33] to represent the stoppage power (and thus the dose) of the protons at various tissue depths. Let R be the target depth. The initial energy generated by the particle accelerator, E0, is defined as a function of R [7],
The dosage at depth z given target depth R, S(z,R), is approximated by
where the functions ϕi(z,R) are defined as
|
ϕ1(z,R)=C1exp(−(R−zτ0)2)θ(z)
|
(5a)
|
|
ϕ3(z,R)=2C3exp(−Qp(R−z))θ(z)
|
(5c)
|
|
ϕ4(z,R)=2C4(zR)2θ(z)
|
(5d)
|
|
ϕ5(z,R)=2C5(1−zR)θ(z)
|
(5e)
|
|
ϕ6(z,R)=(5∑i=2ϕn(R,R))exp(−2(z−R)2)ψ(z).
|
(5f)
|
The coefficients Ci for i=1,…,6, and Qp are functions of E0 (and thus functions of the target depth R) and are given in Table 1. The functions θ(z) and ψ(z) are step functions defined by
|
θ(z)={1,z≤R0z>R and ψ(z)={0,z≤R1z>R.
|
(6)
|
Note that z=R is the depth at which maximum dosage is received, and that the functions ϕ1(z),…,ϕ5(z) provide the approximation of S(z,R) for 0≤z≤R, while the function ϕ6(z) provides the approximation of S(z,R) for z≥R. The Bragg peak curves in Figures 1 and 2 are generated using this approximation.
Table 1. Coefficients and parameters for clinical approximation of the Bethe-Bloch formula (Equations (4)-(6)) as given in [33].
| Parameter |
Value |
Parameter |
Value |
| C1 |
2.277463−0.0018473E0 |
C2 |
0.243100−0.0007000E0 |
| C3 |
1.029500−0.0010300E0 |
C4 |
0.405300−0.0007000E0 |
| C5 |
0.007000 |
τ0 |
10−5 |
| Qp |
π(6.267510+0.0010300E0)R(1+(2.11791×10−5)E0+(0.9192399×10−7)E20) |
3.1.2. Formulating a spread Out Bragg peak (SOBP)
A SOBP curve is formed as a weighted sum of multiple Bragg peak curves. A method for determining the weights of each single Bragg peak curve was developed by Bortfeld [8], and refined by Jette and Chen [17]. For a SOBP created using n+1 Bragg peak curves distributed over a target region [(1−χ)Rmax,Rmax], the target depth of the kth curve is given by
|
Rk=[1−(1−kn)χ]Rmax, for k=0,1,…,n,
|
(7)
|
and thus the kth Bragg peak curve is given by S(z,Rk). Note that R0=Rmax, Rn=(1−χ)Rmax, and χ represents the proportion of the region [0,R0] which is targeted. The SOBP curve represents the dose at tissue depth z (in MeV cm2/g) and is defined as
|
D(z,Rmax,χ)=n∑k=0wkS(z,Rk),
|
(8)
|
with each weight wk defined by
|
wk={1−(1−12n)1−1/pk=0[1−1n(k−12)]1−1/p−[1−1n(k+12)]1−1/p1≤k≤n−1(12n)1−1/pk=n,
|
(9)
|
where the parameter p is adjusted to keep the dose over target region relatively constant. Note that Figure 2 shows a SOBP composed of 12 Bragg peak curves (n=11) with Rmax=12 cm, χ=0.3, and p=2.
For our model (System(2)), the relative dose at depth i due to treatment applied at time step t∗ is approximated by
|
Dit∗=D(z(i)+z(i+1)2,Rmax,χ)Dmax
|
(10)
|
where z(i) is the tissue depth (in cm), and Dmax=maxz[D(z,Rmax,χ)]. Note that the relative dose for tissue depth i is calculated at the midpoint of the ith subinterval [i,i+1].
4. Model parameters for a case of hepatocellular carcinoma
As a sample case, we have used parameters which describe the growth and treatment of Hepatocellular carcinoma (HCC), a common form of liver cancer. Proton therapy has been used to treat HCC, but there remains a need for research and clinical trials to determine the effects of proton therapy used alone and with other treatment options [13]. Using the model proposed in Section 3 with parameters which describe the growth of liver cells (hepatocytes) and the impact of proton therapy on HCC we are able to examine the temporal and spatial effects of treating HCC with proton therapy alone.
All parameters used for the numerical simulation of the growth and treatment of HCC tumors are given in Table 2, with their derivation and/or biological motivation described in detail through the remainder of this section.
Table 2. Values of parameters used in simulations of the model described in Section 3.
| Parameter |
Value |
| kA |
Cancer cell growth rate (hours−1) |
0.008 165 |
| kH |
Healthy cell growth rate (hours−1) |
2.108 703 |
| MA |
Relative carrying capacity of A cells in 1 mm layer of tissue |
0.225 |
| MB |
Relative carrying capacity of B cells in 1 mm layer of tissue |
0.675 |
| μA |
Effective diffusion rate for A cells |
0.133642 |
| μH |
Effective diffusion rate for H cells |
0.131166 |
| α |
Maximum cell death rate at depth i from a single treatment |
0.02 |
| β |
Determines range over which the majority of cell death occurs |
0.0075 |
| δ |
Hours after treatment at which cell death rate is maximized |
47 |
4.1. Parameters defining spatial & temporal scales
We assume that each depth i represents a layer of tissue 1 mm thick. For the simulations shown in Section 5, we use a spatial domain of 20.1 cm, i.e. i∈0,1,…,200. Additionally, each time step t represents the passing of 1 hour.
4.2. subsection{Instrinic growth & effective diffusion rates of H cells
In the absence of cancer cells, when a portion of the liver is surgically removed, the liver cells will regenerate quickly (see liver regeneration studies [25,24,14] for details). Together, the parameters kH (the intrinsic growth rate of H cells) and μH (the effective diffusion rate of H cells) determine how quickly healthy tissue is able to regenerate across the spatial domain. To determine appropriate values of kH and μH we used data for liver cell regeneration provided by Nagasue, et al.[25]. In this study, five patients with normal livers (no chirrosis or chronic hepatitis) had right lobectomies where 60% of the volume of their liver was removed leaving 40% of each patient's original liver volume directly after surgery. Averaging across the five patients, after 8 days liver volumes had recovered to 49% of the original liver volumes, and after 100 days liver volumes had recovered to 98% of the original liver volumes.
To determine the values of kH and μH which would best approximate the averaged patient data presented by Nagasue, et al.[25] we use Latin Hypercube sampling to generate 2000 pairs of (kH,μH) assuming possible values of kH and μH to be uniformly distributed over [0.0005,3] and [0.05,3], respectively (see [5,4,6] for details and examples of Latin Hypercube sampling). Next, we simulate System (2) with no cancer cells (i.e., Ait=Bit=0 for all i and t) and no proton therapy treatment over 100 days (2400 times steps) for each of the (kH,μH) parameter pairs. Each simulation uses a healthy cell initial condition of
|
Hi0={1i=0,…,800i=81,…,200,
|
i.e., we start with 40% of the total possible volume of healthy cells. Lastly, we select kH and μH such that
|
minkH, μH√(H192−0.49)2+(H2400−0.98)2 where Ht=1201∑iHit.
|
This process yields the parameter values kH=2.108703 and μH=0.131166. Note that 8 days is 192 time steps and 100 days is 2400 times steps.
4.3. Relative carrying capacities
Recall that System (2) is constructed such that Ait+Bit+Hit≤1. We further assume that the relative carrying capacities of A and B cells at tissue depth i is MA+MB<1, thus a particular layer can become mostly cancer cells, but cannot be composed entirely of cancer cells. Next, an underlying assumption of linear cancer networks is that A cells proliferate, while B cells accumulate. Thus, we assume that MB>MA. Specifically for the results shown in Section 5 we assume MA+MB=0.9 and MB=3MA, which together yield MA=0.225 and MB=0.675.
4.4. Instrinic growth & diffusion rates of A cells
The tumor volume doubling time (TVDT) of HCCs varies greatly. In a study of 15 patients with small (<5 cm in diameter) HCC tumors by Okazaki, et al.[26] the range in TVDTs was 39—305 days with mean 102±77 days. In study of 39 patients with small (<5 cm in diameter) HCC tumors by Barbara, et al.[3] the range in TVDTs was 27—605 days with mean of 204±135 days. For parameterization of System (2) we assumed a TVDT of 150 days. A doubling in tumor volume is assumed to be equivalent to a doubling in cancer cell density. Thus, if we let
be the average cancer density across all tissue depths at time t, then after 150 days (t=3600) we expect
However, since Model 2 accounts for only one spatial dimension, if we assume the HCCs develop in a volume that can be approximated by sphere, then for a tumor with diameter d0 at time t=0, the diameter t days later will be
where TD is the tumor volume doubling time. For example, if TD=150 and the tumor is 30 mm in diameter at t=0 (i.e., d0=30), then after 150 days (t=3600) the tumor will have a diameter of 38 mm (i.e., d3600=38).
For the purpose of measurement, we assume that tissue depths with Ait+Bit≥0.55 are "visible" as part of the tumor, and thus contribute to the diameter of the tumor. To determine parameter combinations that would result in a tumor volume doubling time of 150 days, we start with a visible 30 mm tumor located in the center of the spatial domain. Specifically, we use initial conditions
|
Ai0={0.1375i=85,…,1140otherwise, Bi0={0.4125i=85,…,1140otherwise, and
|
Notice, for i=85,…,114, Ai0+Bi0=0.55 and Bi0=3Ai0.
To determine values of kA and μA for which C3600≈2C0 and d3600=38, we again use Latin Hypercube sampling to generate 1000 pairs of (kA,μA) assuming possible values of kA and μA to be uniformly distributed over [0.0005,0.1] and [0.05,1.0], respectively. Next, we simulate System (2) with no proton therapy treatment over 150 days (3600 times steps) for each of the 1000 (kA,μA) parameter pairs. Lastly, we select the (kA,μA) parameter pair such that d3600=38 and
This process yields the parameter values kA=0.008165 and μA=0.133642 and result in C3600=2.037C0 and d3600=38.
4.5. Parameters for application of proton therapy
Proton radiation damages the DNA of cells, but does not cause the immediate cell death. An experiment by Lee, et al.[19] on the effects of proton therapy on HCC cell death found that in a culture of HCC cells exposed to a 5 Gy dose proton beam (a typical patient dose) there was virtually no effect on cell death during the first 24 hours, but only about 66.5% of the cells were alive after 72 hours. If the dose was lowered to 2 Gy, there was still virtually not effect on cell death during the first 24 hours, and 74.7% of the cells were alive after 72 hours. Since Lee, et al.[19] do not provide data on cell death after 72 hours, for both doses we have assumed the increase in cell death after 72 hours is minimal.
We approximate the HCC cell death rate at time t and tissue depth i from a single proton therapy treatment applied at time t=0 by the function
where α is the maximum cell death rate at depth i from a single treatment, δ is the hours after a single treatment at which the cell death rate is maximized, and β defines the range over which the majority of the cell death occurs. Let xt be the proportion of the initial HCC cell culture left after time t. If a single treatment of proton therapy is applied at t=0, then
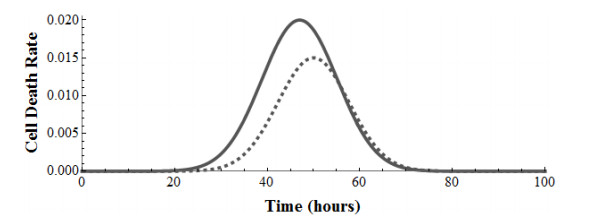
Using Equation (14), we determined estimates for α, β, and γ that fit the data for both the 5 Gy and 2 Gy dose experiments performed by Lee, et al [19].
5 Gy Dose: Parameter values α=0.020, β=0.00750, and δ=47 yield x24=0.999, x72=0.663, and x100=0.662 which approximates the data from Lee, et al.[19] for a 5 Gy dose.
2 Gy Dose: Parameter values α=0.015, β=0.00845, and δ=50 yield x24=1.000, x72=0.748, and x100=0.748 which approximates the data from Lee, et al.[19] for a 2 Gy dose.
Figure 3 shows the time dependent cell death rate at a particular tissue depth due to a single applications of proton therapy treatment using a 5 Gy dose (solid cure) and a 2 Gy dose (dashed curve).
5. Numerical simulations of growth & treatment of an HCC tumor
The parameter values used for each of the simulations discussed here are given in Table 2. Note a single treatment course refers to a set of proton therapy treamtents given to a patient over a 1-2 month period after which there is a period of no treatment so that the patient can recover from any adverse side effects of the treatment. After the period of no treatment the patient is usually re-evaluated to determine how much of the cancer remains.
5.1. Non-conformal treatment course
To simulate the effects of a typical (non-conformal) proton therapy treatment course given to a HCC patient we used a treatment course (multiple doses of proton therapy administered over several weeks) similar to those reported by a retrospective review of proton therapy treatment in 162 HCC patients [11]. Of the 162 patients, the median dose given to a patient was 4.5 Gy, however dose size ranged from 2.9—6.0 Gy. Patients received 10—24 doses over 13—50 days. Typically, the larger the dose size, the fewer doses given. Of the 162 patients, the treatment course given most often was a dose of 4.5 Gy given 16 times over the course of 24 to 43 days. Since the data we used for time dependent cell death rate used a 2.0 Gy dose and a 5.0 Gy dose, we approximated this treatment course with a dose schedule of 5.0 Gy given 16 times over 35 days (5 weeks) with the dosing schedule as shown in Table 3(a). Note a total of 80 Gy of proton radiation are administered over the 5 weeks.
Table 3. Proton therapy treatment course of (a) 16 doses over 35 days (5 weeks), and (b) 20 doses over 49 days (7 weeks). The number in each box indicates the day of the treatment course and shaded boxes indicate the days on which treatment is administered.
| (A)5 week treatment course |
| Week |
S |
M |
T |
W |
T |
F |
S |
| 1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 2 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
| 3 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
| 4 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
| 5 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
| (B)7 week treatment course |
| Week |
S |
M |
T |
W |
T |
F |
S |
| 1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 2 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
| 3 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
| 4 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
| 5 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
| 6 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
| 7 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
The simulation uses initial conditions
|
Ai0={0.1375i=85,…,1140otherwise, Bi0={0.4125i=85,…,1140otherwise, and
|
Notice, for i=85,…,114, Ai0+Bi0=0.55 and Bi0=3Ai0. The simulation allows the tumor to grow for 150 days (3600 times steps), and Day 1 of the treatment schedule begins on Day 151 of the simulation. We assume that treatment is given at noon each day it is scheduled, thus the first dose is administered at noon on Day 152 of the simulation (time step t=152×24+12=3660). After the 35 day treatment period, the simulation continues another 90 days (without treatment) to allow for observation of tumor growth after treatment. Thus, the entire simulation is 275 days (6600 time steps).
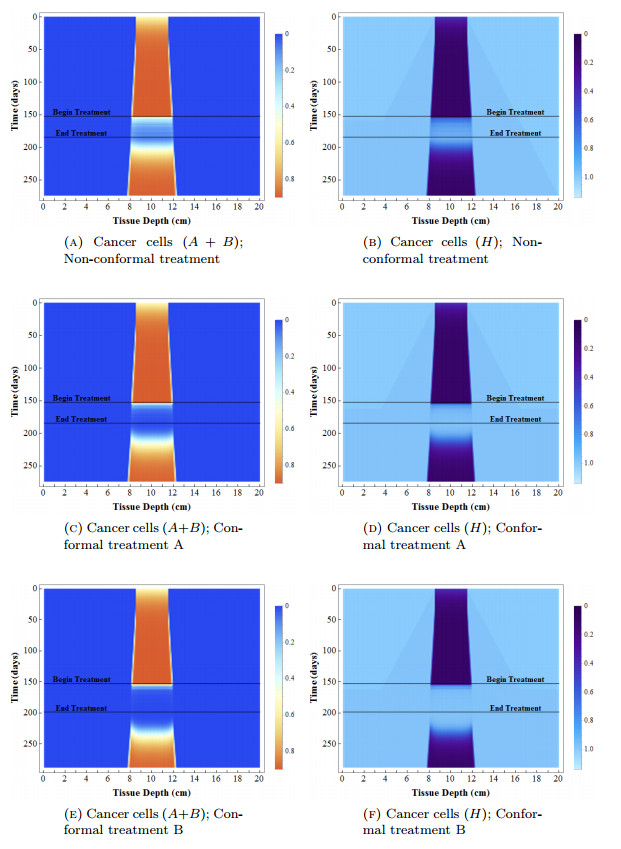
The results of the simulation are shown in Figures 4(a) and 4(b). Again, for the purposes of measurement, we assume that tissue depths with Ait+Bit≥0.55 are "visible" as a part of the tumor, and thus contribute to the diameter of the tumor, dt. At the beginning of the simulation the cancer cells (A and B cells) only exist at tissue depths i=85,…,114 making the diameter of the tumor 30 mm (d0=30). After 150 days of no treatment, there are 2.037 times as many cancer cells present as at the start of the simulation (C3600=2.037 C0, using the notation of Section 4), and the diameter of the visible tumor has grown to 38 mm (d3600=38). After the 35 day treatment period, there are 0.062 times as many cancer cells present as at Day 150 (C4400=0.062 C3600, nearly a 94% reduction in cancer cell density), and the diameter of the visible tumor has shrunk to 0 mm (d4440=0). Though this result seems promising, after the additional 90 day observation period, there are 1.188 times as many cancer cells present as at Day 150 (C6600=1.188 C3600, almost a 19% increase in cancer cell density when compared to right before treatment), and the diameter of visible tumor has increased to 44 mm (d6600=44). These results are summarized in Table 4. Note, if no proton therapy treatment had been given over the 35 day treatment period, then by Day 275 there would be 1.236 times as many cancer cells present as at Day 150 (C6600=1.236 C3600) and the diameter of visible tumor would have increased to 46 mm (d6600=46). This means, the patient is only slightly better off for having undergone the treatment.
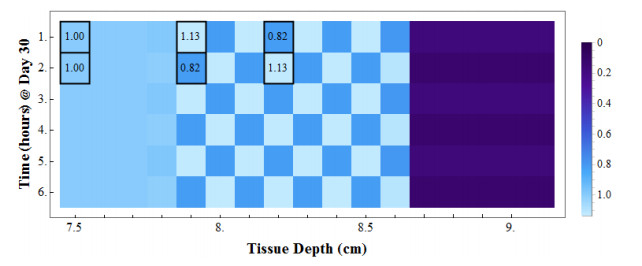
In Figure 4(b) we see the healthy cells quickly rebound into the tumor region during and shortly after treatment, but as the observation period progresses the healthy cells are removed from the tumor region as the tumor re-establishes itself. Upon close inspection of Figure 4(b), a shaded triangle centered around the tumor can be seen. Figure 5 shows a close up of a portion of this region from Figure 4(b). Specifically, it shows tissue depths i=75,…,90 for the first 6 hours of Day 30 of the simulation, that is t=721,…,726. The checkerboard pattern that forms is a result of the combination of the diffusion of healthy cells and the overcrowding effects of logistic growth. For clarity, in hours 1 and 2 of Day 30 (t=721 and t=722) boxes are formed around three tissue depths: 75 mm, 79 mm, and 82 mm. The values shown in each box indicate the value of Hit at that time and tissue depth. Notice, within the checkerboard patterned region the density of healthy cells are switching to values above 1 (the carrying capacity of any single tissue depth) and below 1. When a particular tissue depth gains a healthy cell density greater than 1, diffusion will move healthy cells out of that depth to lower density depths (darker shaded cells) and the overcrowding effects of logistic growth with eliminate cells from that tissue depth causing a lower cell density at that tissue depth in the next time step. Conversely, when the healthy cell density at a particular tissue depth is below 1, diffusion will move healthy cells from higher density depths (lighter shaded cells) into that tissue depth, and the logistic growth will additionally cause the production of some new healthy cells. Together, the effects of diffusion and logistic growth work to create the resulting checkerboard pattern which, over time, grows outward from the tumor region.
5.2. Treatment courses with conformal proton therapy
Since our model contains only one spatial dimension we only have the options of the proton beam originating from the left side of the spatial domain or from the right side. The simulation shown in Section 5.1 assumes that the beam is being fired from the left side of the spatial domain. To simulate the effects of conformal proton therapy where multiple modulated beams are targeted upon the tumor from different angles, we now consider simulations in which the beam is fired from both the left and right sides of the spatial domain.
Typically, when conformal proton therapy is used, the dose of each fired beam is smaller than if only a single beam is used. Recall, the data we used for the time dependent cell death rate used a 2 Gy dose and a 5 Gy dose. For the conformal proton treatment we will assume each fired beam (one from the left and one from the right) is a 2 Gy dose, giving a total dose of 4 Gy (less than was delivered in each dose in the simulation described in Section 5.1). To compare the results of the conformal treatment to the non-conformal treatment simulation of Section 5.1, we use two different treatment courses.
(A) 4 Gy total dose given 16 times over 35 days (5 weeks) as shown in Table 3(a); total of 64 Gy of proton irradiation administered
(B) 4 Gy total dose given 20 times over 49 days (7 weeks) as shown in Table 3(b); total of 80 Gy of proton irradiation administered
Note that treatment course A uses the same scheduling as was used in the Section 5.1 example, but each dose is lower (and being delivered by two 2 Gy beams). Treatment course B delivers the same amount of proton radiation but in smaller doses (and being delivered by two 2 Gy beams) and over a longer period of time.
For both of the following simulations, as with the previous simulation (Section 5.1), we assume that tissue depths with Ait+Bit≥0.55 are "visible" as a part of the tumor, and thus contribute to the tumor diameter at time t, dt. Additionally, the initial conditions are the same as in the previous simulation, and the results for the first 150 days (when no treatment is administered) as the same as described for the previous simulation (that is, C3600=2.037C0 and d3600=38).
5.2.1. Results of treatment course A
The results of the simulation using treatment course A are shown in Figures 4(c) and 4(d). After the 35 day treatment period, there are 0.011 times as many cancer cells present as at Day 150 (C4400=0.011 C0 nearly a 99% reduction in cancer cell density), and the diameter of the visible tumor has shrunk to 0 mm (d4440=0). Note, that though this results is an improvement over the non-conformal treatment course described in Section 5.1, after the additional 90 day observation period, there are 1.161 times as many cancer cells present as at Day 150 (C6600=1.161 C3600, more than a 16% increase in cancer cell density when compared to right before treatment), and the diameter of the visible tumor has increased to 44 mm (d6600=44).
5.2.2. Results of treatment course B
The results of the simulation using treatment course B are shown in Figures 4(e) and 4(f). After the 49 day treatment period (t=4776), there are 0.003 times as many cancer cells present as at Day 150 (C4776=0.003 C0 over a 99% reduction in cancer cell density), and the diameter of the visible tumor has shrunk to 0 mm (d4776=0). Note, that though this results is an improvement over the non-conformal treatment course described in Section 5.1 and conformal treatment course A, after the additional 90 day observation period, there are 1.154 times as many cancer cells present as at Day 150 (C6936=1.154 C3600, slightly more than a 15% increase in cancer cell density when compared to right before treatment), and the diameter of the visible tumor has increased to 44 mm (d6936=44).
The results for conformal treatment courses A and B are summarized in Table 4. As in the simulation described in Section 5.1, in each conformal treatment simulation the healthy cells quickly rebound into the tumor region during and shortly after treatment, but as the observation period progresses the healthy cells are removed from the tumor region as the tumor re-establishes itself.
Table 4. Summary of results from all treatment courses where t=0 is the initial time, ts is the time at which the treatment course starts (ts=3600 for all treatment courses), te is the time at which the treatment course ends (te=4440 for non-conformal and conformal treatment course A, and te=4776 for conformal treatment course B), and to is the time at which the 90-day observation period ends (to=te+2160 for all treatment courses).
|
| t=0 |
ts |
te |
to |
| Non-Conformal |
Cell Density |
C0 |
2.037 C0 |
0.062 Cts |
1.188 Cts |
| Tumor Diameter |
30 mm |
38 mm |
0 mm |
44 mm |
| Conformal A |
Cell Density |
C0 |
2.037 C0 |
0.011 Cts |
1.161 Cts |
| Tumor Diameter |
30 mm |
38 mm |
0 mm |
44 mm |
| Conformal B |
Cell Density |
C0 |
2.037 C0 |
0.003 Cts |
1.154 Cts |
| Tumor Diameter |
30 mm |
38 mm |
0 mm |
44 mm |
6. Discussion
We have proposed a model to simulate the spatial and temporal dynamics of cancer and healthy cells before, during, and after the application of proton therapy. As an example of how the model can be applied, we have used data from in vitro clinical studies of hepatocellular carcinoma to parameterize the model, explore numerical simulations, and compare different treatment courses. Within the numerical simulations we looked at both non-conformal and conformal treatment regimes. In each of the numerical simulations the resurgence of the cancer cells and the tumor after the 90 day observation period suggest the given treatment course is not sufficient. However, there are reasons to remain hopeful.
First, note that the patient's immune response is not included in our proposed model. In the simulation of each of the three treatment courses described in Section 5, the cancer cell density directly after the treatment period was lowered to 6.2% or lower of the cell density directly before treatment was administered. For many forms of cancer, including hepatocellular carcinoma, once of the density of cancer cells is low enough, a sufficiently healthy immune system will work to remove the remaining cancer cells. This suggests a type of Allee effect (see [1], [9], and [12] for details) which causes the decay of the cancer cell population once it falls below a certain threshold. This feature is not included in the model we proposed, but if it were, we may see the elimination of the remaining cancer cells after the proton therapy treatment course is administered.
Secondly, clinical studies show that proton therapy may be administered in conjunction with or sequentially with other forms of treatment. For example, the treatment of hepatocellular carcinomas with proton therapy may be combined with transarterial chemoembolization (TACE) [28]. The model we have proposed here simulates the effects of proton therapy used alone, not in conjunction with other therapies. We hypothesize that an extension of this model which included both proton therapy and TACE used sequentially would show improved results, possibly leading to the elimination of the cancer cells entirely.
In addition to the possible model extensions proposed above, another obvious extension would be to increases the spatial domain of this model to be three-dimensional. Increasing the spatial domain to three dimensions would allow for infinitely more possibilities in the structure of the conformal treatment courses. Other possible model extensions could be informed by the variety of cancer networks proposed by Werner, including exponential cancer networks [36,Section 6], geometric cancer networks which may provide an more accurate model of logistic growth of cancer cells at the network level [36,Section 8], linear cancer networks with stochastic dedifferentiation [36,Section 9], and cancer networks with explicitly modeled cell communication [36,Sections 11-12].
Lastly, in the simulations shown in Section 5, we considered the application of only a single treatment course. However, a patient who shows regeneration of the tumor after a given observation period would likely undergo a second treatment period. An interesting extension of this model would be to consider the optimal length of the observation period before applying a second treatment course. A clinician would need to wait long enough for the patient to recover from the first round of treatment and for there to be evidence of the tumor's regrowth, but waiting too long could result in an even larger tumor as we saw after the 90-day observation period in the simulations in Section 5.
Both conformal treatment courses result in lower densities of cancer cells directly after the treatment period and after the 90 day observation period when compared with the non-conformal treatment course. It should be noted that since conformal treatment course A delivers a lower total amount of proton radiation (64 Gy instead of the 80 Gy) when compared to the non-conformal treatment course and conformal treatment course B, we would expect conformal treatment course A to result in fewer adverse side effects than the other two treatment courses. Additionally since both conformal treatment courses deliver better results than the non-conformal treatment course, when a conformal treatment regime is an option for a patient, our results suggest it will lead to better control of the targeted tumor. Furthermore, since both conformal treatment courses administer a lower dose on each treatment day than the non-conformal treatment course, the conformal treatment courses may be advised in patients with lower tolerances to irradiation.
As the use of proton therapy increases, the need for useful mathematical models which describe both the effectiveness of treatment and the cellular dynamics in the tissues surrounding the tumor are needed. Our model provides a tool which addresses both of these objectives and is novel in its use of both spatial and temporal dynamics in simulating the effects of proton radiation therapy. Though we have used the model here to explore the impact of proton therapy on hepatocellular carcinomas, by following the methods laid out in Section 4 one can reparameterize the model for other types of cancer. Though there are many directions in which this model could be expanded, the ability to use this model to compare different treatment courses (like the comparison of non-conformal and conformal treatment options) make this model a powerful tool.









 DownLoad:
DownLoad: