1. Introduction
Spatial heterogeneity, dispersal patterns, and biotic interactions influence the distribution of species within a landscape [4, 47, 60, 68, 70]. Spatial self-organization results from local interactions between organisms and the environment, and emerges at patch-scales [61, 75]. For example, limited dispersal ability and its related dispersal patterns [57] is considered to be one of the key factors that promote the development of self-organized spatial patterns [1, 42, 71, 72].
In nature, especially for ecological communities of insects, dispersal of a predator is usually driven by its non-random foraging behavior which can often response to prey-contact stimuli [23], including spatial variation in prey density [40] and different types of signals arising directly from prey [76]. For instances, bloodsucking insects respond to the carbon dioxide output and the visual signals of a moving animal, which in tsetse flies (Glossina spp.) lead to the formation of a "following swarm" associated with herds of grazing ungulates [14, 34]. Most mosquitoes were attracted over a larger distance by the odor of the host [17, 18, 19]. The wood-wasp, Sirex noctilio, is attracted by the concentration of the scent [19, 53]. Social ants excite "pheromone trails" to encourage other individuals to visit the same food source [6]. Plant-feeding insects commonly detect food items by gustatory signals [65, 66, 66]. These non-random foraging behaviors driven by prey-mediated patch attractants, prey attractants themselves, and arrestant stimuli following the encounter of a prey, can lead to predation rates that are greater in regions where prey are more abundant (i.e., density-dependent predation), thus regulate population dynamics of both prey and predator.
Recent experimental work on population dynamics of immobile Aphids and Coccinellids by [44] show that the foraging movements of predator Coccinellids are combinations of passive diffusion, conspecific attraction, and retention on plants with high aphid numbers which is highly dependent on the strength of prey-predator interaction. Their study also demonstrates that predation by coccinellids was responsible for self-organization of aphid colonies. Many ecological systems exhibit similar foraging movements of predator. For example, Japanese beetles are attracted to feeding induced plant volatiles and congregate where feeding is taking place [52]. Motivated by these field studies, we propose a two-patch prey-predator model incorporating foraging movements of predator driven by the strength of prey-predator interaction, to explore how this non-random dispersal behavior of predator affect population dynamics of prey and predator.
Dispersal of predator plays an important role in regulating, stabilizing, or destabilizing population dynamics of both prey and predator. There are fair amount literature on mathematical models of prey-predator interactions in patchy environments. For example, see work of [47, 25, 3, 24, 26, 27, 64, 74, 20, 21, 62, 38, 39] and also see [41] for literature review. Many studies examine how the interactions between patches affect the synchronicity of the oscillations in each patch, e.g. see the work of [28, 35], and how interactions may stabilize or destabilize the dynamics. For instances, [37, 35] studied a model with two patches, each with the wellknown prey-predator Rosenzweig-McArthur dynamics, linked by the density independent dispersal (i.e., dispersal is driven by the difference of species' population densities in two patches). His study showed that this type of spatial predator-prey interactions might exhibit self-organization capable of producing stabilizing heterogeneities in prey distribution, and spatial populations can be regulated through the interplay of local dynamics and migration.
However, due to the intricacies that arise in density-dependent dispersal models, there are relatively limited work on models with non-random foraging behavior of predator or non-linear dispersal behavior [40] but see the two patch model with predator attraction to prey, e.g. [32], or predator attraction to conspecific, e.g. [58], or only predators migrate who are attracted to regions with concentrated food resources, see the work of [22, 8]. [40] proposed a non random foraging PDE model through a mechanistic approach to demonstrate that area-restricted search does yield predator aggregation, and explore the the consequences of area-restricted search for predator-prey dynamics. In addition, they provided many supporting ecological examples (e.g. Coccinellids, blackbirds, etc.) that abide by their theory. [32] studied a two-patch predator-prey Rosenzweig-MacArthur model with nonlinear density-dependent migration in the predator. The migration term of the predator is derived by extending the Holling time budget argument to migration. Their study showed that the extension of the Holling time budget argument to movement has essential effects on the dynamics. By extending the model of [32], [16] formulated a similar two patch prey-predator model with density-independent migration in prey and density-dependent migration in the predator. Their study shows that several foraging parameters such as handling time, dispersal rate can have important consequences in stability of prey-predator system. [10] investigated the population-dispersal dynamics for predator-prey interactions in a two patch environment with assumptions that both predators and their prey are mobile and their dispersal between patches is directed to the higher fitness patch. They proved that such dispersal, irrespectively of its speed, cannot destabilize a locally stable predator-prey population equilibrium that corresponds to no movement at all.
In this paper, we formulates a new version of Rosenzweig-MacArthur two patch prey predator model with mobility only in predator. Our model is distinct from others as we assume that the non-random foraging movements of predator is driven by the strength of prey-predator interactions, i.e., predators move towards patches with more concentrated prey and predator. Our model can apply to many insects systems such as Aphids and Coccinellids, Japanese beetles and their host plants, etc. For instance, the experimental work of [5] demonstrated that attraction to uninfested potato plants by Colorado potato beetle does not occur when the plants are small. However, when small plants are infested by conspecific larvae they become highly attractive to adult beetles. Thus predators beetles are are more attracted toward patches with high prey-predator interaction strength. The prey-predation attraction can also be observed in the field work of [44]. The main focus of our study of such prey-predator interactions in heterogeneous environments is to explore the following ecological questions:
1.How does our proposed nonlinear density-dependent dispersal of predator stabilize or destabilize the system?
2.How does dispersal of predator affect the extinction and persistence of prey and predator in both patches?
3.How may dispersal promote the coexistence of prey and predator when predator goes extinct in the single patch?
4.What are potential spatial patterns of prey and predator?
5.How are the effects of our proposed nonlinear density-dependent dispersal of predator on population dynamics different from the effects of the traditional density-independent dispersal?
The rest of the paper is organized as follows: In Section (2), we provide the detailed derivation of our two patch prey-predator model. In Section (3), we perform completed local and global dynamics of our model, and derive sufficient conditions that lead to the persistence and extinction of predator as well as permanence of the model. In Section (4), we perform bifurcation simulations to explore the dynamical patterns and compare the dynamics of our model to the traditional model [26, 27, 37, 35, 36]. In Section (5), we conclude our study and discuss the potential future study. The detailed proofs of our analytical results are provided in the last section.
2. Model derivations
Let ui(t), vi(t) be the population of prey and predator in Patch i at time t, respectively. In the absence of dispersal, we assume that the population dynamics of prey and predator follow the well-known Rosenzweig-MacArthur prey-predator model as follows:
|
duidt=riui(1−uiki)−biuivi1+bihiuidvidt=cibiuivi1+bihiui−δivi
|
(1)
|
where ri is the intrinsic growth of prey at Patch i; ki is the prey carrying capacity at Patch i; bi is the predator attacking rate at Patch i; hi is the predator handling time at Patch i; ci is the energy conversion rate at Patch i; and δi is the mortality of predator at Patch i.
We assume that the dispersal of predator from one patch to the other is driven by the strength of the prey-predator interaction in two patches which is termed as the attraction strength. More specifically, in the presence of dispersal, the dispersal rate of predators from Patch i to Patch j depends on the prey-predator interaction term bjujvj1+bjhjuj in Patch j, and the dispersal term of predators from Patch i to Patch j is modeled by bjujvj1+bjhjujρijvi which gives the net dispersal of predator at Patch i as follows:
|
bjujvj1+bjhjujρijvi−biuivi1+bihiuiρjivj
|
(2)
|
where ρij is the dispersal constant of predators at Patch j moving to Patch i. This assumption of deriving (2) is motivated by the fact that dispersal of a predator is usually driven by its non-random foraging behavior which can often response to prey-contact stimuli [23] which has been supported in many field studies including the recent work by [44]. Note that the dispersal constant ρij is directional and not sysmmetrical, i.e., ρij may not be equal to ρji. In addition, we assume that prey is immobile. This assumption fits in many prey-predator (or plant-insects) interactions in ecosystems such as Aphid and Ladybugs, Japanese beetles and its feeding plants, etc. Based on these assumptions, a two-patch prey-predator model extended from the single patch model (1) is described as the following set of nonlinear equations:
|
du1dt=r1u1(1−u1k1)−b1u1v11+b1h1u1dv1dt=c1b1u1v11+b1h1u1−δ1v1+(b1u1v11+b1h1u1ρ21v2−b2u2v21+b2h2u2ρ12v1)du2dt=r2u2(1−u2k2)−b2u2v21+b2h2u2dv2dt=c2b2u2v21+b2h2u2−δ2v2+(b2u2v21+b2h2u2ρ12v1−b1u1v11+b1h1u1ρ21v2).
|
(3)
|
We use the similar rescaling approach in [51] by letting
|
xi=bihiui,yi=bihicivi,Ki=bihiki,ai=cihi,di=ciδibihi,
|
then we have
|
v1(b1u11+b1h1u1ρ21v2−b2u2v21+b2h2u2ρ12)=v1(b1x1b1h11+x1ρ21c2b2h2y2−b2x2b2h2c2b2h2y21+x2ρ12)=v1(ρ21a1a2c1b2x1y21+x1−ρ12a22c2b2x2y21+x2)
|
and
|
v2(b2u21+b2h2u2ρ12v1−b1u1v11+b1h1u1ρ21)=v2(b2x2b2h21+x2ρ12c1b1h1y1−b1x1b1h1c1b1h1y11+x1ρ21)=v2(ρ12a1a2c2b1x2y11+x2−ρ21a21c1b1x1y11+x1)
|
For mathematical convenience, we assume that ρ12c2=ρ21c1=ρ, then we have
|
v1(ρ21a1a2c1b2x1y21+x1−ρ12a22c2b2x2y21+x2)=v1y2ρa2b2(a1x11+x1−a2x21+x2)
|
and
|
v2(ρ12a1a2c2b1x2y11+x2−ρ21a21c1b1x1y11+x1)=y1v2ρa1b1(a2x21+x2−a1x1y11+x1).
|
Denote that ρ1=ρa2b2 and ρ2=ρa1b1, then the two-patch model (3) could be rewritten as the following equations:
|
dx1dt=r1x1(1−x1K1)−a1x1y11+x1dy1dt=a1x1y11+x1−d1y1+ρ1(a1x1y11+x1⏟attraction strength to Patch 1y2−a2x2y21+x2⏟attraction strength to Patch 2ρ12y1)dx2dt=r2x2(1−x2K2)−a2x2y21+x2dy2dt=a2x2y21+x2−d2y2+ρ2(a2x2y21+x2⏟attraction strength to Patch 2y1−a1x1y11+x1⏟attraction strength to Patch 1y2)
|
(4)
|
where Ki is the relative carrying capacity of prey in the absence of predation; ai is the relative predation rate at Patch i; di is the relative death rate of predator at Patch i; ρi is the relative dispersal rate of predator at Patch i; and ri is the relative maximum growth rate of prey at Patch i. All parameters are nonnegative. In addition, we could scale r1 away by rescaling the time, i.e., t→tr1. Thus, for the future analysis or simulations, we could let r1=1 and r2=r. In summary, the ecological assumptions of Model (4) can be stated as follows:
1.In the absence of dispersal, Model (4) is reduced to the following uncoupled Rosenzweig-MacArthur prey-predator single patch models
|
dxidt=rixi(1−xiKi)−aixiyi1+xidyidt=aixiyi1+xi−diyi
|
(5)
|
where r1=1 and r2=r and its ecological assumptions [63] can be stated as follows:
(a)In the absence of predation, population of prey xi follows the logistic growth model.
(b)Predator is specialist (i.e., predator yi goes extinct without prey xi) and the functional response between prey and predator follows Hollying Type Ⅱ functional response.
2.There is no dispersal in prey species. This assumption fits in many prey-predator (or plant-insects) interactions in ecosystems such as Aphid and Ladybugs, Japanese beetles and its feeding plants, etc.
3.The dispersal of predator from Patch i to Patch j is driven by the prey-predation interaction strength in Patch j termed as the attraction strength.
3. Mathematical analysis
The state space of Model (4) is R4+. Let μi=diai−di,ν1=(K1−μ1)(1+μ1)a1K1,ν2=r(K2−μ2)(1+μ2)a2K2. We have the following theorem regarding the dynamics properties of Model (4):
Theorem 3.1. Assume all parameters are nonnegative and r,ai,Ki,di,i=1,2 are strictly positive. Model (4) is positively invariant and bounded in R4+ with lim supt→∞xi(t)≤Ki for both i=1,2. In addition, it has the following properties:
1.If there is no dispersal in predator, i.e., ρ1=ρ2=0, then Model (4) is reduced to Model (5) whose dynamics can be classified in the following three cases:
(a) Model (5) always has the extinction equilibrium (0,0) which is a saddle.
(b) If μi>Ki or μi<0, then the boundary equilibrium (Ki,0) is globally asymptotically stable.
(c) If Ki−12<μi<Ki, then the boundary equilibrium (Ki,0) is a saddle while the interior equilibrium (μi,νi) is globally asymptotically stable.
(d) If 0<μi<Ki−12, then the boundary equilibrium (Ki,0) is a saddle; the interior equilibrium (μi,νi) is a source, and the system has a unique limit cycle which is globally asymptotically stable. In addition, the Hopf bifurcation occurs at μi=Ki−12.
2.The sets {(x1,y1,x2,y2)∈R4+:xi=0} and {(x1,y1,x2,y2)∈R4+:yi=0} are invariant for both i=1,2. If xj=0, Model (4) is reduced to the single patch model Model (5). If yj=0, Model (4) is reduced to the following two uncoupled models:
|
dxidt=rixi(1−xiKi)−aixiyi1+xidyidt=aixiyi1+xi−diyi
|
(6)
|
where limt→∞xj(t)=Kj and the dynamics of xi,yi is the same as Model (5).
Notes and biological implications. Theorem 3.1 provides a foundation on our further study of local stability and global dynamics of Model (4). More specifically, Item 2 of Theorem 3.1 implies that Model (4) has the same the invariant sets xi=0 and yi=0 for both i=1,2 as the single patch models (5). In addition, the results of the single patch models (5) indicate that prey is always persist while predator i is persist if 0<μi<Ki hold. We would like to point out that the detailed proofs of dynamics of the single patch models (5) has been provided in the work of [30, 31, 51, 77].
3.1. Boundary equilibria and the stability
Now we start with the boundary equilibria of Model (4). Recall that
|
μi=diai−di,ν1=(K1−μ1)(1+μ1)a1K1,ν2=r(K2−μ2)(1+μ2)a2K2.
|
We define the following notations for all possible boundary equilibria of Model (4):
|
E0000=(0,0,0,0),EK1000=(K1,0,0,0),Eμ1ν100=(μ1,ν1,0,0),EK10μ2ν2=(K1,0,μ2,ν2),EK10K20=(K1,0,K2,0),E00K20=(0,0,K2,0),E00μ2ν2=(0,0,μ2,ν2),Eμ1ν1K20=(μ1,ν1,K2,0).
|
The following theorem provides sufficient conditions on the existence and stability of these boundary equilibria:
Theorem 3.2. [Boundary equilibria of Model (4)] Model (4) always has the following four boundary equilibria
|
E0000,EK1000,E00K20,EK10K20
|
where the first three ones are saddles while EK10K20 is locally asymptotically stable if μi>Ki and it is a saddle if (μ1−K1)(μ2−K2)<0 or μi<Ki,i=1,2. Let i,j=1,2,i≠j, and
|
Eb11=Eμ1ν100,Eb12=Eμ1ν1K20,Eb21=E00μ2ν2andEb22=EK10μ2ν2.
|
Then if 0<μi<Ki, then Model (4) has additional two boundary equilibria Ebi1 and Ebi2 where Ebi1 is always a saddle. The boundary equilibrium Ebi2 is locally asymptotically stable if Ki−12<μi<Ki and one of the following conditions holds:
sa: aj≤di,Kj<μj.
sb: 0<Kj<min{μj,diaj−di}.
sc: 0<diaj−di<Kj<μjandρj<dj−Kj(aj−dj)νi[Kj(aj−di)−di].
sd: 0<μj<Kj<diaj−diandρj>Kj(aj−dj)−djνi[di−Kj(aj−di)].
And Ebi2 is a saddle if 0<μi<Ki−12 or one of the following conditions holds:
ua: Kj>max{μj,diaj−di}.
ub: 0<diaj−di<Kj<μjandρj>dj−Kj(aj−dj)νi[Kj(aj−di)−di].
uc: μj<Kj<diaj−diandρj<Kj(aj−dj)−djνi[di−Kj(aj−di)].
In addition, if 0<μi<Ki for both i=1 and i=2, the boundary equilibria Eb12 and Eb22 exist but they cannot be locally asymptotically stable at the same time while if ri=1,ai=a,di=d,Ki=d for both i=1,2, the boundary equilibria Eb12 and Eb22 can not be locally asymptotically stable at all if they exist.
Notes and biological implications. Theorem 3.2 implies the following points regarding the effects of dispersal in predators:
1.Dispersal has no effects on the local stability of the boundary equilibrium EK10K20.
2.Large dispersal of predator in its own patch may have stabilizing effects from the results of Item sd: In the absence of dispersal, the dynamics of Patch j is unstable at (Kj,0) since 0<μj<Kj. However, in the presence of dispersal, large values of ρj can lead to the local stability of the boundary equilibrium Ebi2 where i,j=1,2 and i≠j, under conditions of μj<Kj<diaj−di.
3.Large dispersal of predator in its own patch may have destabilizing effects from the results of Item ub: In the absence of dispersal, the dynamics of Patch j is local stable at (Kj,0) since Kj<μj. However, in the presence of dispersal, large values of ρj can drive the boundary equilibrium Ebj2 being unstable, under conditions of 0<diaj−d1<Kj<μj.
4.Under conditions of μi<Ki, the boundary equilibria Eb12 and Eb22 can not be asymptotically stable at the same time.
3.2. Global dynamics
In this subsection, we focus on the extinction and persistence dynamics of prey and predator of Model (4). First we show the following theorem regarding the boundary equilibrium EK10K20:
Theorem 3.3. Model (4) has global stability at EK10K20 if μi>Ki,i=1,2.
Notes and biological implications. Theorem 3.3 implies that the dispersal of predators does not effect the global stability of the boundary equilibrium EK10K20.
To proceed the statement and proof of our results on persistence, we provide the definition of persistence and permanence as follows:
Definition 3.4 (Persistence of single species)We say species z is persistent in R4+ for Model (4) if there exists constants 0<b<B, such that for any initial condition with z(0)>0, the following inequality holds
|
b≤lim infτ→∞z(τ)≤lim supτ→∞z(τ)≤B.
|
where z can be xi,yi,i=1,2 for Model (4).
Definition 3.5 (Permanence of a system)We say Model (4) is permanent in R4+ if there exists constants 0<b<B, such that for any initial condition taken in R4+ with x1(0)y1(0)x2(0)y2(0)>0, the following inequality holds
|
b≤lim infτ→∞min{x1(τ),y1(τ),x2(τ),y2(τ)}
|
|
≤lim supτ→∞max{x1(τ),y1(τ),x2(τ),y2(τ)}≤B.
|
The permanence of Model (4) indicates that all species in the system are persistence.
Theorem 3.6. [Persistence of prey and predator] Prey xi,i=1,2 of Model (4) are always persistent for all r>0. Predator yj is persistent if one of the following inequalities hold
1.μj<Kj,μi>Ki. Or
2.Ki−12<μi<KiandKj>max{μj,diaj−di}. Or
3.Ki−12<μi<Ki,μj<Kj<diaj−diandρj<Kj(aj−dj)−djνi[di−Kj(aj−di)].
Notes and biological implications. Theorem 3.6 indicates that the dispersal of predators does not affect the persistence of preys, while small dispersal of predator j, under condition of Ki−12<μi<Ki,μj<Kj<diaj−di, can keep the persistence of predator j. This is consistent with the results of Item uc in Theorem 3.2.
Theorem 3.7 [Permanence of the two patch dispersal model] Model (4) is permanent if one of the following inequalities hold
1.Kj−12<μj<Kj,0<djai−dj<Ki<μiandρi>di−Ki(ai−di)νj[Ki(ai−dj)−dj] where i=1,j=2 or i=2,j=1. Or
2.Kj−12<μj<Kj,μi>Ki−12andKi>max{μi,djai−dj} for both i=1,j=2 and i=2,j=1. Or
3.Ki−12<μi<Ki,Ki>max{μi,djai−dj},Kj−12<μj<Kj<diaj−diandρj<Kj(aj−dj)−djνi[di−Kj(aj−di)] where i=1,j=2 or i=2,j=1.
Notes and biological implications. According to Theorem 3.6, we can conclude that Model (4) is permanent whenever both predators are persistent. Theorem 3.7 provides such sufficient conditions that can guarantee the coexistence of bother predator for the two patch model (4), thus provides sufficient conditions of its permanence. Item 1 of this theorem implies that if predator yj is persistent, and large dispersal of predator yi can promote its persistence, thus, promote the permanence since in the absence of dispersals in predator, predator yi goes extinct due to μi>Ki. This is consistent with the results of Item ub of Theorem 3.2 that large dispersal of predator yi can have destabilize effects on the boundary equilibria Ebj2.
3.3. Interior equilibrium and stability
Let pi(x)=aix1+x and qi(x)=ri(Ki−x)(1+x)aiKi, then we have
|
dxidt=rixi(1−xiKi)−aixiyi(1+xi)=aixi1+xi[ri(Ki−xi)(1+xi)aiKi−yi]=pi(xi)[qi(xi)−yi]dyidt=yi[aixi1+xi−di+ρiyj(aixi1+xi−ajxj1+xj)]=yi[pi(xi)−di+ρiyj(pi(xi)−pj(xj))]
|
If (x∗1,y∗1,x∗2,y∗2) is an interior equilibrium of Model (4), then it satisfies the following equations:
|
qi(xi)−yi=0⇔qi(xi)=yi,pi(xi)−di+ρiyj(pi(xi)−pj(xj))=0⇔pi(xi)=aixi1+xi=ρiyjpj(xj)+di1+ρiyj=ρiqj(xj)pj(xj)+di1+ρiqj(xj)
|
(8)
|
which gives:
|
xi=ρiqj(xj)pj(xj)+diai(1+ρiqj(xj))−(ρiqj(xj)pj(xj)+di)
|
(9)
|
|
=ρiqj(xj)pj(xj)+diρiqj(xj)[ai−pj(xj)]+ai−di
|
(10)
|
Since lim supt→∞xi(t)≤Ki for both i=1,2 and yi=qi(xi), therefore, positive solutions of xi∈(0,Ki) for (9) determine interior equilibrium of Model (4). By substituting the explicit forms of pi,qi into (9), we obtain the following null clines:
|
x1=a2[r2ρ1x2(K2−x2)+K2d1]r2ρ1x2(K2a1−K2a2−a1)−r2ρ1x22(a1−a2)+K2(a1r2ρ1+a1a2−a2d1)=ft(x2)fb(x2)=F(x2)x2=a1[r1ρ2x1(K1−x1)+K1d2]r1ρ2x1(K1a2−K1a1−a2)−r1ρ2x21(a2−a1)+K1(a2r1ρ2+a1a2−a1d2)=gt(x1)gb(x1)=G(x1)
|
(11)
|
with r1=1,r2=r and the following properties:
1.F(0)=ft(0)fb(0)=a2K2d1K2(a1r2ρ1+a1a2−a2d1)=a2d1a1r2ρ1+a1a2−a2d1 and F(K2)=ft(K2)fb(K2)=d1a1−d1=μ1.
2.ft(x2)=a2[r2ρ1x2(K2−x2)+K2d1]≥a2K2d1>0 for x2∈[0,K2] and fb(x2)|a1=a2=a=a[r2ρ1(K2−x2)+K2(a−d1)].
3.G(0)=gt(0)gb(0)=a1K1d2K1(a2r1ρ2+a1a2−a1d2)=a1d2a2r1ρ2+a1a2−a1d2 and G(K1)=gt(K1)gb(K1)=d2a2−d2=μ2.
4.gt(x1)=a1[r1ρ2x1(K1−x1)+K1d2]≥a1K1d1>0 for x1∈[0,K1] and gb(x1)|a1=a2=a=a[r1ρ2(K1−x1)+K1(a−d2)].
Theorem 3.8. [Interior equilibrium] If μi>Ki for both i=1,2, then Model (4) has no interior equilibrium. Moreover, we have the following two cases:
1.Assume that ai>aj where i=1,j=2 or i=2,j=1. Define
|
xci=Ki(riρj+ai−dj−√(ai−dj)(riρj+ai−dj))riρj.
|
Model (4) has no interior equilibrium if ai>aj,ρi<4Kjaj(ai−aj)(di−ai)rj(Kjai−Kjaj+ai)2 hold.
And it has at least one interior equilibrium (x∗1,y∗1,x∗2,y∗2) if the following conditions hold for both i=1,j=2 and i=2,j=1
|
ai>max{aj,d1,d2},aj>max{d1,d2},ρj<4Kiai(aj−ai)(dj−aj)ri(Kiaj−Kiai+aj)2,
|
where sufficient conditions for the inequalities F(xc2)<K1,andG(xc1)<K2 hold are
|
ρi≤4(Kiai−Kidi−di)Kjrjandρj<4Kjaj(Kiai−Kidi−di)ajrjK2j+rjKi(Kjaj−Kjai−ai)2.
|
In addition, we have aidjajriρj+aiaj−aidj<x∗j<Kj for both i=1,j=2 and i=2,j=1.
2.Assume that a1=a2=a. Model (4) has no interior equilibrium if d1>a+r2ρ1 or d2>a+r1ρ2 while it has at least one interior equilibrium (x∗1,y∗1,x∗2,y∗2) if the following inequalities hold
|
a1=a2=a>max{d1,d2},F(xc2)<K1,andG(xc1)<K2
|
where sufficient conditions for the inequalities F(xc2)<K1,andG(xc1)<K2 hold are
for both i=1,j=2 and i=2,j=1. In addition, we have djriρj+a−dj<x∗j<Kj for both i=1,j=2 and i=2,j=1.
Notes and biological implications. Theorem 3.8 provides sufficient conditions on the existence of no interior equilibrium when μi>Ki for either i=1 or i=2; and at least one interior equilibrium of Model (4) when μi<Ki for both i=1,2. The results indicate follows:
1.If μi>Ki, then Model (4) has no interior equilibrium if the dispersal of its predator is too small.
2.If μi<Ki for both i=1,2, then large values of the predation rate ai,aj and small values of dispersal of both predators can lead to at least one interior equilibrium.
The question is how we can solve the explicit form of an interior equilibrium of Model (4). The following theorem provides us an example of such interior equilibrium of Model (4).
Theorem 3.9. [Interior equilibrium and the stability] Suppose that d1=d2=d. Let
|
μ1=da1−d,ν1=(K1−μ1)(1+μ1)a1K1,μ2=da2−d,ν2=r(K2−μ2)(1+μ2)a2K2.
|
If 0<μi<Ki for both i=1 and i=2, then Ei=(μ1,ν1,μ2,ν2) is an interior equilibrium of Model (4) and its stability can be classified in the following cases:
1.Ei is locally asymptotically stable if Ki−12<μi<Ki hold for both i=1 and i=2 while it is unstable if the following inequality holds
|
μ1(K1a1−a1−K1d−d)a1K1+rμ2(K2a2−a2−K2d−d)a2K2>0.
|
2.Assume that (K1a1−a1−K1d−d)(K2a2−a2−K2d−d)<0 and
|
μ1(K1a1−a1−K1d−d)a1K1+rμ2(K2a2−a2−K2d−d)a2K2<0.
|
If Kiai−ai−Kid−d>0 (i.e., μi<Ki−12) for either i=1 or i=2, then the large values of ρi can make Ei being locally asymptotically stable, i.e.,
|
ρi>max{−νj−rjμiμj(Kiai−Kid−ai−d)(Kjaj−Kjd−aj−d)(KiKjajνjdνi(ai−d)2),
|
|
−μiνjKj(νiρj+1)(aj−d)2(Kiai−Kid−ai−d)rjμjνiKi(ai−d)2(Kjaj−Kjd−aj−d)−1νj}.
|
If, in addition, a1=a2=a,K1=K2=K,r=1, then μ1=μ2=μ=da−d,ν1=ν2=ν=(K−μ)(1+μ)aK, and Ei=(μ,ν,μ,ν) is the only interior equilibrium for Model (4) which has the same local stability as the interior equilibrium (μ,ν) for the single patch model (5), i.e., Ei is locally asymptotically stable if K−12<μ<K while it is unstable if μ<K−12.
Notes and biological implications. Theorem 3.9 implies Model (4) has an interior equilibrium Ei=(μ1,ν1,μ2,ν2) if d1=d2=d and 0<μi<Ki for both i=1,2. In addition, Theorem 3.9 indicates that dispersal of predators has no effects on the local stability if Ki−12<μi<Ki for both i=1,2 or one of the single patch models (5) is unstable and μ1(K1a1−a1−K1d−d)a1K1+rμ2(K2a2−a2−K2d−d)a2K2>0. However, large dispersal of predator at Patch i can stabilize the interior equilibrium when its single patch model model is unstable at (μi,νi) with μ1(K1a1−a1−K1d−d)a1K1+rμ2(K2a2−a2−K2d−d)a2K2<0.
4. Effects of dispersal on dynamics
From mathematical analysis in the previous sections, we can have the following summary regarding the effects of dispersal of predators for Model (4):
1.Large dispersal of predator at Patch i can stabilize or destabilize the boundary equilibrium of x∗i=Ki,y∗i=0,x∗j=μj,y∗j=νj depending on additional conditions.
2.Small dispersal of predator at Patch i may preserve its persistence under certain conditions. On the other hand, large dispersal of predator at Patch i may promote its persistence when the other predator is already persist even if μi>Ki.
3.Dispersal has no effects on the persistence of prey and the number of boundary equilibrium. It has also no effects on the local stability of the boundary equilibrium EK10K20 and the symmetric interior equilibrium (μ,ν,μ,ν) when it exists.
4.If di>ai, then small dispersal of predator at Patch i prevents the interior equilibrium while if 0<μi<Ki, large predations rates ai,aj and small dispersal of predators at both patches can lead to at least one interior equilibrium.
5.If di=dj and 0<μi<Ki−12,Kj−12<μj<Kj, then large dispersal of predator at Patch i can stabilize the interior equilibrium (μi,νi,μj,νj).
To continue our study, we will perform bifurcations diagrams and simulations to explore the effects on the dynamical patterns and compare dynamics of our model (4) to the classical two patch model (12).
4.1. Bifurcation diagrams and simulations
In this subsection, we perform bifurcation diagrams and simulations to obtain additional insights on the effects of dispersal on the dynamics of our proposed two patch model (4). We fix r1=1,r2=1.5,K1=5,K2=3,d1=0.2,d2=0.1. Then according to Theorem 3.1, we know that in the absence of dispersal, the dynamics of Patch 1 has global stability at (5,0) if 0<a1<0.24; it has global stability at its unique interior equilibrium (0.2a1−0.2,(5−0.2a1−0.2)(1+0.2a1−0.2)5) if 2<0.2a1−0.2<5⇔0.24<a1<0.3; and it has a unique limit cycle if a1>0.3; while the dynamics of Patch 2 has global stability at (3,0) if 0<a2<0.133; it has global stability its unique interior equilibrium (0.1a2−0.1,1.5(3−0.1a2−0.1)(1+0.1a2−0.1)3) if 1<0.1a2−0.1<3⇔0.133<a2<0.2 while it has a unique limit cycle if a2>0.2. Now we consider the following cases:
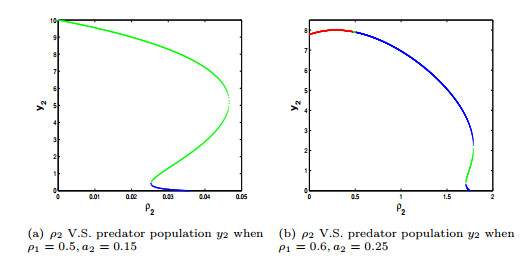
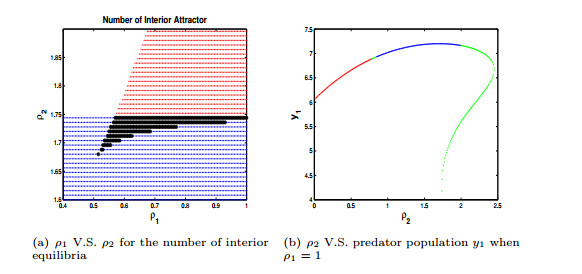
1.Choose a1=0.25 and a2=0.15. In the absence of dispersal, the dynamics at both Patch 1 and 2 have global stability at its unique interior equilibrium (4,1), (2,1.5), respectively. After turning on the dispersal, the coupled two patch model can have one interior equilibrium (see the blue regions in Figure (1a)) which can be locally stable (see the blue dots in Figure (1b)), or be a saddle (see the green dots in Figure (1b)) where the coupled system has fluctuated dynamics; or it can have two interior equilibria (see the red regions in Figure (1a)) which could be saddles and generate bistability between fluctuated interior dynamics and the boundary attractor (4,1,3,0) (see the examples of two interior saddles of Figure (4a)); or it can have three interior equilibria (see the black regions in Figure (1a)) which generate multiple interior attractors (see the examples of two saddles, one sink and two sinks, one saddle of Figure (1b)) or it could have no interior equilibrium (see white and yellow regions of Figure (1a)). Bifurcation diagrams Figure (1a), (1b), and (4b) suggest that dispersal may destabilize system and generate fluctuated dynamics; may generate multiple interior attractors (the case of three interior equilibria), thus generate multiple attractors; or even may drive extinction of predator in one or both patches (he case of two interior equilibria, no interior equilibrium, respectively).
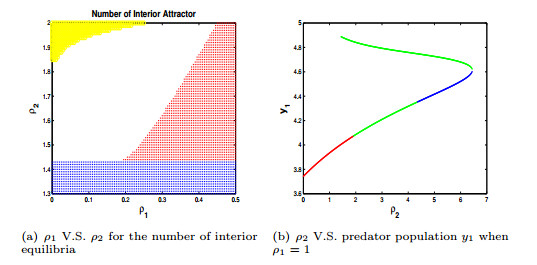
2.Choose a1=0.25 and a2=0.25. In the absence of dispersal, the dynamics of Patch 1 has global stability at its unique interior equilibrium (4,1) while the dynamics of Patch 2 has a unique stable limit cycle around (2,1.5). After turning on the dispersal, the coupled two patch model can have one interior equilibrium (see the blue regions in Figure (2a)) which can be locally stable (see the blue dots in Figure (2b)), or be a saddle (see the green dots in Figure (2b)), or be a source (see the red dots in Figure (2b)) where the coupled system has fluctuated dynamics for the later two cases; or it can have two interior equilibria (see the red regions in Figure (1a)) which could be two saddles or one sink, one saddle and generate bistability between the interior attractor and the boundary attractor (see Figure (2b)); or it can have three interior equilibria (see the black regions in Figure (1a)) which generate multiple interior attractors (see the examples of two sinks and one saddle of Figure (4b)) or it could have no interior equilibrium (see white regions of Figure (2a)). Bifurcation diagrams of Figure (2a), (2b), and (4b) suggest that dispersal may stabilize system and generate equilibrium dynamics; may generate multiple interior equilibria (the case of three interior equilibria), thus generate multiple attractors; or even may drive extinction of predator in one or two both patches (the case of two interior equilibria, no interior equilibrium, respectively).
3.Choose a1=0.35 and a2=0.25. In the absence of dispersal, the dynamics of both Patch 1 and 2 have a unique stable limit cycle. After turning on the dispersal, the coupled two patch model can have one interior equilibrium (see the blue regions in Figure (3a)) which can be a sink (see the red dots in Figure (3b)) where the coupled system has fluctuated dynamics; or it can have two interior equilibria (see the red regions in Figure (2a)) which could be two saddles, one sink v.s. one saddle, one source v.s. one saddle and generate bistability between the interior attractors and the boundary attractor (see Figure (3b)); it could have no interior equilibrium (see white and yellow regions of Figure (3a)). Bifurcation diagrams Figure (2a)-(3b) suggest that dispersal may generate bistability between the interior attractor and the boundary attractor; or even may drive the extinction of predator in one or both patches (the case of two interior equilibria, no interior equilibrium, respectively).
In summary, Figure 1, 2, 3, and 4 suggest that dispersal of predator may stabilize or destabilize interior dynamics; it may drive the extinction of predator in one or both patches; and it may generate the following patterns of multiple attractors via two or three interior equilibria:
1.Multiple interior attractors through three interior equilibria: In the presence of dispersal, Model (4) can have the following types of interior equilibria and the corresponding dynamics:
• Two interior sinks and one interior saddle: Depending on the initial conditions with x1(0)y1(0)x2(0)y2(0)>0, Model (4) converges to one of two sinks for almost all initial conditions (see examples in Figure (1b)-(4b)).
• One interior sink and two interior saddles: Depending on the initial conditions with x1(0)y1(0)x2(0)y2(0)>0, Model (4) either converges to the sink or has fluctuated dynamics for almost all initial conditions (see examples in Figure (1b), (4a)).
We should also expect the case of one sink v.s. one saddle v.s. one source and the case of two source v.s. one saddle when the interior sink(s) become unstable and go through Hopf-bifurcation. In addition, Model (4) seems to be permanent whenever it processes three interior equilibria.
2.Boundary attractors and interior attractors through three interior equilibria:
• one interior sink and one interior saddle: Depending on the initial conditions with x1(0)y1(0)x2(0)y2(0)>0, Model (4) converges either to the interior sinks or to the boundary attractors with one predator going extinct for almost all initial conditions (see examples in Figure (2b), (3b), (4b)).
• two interior saddles: Model (4) converges either to the fluctuated interior attractors or to the boundary attractors with one predator going extinct for almost all initial conditions depending on the initial conditions with x1(0)y1(0)x2(0)y2(0)>0 (see examples in Figure (2b), (3b), 4).
• one interior source and one interior saddle: Depending on the initial conditions with x1(0)y1(0)x2(0)y2(0)>0, Model (4) converges either to the fluctuated interior attractors or to the boundary attractors with one predator going extinct for almost all initial conditions (see examples in Figure (3b)).
Model (4) has bistability between interior attractors and the boundary attractors whenever it processes two interior equilibria. This implies that depending on the initial conditions, predator at one patch can go extinct when the system has two interior equilibria.
In general, simulations suggest that Model (4) is permanent when it processes one or three interior equilibria while it has bistability between interior attractors and the boundary attractors whenever it processes two interior equilibria.
4.2. Comparisons to the classic model
The dispersal of predator in our model is driven by the strength of prey-predator interactions. This is different from the classical dispersal model such as Model (12) which has been introduced in [36]:
|
dxidt=rixi(1−xiKi)−aixiyi1+xidyidt=aixiyi1+xi−diyi+ρi(yj−yi)dxjdt=rjxj(1−xjKj)−ajxjyj1+xjdyjdt=ajxjyj1+xj−djyj−ρj(yj−yi)
|
(12)
|
where i=1,j=2 or i=2,j=1 with r1=1,r2=r. The symmetric case of Model (12) (i.e., ri=rj, ai=aj, Ki=Kj, di=dj, and ρi=ρj) has been discussed and studied by [36] through simulations of different scenarios of local bifurcation analysis. Jansen's study shows that the classical two-patch model (12) has a rich dynamical behavior where spatial predator-prey populations can be regulated through the interplay of local dynamics and migration: (ⅰ) for very small migration rates the oscillations always synchronize; (ⅱ) For intermediate migration rates the synchronous oscillations are unstable and there are periodic, quasi-periodic, and intermittently chaotic attractors with asynchronous dynamics; and (ⅱ) For large predator migration rates, attractors in the form of equilibria or limit cycles exist in which one of the patches contains no prey.
Recently, [51] studied Model (12) with both dispersal in prey and predator. Liu provide global stability of the interior equilibrium for the symmetric case and performed simulations for the asymmetric cases. Here we provide rigorous results on the persistence and permanence conditions that can be used for the comparisons to our Model (4) in the following theorem:
Theorem 4.1. [Summary of the dynamics of Model (12)] Define
|
^μi=^diai−^di,^νi=qi(^μi)=ri(Ki−^μi)(1+^μi)aiKiandˆνij=ρj^νidj+ρj
|
where ^di=di+ρidjdj+ρj. Let Eb1=Ex1y10y2=(^μ1,^ν1,0,ˆν12) and Eb2=E0y1x2y2=(0,ˆν21,^μ2,ˆν2). Then we have the following summary on the dynamics of Model (12)
1.Model (12) is positively invariant and bounded in its state space R4+ with lim supt→∞xi(t)≤Ki for both i=1 and i=2.
2.Boundary equilibria: Model (12) always has the following four boundary equilibria
|
E0000,EK1000,E00K20,EK10K20
|
where the first three ones are saddles while EK10K20 is locally asymptotically stable if
|
d1+d2+ρ1+ρ2>a1K11+K1+a2K21+K2
|
and
|
ˆd1−a1K11+K1+K2a2(a1K11+K1−d1−ρ1)(d2+ρ2)(1+K2)>0⇔[d1−a1K11+K1][1−K2a2(d2+ρ2)(1+K2)]+ρ1d2+ρ2[d2−K2a2(1+K2)]>0.
|
and it is a saddle if one of the above inequalities does not hold. If 0<ˆμi<Ki, then the boundary equilibrium Ebi exists which is locally asymptotically stable if Ki−12<^μi<Ki,rj<ajˆνij.
3.Subsystem i: If xj=0, then Model (12) reduces to the following subsystem (13) with three species xi,yi,yj:
|
dxidt=rixi(1−xiKi)−aixiyi1+xidyidt=aixiyi1+xi−diyi+ρi(yj−yi)dyjdt=−djyj−ρj(yj−yi)
|
(13)
|
whose global dynamics can be described as follows:
3a Prey xi is persistent for Model (13) with lim supt→∞xi(t)≤Ki.
3b Model (13) has global stability at (Ki,0,0) if ^μi>Ki.
3c Model (13) has global stability at (^μi,^νi,ˆνij) if Ki−12<^μi<Ki.
4.Persistence of prey: Prey xi persists if ^μj<0, or ^μj>Kj, or Kj−12<^μj<Kj,ri>aiˆνji hold.Both prey xi and xj persist if one of the following three conditions hold
4(a) ^μi>Ki for both i=1 and i=2. Or ^μi<0 for both i=1 and i=2.
4(b)Ki−12<^μi<Ki,rj>ajˆνij for both i=1,j=2 and i=2,j=1.
4(c) ^μi>Ki, or ^μi<0, and Kj−12<^μj<Kj,ri>aiˆνji for either i=1,j=2 or i=2,j=1.
5.Extinction of prey xi: Prey xi goes to extinction if Kj−12<^μj<Kj and ri(Ki+1)24aiKi<ˆνij. In addition, under these conditions, Model (12) has global stability at (0,ˆνji,^μj,^νj).
6.Persistence and extinction of predators: Predator yi and yj have the same persistence and extinction conditions. Predators persist if 0<μi<Ki for both i=1 and i=2 while both predators go extinct if μi>Ki for both i=1 and i=2. In addition, Model (12) has global stability at (K1,0,K2,0) for the later case.
7.Permanence of Model (12): Model (12) is permanent if 0<μi<Ki for both i=1 and i=2 and one of 4(a), 4(b), 4(c) hold.
8.The symmetric case: Let r1=r2=1,a1=a2=a,b1=b2=b,d1=d2=d and K1=K2=K, then μ1=μ2=μ and ν1=ν2=ν. Therefore, we can conclude that Model (13) has global stability at (μ,ν,μ,ν) if K−12<μ<K. In addition, the local stability of (μ,ν,μ,ν) for Model (12) is the same as the local stability of (μ,ν) for single patch models when ρ1=ρ2=0 of Model (12).
Notes. Theorem 4.1 indicates follows:
1.If μi>Ki and 0<μj<Kj, then the large dispersal of predator at Patch i stabilizes EK10K20.
2.Proper dispersal of predators can drive the extinction of prey in one patch.
3.Dispersal has no effects on the persistence of predator. This is different from our proposed model (12).
To see how different types of strategies in dispersal of predators affect population dynamics of prey and predator, we start with the comparison of the boundary equilibria of our model (4) and the classic model (12). Both Model (4) and (12) always have four boundary equilibria E0000=(0,0,0,0), EK1000=(K1,0,0,0), E00K20=(0,0,K2,0) and EK10K20=(K1,0,K2,0) among which first three are saddles in both the cases. If 0<μi<Ki for i=1,2, then Model (4) has another two boundary equilibria Ebi1 and Ebi2 where Ebi1 is a saddle. If 0<ˆμi<Ki, then Model (4) has another boundary equilibrium Ebi. We summarize and compare the dynamics of our model (4) with dispersal in predator driven by the strength of predation and the classical model (12) with dispersal in predator driven by the difference of predator densities in Table 1-Table 3. We highlight effects of dynamical outcomes due to different dispersal strategies in predators between Model (4) and (12) as follows:
Table 1. The comparison of boundary equilibria between Model (4) and Model (12). LAS refers to the local asymptotical stability, and GAS refers to the global stability.
| Scenarios |
Model (4) whose dispersal is driven by the strength of prey-predator interactions |
Classical Model (12) whose dispersal is driven by the density of predators |
| EK10K20 |
LAS and GAS if μi>Ki for both i=1,2. Dispersal has no effects on its stability. |
GAS if μi>Ki for both i=1,2; While LAS if d1+d2+ρ1+ρ2>a1K11+K1+a2K21+K2 and [d1−a1K11+K1][1−a2K2(d2+ρ2)(1+K2)]+ρ1d2+ρ2[d2−a2K21+K2]>0. Large dispersal may be able to stabilize the equilibrium. |
| Ebi2 (yi=0) |
LAS if Ki−12<μi<Ki and one of the conditions sa, sb, sc, sd in Theorem 3.2 holds. Large dispersal has potential to either stabilize or stabilize the equilibrium. |
Does not exists |
| Ebi (xi=0) |
Does not exists |
LAS if Ki−12<ˆμi<Ki and rj<ajˆνij. GAS if Ki−12<ˆμi<Ki and rj(Kj+1)24ajKj<ˆνji. Large dispersal of predator in Patch i will either destroy or destabilize the equilibrium while large dispersal of predator in Patch j may stabilize the equilibrium. |
Table 2. The comparison of prey persistence and extinction between Model (4) and Model (12).
| Scenarios |
Model (4) whose dispersal is driven by the strength of prey-predator interactions |
Classical Model (12) whose dispersal is driven by the density of predators |
| Persistence of prey |
Always persist, dispersal of predator has no effects |
One or both prey persist if conditions 4. in Theorem (4.1) holds. Small dispersal of predator in Patch i and large dispersal of predator in Patch j can help the persistence of prey in Patch i. |
| Extinction of prey |
Never extinct |
xi extinct if Kj−12<ˆμj<Kj and ri(Ki+1)24aiKi<ˆνji. Large dispersal of predator in Patch i can promote the extinction of prey in Patch i. |
Table 3. The comparison of predator persistence and extinction between Model (4) and Model (12).
| Scenarios |
Model (4) whose dispersal is driven by the strength of prey-predator interactions |
Classical Model (12) whose dispersal is driven by the density of predators |
| Persistence of predator |
Predator at Patch j is persistent if Conditions in Theorem 3.6 holds. Small dispersal of predator in Patch j can help the persistence of predator in that patch. Dispersal is able to promote the persistence of predator when predator goes extinct in the single patch model. |
Predators in both patches have the same persistence conditions. They persist if 0<μi<Ki for i=1,2. Dispersal seems to have no effects in the persistence of predator. |
| Extinction of predator |
Simulations suggestions (see the yellow regions of Figure (1a) and Figure (3a)) that the large dispersal of predator in Patch i may lead to the its own extinction. |
Predators in both patches have the same extinction conditions. They go extinct if μi>Ki or μi<0 for i=1,2 |
1.The boundary equilibria: EK10K20, Ebi2 and Ebi. The comparisons listed in Table 1 suggest that dispersal of predator has larger effects on the boundary equilibrium of the classic model than ours.
2. Persistence and extinction of prey. According to the comparison of sufficient conditions leading either persistence or extinction of prey in a patch listed in Table 2, we can conclude that the strength of dispersal ability of predator has huge impact on the prey for the classical model (12) but not for our model (4).
3. Persistence and extinction of predator. Simulations and the comparison of sufficient conditions leading either persistence or extinction of predators in a patch listed in Table 3, suggest that the strength of dispersal ability of predator has profound impacts on the persistence of predator for our model (4) while it has no effects on the persistence of predator for the classical model (12).
4.Permanence of a system depends on the persistence of each species involved in the system. Our comparisons of sufficient conditions leading to the persistence of prey and predator listed in Table 2-3, indicate that dispersal of predator has important impacts in the persistence of predator in our model (4) while it has significant effects on the persistence of prey of the classical model (12). We can include that (ⅰ) the large dispersal of predator in a patch has potential lead to the extinction of prey (the classical model (12)) or predator (our model (12)) in that patch, thus destroy the permanence of the system; (ⅱ) the small dispersal of predator in Patch i with the large dispersal in Patch j can promote the persistence of prey (the classical model (12)) or predator (our model (12)) in Patch i, thus promote the permanence of the system.
5.Interior equilibria: Both our model (4) and the classical model (12) have the maximum number of three interior equilibria. However, for the symmetric case, our model (4) can have the unique interior equilibrium (see Theorem 3.9) while the classical model can potentially process three interior equilibria [36].
6.Multiple attractors: Both our model (4) and the classical model (12) have two types bi-stability: (a) The boundary attractors where one of prey or predator can not sustain and the interior attractors where all four species can co-exist; and (b) Two distinct interior attractors. One big difference we observed is that for the symmetric case when each single patch model has global stability at its unique interior equilibrium, our model (4) can have only one interior attractor while the classical model can potentially have two distinct interior attractors. This is due to the fact that Model (4) has unique interior equilibrium while Model (12) can potentially process three interior equilibria as we mentioned earlier.
5. Conclusion
The idea of "metapopulation" originated from [48] where R. Levins used the concept to study the dynamics of pests in agricultural field in which insect pests move from site to site through migrations. Since Levin's work, many mathematical models have been applied to study prey-predator interactions between two or multiples patches that are connected through random dispersion, see examples in [37, 36, 7, 43, 35, 46, 47, 59, 9, 26, 2, 55, 29]. The study of these metapopulation models help us get a better understanding of the dynamics of species interacting in a heterogeneous environment, and allow us to obtain a useful insight of random dispersal effects on the persistence and permanence of these species in the ecosystem. Recently, there has been increasing empirical and theoretical work on the non-random foraging movements of predators which often responses to prey-contact stimuli such as spatial variation in prey density [11, 40], or different type of signals arising directly from prey [76]. See more related examples of mathematical models in [49, 45, 12, 8, 13, 22, 10, 44, 16, 32, 28, 56]. Kareiva [41] provided a good review on varied mathematical models that deal with dispersal and spatially distributed populations and pointed out the needs of including non-random foraging movements in meta-population models. Motivated by this and the recent experimental work of immobile Aphids and Coccinellids by [44], we formulate a two patch prey-predator model (4) with the following assumptions: (a) In the absence of dispersal the model reduced to the two uncoupled Rosenzweig-MacArthur prey-predator single patch models (5); (b) Prey is immobile; and (c) Predator foraging movements are driven by the strength of prey-predator interaction. We provide basic dynamical properties such positivity and boundedness of our model in Theorem 3.1.
Based on our analytic results and bifurcation diagrams, we list our main findings regarding the following questions stated in the introduction how our proposed nonlinear density-dependent dispersal of predator stabilizes or destabilizes the system; how it affects the extinction and persistence of prey and predator in both patches; how it may promote the coexistence; and how it can generate spatial population patterns of prey and predator:
1.Theorem (3.2) provides us the existence and local stability features of the eight boundary equilibria of our model (4). This result indicates that large dispersal of predator in its own patch may have both stabilizing and destabilizing effects on the boundary equilibrium depending on certain conditions. Theorem (3.3) gives sufficient conditions on the extinction of predator in both patches, which suggest that predator can not survive in the coupled system if predator is not able to survive at its single patch. In this case, dispersal of predator has no effect on promoting the persistence of predator but dispersal may drive predator extinct even if predator is able to persist at the single patch state (see white regions of Figure (1a), (2a), and (3a)).
2.Theorem (3.6) provides sufficient conditions of the persistence of prey and predator while Theorem (3.7) provides sufficient conditions of the permanence of our two patch model. These results imply that under certain conditions, large dispersal of predator can promote its persistence, thus, promote the permanence of the coupled system while predator in that patch goes extinct in the absence of dispersal. Our numerical studies also suggests that large dispersal can also drive the extinction of predators in both patches (see white regions of Figure (1a), (2a), and (3a)).
3.Theorem (3.8) and Theorem (3.9) provide sufficient conditions on the existence and the local stability of the interior equilibria under certain conditions. Our analytic study shows that large dispersal of predator may be able to stabilize the interior equilibrium when one of the single patch has global stable interior equilibrium while the other one has limit cycle dynamics. At the mean time, our bifurcation diagrams (see Figure (1b), (2b), and (2b)) suggest that the stabilizing or destabilizing effects of predator's dispersal are not definite, i.e., dispersal can either stabilize or destabilize the system depending on other life history parameters. Moreover, our simulations also suggest that the dispersal of predator can either generate multiple interior equilibria or destroy the interior equilibrium which leads to the extinction of predator in one patch or predators in both patches.
Comparisons to the classic model (12). We provide detailed comparison between the dynamics of our model (4) to the classic model (12). These comparisons suggest that the mode of forging movement of predator has profound impacts on the dynamics of the coupled two patch model.Here we highlight two significant differences: (1) the strength of dispersal ability of predator has profound impacts on the persistence of predator for our model (4) while it has no effects on the persistence of predator for the classical model (12). However, the dispersal of predator has huge impacts on the persistence of prey for the classical model (12) while it has little or no effects on the persistence of prey for our model (4). And (2) for the symmetric case, our model (4) has a unique interior equilibrium while the classical model (12) can have up to three interior equilibria thus it is able to generate different spatial patterns.
6. Proofs
Proof of Theorem 3.1
Proof.Notice that both dxidt|xi=0=0 and dyidt|yi=0=0 for i=1,2, thus according to Theorem A.4 (p.423) in [73], we can conclude that the model (4) is positive invariant in R4+. Now we can go ahead to show the boundedness of the system. First, we have the following inequalities due to the property of positive invariance:
|
dxidt=rixi(1−xiKi)−aixiyi1+xi≤rixi(1−xiKi)
|
which implies that
Define V=ρ2(x1+y1)+ρ1(x2+y2), then we have
|
dVdt=rho2d(x1+y1)dt+ρ1d(x2+y2)dt=ρ2x1(1−x1K1)+ρ1rx2(1−x2K2)−ρ2d1y1−ρ1d2y2=ρ2x1(1−x1K1)+ρ1rx2(1−x2K2)+ρ2d1x1+ρ1d2x2−ρ2d1(x1+y1)−ρ1d2(x2+y2)≤M−d[ρ2(x1+y1)+ρ1(x2+y2)]=M−dV
|
where d=min{d1,d2} and
|
M=max0≤x1≤K1{ρ2x1(1−x1K1+d1)}+max0≤x2≤K2{ρ1x2(1−x2K2+d2)}.
|
Therefore, we have
|
lim supt→∞V(t)=lim supt→∞ρ2(x1(t)+y1(t))+ρ1(x2(t)+y2(t))≤Md
|
which implies that Model (5) is bounded in R4+.
If there is no dispersal in predator, i.e., ρi=0,i=1,2, we can easily check that Model (4) is reduced to the two uncoupled Rosenzweig-MacArthur prey-predator single patch models (5) with r1=1 and r2=r. The global dynamics of the single patch model (5) can be summarized from the work of [50, 51, 30, 31]. Thus, we omit the detailed proof here.
Recall that both dxidt|xi=0=0 and dyidt|yi=0=0 for i=1,2, therefore, the sets {(x1,y1,x2,y2)∈R4+:xi=0} and {(x1,y1,x2,y2)∈R4+:yi=0} are invariant. This indicates that if xj(0)=0, then xj(t)=0 for all t>0. Therefore, the population of yj converges to 0 since
|
dyjdt=−djyj−ρjaixiyi1+xiyj≤0⇒lim supt→∞yj(t)=0.
|
Applying the results in [69], we can conclude that Model (4) is reduced to the single patch model (5) when xj=0.
In the case that yj=0, Model (4) is reduced to Model (7) by replacing yj=0 in Model (4).
Summarizing the discussions above, we can conclude that the statement of Theorem 3.1 holds.
Proof of Theorem 3.2.
Proof.According Theorem 3.1, sufficient condition for the single patch model (5) having the unique interior equilibrium (μi,νi),i=1,2 is μi<Ki. Therefore, sufficient condition for Model (4) having boundary equilibria Eμ1ν100 andEμ1ν1K20 is μ1<K1. Similarly, sufficient condition for Model (4) having boundary equilibria E00μ2ν2 and EK10μ2ν2 is μ2<K2.
The local stability of an equilibrium (x∗1,y∗1,x∗2,y∗2) can be determined by the eigenvalues λi, i=1, 2, 3, 4 of the Jacobian matrix J(x∗1,y∗1,x∗2,y∗2) (14) of Model (4) evaluated at the equilibrium.
|
J(x∗1,y∗1,x∗2,y∗2)=|(1−2x∗1K1)−a1y∗1(1+x∗1)2−a1x∗11+x∗100a1y∗1(1+ρ1y∗2)(1+x∗1)2a1x∗1(1+ρ1y∗2)1+x∗1−ρ1a2x∗2y∗21+x∗2−d1−ρ1a2y∗1y∗2(1+x∗2)2ρ1y∗1(a1x∗11+x∗1−a2x∗21+x∗2)00r(1−2x∗2K2)−a2y∗2(1+x∗2)2−a2x∗21+x∗2−ρ2a1y∗1y∗2(1+x∗1)2ρ2y∗2(a2x∗21+x∗2−a1x∗11+x∗1)a2y∗2(1+ρ2y∗1)(1+x∗2)2a2x∗2(1+ρ2y∗1)1+x∗2−ρ2a1x∗1y∗11+x∗1−d2|
|
(14)
|
After substituting the boundary equilibria E0000, EK1000, E00K20, Eμ1ν100 and E00μ2ν2 into the Jacobian Matrix (14), we can conclude that these equilibria are saddles since they have both positive and negative eigenvalues.
The eigenvalues of (14) evaluated at EK10K20 are as follows:
|
λ1=−1 (<0), λ2=a1K11+K1−d1<0⇔μ1>K1,
|
|
λ3=−r (<0), λ4=a2K21+K2−d2<0⇔μ2>K2.
|
Therefore, EK10K20 is locally asymptotically stable if μi>Ki,i=1,2 while it is a saddle if either (μ1−K1)(μ2−K2)<0 or μi<Ki,i=1,2 holds.
Now we focus on the local stability of Eμ1ν1K20 and EK10μ2ν2 when they exist. After substituting the boundary equilibrium Eμ1ν1K20 to (14), we can obtain the eigenvalues of the Jacobian matrix evaluated at this boundary equilibrium as follows:
|
λ1=−r,λ2=K2(a2−d2)−d21+K2+ρ2ν1[K2(a2−d1)−d1](1+K2)
|
and
|
λ3+λ4=K1(a1−d1)−(a1+d1)a1K1(a1−d1),λ3λ4=d1(K1(a1−d1)−d1)a1K1.
|
Notice that the eigenvalues of λ3 and λ4 being negative is equivalent to the case that the unique interior equilibrium (μ1,ν1) being locally asymptotically stable for the single patch model (5) when i=1. Thus, we can conclude that K1−12<μ1<K1 are sufficient conditions for λ3 and λ4 being negative. Now we explore sufficient conditions for λ2 being negative. First, we have μ1<K1 due to the existence of Eμ1ν1K20. We have the following three cases:
1.If μ2>K2⇔K2(a2−d2)−d2<0, then the first term of λ2 is negative. This also implies that Model (4) has no boundary equilibria of E00μ2ν2 and EK10μ2ν2. Since μ1<K1, therefore, we have λ2<0 for all ρ2>0 if a2≤d1 or K2<d1a2−d1 since
|
K2(a2−d1)−d1<0⇔eithera2≤d1 or K2<d1a2−d1.
|
Therefore, we can conclude that λ2 is negative if either a2≤d1,K2<μ2 or K2<min{μ2,d1a2−d1}. Assume that K2(a2−d1)−d1>0 (i.e., K2>d1a2−d1>0), then λ2<0 if ρ2 is small enough, i.e., satisfies the condition of ρ2<d2−K2(a2−d2)ν1[K2(a2−d1)−d1]. In this case, we can conclude that λ2 is negative if
|
0<d1a2−d1<K2<μ2andρ2<d2−K2(a2−d2)ν1[K2(a2−d1)−d1].
|
2.If μ2<K2⇔K2(a2−d2)−d2>0, then the first term of λ2 is positive. This also implies that Model (4) has two boundary equilibria of E00μ2ν2 and EK10μ2ν2. In this case, sufficient conditions for λ2 being negative are K2<d1a2−d1 and ρ2 large enough. More specifically, ρ2 has to satisfy the following inequality:
|
ρ2>K2(a2−d2)−d2ν1[d1−K2(a2−d1)].
|
Therefore, λ2 is negative if μ2<K2<d1a2−d1andρ2>K2(a2−d2)−d2ν1[d1−K2(a2−d1)].
Summarizing the discussions above, we can conclude that the boundary equilibrium Eμ1ν1K20 is locally asymptotically stable if K1−12<μ1<K1 and one of the following conditions holds:
1.a2≤d1,K2<μ2.
2.K2<min{μ2,d1a2−d1}.
3.0<d1a2−d1<K2<μ2andρ2<d2−K2(a2−d2)ν1[K2(a2−d1)−d1].
4.μ2<K2<d1a2−d1andρ2>K2(a2−d2)−d2ν1[d1−K2(a2−d1)].
And Eμ1ν1K20 is a saddle if μ1<K1−12 or one of the following conditions holds:
1.K2>max{μ2,d1a2−d1}.
2.0<d1a2−d1<K2<μ2andρ2>d2−K2(a2−d2)ν1[K2(a2−d1)−d1].
3.μ2<K2<d1a2−d1andρ2<K2(a2−d2)−d2ν1[d1−K2(a2−d1)].
Similarly, we can obtain sufficient conditions for the local stability of the boundary equilibrium EK10μ2ν2 as the statement.
If μi<Ki, then Model (4) has the boundary equilibria Eμ1ν1K20 and EK10μ2ν2 according to Theorem 3.2 and the discussions above. If both Eμ1ν1K20 and EK10μ2ν2 are locally stable, then the following inequalities are satisfied:
|
μ1<K1<d2a1−d2⇒d1a1−d1<d2a1−d2⇒d1<d2
|
and
|
μ2<K2<d1a2−d1⇒d2a2−d2<d1a2−d1⇒d2<d1
|
which are contradiction. Therefore, Eμ1ν1K20 and EK10μ2ν2 can not be local stable at the same time.
Now if ri=1,ai=a,di=d,Ki=d for both i=1,2, then Ebi2,i=1,2 exist if Ka−Kd−d>0. This implies that one of the eigenvalues of the Jacobian matrix of Model (4) evaluated at Ebi2 is positive, i.e.,
|
K(a−d)(Ka−Kd−d)+ρj(Ka−Kd−d)2K(K+1)(a−d)2>0
|
which indicates that Ebi2 can not be stable for both i=1 and i=2.
Proof of Theorem 3.3.
Proof.Let pi(x)=aix1+x and qi(x)=ri(Ki−x)(1+x)aiKi, then we have
|
rixi(1−xiKi)−aixiyi(1+xi)=aixi1+xi[ri(Ki−xi)(1+xi)aiKi−yi]
|
We construct the following Lyapunov functions
|
V1(x1,y1)=ρ2∫x1K1p1(ξ)−p1(K1)p1(ξ)dξ+ρ2y1
|
(15)
|
and
|
V2(x2,y2)=ρ1∫x2K2p2(ξ)−p2(K2)p2(ξ)dξ+ρ1y2
|
(16)
|
Now taking derivatives of the functions (15) and (16) with respect to time t, we get
|
ddtV1(x1(t),y1(t))=ρ2p1(x1)−p1(K1)pi(x1)dx1dt+ρ2dy1dt=ρ2[p1(x1)−p1(K1)][q1(x1)−y1]+ρ2y1[p1(x1)−d1]+ρ1ρ2y1y2[p1(x1)−p2(x2)]=ρ2[p1(x1)−p1(K1)]q1(x1)+ρ2y1[p1(K1)−d1]+ρ1ρ2y1y2[p1(x1)−p2(x2)]
|
(17)
|
and
|
ddtV2(x2(t),y2(t))=ρ1p2(x2)−p2(K2)p2(x2)dx2dt+ρ1dy2dt=ρ1[p2(x2)−p2(K2)][q2(x2)−y2]+ρ1y2[p2(x2)−d2]+ρ1ρ2y1y2[p2(x2)−p1(x1)].=−ρ1[p2(x2)−p2(K2)]q2(x2)+ρ1y2[p2(K2)−d2]+ρ1ρ2y1y2[p2(x2)−p1(x1)]
|
(18)
|
Let V=V1+V2. Now adding (17) and (18), we get
|
ddtV=ddtV1(x1(t),y1(t))+ddtV2(x2(t),y2(t))=ρ2[p1(x1)−p1(K1)]q1(x1)+ρ2y1[p1(K1)−d1]+ρ1[p2(x2)−p2(K2)]q2(x2)+ρ1y2[p2(K2)−d2].
|
Since μi>Ki⇔diai−di>Ki⇔aiKi1+Ki=pi(Ki)<di, thus, we have pi(Ki)−di<0. Notice that pi(xi) is an increasing function in xi, therefore, [pi(xi)−pi(Ki)] is positive for xi>Ki and it is negative for xi<Ki. At the mean time, we have qi(xi) is positive for xi<Ki and it is negative for xi>Ki. This implies that [pi(xi)−pi(Ki)]qi(xi)≤0 for all xi≥0. Therefore, we have ddtV<0 in R4+. This implies that both V1 and V2 are Lyapunov functions, and the boundary equilibrium EK10K20=(K1,0,K2,0) is globally stable when μi>Ki according to Theorem 3.2 in [31].
Proof of Theorem 3.6.
Proof.
According to Theorem 3.1, we know that Model (4) is attracted to a compact set C in R4+. Moreover, if yj=0, Model (4) is reduced to the two uncoupled models (7) while if xj=0 it is reduced to a single patch model (5).
First we focus on the persistence conditions for prey x1. Model (4) is reduced to a single patch model (5) when x1(0)=0, i.e., we have x1=y1=0. Notice that
|
dx1x1dt|x1=0,y1=0=(1−x1K1)−a1y11+x1|x1=0,y1=0=1>0.
|
According to Theorem 2.5 of [33], we can conclude that prey x1 is persistent. Similarly, we can show that prey x1 is persistent for all r>0.
Since both x1 and x2 are persistent, then we can conclude that Model (4) is attracted to a subcompact set Cs of C that excludes E0000,EK1000andE00K20. Therefore, we can restrict the dynamics of Model (4) on the compact set Cs. Now we focus on the persistence conditions for predator y1. According to Theorem 3.1, if y1=0, Model (4) is reduced to the two uncoupled models (7). In this case, according to both Theorem 3.1 and 3.2, the omega limit sets of (4) on the compact set Cs are EK1000,,EK10K20,EK10μ2ν2 if K2−12<μ2<K2 while they are EK1000,EK10K20 if μ2>K2. Now we consider the following two cases:
1.If μ2>K2, according to Theorem 2.5 of [33], we can conclude that predator y1 is persistent if all of the following equations are strictly positive:
|
dy1y1dt|EK1000=[a1x11+x1−d1+ρ1(a1x1y21+x1−a2x2y21+x2)]|EK1000=a1K11+K1−d1dy1y1dt|EK10K20=[a1x11+x1−d1+ρ1(a1x1y21+x1−a2x2y21+x2)]|EK10K20=a1K11+K1−d1.
|
Since a1K11+K1−d1>0⇔μ1<K1, therefore, we can conclude that predator y1 is persistent if μ1<K1 and μ2>K2.
2.If K2−12<μ2<K2, according to Theorem 2.5 in [33] and discussions above, we can conclude that predator y1 is persistent if μ1<K1 and the following equation is strictly positive:
|
dy1y1dt|EK10μ2ν2=[a1x11+x1−d1+ρ1(a1x1y21+x1−a2x2y21+x2)]|EK10μ2ν2=a1K11+K1−d1+ρ1(a1K1ν21+K1−a2μ2ν21+ν2)=a1K11+K1−d1+ρ1ν2(a1K11+K1−a2μ21+μ2)=a1K11+K1−d1+ρ1ν2(a1K11+K1−d2)>0.
|
According to the proof of Theorem 3.2, we can see that sufficient condition that dy1y1dt|EK10μ2ν2>0 holds is the same as sufficient condition for the boundary equilibrium EK10μ2ν2 being unstable when μ1<K1. Therefore, we can conclude that predator y1 is persistent if one of the following inequalities hold
(a)μj<Kj,μi>Ki. Or
(b)Ki−12<μi<KiandKj>max{μj,diaj−di}. Or
(c)Ki−12<μi<Ki,μj<Kj<diaj−diandρj<Kj(aj−dj)−djνi[di−Kj(aj−di)].
where i=1,j=2 or i=2,j=1.one of the following inequalities hold.
Based on the discussion above, we can conclude that the statement of Theorem 3.6 holds.
Proof of Theorem 3.7.
Proof. If Kj−12<μj<Kj,μi>Ki, then according to Theorem 3.6, we can conclude that prey xi for both i=1,2 and predator yj is persistent. This implies that Model (4) is permanent if predator yi is persistent. Since Kj−12<μj<Kj, then Theorem 3.2 indicates that the omega limit set of Model (4) when yi=0 is Eμ1ν1K20 when i=2,j=1 while its omega limit set is EK10μ2ν2 when i=2,j=1. Now let i=1,j=2, then according to Theorem 2.5 of [33], we can conclude that predator y1 is persistent if the following equation is strictly positive:
|
dy1y1dt|EK10μ2ν2=[a1x11+x1−d1+ρ1(a1x1y21+x1−a2x2y21+x2)]|EK10μ2ν2=a1K11+K1−d1+ρ1(a1K1ν21+K1−a2μ2ν21+ν2)=a1K11+K1−d1+ρ1ν2(a1K11+K1−a2μ21+μ2)=a1K11+K1−d1+ρ1ν2(a1K11+K1−d2)>0.
|
Since μi>Ki⇔a1K11+K1−d1<0, therefore, sufficient conditions for dy1y1dt|EK10μ2ν2>0 is
|
a1K11+K1−d2>0⇔K1>d2a1−d2andρ1>d1−K1(a1−d1)v2[K1(a1−d2)−d2].
|
Similarly, we can show that predator y2 is persistent when i=2,j=1. Therefore, Model (4) is permanent if the following inequalities hold for either i=2,j=1 or i=1,j=2,
|
Kj−12<μj<Kj,μi>Ki,0<djai−dj<Ki<μi
|
|
andρi>di−Ki(ai−di)νj[Ki(ai−dj)−dj].
|
According to Theorem 3.6, we can conclude that prey xi for both i=1,2 and predator yi is persistent if the following inequalities hold
|
Ki−12<μi<Ki,μj>Kj−12andKj>max{μj,diaj−di}.
|
Therefore, Model (4) is permanent if the above inequalities hold for both i=1,j=2 and i=2,j=1. On the other hand, predator yj is persistent if the following inequalities hold
|
Ki−12<μi<Ki,Kj−12<μj<Kj<diaj−diandρj<Kj(aj−dj)−djνi[di−Kj(aj−di)].
|
Therefore, both predator yi and yj are persistent if the following inequalities hold for either i=1,j=2 or i=2,j=1,
|
Ki−12<μi<Ki,Ki>max{μi,djai−dj},
|
|
Kj−12<μj<Kj<diaj−diandρj<Kj(aj−dj)−djνi[di−Kj(aj−di)].
|
Based on the discussion above, we can conclude that the statement of Theorem 3.7 holds.
Proof of Theorem 3.8.
Proof.If μi>Ki for both i=1,2, then Model (4) has global stability at (K1,0,K2,0) according to Theorem (3.3). This implies that Model (4) has no interior equilibrium when μi>Ki for both i=1,2.
The interior equilibrium (x∗1,y∗1,x∗2,y∗2) is determined by the positive intersections of the nullclines (11) x1=F(x2)=ft(x2)fb(x2) and x2=G(x1)=gt(x1)gb(x1) where
|
ft(x2)=a2[r2ρ1x2(K2−x2)+K2d1],fb(x2)=r2ρ1x2(K2a1−K2a2−a1)−r2ρ1x22(a1−a2)+K2(a1r2ρ1+a1a2−a2d1)
|
and
|
gt(x1)=a1[r1ρ2x1(K1−x1)+K1d2],gb(x1)=r1ρ2x1(K1a2−K1a1−a2)−r1ρ2x21(a2−a1)+K1(a2r1ρ2+a1a2−a1d2).
|
Notice that the nullclines x1=F(x2)=ft(x2)fb(x2) and x2=G(x1)=gt(x1)gb(x1) has the following properties:
1.F(0)=ft(0)fb(0)=a2K2d1K2(a1r2ρ1+a1a2−a2d1)=a2d1a1r2ρ1+a1a2−a2d1 and F(K2)=ft(K2)fb(K2)=d1a1−d1=μ1.
2.ft(x2)=a2[r2ρ1x2(K2−x2)+K2d1]≥a2K2d1>0forx2∈[0,K2] and
|
fb(x2)|a1=a2=a=a[r2ρ1(K2−x2)+K2(a−d1)].
|
3.G(0)=gt(0)gb(0)=a1K1d2K1(a2r1ρ2+a1a2−a1d2)=a1d2a2r1ρ2+a1a2−a1d2 and G(K1)=gt(K1)gb(K1)=d2a2−d2=μ2.
4.gt(x1)=a1[r1ρ2x1(K1−x1)+K1d2]≥a1K1d1>0 for x1∈[0,K1] and
|
gb(x1)|a1=a2=a=a[r1ρ2(K1−x1)+K1(a−d2)].
|
According to Theorem 3.1, we know that population of prey xi for i=1,2 has the following properties:
Thus, we can restrict the function F(x2) on the domain of [0,K2] and G(x1) on the domain of [0,K1]. Since ft(x2)≥a2K2d1>0forx2∈[0,K2] and gt(x1)≥a1K1d1>0 for x1∈[0,K1], thus, Model (4) has no interior equilibrium if fb(x2)<0forx2∈[0,K2] or gb(x1)<0forx1∈[0,K1].
Now we assume that a1>a2, then we have fb(x2)<0forx2∈[0,K2] if
|
r22ρ21(K2a1−K2a2−a1)2<4K2r2ρ1(a2−a1)(a1r2ρ1+a1a2−a2d1)
|
|
⇔ρ1<4K2a2(a1−a2)(d1−a1)r2(K2a1−K2a2+a1)2
|
while fb(x2)>0forx2∈[0,K2] if a1>d1 since
|
fb(0)=K2(a1r2ρ1+a2(a1−d1))>0andfb(K2)=a2K2(a1−d1)>0.
|
And gb(x1)>0 for x1∈[0,K1] if
|
r21ρ22(K1a2−K1a1−a2)2<4K1r1ρ2(a1−a2)(a2r1ρ2+a1a2−a1d2)
|
|
⇔ρ2<4K1a1(a1−a2)(a2−d2)r1(K1a2−K1a1+a2)2.
|
Similar cases can be made for a1<a2, therefore we can conclude that Model (4) has no interior equilibrium if either
|
a1>a2,ρ1<4K2a2(a1−a2)(d1−a1)r2(K2a1−K2a2+a1)2
|
or
|
a2>a1,ρ2<4K1a1(a2−a1)(d2−a2)r1(K1a2−K1a1+a2)2
|
hold.
Now we focus on sufficient conditions lead to both fb(x2)>0 for x2∈[0,K2] and gb(x1)>0forx1∈[0,K1]. Assume that a1>a2 and ai>di for both i=1,2. Notice that fb(0)=K2(a1r2ρ1+a2(a1−d1))>fb(K2)=a2K2(a1−d1)>0 with
|
fb(x2)=r2ρ1x2(K2a1−K2a2−a1)−r2ρ1x22(a1−a2)+K2(a1r2ρ1+a1a2−a2d1).
|
Therefore, we have fb(x2)>fb(K2) for all x2∈[0,K2]. Since gb(x1) is a degree 2 polynomial with the positive coefficient in the degree 2 and gb(0)=K1(a2r1ρ2+a1(a2−d2))>gb(K1)=a1K1(a2−d2)>0. Therefore, we have gb(x1)>0 for all x1∈[0,K1] if the following conditions hold
|
ρ2<4K1a1(a2−a1)(d2−a2)r1(K1a2−K1a1+a2)2.
|
The discussion so far also indicates that we have both fb(x2)>0forx2∈[0,K2] and gb(x1)>0forx1∈[0,K1] if the following inequalities hold for i=1,j=2 or i=2,j=1
|
ai>max{aj,di},ρj<4Kiai(aj−ai)(dj−aj)ri(Kiaj−Kiai+aj)2.
|
Now assume that these conditions hold, then we have F(x2) and G(x1) are positive on their restricted domain. By algebraic calculations, if ai>max{d1,d2} for both i=1,2, then both F(x2) and G(x1) have its unique critical points xci,i=1,2 in their restricted domain where
|
xc1=K1(r1ρ2+a1−d2−√(a1−d2)(r1ρ2+a1−d2))r1ρ2∈(0,K1)
|
and
|
xc2=K2(r2ρ1+a2−d1−√(a2−d1)(r2ρ1+a2−d1))r2ρ1∈(0,K2).
|
If F(xc2)<K1andG(xc1)<K2, then we can conclude that both maps x1=F(x2) and x2=G(x1) are unimode and the skew product of F×G maps [0,K2]×[0,K1] to its compact subset. Since both F and G are continuous and differentiable, therefore, x1=F(x2) and x2=G(x1) has at least one positive intersection for x2∈[0,K2],x1∈[0,K1]. Now we focus on sufficient condition that leads to F(xc2)<K1andG(xc1)<K2 when a1>a2. Since
|
max0≤x2≤K2{F(x2)}=F(xc2)≤max0≤x2≤K2{ft(x2)}min0≤x2≤K2{fb(x2)}=fb(K2/2)fb(K2)=K2r2ρ1+4d14(a1−d1)
|
and
|
max0≤x1≤K1{G(x1)}=G(xc1)≤max0≤x1≤K1{gt(x1)}min0≤x1≤K1{gb(x1)}=gt(K1/2)gb(K2a1−K2a2−a12(a1−a2))
|
|
=a1K1(r1K1ρ2/4+d2)K1a1(a2−d2)−r1ρ2(K1a1−K1a2−a2)24(a1−a2),
|
therefore, we have F(xc2)<K1andG(xc1)<K2 when a1>a2 if the following inequalities hold
|
K2r2ρ1+4d14(a1−d1)≤K1⇔ρ1≤4(K1a1−K1d1−d1)K2r2.
|
and
|
K2≥a1K1(r1K1ρ2/4+d2)K1a1(a2−d2)−r1ρ2(K1a1−K1a2−a2)24(a1−a2)⇔ρ2≤4K1a1(K2a2−K2d2−d2)a1r1K21+r2K2(K1a1−K1a2−a2)2.
|
Therefore, we can conclude that Model (4) has at least one interior equilibrium (x∗1,y∗1,x∗2,y∗2) if the following inequalities hold
|
ai>max{aj,d1,d2},aj>max{d1,d2},ρi≤4(Kiai−Kidi−di)Kjrj
|
and
|
ρj<min{4Kiai(aj−ai)(dj−aj)ri(Kiaj−Kiai+aj)2,4Kiai(Kjaj−Kjdj−dj)airiK2i+rjKj(Kiai−Kiaj−aj)2}.
|
In addition, since both F(x2) and G(x1) are unimode maps in their domain with unique local maximum, thus, we have
|
x1=F(x2)≥F(0)=a2d1a1r2ρ1+a1a2−a2d1
|
|
andx2=G(x1)≥G(0)=a1d2a2r1ρ2+a1a2−a1d2.
|
Therefore, we have aidjajriρj+aiaj−aidj<x∗j<Kj for both i=1,j=2 and i=2,j=1.
Now assume that a1=a2=a, then both fb and gb are reduced to linear decreasing functions, i.e.,
|
fb(x2)|a1=a2=a=a[r2ρ1(K2−x2)+K2(a−d1)]andgb(x1)|a1=a2=a
|
which indicates that fb(x2)<0 for x2∈[0,K2] if d1>a+r2ρ1 and gb(x1)<0forx1∈[0,K1] if d2>a+r1ρ2. Therefore, if a1=a2=a and either d1>a+r2ρ1 or d2>a+r1ρ2 holds, then Model (4) has no interior equilibrium. On the other hand, both fb(x2)>0forx2∈[0,K2] and gb(x1)>0forx1∈[0,K1] if a>max{d1,d2}. Then apply the discussions for the case a1≠a2, then we can conclude that Model (4) has at least one interior equilibrium if
|
a>max{d1,d2},F(xc2)<K1,andG(xc1)<K2.
|
Applying the similar arguments for the case ai>aj, we have
|
max0≤x2≤K2{F(x2)}=F(xc2)≤max0≤x2≤K2{ft(x2)}min0≤x2≤K2{fb(x2)}=fb(K2/2)fb(K2)=K2r2ρ1+4d14(a1−d1)
|
and
|
max0≤x1≤K1{G(x1)}=G(xc1)≤max0≤x1≤K1{gt(x1)}min0≤x1≤K1{gb(x1)}=gt(K1/2)gb(K1)=K1r1ρ2+4d24(a2−d2).
|
Therefore, we can conclude that Model (4) has at least one interior equilibrium (x∗1,y∗1,x∗2,y∗2) if the following inequalities hold
|
a1=a2=a>max{d1,d2},ρi<4(Kia−Kidi−di)Kjrj
|
for both i=1,j=2 and i=2,j=1. In addition, djriρj+a−dj<x∗j<Kj hold for both i=1,j=2 and i=2,j=1.
Proof of Theorem 3.9.
Proof.Suppose that min{a1,a2}>d, then we have μi=dai−d,νi=ri(Ki−μi)(1+μi)aiKi where (μi,νi) is the unique interior equilibrium of the single patch model (5) in the absence of the dispersal in predator for both i=1,2. Now recall from the null clines (9), we have
|
xi(xj)=ρiqj(xj)pj(xj)+diai(1+ρiqj(xj))−(ρiqj(xj)pj(xj)+di)=ρiqj(xj)pj(xj)+diρiqj(xj)[ai−pj(xj)]+ai−di
|
which indicates that
|
xi(μj)=ρiqj(μj)pj(μj)+dρiqj(μj)[ai−pj(μj)]+ai−d=dai−d=μi.
|
This implies that xi=μi for i=1,2 is the positive solutions of the null clines (9). Therefore, we can solve that (μ1,ν1,μ2,ν2) is an interior solution of Model (4) if min{a1,a2}>d=d1=d2. By substituting the equilibrium (μ1,ν1,μ2,ν2) into the Jacobian matrix (14), we obtain its characteristic equation as follows:
|
H(λ)=λ4+(α1+α2)λ3+[α1α2+d(β1+β2)]λ2+d(α1β2+α2β1)λ+d2(β1β2−γ1γ2=0
|
where
|
αi=−riμi(Kiai−Kid−ai−d)Kiai⇒[αi>0⇔Kia1−Kid−ai−d<0⇔Ki−12<μi<Ki]βi=νi(νjρi+1)(ai−d)2ai>0γi=ρiνiνj(aj−d)2aj>0β1β2−γ1γ2=ν1ν2(a1−d)(a2−d)2(ν1ρ2+ν2ρ1+1)a1a2>0.
|
Then the real parts of the solutions of H(λ) are all negative if α1+α2>0 while the solutions of H(λ) has positive if α1+α2<0. Notice that the single patch i (5) has global stability at (μi,νi) if αi>0⇔Ki−12<μi<Ki. Therefore, the interior equilibrium is locally asymptotically stable of Ki−12<μi<Ki for both i=1,2 while it is unstable if
|
μ1(K1a1−K1d−a1d)K1a1+rμ2(K2a2−K2d−a2−d)K2a2>0.
|
Assume that α1α2<0and α1+α2>0. Then the real parts of all solutions of H(λ) can be still negative if α1α2+d(β1+β2)>0 and d(α1β2+α2β1). By algebraic calculations, we can conclude that if αi<0 and the dispersal of predator yi is large enough, then the interior equilibrium (μ1,ν1,μ2,ν2) can still be locally asymptotically stable, where ρi should satisfy the following condition:
|
ρi>max{−νj−rjμiμj(Kiai−Kid−ai−d)(Kjaj−Kjd−aj−d)(KiKjajνjdνi(ai−d)2),
|
|
−μiνjKj(νiρj+1)(aj−d)2(Kiai−Kid−ai−d)rjμjνiKi(ai−d)2(Kjaj−Kjd−aj−d)−1νj}.
|
Now if a1=a2=a,r1=r2=1,K1=K2=K,d1=d2=d. The discussions above implies that Model (4) has the same stability at Ei=(μ,ν,μ,ν) as the stability of the single patch model (5) at (μ,ν) where μ=da−d and ν=(K−μ)(1+μ)aK. Therefore, Ei is locally asymptotically stable if K−12<μ<K while it is unstable if μ>K−12.
Now we should show that Model (4) has the unique Ei=(μ,ν,μ,ν) whenever a>d. Notice that F(x2) and G(x1) have the following properties in the symmetric case (i.e., a1=a2=a,r1=r2=1,K1=K2=K,d1=d2=d):
1.F(x2)=ρ1x2(K−x2)+Kdρ1(K−x2)+aK(1−d) with F(0)=dρ1+a−d and F(μ)=F(K)=μ. In addition, F(x2)>0 for all x2∈[0,K] and F(x2) has a unique critical point xc2 for x2∈[0,K] where
|
μ<xc2=K(ρ1+a−d−√(a−d)(ρ1+a−d))ρ1∈(0,K).
|
2.G(x1)=ρ2x1(K−x1)+Kdρ2(K−x1)+aK(1−d) with G(0)=dρ2+a−d and G(μ)=G(K)=μ. In addition, G(x1)>0 for all x1∈[0,K] and G(x1) has a unique critical point xc1 for x1∈[0,K] where
|
μ<xc1=K(ρ2+a−d−√(a−d)(ρ2+a−d))ρ2∈(0,K).
|
The discussions above indicate that both F(x2) and G(x1) are unimode maps with a unique interception at x1=x2=μ.
Proof of Theorem 4.1.
Proof.Proof of Item 1 can be obtained by adopting the proof provided in Theorem 3.1. We omit details.
The stability of E0000,EK1000,E00K20,EK10K20 can be obtained from eigenvalues of the Jacobian matrix of Model (12) evaluated at these equilibria through simple algebraic calculations. We omit details. But we will return to the local stability of Ebi when we prove Item 4.
Item 3(a): If xi=0, then we have limt→∞y1(t)=limt→∞y2(t)=0. This implies that the omega limit set of Model (13) is y1=y2=0. Therefore, prey xi persists by applying Theorem 2.5 of [33] since
Item 3(b): Recall pi(x)=aix1+x and qi(x)=ri(Ki−x)(1+x)aiKi for i=1,2. Then we construct the following Lyapunov function
|
Vij(xi,yi,yj)=(ρj+dj)∫xiKipi(ξ)−pi(Ki)pi(ξ)dξ+(ρj+dj)yi+ρiyj.
|
If ^μi>Ki, then we have
|
dVij(xi,yi,yj)dt=(ρj+dj)[(pi(xi)−pi(Ki)]qi(xi)+yi(pi(Ki)−ˆdi)<0
|
since pi(Ki)−ˆdi<0⇔^μi>Ki. Therefore, Model (13) has global stability at (Ki,0,0) if ^μi>Ki.
Item 3(c): We construct the following Lyapunov function
|
Vij(xi,yi,yj)=(ρj+dj)∫xiˆμipi(ξ)−pi(ˆμi)pi(ξ)dξ+(ρj+dj)∫yiˆνiηi−ˆνiηidηi+ρi∫yjˆνijηj−ˆνijηjdηj.
|
If Ki−12<^μi<Ki, then we have
|
=(ρj+dj)[(pi(xi)−pi(ˆμi)][qi(xi)−ˆνi]−ρiˆνi((ρj+dj)yj−ρjyi)2(ρj+dj)yiyj<0.
|
Therefore, Model (13) has global stability at (^μi,^νi,ˆνij) if Ki−12<^μi<Ki.
Item 4: If xj=0, then Model (12) reduces to Model (13) who has global stability at (Ki,0,0) if ^μi>Ki while has (^μi,^νi,ˆνij) if Ki−12<^μi<Ki. Therefore, by applying Theorem 2.5 of [33], prey xj persists if
|
dxjxjdt|xj=0,yj=0=rj>0 when ^μi>Ki
|
and
|
dxjxjdt|xj=0,yj=ˆνij=rj−ajˆνij>0 when Ki−12<^μi<Ki.
|
The persistence of both prey can be easily obtained from the persistence of one prey.
If Ki−12<^μi<Ki and rj−ajˆνij<0, then dxjxjdt|xj=0,yj=ˆνij=rj−ajˆνij<0. According to Theorem 2.18 by [34], we can conclude that the boundary equilibrium (^μi,^νi,0,ˆνij) is locally asymptotically stable. This proves the stability condition of Ebi of Item 2.
Item 5: We construct the following Lyapunov function
|
V(xi,yi,xj,yj)=(ρi+di)∫xjˆμjpj(ξj)−pj(ˆμj)pj(ξj)dξj+(ρi+di)∫yjˆνjηj−ˆνjηjdηj+ρixi+∫yiˆνjiηi−ˆνjiηidηi.
|
Then we have
|
dV(xi,yi,xj,yj)dt=(ρj+dj)[(pi(xi)−pi(ˆμi)][qi(xi)−ˆνi]−ρiˆνi((ρj+dj)yj−ρjyi)2(ρj+dj)yiyj+ρjpi(xi)[qi(xi)−ˆνji]<(ρj+dj)[(pi(xi)−pi(ˆμi)][qi(xi)−ˆνi]−ρiˆνi((ρj+dj)yj−ρjyi)2(ρj+dj)yiyj+ρjpi(xi)[qi(Ki−12)−ˆνji]=(ρj+dj)[(pi(xi)−pi(ˆμi)][qi(xi)−ˆνi]−ρiˆνi((ρj+dj)yj−ρjyi)2(ρj+dj)yiyj+ρjpi(xi)[ri(Ki+1)24aiKi−ˆνji].
|
Therefore, if Kj−12<^μj<Kjandri(Ki+1)24aiKi<ˆνij hold, then we have dV(xi,yi,xj,yj)dt<0. This implies that Model (13) has global stability at (0,ˆνji,^μj,^νj).
Item 6: Define V(y1,y2)=ρ2y1+ρ1y2, then we have
|
dVdt=ρ2(p1(x1)−d1)y1+ρ1(p2(x2)−d2)y2.
|
Notice that lim supt→∞xi(t)≤Ki for both i=1,2. Then if μi>Ki for both i=1,2, then we have max{p1(K1)−d1,p2(K2)−d2}<−δ<0. This implies that
|
dVdt=ρ2(p1(x1)−d1)y1+ρ1(p2(x2)−d2)y2<−δ(ρ2y1+ρ1y2).
|
Therefore, both predators go extinct if μi>Ki for both i=1 and i=2. Since both lim supt→∞yi(t)=0 for both i=1,2. Then we have Model (12) reduced to the following uncoupled prey model
which converges to xi=Ki. Thus, Model (13) has global stability at (K1,0,K2,0) when μi>Ki for both i=1,2.
On the other hand, if 0<μi<Ki for both i=1,2, then we have max{p1(K1)−d1,p2(K2)−d2}>δ>0. This implies that
|
dVdt=ρ2(p1(x1)−d1)y1+ρ1(p2(x2)−d2)y2>δ(ρ2y1+ρ1y2).
|
Therefore, both predators persist if 0<μi<Ki for both i=1 and i=2.
Item 7 can be obtained from Item 4 and Item 6.
Item 8 can be obtained from eigenvalues of the Jacobian matrix of Model (12) evaluated at the symmetric interior equilibrium (μ,ν,μ,ν) through simple algebraic calculations. We omit details. The global stability of (μ,ν,μ,ν) when K−12<μ<K can be obtained by constructing the following Lyapunov function
|
V(x1,y1,x2,y2)=ρ2∫x1μp1(ξ1)−p1(μ)p1(ξ1)dξ1+ρ2∫y1νη1−νη1dη1+ρ1∫x2μp2(ξ2)−p2(μ)p2(ξ2)dξ2+ρ1∫y2νη2−νη2dη2
|
which gives
|
dV(x1,y1,x2,y2)dt=ρ2(p1(ξ1)−p1(μ))(q1(x1)−K)+ρ1(p2(ξ2)−p2(μ))(q2(x2)−K)
|
|
+ρ1ρ2ν(y1−y2)(1y1−1y2)y1y2.
|
Acknowledgments
This research is partially supported by NSF-DMS(1313312); NSF-IOS/DMS (1558127) and The James S. McDonnell Foundation 21st Century Science Initiative in Studying Complex Systems Scholar Award (UHC Scholar Award 220020472). We also would like to acknowledge the partial support from Natural Science Foundation of Jiangsu Province (BK20140927), Tianyuan Fund for Mathematics of NSFC (11426132, 11601226), and from Nanjing Tech University. The research of K.M is also partially supported by the Department of Education GAANN (P200A120192). S.K.S. is partially supported by the NBHM post-doctoral fellowship. All authors would like to thank Dr. Andrea Bruder for the discussions on the modeling dispersal strategies in the early stage of this manuscript.









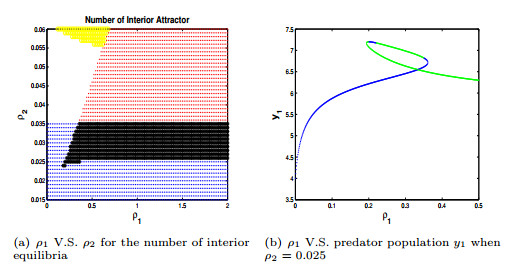
 DownLoad:
DownLoad: