COVID-19 pandemic containment in the Caribbean Region: A review of case-management and public health strategies

1.   Introduction

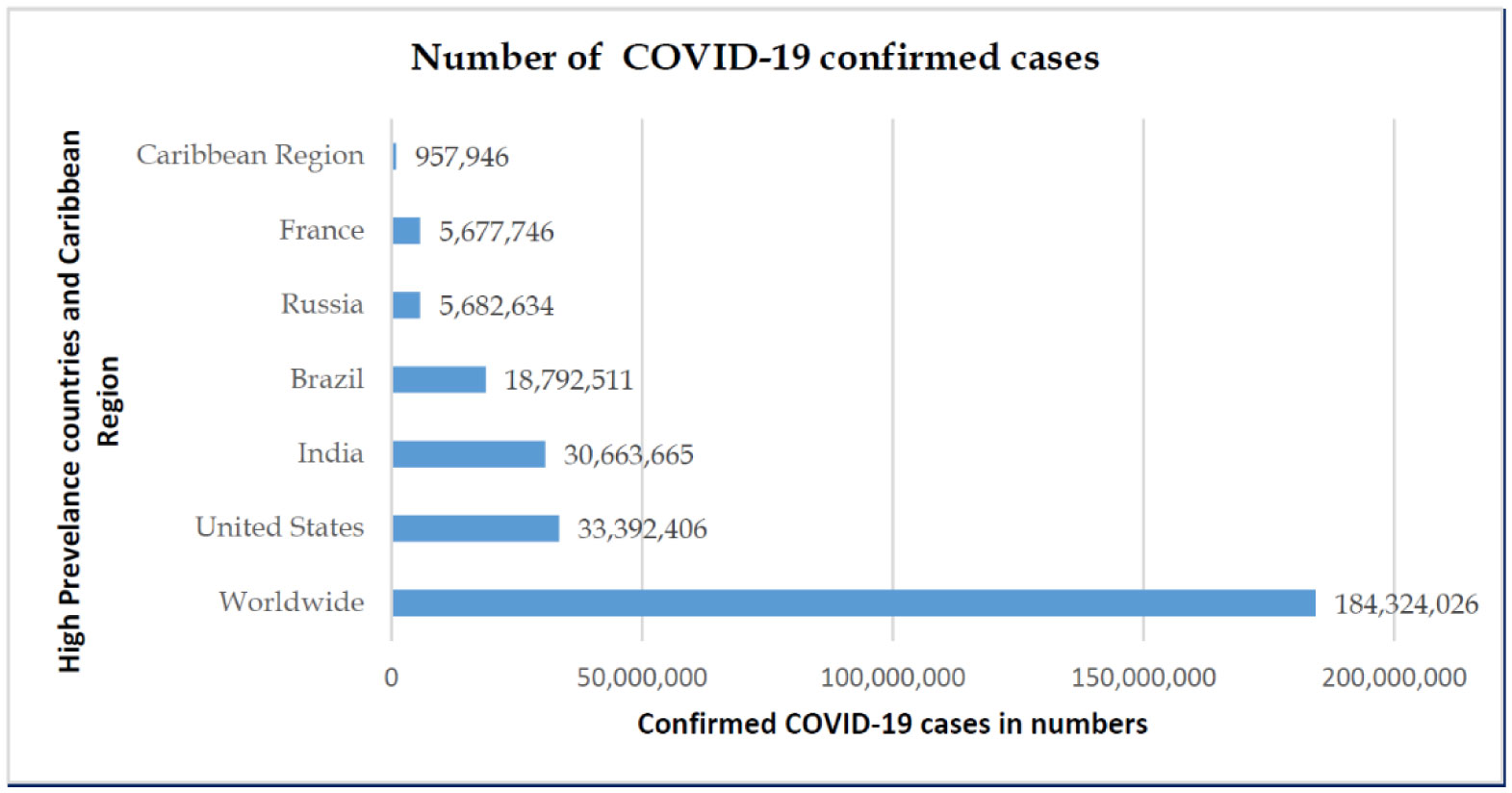
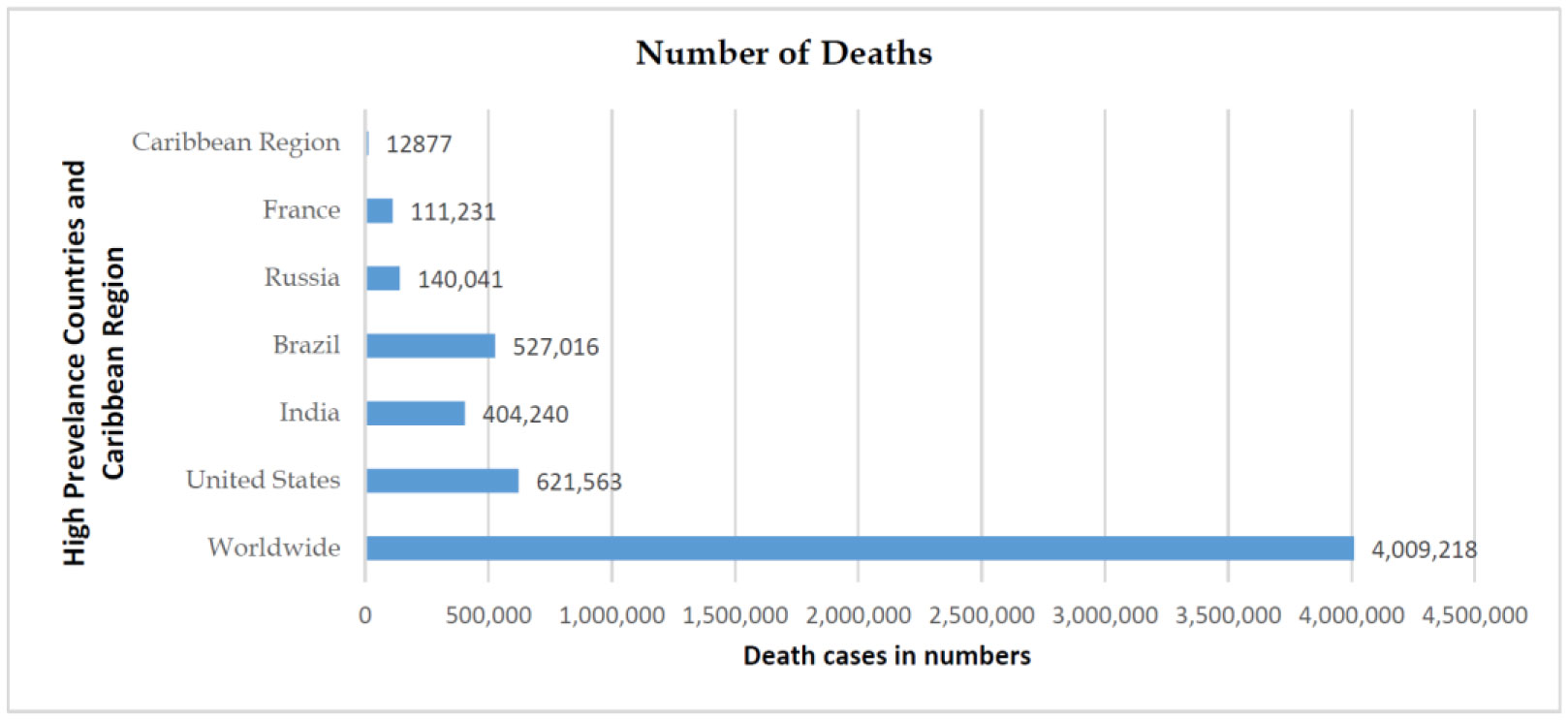
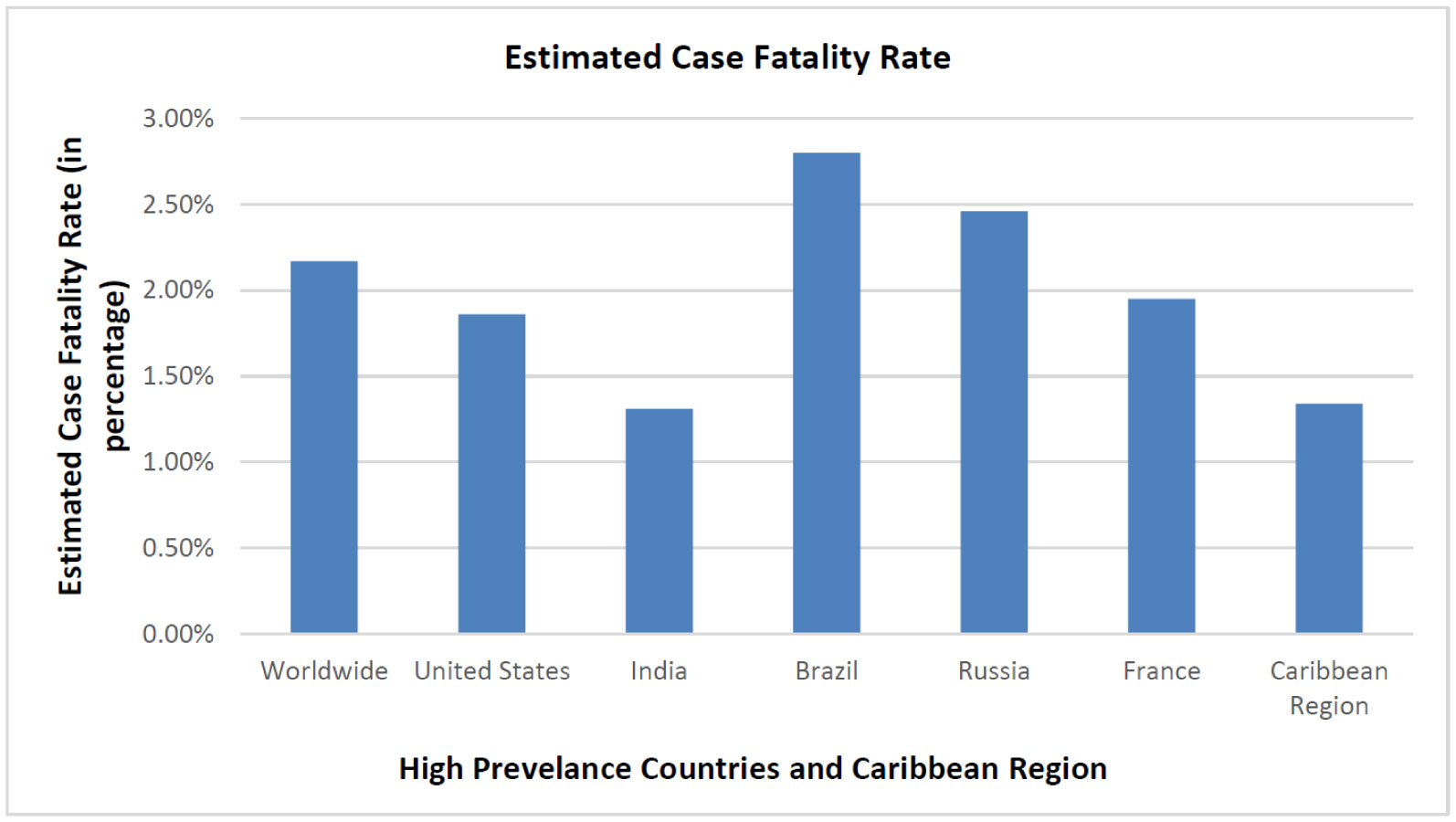
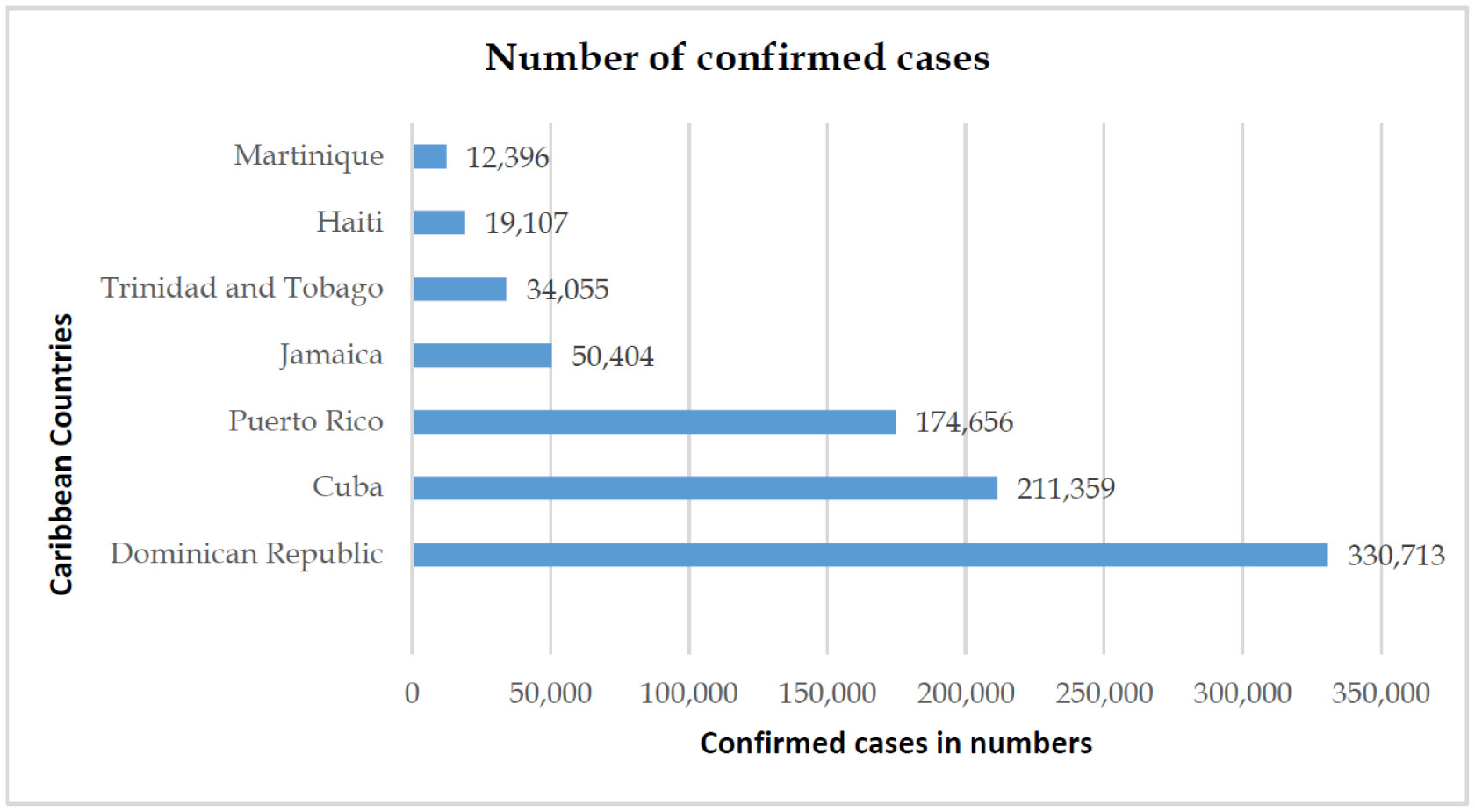
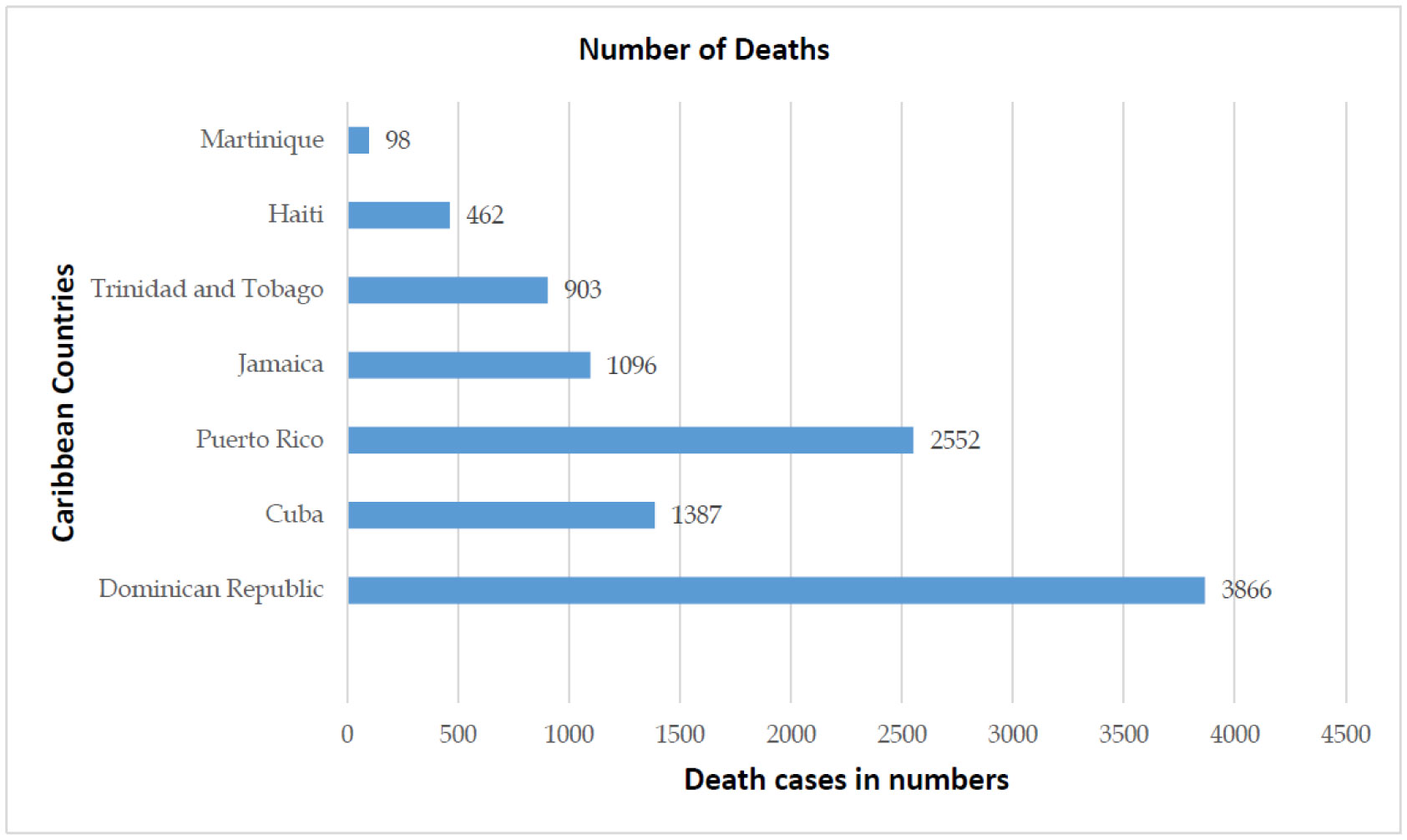
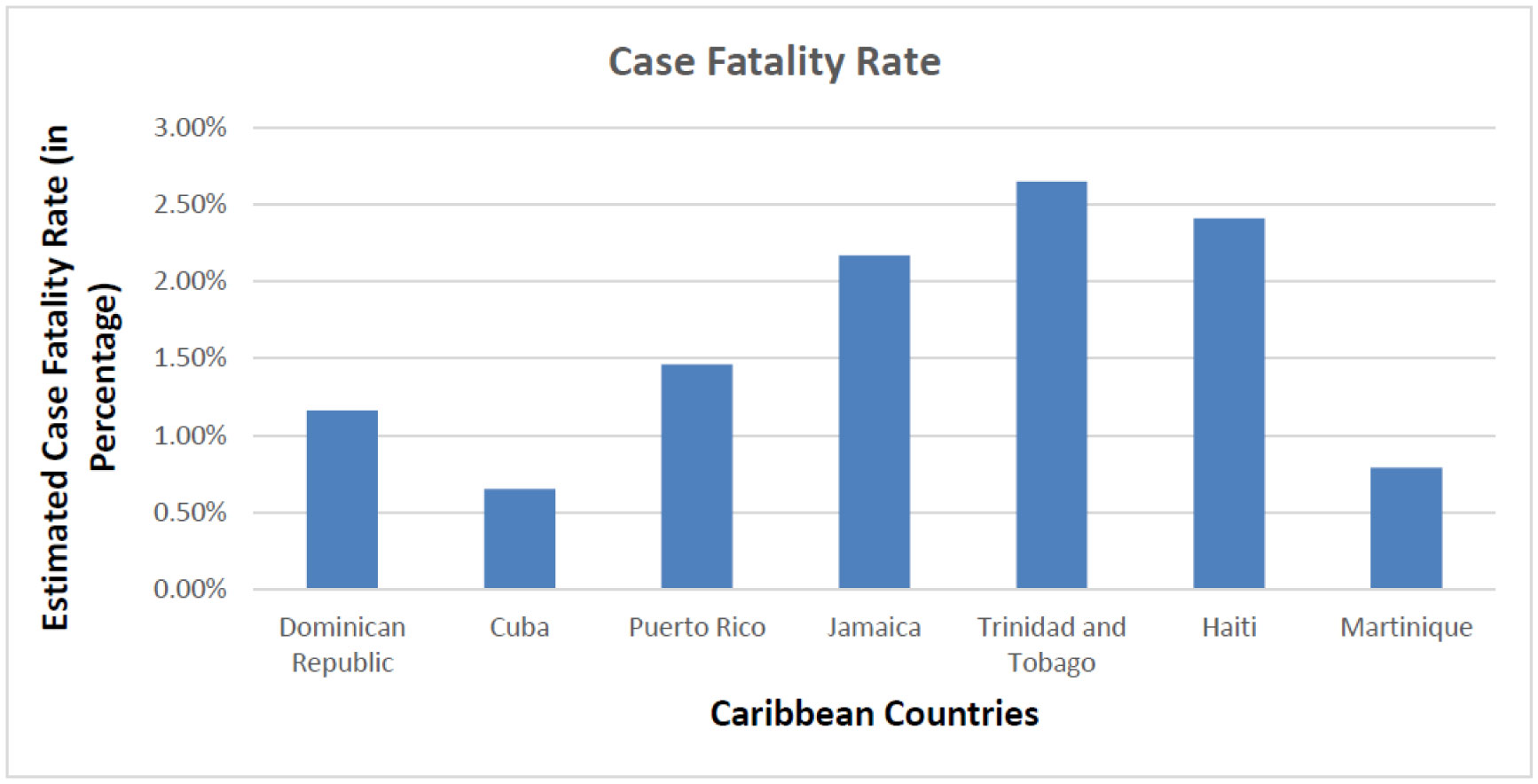
On December 31, 2019, a highly contagious pneumonia case with unknown origin was reported in Wuhan City, Hubei Province of China. Wuhan has been the focus of worldwide attention due to the outbreak of Coronavirus Disease 2019 (COVID-19), caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). The number of infections and deaths has been growing rapidly since then. COVID-19 has become a pandemic ^[1] and disease is creating unprecedented public health challenges worldwide. As of August 30, 2020, the disease has caused over 12.5 million confirmed cases and 843 thousand deaths in at least 188 countries and territories.

COVID-19 is a new disease. The origin and etiology of the infection is still uncertain. There were likely substantial proportions of undetected cases in early periods ^[2,3,4]. Moreover, the disease incubation period ranges from 2 to 14 days ^[5]. During this period of time, infected individuals may not show any symptoms; thus, they may not have awareness of the infection, but they are capable of transmitting the disease to other people. Therefore, we are facing unprecedented challenges in the prevention and control of the disease. To that end, a large number of mathematical models have being proposed to improve our understanding in mitigating the pandemic (see, e.g., ^{[1,3,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]} and the references therein). Some of these works are summarized below. Chen et al. ^[13] cataloged the symptoms and physical characteristics of the first 425 laboratory-confirmed cases in Wuhan. Their study shows that the basic reproduction number $\mathcal{R}_0$ is 2.2 and the incubation period of these early cases to be $7.5\pm 3.4$ days. Wu et al. ^[4] presented a susceptible-exposed-infectious-recovered (SEIR) model in which the reported value of $\mathcal{R}_0$ is 2.68 and they estimated that the COVID-19 epidemic was doubling every 6.4 days. Their study helped to forecast the potential domestic and international spread of COVID-19. Ndairou et al. ^[18] used a compartmental epidemic model to study the spread of the COVID-19 with an inclusion of super spreaders. In their case study of Wuhan, the reported value of the basic reproduction number is 0.945, indicating that the containment within Wuhan was well-controlled by the Chinese authorities. A modeling study in ^[4] inferred the basic reproduction number, outbreak size in Wuhan, exported cases from Wuhan, forecasting the spread in China. In ^[21], a modified SEIR model and an AI trained model on SARS 2003 data were proposed to predict the epidemic curve and promise for future prediction of epidemics. Lin et al. ^[22] used a variation of the SEIR model to study the outbreak of COVID-19 in Wuhan by incorporating individual behavioral change and governmental actions towards the spread of the disease. Hao et al. ^[23] employed a more detailed epidemic model to help understand the vigorous non-pharmaceutical intervention that has helped in keeping infection spread at the lowest in Wuhan. However, most of these mathematical models of COVID-19 dynamics are deterministic. To capture the discrete nature of human population and heterogeneity among individual hosts, a stochastic modeling approach may be more appropriate, particularly during the initiation of the infection. That motivates our work.

The goal of this article is to develop deterministic and stochastic models to study the evolution of the disease in both short and long terms. Our focus is mathematical modeling and analysis of disease epidemic, which aims to address the important questions such as how long will it take to disease extinction and how likely the second wave of the pandemic would occur if the reopening of Wuhan is not well contained?

The remainder of this paper is organized as follows. Section 2 presents the deterministic ordinary differential equation (ODE) model and performs a detailed analysis on the local and global dynamics of the ODE model with constant parameters. Section 3 is dedicated to the formulation of the stochastic model and a theoretical estimate of the probability of disease extinction. In Section 4, parameter estimation is carried out to fit the publicly reported data and numerical simulations of deterministic and stochastic models are performed. Finally we conclude the paper with some discussion in Section 5.

2.   Deterministic model

To study the transmission dynamics of the COVID-19 epidemic, we employ the classical SEIR epidemic modeling framework where the total human population is composed of four compartments: the susceptible, the exposed, the infected and the recovered. Let $S$, $E$, $I$, $R$ denote the number of human individuals in each of the classes; thus, our deterministic model takes the form:

Here $N = N(t)$ is the total population size at time $t$. The parameter $b$ and $d$ are the natural birth and death rates, respectively. Let $N_0 = b/d$ denote the initial population size. The function $\beta(t)$ is the transmission rate. This function is time dependent and assumed to be piecewise constant, which is to capture the dramatic change in the prevention and control policy in Wuhan, such as city lockdown, hospitalization and quarantine. Parameter $\alpha^{-1}$ denotes the latent period, $\tau^{-1}$ is the (mean) infectious period and $\gamma_I$ is the disease-induced mortality rate. For simplicity of analysis, in the rest of this section, we assume that $\beta(t) = \beta$ is constant.

2.1.   Basic reproduction number $\mathcal{R}_0$

The basic reproduction number $\mathcal{R}_0$ in epidemic models is an important threshold parameter to understand the extinction and persistence of a disease. It is defined as the expected number of secondary infectious cases produced by a primary infected individual in an otherwise susceptible population. Using the next generation matrix method ^[24], we compute $\mathcal{R}_0$ and it is given by

2.2.   Equilibrium analysis

It is easy to verify that the deterministic model (2.1) admits at most two biologically feasible equilibrium solutions which depends on the value of $\mathcal{R}_0$.

The disease-free equilibrium (DFE) $\mathcal{E}_0 = (N_0, 0, 0, 0)$ always exists and $\mathcal{E}_0$ is the only feasible equilibrium when $\mathcal{R}_0\le 1$. An endemic equilibrium (EE)

for which $I^* = \frac{b}{\beta-\gamma_I}(\mathcal{R}_0 -1)$ exists when $\mathcal{R}_0 > 1$. Note that $\mathcal{R}_0 > 1$ implies $\beta > \gamma_I$.

2.2.1.   Local stability

The local stability of the DFE is an immediate consequence of [24,Theorem 2]. More specifically, the DFE is locally asymptotically stable for $\mathcal{R}_0 < 1$ and unstable for $\mathcal{R}_0 > 1$. The following theorem establishes the local stability of the EE of model (2.1).

Theorem 2.1. The EE, $\mathcal{E}_1$, of the system (2.1) is locally asymptotically stable for $\mathcal{R}_0 > 1$.

Proof. Let ${S}^*, {E}^*, {I}^*, {R}^*$ be as defined above as in (2.2). Note that the Jacobian matrix of the linearized system of (2.1) at the EE $\mathcal{E}_1$ is

Hence the corresponding characteristic equation is

where

By the Routh-Hurwitz criterion, the EE is locally stable when $a_1 > 0$, $a_3 > 0$ and $a_1 a_2 > a_3$. Clearly $a_1 > 0$, since $\alpha, d, \tau, b, \gamma_I,$ and $S^* > 0$. Similarly, $a_3 > 0$, for $\alpha, \beta, b, N^* > 0$ and $\mathcal{R}_0 > 1.$ Now it remains to show that $a_1 a_2-a_3 > 0$. Let $u = \alpha+d$ and $v = d+\tau+\gamma_I$. Thus,

This shows that $a_1a_2 - a_3 > 0$.

Thus, the local stability result of the EE follows when $\mathcal{R}_0 > 1$.

2.2.2.   Global stability

It is clear that the biologically feasible region

is the positive invariant for model (2.1). The global stability of the DFE and the EE is established in the following two theorems.

Theorem 2.2. If $\mathcal{R}_0 \le 1$, then the DFE $\mathcal{E}_0$ is globally asymptotically stable in $\Omega$.

Proof. One can verify that

where

Define $\mathbf{x} = \begin{bmatrix} E &I \end{bmatrix}^T$, and $\mathbf{u} = (0, \beta)$. Consider a Lyapunov function $L = \mathbf{u} V^{-1} \mathbf{x}.$ Taking the derivative of $L$ along the solution of model (2.1) in $\Omega$ leads to

Note that $\mathbf{u}$ is the left eigenvector of the matrix $V^{-1} F$ corresponding to the spectral radius of $V^{-1} F$. Since $\mathcal{R}_0 = \rho(FV^{-1}) = \rho(V^{-1} F)$, $\mathbf{u}V^{-1} F = \mathcal{R}_0\mathbf{u}$. Thus,

If $\mathcal{R}_0 < 1$, $\dot{L} \le 0$ and $\dot{L} = 0$ implies that $\mathbf{u}\mathbf{x} = 0$. This shows that $I = 0$. Using the second, fourth and the first equations of model (2.1), we have $E = 0$, $R = 0$ and $S = N_0$. This shows that the largest invariant set on which $\dot{L} = 0$ is the singleton $\mathcal{E}_0$.

If $\mathcal{R}_0 = 1$, $\dot{L} = 0$ and the fact $\mathbf{u}V^{-1} > 0$ yield $S = N$. By the definition of $N = S+E+I+R$ and $E, I, R\ge 0$, $E = I = R = 0$. In view of the first equation of model (2.1), $S = N_0 = b/d$. Hence, the largest invariant set on which $\dot{L} = 0$ is the singleton $\mathcal{E}_0$. Therefore, by LaSalle's invariance principle ^[25], the DFE is globally asymptotically stable in $\Omega$ when $\mathcal{R}_0\le 1$.

Theorem 2.3. If $\mathcal{R}_0 > 1$ and $\gamma_I = 0$, then the unique endemic equilibrium $E_1$ is globally asymptotically stable in the interior of $\Omega$.

Proof. By $\gamma_I = 0$, $dN/dt = b-dN$. Since $N(0) = N_0 = b/d$, $N(t)\equiv N_0$ for all $t\ge 0$. Recall that $\mathcal{E}_1 = ({S}^*, E^*, {I}^*, R^*)$. Consider a Lyapunov function $V$ as follows:

where $c = \frac{\beta S^* I^*}{\alpha E^*N}$. It is clear that $V\ge 0$ and $V = 0$ if and only if $U = U^*$ for $U = S, E, I$. Taking the derivative of (2.3) along the solutions of model (2.1), we have the following,

Using the equilibrium equations of model (2.1) yields

By the arithmetic-geometric mean inequality,

and the quantities hold if and only if $S = S^*$, $E = mE^*$ and $I = mI^*$ for some $m > 0$. Substituting $I = mI^*$ into the fourth equation of model (2.1) yields $R = mR^*$. Using the first equations leads to $m = 1$. Hence the largest invariant set where $\dot{V} = 0$ is the singleton $\mathcal{E}_1 = (S^*, E^*, I^*, R^*)$. It follows from the LaSalle's Invariance Principle ^[25], the EE $\mathcal{E}_1$ is globally asymptotically stable in the interior of $\Omega$ when $\mathcal{R}_0 > 1$.

Theorems 2.2 and 2.3 show that $\mathcal{R}_0$ serves as a sharp threshold for disease dynamics. More specifically, the disease will die out if $\mathcal{R}_0 < 1$ and persist if $\mathcal{R}_0 > 1$.

3.   Stochastic process

Epidemic ODE models typically assume that the sizes of the compartments are large enough that the mixing of members is homogeneous, or at least that there is homogeneous mixing in each subetaoup if the population is stratified by activity levels. However, at the beginning of a disease outbreak, there is a very small number of infectious individuals and the transmission of infection is indeed a stochastic event depending on heterogeneity among individuals in the population (e.g., variations in individual health conditions and disease transmissibility) and patterns of contacts between them. This suggests that the homogeneous mixing at the beginning of an epidemic may not be a good assumption and hence the ODE models may not be appropriate when the initial infection is small. To that end, we use a continuous time Markov chain (CTMC) model to study the variability of the disease dynamic, and then we apply the theory of the multitype branching process (e.g., see ^[26,27,28] and references therein) to approximate the dynamics of the CTMC model near the DFE.

3.1.   Continuous time Markov chain (CTMC) model

We use the ODE model (2.1) with constant parameters as a framework to formulate a CTMC model, which is composed of nine independent events. For simplicity, we use the same notation as in the ODE model (2.1). Let $\boldsymbol{Z}(t) = (S(t), E(t), I(t), R(t))$ be a discrete random vector and $\Delta \boldsymbol{Z}(t) = \boldsymbol{Z}(t+\Delta t)-\boldsymbol{Z}(t)$ denote the change during $[t, t+\Delta t]$, for $t\in [0, \infty)$. The infinitesimal transition probabilities are defined based on the ODE rates. The changes and the corresponding transition probabilities are summarized in Table 1.

3.2.   Branching process approximation (BP)

To investigate the dynamics of the CTMC model near the DFE (i.e., $S\approx N_0$), we employ the multitype branching process theory by approximating the "birth and death'' of the infection process near the origin. Assume that $S = N_0$ and $R = 0$ and consider only the events in Table 2. The transition rates in this table follow directly from the rates in the linearized ODE model (2.1). This leads to a multitype branching process for the exposed and infected human individuals, where a transition occurs in one of the infectious random variables, $E$ or $I$.

In general, let $\boldsymbol{X} = (X_1, X_2, \cdots, X_n)$ denote a vector of discrete-state random variables where $X_i$ is the random variable corresponding to the infectious group $i$ for $i = 1, 2, \cdots, n$. Let $X_i(0) = \delta_{ij}$ where $\delta_{ij}$ is the Kronecker delta with $\delta_{ij} = 1$ if $i = j$ and zero otherwise, for $1\le i, j\le n$. The offspring pgf for the infectious individuals of type $i$ is a function $f_i: [0, 1]^n\to [0, 1]$ and

where $p_i(k_1, k_2, \cdots, k_n)$ denotes the probability that the individual of type $i$ gives "birth" to $k_j$ individuals of type $j$, for $j = 1, 2, \cdots, n$. In our case, $\boldsymbol{X} = (X_1, X_2) = (E, I)$ and $n = 2$.

By Table 2, the offspring pgf for $E$ is given $(E(0), I(0)) = (1, 0)$ is

and the offspring pgf for $I$ given $(E(0), I(0)) = (0, 1)$ is

It follows from branching process theory that the key of estimating the probability of disease extinction is to determine the fixed point of the offspring pgf on $[0, 1]$. Solving $f_i(q_1, q_2) = q_i$ for $i = 1, 2$ on $[0, 1]$ leads to

where $c_1 = \alpha \beta$ and $c_2 = -(d+\alpha)(\tau+\gamma_I+d)$.

Thus fixed points in terms of $q_2$ on $[0, 1]$ are $1$ and $q_2^* = -c_2/c_1 = 1/\mathcal{R}_0$. It is clear that $0 < q_2^* < 1$ if and only if $\mathcal{R}_0 > 1$, which shows that the minimal fixed point of $q_2$ is $q_2^* = \min\{1/\mathcal{R}_0, 1\}$. Thus the fixed point $(q_1^*, q_2^*)$ of $f_i(q_1, q_2) = q_i$ ($i = 1, 2$) in $[0, 1]^2\backslash\{(1, 1)\}$ is given by

when $\mathcal{R}_0 > 1$.

By the theory of the multitype branching process approximation, an estimate of the probability of disease extinction is given by

and consequently, the probability of an outbreak is

where $e_0, i_0$ corresponds to the initial population size of the exposed class and the infected class respectively. This particularly shows that the outbreak probability is $1-q_1^*$ (resp. $1-q_2^*$) when the infection is initiated by one exposed (resp. infected) individual.

The above results highlight the difference between the deterministic and stochastic dynamics; i.e., unlike the deterministic dynamics showing that the disease persists and reaches an endemic equilibrium when $\mathcal{R}_0 > 1$, the stochastic model indicates there is a positive probability of disease extinction when $\mathcal{R}_0 > 1$.

4.   Numerical simulations

In this section, we fit our ODE model to the public reported data, conduct a sensitivity analysis for the model parameters and predict the second wave of the pandemic in terms of the time, duration and strength. On the other hand, numerical simulations of the CTMC model are performed. In particular, we use the stochastic model to investigate the disease extinction and the first and second waves of the disease epidemics in terms of the time and the likelihood.

4.1.   Deterministic model

4.1.1.   Parameter estimation

Using the method of iterated filtering ^[29], we fit our ODE model to COVID-19 data published daily by WHO and other sources ^{[30,31,32,33,34]} from December 31, 2019 to June 28, 2020. It has been estimated that the population of Wuhan was approximately 9,000,000 people ^[35], so that we set $N(0) = 9,000,000$ in our model. The model parameters are taken from ^[36,37,38], which is summarized in Table 3. The other initial compartment values are set as $S(0) = 8,999,768, \, E(0) = 39, \, I(0) = 193,$ and $R(0) = 0$.

We assume that $\beta(t)$ is a piecewise constant function of time. We estimate $\beta(t)$ by fitting to our data sets in five time intervals: days 0–17, days 17–28, days 28–37, days 37–42, and days greater than 42. These days were chosen as follows. Day 17 corresponds to January 23, 2020 which is the day that the citywide lockdown began in Wuhan, China ^[39]; Day 28 corresponds to February 2, 2020 which is the day that the centralized quarantine and treatment began ^[39] (and also this is the end of Period 1 in ^[2]); Day 37 corresponds to the first day in which clinical diagnosis of COVID-19 were included in the dataset on February 12, 2020 ^[40]; Day 42 corresponds to February 17, 2020 which is the day that the community universal symptom survey began and is the peak in daily active infected cases from our calculations ^[39]. It is well-known that the dataset of confirmed cases for COVID-19 is greatly underestimated due to various reasons such as high transmissibility, long incubation periods, low levels of testing, particularly, in the beginning and high levels of asymptomatic infections (e.g., see ^[2,41,42,43] and the references therein). To account for under-reported cases, we assume an ascertainment rate of $14 \%$ before January 23, 2020 and then linearly increase the ascertainment rate from $14 \%$ to $65 \%$ until February 12, 2020 ^[2]. After February 12, 2020, the ascertainment rate is assumed to be $100\%$ ^[44]. The cumulative infections in Wuhan estimated from our model are 3049 people by January 18, 2020 and cumulative cases are estimated at 36,091 people by January 27, 2020, which is in line with the results from other studies ^[22,43].

Figure 1 presents our fitted result to the data. It shows that (1) the onset of the epidemic occurs in January of 2020; (2) the epidemic lasts for about two months; (3) the situation of the epidemic is under control by March of 2020 and the disease tends to be extinct after July of 2020.

Figure 2 plots the time-dependent effective reproduction number $\mathcal{R}_0(t)$ over the first 60 days, where

This indicates that the effective reproduction number is $2.4$ during $[0, 17)$ days, and it is gradually reduced to $1.25$ by February 12, 2020 (Day 42) and and dropped to $0.625$ afterward. The details of the estimated $\beta$ and $\mathcal{R}_0$ values are provided in Table 4.

4.1.2.   Prediction

As shown in Figure 3, the ODE model predicts the disease extinction after June of 2020, which is a direct consequence of the effective intervention, prevention and control strategies currently implemented in Wuhan. There arises a question: Will the second wave take place if these strategies can't be implemented properly, for instance due to economic reopening?

To address this question, we elevate the basic reproduction number $\mathcal{R}_0$ by increasing $\beta(t)$ after June 28, 2020 (175 days) at which $\mathcal{R}_0 = 0.625$. The simulated result of our ODE model is illustrated in Figure 3. Our fitted solution (based on the data until June 28, 2020) is displayed in black and the curves in blue (resp. orange, green, red) shows the evolution of the infected cases over time when the value of $\mathcal{R}_0$ is increased to $1.5$ (resp. $2.0$, $2.5$, $3.0$) after June 28, 2020. The prediction of our ODE model shows that (a) the second wave may be much stronger than the first one; (b) the higher of the $\mathcal{R}_0$ value, the sooner the second wave would take place with higher peak value. This result indicates the second wave of the pandemic would happen if the infection risk goes up, for instance, due to changes in control strategy or human behavior.

Additionally, in this section, we conduct numerical simulations using stochastic models.

First, we study the probability of a disease outbreak. The outbreak is assumed to be attained when the cumulative sum of $E$ and $I$ reaches $10,000$. The outbreak probability is estimated from the proportion of the sample paths (out of $10,000$) of the CTMC model. Then the obtained estimate is compared to the theoretical approximation computed by the multitype branching process theory. Figure 4 displays the probability of a disease outbreak as a function of $\mathcal{R}_0$ when the infection is initiated by an individual from the infected class ($I(0) = 1$), where $\mathcal{R}_0$ is changed by varying $\beta$. In the case where the infection is initiated by an exposed individual ($E(0) = 1$), the result is nearly identical to the case begun with an infected individual. This happens because of $d\ll \alpha$. Note that when $d\ll \alpha$, $\frac{d}{\alpha+d} \approx 0$ and $\frac{a}{a+d} \approx 1$ and hence it follows from (3.1) that $q_1^* = \frac{d}{d+\alpha}+\frac{\alpha}{d+\alpha}\frac{1}{\mathcal{R}_0}\approx \frac{1}{\mathcal{R}_0} = q_2^*$, which implies $1-q_1^*\approx 1-q_2^*$. This result indicates that the outbreak probability is (approximately) $1-1/\mathcal{R}_0$ when $\mathcal{R}_0 > 1$, which is regardless of the initial condition of the infection (beginning with $E(0) = 1$ or $I(0) = 1$), since the human lifespan ($1/d$) is much longer than the disease latent period ($1/\alpha$). In both cases, (1) we find a strong agreement between the theoretical estimate (using branching process theory) and the numerical simulation of the CTMC model (using Gillespie simulation algorithm); (2) the chance of an outbreak increases as $\mathcal{R}_0$ increases; (3) the disease extinction occurs with probability one (i.e., the probability of an outbreak is zero) when $\mathcal{R}_0 < 1$; (4) unlike the deterministic model that predicts the persistence of the disease, the stochastic model indicates there is a positive chance for disease extinction.

Secondly, we study the time to the disease extinction and an outbreak by using the CTMC models for 10,000 simulation runs in each scenario. Figure 5 displays the conditional probability distribution of the extinction time given the extinction takes place during $[0,400]$ days, where the left (resp. right) panel displays the result when the infection starts with one exposed $E$ (resp. infected $I$) individual. It shows that there is a delay in the time to extinction when the infection is initiated by an exposed individual $E(0) = 1$ as compared to that by an infected individual $I(0) = 1$. Besides, in the case of $I(0) = 1$, the probability distribution of extinction time undergoes an immediate peak in the beginning and then declines rapidly as time increases. This indicates that disease extinction is expected to occur sooner with higher probability if the infection starts with one infected person. A biological interpretation of this result is that exposed individuals have to pass the incubation period to be capable of transmitting the disease to others and hence it delays the time to extinction. Figure 6 illustrates the conditional probability distribution of an outbreak given the occurrence of an outbreak during $[0,400]$ days. If we fix a time during this investigation period, we see the that the outbreak probability (the corresponding area in Figure 6) is higher in the case where infection is initiated by a person from the infected class, as compared to that initiated with a person from the exposed class.

Additionally, we investigate the time to the second wave of the pandemic. The current $\mathcal{R}_0$ is below one (from our investigation on the ODE model). Hence, to account for the change in restrictions and intervention and human behavior after reopening, we consider four different scenarios by assuming that $\mathcal{R}_0$ is elevated to $2.0$, $1.75$, $1.5$ and $1.25$. Figure 7 shows the conditional probability distribution of time to the second outbreak under these four scenarios when the infection starts with one $I$. Our result indicates that the second wave is likely to happen sooner with the higher value $\mathcal{R}_0$ after reopening. The mean and standard derivation for the time to extinction and the time to the second outbreak that are associated with the two initial conditions (i.e., either $E(0) = 1, I(0) = 0$ or $E(0) = 0, I(0) = 1$) are summarized in Table 5 for the selected $\mathcal{R}_0$ values. For instance, in the case where $\mathcal{R}_0$ is elevated to $1.5$ after reopening, there would be about a $34\%$ chance of a second outbreak and the standard deviation of the time to extinction is about $9$ days. If we compare the infection initiated by an exposed individual to that initiated by an infected individual, as shown in Table 5, the average extinction time is reduced from $8.03$ to $6.04$ days, the average time to outbreak decreases from $113.57$ to $111.36$ days and the corresponding standard deviation is dropped slightly from $16.11$ to $15.81$ days. In these two scenarios, we see the difference in terms of time to extinction or outbreak is small. As $\mathcal{R}_0$ increases, both disease extinction and outbreak are likely to occur sooner. More specifically, if $\mathcal{R}_0$ is increased from $1.25$ to $2.4$, the average time to the second outbreak (resp. extinction) is decreased from $201.85$ to $47.38$ days (resp. from $9.05$ to $2.96$ days) in the case of the infection starting with an infected individual. Nevertheless, our results from deterministic and stochastic models indicate that there is a possibility of the second wave if the reopening is not handled properly.

5.   Discussion

In this paper, we propose a deterministic and stochastic modeling framework to study the ongoing epidemic dynamics of the COVID-19 in the city of Wuhan, China. The deterministic model is formulated by a system of ODEs model that is built upon the classical SEIR framework. The stochastic model is formulated by a CTMC that is derived based on the ODE model with constant parameters during the early stage of the infection. We obtain a theoretical estimate for the probability of a disease outbreak by using multitype branching process approximation. Then we conduct a detailed mathematical analysis to the ODE model with constant model parameters, and our result indicates that the basic reproduction number $\mathcal{R}_0$ is served as a sharp disease threshold: the disease dies out if $\mathcal{R}_0\le 1$ and persists if $\mathcal{R}_0 > 1$. In contrast, the stochastic dynamics indicate that the disease may not persist when $\mathcal{R}_0 > 1$. A parameter estimation and validation is performed to fit our ODE model to the public reported data that is corrected to address underestimation issue. Additionally, we use numerical simulations of the CTMC model to study the disease extinction and an outbreak. Our results show that if the non-pharmaceutical interventions such as quarantine and social distancing were not implemented properly, the second wave is likely to take place. There are several limitation of this work. First, our model is based on the classical SEIR epidemic framework. It would be more realistic if more compartments representing variations in the population (e.g., asymptomatic, symptomatic, hospitalized individuals and different age groups) are included. Second, it would be interesting to study the ongoing pandemic under various prevention and control strategies (e.g., the stay-at-home order, the reopening of schools and social distancing measures) with data available. Third, the epidemic patterns of COVID-19 vary significantly by countries and regions. The impact of spatial heterogeneity on the transmission and spread of COVID-19 will provide an interesting topic in future research.

Acknowledgements

We thank the editor and reviewers for their helpful suggestions.

Conflict of interests

The authors declare that they have no conflict of interests.

Data availability

All data can be supplied by the authors upon request.