Dysbiosis, small intestinal bacterial overgrowth and biofilms in autism and chronic illness

1.   Introduction

Impulsive systems are a class of dynamical systems characterized by sudden changes in state or input at discrete time points. Such dynamical properties of impulsive systems have generated widespread applications in fields such as electrical engineering ^[1], digital signal processing ^[2], and biomedical engineering ^[3]. In impulsive systems, impulses are typically categorized into stabilizing impulses and disturbance impulses. Stabilizing impulses represent the stabilizing effect and optimal performance achieved by the nonlinear system under specific impulsive control, positively influencing system stability (see, e.g., ^[4,5]). Conversely, disturbance impulses may occur when the nonlinear system is subjected to external perturbations, negatively affecting system stability and potentially leading to instability (see, e.g., ^[6,7]). To maintain system stability and performance, corresponding control strategies are required to suppress or compensate for such disturbance impulses.

In certain practical engineering applications, such as wind power management, vehicle control, and spacecraft trajectory adjustments, continuously feeding control signals into the plant system is not realistic. Compared to traditional continuous control methods, intermittent control (IC) allows for inputting control signals into the plant system only at specific control time intervals, making it more suitable for these actual applications. IC can be divided into periodic intermittent control (PIC) (see e.g., ^[8,9,10]) and aperiodic intermittent control (APIC) (see, e.g., ^[11,12,13]). PIC inputs control signals into the plant system at fixed control period and control width, while APIC is more flexible, allowing for dynamic adjustments of control strategies as needed. In ^[14], exponential stability of nonlinear systems under PIC was investigated, and stability criteria based on linear matrix inequalities (LMI) and scalar inequalities were proposed. Given that the control period and width in PIC are fixed and known, the derived conditions may be too conservative. Consequently, there is an urgent need to introduce the APIC to replace PIC. In ^[15], the stabilization problem of continuous systems achieving exponential input-to-state stability through APIC was studied. In ^[16], the concept of aperiodic time-triggered IC was introduced, and a lower conservative exponential stability theorem was formulated for the considered aperiodic time-triggered IC system through the construction of a hybrid time-dependent Lyapunov functional. In the light of these reporting-based works, the APIC has become a highly regarded area of interest.

In current research, traditional time-triggered control (TC) and event-triggered control (EC) employ different approaches for control system design. TC involves sending and executing control signals at regular intervals, which, although simple and convenient, may lead to resource wastage and performance degradation due to its fixed-time interval signal transmission. In contrast, EC significantly reduces resource consumption and enhances system performance by updating control signals under specific triggering conditions. Recently, EC has achieved significant progress in achieving the satisfied dynamic performances of control systems (see, e.g., ^{[17,18,19,20]}). However, EC is unnecessary and energy-consuming as the event generator and controller continue to keep on running when the control execution is not required. Hence, an event-triggered intermittent control (EIC) strategy combining IC with EC has emerged. This strategy operates within specific time periods, allowing for intermittent updating of control signals, thereby further reducing resource consumption. A dynamic EIC scheme with input delays was introduced to stabilize the delayed dynamical systems in ^[21]. The time-triggered APIC and event-triggered APIC (EAPIC) schemes were developed to achieve exponential stabilization of continuous-time dynamical systems in ^[22].

Within a finite-time control framework, two particular stability concepts are under scrutiny: asymptotic stability, where system trajectories converge to equilibrium states (see, e.g., ^[23,24]), and finite-time stability (FTS), where the system does not exceed a predefined threshold in finite-time. Building upon the FTS concept, finite-time contraction stability (FTCS) further emphasizes the "boundedness" and "contraction" nature of the system itself. Numerous theoretical results exist regarding FTS and FTCS (see, e.g., ^[25,26,27]). Additionally, some guidelines for FTS and FTCS are also presented for impulsive systems (see, e.g., ^[28,29,30]). In ^[31], some sufficient conditions of FTS/FTCS for nonlinear impulsive systems were constructed via the Lyapunov function method. In ^[32], FTS and FTCS of nonlinear systems subject to impulsive disturbances with parameter uncertainties were obtained by designing APIC. A further exploration about FTS for nonlinear systems involving impulsive disturbances under the EAPIC strategy faces a series of challenges. This includes how to build the relationship between the IC parameters and event-triggering mechanism (ETM) threshold under EAPIC, as well as whether the designing APIC can suppress the effects of impulsive disturbance. These issues constitute the focal points of further study. From the above discussion, the strengths of this paper can be concluded as below:

(1) Based on the Lyapunov method and LMI techniques, this paper combines EC and APIC to investigate the FTS and FTCS of uncertain systems with uncertain impulsive disturbance using EAPIC, where the impulsive instants are generated by the predesigned ETM.

(2) Four elements of uncertain systems–FTS/FTCS, APIC, and impulse disturbances–are combined simultaneously. Moreover, under EAPIC, the correlation among finite-time interval, impulsive disturbance, inspection period, and ETM threshold is revealed. Additionally, the adopted EAPIC can exclude the Zeno phenomenon.

(3) You et al. ^[32] apply time-triggered APIC to stabilize uncertain nonlinear systems with impulse disturbance. This method involves control actions at fixed time intervals, which can lead to unnecessary computations and communications. In contrast, the EAPIC considered in this paper triggers control based on the actual changes in the system state, thus being more universal and flexible.

Notations: $ \mathcal{R} $ and $ \mathcal{R}_+ $ represent the sets of real and non-negative real numbers, respectively. $ \mathcal{Z}_+ $ stands for the set of positive integers. $ \mathcal{R}^n $ denotes the $ n $-dimensional real space with the Euclidean norm $ \vert\vert\cdot\vert\vert $. $ \mathcal{R}^{n\times m} $ indicates the $ n\times m $ dimensional real space. $ Y\geq 0 $ or $ Y\leq 0 $ means that matrix $ Y $ is a positive definite or negative definite symmetric matrix. $ Y^{T} $ and $ Y^{-1} $ are used to describe the transpose and inverse of $ Y $ separately. $ \lambda_{max}(Y) $ and $ \lambda_{min}(Y) $ represent the maximum and minimum eigenvalues of matrix $ Y $, respectively. $ \ast $ stands for a symmetric block within a symmetric matrix. $ \mathcal{I} $ denotes the unit matrix possessing suitable dimension. $ C([-\theta, 0]; \mathcal{R}^n) $ is the family of continuous functions $ \psi: [-\theta, 0]\to\mathcal{R}^n $. A locally Lipschitz function $ \nu: \mathcal{R}^n\to\mathcal{R}_+ $ has the upper right-hand Dini derivative determined by

2.   Model description and preliminaries

The uncertain system is considered as follows:

where $ \iota(t)\in\mathcal{R}^n $ is state vector, $ \mathcal{A}(t), \mathcal{B}(t)\in\mathcal{R}^{n\times n} $, as well as $ \mathcal{C}(t)\in\mathcal{R}^{n\times m} $. Assume that $ \mathcal{A}(t) = $ $ \mathcal{A}+\Delta \mathcal{A}(t) $, $ \mathcal{B}(t) = \mathcal{B}+\Delta \mathcal{B}(t) $, and $ \mathcal{C}(t) = \mathcal{C}+\Delta \mathcal{C}(t) $, in which $ \mathcal{A}, \mathcal{B} $, and $ \mathcal{C} $ are known real matrices, whereas $ \Delta \mathcal{A}(t), \Delta \mathcal{B}(t) $, and $ \Delta \mathcal{C}(t) $ are uncertain unknown matrices. $ \sigma(\iota(t)) = \left(\sigma_1(\iota_1(t)), \sigma_2(\iota_2(t)), \cdots, \sigma_n(\iota_n(t))\right)^T\in\mathcal{R}^n $ with $ \sigma(0) = 0 $. $ \theta $ denotes time delay. The APIC $ u(t)\in\mathcal{R}^m $ is given as below

in which $ \mathcal{H} $ signifies the control strength. $ t_k, \tau_k $ respectively denote the start time and control width of each control period, which satisfy $ 0 < \tau_k < t_{k+1}-t_k $. It can be noted that the controller (2.2) requires operation only on control intervals. That is, the absence of transmitting control input information during the rest interval implies that system (2.1) operates alternately between the open-loop control mode and the closed-loop control mode. Moreover, it is considered that the state of system (2.1) jumps in certain cases due to the activation of the aperiodic interval controller, namely, the generation of impulsive phenomena, and we regard them as disturbance impulses. Thus, system (2.1) with impulses involved can be formulated as

where $ \mathcal{D}(t) $ represents the impulse gain matrix, which satisfies $ \mathcal{D}(t) = \mathcal{D}+\Delta \mathcal{D}(t) $. $ \mathcal{D} $ is a known matrix, and $ \Delta \mathcal{D}(t) $ is an unknown matrix. Assume system (2.3) is right continuous. Put $ \iota(t, 0, \varsigma) $ to indicate the solution of system (2.3) through $ (0, \varsigma), \varsigma\in \mathcal{R}^n $. The series $ \left\{t_k\right\}_{k = 1}^{+\infty} $ fulfills $ 0 = t_0 < t_1 < \cdots < t_k < \cdots $ and $ \lim_{k\to+\infty} = +\infty $.

It is assumed that the intermittent sequence $ \left\{t_k\right\} $ is created through the ETM as follows:

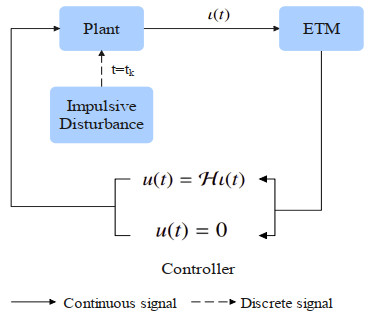
where $ \Gamma_k(\varepsilon, t] = \left\{t: t > \varepsilon+\tau_k, \mathcal{U}(\iota(t))\geq e^\zeta \mathcal{U}(\iota(\varepsilon+\tau_k))\right\} $, $ e^\zeta, \zeta > 0 $ denotes the threshold value, $ \omega > 0 $ stands for the inspection period, which is generally devised as a constant large enough, as well as $ \mathcal{U}(\cdot) $ indicates the Lyapunov function with respect to the state of the system (2.3). Figures 1 and 2 describe the EAPIC loop and framework of EAPIC, respectively.

The following describes some assumptions, definitions, and lemmas.

Assumption 2.1 (^[29]). Suppose there are positive constants $ \varpi_j $, which make

hold.

Assumption 2.2 (^[32]). The parameter uncertainties $ \Delta \mathcal{A}(t), \Delta \mathcal{B}(t), \Delta \mathcal{C}(t) $, and $ \Delta \mathcal{D}(t) $ satisfy

where $ \mathcal{N}, \mathcal{F}, \mathcal{M}_1, \mathcal{M}_2, \mathcal{M}_3 $, and $ \mathcal{M}_4 $ are known matrices as well as $ \mathcal{K}_i(t) $ is an uncertain matrix-valued function of suitable dimension fulfilling

Definition 2.1. For specified constants $ \mathcal{T}, \delta_1, \delta_2, \pi, \rho $ with $ 0 < \rho < \delta_1 < \delta_2 $ and $ \pi\in(0, \mathcal{T}) $, along with an arbitrary trajectory $ \iota(t) $, the existence of a controller making $ \vert\vert\iota(0)\vert\vert\leq\delta_1 $ implies that $ \vert\vert\iota(t)\vert\vert\leq\delta_2 $ for $ t\in[0, \mathcal{T}] $, then system (2.3) is called FTS with respect to (w.r.t) $ (\mathcal{T}, \delta_1, \delta_2) $. Moreover, for $ t\in[\mathcal{T}-\pi, \mathcal{T}] $, if $ \vert\vert\iota(t)\vert\vert\leq\rho $, then system (2.3) is called FTCS w.r.t $ (\mathcal{T}, \delta_1, \delta_2, \rho, \pi) $.

Remark 2.1. According to ^[33], FTS depicts the "boundedness" of the described systems. In contrast, FTCS demonstrates the "boundedness" and "contraction" of the described systems simultaneously. In particular, to attain the "contraction" feature, FTCS requires the additional condition that the reasoned systems can remain in a comparatively smaller boundary than the initial boundary until the end time is implemented. Figure 3 visually depicts the FTS and FTCS, which also consider the possible impact on the system of impulsive disturbance.

Lemma 2.1 (^[34]). For matrices $ \mathcal{D}, \mathcal{S}, \mathcal{F}, \mathcal{M} $, and $ \mathcal{K}(t) $ with appropriate dimensions and $ \mathcal{S}>0, \mathcal{K}^{T} \mathcal{K}(t)\leq\mathcal{I} $, scalars $ \kappa>0 $ and $ \mathcal{S}-\kappa \mathcal{F} \mathcal{F}^T>0 $, it follows that

Lemma 2.2 (^[35]). For a symmetric and positive matrix $ \mathcal{Q} $, constant $ \varrho > 0 $, one has

Lemma 2.3 (^[36]). The $ \mathcal{N} $ and $ \mathcal{M} $ are matrices with proper dimensions. Let $ \mathcal{K}(t) $ meet $ \mathcal{K}^{T} \mathcal{K}(t)\leq\mathcal{I} $. For any $ \gamma > 0 $, then

Lemma 2.4 (^[29]). Let $ \iota\in C([\chi-\theta, \infty); [0, \infty)) $ satisfy

If $ c > d > 0 $, then

in which $ \max\left\{\iota_t\right\} = \sup_{t-\theta\leq\phi\leq t}\iota(\phi) $, and $ \lambda $ is the smallest positive real root in the following equation

Lemma 2.5 (^[37]). For $ t\in(-\theta, +\infty) $, if function $ \iota\geq 0 $ meets

it follows that

3.   Main results

In this section, sufficient conditions for FTS and FTCS of system (2.3) are obtained through EAPIC.

Theorem 3.1. Suppose that Assumptions 2.1 and 2.2 hold, there exists symmetric and positive matrix $ \mathcal{P} $, positive constants $ \lambda, \delta_1, \delta_2, \mathcal{T}, \rho, \pi, \mu_1, \mu_2, \gamma_1, \gamma_2, \gamma_3, \gamma_4, \alpha_1, \alpha_2, \eta_1, \eta_2, \vartheta $, where $ \rho < \delta_1 < \delta_2, \pi\in(0, \mathcal{T}), \mu_1\leq\mu_2, $ and $ \vartheta\geq1 $ to satisfy

$ (A)\; \mu_1\mathcal{I}\leq\mathcal{P}\leq\mu_2\mathcal{I}; $

$ (B)\;

$$\begin{pmatrix} -\vartheta\mathcal{P} & \mathcal{D}^T\mathcal{P} & \mathcal{M}_4^T \\ \ast & -\mathcal{P}+\gamma_4\mathcal{P} \mathcal{F} \mathcal{F}^T\mathcal{P} & 0 \\ \ast & \ast & -\gamma_4\mathcal{I} \end{pmatrix}$$ < 0; $

$ (C)\;

$$\begin{pmatrix} \tilde{\psi}_1 & \mathcal{P} \mathcal{B}\\ \ast & -\alpha_1\mathcal{I}+\gamma_2^{-1} \mathcal{M}_2^T \mathcal{M}_2 \end{pmatrix}$$ < 0 $, where

$ (D)\;

$$\begin{pmatrix} \tilde{\psi}_2 & \mathcal{P} \mathcal{B}\\ \ast & -\alpha_2\mathcal{I}+\gamma_2^{-1} \mathcal{M}_2^T \mathcal{M}_2 \end{pmatrix}$$ < 0 $, where

$ (E)\; \frac{\zeta}{\lambda}\leq\bar{\tau}\leq\tau_k\leq\omega-\frac{\zeta}{\eta_2+h_2}; $

$ (F)\; n(0, t)\ln\vartheta-\lambda(\sum_{i = 0}^{n(0, t)}\tau_i)+(n(0, t)+1)\zeta\leq\ln(\mu_1\delta_2^2)-\ln(\mu_2\delta_1^2), \; \; t\in[0, \mathcal{T}] $,

in which $ \lambda $ is the smallest positive solution of the formula $ \eta_1-\lambda-h_1e^{\lambda\theta} = 0 $ and $ \eta_1 > h_1 $. $ \bar{\tau} = \liminf\frac{\sum_{i = 0}^{k-1}\tau_i}{k} $ denotes the minimum average control width. $ n(0, t) $ represents the control period count on $ (0, \mathcal{T}], \; \mathcal{T}\neq t_k $. Thus, the Zeno phenomenon is ruled out, and system (2.3) is FTS w.r.t $ (\mathcal{T}, \delta_1, \delta_2) $ under APIC (2.2). Besides, for $ t\in[\mathcal{T}-\pi, \mathcal{T}] $, if the following relation.

$ (G)\; n(0, t)\ln\vartheta-\lambda(\sum_{i = 0}^{n(0, t)}\tau_i)+(n(0, t)+1)\zeta\leq\ln(\mu_1\rho^2)-\ln(\mu_2\delta_1^2) $ holds, then system (2.3) is FTCS w.r.t $ (\mathcal{T}, \delta_1, \delta_2, \rho, \pi) $ under APIC (2.2).

Proof. For $ 0 < \vert\vert\iota(0)\vert\vert\leq\delta_1 $, assume that $ \iota(t) = \iota(t, 0, \varsigma) $ is a solution of system (2.3) via $ (0, \varsigma) $. Consider the Lyapunov function as follows:

From $ (B) $ in Theorem 3.1, it follows that

For $ t = t_k $, by using Lemma 2.1, we obtain

For $ t\neq t_k $, when $ t\in[t_k, t_k+\tau_k) $, we obtain

Next, together with Assumption 2.2, Lemma 2.2, and Lemma 2.3 to obtain

Bringing (3.3)–(3.5) into (3.2), we have, according to $ (C) $ in Theorem 3.1, that

where $ h_1 = \alpha_1\varpi_{\sigma}\lambda_{max}(\mathcal{P}^{-1}) $ with $ \varpi_{\sigma} = \max\left\{\varpi_1^2, \varpi_2^2, \dots, \varpi_n^2\right\} $. For $ t\in[t_k, t_k+\tau_k) $, by Lemma 2.4, one has

Similarly, for $ t\in[t_k+\tau_k, t_{k+1}) $, it follows that

where $ h_2 = \alpha_2\varpi_{\sigma}\lambda_{max}(\mathcal{P}^{-1}) $. Based on Lemma 2.5, when $ t\in[t_k+\tau_k, t_{k+1}) $, we obtain

Thus,

If $ \Gamma_k(t_k+\tau_k, t_k+\omega]\neq\emptyset $, then $ t_{k+1}-t_k\leq\omega $ and only when the event occurrence function to be zero will trigger the next event, namely

Consequently, together with (3.8) and (3.9), we derive

If $ \Gamma_k(t_k+\tau_k, t_k+\omega] = \emptyset $, then $ t_{k+1}-t_k = \omega $, (3.10) still stands. Because $ \frac{\zeta}{\eta_2+h_2} > 0 $, combining (3.10) with $ (E) $ in Theorem 3.1, it follows that

Therefore, the Zeno behavior of system (2.3) is excluded.

For $ t\in[t_k+\tau_k, t_{k+1}) $, by ETM (2.4), we obtain

When $ t\in[0, \tau_0) $, by (3.6), it is obtained that

and

When $ t\in[\tau_0, t_1) $, based on (3.12), one obtains

and

When $ t\in[t_1, t_1+\tau_1) $, it follows from (3.1) and (3.6) that

and

When $ t\in[t_1+\tau_1, t_2) $, we obtain

and

When $ t\in[t_2, t_2+\tau_2) $, one has

and

When $ t\in[t_2+\tau_2, t_3) $, there holds

By mathematical induction, when $ t\in[t_k+\tau_k, t_{k+1}) $, one obtains

which means

Using $ (A) $ and $ (F) $ in Theorem 3.1, we derive

which implies $ \vert\vert\iota(t)\vert\vert\leq\delta_2 $, and hence, $ \vert\vert\iota(t)\vert\vert\leq\delta_2 $ holds on $ [0, \mathcal{T}] $. So, system (2.3) can achieve FTS under APIC (2.2). When $ t\in[\mathcal{T}-\pi, \mathcal{T}] $, if $ (G) $ in Theorem 3.1 is satisfied, it follows from (3.13) that

which shows that $ \vert\vert\iota(t)\vert\vert\leq\rho $ for all $ t\in[\mathcal{T}-\pi, \mathcal{T}] $. Then, system (2.3) can achieve FTCS under APIC (2.2). □

Remark 3.1. It is important to note that conditions $ (C) $ and $ (D) $ in Theorem 3.1 regulate the continuous dynamics so that (3.6) and (3.7) hold, where the parameters $ \eta_1 $ and $ \eta_2 $ imply the decay rate and potential growth for system (2.3), respectively. This means that system (2.3) shows a decreasing trend in the control intervals, which makes system (2.3) to some extent divergent in the resting intervals. Furthermore, $ \vartheta\geq 1 $ in condition $ (B) $ of Theorem 3.1 suggests that impulses may have destabilizing effects.

As a matter of fact, when $ \tau_k = \tau, t_{k+1}-t_k-\tau = c $ with $ \tau, c > 0 $, APIC (2.2) can be turned into PIC as follows:

where $ \mathcal{J} > 0 $ denotes the control period as well as $ 0 < \tau < \mathcal{J} $ indicates the control width, then the following corollary is obvious.

Corollary 3.1. Suppose that Assumptions 2.1 and 2.2 hold, there exists symmetric and positive matrix $ \mathcal{P} $, positive constants $ \lambda, \delta_1, \delta_2, \mathcal{T}, \rho, \pi, \mu_1, \mu_2, \gamma_1, \gamma_2, \gamma_3, \gamma_4, \alpha_1, \alpha_2, \eta_1, \eta_2, \vartheta $, where $ \rho < \delta_1 < \delta_2, \pi\in(0, \mathcal{T}), \mu_1\leq\mu_2, $ and $ \vartheta\geq1 $ to satisfy $ (A)-(D) $ in Theorem 3.1, and for any $ t\in[0, \mathcal{T}] $, if the following relation

holds, then system (2.3) is FTS w.r.t $ (\mathcal{T}, \delta_1, \delta_2) $ under PIC (3.14). Besides, for $ t\in[\mathcal{T}-\pi, \mathcal{T}] $, if

holds, then system (2.3) is FTCS w.r.t $ (\mathcal{T}, \delta_1, \delta_2, \rho, \pi) $ under PIC (3.14).

Remark 3.2. It should be noted that (3.14), as a special case of (2.2), is time-triggered, meanwhile, both $ \mathcal{J} $ and $ \tau $ are fixed.

Next, when parameter uncertainties $ \Delta \mathcal{A}(t) = \Delta \mathcal{B}(t) = \Delta \mathcal{C}(t) = \Delta \mathcal{D}(t) = 0 $, the uncertain system (2.3) is transformed into the following deterministic system:

Corollary 3.2. Suppose that Assumption 2.1 holds and there exists symmetric positive matrices $ \mathcal{P} $, positive constants $ \lambda, \delta_1, \delta_2, \mathcal{T}, \rho, \pi, \mu_1, \mu_2, \alpha_1, \alpha_2, \eta_1, \eta_2, \vartheta $, where $ \rho < \delta_1 < \delta_2, \pi\in(0, \mathcal{T}), \mu_1\leq\mu_2, $ and $ \vartheta\geq1 $ such that $ (A) $ in Theorem 3.1 and

$ (B')\;

$$\begin{pmatrix} -\vartheta\mathcal{P} & \mathcal{D}^T\mathcal{P} \\ \ast & -\mathcal{P} \end{pmatrix}$$ < 0; $

$ (C')\;

$$\begin{pmatrix} \tilde{\psi}_1 & \mathcal{P} \mathcal{B}\\ \ast & -\alpha_1\mathcal{I} \end{pmatrix}$$ < 0 $, where $ \tilde{\psi}_1 = \mathcal{P} \mathcal{A}+ \mathcal{A}^T\mathcal{P}+\mathcal{P} \mathcal{C} \mathcal{H}+ \mathcal{H}^T \mathcal{C}^T\mathcal{P}+\eta_1\mathcal{P}; $

$ (D')\;

$$\begin{pmatrix} \tilde{\psi}_2 & \mathcal{P} \mathcal{B}\\ \ast & -\alpha_2\mathcal{I} \end{pmatrix}$$ < 0 $, where $ \tilde{\psi}_2 = \mathcal{P} \mathcal{A}+ \mathcal{A}^T\mathcal{P}-\eta_2\mathcal{P}; $

$ (E')\; \frac{\zeta}{\lambda}\leq\bar{\tau}\leq\tau_k\leq\omega-\frac{\zeta}{\eta_2+h_2}; $

hold, then system (3.15) is FTS w.r.t $ (\mathcal{T}, \delta_1, \delta_2) $ under APIC (2.2) if $ (F) $ in Theorem 3.1 is true and the Zeno phenomenon is excluded. Furthermore, system (3.15) is FTCS w.r.t $ (\mathcal{T}, \delta_1, \delta_2, \rho, \pi) $ under APIC (2.2) if $ (G) $ in Theorem 3.1 is satisfied when $ t\in[\mathcal{T}-\pi, \mathcal{T}] $.

4.   Numerical examples

The validity of the theoretical results will be verified by two numerical examples.

Example 4.1. Consider the uncertain system as follows:

on $ t\geq 0 $, where

Consider the initial condition $ \iota(0) = (1.05, 0.6)^{T} $, parameters $ \delta_1 = 1.21, \delta_2 = 2 $, and $ \mathcal{T} = 9.5 $. Based on the state trajectories of system (4.1) shown in Figure 4, we know that system (4.1) is not FTS w.r.t (9.5, 1.21, 2).

When APIC $ u(t) $ and impulsive disturbance are accounted for, system (4.1) can be rewritten as

where

and

Let $ \varpi_1 = \varpi_2 = 0.51, \mathcal{N} = \mathcal{F} = \mathcal{I}_2, \mathcal{M}_1 = \mathcal{M}_2 = \mathcal{M}_4 = 0.1\mathcal{I}_2, \mathcal{M}_3 = (0.1;0), \mathcal{K}_i(t) = (\sin(0.5t), 0;0, \sin(0.5t)) $ and $ \mathcal{K}_i^{T}(t) \mathcal{K}_i(t)\leq\mathcal{I}_2\; (i = 1, 2) $, in which case Assumptions 2.1 and 2.2 hold.

Assume that $ \mu_1 = 5.2, \mu_2 = 5.5, \vartheta = 2, \gamma_1 = 0.0425, \gamma_2 = 0.043, \gamma_3 = 0.0358$, $\gamma_4 = 0.018, \alpha_1 = 1.8266, \alpha_2 = 2.3013, \eta_1 = 0.3665, \eta_2 = 1.1 $. Under conditions $ (A)-(D) $ of Theorem 3.1, it can be obtained by using the MATLAB toolbox

Additionally, by calculating, we can obtain $ h_1 = 0.0888, h_2 = 0.1119 $, and $ \lambda = 0.2651 $.

Design $ \omega = 5, \zeta = 0.1 $ as well as $ \tau_k = 3.5 $, then the intermittent sequence $ \left\{t_k\right\} $ is decided by the following ETM

where

and $ \mathcal{U}(\iota(t)) = \iota^{T}(t) \mathcal{P}\iota(t) $. Obviously, the condition $ (E) $ in Theorem 3.1 is satisfied. According to Figure 5, we can obtain the intermittent times as $ t_1 = 3.6359, t_2 = 7.4563 $. Furthermore, when $ t\in[0, 9.5] $, we have that the intermittent sequences $ \left\{t_k\right\} $ and control span $ \tau_k $ meet

By Theorem 3.1, we can conclude that system (4.2) is FTS w.r.t (9.5, 1.21, 2) under APIC (4.3). Moreover, take $ \pi = 2, \rho = 1.15 $. When $ t\in\left[7.5, 9.5\right] $, the intermittent sequences $ \left\{t_k\right\} $ and control span $ \tau_k $ satisfy

Based on Theorem 3.1, we can deduce that system (4.2) is FTCS w.r.t (9.5, 1.21, 2, 1.15, 2) under APIC (4.3). The relevant simulation results for $ \iota(0) = (1.05, 0.6)^T $ are displayed in Figure 5, where Figure 5(a) portrays the trajectories of $ \iota_1, \iota_2 $; Figure 5(b, c) shows the trajectories of $ \vert\vert\iota(t)\vert\vert $ and $ u(t) $, respectively.

Example 4.2. Let us consider the two degrees of freedom damped dual-mass spring system illustrated in Figure 6, which has the following mathematical expression:

where $ m_1, m_2\in \mathcal{R}_+ $ denote two masses, $ \iota_1, \iota_2\in \mathcal{R}_+ $ represent displacements of masses $ m_1, m_2 $, $ k_1, k_2\in \mathcal{R}_+ $ indicate elasticity coefficients of two springs, $ c_1, c_2\in \mathcal{R}_+ $ signify damping coefficients of two dampers, as well as $ u $ stands for the control input as shown in (2.2). Setting $ \dot{\iota}_1 = \iota_3, \dot{\iota}_2 = \iota_4 $, and $ \iota = (\iota_1, \iota_2, \iota_3, \iota_4)^T $, then we obtain

In real applications, the damped dual-mass spring system may experience transient disturbances in the control mass $ m_1 $ caused by input noise and uncertainty. We treat such transient disturbances as impulsive disturbances that induce an instantaneous change in velocity, namely, $ \iota(t_k) = \mathcal{D}\iota(t_k^-) $, where $ \mathcal{D} = diag\left\{1, 1, d, 1\right\} $. Moreover, the sequence of impulsive moments is given by ETM (4.4). Assume that $ \sigma_1 = \sin(0.1\iota_1(t)), \sigma_2 = \sin(0.1\iota_2(t-\theta)) $, where $ \theta = 0.2 $. Let $ \mu_1 = 1, \mu_2 = 3, \eta_1 = 0.6513, \eta_2 = 1.961, \vartheta = 1.8$, $\alpha_1 = 1.6371, \alpha_2 = 1.5088, k_1 = 2.5, k_2 = 2$, $m_1 = 3.5, m_2 = 1.2, c_1 = 0.5, c_2 = 3, d = 1.3. $ According to $ (A), (C')-(D') $ in Corollary 3.2, using the MATLAB toolbox, one has

By further calculations, it follows that $ h_1 = 0.0159, h_2 = 0.0147, $ as well as $ \lambda = 0.6333 $. Therefore, $ (E') $ in Corollary 3.2 holds. As can be seen from Figure 7, the impulsive instants are $ t_1 = 4.6267, t_2 = 9.6267 $. Let $ \mathcal{T} = 6, \delta_1 = 2.17, \delta_2 = 4, \rho = 1.85, \pi = 1.2 $, and the initial value is $ \iota_0 = (1.8, 0.8, -0.1, -0.9) $. When $ t\in[0, 6] $, we have that the impulsive sequences $ \left\{t_k\right\} $ and control span $ \tau_k $ meet

From Corollary 3.2, we can deduce that under APIC (2.2), system (4.6) is FTS w.r.t (6, 2.17, 4). Moreover, when $ t\in\left[4.8, 6\right] $, the impulsive sequences $ \left\{t_k\right\} $ and control span $ \tau_k $ satisfy

According to Corollary 3.2, we can infer that system (4.6) is FTCS w.r.t (6, 2.17, 4, 1.85, 1.2) under APIC (2.2). The associated simulation results are exhibited in Figure 7.

Remark 4.1. Without considering the control input $ u $ and impulsive disturbance, it can be seen from Figure 8 that system (4.6) is not FTCS w.r.t (6, 2.17, 4, 1.85, 1.2).

5.   Conclusions

Due to traditional PIC methods, which execute control actions at fixed time intervals regardless of system state changes, inefficiencies may arise. To overcome these restrictions, this paper proposes the EAPIC method by combining APIC with EC. Through this approach, the FTS and FTCS of parameter-uncertain systems with impulsive disturbance are investigated. With the aid of Lyapunov methods and LMI techniques, criteria for FTS and FTCS of parameter uncertain systems are derived. Additionally, under EAPIC conditions, relationships among impulsive disturbance, intermittent control parameters, and ETM threshold are established. The sequence of impulsive instants is determined by predefined ETM, and the Zeno phenomenon is ruled out. In future work, we will focus on how to incorporate external disturbances, such as random noise, into the EAPIC system. We plan to adapt the existing event-triggered control strategy to enhance the robustness of the system to these disturbances and ensure that the control strategy remains effective under various disturbance conditions.

Author contributions

Tian Xu: Writing-original draft; Jin-E Zhang: Supervision, writing-review & editing. Both authors have read and approved the final version of the manuscript for publication.

Acknowledgments

The authors would like to thank the editors and referees for their very helpful comments and suggestions.

Conflict of interest

The authors declare that there are no conflicts of interest.