microRNA (miRNA) is a small non-coding RNA molecule that plays a role in the post-transcriptional regulation of gene expression. Recent evidence shows that miRNAs are involved in various diseases,including neurodegenerative diseases (NDs) such as: Parkinson's disease,Alzheimer's disease,Huntington's disease,Amyotrophic lateral sclerosisand multiple system atrophy (MSA).
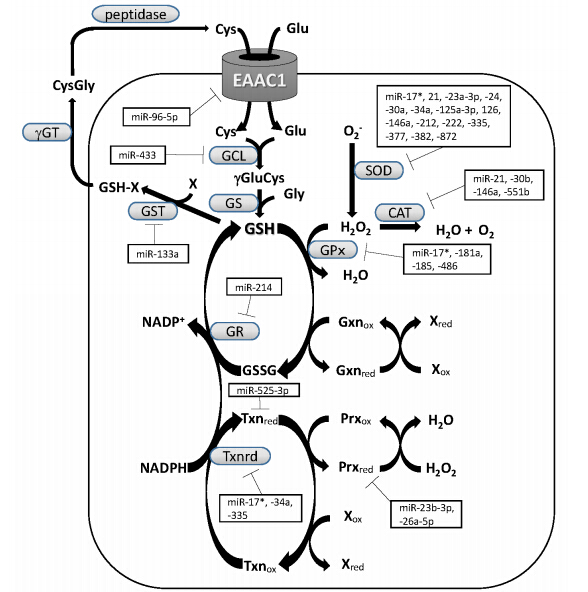
The initiation and progression of NDs is generally considered to be induced by oxidative stress arising from an imbalance of oxidants and antioxidants. One of the most important antioxidants against oxidative stress is glutathione (GSH),which is a tripeptide composed of cysteine,glutamate and glycine. Among these precursor amino acids,cysteine is the determinant of neuronal GSH synthesis. Cysteine uptake in the neurons is mostly mediated by excitatory amino acid carrier 1 (EAAC1),a member of the sodium-dependent excitatory amino acid transporters. Interestingly,it has been reported that one miRNA,miR-96-5p,regulates the neuroprotective effect of GSH by directly regulating EAAC1 expression. Furthermore,the expressions of miR-96-5p and its target EAAC1 are specifically deregulated in the brains of patients with MSA,suggesting that deregulated miR-96-5p induces MSA via EAAC1 down-regulation. Since miR-96-5p regulation of EAAC1 expression and GSH level is indicated to be under circadian control,a greater understanding of rhythmic miRNA regulation could lead to the use of miRNA in chronotherapy for ND.
In this review,we focus on the role of miRNA in the mechanism of GSH synthesis and metabolism; particularly with respect to a critical transport system of its rate-limiting substrate via EAAC1,as well as on the implications and chronotherapeutic potential of miRNA for NDs.
1.
Introduction
The constituent members in a system mainly found in nature can be interacting with each other through cooperation and competition. Demonstrations for such systems involve biological species, countries, businesses, and many more. It's very much intriguing to investigate in a comprehensive manner numerous social as well as biological interactions existent in dissimilar species/entities utilizing mathematical modeling. The predation and the competition species are the most famous interactions among all such types of interactions. Importantly, Lotka [1] and Volterra [2] in the 1920s have announced individually the classic equations portraying population dynamics. Such illustrious equations are notably described as predator-prey (PP) equations or Lotka-Volterra (LV) equations. In this structure, PP/LV model represents the most influential model for interacting populations. The interplay between prey and predator together with additional factors has been a prominent topic in mathematical ecology for a long period. Arneodo et al. [3] have established in 1980 that a generalized Lotka-Volterra biological system (GLVBS) would depict chaos phenomena in an ecosystem for some explicitly selected system parameters and initial conditions. Additionally, Samardzija and Greller [4] demonstrated in 1988 that GLVBS would procure chaotic reign from the stabled state via rising fractal torus. LV model was initially developed as a biological concept, yet it is utilized in enormous diversified branches for research [5,6,7,8]. Synchronization essentially is a methodology of having different chaotic systems (non-identical or identical) following exactly a similar trajectory, i.e., the dynamical attributes of the slave system are locked finally into the master system. Specifically, synchronization and control have a wide spectrum for applications in engineering and science, namely, secure communication [9], encryption [10,11], ecological model [12], robotics [13], neural network [14], etc. Recently, numerous types of secure communication approaches have been explored [15,16,17,18] such as chaos modulation [18,19,20,21], chaos shift keying [22,23] and chaos masking [9,17,20,24]. In chaos communication schemes, the typical key idea for transmitting a message through chaotic/hyperchaotic models is that a message signal is nested in the transmitter system/model which originates a chaotic/ disturbed signal. Afterwards, this disturbed signal has been emitted to the receiver through a universal channel. The message signal would finally be recovered by the receiver. A chaotic model has been intrinsically employed both as receiver and transmitter. Consequently, this area of chaotic synchronization & control has sought remarkable considerations among differential research fields.
Most prominently, synchronization theory has been in existence for over $ 30 $ years due to the phenomenal research of Pecora and Carroll [25] established in 1990 using drive-response/master-slave/leader-follower configuration. Consequently, many authors and researchers have started introducing and studying numerous control and synchronization methods [9,26,27,28,29,30,31,32,33,34,35,36] etc. to achieve stabilized chaotic systems for possessing stability. In [37], researchers discussed optimal synchronization issues in similar GLVBSs via optimal control methodology. In [38,39], the researchers studied the adaptive control method (ACM) to synchronize chaotic GLVBSs. Also, researchers [40] introduced a combination difference anti-synchronization scheme in similar chaotic GLVBSs via ACM. In addition, authors [41] investigated a combination synchronization scheme to control chaos existing in GLVBSs using active control strategy (ACS). Bai and Lonngren [42] first proposed ACS in 1997 for synchronizing and controlling chaos found in nonlinear dynamical systems. Furthermore, compound synchronization using ACS was first advocated by Sun et al. [43] in 2013. In [44], authors discussed compound difference anti-synchronization scheme in four chaotic systems out of which two chaotic systems are considered as GLVBSs using ACS and ACM along with applications in secure communications of chaos masking type in 2019. Some further research works [45,46] based on ACS have been reported in this direction. The considered chaotic GLVBS offers a generalization that allows higher-order biological terms. As a result, it may be of interest in cases where biological systems experience cataclysmic changes. Unfortunately, some species will be under competitive pressure in the coming years and decades. This work may be comprised as a step toward preserving as many currently living species as possible by using the proposed synchronization approach which is based on master-slave configuration and Lyapunov stability analysis.
In consideration of the aforementioned discussions and observations, our primary focus here is to develop a systematic approach for investigating compound difference anti-synchronization (CDAS) approach in $ 4 $ similar chaotic GLVBSs via ACS. The considered ACS is a very efficient yet theoretically rigorous approach for controlling chaos found in GLVBSs. Additionally, in view of widely known Lyapunov stability analysis (LSA) [47], we discuss actively designed biological control law & convergence for synchronization errors to attain CDAS synchronized states.
The major attributes for our proposed research in the present manuscript are:
● The proposed CDAS methodology considers four chaotic GLVBSs.
● It outlines a robust CDAS approach based active controller to achieve compound difference anti-synchronization in discussed GLVBSs & conducts oscillation in synchronization errors along with extremely fast convergence.
● The construction of the active control inputs has been executed in a much simplified fashion utilizing LSA & master-salve/ drive-response configuration.
● The proposed CDAS approach in four identical chaotic GLVBSs of integer order utilizing ACS has not yet been analyzed up to now. This depicts the novelty of our proposed research work.
This manuscript is outlined as follows: Section 2 presents the problem formulation of the CDAS scheme. Section 3 designs comprehensively the CDAS scheme using ACS. Section 4 consists of a few structural characteristics of considered GLVBS on which CDAS is investigated. Furthermore, the proper active controllers having nonlinear terms are designed to achieve the proposed CDAS strategy. Moreover, in view of Lyapunov's stability analysis (LSA), we have examined comprehensively the biological controlling laws for achieving global asymptotical stability of the error dynamics for the discussed model. In Section 5, numerical simulations through MATLAB are performed for the illustration of the efficacy and superiority of the given scheme. Lastly, we also have presented some conclusions and the future prospects of the discussed research work in Section 6.
2.
Problem formulation
We here formulate a methodology to examine compound difference anti-synchronization (CDAS) scheme viewing master-slave framework in four chaotic systems which would be utilized in the coming up sections.
Let the scaling master system be
and the base second master systems be
Corresponding to the aforementioned master systems, let the slave system be
where $ w_{m1} = (w_{m11}, w_{m12}, ..., w_{m1n})^T\in R^n $, $ w_{m2} = (w_{m21}, w_{m22}, ..., w_{m2n})^T\in R^n $, $ w_{m3} = (w_{m31}, w_{m32}, ..., w_{m3n})^T\in R^n $, $ w_{s4} = (w_{s41}, w_{s42}, ..., w_{s4n})^T\in R^n $ are the state variables of the respective chaotic systems (2.1)–(2.4), $ f_1, f _2, f_3, f_4: R^n \rightarrow R^n $ are four continuous vector functions, $ U = (U_1, U_2, ..., U_n)^T : R^n\times R^n\times R^n\times R^n \rightarrow R^n $ are appropriately constructed active controllers.
Compound difference anti-synchronization error (CDAS) is defined as
where $ P = diag(p_1, p_2, ....., p_n), Q = diag(q_1, q_2, ....., q_n), R = diag(r_1, r_2, ....., r_n), S = diag(s_1, s_2, ....., s_n) $ and $ S\neq 0 $.
Definition: The master chaotic systems (2.1)–(2.3) are said to achieve CDAS with slave chaotic system (2.4) if
3.
Stability analysis via active control strategy
We now present our proposed CDAS approach in three master systems (2.1)–(2.3) and one slave system (2.4). We next construct the controllers based on CDAS approach by
where $ \eta_i = p_i{(f_1)}_i({r_iw_{m3i}-q_iw_{m2i}})+p_iw_{m1i} ({r_i{(f_{3})_i-q_i{(f_{2}})_i}}) $, for $ i = 1, 2, ..., n. $
Theorem: The systems (2.1)–(2.4) will attain the investigated CDAS approach globally and asymptotically if the active control functions are constructed in accordance with (3.1).
Proof. Considering the error as
Error dynamical system takes the form
where $ \eta_i = p_i{(f_1)}_i({r_iw_{m3i}-q_iw_{m2i}})+p_iw_{m1i} ({r_i{(f_{3})_i-q_i{(f_{2}})_i}}) $, $ i = 1, 2, 3, ...., n. $ This implies that
The classic Lyapunov function $ V(E(t)) $ is described by
Differentiation of $ V(E(t)) $ gives
Using Eq (3.2), one finds that
An appropriate selection of $ (K_1, K_1, ......., K_n) $ makes $ \dot{V}(E(t)) $ of eq (3.3), a negative definite. Consequently, by LSA [47], we obtain
Hence, the master systems (2.1)–(2.3) and slave system (2.4) have attained desired CDAS strategy.
4.
An illustration
We now describe GLVBS as the scaling master system:
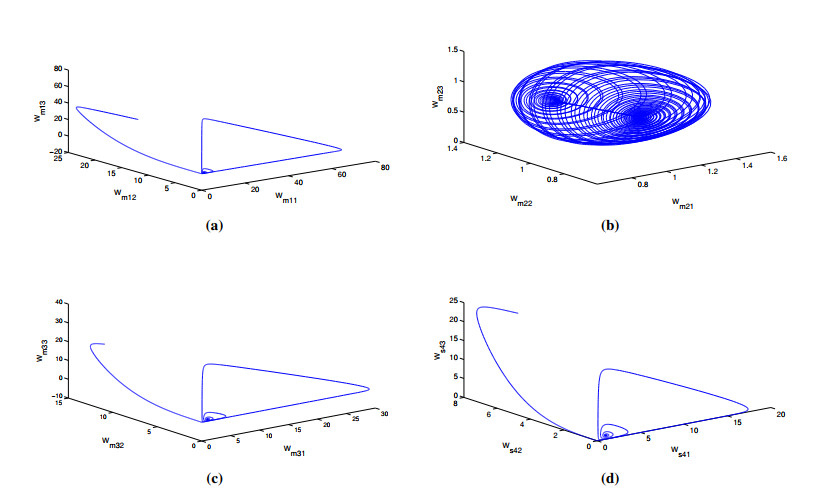
where $ (w_{m11}, w_{m12}, w_{m13})^T\in R^{3} $ is state vector of (4.1). Also, $ w_{m11} $ represents the prey population and $ w_{m12} $, $ w_{m13} $ denote the predator populations. For parameters $ b_1 = 2.9851 $, $ b_2 = 3 $, $ b_3 = 2 $ and initial conditions $ (27.5, 23.1, 11.4) $, scaling master GLVBS displays chaotic/disturbed behaviour as depicted in Figure 1(a).
The base master systems are the identical chaotic GLVBSs prescribed respectively as:
where $ (w_{m21}, w_{m22}, w_{m23})^T\in R^{3} $ is state vector of (4.2). For parameter values $ b_1 = 2.9851 $, $ b_2 = 3 $, $ b_3 = 2 $, this base master GLVBS shows chaotic/disturbed behaviour for initial conditions $ (1.2, 1.2, 1.2) $ as displayed in Figure 1(b).
where $ (w_{m31}, w_{m32}, w_{m33})^T\in R^{3} $ is state vector of (4.3). For parameters $ b_1 = 2.9851 $, $ b_2 = 3 $, $ b_3 = 2 $, this second base master GLVBS displays chaotic/disturbed behaviour for initial conditions $ (2.9, 12.8, 20.3) $ as shown in Figure 1(c).
The slave system, represented by similar GLVBS, is presented by
where $ (w_{s41}, w_{s42}, w_{s43})^T\in R^{3} $ is state vector of (4.4). For parameter values, $ b_1 = 2.9851 $, $ b_2 = 3 $, $ b_3 = 2 $ and initial conditions $ (5.1, 7.4, 20.8) $, the slave GLVBS exhibits chaotic/disturbed behaviour as mentioned in Figure 1(d).
Moreover, the detailed theoretical study for (4.1)–(4.4) can be found in [4]. Further, $ U_1 $, $ U_2 $ and $ U_3 $ are controllers to be determined.
Next, the CDAS technique has been discussed for synchronizing the states of chaotic GLVBS. Also, LSA-based ACS is explored & the necessary stability criterion is established.
Here, we assume $ P = diag(p_1, p_2, p_3) $, $ Q = diag(q_1, q_2, q_3) $, $ R = diag(r_1, r_2, r_3) $, $ S = diag(s_1, s_2, s_3) $. The scaling factors $ p_i, q_i, r_i, s_i $ for $ i = 1, 2, 3 $ are selected as required and can assume the same or different values.
The error functions $ (E_1, E_2, E_3) $ are defined as:
The major objective of the given work is the designing of active control functions $ U_i, (i = 1, 2, 3) $ ensuring that the error functions represented in (4.5) must satisfy
Therefore, subsequent error dynamics become
Using (4.1), (4.2), (4.3), and (4.5) in (4.6), the error dynamics simplifies to
Let us now choose the active controllers:
where $ \eta_1 = p_1{(f_1)}_1({r_1w_{m31}-q_1w_{m21}})+p_1w_{m11} ({r_1{(f_{3})_1-q_1{(f_{2}})_1}}) $, as described in (3.1).
where $ \eta_2 = p_2{(f_1)}_2({r_2w_{m32}-q_2w_{m22}})+p_2w_{m12} ({r_2{(f_{3})_2-q_2{(f_{2}})_2}}) $.
where $ \eta_3 = p_3{(f_1)}_3({r_3w_{m33}-q_3w_{m23}})+p_3w_{m13} ({r_3{(f_{3})_3-q_3{(f_{2}})_3}}) $ and $ K_1 > 0, K_2 > 0, K_3 > 0 $ are gaining constants.
By substituting the controllers (4.8), (4.9) and (4.10) in (4.7), we obtain
Lyapunov function $ V(E(t)) $ is now described by
Obviously, the Lyapunov function $ V(E(t)) $ is +ve definite in $ R^3 $. Therefore, the derivative of $ V(E(t)) $ as given in (4.12) can be formulated as:
Using (4.11) in (4.13), one finds that
which displays that $ \dot V(E(t)) $ is -ve definite.
In view of LSA [47], we, therefore, understand that CDAS error dynamics is globally as well as asymptotically stable, i.e., CDAS error $ E(t)\rightarrow 0 $ asymptotically for $ t\rightarrow \infty $ to each initial value $ E(0)\in R^3 $.
5.
Numerical simulation & discussion
This section conducts a few simulation results for illustrating the efficacy of the investigated CDAS scheme in identical chaotic GLVBSs using ACS. We use $ 4^{th} $ order Runge-Kutta algorithm for solving the considered ordinary differential equations. Initial conditions for three master systems (4.1)–(4.3) and slave system (4.4) are $ (27.5, 23.1, 11.4) $, $ (1.2, 1.2, 1.2) $, $ (2.9, 12.8, 20.3) $ and $ (14.5, 3.4, 10.1) $ respectively. We attain the CDAS technique among three masters (4.1)–(4.3) and corresponding one slave system (4.4) by taking $ p_i = q_i = r_i = s_i = 1 $, which implies that the slave system would be entirely anti-synchronized with the compound of three master models for $ i = 1, 2, 3 $. In addition, the control gains $ (K_1, K_2, K_3) $ are taken as 2. Also, Figure 2(a)–(c) indicates the CDAS synchronized trajectories of three master (4.1)–(4.3) & one slave system (4.4) respectively. Moreover, synchronization error functions $ (E_1, E_2, E_3) = (51.85, 275.36, 238.54) $ approach 0 as $ t $ tends to infinity which is exhibited via Figure 2(d). Hence, the proposed CDAS strategy in three masters and one slave models/systems has been demonstrated computationally.
6.
Concluding remarks
In this work, the investigated CDAS approach in similar four chaotic GLVBSs using ACS has been analyzed. Lyapunov's stability analysis has been used to construct proper active nonlinear controllers. The considered error system, on the evolution of time, converges to zero globally & asymptotically via our appropriately designed simple active controllers. Additionally, numerical simulations via MATLAB suggest that the newly described nonlinear control functions are immensely efficient in synchronizing the chaotic regime found in GLVBSs to fitting set points which exhibit the efficacy and supremacy of our proposed CDAS strategy. Exceptionally, both analytic theory and computational results are in complete agreement. Our proposed approach is simple yet analytically precise. The control and synchronization among the complex GLVBSs with the complex dynamical network would be an open research problem. Also, in this direction, we may extend the considered CDAS technique on chaotic systems that interfered with model uncertainties as well as external disturbances.
Acknowledgments
The authors gratefully acknowledge Qassim University, represented by the Deanship of Scientific Research, on the financial support for this research under the number 10163-qec-2020-1-3-I during the academic year 1441 AH/2020 AD.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: