Dynamical analysis of COVID-19 and tuberculosis co-infection using mathematical modelling approach

1.   Introduction

COVID-19 began its widespread propagation in Wuhan, China in December 2019 and spread throughout the World, with devastating effects on the health and lives of people. Currently, there are 760 million confirmed cases of the COVID-19 in the world, and 6.9 million people have been reported to have died from the infection ^[1]. COVID-19 is a contagious disease caused by SARS-CoV-2. The disease is characterized by respiratory symptoms which are similar to the flu, a cold, or pneumonia, and it spreads primarily through the droplets from an infected person. It mainly attacks the lungs and respiratory organs ^[2].

Tuberculosis (TB) is a serious respiratory disease which has continued to impact the health of people negatively. The causative agent of TB is Mycobacterium TB, which attacks the lungs ^[3]. One of the main barriers to the fight against TB is the resistance of Mycobacterium TB to drugs. Globally, TB ranks thirteenth among diseases with a high mortality rate, and it is the second infectious killer disease after COVID-19. In 2021, about 10.6 million people contracted TB, and a total of 1.6 million deaths occurred as a result of TB worldwide ^[4].

Both COVID-19 and TB are infectious diseases and they attack the lungs. The two diseases have similar manifestations, such as fever, cough, and breathing problems. However, the latency period of COVID-19 is shorter than that of TB ^[4]. The experience of COVID-19 infection in people with TB is still limited, but it is expected that people with COVID-19-TB co-infection will experience worse treatment results, especially if TB treatment is interrupted ^[4].

Clinical studies have reported and discussed the possibility, interaction, and facilitation of dual infections. According to Yang and Lu ^[5], they opined that the intake of immunosuppressive drugs by people infected with the COVID-19 can temporarily alter immunological functionality, introducing vulnerability to active TB via a new infection or reinfection. Also, from the pathological point of view, the immunomodulation-related disorders caused by the pathogens of COVID-19 and TB lead to an unstable inflammatory response and progression and worsening of the two diseases ^[6]. According to ^[7], there is a huge reduction in T cell counts in patients with COVID-19, and Khayat et al. ^[8] stated that T cell depletion can cause the patient to develop active TB if the patient is living with latent TB. In a pilot study carried out by the Global Tuberculosis Network, the diagnosis of TB and COVID-19 was concurrently carried out in patients, and a clinical investigation of COVID-19 in patients led to the discovery of TB ^[9].

Opportunistic infections typically refer to infections that occur in people with weak immune systems, such as those with HIV/AIDS or those on immunosuppressants therapy. According to a previous study ^[10], COVID-19 can also be referred to as an opportunistic infection. These infections take advantage of the compromised immune system to cause illness. In the case of a co-infection of COVID-19 and TB, COVID-19 is considered to be an opportunistic infection; similarly, both diseases can independently cause illness in individuals with normal or compromised immune systems. However, having both infections simultaneously could potentially exacerbate symptoms and increase the severity of the disease, particularly in people with underlying health conditions or weak immune systems. The estimated efficacy of the Bacillus Calmette-Guérin (BCG) vaccine is about 50–60% in childhood TB prevention.

Recently, the modeling of the spread of contagious diseases has come to influence the theory and practice of disease control and management. Mathematical modeling now plays an important role in epidemiology-related policy decision-making for diseases in many countries ^[11]. Several studies have been carried out on TB and COVID-19 dynamics, with remarkable results. The authors of ^[12] proposed a model for the prevention and control of TB by using cases from US citizens. Also, Nkamba et al. ^[13] worked on the TB mathematical model to examine the influence of vaccination and the effective contact rate. In addition, Liu et al. ^[14] formulated a mathematical model to study China's transmission of TB. The authors used data from reported cases of TB in China from 1998 to 2017 to calibrate the model. In a study by Chong et al. ^[15], a model was used to investigate the effect of treatment on latent TB infection in the elderly population. Researchers including Perkins and España ^[16], Oke et al. ^[17], Zamir et al. ^[18], Masandawa et al. ^[19], Atede et al. ^[20] etc., have worked on the modelling of COVID-19. Also, Yang et al. ^[21] investigated the impact of vaccination in the COVID-19 transmission model, and the model was later extended to incorporate isolation as an intervention. The work of Kouidere et al. suggested that the awareness and quarantine of people infected with COVID-19 are the most effective means of reducing infection ^[22]. Furthermore, Ngonghala et al. ^[23] examined the impact of nonpharmaceutical measures on mitigating the burden of COVID-19. They concluded that early implementation, strict adherence, and high coverage of measures such as combinations of face mask use and social distancing in the public can reduce disease transmission.

Many models of co-infection of diseases have been formulated and studied ^{[24,25,26,27,28]}. The authors of ^[29] presented a mathematical analysis and numerical solutions of a model for the co-infection of TB-HIV. The authors of ^[30] studied the optimal control and cost-effectiveness of the human papillomavirus and syphilis co-infection model. The authors of ^[31] presented the COVID-19 and TB co-infection model by using the Atangana–Baleanu derivative in the fractional-order approach. In the same vein, the authors of ^[32] developed a fractional-order COVID-19 and hepatitis B virus co-infection model; they compared the approximate solutions of models of integer and fractional order. Another group of authors ^[33] developed the SARS-CoV-2 and TB co-infection model to study its optimal control by using a case from Indonesia. Also, Gweryina et al. ^[34] worked on a model of TB co-infected with pneumonia. The authors of ^[35] presented a seven-compartment TB-COVID-19 co-infection model. Similarly, Mekonen et al. ^[36] studied and analyzed a mathematical model of TB and COVID-19 co-infection, and their analysis revealed that minimizing the contact rate and increasing treatments can reduce the cases of co-infection with COVID-19-TB. The authors of ^[37] studied a fractal-fractional model of TB and COVID-19 co-infection by using the Atangana-Baleanu fractal-fractional operator; additionally Lagrange polynomial interpolation was used to obtain the numerical scheme for the co-infection model. Also, Bandekar and Ghosh conducted optimal control and sensitivity analysis of the TB-COVID-19 co-infection model ^[38]. Their work emphasized that the treatment of other diseases should be implemented in times of a pandemic. Furthermore, Inayaturohmat et al. ^[39] examined the effects of treatment and isolation on a co-infection model of TB and COVID-19. Their results revealed that the impact of isolation is immediate, whereas the treatment takes a longer time for its effect to be felt.

In another study, Kifle and Obsu ^[40] applied optimal control in their COVID-19-TB co-infection model. They incorporated exogenous TB reinfection and COVID-19 vaccination into the model.

The authors of^[41] developed a compartmental model to analyze the spread of HIV/AIDS-TB co-infection. They considered preventive measures and the treatment of infected individuals and assessed the impact of co-infection and single-infection treatment on the spreading dynamics of HIV/AIDS-TB co-infection and single infection. The study concluded that therapeutic controls were more effective for infected individuals, whereas preventive controls were more effective for noninfected individuals. In another study, Kotola et al. ^[42] formulated and analyzed a mathematical model for the transmission dynamics of HIV/AIDS and COVID-19 co-infection. Their model incorporated protection and treatment for infected groups. The results showed that applying combinations of all possible protective and treatment strategies was the most effective strategy to minimize the transmission of HIV/AIDS and COVID-19 co-infection in the community.

Similarly, Teklu ^[43] investigated the respective impacts of vaccination, other protective measures, home quarantine with treatment, and hospital quarantine with treatment strategies simultaneously by using a deterministic mathematical modeling approach. They found that, among all parameters, the transmission rate is the most sensitive to control, and that vaccination, other protective measures, home quarantine with treatment, and hospital quarantine with treatment greatly minimize COVID-19 transmission in the community.

In addition, the authors of ^[44] studied a compartmental model of co-infection of pneumonia and HIV/AIDS with optimal control strategies by using a system of ordinary differential equations. They investigated various optimal control strategies to predict the best strategy to minimize and possibly eradicate HIV/AIDS and pneumonia co-infection from the community.

However, none of the studies has incorporated a vaccination program for the two diseases, and this makes our current research differ from the existing works. Since TB and COVID-19 are infectious diseases with similar clinical manifestations, they mainly attack the lungs. Clinical studies have revealed that the immunosuppressive drugs taken by COVID-19 patients can affect the immunological functions in the body, which can make patients vulnerable to active TB via a new infection or reinfection; also, the co-infection of the two diseases portends a clinical complexity in the management of the patients. This has motivated us to present a mathematical model that studied the dynamics and control of COVID-19-TB co-infection.

We also aimed to identify which parameters actually trigger the burden of COVID-19-TB co-infection, as well as the parameters that must be targeted in order to reduce the incidence of either disease in the population as this will allow us to appropriately advise policymakers, health workers, and government agencies.

It is important to note that this study is limited to the use of classical ordinary differential equations in the modeling process.

The other part of this work is fragmented into sections as follows: Section 2 presents the formulation of the model, the analysis of the model is given in Section 3, the discussion of the results follows in Section 4, and the conclusion is in Section 5.

2.   Mathematical formulation and the assumptions of the model

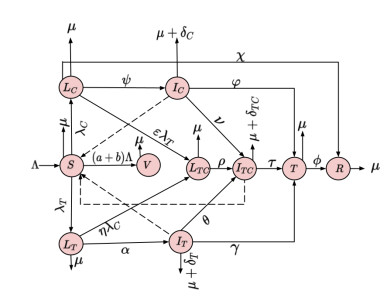
The total human population $(N)$ at time $(t)$ is separated into the following classes: the susceptible $(S(t))$ class, the latent TB $(L_{T}(t))$ class, the TB infectious class $(I_{T}(t))$, the latent COVID-19 $(L_{C}(t))$ class, the COVID-19 infectious class $(I_{C}(t))$, the latent COVID-19-TB co-infected class $(L_{TC}(t))$, the infectious COVID-19-TB co-infected class $(I_{TC}(t))$, the treatment $(T(t))$ class, the class of individuals who are vaccinated $(V(t))$, and the recovered class $(R(t))$. It is assumed that the susceptible class $(S(t))$ is increased by the recruitment of people (at the rate $\Lambda$). This class diminishes as a result of infections following contact with TB-infectious individuals, COVID-19-infectious individuals, infectious COVID-19-TB co-infected individuals at the rates $\lambda_C$ and $\lambda_T$, given by

where $\beta_1$ and $\beta_2$ are the transmission rates of TB and the COVID-19 infections, respectively. Also, $m$ and $n$ are the modification parameters accounting for reduced infectivity of the $I_{TC}$ class relative to the $I_T$ and $I_C$ classes, respectively. The class further reduces due to the vaccination of proportions $a$ and $b$ of the newly recruited individuals against TB and COVID-19 infection respectively. It is also assumed that all humans die naturally (at the rate $\mu$), which causes every compartment to reduce. Therefore,

The class $L_T$ of people with latent TB is assumed to be populated by the newly infected TB individuals who have acquired TB (at the rate $\lambda_T$). The size of the class diminishes due to transfer (at the rates $\alpha$ and $\eta$) to the $I_T$ class and $L_{TC}$ class, respectively. Thus,

The TB infectious class $(I_T)$ is assumed to be composed of those who have transitioned from the latent class (at the rate $\alpha$); additionally, the size of the class shrinks due to progression (at the rates $\gamma$ and $\theta$). Thus,

The latent COVID-19 class $(L_C)$ comprises those who just contracted COVID-19 (at the rate $\lambda_C$). This population is decreased by transition to the $I_C$ and $L_{TC}$ classes (at the rates $\psi$ and $\varepsilon$, respectively). Also, the population of individuals with latent COVID-19 declines (at the rate $\chi$) as they recover naturally without treatment. Hence,

The class $I_C$, of infectious COVID-19 individuals is occupied by those who have transitioned into the class from the $L_C$ compartment (at the rate $\psi$). The reductions in the $I_C$ population are caused by mortality (at the rate $\delta_C$) and transition to the $I_{TC}$ and $T$ classes (at the rates $\upsilon$ and $\varphi$, respectively). Therefore,

The $L_{TC}$ population of the latent COVID-19-TB co-infected individuals is assumed to be generated by the latent COVID-19 individuals who contracted TB and latent-TB-infected individuals who contracted COVID-19 as well. The transition to the class $I_{TC}$ (at the rate $\rho$) lowers this population. Hence,

The $I_{TC}$ class is increased by the contributions of the $L_{TC}$, $I_T$, and $I_C$ classes (at the rates $\gamma$, $\theta$, and $\upsilon$, respectively), indicating infectious COVID-19-TB co-infected. The treatment and death due to the co-infection (at the rates $\tau$ and $\delta_{TC}$, respectively) cause the population to reduce. Thus,

The treatment class is filled with those who are receiving treatment in the $I_T$, $I_C$, and $I_{TC}$ classes (at the rates $\gamma$, $\varphi$, and $\tau$, respectively). The class is decreased by recovery at the rate $\phi$. Then,

It is assumed that the vaccinated class $V$ has the proportions $a$ and $b$ of those that are recruited who have been vaccinated against TB and COVID-19. Then,

Last, the recovered compartment comprises those recovered from treatment at the rate $\phi$ and those who recover at the rate $\chi$ from latent COVID-19 naturally without treatment. Thus,

The schematic diagram illustrating the dynamics in the models is given in Figure 1. Also, all of the parameters and variables used in the model are defined in Tables 1 and 2.

Summarily, combining all of the assumptions together, we have the following system of equations:

where

2.1.   Positivity of the solutions

Since the model (2.12) tracks the populations of humans, the solutions to the model (2.12) have to be positive. Hence, the following theorem is proved to ensure that the solutions are all positive.

Theorem 2.1. All solutions

having positive starting values continue to be positive at all times.

Proof. Let $t_1 = sup\{t > 0:S(t) > 0, L_T(t) > 0, I_T(t) > 0, L_C(t) > 0$, $I_C(t) > 0, L_{TC}(t) > 0$, $I_{TC}(t) > 0, T(t) > 0$, $V(t) > 0, R(t) > 0\} > 0$.

So, from the equation for the first compartment of the model (2.12), we have

Then,

By applying the same approach, all other variables of the model (2.12) can be shown to stay positive for all time $t > 0$; therefore, this ends the proof. □

2.2.   Invariant region of the model

Lemma 2.1. Consider

Then, the closed set $D$ is positively-invariant and attracting for the model (2.12).

Proof. The summation of the rates of change of all classes in (2.12) gives

So,

Then

If

then

Hence, all solutions possessing initial values in $D$ stay in $D$ for $t > 0$. This signifies that $D$ is positively-invariant, and that, in region $D$, the model is deemed to be epidemiologically meaningful and mathematically well-posed. □

3.   Mathematical analysis of the models

The full co-infection model is split into 2 sub-models namely, the TB-only model and the COVID-19-only model. We will first explore the dynamics of the 2 sub-models separately (i.e., the TB-only model and the COVID-19-only model) before proceeding to the co-infection model.

3.1.   TB-only model

The TB-only model is obtained from the co-infection model (2.12) by setting $b = \theta = 0 \text{ and } L_C = I_C = L_{TC} = I_{TC} = 0$; thus we have the TB-only model as follows:

where

Consider the feasible region

It can be shown that all solutions in $D_T$ stay in $D_T$ for all values of $t > 0$. Hence, $D_T$ is positively-invariant. Now, we can proceed to explore the model's dynamics in $D_T$.

3.1.1.   Disease-free equilibrium and reproduction number of TB-only model

When TB infection does not exist, the disease-free equilibrium is obtained, and it is given by

By adopting the next-generation matrix method of ^[50] to find the reproduction number, we can respectively define the matrices $F$ and $V$ as follows:

Differentiating $F$ and $V$ in (3.5) with respect to $L_T, I_T, \text{ and } T$ at the disease-free equilibrium $E_T^{o}$, leads to

and

where

Then, the control reproduction number in the presence of the vaccine, denoted by $R_{o}^{TV}$, is given by

The $\rho$ parameter in (3.9) is the spectral radius of the dominant eigenvalue of the matrix $FV^{-1}$. When there is no vaccination, the basic reproduction number is represented by $R_{o}^{T}$, which is given by

Then, from (3.9) and (3.10), we have that

If we denote the critical vaccination proportion to be $a_c$, then, the critical number of individuals that must be vaccinated to guarantee the elimination of the disease is given by

provided that $R_{o}^{TV} \leq 1$ whenever $a\geq a_c$.

The epidemiological quantity $R_{o}^{TV}$ is the control reproduction number, which is the average number of secondary TB infections that stem from one primary infection source when introduced into the population of susceptible individuals where a proportion $a$ has been vaccinated. On the other hand, the quantity $R_{o}^{T}$ is the basic reproduction number of the TB-only model. This is the average number of secondary TB infections that stemmed from a single infectious person in a group of susceptible individuals ^[50]. Therefore, employing Theorem 2 of ^[51], we arrive at the following result:

Lemma 3.1. If $R_{o}^{TV} < 1$, then the disease-free equilibrium of TB-model (3.1) is locally asymptotically stable.

The meaning of Lemma 3.1 is that the eradication of TB is possible if the starting values of the sub-classes of the model are in the basin of attraction of $E_{T}^{o}$. Therefore, an introduction of a small group of TB-infectious people into the population will not produce an outbreak of TB; therefore, it vanishes.

3.1.2.   Endemic equilibrium of TB-only model

The endemic equilibrium of the TB-only model represented by

is obtained as follows:

where $G_1, G_2$, and $G_3$ have been defined in (3.8); similarly,

From (3.13), it is clear that $E_{T}^{e}$ has a unique positive endemic equilibrium when $R_{o}^{TV} > 1$.

3.1.3.   Global stability of disease-free equilibrium of TB-only model

The global asymptotic stability of the disease-free equilibrium of the TB-only model is investigated here for $R_{o}^{TV} < 1$, to determine whether the disappearance of TB is independent of the starting values of the sub-classes of the TB-only model.

Theorem 3.1. The disease-free equilibrium (3.4) of the TB-only model (3.1) is globally asymptotically stable when $R_{o}^{TV} < 1$, but not when $R_{o}^{TV} > 1$.

Proof. We apply linear Lyapunov function, which is given by

The time derivative of (3.14) is given by

Then, by substitution and simplification, we have

Therefore, $Z^{\prime} < 0$ if $R_{o}^{TV} < 1$ and $Z^{\prime} = 0$ if $T = 0$. Thus, $Z$ is a Lyapunov function in $D_T$. Also, the largest invariant set in

is the singleton $E_{T}^{o}$. According to LaSalle's invariance principle ^[52], every solution that possesses initial values in $D_T$ tends to $E_{T}^{o}$ as $t$ becomes large. □

Theorem 3.1, epidemiologically, means that TB can be curtailed regardless of the starting sizes of the sub-classes of the model (3.1) when $R_{o}^{TV} < 1$.

3.1.4.   Global stability of endemic equilibrium of the TB-only model

Consider the model (3.1) with $\delta_T = 0$. Let

and the endemic equilibrium be denoted by

If the associated reproduction number of the model is given by

Then, we prove the global stability of $E_{T}^{e*}$.

Theorem 3.2. For $D_T \backslash D^*$, the endemic equilibrium of the model (3.1) with $\delta_T = 0$ is globally asymptotically stable if $\tilde{R}_{o}^{TV} > 1$, where

Proof. We apply the Lyapunov function in (3.16) to prove Theorem 3.2

By differentiation, (3.16) becomes

With the arithmetic mean surpassing the geometric mean, we have the following inequalities:

and

Hence, $Q^{\prime}\leq$ 0 for $\tilde{R}_{o}^{TV} > 1$. Therefore, Q is a Lyapunov function in $D_T$, and, from LaSalle's invariance principle ^[52], every solution possessing starting values in $D_T \backslash D^{*}$ tends to $E_{T}^{e*}$ as the time moves closer to infinity for $\tilde{R}_{o}^{TV} > 1$. □

The biological interpretation of Theorem 3.2 is that TB will continue to exist in the community regardless of the initial population levels whenever $\tilde{R}_{o}^{TV} > 1$.

3.2.   COVID-19-only model

The COVID-19-only model can be obtained from the co-infection model (2.12) when

and

We have the COVID-19-only model as follows:

where

Regarding model (3.20), it can be shown that the region given by

is positively-invariant and attracting. Then, the COVID-19-only model (3.20) will be considered in the region $D_C$.

3.2.1.   Disease-free equilibrium and reproduction number of COVID-19-only model

In a case in which there is no COVID-19, we have a disease-free situation, and its equilibrium is given by

The control reproduction number of COVID-19 is obtained by employing the next-generation matrix method as in ^[50]. Let $F$ and $V$ be defined as follows:

and

Then, the control reproduction number is given by

where

and $\rho$ is the spectral radius of the dominant eigenvalue of the matrix $FV^{-1}$. In the absence of a vaccine, the basic reproduction number is obtained, which is represented by $R_{o}^{C}$. Then,

We can re-write (3.26) as follows:

Thus, the critical number of individuals who need to be vaccinated to eliminate the disease is given by

such that $R_{o}^{CV} \leq 1$ whenever $b\geq b_c$. Then, by adopting Theorem 2 of ^[51], we obtain the following result:

Lemma 3.2. If $R_{o}^{CV} < 1$, then the disease-free equilibrium of the COVID-19-only model (3.20) is locally asymptotically stable.

Lemma 3.2 basically states that the eradication of the COVID-19 is possible if the starting values of the different populations that make up the model are in the basin of attraction of $E_{C}^{o}$. Hence, an introduction of a few numbers of infected people into the population will not lead to an outbreak of COVID-19; then, the disease vanishes.

3.2.2.   Endemic equilibrium of COVID-19-only model

Let the endemic equilibrium of the COVID-19-only model be represented by $E_{C}^{e}$. We obtain the following for $E_{C}^{e}$:

where

where

and $H_1$ and $H_2$ have been defined in (3.27).

Evidently, from (3.31), we have a unique positive endemic equilibrium when $R_{o}^{CV} > 1$.

3.2.3.   Global stability of disease-free equilibrium of COVID-19-only model

We shall investigate whether the elimination of COVID-19 relies on the starting values of the sub-classes through the exploration of the global asymptotic stability of the disease-free equilibrium of the COVID-19-only model.

Theorem 3.3. The disease-free equilibrium (3.23) of the COVID-19-only model (3.20) is globally asymptotically stable when $R_{o}^{CV} < 1$, but not when $R_{o}^{CV} > 1$.

Proof. We adopt the linear Lyapunov function defined by

Taking the derivative of (3.32) leads to

Then, by substitution and simplification, we have

Therefore,

if $R_{o}^{CV} < 1$ and

if $T = 0$. Thus, $J$ is a Lyapunov function in $D_C$. Also, the largest invariant set in

is the singleton $E_{C}^{o}$. According to LaSalle's invariance principle ^[52], all solutions having initial values in $D_C$ move toward $E_{C}^{o}$ as $t$ becomes large. □

Theorem 3.3 can be interpreted epidemiologically to mean that COVID-19 can be curbed regardless of the starting sizes of the sub-classes of the model (3.1) when $R_{o}^{CV} < 1$.

3.2.4.   Global stability of endemic equilibrium of the COVID-19-only model

Consider the model (3.20) with $\delta_C = 0$. Let the associated transmission rate

and the endemic equilibrium be denoted by

Let the associated reproduction number of the model be given by

Then, we explore the global asymptotic behavior of $E_{T}^{e*}$.

Theorem 3.4. For $D_C \backslash D^{**}$, the endemic equilibrium of the model (3.20) with $\delta_C = 0$ is globally asymptotically stable if $\tilde{R}_{o}^{CV} > 1$, where

Proof. We consider the Lyapunov function for the proof. We define the Lyapunov function as follows:

By differentiation, (3.34) becomes

Given that the arithmetic mean surpassing the geometric mean, the following inequalities hold:

Thus, $X^{\prime}\leq$ 0 for $\tilde{R}_{o}^{CV} > 1$. Then, $X$ is a Lyapunov function in $D_C$, and from LaSalle's invariance principle ^[52], every solution with starting values in $D_C \backslash D^{**}$ tends to $E_{C}^{e*}$ as the time moves closer to infinity for $\tilde{R}_{o}^{CV} > 1$. □

The biological interpretation of Theorem 3.4 is that COVID-19 will continue to exist in the population regardless of the starting values of the classes whenever $\tilde{R}_{o}^{CV} > 1$.

3.3.   Analysis of the COVID-19-TB co-infection model

3.3.1.   Disease-free equilibrium and reproduction of the co-infection model

The disease-free equilibrium of the COVID-19-TB co-infection model (2.12) is given by

Then, using the next-generation matrix method as in ^[50], the associated reproduction number is given by

where

and

Hence, given Theorem 2 of ^[51,53], we claim the following result:

Lemma 3.3. The disease-free equilibrium $E_{F}^{o}$ of the COVID-19-TB-model (2.12) is locally asymptotically stable if $R_{o}^F < 1$, but not if $R_{o}^F > 1$.

The epidemiological interpretation of Figure 2 indicates that the disease may dies out in the population regards of the initial size. The following Theorem 3.3 confirms the disease free equilibrium in the case $\mathcal R_{0}^{CV} < 1$, while that of Figure 3 shows that the disease may keep persistent in the population irrespective of the initial size of the infected individual. The following Theorem 3.4 affirms the persistence of the disease in the case $\tilde{\mathcal R}_{0}^{CV} > 1$.

3.3.2.   Global stability of disease-free equilibrium of COVID-19-TB co-infection model

Using the method presented by Castillo-Chavez et al. ^[50], we can write the model (2.12) as follows:

Then, the global asymptotic stability of the disease-free equilibrium is guaranteed if the following conditions hold:

Y1. For $\dfrac{dP}{dt} = A(P, 0), P^*$ is globally asymptotically stable;

Y2. $B(P, I) = HI-\tilde{B}(P, I)\geq0$ for $(P, I)\in D$,

where

is an M-matrix (the off-diagonal elements of H are non-negative) and $D$ is the feasible region in which the model makes sense.

Theorem 3.5. If the disease-free equilibrium $E_{F}^{o}$ of the COVID-19-TB co-infection model (2.12) is locally asymptotically stable, then, it is also globally asymptotically stable if the conditions $(Y1)$ and $(Y2)$ are satisfied.

Proof. For model (2.12),

and

where $K_5 = \mu+\rho, \ K_7 = \phi+\mu$, and $K_1, K_2, K_3 K_4, K_6$ have been defined in (3.41).

Then,

From (3.45), $\tilde{B}_5 (P, I) < 0$, which means that (Y2) is not satisfied. Hence, the disease-free equilibrium $E_{F}^{o}$ may not be globally asymptotically stable. This implies that multiple endemic equilibria may exist; thus, we decided to investigate the possibility of backward bifurcation. □

3.3.3.   Bifurcation analysis of the COVID-19-TB co-infection model

The approach presented by Castillo-Chavez and Song ^[54] is adopted to determine the type of bifurcation in the co-infection model. The method used was derived from the centre manifold theory. Now, we can establish the following result:

Theorem 3.6. The model (2.12) exhibits backward bifurcation at $R_{o}^F = 1$ if $a > 0$ when $R_{o}^F < 1$; otherwise, it exhibits forward bifurcation, where

Proof. The approach of Castillo-Chavez and Song ^[54] will be followed. We start by changing the variables as follows:

and establishing that

So, if we use the vector form

then the model (2.12) is represented as follows:

Thus, model (2.12) becomes

where

If $\beta_1$ is taken as the bifurcation parameter at $R_{o}^F = 1$, then

The Jacobian of (3.46), evaluated at $E_{F}^{o}$, is denoted by $J(E_{F}^{o})$; also by adopting the method in ^[54,55], the Jacobian $J(E_{F}^{o})$ has right and left eigenvectors $w$ and $v$ that correspond to the simple zero eigenvalue such that $w.v = 1$. The right eigenvector is given by

where

The left eigenvector $v$ is given by

where

where $K_5 = \mu+\rho, K_7 = \phi+\mu$ and $K_1, K_2, K_3 K_4, K_6$, have been defined in (3.41).

We then compute the bifurcation coefficients $a$ and $b$, defined as follows:

Thus,

and

From (3.50), $b > 0$; consequently, from Theorem 3.6, the COVID-19-TB co-infection model will exhibit backward bifurcation if $a$ in (3.49) is positive. The parameters that lead to the backward bifurcation observed in the co-infection model when $R_{o}^F < 1$ are $\eta$, i.e., rate at which latent TB individuals become latently infected with COVID-19, and $\varepsilon$, i.e., rate at which latent COVID-19 individuals become latently infected with TB. □

This means that the classical condition $R_{o}^F < 1$ required for the elimination of the co-infection is necessary but not sufficient to guarantee adequate control of COVID-19-TB co-infection. This implies that it will be difficult to manage COVID-19-TB co-infection. Figure 4 is a diagrammatic representation of the contents of Subsection 3.3.3.

3.4.   Uncertainty and sensitivity analysis

As a result the model (2.12) comprising many parameters, uncertainty will arise. To ascertain the impact of different parameters of the model, uncertainty and sensitivity analysis was performed by using Latin hypercube sampling (LHS) and the partial rank correlation coefficient (PRCC). LHS was used to sample the 17 parameters required to determine the reproduction number $R_{o}^F$, and the PRCC was used for the global sensitivity analysis of $R_{o}^F$. For more details on this method, see ^[56,57,58]. The significance of this analysis is that it helps to identify the parameters that contribute massively to the spread and control of the co-infection ^[59]. The signs of the PRCCs indicate the relationship between the response function $R_{o}^F$ and the parameters. It is important to note that this analysis helps to predict the necessary policy measures. The parameters with negative PRCCs show that they are negatively correlated, and parameters with positive PRCCs indicate that they are positively correlated. If the absolute value of a PRCC of a parameter is greater than or equal to 0.5, then such a parameter is statistically important. The results of the computed PRCCs are given in Table 3.

4.   Results and discussion

Various simulation experiments were carried out by employing ODE45 in Matlab with the parameter values in Table 2; the results are presented in Figures 2–12.

The parameter values used were obtained from the literature, with the references stated in Table 2. It should be noted that the initial data of the sub-populations used were hypothetical values. Figure 2 shows to us the possibilities of eliminating COVID-19 in the population regardless of the initial size of infected individual provided that $\mathcal R_0^{CV} < 1$. on the other-hands, if $\tilde{\mathcal R}_0^{CV} > 1$ the diseases will persist in the population, this is clearly shown in Figure 3. Figure 4 shows the co-existence of the stable disease-free equilibrium and endemic equilibrium. Thus, The classical condition $R_{o}^F <1$ required for the elimination of the co-infection is necessary but not sufficient to guarantee adequate control of COVID-19-TB co-infection. Then, this will make it difficult to manage the COVID-19-TB co-infection.

The results of the uncertainty and sensitivity analysis using LHS/PRCC are given in Table 3, and the bar plot of the results is depicted in Figure 5. From the analysis, the most important parameters, i.e., with $|\mbox{PRCC}|\geq 0.5$, are $\beta_{2}, \delta_{C}, b, \mbox{ and } a$, which are the rate of transmission of the COVID-19, death from COVID-19, the proportion vaccinated against the COVID-19, and the proportion vaccinated with BCG. $\beta_{2}$ was found to be positively correlated, which means that its increase will give rise to a corresponding increase in the value of $R_{o}^F$. Hence, non-pharmaceutical measures should be put in place to minimize the transmission rate $\beta_{2}$. However, $a \mbox{ and } b$ were found to be negatively correlated, which signifies that they have decreasing effects on $R_{o}^F$, when they are increased. Thus, increasing the proportion of people vaccinated against COVID-19 and TB can also control the incidence of the COVID-19-TB co-infection. Hence, interventions that can help to increase the vaccinated proportion should be considered (e.g., adequate funding and manpower, use of media, community engagement, and improved access to vaccine).

Figure 6 presents the contour graph to illustrate the impact of $a$ and $b$ on the reproduction number $R_{o}^F$ of the complete model. The associated reproduction number $R_{o}^F$ increases as the proportions $a$ and $b$ of vaccinated people decrease; this is consistent with the results of the sensitivity analysis. Figure 7 indicates that, with a low transmission rate of COVID-19 infection, the proportion of people required to be vaccinated with BCG and against COVID-19 to have the reproduction number $R_{o}^F$ be less than unity will be small. The illustration in Figure 8 depicts the effects of the COVID-19 transmission rate and vaccination proportions $a$ and $b$ on the associated reproduction number $R_{o}^F$. It is observed that lowering the transmission rate and increasing the proportions $a$ and $b$ reduce the reproduction number $R_{o}^F$. This means that a smaller number of people will be co-infected with the COVID-19-TB if the proportions of people vaccinated with BCG and against COVID-19 are large and there is a reduced COVID-19 transmission rate.

The long-term dynamics of the infectious COVID-19-TB co-infected population depicted in Figure 9 indicate that co-infection will persist in the population whenever $R_o^{F} > 1$. Moreover, the effect of the rate of transmission of COVID-19 is illustrated in Figure 10. The infectious population of the co-infected individuals was found to reach the highest peak within a very short time under the maximum transmission rate. Hence, the large number of infectious COVID-19-TB co-infected populations that is subject to a high transmission rate of COVID-19 should be addressed by implementing interventions that can reduce the transmission rate.

Furthermore, the solution lines of infectious COVID-19-TB co-infected population when the proportions $a$ and $b$ were varied simultaneously are depicted in Figure 11. The population declines as these proportions increase, and this is related to the interpretation of the sensitivity analysis results. The plot in the Figure 12 shows the infectious COVID-19-TB co-infected population when the transmission rate $\beta_2$ is varied with different values of $a$ and $b$. A decrease in population size was observed, and it is attributed to the increase in the proportions $a$ and $b$ of vaccinated people. Hence, interventions that can reduce the rate of transmission of COVID-19 and interventions targeted at increasing the proportion of people vaccinated should be concurrently considered to mitigate the burden of the co-infection.

5.   Conclusions

A mathematical model of the dynamics of COVID-19-TB co-infection has been presented and studied. The disease-free and endemic equilibria of the two sub-models have been obtained and found to be globally asymptotically stable when their control reproduction numbers $R_{o}^{TV}, R_{o}^{CV} < 1$ and $\tilde{R}_{o}^{TV}, \tilde{R}_{o}^{CV} > 1$, respectively. However, the co-infection model was found to exhibit backward bifurcation. Furthermore, uncertainty and sensitivity analysis was performed by using LHS and the PRCC to determine the impact of different parameters of the model. The simulation results suggest that a reduction in the rate of transmission and an increment in the proportions of people vaccinated with BCG and against TB can lower the number of COVID-19 cases. Therefore, interventions aimed at reducing the transmission rate and increasing the proportion of people vaccinated against TB and COVID-19, such as the use of face masks, good sanitation practices, massive vaccination funding, programs, and campaigns, should be prioritized. Based on the limitations stated earlier, we wish to explore the fractional order of the model and use real data to simulate and predict the dynamics of the model in our future research.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

Authors declare no conflicts of interest.