1.
Introduction
Malaria is a vector-borne disease of global public health concern with high level of morbidity and mortality in the tropical regions of the world. The disease is caused by several species of parasites of the Plasmodium genus type and transmitted to humans by the bite of a female anopheles mosquito when taking the blood meal necessary for egg production. In 2018, there was an estimated 228 million cases of malaria worldwide with about 405,000 deaths attributable to malaria[39]. Various mathematical models of the transmission dynamics of malaria and its control have been proposed in the literature [2,3,5,8,10,15,16,20,34,38]. The very first model is that of Ross-MacDonald who laid the foundations for modeling malaria [26,35]. Models that include therapeutic (treatment and vaccination) and non-therapeutic (insecticide-treated bed net) measures have also flourished in the literature [12,17,19,33]. Because insecticide-treated nets (ITNs) reduce human/mosquito contacts, distribution campaigns have been organized in affected countries, including Cameroon. However, the use of these mosquitoes treated bednets have not always been satisfactory as several people let holes in the bednets, do not use them every night (poor adherence), or use these bednets for other activities such as fishing [36]. Mosquitoes insecticide-treated bednets could influence the force of infection, the rate of recruitment of new females mosquito, or the death rate of mosquitoes [6,10,11,17,19]. Moreover, the use of these treated bednets could influence the rate of loss of immunity.
We formulate a mathematical model for the transmission dynamics of malaria in human populations, which takes the (good or poor) use of bednets as a control measure. First, we formulate the autonomous model with a constant proportion of bednets usage as control strategy. Next, we compute the basic reproduction number T0, and investigate the existence and stability of the equilibria. Analytical results show that both model equilibria; the disease-free and the endemic states are locally asymptotically stable when T0< and when T0>1, respectively. However, the model could exhibit the phenomenon of backward bifurcation when T0<1, an epidemiological situation where, although necessary, having the basic reproduction number less than unity is not sufficient for malaria elimination [38].
We then extend our autonomous model by considering a time-dependent control of the proportion of bednets usage. Optimal control theory is used to establish conditions under which the spread of malaria can be mitigated. The characterization of the optimal control is obtained by the application of Pontryagin's maximum principle. We use the Forward-backward fourth-order Runge-Kutta method for numerical simulations to determine an optimal control strategy. In addition, we focus on a bednet control strategy since the other controls measures are expensive. By other vector controls, we mean outdoor application of larvicides (chemical or biological), breeding habitat reduction (e.g., draining standing water), outdoor vector control (mosquito fogging, attractive toxic sugar bait (ATSB)), indoor residual spraying (IRS), repellents, including topical repellents, mosquito coils, etc, rapid diagnosis and treatment (RDT), preventative drugs like seasonal malaria chemo-prevention (SMC), intermittent preventative treatment (IPT) [19]. Generally, the bednet control in the literature concerns the bednets usage, including insecticide-treated bed nets (ITNs), long-lasting insecticide-treated nets (LLINs), and untreated bednets (UBNs) [19]. Some of these other vector controls do not respectful the ecological population environment. But, the use of these other vector control require periodic actions on a short time (1 day, 1 week, 1 month, 1 year) that is less effective and practicable than the three years' use of the LLNs. We observe that the disadvantage (loss of immunity, even at its maximum) in the use of bednets is compensated by the benefit of the number of susceptible/infected individuals excluded from the malaria disease dynamics, the only danger being the poor use of the long-lasting bednets. In fact, the model suggests that if one family fails to use accurately the LLNs, then the number of infectious will increase (sometimes exponentially) since the protection of the bednets would drop down. However, it is possible to come close to the optimal results with a realistic strategy.
The rest of the paper is organized as follows. In Section 2, we present the mathematical model for malaria transmission dynamics with a parameter w that represents the proportion of persons having and using the treated mosquito bednets correctly. In Section 4, we propose an optimal control problem for the minimization of the number of infected humans while controlling the cost of control interventions with bednets. Finally, in Section 4.4, some numerical simulations provided to support the analytical results are interpreted from the epidemiological point of view. Section 5 is the conclusion.
2.
Modeling of the LLITN controlled dynamics of malaria
2.1. Description of involved phenomena
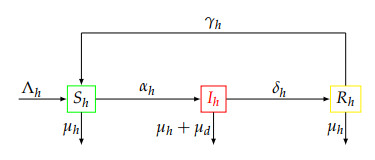
In this section, we consider two populations, namely human hosts and female mosquitoes that are assumed homogeneously distributed. We suppose that female mosquitoes only feed with human blood. The human population is subdivided into three classes, namely the susceptible Sh, the infectious Ih and the immune Rh as shown in Figure 1. According to [20], we do not consider an exposed compartment because it does not significantly influence qualitatively the evolution of infections in the human population. The recruitment is done only in the susceptible class at a rate Λh. In all compartments, there is an output of μh due to natural death, with an additional death rate μd in the infectious compartment. When in contact with an infectious mosquito, a susceptible humans become infected at a rate αh representing the force of infection. Infectious humans recover and gain immunity at a rate δh, while the rate of loss of immunity is γh.
Following the work in [17,19,37], we distinguish the questing anopheles (looking for the blood meal) from the resting one. As depicted in Figure 2, the new mosquitoes arrive through the compartment of questing susceptible at rate Λv. The natural death rate is μv. When in contact with an infectious human, a susceptible mosquito can become infected at a rate of αv corresponding to the strength of infection of the mosquitoes. Once infected, a mosquito will alternate (at most 12 times) during its period of latency between the resting status and the questing status. Hence, we consider 6 resting infected compartments and 6 questing infected compartments. The transition rate from resting status to questing status is χ, and the transition rate from questing to resting is β. Assuming that the number of bites on a human by female mosquitoes per day is a, the fraction of persons having a long-lasting insecticide-treated net is b∈[0,1], and the sub-fraction of persons using it effectively is u∈[0,1]. Hence, the proportion of people who own a mosquito net and use it adequately is w:=b×u∈[0,1]. We suppose that the dependence of some parameters with respect to w can be express as
Indeed, the adequate use of mosquito bednet reduces transmission forces αh and αv through the factor a. It also limits indirectly the horizontal immigration of mosquitoes in the human environment via the rate Λv. Finally, w indirectly increases the rate of death in the population of mosquitoes since it reduces mosquito-human contacts, and then there is a reduction of mosquito's blood meal leading to additional death rate.
The variables and parameters of the model are presented in detail in Table 1, Table 2 and Table 3.
2.2. Mathematical model and preliminary properties
According to the above description and assumptions, we proposed the following system of non-linear ordinary differential equations (5).
By setting xS=(Sh,Sq)∈R2 and xI≡((Eir,Eiq)1≤i≤6,E7r,Ir,Iq,Ih,Rh)∈R17, the system (5) can be rewritten as
More precisely, we have
ASI is the 2×17 matrix with all its coefficients null, except ASI(1,15)=−amShNh, ASI(1,17)=γh, ASI(2,16)=−acSqNh and ASI(2,17)=−~acSqNh.
A11 is a 13×13 matrix satisfying
A12 is the 13×4 matrix defined by A12(1,3)=acSqNh, A12(1,4)=a˜cSvNh and A12(i,j)=0 for other cases. The matrix A21 is the 4×13 matrix defined by A21(2,13)=χ and A21(i,j)=0 for the other cases. The matrix A22 is the 4×4 square matrix defined by
Proposition 2.1. The non-negative cone (R+)19 is positively invariant for system (7).
Proof 2.0.1. The result comes from the fact that A(x) is a Metzler matrix for allx∈(R+)19, i.e., aij(x)=A(x)(i,j)≥0 for i≠j. Indeed, since the solution of the system (7) is continuous, it suffices to check that every trajectory starting at the boundary of (R+)19 remains in (R+)19. That boundary is defined as ∪19i=1Hi where Hi≡{x∈(R+)19,∣xi=0}. For x∈Hi, x′i=∑19j=1aij(x)xi+bi=∑19j=1,i≠jaij(x)xi+bi≥0. This means that xi moves from 0 to non-negative values.
Proposition 2.2. The set Ω={(Sh,Sq,(Eir,Eiq)1≤i≤6,E7r,Ir,Iq,Ih,Rh)∈R19+/0≤Nh ≤Λhμh,0≤Nv≤Λvμv} is a compact forward-invariant and absorbing set for the model system (5).
Proof 2.0.2. Adding respectively the human sub-populations equations and then the mosquitoes sub-populations equations, we have
From Proposition 2.1, we have Nh,Nv≥0. Applying Gronwall's inequality, we have
Assuming that Nh(0)≤Λhμh and Nv(0)≤Λvμv. it follows that Nh≤Λhμh and Nv≤Λvμv.
Proposition 2.3. At any time t, the model system (5) is well-posed, i.e., it admits a non-negative global unique C1-solution on the set R+.
Proof 2.0.3. Applying the Cauchy-Lipschitz theorem, Proposition 2.1 and Proposition 2.2, the result is immediate.
3.
Asymptotic and bifurcation analyses
In this section we study the existence of equilibria and their stability using the theory of bifurcation.
3.1. Disease-free equilibrium and threshold condition
This section is devoted to local and global stability of the disease-free equilibrium which unconditionally exists.
Proposition 3.1. System (5) admits a disease-free equilibrium (DFE) given by x∗=(x∗S,x∗I) with
Proof 3.0.1. An equilibrium is obtained by solving x′=A(x)x+b=0. A DFE corresponds to any solution satisfying xI=0R17.
Proposition 3.2. The system x′=AS(x∗).(x−x∗S) is globally asymptotically stable (GAS) at x∗S on R2+.
Proof 3.0.2. The proof is immediate since the matrix
has all its eigenvalues −μh and −~μv negative.
In the following, we determine a stability threshold condition using a technique well described and used in [17,37]. In our case, this threshold can be biologically interpreted as the basic reproduction number T0 [19].
Let us define the threshold
Theorem 3.1. T0 is equivalent to the basic reproduction number T0 of the model system (5). Moreover, the DFE is locally asymptotically stable (LAS) if T0≤1.
Proof 3.1.1. According to Gautier-Sallet's algorithm in [18] and Proposition 3.2, it is sufficient to obtain condition ensuring that AI(x∗) is stable (all its eigenvalues are negative). Looking carefully at A11 and A22, they are Metzler stable. Thus, letN=A22(x∗)−A21(x∗)×A−111(x∗)×A12(x∗). Using formal calculus (under Sagemath software for instance), we have
Let us consider the 2×2 blocks in N. Since N11 is Metzler stable, let L=N22−N21×N−111×N12.
AI(x∗) is stable if
Since N∗h=S∗h, this is equivalent to
Theorem 3.2. The DFE is GAS in Ω when T0<μhμh+μd≡ζ.
Proof 3.2.1. Our proof relies on Theorem 4.3 in [18], which establishes global asymptotic stability (GAS) for epidemiological systems that can be expressed in matrix form (7). The demonstration is completely similar to that made in [37].
3.1.1. Endemic equilibrium
Theorem 3.3. There exists R−,Rc,R+∈R such that the model system (5) has
(a) a unique endemic equilibrium if R0>1,
(b) a unique endemic equilibrium if R0=1 and Rc<1,
(c) two endemic equilibria if Rc<R0<min(1,R−) or max(Rc,R+)<R0<1,
(d) No endemic equilibrium elsewhere.
Proof 3.3.1. An endemic equilibrium is any non-zero and positive solution of the following system
The equations (15) and (16) allow us to write S⋆h and R⋆h in function of I⋆h as follows: S⋆h=δh+μh+μdα⋆hI⋆h and R⋆h=δhγh+μhI⋆h.
To simplify the expressions, let D=δh+μh+μd, C=δhγh+μh and F=γhC.
By subsequently replacing S⋆h and R⋆h by their values in (14), we then obtain the expression of I⋆h with respect to α⋆h.
Also, α⋆v=a(cI⋆h+˜cR⋆h)N⋆h=a(C˜c+c)α⋆h(C+1)α⋆h+D. Using equations (17), (18), (19), (20), (21) and (22), we have
S⋆q=Λv(w)α⋆v+(μv+wΔμv), E1⋆r=α⋆vS⋆qχ+μv, Ei⋆q=χEi⋆rβ+(μv+wΔμv)for1≤i≤6, Ej⋆r=βE(j−1)⋆qχ+μvfor2≤j≤7; I⋆q=χfqE7⋆rβ(1−fqfr) et I⋆r=βI⋆qχ+μv.
So all our unknowns are expressed in terms of α⋆h, and it only remains to determine the value of α⋆h.
By definition, we have αh⋆=amI⋆qN⋆hand by replacing I⋆q and N⋆h by their values, and after simplification and re-arrangement, we obtain
where
Equation (23) has solution α⋆h=0 and solutions of the equation (E):P2(α⋆h)2+P1α⋆h+P0=0.
The case α⋆h=0 leads us to the equilibrium without disease. We are interested in the equation (E), of which we are going to analyze the number of positive solutions as a function of the value of T0.
1. If T0>1 then, P0>0 and since P2<0, the discriminant Δ=P21−4P2P0 of the equation (E) is positive, hence the equation (E) has two different real solutions. In addition, the product of the solutions is p=P0P2<0. Hence, equation (E) has a unique positive solution.
2. if T0=1, then, equation (E) has two different real solutions, which are zero and −P1P2. But P2<0, so this solution is positive if P1>0, that is to say if T0>Tc.
3. if T0<1 and Δ=P21−4P2P0>0 and T0>Tc, then, equation (E) admits two different positive solutions.
Let P2=−b2 P1=b1(T0−Tc) and P0=b0(T0−1); b2,b1andb0 are all positive coefficients. We have, Δ=P21−4P2P0=b21T20−(2b21Tc−4b0b2)T0−4b0b2+b1T2c.
The last condition can be re-written as follows {Tc<T0<1,Δ=b21T20−(2b21Tc−4b0b2)T0−4b0b2+b1T2c>0.
Let us study the sign of Δ in relation to the values of T0. Consider the equation
(ET0) has as discriminant Δr=(2b21Tc−4b0b2)2−4b21(−4b0b2+b21T2c)=16b2b0[b2b0+b21(1−Tc)] which is positive for Tc<1, and the equation (ET0) has two solutions T− and T+.
We then have {Tc<T0<1,T0∈]−∞,T−[∪]T+,+∞[,
which yields Tc<T0<min(1,T−), where max(Tc,T+)<T0<1.
Remarks 3.1. For the (global) stability of the endemic equilibrium, one could follow the approach in [19] by using a suitable Lyapunov-type functional along the positive flow of the model 5 on a "two domains" subdivision of the phase state R19, under appropriate conditions.
Note that the disease-free equilibrium is only globally asymptotically stable when T0<ζ<1, so it is possible that if this condition is violated, bistability could occur. That is, for ζ<T0<1, a stable DFE could co-exist with a stable endemic equilibrium, a phenomenon known as backward bifurcation [7,9,14,21,38]. In this case, the condition T0<1, although necessary is insufficient to mitigate the spread of malaria in a community.
The following figure depicts the backward bifurcation for model system (5), representing the plotting of I⋆h as a function of T0 for values of the bifurcation parameter m ranging from 0.001 to 0.01, μd=4.54×10−3 and Tc=0.388975.
4.
Optimal control model
To find the solution to the model (5), following four steps are followed. (i) Description the optimal control (ii) Proof of the existence of optimal control problem (iii) Proof of the uniqueness of the optimal control (iv) Numerically solve the optimal control and show these graphically.
4.1. Description of optimal control
There are several methods to mitigate the prevalence of malaria in a community by reducing the mosquito density, contact, longevity and competence. Among all these methods, the possession and correct use of insecticide-treated mosquito bednets is the strategy that considers three of the biological elements mentioned above [27]. Therefore, we consider as control the function w representing the fraction of population that owns and properly use a mosquito net.
Consider the following objective functional
The terms A1Ih and A2(6∑i=1Eiq+Iq) are the cost of infection while Bw2(t) is a quadratic cost related to the effort of using bednets. Our main goal is to find an optimal control function w∗ such that J(w∗)=min{J(w)∣w∈Γ(T)}, with Γ(T) the set of admissible controls defined as
4.2. Existence and characterization of an optimal control
The aim of this section is to prove the existence of an optimal control for the model system (5) and then derive the optimality system. The existence of optimal control of the system (5) will be considered by applying the following theorem [4,22,23,25,29].
Theorem 4.1. Consider the objective functional J given by equation (25), with w∈Γ subject to the constraint state system (5). There exists w∗∈Γ(T) such thatJ(w∗)=min{J(w)∣w∈Γ(T)} subject to thecontrol system (5) with initial conditions at t=0.
Proof 4.1.1. The state and control variables of the system (5) are positive and thecontrol set Γ(T) is closed and convex. Therefore, the integrand of the objectivefunctional J in which it was expressed in the system (5) is a convex function of ω on the control set Γ(T). Since the state solutions are bounded, the Lipschitz property of the state system with respect to the state variables is satisfied. It can also be seen that there exist positive numbers η1 and η2, and a constant ε>1 such that J(ω)≥η1∣ω∣ε−η2. Therefore, the state variables are bounded and the existence of optimal control of the model system (5) is concluded.
4.3. The uniqueness of optimal control
To derive the necessary conditions that the three controls and corresponding state variables must satisfy, we use Pontryagin's maximum principle [31]. To this end, we define the Hamiltonian function for the system, where λi,i=1,…,19 are the adjoint variables or co-state variables
The following result presents the adjoint system and control characterization.
Theorem 4.2. Given an optimal control w∗, and the corresponding state solutions
of the corresponding state system (5), there exists adjoint variables, λi,i=1,…,19, satisfying
The control w∗ satisfies the optimality condition.
where α∗v=mI∗qN∗h and α∗h=cI∗h+˜cR∗hN∗h.
Proof 4.2.1. The differential equations governing the adjoint variables are obtained by differentiation of the Hamiltonian function, evaluated at the optimal control. Then, the adjoint system can be written as
with zero final time conditions (transversality) λi(T)=0. The characterization of the optimal control given by (28) is obtained by solving the equations on the interior of the control set, where 0<w<1. That is,
with ∂H∂ω=0, where α∗v=mI∗qN∗h and α∗h=cI∗h+˜cR∗hN∗h.Hence, we obtain
4.4. Numerical simulations: the biological admissibility and approximate controls
We numerically solve the optimal transmission parameter control for the malaria model. The optimal control is obtained by solving the optimality system, consisting of 19 non-linear ordinary differential equations from the state and adjoint equations. An iterative scheme is used for solving the optimality system [24]. For the simulations, we consider the initial (and arbitrary) number of individuals at time t=0: Sh(0)=100000,Ih(0)=100,Rh(0)=1000,Sq(0)=100000, E1r(0)=10, E2r(0)=9,E3r(0)=8, E4r(0)=7,E5r(0)=6,E6r(0)=5,E7r(0)=4, E1q(0)=3,E2q(0)=3,E3q(0)=3,E4q(0)=3, E5q(0)=3, E6q(0)=2,Ir(0)=35,Iq(0)=800.
For the cost weight in the objective functional J, we take B=$4.5USD (for three years) which represents what the state of Cameroon spends on the purchase of an insecticide-treated mosquito net for two individuals [32]. This is somehow comparable to B=$3.95USD for the average cost for a household (with about 5.5 individuals) per month (for the first two largest cities of Cameroon in terms of population - Douala and Yaounde [28]). The main practical problem is the difficulty to provide bednets to everybody in the household as well as individuals complain of feeling excessive heat when sleeping under a bednet [28], the latter being a potential reason why some individuals use other vector control measures. We could consider the cost per household2 for T=3years, and finally discuss the impact of the optimal controls associated to B1=4.5∗5.52 and B2=3.95∗36. Clearly, from the economic stand point, the other vector control strategies are more expensive than the bednet control. Thus, we focus on the bednet control strategies. The simulations are carried out with T = 3 years, the duration of one LLIN (Long-lasting insecticide-treated bednet) efficacy [32]. We define the uniform control uunif(t)=k and the multi-intervals ("stage") one ustages(t)={u1fflt∈[0;365.25 days ],u2fflt∈]365.25;730.5 months ],u3fflt∈]730.5;1080.75 months ], over three years with k,u1,u2,u3∈R+ and 11080.75∫1080.750ustages(t)dt=k as the mean value. uoptimal is an optimal control for our optimal problem in Theorem 4.1. uforced is an administrative control of distribution of the bednets over three years (it is imposed or "forced"); it is either uunif or ustages. We also define the following in percentage:
1. tuoptimals(uforced)=100×Total of susceptible humans on [ 0;T] under uforced Total of susceptible humans on [ 0;T] under uoptimal;
2. tuoptimalIh(uforced)=100×Total of infectious humans on [ 0;T] under uoptimal Total of susceptible humans on [ 0;T] under uforced;
3. tuoptimalRh(uforced)=100×Total of recovered humans on [ 0;T] under uoptimalTotal of recovered humans on [ 0;T] under uforced.
Definition 4.1. Let Γ(T) be the set of admissible controls relative to a dynamical system D(u(.)), u(.)∈Γ(T). An optimal control, mathematically admissible, is biologically admissible if tuoptimals(uforced)≤100, tuoptimalIh(uforced)≤100 and tuoptimalRh(uforced)≤100.
It is easy (even numerically) to study the biological admissibility to an (mathematically) admissible control uforced. But (for all uforced), the biological admissibility is a challenge related to the choice of the objective function.
Numerically, for T=1080.75 days, uunif(t)=0.65 and ustages(t)={u1=0.9t∈[0;365.25 days ],u2=0.6t∈]365.25;730.5 days ],u3=0.45t∈]730.5;1080.75 days ]. For all our numerical simulations, graphs related to optimal control are in black solid lines, while those linked to the "forced" control are in solid green lines. The effects of the "uniform" control are graphically represented in Figures 4-9 while the "stage" control effects are shown in Figures 10-15.
Practically, the common strategies uforced in malaria affected countries are decreasing functions of time (as trends), due to the difficulty to maintain a constant or high (>90%) level of possession and use of bednets throughout a 3-year campaign of LLINs distribution.
Table 4 suggests that, even if the "stage" and uniform controls have the same mean, it is better to use a "stage" control with emphasis on the first few months of the 3 years. Clearly, the effort should be done to cover the gap (between the results of the system state following uforced and uoptimal) in Table 4. This approach, based on the reality of the malaria programs in each country, could support health policies and decision-makers in order to obtain an accurate threshold in the percentage ϵuforced of the "administrative/public planners controls" uforced (ustage or uunif) applications compared to optimal effects, such that 100−tuoptimals(uforced)≤ϵuforced, 100−tuoptimalIh(uforced)≤ϵuforced and 100−tuoptimalRh≤ϵuforced. This allows us to introduce the definitions of the ϵuforced-approximate weak or strong "sub-optimal" controls.
Definition 4.2. (Approximate controlability) Let Γ(T) be the set of admissible controls relative to a dynamical system D(u(.)), u(.)∈Γ(T), for T>0. For Vuoptimaluforced=(tuoptimals(uforced),tuoptimalIh(uforced),tuoptimalRh(uforced)), let define
also written as
and
That is,
A biologically admissible control uforced is ϵuforced-approximate weak "sub-optimal" if
A biologically admissible control uforced is ϵuforced-approximate strong "sub-optimal" if
Remarks 4.1. These definitions in 4.2 improve on the efficiency index [1]. It is possible to consider the reduction of noise Nmosq (similar to Norm. for mosquitoes) produced by mosquitoes as the percentage of mosquitoes with optimal control compared to the states with forced control: then the new index would be Normα,β.:=αNorm.+βNmosq such that α+β=1. The coefficients α and β relate respectively the importance of the humans' group and mosquitoes' group. Herein, we focus on the optimal impact on humans and consider α=1.
Straightforward computations lead to the following proposition 4.1.
Proposition 4.1. There is an equivalence between Normweak and Normweak:
In Table 4,
and
We see that for ϵuforced=35%, the Vuoptimaluunif is 35%-approximate weak "sub-optimal" like Vuoptimalustage. But only Vuoptimalustage is 35%-approximate strong "sub-optimal" and not Vuoptimaluunif. Another interesting point is the fact that Normweak(Vuoptimalustage)=18.186947, and this comes from the fact that the "weak" deviation from the optimal strategy is only about 18.187% in total (with the collective effort/contribution of Sh,Ih and Rh to reach the optimal strategy). By the way, Normstrong(Vuoptimalustage)=31.410, and this corroborates the fact that the "weak" deviation from the optimal strategy is only about 31.410% following the individual efforts/contributions of Sh,Ih and Rh to reach the optimal objective. We observe that the disadvantage (loss of immunity) in the use of bednets is compensated by the benefit of the number of susceptible/infected individuals excluded from the malaria disease dynamics. Then, it is possible to get closer to the optimal results with a realistic strategy.
5.
Conclusion
We formulated and rigorously analyzed a vector multi-stage malaria model with the use of mosquito treated bednets as preventive measure. The proposed model is biologically meaningful and mathematical well-posed. We investigated the local and global stability of equilibria. The analytical results reveal the possibility of bistability when T0<ζ<1 (see subsection 3.1.1 with additional mortality δh less than 10−5 see discussion in [6]). That is, the model could exhibit the phenomenon of backward bifurcation, an epidemiological situation which although necessary, having the basic reproduction number less than unity is no longer sufficient to mitigate the malaria transmission dynamics [38]. Thus, a low level of additional (disease-induced) mortality could lead to the existence of an endemic equilibrium even if the basic reproduction number is less than one.
Next, an optimal control strategy is investigated with the proper usage of LLINs (during three years compared to a "forced" control) as the control parameter. We observe that the disadvantage (loss of immunity) in the use of bednets is compensated by the benefit of the number of susceptible/infected individuals excluded from the malaria disease dynamics. Moreover, it is possible to get close to the optimal results with a realistic strategy.
Results from this study could help inform health policy and decision-makers on the potential optimum strategies to mitigate malaria transmission dynamics in affected communities by designing reachable malaria program implementation objectives "close" to the optimal strategies ϵu.% by the "weak" collective contribution or the "strong" individual effort to achieve the optimal objective. The notions of ϵuforced-approximate strong/weak "sub-optimal" control are more practical than the theoretical optimal control which remains a daunting task to health officials. The upper bound ϵuforced of the gap, from the "sub-optimal" results to the optimal ones, is of great interest practically since it delineates the acceptable error one could essentially make if we apply uforced instead of uoptimal.
The proposed model is not exhaustive. One could consider splitting the human population into adults and juveniles since malaria disproportionately affects children under five years of age. The model could then be fitted with real data from an affected region/country with most model parameter values estimated for the purpose. Also, because of uncertainties in most parameter values, a detailed sensitivity and uncertainty analysis could be carried out to understand the dependence of the basic reproduction number and model state variables on their components [30].
Conflict of interest
The authors declare that they have no conflicts of interest to this work.









 DownLoad:
DownLoad:
















