A locally conservative staggered least squares method on polygonal meshes

1.   Introduction

Staggered discontinuous Galerkin (SDG) methods on triangular meshes have been actively studied since the pioneering works of Chung and Engquist ^[20,21]. SDG methods earn many desirable features, such as local and global conservations, superconvergence and preservation of physical laws. Recently, a lowest order SDG method on general meshes has been developed for Poisson equation ^[31,39], the Stokes equations ^[40], linear elasticity equations ^[43], respectively. The key idea of the lowest order SDG method on general meshes is to divide the initial partition into the union of triangles by connecting the interior point to the vertices of the initial partition. Then two finite element spaces are defined on the resulting triangulations, and the continuity of them are staggered on the interelement boundaries. The construction of the SDG method on triangular meshes and on polygonal meshes shares some similarities, while the lowest order SDG method on polygonal meshes is more competitive for practical applications. The lowest order SDG method enfolds the following features: First, it allows arbitrary shapes of polygons. Second, it can be flexibly applied to rough grids. Third, hanging nodes are allowed, which can be simply treated as additional vertices. Very recently, arbitrarily high order SDG methods have been developed for various problems of interest ^{[30,41,42,44]}.

Although SDG methods earn many desirable features, one of the disadvantages is that the inf-sup condition is needed to establish the stability, which is usually not an easy task. Least squares method is considered as an alternative to the saddle point formulations and can circumvent the inf-sup condition. Examples of application of least squares to scalar elliptic equations, Helmholtz equation, linear elasticity, the Stokes equations and the Navier-Stokes equations can be found in ^{[6,7,13,14,19]}. The purpose of this paper is to develop a first-order staggered least squares method for Poisson equation on polygonal meshes. Different from the standard SDG methods, our method employs the locally conforming Raviart-Thomas (RT) element and locally conforming linear element as the function spaces. And the construction of locally conforming RT elements is much simpler than the flux space employed in the standard SDG methods. Since continuity of the function spaces are staggered on the interelement boundaries, we impose the flux jump term and potential jump term to stabilize the least squares functional. The resulting staggered least squares method inherits the aforementioned features of the lowest order SDG method. Stability and optimal a priori error estimates in energy norm are developed. It is worth mentioning that in the first-order least squares method, the built-in functional provides a natural error estimator. One can refer to ^[22,38] for related works on guaranteed a posteriori error estimators for the SDG method and to ^{[11,17,18,29,32,34]} for a posteriori error estimators for the least squares method.

Superconvergence of finite element methods has drawn great attention for a few decades. It has strong relevance to a posteriori error estimation. Most of the existing works are devoted to superconvergence on rectangular meshes, among these, we cite in particular the works ^[26,27,35]. Superconvergence on triangular meshes can be referred to ^[3,9,33,37]. Superconvergent estimates for RT elements on triangular meshes are not an easy task, and the variational error expansion for RT elements on a local triangle in terms of the normal trace (cf. ^[33]) is the key ingredient. Our superconvergent estimate in energy norm is motivated by the work given in ^[33], while some new techniques are also exploited due to the different expressions of least squares functional. One of the major differences is Eq (3.9), which can not be bounded by direct application of Lemma 3.4. To overcome this issue, we introduce piecewise constant projections and employ the equivalence between the energy norm and divergence norm of RT elements.

Another new contribution is to study the $L^2$ norm error estimates via a duality argument. It is straightforward for the standard SDG method, while it is less obvious for the staggered least squares method. Our staggered least squares method is nonconforming in the sense that the function spaces are partially continuous over the interelement boundaries. If we proceed as in ^[12], then the $L^2$ norm of the potential will be expressed in terms of the bilinear form and the edge integration for the potential error and flux error (see Lemma 3.6). The standard trace theorem will lead to the loss of the optimal convergence rates for $L^2$ error. To overcome this issue and achieve the optimal convergence rates in $L^2$ error, the superconvergent estimates measured in energy norm as well as the standard trace theorems are exploited.

On the other hand, local and global conservations are attractive properties in practical applications, while standard least squares method can not preserve the conservation properties. The staggered least squares method also fails to preserve the local and global conservations. Therefore, we attempt to develop a postprocessing scheme which can ensure local and global conservations. The postprocessing scheme developed in this paper takes advantage of the single valued flux over the outer boundary of the dual partition, which can be corrected by using some simple local procedure, yielding locally conservative flux over the dual partition. Then the locally conservative flux over the resulting triangulations can be constructed by using direct calculations. We remark that the postprocessing scheme developed in this paper mimics the one proposed in ^[8], where quadrilateral elements are considered. We modify the scheme proposed therein to fit it into polygonal meshes.

The rest of the paper is organized as follows. In the next section, we introduce the staggered least squares method and present some preliminary results. Then in Section 3, some error estimates, superconvergent estimates and $L^2$ norm error estimate are proposed. In Section 4, a postprocessing scheme for flux is established, which ensures the local and global conservations. Several numerical experiments are carried out in Section 5 to confirm the theoretical findings. Finally, a conclusion is given at the end of the paper.

2.   Least squares method on staggered mesh

Let $\Omega$ be a bounded domain in $\mathbb{R}^2$ with Lipschitz continuous boundary $\partial \Omega$. We consider the Dirichlet boundary value problem

By introducing a new variable $\mathit{\boldsymbol{u}} = -\nabla p$, the original problem can be recast into the first order system:

Next, we introduce some notations that will be used throughout the paper. Let $D\subset \mathbb{R}^d, d = 1, 2$, we adopt the standard notations for the Sobolev spaces $H^s(D)$ and their associated norms $\|\cdot\|_{s, D}$, and semi-norms $|\cdot|_{s, D}$ for $s\geq 0$. The space $H^0(D)$ coincides with $L^2(D)$, for which the norm and inner products are denoted as $\|\cdot\|_D$ and $(\cdot, \cdot)_D$, respectively. If $D = \Omega$, the subscript $\Omega$ will be dropped unless otherwise mentioned. In the sequel, we use $C$ to denote a generic positive constant which may have different values at different occurrences.

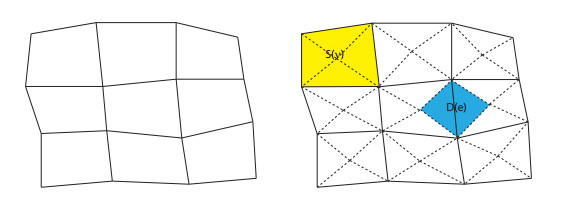
Now we can define our staggered least squares method. We start by introducing the meshes employed in our construction, which is also one of the key ingredients. Following ^[21,39], three meshes will be constructed: the primal mesh $\mathcal{T}_{prm}$, the dual mesh $\mathcal{T}_{dl}$ and the primal simplicial submeshes $\mathcal{T}_{h}$. We first let $\mathcal{T}_{prm}$ be the initial (primal) partition of the domain $\Omega$ into non-overlapping simple quadrilateral/polygonal elements. We let $\mathcal{F}_{prm}$ be the set of all primal edges in this partition and $\mathcal{F}_{prm}^{0}$ be the subset of all interior edges, that is, the set of edges in $\mathcal{F}_{prm}$ that do not lie on $\partial\Omega$. For each quadrilateral/polygon $E$ in the initial partition $\mathcal{T}_{prm}$, we select an interior point $\nu$ and create new edges by connecting $\nu$ to the vertices of quadrilateral/polygon, and the set collecting all the interior point is denoted as $\mathcal{N}_1$. This process will divide $E$ into the union of triangles, where the triangle is denoted as $\tau$, and we rename the union of these triangles by $S(\nu)$. We remark that $S(\nu)$ are the quadrilaterals/polygons in the initial partition (primal mesh). Moreover, we will use $\mathcal{F}_{dl}$ to denote the set of all the dual edges generated by this subdivision process and use $\mathcal{T}_{h}$ to denote the resulting triangulations, on which our basis functions are defined. For each triangle $\tau\in \mathcal{T}_h$, we let $h_\tau$ be the diameter of $\tau$ and $h = \max\{h_\tau, \tau\in \mathcal{T}_h\}$. Furthermore, $\mathcal{T}_h$ is assumed to satisfy the local quasi-uniform assumption in the sense that for any pair of elements $\tau$ and $\tau'$ in $\mathcal{T}_h$ which share an edge, there exists a constant $\kappa$ independent of $h_\tau$ and $h_{\tau'}$ such that $\kappa^{-1}\leq h_\tau/h_{\tau'}\leq \kappa$. In addition, we define $\mathcal{F}: = \mathcal{F}_{prm}\cup \mathcal{F}_{dl}$ and $\mathcal{F}^{0}: = \mathcal{F}_{prm}^{0}\cup \mathcal{F}_{dl}$. This construction is illustrated in Figure 1, where solid lines are edges in $\mathcal{F}_{prm}$ and dotted lines are edges in $\mathcal{F}_{dl}$.

For each interior edge $e\in \mathcal{F}_{prm}^0$, we use $D(e)$ to denote the union of the two triangles in $\mathcal{T}_h$ sharing the edge $e$ (dual mesh), and for each boundary edge $e\in\mathcal{F}_{prm}\backslash\mathcal{F}_{prm}^0$, we use $D(e)$ to denote the triangle in $\mathcal{T}_h$ having the edge $e$, see Figure 1. We write $\mathcal{T}_{dl}$ as the union of all $D(e)$. In addition, we define $\mathcal{T}_{dl}^{int}$ as the set collecting $D(e)$ for all interior edges $e\in \mathcal{F}_{prm}^0$ and $\mathcal{T}_{dl}^{ext}$ as the set collecting $D(e)$ for all boundary edges $e\in \mathcal{F}_{prm}\backslash \mathcal{F}_{prm}^0$. In the sequel, we use $\nabla_h$ and $\nabla_h\cdot$ to denote element-wise defined gradient and divergence operators with respect to $\mathcal{T}_h$ respectively.

For each edge $e$, we define a unit normal vector $n_{e}$ as follows: If $e\in \mathcal{F}\setminus \mathcal{F}^{0}$, then $\mathit{\boldsymbol{n}}_{e}$ is the unit normal vector of $e$ pointing towards the outside of $\Omega$. If $e\in \mathcal{F}^{0}$, an interior edge, we then fix $\mathit{\boldsymbol{n}}_{e}$ as one of the two possible unit normal vectors on $e$. When there is no ambiguity, we use $\mathit{\boldsymbol{n}}$ instead of $\mathit{\boldsymbol{n}}_{e}$ to simplify the notation.

The following mesh regularity assumptions are also needed throughout the paper (cf. ^[5,15]).

Assumption 2.1. We assume there exists a constant $\rho > 0$ such that

(1) For every element $S(\nu)\in \mathcal{T}_{prm}$ and every edge $e\in \partial S(\nu)$, it satisfies $h_e\geq \rho h_{S(\nu)}$, where $h_e$ denotes the length of edge $e$ and $h_{S(\nu)}$ denotes the diameter of $S(\nu)$.

(2) Every element $S(\nu)$ in $\mathcal{T}_{prm}$ is star-shaped with respect to a ball of radius $\geq \rho h_{S(\nu)}$.

We remark that the above assumptions ensure that the triangulation $\mathcal{T}_h$ is shape-regular.

Let $k\geq 0$ be the order of approximation. For every $\tau \in \mathcal{T}_{h}$ and $e\in\mathcal{F}$, we define $P^{k}(\tau)$ and $P^{k}(e)$ as the spaces of polynomials of degree less than or equal to $k$ on $\tau$ and $e$, respectively. For $w$ and $\mathit{\boldsymbol{v}}$ belonging to broken Sobolev space, the jump $[v]$ and the jump $[\mathit{\boldsymbol{v}}\cdot\mathit{\boldsymbol{n}}]$ are defined respectively as

where $v_{i} = v\mid_{\tau_{i}}$, $\mathit{\boldsymbol{v}}_{i} = \mathit{\boldsymbol{v}}\mid_{\tau_{i}}$ and $\tau_{1}$, $\tau_{2}$ are the two triangles in $\mathcal{T}_h$ having the edge $e\in \mathcal{F}$. In the above definitions, we assume $\mathit{\boldsymbol{n}}$ is pointing from $\tau_1$ to $\tau_2$.

In addition, we let $H_r(\text{div}; D)$ be the Banach space

which can be denoted as $H(\text{div}; D)$ when $r = 2$.

Finally, we introduce the finite dimensional spaces earning staggered continuity for defining our scheme. We first define the following locally $H^{1}(\Omega)$ conforming space $S_h$:

Here, for $w\in S_h$, we have $w|_{D(e)}\in H^1(D(e))\; \forall D(e)\in \mathcal{T}_{dl}, {\forall e\in \mathcal{F}_{prm}}$. We next define the following locally $H(\mbox{div}; \Omega)-$conforming SDG space $\mathit{\boldsymbol{V}}_h$:

where $R^0(\tau) = P^0(\tau)^2 \oplus (x, y)^TP^0(\tau)$. Note that if $\mathit{\boldsymbol{v}}\in \mathit{\boldsymbol{V}}_h$, then $\mathit{\boldsymbol{v}}\mid_{S(\nu)}\in H(\text{div}; S(\nu))$ for each $\nu\in \mathcal{N}_1$.

Based on the above preparations, we define a least squares functional for $(\mathit{\boldsymbol{v}}, q)\in \mathit{\boldsymbol{V}}_h\times S_h$

The finite element discretization of our staggered least squares corresponding to the $L^2$ norm least squares functional is to minimize functional (2.3) over $S_h\times \mathit{\boldsymbol{V}}_h$ such that

Then, (2.4) can be equivalently written as follows: Find $(\mathit{\boldsymbol{u}}_h, p_h)\in \mathit{\boldsymbol{V}}_h\times S_h$ such that

where

We mention the existing methods supporting polygonal meshes with arbitrary polynomial orders such as DG ^[1,4,16,24], HHO ^[25], VEM ^[5], and WG ^[36]. Advantages of our formulation are as follows. First, the current least squares formulation does not require any stabilization parameters as opposed to the existing polygonal methods. Second, the least square functional itself provides an a posteriori error estimator for adaptive mesh refinements ^[17,18].

For later analysis, we define

The following discrete Poincaré inequality will be used for the subsequent analysis (cf. ^[10])

Lemma 2.1. There exists a positive constant $C$ such that for all $(\mathit{\boldsymbol{v}}, q)\in \mathit{\boldsymbol{V}}_h\times S_h$ one has

Proof. Integration by parts leads to

and

The Cauchy-Schwarz inequality and norm equivalence imply

The preceding arguments and the discrete Poincaré inequality (2.6) lead to

Therefore

It is trivial that

Thus, the proof is complete by combining the above estimates. □

Theorem 2.1 (Existence and uniqueness). There exists a unique solution to (2.5).

Proof. Since (2.5) is equivalent to a square linear system, existence follows from uniqueness, it suffices to prove the uniqueness. Let $f = 0$ in (2.5) and then $(\mathit{\boldsymbol{u}}_h, p_h)$ satisfies

By letting $\mathit{\boldsymbol{v}} = \mathit{\boldsymbol{u}}_h$ and $q = p_h$ in the above equation, we can obtain $\mathit{\boldsymbol{u}}_h = \mathit{\boldsymbol{0}}$ and $p_h = 0$ (cf. Lemma 2.1). This completes the proof. □

3.   Error analysis

3.1.   Energy error estimates

This section presents the convergence estimates for both potential and flux. To begin, we define the projection operator such that it satisfies

The following approximation properties hold (cf. ^[21,23])

A projection operator, denoted by $\Pi_h$, is defined as a linear mapping from $H_r(\text{div}; \Omega)$ to $\mathit{\boldsymbol{V}}_h$ for some $r > 2$ such that on each element $\tau\in \mathcal{T}_h$

It satisfies

In addition, we remark that $\Pi_h \mathit{\boldsymbol{v}}\in H(\text{div}; \Omega)$.

For $\mathit{\boldsymbol{v}}\in H^1(\tau)^2, \forall\tau\in \mathcal{T}_h$, the local Crouzeix-Raviart interpolant $I_h^{CR}\mathit{\boldsymbol{v}}$ on $\tau$ is the unique element in $P^1(\tau)^2$ such that

Standard approximation theory yields (cf. ^[23])

and

In addition, they satisfy (cf. ^[33])

Lemma 3.1. $\Pi_hI_h^{CR}\mathit{\boldsymbol{v}} = \Pi_h\mathit{\boldsymbol{v}}.$

Theorem 3.1. Assume that $(\mathit{\boldsymbol{u}}, p)$ is in $H^1(\Omega)^2\times H^2(\Omega)$ and that the divergence of the flux $\nabla \cdot\mathit{\boldsymbol{u}}$ is in $H^1(\Omega)$. Let $(\mathit{\boldsymbol{u}}_h, p_h)$ denote the numerical solution of (2.5). Then, we have

Proof. Replacing $(\mathit{\boldsymbol{u}}_h, p_h)$ by $(\mathit{\boldsymbol{u}}, p)$ in (2.5), we can obtain

It then yields the following error equation

which gives

Lemma 2.1 and the definition of the bilinear form $A$ lead to

We have from (3.2)

Standard approximation theory yields

Trace inequality and standard approximation theory (3.1) imply

Finally, we have from the definition of $\Pi_h$

The preceding arguments, the triangle inequality and the interpolation error estimates (cf. (3.3)–(3.5)) yield the desired estimate. □

Theorem 3.2. Let $(\mathit{\boldsymbol{u}}, p)$ satisfy the assumption of Theorem 3.1 and let $(\mathit{\boldsymbol{u}}_h, p_h)$ be the numerical solution of (2.5). Then, we have

Proof. Given $\phi\in H^1(\Omega)$, let $\alpha$ solve $-\Delta \alpha = \phi$ in $\Omega$, $\alpha = 0$ on $\partial \Omega$, and let $\mathit{\boldsymbol{\beta}} = -\nabla \alpha$, so $\nabla \cdot \mathit{\boldsymbol{\beta}} = \phi$. Then $\|\alpha\|_2\leq C \|\phi\|_1$, $\|\nabla\cdot\mathit{\boldsymbol{\beta}}\|_1\leq C\|\phi\|_1$. We have from the definition of the dual norm

Thus,

which together with (3.7) yields the desired estimate. □

3.2.   Superconvergence and $L^2$ error estimate

In this section, we aim to derive the superconvergent estimates. Most of the existing literatures are devoted to the rectangular cases. The function spaces exploited in our method is essentially defined on the triangular meshes, which makes it more complicated to derive the superconvergent estimate. To this end, we employ the variational error expansions for $RT$ elements on a local triangle in terms of the normal trace.

The next two lemmas are given in ^[33].

Lemma 3.2. For $\mathit{\boldsymbol{v}}_L\in P^1(\tau)^2$,

where

and $\{e_k\}_{k = 1}^3$ denote the edges of triangle $\tau\in \mathcal{T}_h$, $\{\mathit{\boldsymbol{n}}_k\}_{k = 1}^3$ the unit outward normal vectors, $\{\mathit{\boldsymbol{t}}_k\}_{k = 1}^3$ the unit tangent vectors with counterclockwise orientation, and $\{\lambda_k\}_{k = 1}^3$ are barycentric coordinate functions. In addition, $k\pm1$ permuted cyclically.

Lemma 3.3. For $\mathit{\boldsymbol{v}}_h\in P^0(\tau)^2$ and $\mathit{\boldsymbol{v}}_L\in P^1(\tau)^2$

where

and $A_k^{(j)}$ are operators defined by

Now we are ready to prove the next lemma, which is crucial in the proof of the superconvergence.

Lemma 3.4. For $\mathit{\boldsymbol{v}}_h\in P^0(\mathcal{T}_h)^2$, the following estimate holds

Proof. Lemmas 3.1 and 3.3 imply

Standard interpolation theory (3.5) yields

The elementary identity

leads to

The Cauchy-Schwarz inequality and trace inequality yield

□

Let $Q_h$ denote the standard linear interpolation operator, and we find the following lemma useful for the subsequent analysis (cf. ^[28]).

Lemma 3.5. For any quadratic function $p_Q$, we have

Let $\Pi_0$ denote the $L^2$ orthogonal projection onto the piecewise constants $P^0(\mathcal{T}_h)^2$, and it satisfies

The superconvergent estimate can be stated in the next theorem.

Theorem 3.3. (superconvergence) Let $(\mathit{\boldsymbol{u}}_h, p_h)$ be the numerical solution of (2.5). Then, we have

Proof. We can infer from Lemma 2.1

It follows from (3.2)

Any function $\mathit{\boldsymbol{v}}_h\in \mathit{\boldsymbol{V}}_h$ can be expressed in the following form on each triangle $\tau\in \mathcal{T}_h$:

We have

Then, Lemma 3.4 and (3.8) yield

and

Integration by parts implies

Without loss of generality, we assume that $p\in P^2$, then the first term of (3.10) can be bounded by Lemma 3.5

Standard interpolation theory and the Cauchy-Schwarz inequality yield the upper bound for the second term of (3.10)

Assume that $p\in P^2$, then we have from Lemma 3.5 and integration by parts

The proof is complete by combining the preceding arguments. □

Lemma 3.6. Let $(\mathit{\boldsymbol{u}}, p)$ be the solution of (2.2) and $(\mathit{\boldsymbol{u}}_h, p_h)$ be the numerical solution of (2.5). Then there exists $(\mathit{\boldsymbol{\gamma}}, w)$ and $z$ such that

and that

Proof. Let $z\in H^1_0(\Omega)$ be the solution of the following problem

We assume that the following regularity estimate holds

Multiplying both sides of (3.12) by $p-p_h$, adding and subtracting $(\mathit{\boldsymbol{u}}-\mathit{\boldsymbol{u}}_h, \nabla z)$, and integration by parts imply

It suffices to find $(\mathit{\boldsymbol{\gamma}}, w)\in H_r(\text{div}; \Omega)\times H^1_0(\Omega), r > 2$ such that

and that

To do so, let $w\in H^1_0(\Omega)$ be the solution of the scalar elliptic problem (2.1) with the right hand side $f = z-\Delta z$. The regularity estimate (3.13) and the triangle inequality imply

Let $\mathit{\boldsymbol{\gamma}} = \nabla (z-w)$. It is then easy to check that $(\mathit{\boldsymbol{\gamma}}, w)$ satisfies (3.14). Now (3.15) follows from (3.13), (3.16), and the facts that

and that

The proof is complete by combining the preceding arguments. □

Now we are ready to prove the $L^2$ norm error estimate, which is also the main result of this section.

Theorem 3.4. Let $(\mathit{\boldsymbol{u}}, p)$ be the solution of (2.2) and $(\mathit{\boldsymbol{u}}_h, p_h)$ be the numerical solution of (2.5). Then, we have

Proof. We have from (3.6), (3.11), the Cauchy-Schwarz inequality and standard interpolation theory

On the other hand, we have from the definition of dual norm, trace theorem and the discrete Poincaré inequality (2.6) that

where $\|\cdot\|_{\Sigma, \tau}$ denotes $\|\cdot\|_\Sigma$ restricted to each element $\tau\in \mathcal{T}_h$.

Proceeding analogously, we have

The assertion follows by combining the preceding arguments, Theorems 3.1, 3.3 and Lemma 3.6. □

Remark 3.1. The $L^2$ norm error estimate for potential given in Theorem 3.4 is constructed by exploiting duality argument and superconvergent estimate (cf. Theorem 3.3). The optimal convergence estimate in $L^2$ norm proposed above requires higher regularity than the one given in ^[12], which is due to the superconvergent estimate.

4.   Locally conservative flux correction

In this section, we aim to formulate a simple, local procedure that replaces $\mathit{\boldsymbol{u}}_h$ by a field $\tilde{\mathit{\boldsymbol{u}}}_h\in H(\text{div}; \Omega)$ and satisfy

The construction proposed in this section can be flexibly applied to general meshes. There are two steps involved in our postprocessing scheme: first, inspired by the work given in ^[8], we construct a function which satisfies

where $\mathit{\boldsymbol{n}}$ denotes the unit outward normal vector of $D(e)$; then, we can construct a function $\tilde{\mathit{\boldsymbol{u}}}_h\in H(\text{div}; \Omega)$ satisfying

To complete the first step, we proceed as follows. Let $D(e)$ denote an arbitrary dual mesh belonging to $\mathcal{T}_{dl}^{int}$. Let $e_i, i = 1, \ldots, 4$ denote the (oriented) edges lying on $\partial D(e)$, let $\phi_{e_i}, i = 1, \ldots, 4$ denote the flux of $\mathit{\boldsymbol{u}}_h$ across the edge $e_i$ and let $\mathit{\boldsymbol{n}}$ denote the unit outward normal vector of $\partial D(e)$. In addition, $\sigma_i = 1$ if orientation of $e_i$ coincides with the outer normal on $\partial D(e_i)$ and $\sigma_i = -1$ otherwise. A function $\mathit{\boldsymbol{u}}_h\in \mathit{\boldsymbol{V}}_h$ satisfies

which immediately leads to

where $h_{e_i}, i = 1, \ldots, 4$ denotes the length of the respective edges.

We seek to define modified flux values $\tilde{\phi}_{e_i} = \phi_{e_i}-\sigma_i\delta\phi_{e_i}$ and a function $\tilde{\mathit{\boldsymbol{u}}}_h$ which satisfies

such that

To define the corrected flux values for an element $D(e)$, we proceed as follows. If, for a given edge $e_i$, the flux $\phi_{e_i}$ has already been corrected, we set $\delta \phi_{e_i} = 0$. If the flux on $e_i$ has not yet been corrected, we set

where $n_{D(e)} > 0$ is the summation of the length of all the edges on $\partial D(e)$ whose fluxes have not been corrected.

Consider now a dual partition $\mathcal{T}_{dl}^{int}$ of $\Omega$ with $n_h$ interior dual elements. To define the flux-correction algorithm, some additional notation is necessary. Let

denote the set of all edges in the union of the dual elements indexed by $i_1, \cdots, i_k$. For example, $e(i_l) = \partial D_{i_l}$ is the set of all outer edges of element $D_{i_l}\in \mathcal{T}_{dl}^{int}$. Define

Given $\mathit{\boldsymbol{u}}_h\in \mathit{\boldsymbol{V}}_h$, the following algorithm finds $\tilde{\mathit{\boldsymbol{u}}}_h$ that is locally conservative over each $D(e)\in \mathcal{T}_{dl}$:

(1) Define a permutation $\pi = \{i_1, i_2, \ldots, i_{nel}\}$ of all elements in $\mathcal{T}_{dl}^{int}$ such that

(2) For $k = 1, \ldots, n_h$, apply the element flux correction procedure to element $D_{i_k}$.

We remark that the above procedure constructs a function $\tilde{\mathit{\boldsymbol{u}}}_h$ satisfying

for $D(e)\in \mathcal{T}_{dl}^{int}$. For elements $D(e)$ in $\mathcal{T}_{dl}^{ext}$, if the flux value over $\partial D(e)\backslash\partial \Omega$ has not been corrected, then we set the flux value to be equal to the flux value of $\mathit{\boldsymbol{u}}_h$ over that edge. At this point, we have determined the flux values of $\tilde{\mathit{\boldsymbol{u}}}_h$ over all the edges belonging to $\mathcal{F}_{dl}$. To calculate the flux values over the edges belonging to $\mathcal{F}_{prm}$, we number the edges of an arbitrary element $\tau\in \mathcal{T}_h$ as $e_i, i = 1, \ldots, 3$ and $e_1$ denotes the edge that belongs to $\mathcal{F}_{prm}$. The flux values over $e_2$ and $e_3$ have already been corrected, which we denote as $\tilde{\phi}_2$ and $\tilde{\phi}_3$, respectively. We can define the flux value over $e_1$ by

Then, $\tilde{\mathit{\boldsymbol{u}}}_h$ in each element can be represented as

where $W_{e_i}$ is the RT shape function associated with edge $e_i$. The above procedure yields a function $\tilde{\mathit{\boldsymbol{u}}}_h\in H(\text{div}; \Omega)$ and satisfies the local conservation.

Remark 4.1. Our locally conservative flux correction is motivated by the work given in ^[8], while some modifications are made. First, different from the work in ^[8], our locally conservative flux correction is essentially defined on triangular meshes, which makes it well suited to general meshes. Second, our construction is based on locally conforming $H(\text{div}; \Omega)$ elements, thus, locally conservative flux on dual partitions are considered first and then locally conservative flux on each triangle can be constructed by applying some simple local procedure.

5.   Numerical experiments

In this section, we present several numerical examples to test the performance of the proposed method. The convergence history for various errors under uniform refinement are displayed. In addition, some numerical experiments are carried out to test the performance of the adaptive mesh refinement guided by the least squares functional estimator. Moreover, the adaptive mesh refinement can be pursued by connecting the midpoint of each planar face of its boundary to the barycenter of the element, and more details regarding the adaptive mesh refinement strategies can be found in ^[39]. By refining in this fashion, hanging nodes may be introduced, which can be simply treated as new nodes since adjacent co-planar elemental interfaces are perfectly acceptable for our method.

Example 5.1 (Smooth solution on unit square domain). In this example, we consider $\Omega = (0, 1)^2$, and the exact solution is given by $p = x(1-x)y(1-y),$ where the right hand side $f$ can be calculated correspondingly.

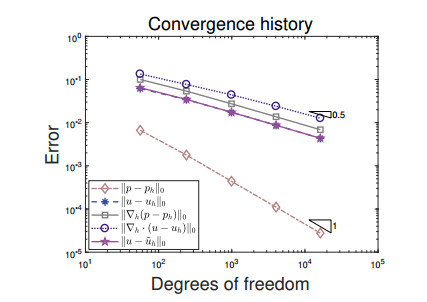
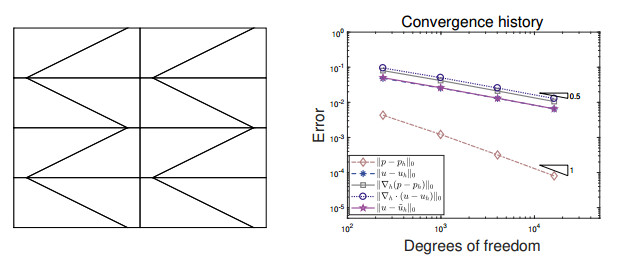
We first partition the domain $\Omega$ into uniform square grids. Note that the mesh size $h\approx N^{-1/2}$, where $N$ represents the number of degrees of freedom. The convergence history for various errors against the number of degrees of freedom are displayed in Figure 2, where optimal convergence rates can be achieved. In addition, we can observe from the numerical tests that the postprocessed flux has first order convergence and the $L^2$ accuracy is not influenced. Then, we partition the domain $\Omega$ into trapezoidal grids of base $h$ in vertical direction and parallel horizontal edges of size $0.2\; h$ and $1.8\; h$, as proposed in ^[2,39] and shown in Figure 3. We can observe from the numerical results that optimal convergence rates can be obtained. Next, we test the performance of the proposed method by using Voronoi mesh as shown in Figure 4, again, optimal convergence rates can be achieved. The numerical results in Table 1 indicate that the postprocessed flux can recover local and global conservations for rough grids. Here, $\mbox{Dofs}$ denotes the number of degrees of freedom.

Let

then we have:

Example 5.2 (Classical $L$-shaped domain). In this example, we consider the $L$-shaped domain

The exact solution in polar coordinates is given by

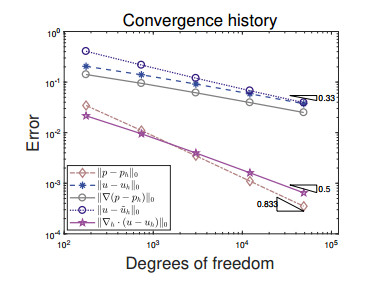
The convergence history under uniform refinement are reported in Figure 5. As expected, reduced convergence rates are achieved, which is due to the reduced regularity. In addition, as shown in Table 2, the postprocessed flux ensures local and global conservations.

To restore the optimal convergence rates, we aim to exploit the adaptive mesh refinement guided by least squares functional estimator which is defined by

and the error is defined as

Indeed, it follows from (2.3) and (2.2) that $E(p-p_h, \mathit{\boldsymbol{u}}-\mathit{\boldsymbol{u}}_h) \approx\eta^2$. Interested readers can also refer to ^[17] for the discussions on the equivalence of the error estimator and the error in the least-square methods. The adaptive mesh pattern and convergence history under adaptive mesh refinement are reported in Figure 6, where the singularity is well-captured and optimal convergence rates can be recovered by using adaptive mesh refinement.

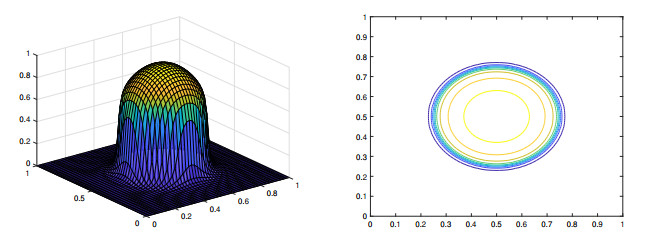
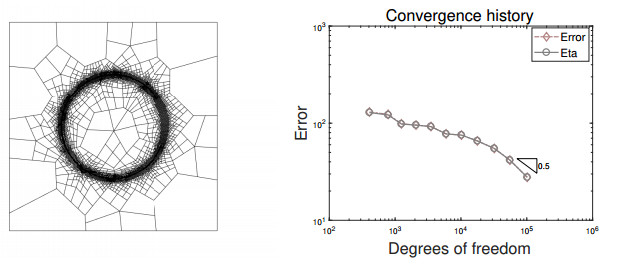
Example 5.3 (Solution with circular inner layer). In this example, we set $\Omega = (0, 1)^2$ and the exact solution is given by

and $f$ can be calculated correspondingly. The solution possesses a circular inner layer where its gradient behaves like $O(\epsilon^{-1/2})$. In our numerical simulation, we set $\epsilon = 10^{-4}$.

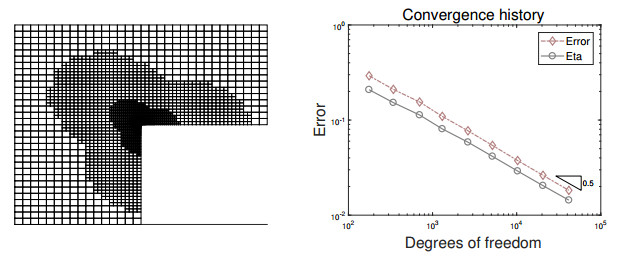
The plots of the exact solution are shown in Figure 7. The adaptive mesh pattern and convergence history are reported in Figure 8, and we can observe from the numerical results that the circular inner layer can be well captured and optimal convergence rates can be restored.

6.   Conclusions

In this paper, we have developed a staggered least squares method for elliptic equations on general meshes. Optimal a priori error estimates in energy norm and $L^2$ norm are derived. A postprocessing scheme is introduced to ensure local and global conservations on general meshes. The numerical results indicate that the proposed method can be flexibly applied to rough grids, and the postprocessed flux earns local and global conservations on general meshes. In addition, the adaptive mesh refinement guided by the least squares functional estimator is efficient in dealing with problems with singularities. Finally, we remark that the RT element exploited in this paper can also be replaced by $BDM_1$ element, then optimal convergence rates in energy norm can be proved similarly. Our (undisplayed) numerical tests indicate that optimal convergence rates in $L^2$ norm can be obtained for $BDM_1$ element, while the proof for it remains open.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The research of the the first author was supported by the Research Grants Council of the Hong Kong Special Administrative Region, China [Project No. CityU 21309522]. The research of the second author was supported by the National Research Foundation of Korea (NRF) grant funded by the Ministry of Science and ICT (NRF-2022R1A2B5B02002481).

Conflict of interest

The authors declare no conflicts of interest.