The incidence of pulmonary tuberculosis in patients with anthracosis

1.   Introduction

Avian influenza is a viral infectious disease induced by type A virus, which can be divided into the low pathogenic avian influenza and highly pathogenic avian influenza ^[1,2]. Both types of viruses commonly occur among wild birds around the world and can infect domestic poultry (such as turkeys, quails, chickens) and other bird species. To date, some avian influenza viruses, such as A (H5N1, H5N6, H7N9) ^[3,4,5,6] have been frequently reported to cross the species barrier, causing severe infections in humans and other mammals, and causing serious problems. For example, Hong Kong first reported 18 human cases (including 6 deaths) of avian influenza A (H5N1) in 1997, which attracted global attentions ^[7]. Since then, avian influenza viruses (such as H7N9, H5N6, etc.) have also been reported to pose a great potential threat to human. For example, H1N1 flu struck the United States and spread to 214 countries and territories, killing nearly 200,000 people in 2009; there are 132 cases of infected H7N9 virus were found, including 37 deaths in 2013; as of December 2019, the global cumulative number of cases of human infection with H5N1 avian influenza arrives 861, including 455 deaths ^[8,9,10]. Epidemiological investigations confirmed that the majority of people infected with H7N9 and H5N6 have had contact with infected poultry ^[11,12]. Avian influenza viruses, such as H7N9, H5N6 and H5N1, have not yet been found to be transmissible between humans, but sporadic outbreaks in human remain a enormous threat to world public health security. Live poultry markets and backyard poultry flocks are two main places of risk major for sporadic outbreaks of avian influenza in human ^[13,14]. It has also been noted that a mass of people infected with the avian influenza viruses has gradually declined after the closure of live poultry markets in many provinces ^[15]. Because of the frequent outbreaks of avian influenza worldwide, we need to have an in-depth understanding of the transmission dynamics of avian influenza and further propose the better control scheme to control its spread.

On the one hand, avian influenza has posed enormous economic pressures on society, mainly including opportunity loss, health-related expenditures and unemployment. On the other hand, the cost of implementing control measures, such as vaccination, treatment and educational campaigns, is also high. Hence, it is an important and meaningful problem to establish optimal control mechanisms of avian influenza with balance of costs and benefits from the epidemiological and social economic viewpoint. To address these issues, many researchers addressed the optimal control problems of avian influenza by introducing lots of control variables and applying the Pontryagin's maximum principle, and proposed the corresponding control strategies (both pharmaceutical and non-pharmaceutical) ^[8,16,17,18]. It should be pointed out that for optimal control, the control variables are obtained by setting the objective function. If the control objective is set as desired number of infected poultry or humans, the optimal control theory is invalid. Adaptive control, as one of the important control methods ^[19,20], allows us to preset the control objective concerning the number of infected poultry or humans ^[21,22]. Besides, different from the optimal control, where all the parameters are assumed to be completely known, the adaptive control can effectively estimate the system parameters through the designed adaptive laws and the control input is determined by the estimated parameters, which can overcome the problem of parameter uncertainties in the common transmission of avian influenza viruses. Since the theory of adaptive control was put forward in the field of engineering, its theoretical development is more and more perfect, and it can accurately deal with the control problems of nonlinear systems in engineering. Unfortunately, there are few studies on adaptive control strategies for biological systems ^[21,22,23], where the nonlinear adaptive control problems were studied for cancer chemotherapy, COVID-19, tuberculosis model, respectively. To our knowledge, for the adaptive control issue of avian influenza model, there is no relevant research results, which is the main motivation of this study.

Poultry is the main source responsible for the transmission of avian influenza virus to humans. Because of the difficulty in tracing and diagnosing infected poultry, control measures should be implemented for both susceptible and infected poultry populations. Especially, slaughter is a reactive control strategy aimed at eliminating infected poultry early in the outbreak, and the specific implementation policies of different regions should be different since slaughter is a high socio-economic losses control measure ^[24]. At the same time, the government departments will disseminate the avian influenza information through the mass media and internet in the early stage of the outbreak, so as to enhance the humans' public health awareness. Based on the avian influenza information disseminated by the government, some populations will change their behavior to reduce contact with the source of infection, which can reduce their risk of contracting avian influenza ^[25,26]. Moreover, timely treatment of infected humans during avian influenza outbreaks can effectively reduce mortality ^[27]. In conclusion, different control measures are of great significance in controlling the practical spread of avian influenza at different stages of avian influenza outbreaks, so it is necessary to explore the existed control effect of mixed control measures (educational campaigns to the susceptible human population, slaughtering to poultry and treatment to infected humans).

For all we know, there is no research result about the adaptive control strategies of avian influenza models. Hence, the main purpose of this paper is to design precise adaptive controllers and obtain the estimation values of unknown parameters according to the designed adaptive laws. The structure of this paper is arranged as follows: the avian influenza model is established and the adaptive control problem is formulated in Section 2. In Section 3, the stability of the closed-loop system under the adaptive laws and the designed controllers is analyzed. In Section 4, the effectiveness of the designed controllers is verified. Finally, a brief summary is presented in Section 5.

2.   Avian influenza model structure analysis

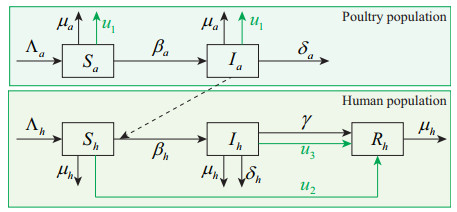
Because poultry is the most important infectious source to human, we only consider the transmission of avian influenza between poultry and human in this paper. The total poultry population $ N_{a}(t) $ is divided into the susceptible poultry $ S_{a}(t) $ and the infected poultry $ I_{a}(t) $, and the total human population $ N_{h}(t) $ is classified into susceptible human $ S_{h}(t) $, infected human $ I_{h}(t) $ and $ R_{h}(t) $, where $ R_h $ represents human with certain immunity to avian influenza virus, which includes physiological immunity (due to infection and then recovery) and psychological immunity (due to changes in their own behavior under educational campaigns). The mathematical model is formulated as follows

where all parameters are assumed non-negative and described as follows: $ \Lambda_{a} $ ($ \Lambda_{h} $) stands for the new recruitment of poultry (human); $ \beta _{a} $ and $ \beta _{h} $ are transmission rates from infectious poultry to susceptible poultry and human; $ \mu_{a} $ ($ \mu_{h} $) and $ \delta_{a} $ ($ \delta_{h} $) are natural and disease-related death rates of poultry (human), respectively; $ \gamma $ is the recovery rate of the infectious human. Control variable $ u_{1}(t) $ represents slaughter to susceptible and infected poultry, $ u_{2}(t) $ represents educational campaigns to susceptible humans and $ u_{3}(t) $ denotes treatment for infected humans. The control variables $ u_1(t) $, $ u_2(t) $ and $ u_3(t) $ are defined to decrease the number of infected poultry and infected humans, respectively. We denote $ S_a(t), I_a(t), S_h(t), I_h(t), R_h(t) $ as $ S_a, I_a, S_h, I_h, R_h $ for convenience. In order to more clearly demonstrate the transmission process of avian influenza described in model (2.1), we also provide a schematic diagram as shown in Figure 1.

Figure 1.  Schematic diagram of the model (2.1) (The green arrows denote the control measures adopted in model (2.1)).

DownLoad: Full-Size Img PowerPoint

The reasons why we set $ u_1(t), u_2(t) $ and $ u_3(t) $ as control variables are summarized as follows:

(i) For human, the infected poultry is the most important spreading source of avian influenza, and in practice, the susceptible and infected poultry may not be effectively distinguished. Thus, in order to quickly eliminate the spreading source, the slaughter to both susceptible and infected poultry is a necessary and effective strategy, which can be described by the control variable $ u_1(t) $.

(ii) When avian influenza spreads in poultry, it is necessary to warn people not to contact infected poultry or contaminated poultry markets through educational campaigns to prevent the spread of avian influenza among human. Therefore, the control variable $ u_2(t) $ is introduced into (2.1).

(iii) Once diagnosed with avian influenza, patients are hospitalized. The specific treatment method, either single or combination treatment, should be applied by the severity of the patient's conditions. Furthermore, the dosage of medicine and length of hospitalization also vary with the severity of the patient's conditions. Thus, the treatment measure is a necessary strategy for the infected humans, which is described by control variable $ u_3(t) $.

The control objective of this paper is to make the number of susceptible and infected poultry (humans) achieve the preset goals with appropriate speed by adopting control measures $ u_1(t), u_2(t) $ and $ u_3(t) $.

3.   Control schemes design and stability analysis

In this section, we will design the schemes of control variables $ u_1(t), u_2(t) $ and $ u_3(t) $ to achieve the control objective, and analyze the stability of model (2.1) under the designed control schemes.

3.1.   Design of adaptive control schemes

Compared with the classical optimal control, it is allowable to adaptive control that we can adjust the values of system states to set the control variables $ u_1(t) $, $ u_2(t) $ and $ u_3(t) $, and the purpose of which is to gradually reduce the number of susceptible poultry, susceptible humans and infected humans to reach the desired values. Additionally, the uncertainty of system parameters is inevitable for the practical avian influenza model. Thus, in order to indicate the robust of the presented control schemes, we also take some difference of parameters into account and analyze the stability of controlled system.

To give the final control schemes of $ u_1(t), u_2(t) $ and $ u_3(t) $, we first formulate the control inputs in avian influenza model (2.1) as follows

Since the terms $ \dot{N}_a, \dot{S}_h $ and $ \dot{I}_h $ in (3.1)–(3.3) cannot be directly obtained, we now replace them by $ x_1 $, $ x_2 $ and $ x_3 $, respectively, and the forms of $ x_1 $, $ x_2 $ and $ x_3 $ will be specified later. Therefore, by rearranging (3.1)–(3.3) in the linearly parameterized forms, we can get

where vectors $ \Psi_1(x_1, S_a, I_a) $, $ \Psi_2(x_2, S_h, I_a) $ and $ \Psi_3(x_3, S_h, I_a, I_h) $ consist of known and measurable functions, and vectors $ \theta_i \, (i = 1, 2, 3) $ include the unknown parameters in model (2.1) and can be estimated by the adaptive laws. Based on (3.1)–(3.3), $ \Psi_i $ and $ \theta_i \, (i = 1, 2, 3) $ can be expressed as follows

Now, the variables $ x_1 $, $ x_2 $ and $ x_3 $ are defined as

where $ \alpha_i > 0 \, (i = 1, 2, 3) $ are the designed parameters, $ N_{ad}, S_{hd} $ and $ I_{hd} $ are the desired values of $ N_a, S_h $ and $ I_h $, respectively, $ \tilde{N}_a = N_a - N_{ad} $, $ \tilde{S}_h = S_h - S_{hd} $ and $ \tilde{I}_h = I_h - I_{hd} $ are defined as the tracking errors related to the desired values $ N_{ad}, S_{hd} $ and $ I_{hd} $, respectively.

Remark 1. The optimal control ^[16] obtains the values of control variables by setting objective function, which cannot preset the number of infected poultry or human as control objective, while for the adaptive control, the values of $ N_a, S_h, I_h $ can converge to the desired values $ N_{ad}, S_{hd}, I_{hd} $, respectively. Thus, we can set the values of $ N_{ad}, S_{hd}, I_{hd} $ such that $ N_a, S_h, I_h $ achieve the given number of infected poultry or human.

Considering uncertainty of parameters in the avian influenza model, the schemes of control variables can be designed as follows

where $ \hat{\theta}_i \, (i = 1, 2, 3) $ are the estimations of vectors $ \theta_i $ with the following forms

From (3.10)–(3.12), we see that if $ N_a, S_h $ or $ I_h $ tends to zero, the values of $ \hat{u}_1(t), \hat{u}_2(t) $ or $ \hat{u}_3(t) $ may tend to infinity. Thus, we modify them as follows

where $ \kappa_1, \kappa_2 $ and $ \kappa_3 $ are small positive constants. For poultry, if $ N_a $ tends to zero, then almost all of poultry has been slaughtered, which means that the control measure $ u_1 $ can be canceled. Thus, the modification for $ \hat{u}_1(t) $ is reasonable. Similarly, the rationality of modifications for $ \hat{u}_2(t) $ and $ \hat{u}_3(t) $ can be analyzed. Since these modifications do not influence on the stability of controlled system, we also adopt (3.10)–(3.12) during stability analysis. The adaptive laws of parameter vectors $ \hat{\theta}_i (i = 1, 2, 3) $ are designed as follows

where positive definite matrices $ \Gamma_i \, (i = 1, 2, 3) $ denote adaptive gain matrices. From the adaptive laws (3.16)–(3.18), we can obtain the estimations of vectors $ \hat{\theta}_1, \hat{\theta}_2 $ and $ \hat{\theta}_3 $, and thus the control inputs $ \hat{u}_1(t), \hat{u}_2(t) $ and $ \hat{u}_3(t) $ can be calculated, which will be used to control the model (2.1) such that the state variables $ N_a, S_h $ and $ I_h $ converge to $ N_{ad}, S_{hd} $ and $ I_{hd} $, respectively.

3.2.   Stability analysis of closed-loop system

In this section, we will investigate the stability of the presented closed-loop system under the designed adaptive control strategy by constructing the appropriate Lyapunov function.

Theorem 1. For the avian influenza model (2.1), the designed control schemes (3.10)–(3.12) and parameter adaptive laws (3.16)–(3.18) can ensure that:

(i) All variables in the presented closed-loop system are bounded;

(ii) $ N_a = S_a+I_a, S_h $ and $ I_h $ asymptotically converge to $ N_{ad}, S_{hd} $ and $ I_{hd} $.

Proof. Consider the following Lyapunov function candidate:

where $ \tilde{N}_a = N_a - N_{ad}, \tilde{S}_h = S_h - S_{hd}, \tilde{I}_h = I_h - I_{hd}, \tilde{\theta}_i = \hat{\theta}_i - \theta_i \, (i = 1, 2, 3) $. Since $ \theta_i $ are constants, we have $ \dot{\tilde{\theta}}_i = \dot{\hat{\theta}}_1 \, (i = 1, 2, 3) $. Therefore, the derivative of $ V $ is calculated as

Substituting (3.10)–(3.12) into (3.19) and rearranging its terms, one has

It then follows from $ \tilde{\theta}_i = \hat{\theta}_i - \theta_i \, (i = 1, 2, 3) $ and (3.4)–(3.9), (3.13)–(3.15) that

Substituting (3.16)–(3.18) into (3.20), the time derivative of the presented Lyapunov function is calculated as

From the inequality (Eq 3.21), we have $ V(\Upsilon(t)) \leq V(\Upsilon(0)) $ with $ \Upsilon = (\tilde{N}_a, \tilde{S}_h, \tilde{I}_a, \tilde{\theta}_1^T, \tilde{\theta}_2^T, \tilde{\theta}_3^T)^T $, which implies the boundedness of $ \tilde{N}_a, \tilde{S}_h, \tilde{I}_a, \tilde{\theta}_1, \tilde{\theta}_2 $ and $ \tilde{\theta}_3 $. Since $ \theta_1, \theta_2 $ and $ \theta_3 $ are constant vectors, $ \hat{\theta}_1, \hat{\theta}_2 $ and $ \hat{\theta}_3 $ are bounded. Besides, it follows from the boundedness of $ N_{ad}, S_{hd} $ and $ I_{hd} $ that $ N_a, S_h $ and $ I_h $ are bounded. From (2.1), $ S_a(t), I_a(t), S_h(t), I_h(t) $ and $ R_h(t) $ are non-negative for any non-negative initial values $ S_a(0), I_a(0), S_h(0), I_h(0) $ and $ R_h(0) $. Thus, $ S_a $ and $ I_a $ are bounded. In addition, from the last three equations of (2.1), we have $ S_h + I_h + R_h \leq \frac{\Lambda_h}{\mu_h} $, so $ R_h $ is also bounded. Hence, all variables in the closed-loop system are bounded.

Now, we show the asymptotic convergence of $ N_a, S_h $ and $ I_h $. The time derivative of $ \dot{V} $ can be calculated as

Since $ S_a(t), I_a(t), S_h(t), I_h(t) $ and $ R_h(t) $ are non-negative and bounded, we obtain from (2.1) that $ \dot{N}_a, \dot{S}_h $ and $ \dot{I}_h $ are bounded, which, together with $ \tilde{N}_a = N_a - N_{ad} $, $ \tilde{S}_h = S_h - S_{hd} $ and $ \tilde{I}_h = I_h - I_{hd} $, imply the boundedness of $ \dot{\tilde{N}}_a, \dot{\tilde{S}}_h $ and $ \dot{\tilde{I}}_h $. Thus, from (3.22), we know that $ \ddot{V} $ is bounded, which means that $ \dot{V} $ is uniformly continuous. By feat of the Barbalat's lemma ^[28], we conclude that the tracking errors $ \tilde{N}_a, \tilde{S}_h $ and $ \tilde{I}_h $ will converge to zero when $ t \to \infty $, i.e., $ N_a \to N_{ad} $, $ S_h \to S_{hd} $ and $ I_h \to I_{ad} $. This completes the proof.

4.   Numerical simulations

This section is devoted to illustrating the effectiveness of the designed controllers. The parameter values of model (2.1) are presented in Table 1, and the initial value is $ (S_a(0), I_a(0), S_h(0), I_h(0), R_h(0)) = (3,363,000,100, 52,000, 10, 1) $. The designed parameters are chosen as: $ \kappa_1 = \kappa_2 = \kappa_3 = 1 $, $ \alpha_1 = 310, \alpha_2 = 23.5, \alpha_3 = 20 $ and

Table 1.  The parameter values of model (2.1).

Parameter	Value	Source of data
$ \Lambda_{a} $	1000/245 day$ ^{-1} $	[8,29]
$ \beta_{a} $	$ 8.1\times 10^{-6} $ day$ ^{-1} $	Assumed
$ \mu_{a} $	$ 1/245 $ day$ ^{-1} $	[8,29]
$ \delta_{a} $	$ 6/400 $ day$ ^{-1} $	Assumed
$ \Lambda_{h} $	$ 2000/36,500 $ day$ ^{-1} $	[8,29]
$ \beta_{h} $	$ 2\times 10^{-9} $ day$ ^{-1} $	[8,29]
$ \mu_{h} $	$ 5.48\times 10^{-5} $ day$ ^{-1} $	[8,30]
$ \delta_{h} $	$ 0.001 $ day$ ^{-1} $	[8,30]
$ \gamma $	$ 0.1 $ day$ ^{-1} $	[8,30]

---

 | Show Table

DownLoad: CSV

The minimum eigenvalues of $ \Gamma_1, \Gamma_2 $ and $ \Gamma_3 $ are $ 0.8760, 1.7992 $ and $ 0.9693 $, respectively. Thus, $ \Gamma_1, \Gamma_2 $ and $ \Gamma_3 $ are positive definite matrices, which satisfy the condition of Theorem 3.1. The desired values are selected as

where $ a_1 = 1500, a_2 = 0.6 $, $ b_1 = 25,000, b_2 = 0.01 $, $ \tau = 5, r = 0.6 $.

Remark 2. The forms of desired values $ N_{ad} $, $ S_{hd} $ and $ I_{hd} $ are selected based on the practical requirements. In fact, for $ N_{ad} $ ($ S_{hd} $) (they have similar forms):

(i) $ a_1 $ ($ b_1 $) represents the finally desired value of total poultry population $ N_a $ (susceptible human $ S_h $);

(ii) since the slaughtering to poultry and educational campaigns to human can not work immediately, we introduce the terms $ e^{-a_2 t} $ and $ e^{-b_2 t} $ to describe the process of the number of poultry and susceptible human falling from the initial value to the finally desired values, where $ a_2 $ and $ b_2 $ denote the descending rates.

In addition, $ r $ and $ \tau $ denote the treatment efficiency and treatment duration for infected human ($ I_{hd} $), respectively. Meanwhile, the number of infected humans needing treatment is related to the number of infected people from $ t - \tau $ to $ t $ and the treatment efficiency, so the form of $ I_{hd} $ can be obtained. It is worth noting that the above mentioned parameters $ a_1, a_2, b_1, b_2, \tau $ and $ r $ can be adjusted according to the cost of epidemic prevention and control.

Example 1. The effects of different control combination.

In order to reveal the effect of each control variable, consider the following eight control combinations: Case A1, $ u_1 = u_2 = u_3 = 0 $; Case A2, $ u_1 \neq 0, u_2 = u_3 = 0 $; Case A3, $ u_2 \neq 0, u_1 = u_3 = 0 $; Case A4, $ u_1 = u_2 = 0, u_3 \neq 0 $; Case A5, $ u_1, u_2 \neq 0, u_3 = 0 $; Case A6, $ u_1, u_3 \neq 0, u_2 = 0 $; Case A7, $ u_1 = 0, u_2, u_3 \neq 0 $; Case A8, $ u_1, u_2, u_3 \neq 0 $. Here, $ u_i \neq 0 $ ($ i = 1, 2 $ or $ 3 $) denotes that the corresponding control measure is adopted instead of $ u_i(t) \neq 0 $ for all $ t \geq 0 $. The simulation results are shown in Figures 2–9.

Figure 2.  The trajectories of $ S_a(t) $.

DownLoad: Full-Size Img PowerPoint

Figure 3.  The trajectories of $ I_a(t) $.

DownLoad: Full-Size Img PowerPoint

Figure 4.  The trajectories of $ S_h(t) $.

DownLoad: Full-Size Img PowerPoint

Figure 5.  The trajectories of $ I_h(t) $.

DownLoad: Full-Size Img PowerPoint

Figure 6.  The trajectories of $ R_h(t) $.

DownLoad: Full-Size Img PowerPoint

Figure 7.  The trajectories of $ u_1(t) $.

DownLoad: Full-Size Img PowerPoint

Figure 8.  The trajectories of $ u_2(t) $.

DownLoad: Full-Size Img PowerPoint

Figure 9.  The trajectories of $ u_3(t) $.

DownLoad: Full-Size Img PowerPoint

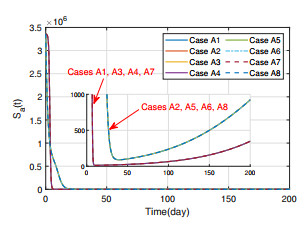
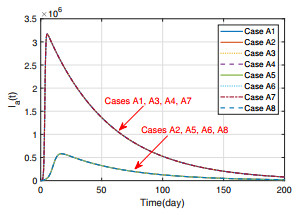
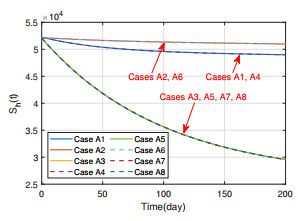
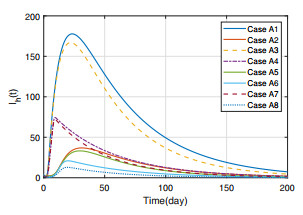
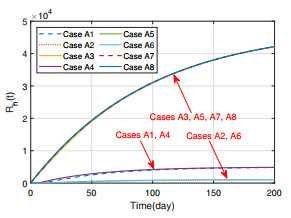
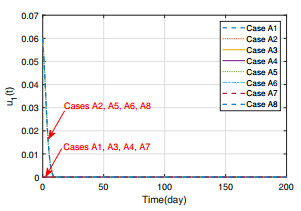
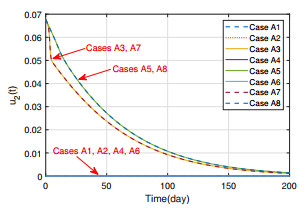
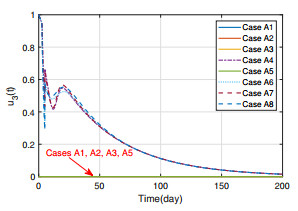
Figures 2 and 3 present the trajectories of $ S_a(t) $ and $ I_a(t) $ under different control combinations, from which we see that once the control measure $ u_1(t) $ is adopted (i.e., Cases A2, A5, A6 and A8), the infected poultry $ I_{a}(t) $ will decrease significantly. Since the control measures $ u_2(t) $ and $ u_3(t) $ only act on the human population, they cannot influence the poultry population. From Figure 4, we can see the effect of control measure $ u_2(t) $. In Cases A1, A2, A4 and A6, $ u_2(t) $ is in absence, so the trajectories of susceptible human $ S_{h}(t) $ drop slowly, while in other cases, the trajectories of $ S_h(t) $ drop rapidly, since some people move into $ R_h $ through educational campaigns. Figure 5 gives the trajectories of $ I_h(t) $, which shows the effect of each control combination more clearly. When all of control measures are in absence (i.e., Case A1), the peak value of infected human $ I_{h}(t) $ is more than $ 150 $, while the peak value of $ I_a(t) $ is not more than $ 20 $ when all control measures are adopted (i.e., Case A8), which shows that the adopted control measures have a significant impact on the spread of the avian influenza. Besides, in Figure 5, the peak values of $ I_h(t) $ in Case A2 (A5, A6, A8), where $ u_1(t) \neq 0 $, are less than that in Case A1 (A3, A4, A7). This, together with Figure 3, indicate that slaughter (i.e., the measure $ u_1(t) $) to poultry population can suppress the outbreak of avian influenza in both poultry and human populations, which is because poultry population is the critical source of avian influenza virus. Figure 6 gives the trajectories of $ R_h(t) $, which also shows that the control measures can raise the individual number of $ R_{h}(t) $. From (3.10)–(3.12), we know that the values of $ u_1(t), u_2(t) $ and $ u_3(t) $ may be negative, which is unrealistic. Thus, when $ u_i(t) \, (i = 1, 2, 3) $ are negative, we take their values as zero, and the trajectories of them are shown in Figures 7–9.

Remark 3. As stated in Section 2, $ u_1(t) $ represents slaughter rate to susceptible and infected poultry. Therefore, the value of $ u_1(t) $ can be determined according to the slaughtering range, for example, $ u_1(t) = 0.05 $ means the epidemic can be controlled if 5% of the total number of poultry are slaughtered, which is exactly the total number of poultry in the farm where the first case occurred. $ u_2(t) $ indicates the frequency of educational campaigns to susceptible humans through television, internet, loudspeakers and other medias. Thus, if we take the frequency of epidemic information broadcast by the loudspeaker (from 6 am to 10 pm (960 minutes)) as the values of $ u_2(t) $, for example, $ u_2(t) = 0.008 $ indicates that the message is broadcasted every 8 minutes. The values of $ u_3(t) $ depend on the treatment plan the doctor takes. For example, $ u_3(t) = 1 $ indicates that the effective rate of treatment is 100%, which is because doctors take antiviral and traditional Chinese medicine treatment in order to control the disease in a short time in the early stage of treatment (1–3 days). $ u_3(t) = 0.8 $ means that the effective rate of traditional Chinese medicine treatment is 80%, which can be determined by the way of taking Chinese medicine, for example, from one dose a day to one dose every two days to one dose every three days.

Example 2. The effects of uncertainty parameters.

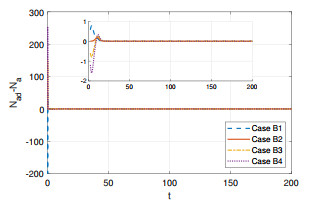
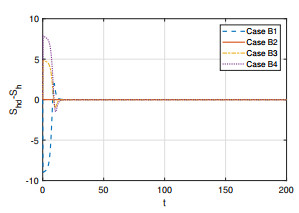
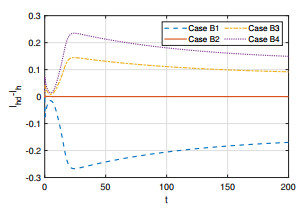
All the parameters in Example 1 are assumed to be completely known, which are used to determine the initial values of adaptive laws of parameter vectors in (3.16)–(3.18). However, in practice, there are some errors between the obtained parameters and true ones. Therefore, we consider the tracking performance when the parameters have some deviations, which is reflected by the initial value of the adaptive laws, namely, the initial value is equal to the true value of the parameter plus a certain deviation. Let $ \hat{\theta}_i(0) = (1 + \eta) \theta_i \, (i = 1, 2, 3) $ and consider the following four cases: Case B1, $ \eta = -0.3 $; Case B2, $ \eta = 0.0 $ (i.e., No deviation); Case B3, $ \eta = 0.3 $; Case B4, $ \eta = 0.6 $. The tracking errors in each case are shown in Figures 10–12, from which we see that the tracking error in Case B2 is closest to 0, because the true values of $ \theta_i \, (i = 1, 2, 3) $ are used. Although there exist some errors in Cases B1, B3 and B4, compared with the population size of poultry and human, the errors are very small, which are tolerable. This also indicates the robustness of the proposed controllers.

Figure 10.  The trajectories of $ N_{ad} - N_a $.

DownLoad: Full-Size Img PowerPoint

Figure 11.  The trajectories of $ S_{hd} - S_h $.

DownLoad: Full-Size Img PowerPoint

Figure 12.  The trajectories of $ I_{hd} - I_h $.

DownLoad: Full-Size Img PowerPoint

5.   Concluding remarks

On account of slaughtering to poultry, educational campaigns to susceptible human and treatment to the infected human, we investigate the adaptive control problem of avian influenza model in this paper. First, the designed controllers can achieve the preset control goal and ensure the stability of the achieved closed-loop system. Then, the effectiveness and robustness of the designed controllers are verified by several numerical examples. The numerical results indicate that comprehensive control strategies are essential to quickly and effectively curb the spreading of avian influenza in both human and poultry population, and the slaughter to poultry population is critical to eliminate the source of avian influenza virus. At present, there are few research achievements on adaptive control of biological models, so this paper only studies adaptive control of ordinary differential avian influenza model. However, many other factors (such as time delay, random environmental noise, etc.) also affect the spread of avian influenza, so how to investigate the adaptive control of delayed avian influenza model and stochastic avian influenza model will be carried put in the future research perspectives.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the Natural Science Foundation of China (12201330 and 12161068).

Conflict of interest

The authors declare there is no conflicts of interest.