An adaptive type-2 fuzzy sliding mode tracking controller for a robotic manipulator

1.   Introduction

The industrial manipulator is a multivariate nonlinear system and it has various uncertainties in the dynamics, which deteriorate the performance and stability of the system, such as external disturbances, nonlinear friction, height time variation and payload variation. Frequent and uncertain disturbances will reduce the tracking accuracy of each joint controller of the manipulator. Repetitive motions will accumulate errors and lead to changes in the stability of the industrial manipulator system. Therefore, improving the trajectory tracking accuracy and maintaining the excellent dynamic performance of the manipulator are important indicators for industrial development.

There are several conventional and effective control strategies for nonlinear uncertain systems, including SMC, robust control and adaptive control ^[1,2,3]. In addition, Azizi ^[4] proposed an artificial neural network structure to simulate the behavior of genetic algorithm for industrial robot parameter optimization. In reference ^[5], fuzzy controller and sliding mode controller are proposed to reduce the external vibration and they are also widely used in motor servo control ^[6]. For the robustness of fuzzy SMC, Rosales et al. ^[7] deduced the calculation of phase margin and gain margin in detail. For uncertain parameters systems, a method combining the finite time robust tracking theory with the composite nonlinear feedback method is proposed in reference ^[8]. The control law of SMC can drive the system into the sliding mode surface, which has strong robustness to the changes of system parameters and disturbances ^[9,10], it has been widely used owing to its attractive features of low sensitivity to uncertainties, fast response and easy realization. In ^[11], a new generalized sliding mode observer is proposed to suppress actuator failures in a class of Markovian jump systems by synthesizing discontinuous inputs. Van ^[12] proposed a novel high-order FTSM combined with adaptive fuzzy neural network to solve the design uncertainty in the accurate dynamic model. Then it is applied to uncertain and nonlinear third-order systems with external disturbances ^[13]. In order to solve the chattering problem of nonlinear systems with positive function boundary, Ding et al. ^[14] proposed two second-order SMC algorithms, which are discontinuous and quasi continuous respectively. In paper ^[15], a higher order sliding mode is proposed, which has the advantages of easy implementation, strong robustness and early selection of time convergence in uncertain nonlinear systems. In ^[16], a non-singular terminal sliding mode manifold was introduced to optimize the performance of the speed loop of the PMSM servo system. In reference ^[17], a novel SMC method is proposed to control cascaded underactuated systems with external disturbances. Liu et al. ^[18] designed an adaptive gain second-order sliding mode observer, which is robust to disturbance with unknown boundary. In order to keep the power factor of full bridge boost power converter stable, reference ^[19] has proposed a Super-twisting sliding mode observer. Bao et al. ^[20] designed a new control strategy combining fuzzy system and sliding mode controller to improve the stability of service robot and realize high-precision control. It can be seen that for the motion control system, a single control method is difficult to meet the complex working conditions, and the existing controllers are designed based on a mixture of multiple control methods, so that the advantages of various methods can be met simultaneously to a certain extent.

The SMC is an effective method with simple design and high robustness for complex uncertain perturbations present in industrial manipulator motion controllers. Existing SMC research mainly focuses on the linear sliding surface. When time is close to infinity, the state exponent on the sliding surface converges to the origin. Model can maintain excellent performance under uncertain disturbances that is one of important characteristics of SMC, so it has been widely used in nonlinear systems. In ^[21], a radial basis function neural network for nonlinear dynamics of manipulator is mentioned. In ^[22], it is not always practical to assume the availability of manual mechanics for industrial robotic manipulator. Therefore, an adaptive observer based on neural network is designed. In ^[23,24], an adaptive sliding mode control scheme using time delay estimation is proposed to suppress the disturbance and make the adaptive law converge rapidly. Recently, an adaptive fuzzy observer is proposed and combined with sliding mode control to apply to the control system of a new one degree of freedom micro manipulator ^[25]. The adaptive fuzzy sliding mode control has also been applied in manipulator control system recently. Reference ^[26] uses fuzzy logic component and adaptive reaching law to approximate the uncertainty in micro/nano manipulator motion system and compensate the influence of nonlinear terms. Reference ^[27] has designed an improved adaptive integral sliding mode controller, the noise sensitive switching action and adaptive gain dynamics are reduced by time delay estimation in this reference. In order to estimate the law of unknown torque, reference ^[28] proposed two kinds of sliding mode observer to determine the trajectory control law. A robust control method with sliding mode nonlinear disturbance observer is designed by Al-Jodah et al. ^[29]. This method can compensate the motion error and track the complex trajectory well. The bottleneck of the application of SMC in industrial manipulators is the threat to motion accuracy and safety caused by the chattering of the controller. The complex filters and observers in the existing research are too computationally intensive to be widely used in low-cost industrial manipulators.

With the diversification of robotic operations, the complexity of motion control has led to the design of more and more controllers based on artificial intelligence algorithms. Latifinavid and Azizi ^[30,31] proposed the design of robotic motion controllers using image processing and fuzzy logic to improve robot motion accuracy and anti-disturbance. This method compensates for the unknown external disturbance through the on-line adaptive mechanism, and is applied to the attitude tracking control system of flexible spacecraft to eliminate the influence of actuator nonlinearity and quantization error ^[32]. Based on a new event triggered sliding mode control scheme, ^[33] optimizes the sliding mode control scheme of fuzzy system with communication delay and determines the control content by event triggered method to solve the control problem of aperiodic sampling. Liu et al. ^[34] proposed a robust fuzzy sliding mode controller to improve the control accuracy and the robustness of the robotic manipulator. In reference ^[35], an adaptive controller is used to estimate the uncertain disturbance and an adaptive sliding mode controller is designed to maintain the attitude stability of the spacecraft system without prior inertia torque. In reference ^[36], a sliding mode controller based on TS fuzzy model considering the uncertainty of motor parameters and unknown external noise is proposed, and the application effect of this method in actual motor driver is demonstrated. Qu et al. ^[37] proposed a method combining active disturbance rejection control and adaptive fuzzy SMC, which is applied to the photoelectric platform to improve the target tracking ability. However, when the uncertainties and nonlinearities of nonlinear systems such as industrial manipulator appear frequently, the parameters of sliding mode control will fluctuate in the membership function, and the parameters obtained by fuzzy logic will not be suitable for the controlled object, which is the motivation of this paper.

In general, the characteristics of SMC are very suitable for nonlinear systems, but in some complex systems, the conventional SMC is difficult to operate perfectly. First, due to the complexity of applications, there are strong coupling nonlinear and uncertain dynamics in physical systems ^[38], and even it is difficult to obtain a complete mathematical model ^[39]. Second, the advanced sliding mode controller is applied in the case of model uncertainty and strong robustness to external disturbances. In order to keep the control system running on the sliding mode surface, the input of the controller changes instantaneously. The discontinuity of control action will become the cause of vibration ^[40]. Finally, in practical application, the controller may output unnecessary control signals when the uncertainty of the system is strong, which may cause damage to system components, such as actuators ^[41]. Thus, the vibration has to be eliminated or alleviated as much as possible to improve the accuracy of repeated positioning and protect the actuator. In summary, the application of sliding mode control in nonlinear systems gives the system favorable robustness, but the application on motion control systems is similar to industrial manipulators and presupposes that chattering must be eliminated or mitigated as much as possible to ensure the accuracy of end-repeat positioning and to protect the actuator. The low-pass filter with adaptive type-2 fuzzy sliding mode controller and adaptive boundary layer adjustment method proposed in this paper can provide solutions to the above-mentioned problems in this field and can provide solutions for related product development and controller design.

The contributions of this paper are as follows.

● A type-2 fuzzy sliding-mode controller is proposed for the uncertain disturbance problem in the industrial manipulator control system, which further improves the system robustness and makes the control surface of the controller smoother when it is close to the steady state.

● The adaptive boundary of the SMC is introduced to reduce the trajectory error caused by the SMC chattering during the motion of the manipulator control system.

● The feasibility of the proposed controller in three scenarios is verified by numerical simulation. Further, the simulation model is constructed according to the physical characteristics of the manipulator, and the effectiveness and advantages of the control method proposed in this paper are illustrated by comparing with other control methods in the same field.

2.   Manipulator model derivation

Based on the derivation of manipulator in reference ^[42]. In this paper, a 2-DOF manipulator model is established, in which the posture and dynamics of the manipulator are described by matrix method. The dynamic model of the manipulator system is established by Lagrange method, and the characteristics of the dynamic model are analysed.

In this paper, the following assumptions are put forward for the model of industrial robotic manipulator:

● The position of the base is fixed during the movement of the manipulator;

● According to the platform coordinates and trajectory coordinates to determine the model parameters, but they can't be defined with coordinates of the system;

● The vibration of servo motor caused by torque fluctuation in the joint of manipulator is ignored.

For the conventional industrial manipulator systems, they are often simplified as dynamic models to intuitively and simply explain the characteristics of the system ^[43].

In Eq (1), $\dot{\theta }\left(t\right)$ means angular velocity of the manipulator joint and $\ddot{\theta }\left(t\right)$ means angular acceleration of the manipulator joint; $\mathbf{M}\left(\theta \left(t\right)\right)$ means the positive definite inertia matrix of the manipulator; $\mathbf{C}\left(\theta \left(t\right), \dot{\theta }\left(t\right)\right)$ stands for the manipulator's Coriolis force and centrifugal force matrix; $\mathbf{g}\left(\theta \left(t\right)\right)$ stands for the manipulator's the gravity matrix; $\tau \left(t\right)$ stands for the manipulator joint's control torque.

In addition, the industrial robotic manipulator is used in many complicated application scenarios, and there are many uncertain disturbances without controlling, including external interference and friction as well as parameter changing. For instance, production process, assembly error, joint friction, workpiece wear and so on will lead that design tolerance exists in the manipulator parts; in the complete motion cycle, the difference of load and position will affect the centre of gravity that results some parameters of the manipulator is unstable; the manipulator will have elastic deformation due to the influence of load and inertia. A plenty of external disturbances also exist in the working process. These factors make it difficult for the manipulator to track the given trajectory. Therefore, this paper mainly considers that lateral and longitudinal vibration produces external disturbance characteristics, and there are two kinds total. Uncertainty factors in the system is also included in the dynamic model of the manipulator. We can build a mathematical model as follows.

where, $\mathbf{f}\left(\dot{\theta }\left(t\right)\right)$ means the friction matrix; ${\boldsymbol{\tau }}_{d}\left(t\right)$ means the external disturbances without controlling.

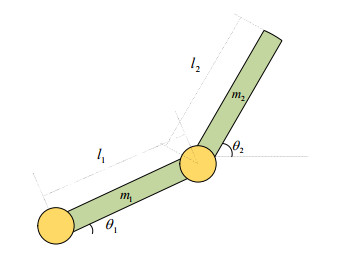
As Figure 1 shows, ${l}_{1}$ and ${l}_{2}$ are the length of the manipulator links, ${m}_{1}$ and ${m}_{2}$ are the mass of the manipulator links. Therefore, Lagrange method describes equation for dynamic model of 2-DOF manipulator can be expressed as:

3.   Controller design

3.1.   Design of low-pass filter

In this part, according to the characteristics of the external disturbance and the vibration of the sliding mode controller on the sliding mode surface, the basic structure of the low-pass filter is as follows.

where, $\lambda$ > 0. The ideal position instruction is ${\theta }_{d}\left(t\right)$ and the position tracking precision is:

where $e$ means tracking error and ${\theta }_{r}$ means additional signal, and $\varLambda$ stands for the definite matrix, so the sliding mode variable function can be described below equation:

It can be obtained by formulae (Eqs (2), (6) and (7)).

The main two characters in the closed-loop system, the stability and transient performance, get optimized due to the function of the first and second terms in Eq (10). Compensating the tracking error produced by motion and other dynamic turbulence is the main purpose and improve the filtering effect in industrial robotic manipulator system. The last term is to introduce sliding mode and keep the function of sliding mode control in the whole process, so that when the system reaches the sliding surface, the manipulator system is absolutely robust to any disturbance. Thus, the robustness of the manipulator system is improved.

The SMC is divided into two stages: one is to make the industrial robot system converge from the initial state to the specified sliding surface, and the other is to reach the system equilibrium point on the sliding surface. Due to the influence of parameter variation and disturbance, the whole function parameters how to be estimated effectively should seriously consider, so fuzzy control is needed. Therefore, fuzzy logic control algorithm plays a significant role for reducing chattering phenomenon and estimating the whole conversion gain ${k}_{\mu }$.

3.2.   Adaptive control law design

The control law is designed as follows because of disturbance characteristics of the manipulator control system:

where, the meaning of $\boldsymbol{J}$ is Jacobian matrix, which can also be written:

where, ${\boldsymbol{J}}_{x}$ represents the forward Jacobian matrix of the manipulator and ${\boldsymbol{J}}_{q}$ represents the reverse Jacobian matrix of the manipulator. It can be concluded as follows:

where, $\left\{\begin{array}{l}{a}_{i1} = x+Rcos{\varphi }_{i}-{L}_{i}cos{\varphi }_{i}cos{\theta }_{i}\\ {a}_{i2} = y+Rsin{\varphi }_{i}-{L}_{1}sin{\varphi }_{i}cos{\theta }_{i}\\ {m}_{i} = -{a}_{i1}{L}_{1}cos{\varphi }_{i}sin{\theta }_{i}-{a}_{i2}sin{\varphi }_{i}sin{\theta }_{i}\end{array}\right.$.

Considering the characteristics of the manipulator closed-loop system with random disturbance and dynamic uncertainty, in order to ensure the asymptotic robust stability of the control system, we propose the following equations,

According to the Eqs (12) and (15), we can deduce the following:

Defined the associated state as follows, only ${k}_{\mu }$ is considered, and we can obtain ${k}_{v}$ by the same token:

It can be obtained:

Use fuzzy Controller ${\widehat{k}}_{\mu }$ to estimate ${k}_{\mu }$ :

Many studies use other switching functions instead of $\mathrm{s}\mathrm{g}\mathrm{n}\left(\bullet \right)$ to reduce the influence of chattering in sliding mode control, such as saturation function, hyperbolic tangent function, etc. However, in practical applications, SMC is accompanied by chattering and changing the switching function cannot completely eliminate chattering, so the switching function is not improved in the controller in this paper, Instead, the following method of designing adaptive boundary layer is adopted to reduce the influence of chattering without affecting the control signal.

3.3.   Boundary layer

In the design of SMC control law, the tracking accuracy of the system is closely related to the boundary layer thickness. In addition, when the controller fails or the output signal is unstable, the appropriate boundary layer thickness plays an important role in maintaining the stability of the system. When the uncertainty and disturbance of the system are serious, due to the overestimation of the adaptive control parameters, only using the conventional adaptive control strategy mentioned above may not maintain the stability of the system. For this case, the general solution is to expand the boundary layer thickness sufficiently, but the trajectory tracking accuracy will be sacrificed. Therefore, this paper designs an adaptive method to adjust the boundary layer thickness and keep the controller signal smooth ^[44]. Compared with the boundary layer thickness determined by experience and test, the dynamic adjustment method of boundary layer thickness in this paper keeps a proper balance between system stability and tracking accuracy.

Denoting ${\widehat{\boldsymbol{k}}}_{\boldsymbol{\mu }}\left({s}_{i}, \boldsymbol{q}\right) = {\widehat{\boldsymbol{q}}}_{\gamma i}^{T}{\xi }_{\gamma i}\left({s}_{i}\right)$, the adaptive law of boundary layer thickness is as below:

where $\boldsymbol{A}$ and $\boldsymbol{B}$ are diagonal matrices containing positive design parameters, and $\psi \left(0\right) = {\boldsymbol{B}}^{-1}\boldsymbol{A}{k}_{\mu }$.

As mentioned in this paper, the main purpose of the designed adaptive boundary layer is to avoid overestimation of adaptive parameters when the system is under strong interference. The initial value of $\psi$ is chosen as $\psi \left(0\right) = {\boldsymbol{B}}^{-1}\boldsymbol{A}{k}_{\mu }$, which is greater than zero and $\dot{\psi } = 0$. When the output signal of the controller has obvious fault, ${k}_{\mu }$ will be increased to compensate the faults, which can be denoted as ${k}_{\mu }^{\mathrm{\text{'}}}$ with ${k}_{\mu }^{\mathrm{\text{'}}} > {k}_{\mu } > 0$. In the equilibrium state, the conventional formula for calculating the boundary layer thickness is $\psi \left(0\right) = {\boldsymbol{B}}^{-1}\boldsymbol{A}{k}_{\mu }$. In this case, substituting ${k}_{\mu }^{\mathrm{\text{'}}}$ into Eq (19) leads to:

Therefore, the boundary layer is updated to: $\psi = {\boldsymbol{B}}^{-1}\boldsymbol{A}{k}_{\mu }^{\mathrm{\text{'}}} > 0$.

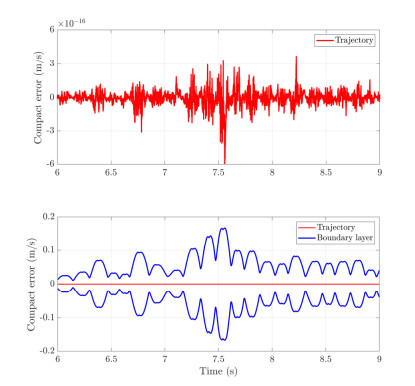
This paper intercepts the more serious error signal of the controller, as shown in Figure 2. After adding the boundary layer according to the method in this paper, the error signal is reduced and the system stability and tracking accuracy are ensured.

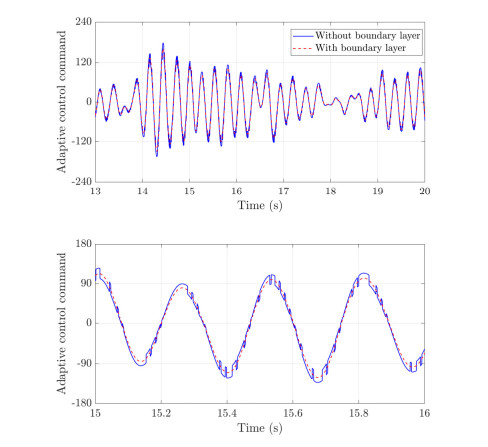
Through the scheme of adaptive boundary layer law, the trigger condition of adaptive law is that the sliding variable leaves the specified boundary layer, and the sliding variable back drive by controller into the boundary layer to ensure the trajectory tracking accuracy. On the contrary, if the sliding variable runs or stays in the boundary layer where the tracking performance is allowed, the adaptive law will not start. Compared with the existing adaptive SMC scheme, the adaptive law proposed in this paper can simply avoid the error of the controller signal ^[45,46,47]. If the sliding variable is used to construct the adaptive law to control the smoothness of the output signal, it is difficult to ensure the adaptive convergence. In addition, as shown in Figure 3, the output signal of the controller using the dynamic boundary layer is smoother, which significantly improves the disturbance suppression ability of the control system. The position tracking accuracy is effectively improved and is conducive to the industrial manipulator system works in stable operation condition. But the adaptive law of this dynamic boundary layer is simplified, which is easy to reduce the loss of some control signals when buffeting. Using neural network to design the adaptive law can solve this problem to a certain extent, but the computational complexity is high. Therefore, this paper proposes the following scheme to design the dynamic boundary layer adaptive law by using type-2 fuzzy logic.

3.4.   Type-2 fuzzy logic control model

The uncertainty of model in nonlinear system is main factor to be solved by fuzzy logic control, adopts logic reasoning, formulates and follows relevant logic rules to draw accurate conclusions according to some imprecise conditions. Based on the type-2 fuzzy logic model proposed by Mendal ^[48], this paper optimizes the type-2 fuzzy logic that is useful for decreasing the chattering phenomenon produced by sliding mode variable structure control. According to the simulation results, we can see that the performance of the system has been improved, especially in the aspect of tracking accuracy.

Based on the relevant analysis, a fuzzy logic control system is designed in this paper, with ${s}_{i}$ and ${\dot{s}}_{i}$ as inputs in the whole type-2 fuzzy logic control, ${\gamma }_{i}$ as an output. The definition of fuzzy control rules is shown in Table 1, and the membership function is shown in Figures 4 and 5.

There are three parts in the fuzzy system, including fuzzy, fuzzy inference machine and correction method of type center of gravity, we can get below fuzzy output ${\boldsymbol{q}}_{\gamma i}$ as follows:

where, ${\boldsymbol{q}}_{\gamma i}^{T}$ is the adjusted parameter and expressed as following formulas:

Below formulas is got with the errors mentioned,

where, $\varepsilon$ is a bounded vector.

The definition of $\beta \text{ = }\text{}a+b‖\dot{\theta }‖+c+\varepsilon$ as an adaptive boundary, can also be written in the following form:

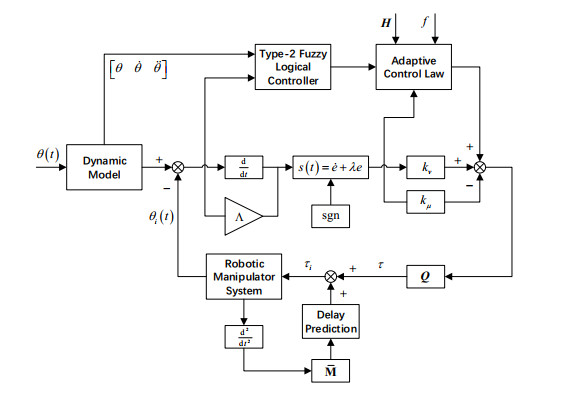
The $\boldsymbol{Q}$ is a vector function of the joint velocity $\dot{\theta }$, and the $\boldsymbol{\varphi }$ is a parameter vector (in Figure 6).

In order to achieve the purpose of the desired trajectory and sub-task tracking, we can write the input torque as follows:

In this paper, the design of adaptive type-2 fuzzy sliding mode controller is studied from the perspective of controller design method. Thus, the inevitable severe jitter problem in the application of sliding mode control of manipulator is solved. So far, there is little research on the controller design of adaptive interval type-2 fuzzy sliding mode control for nonlinear systems. The research content of this paper is very important for the application of nonlinear systems. From the perspective of a nonlinear system, the design results of the controller are obtained by various methods. Compared with previous work, our work combines adaptive interval type-2 fuzzy logic. Then, according to Lyapunov method, it is proved that the controller design method is effective.

3.5.   Stability analysis

In this section, we will use the popular Lyapunov stability technology to prove the stability of the controller proposed in this paper.

Similarly, the derivative of the Lyapunov stability function of the system can be written as:

According to the characteristics of low-pass filter, we will consider the following Lyapunov function to analyze the Lyapunov stability of low-pass filter:

We make the differential operation for $V$, the formula is changed to as follow,

According to the characteristics of the adaptive control law proposed in this paper, we will prove the stability of the adaptive control law through the following Lyapunov functions:

where ${\stackrel{~}{\boldsymbol{q}}}_{\gamma i} = \left|{s}_{i}\right|{\xi }_{\gamma i}\left({s}_{i}\right)$, make the differential operation for $V$, the formula is changed to as follow,

The state of the fuzzy closed-loop system proposed in this paper will reach the sliding mode surface in a finite time through the fuzzy dynamic sliding mode controller. On the premise of considering the error boundary, by solving the time derivative of the path along the fuzzy closed-loop system, we can get:

where ${\psi }_{l}$ is the minimum approximation error, and ${\psi }_{u}$, ${\psi }_{l}$ are assumed to be bounded.

In order to ensure that ${V}_{2}\le 0$, ${V}_{2}\left(0\right)$ is bounded, ${V}_{3}$ is not incremented and bounded, we can infer the boundedness and convergence from the Barbarat lemma and conclude that the proposed adaptive law meets condition defined in the Lyapunov stability.

Below equation can be obtained though Eqs (28), (30) and (32),

Since ${\stackrel{~}{f}}_{e}$ is bounded, we can express the conversion gain of SMC as follows:

Bringing the Eq (35) into the Eq (34), we can obtain:

In terms of stability, the input-output analysis allows us to analyze the stability of a given system without knowing the internal state. This means that the norm bounded input inevitably leads to the norm bounded output. Because the system dynamic state information is not involved in the tuning process, it is suitable for the proposed AT2FSMC method. The proposed AT2FSMC method ensures the stability of closed-loop system of industrial manipulator, that is, the stability of bounded input and bounded output. This completes the proof. In conclusion, it is proved that the sliding variable and the 2-DOF manipulator make the tracking errors consistent and ultimately bounded. Therefore, we obtain conclusion that the stability in whole manipulator control system is strong.

4.   Simulation and discussion

The simulation is run using MATLAB 2020a on a personal computer with Intel Core, CPU i5-6500 @ 3.20 GHz, 16 GB RAM. The Simscape Multibody module was used in MATLAB to model the mechanical structure of industrial robotic manipulators, and industrial task scenarios and motion designs were established in V-REP (CoppeliaSim).

As described in this paper, the model of industrial manipulator is derived, and the effectiveness of the proposed control algorithm is analysed. The dynamic equations used in the simulation are as follows:

where, $d$ means the external disturbance. The simulation parameters of the industrial manipulator are shown in Table 2.

For the sake of implementing the tracking control in the joint space, based on the content described in Section 2, the expected trajectory and the initial joint angle of the joint are obtained by the welding examples of industrial components in Robotics System Toolbox.

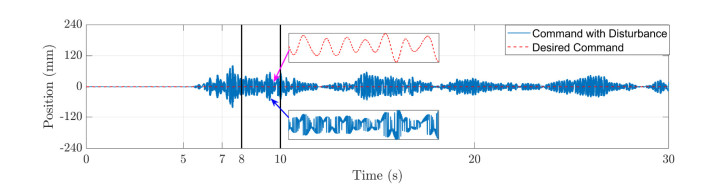
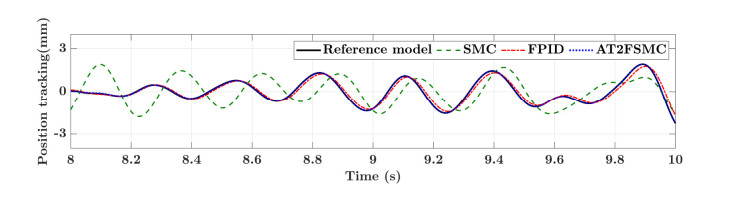
As shown in Figure 7, the red dotted line is the desired trajectory of the end of the manipulator in the case 1 of ${a}_{1}$, and the blue solid line is the output result of the sliding mode controller without using the dynamic boundary layer. In the subsequent simulation part, we will intercept the data of 8-10 seconds to compare the performance of various methods.

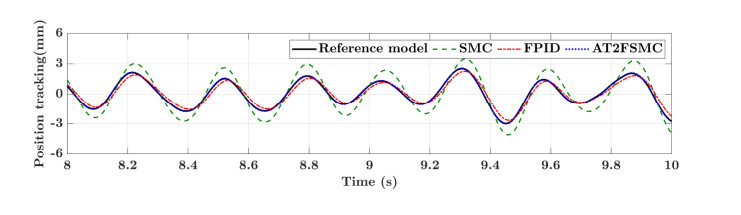
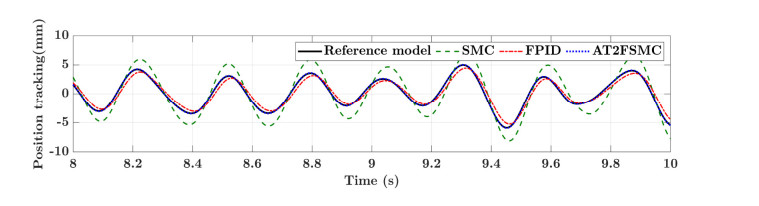
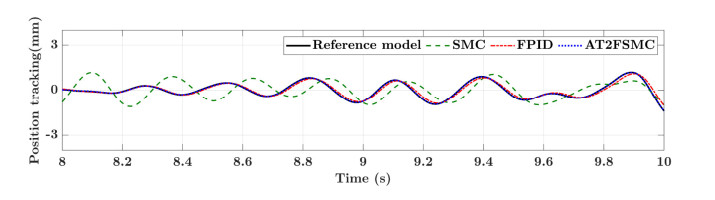
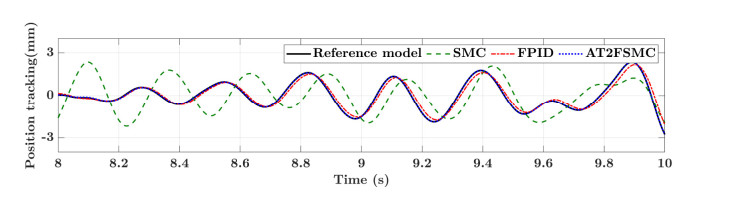
The adaptive type-2 fuzzy sliding mode controller proposed in this paper is used for trajectory tracking of the industrial two-joint manipulator. The simulation results are demonstrated in Figures 8-10. Among them, Figures 11-13 display the position tracking when the external disturbance $d = \mathrm{asin}\left(\pi t\right)$. Figures 8-10 display the position tracking of when the external disturbance ${d}_{x} = \mathrm{asin}\left(\pi t\right)$, ${d}_{y} = \mathrm{asin}\left(2\pi t\right)$. Here, $a$ is a random number formulated within the allowable range of industrial standards, and the parameter values in simulation experiments are shown in Table 3.

where $\mathrm{\lambda }$ and $\mu$ represents the parameters in the FPID controller.

In order to show the application effect of the proposed controller, a comparison is made with the fractional-order fuzzy PID (FPID) controller proposed in reference ^[41]. According to the method in reference ^[49], the multi-objective particle swarm optimization algorithm is used to find the optimal parameters of fractional operator order. The specific parameters are shown in the Table 4.

The simulation results of the trajectory tracking process in Figures 8-10 show that the industrial manipulator system can track the reference trajectory well in a short enough time with the initial error. Both linear motion and turning of direction can travel along the given path more accurately. In the case of external disturbance, the system can still show good tracking performance. In the process of trajectory tracking, the turning direction of the manipulator has been changed many times, while industrial manipulator system with adaptive fuzzy controller can still track the reference trajectory well, compared with the FPID and conventional SMC, it has higher advantages. In actual industrial applications, there are various reasons for external disturbances, so more complex external disturbances continue to be added. Figures 11-13 show that under the action of complex disturbances, the control method proposed in this paper can still maintain a good tracking effect and better than FPID. The conventional SMC not only has large problems in tracking accuracy, but also has a relatively serious delay. If the industrial manipulator is offline, it needs to consume a lot of computing power to solve the time non-synchronization problem, which increases the cost of the sensors. From all the simulation results, it can be seen that the overshoot and oscillation of the proposed method are less than those of the FPID controller, which indicates that AT2FSMC has better performance than SMC or FPID control schemes in tracking the end effector. However, the method proposed in the simulation process cannot provide better computing speed.

According to the above results, the AT2FSMC controller proposed in this paper still has good robustness in spite of the nonlinearity and uncertainty of the industrial manipulator model and the change of dynamic characteristics, which shows that the scheme is effective. In addition, through the stability analysis of the closed-loop system based on Lyapunov theory, the regulation law of the system can be summarized. Another interesting conclusion is that choosing appropriate boundary layer selection rules can effectively improve the trajectory control accuracy.

In this proposal for intelligent control, it can be considered as a general solution for the control of nonlinear systems. Its uses can be highlighting in industrial manipulator systems, in situations where the dynamics are variable or when there are uncertainties associated with the dynamic model.

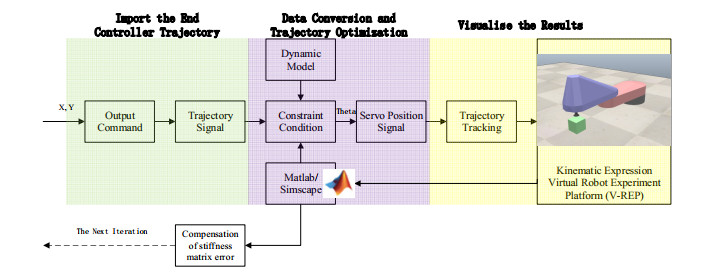
According to the coordinate data of the given trajectory extracted, assuming that there are no singular points in the data extracted from the teaching software, the constraint fitting is carried out according to the dynamic model of the manipulator and the physical model established in simscape. The V-REP module connection is established in MATLAB, and the converted manipulator servo motor control signal is provided to the joint controller. Finally, the motion is visualized in V-REP, as shown in Figure 14.

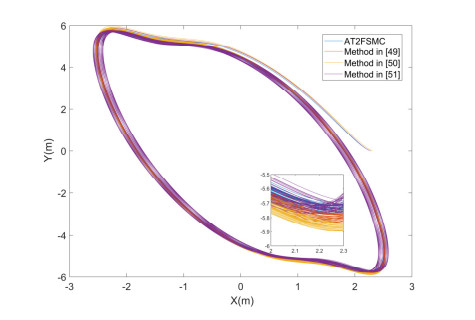
The experiment of two closed curves is designed according to the process in Figure 14. In the application process of industrial manipulator, when repeated operation is complete, the corresponding standards still is satisfied. In fact, each cycle will correct the error through using compensation algorithm. The compensation mechanism is not added to the simulation, and is compared with the methods proposed in ^[49,50,51]. The result is to illustrate the application effect of the scheme proposed in this paper.

In ^[50,51], the canonical normalized symbolic function replaces the general symbolic function. In ^[50], a time-synchronized control mechanism is added that allows the system state elements to converge to the origin simultaneously, resulting in a good trajectory tracking. Figure 15 shows that the motion trajectories largely coincide by persistent operations using the method proposed in this paper. This shows that the trajectory error per cycle is small, especially by comparison with the FPID mentioned in ^[49]. In the simulation experiments, the trajectory errors of the methods in ^[49,50,51] are 0.09, 0.17 and 0.25 m, respectively, while the trajectory error of the method proposed in this paper is 0.05 m. It can be seen that the trajectory error of the method proposed in this paper is the smallest under the influence of uncertain perturbations. It should be noted that the main purpose of this experiment is to discuss the performance of the control method of the motion controller, so no trajectory error compensation mechanism is incorporated. Therefore, in practical applications, the method proposed in this paper can have an important positive impact on the motion accuracy of the industrial robot arm and can characterize the robustness of the proposed method.

5.   Conclusions

In this paper, an adaptive type-2 fuzzy sliding mode controller based on low-pass filter is designed to solve the uncertainty problem of high-precision position tracking in industrial robots. The operating environment of the system is determined by considering several problems, such as parameter uncertainty, sensor induced interference and noise. The purpose of the controller is to provide accurate tracking in the presence of noise and interference, and to limit the minimum change of control signal. The proposed method can consider the important practical functions of the actual robot, such as achieving the required accuracy and avoiding the torque of the actuator beyond its functional range. The performance of the proposed fuzzy scheme is verified by the simulation test of a two degree of freedom direct drive robotic manipulator. In addition, the boundary layer method is proposed to limit the fluctuation of the adaptive law during switching, which makes the controller signal smoother and solves the problem that the control signal often fluctuates violently in the regulation process. Simulation results show that the proposed control scheme can achieve high precision position tracking and good robustness in trajectory tracking control.

Future work may focus on deriving the range of variation of uncertainties through mathematical derivations to ensure robustness, establishing analytical stability conditions and further considering the further applicability of the controller in complex systems with nonlinear properties (in particular, time-lagged systems, fractional-order dynamical systems and chaotic systems). In addition to this, the subdivision of the actual working conditions of industrial manipulators and the selection of different control schemes according to specific signal characteristics is an interesting research direction.

Acknowledgments

The authors would like to acknowledge the editors and reviewers for their extremely valuable inputs.

Conflict of interest

The authors declare there is no conflict of interest.