Displacement identification of oil storage tank and calibration of tank capacity table model based on indicator function integral

1.   Introduction

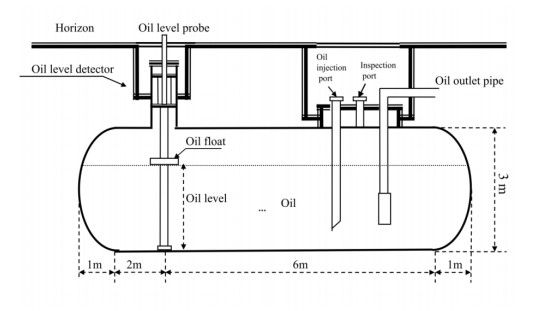
In daily life, the long-term use of equipment can gradually produce small errors, which has a growing impact on many large equipment, especially those requiring high-precision measurement. For example, the oil storage tank of the underground automobile gas station is a horizontal cylinder, and its two ends are composed of spherical surfaces, as shown in Figure 1. Each oil storage tank will be attached with a tank capacity scale after factory installation, showing the height of oil stored in the tank and the corresponding capacity, to ensure the measurement accuracy of gasoline sales and storage. After the oil storage tank is placed underground for a period of time, the position of the oil storage tank will change in longitudinal tilt and lateral deflection, due to geological changes or minor earthquakes, resulting in changes in the calibrated value of the tank volume. Therefore, it is necessary to recalibrate the tank volume table. However, before recalibration, the displacement state of the oil tank must be identified, which is the problem of displacement identification of the oil tank ^[1].

The basic principle of underlying displacement identification and calibration of the tank volume meter in oil storage tanks is to establish an integral relationship among oil storage capacity, oil level height, and displacement parameters based on the concept of the micro-element method. Different numerical techniques are then used to solve the problem and determine the displacement parameters, with the aim of re-calibrating the tank volume meter.

Based on the different positions of the oil level in the oil tank, most of the studies divided the entire oil tank into three parts ^[2,3]: the middle cylinder and the spherical crowns on both sides respectively, to establish the double integral relationship model between oil storage capacity and oil level height ^[4,5,6,7], and to carry out numerical calculation via approximate integration methods such as complex quadrature ^[8], Lagrange interpolation ^[9], Simpson formula ^[10], and so on.

Z. Yao et al. ^[11] developed a deformation integral model for an actual tank based on measured data, and used the nonlinear least squares method to estimate the deformation parameters of the tank. They then calculated the accurate calibration value of the tank capacity table for the actual tank.

L. Qi et al. ^[12] employed mathematical modeling techniques and MATLAB software to address the issue of tank displacement identification and calibration of the capacity map. By focusing on the study of a small elliptical cylinder oil tank, they investigated the calibration of the tank capacity diagram in situations where the actual tank experiences vertical or horizontal displacement.

Z. Liu et al. ^[13] developed a computational fluid dynamics (CFD) model to simulate liquid sloshing. This numerical model was validated through an experimental study of liquid sloshing in an apparent vessel. Based on the selected sloshing experiment, the effects of numerical time step and phase transition factor on liquid sloshing were investigated. It was found that time steps of 0.001 and 0.002 s, in conjunction with a phase transition factor of 0.1 s^-1, were sufficient to meet the requirements for predicting liquid sloshing behavior.

It was found that the first method to calculate the oil volume in the tank via integration method was the analytical method (multiple integration and differentiation), but this traditional functional integration model was complex to build and prone to errors in derivation ^[14]. During the modeling and calculation operation, the calculation of the oil volume in the displacement oil tank was relatively complex and difficult. In addition to functional integration formulas ^[15,16], indicative functions ^[17], Monte Carlo ^[18], and other methods can also be used for volume calculation. The Monte Carlo method is simple, but it requires a long time to obtain the result, and it is difficult to meet the accuracy as required. While indicator functions are commonly used in fields such as mathematics, physics, and computer science to represent the existence or characteristics of a set or region at a certain point, in order to define the properties of the set, such as topological, connectivity, and geometric properties. They can also be extended to multidimensional spaces or more general situations, for example, its indicator function can be represented as a Boolean function or a feature function for a region ^[19].This paper is based on a specific example of identifying the displacement of a mailbox in the calibration of oil storage tank volume in daily life. A mathematical model is established via integration method of indicator functions to analyze the specific situation of liquid oscillation in the container for the first time ^[20], and the model of the oil storage tank volume table is established as well. This method has a simple model, is easy to design algorithms, and has significantly improved calculation accuracy. And the effective combination of mathematical functions and practical applications has great potential significance for the application of mathematical methods in daily life examples

2.   Calibration of tank capacity table model

Considering that the capacity of a set (also known as Jordan measure) can be expressed by the integral of the characteristic function and taking advantage of the powerful computational capabilities of MATLAB ^[21], the construction model becomes very simple. The key lies in selecting an appropriate Cartesian coordinate system to determine the rectangular coordinate representation of the area occupied by the oil in the storage tank. Although the amount of calculation involved is significant, MATLAB can handle it with ease.

The specific algorithm for calculating oil quantity using the Matlab function triplequad is as follows:

1) A three-dimensional rectangular coordinate system is established, with the center of the oil storage tank as the origin and rotated with the oil storage tank.

2) The integration region E is determined according to the three-dimensional space area occupied by the oil volume in the tank.

3) Define the characteristic function of the integral area E as Formula (1):

4) In the integral range D of the Matlab function triplequad, only the region E can be included completely. In order to improve the calculation efficiency, D is set to be the smallest cuboid that can contain E.

5) Take the indicator function as the integrand and integrate it on D to calculate the corresponding oil quantity for the oil level height h.

3.   Results and discussion

3.1.   Displacement identification and tank capacity calibration of actual oil storage tank

The study is based on the actual inspection data during the oil inlet/outlet process after the displacement of a given oil storage tank, including the oil intake, oil output, the oil level display height in the tank, and the actual displayed oil volume. Appendix 1 can be seen for specific values.

3.1.1.   Model preparation

In order to study the displacement identification of oil storage tanks, it is necessary to determine whether the tank has shifted to some extent based on the measured data. The attached Excel table provides the volume label table without displacement for the "Oil Height Displayed" (in millimeters, mm) and "Oil Capacity Displayed" (in liters, L = dm³). The "Oil Output" column records several times of oil output, and the corresponding "Oil Height Displayed" in each row provides the corresponding oil level display height after oil output. The corresponding "Oil Volume Displayed" provides the tank volume gauge value under the oil level display height in the tank after the oil is discharged. If the oil storage tank has not displaced, the "Oil Volume Displayed" before oil output minus the "Oil Volume Displayed" after oil output shall be equal to the current oil output. The data is divided into two sets based on the supplementary intake. The first set contains 302 oil output data points, and the second set contains 300 oil output data points. The error images shown in Figure 2 are obtained by checking the two groups of data respectively.

According to the calculation results, the errors of the two groups of data are among the range of 17.51–16.46 liters, with the maximum relative errors of the two groups being 2.4 and 2.8 per mill, respectively. The error chart shows that the errors mainly occur at the two ends of the oil tank, where the oil height is lower or higher, and present obvious systematic error rules. It can be concluded that the oil tank did not deform but displaced.

3.1.2.   Model building

The mathematical model for the calibration of the tank volume table after the oil tank displacement is established, which is the relationship between the oil storage quantity in the tank and the oil level height within the displacement parameters (longitudinal inclination angle and lateral deflection angle). First, a three-dimensional rectangular coordinate system is established according to the right-handed law, with the center of the oil tank cylinder without displacement taken as the origin, the cylinder axis taken as the Z-axis, and the upward direction of the oil level probe taken as the positive direction of the Z-axis. The unit of measurement is meters, as shown in Figure 3.

Assuming that the section radius of the oil tank, the length of the cylinder, the radius of the spherical crowns at both ends, the distance from the oil level probe to the left end of the oil tank cylinder, the distance from the origin of the coordinates to the spherical center of the spherical crown, and the oil height respectively refers to r, L, R, d, c, h, the cylindrical oil tank with spherical crowns at both ends consists of the cylinder ${\mathrm{x}}^{2}+{\mathrm{z}}^{2} = {\mathrm{r}}^{2}, -\frac{\mathrm{L}}{2}\le \mathrm{y}\le \frac{\mathrm{L}}{2}$ (r = 1.5m, L = 8m) and spherical crowns at both ends, the spherical crown radius is R = 1.625m, and the coordinates of the two spherical centers are (0, $-\mathrm{c}$, 0) and (0, c, 0) (c = 3.375m). When the oil level height is h, if the oil tank has no displacement, the coordinate of the oil float is $(0, -(\frac{\mathrm{L}}{2}-\mathrm{d}), h-\mathrm{r})$ ($d$ = 2m) and the expression of the oil level equation is $\mathrm{z} = h-\mathrm{r}$.

Figure 4 shows the longitudinal inclination and lateral deflection of the oil storage tank. Assuming that the oil level probe entering the oil tank is fixed when the oil storage tank displaces, it can be seen from Figure 5 that:

1) The oil tank has only longitudinal displacement, and the coordinate of the oil float is

2) The oil tank has only lateral displacement, and the coordinate of the oil float is

3) The oil tank has both longitudinal and lateral displacement, and the coordinate of the oil float is

If the oil tank displaces, the oil plane equation in the oil tank $\mathrm{F}(\mathrm{x}, \mathrm{y}, \mathrm{z}) = 0$ is relatively complex and can be obtained through coordinate transformation $(\mathrm{x}, \mathrm{y}, \mathrm{z})\to ({\rm{ \mathsf{ ξ}}}, {\rm{ \mathsf{ η}}}, {\rm{ \mathsf{ζ}}})$. By translating the origin of the coordinate to the position $({\mathrm{x}}_{0}, {\mathrm{y}}_{0}, {\mathrm{z}}_{0})$ of the oil float, and then rotating $\mathrm{y}\mathrm{z}$ - plane around the $\mathrm{x}$-axis by anticlockwise direction angle ${\rm{ \mathsf{ α}}}$, the oil plane equation ${\rm{ \mathsf{ζ}}} = 0$ in the new coordinate system can be obtained, because on the cross section of the oil tank, the section of the oil plane remains parallel to the $\mathrm{x}$-axis regardless of the displacement of the oil tank. Therefore, through coordinate transformation,

the oil plane equation ${\rm{ \mathsf{ζ}}} = 0$ can be obtained, and the expression in the $\mathrm{x}\mathrm{y}\mathrm{z}$ space is $(\mathrm{y}-{\mathrm{y}}_{0})\sin {\rm{ \mathsf{ α}}}+(\mathrm{z}-{\mathrm{z}}_{0})\cos {\rm{ \mathsf{ α}}} = 0$. Thus, when the oil level height is $h$, the area occupied by oil in the tank can be expressed as Formula (7).

The model of the tank capacity table is obtained via the method of indicator function integration, which is expressed as the volume function of oil volume in Formula (8).

The volume unit obtained by integration here is "m³", which is converted into the volume unit "L" adopted by the actual data. The integral value needs to be multiplied by 1000, where ${{\rm{ \mathsf{χ}}}}_{{{\mathit{\Omega}} }_{h}}$ is to use the logical operation of the matrix to define the region ${{\mathit{\Omega}} }_{h}$ of the indicator function (Formula 9):

Because the area ${{\mathit{\Omega}} }_{h}$ of oil in the tank can be placed in the region minimum cuboid $\mathrm{D}$, the volume of ${{\mathit{\Omega}} }_{h}$ can be obtained by integrating ${{\rm{ \mathsf{χ}}}}_{{{\mathit{\Omega}} }_{h}}$ over $\mathrm{D}$.

To verify the correctness of the storage tank capacity table model without displacement, the model-calculated capacity is compared with the "display oil capacity" data. The results of the first set of data are shown in Figure 6, with a maximum deviation value of 0.1063. The maximum deviation value obtained from the second set of data is 0.1076, indicating that the calculation precision of this model meets the requirements.

3.2.   Determination of the displacement parameters

3.2.1.   Sensitivity analysis

First, the influence of tank displacement on the oil capacity function is analyzed. The sensitivity of the oil capacity function to displacement parameters such as the longitudinal inclination angle ${\rm{ \mathsf{ α}}}$ and lateral deflection angle ${\rm{ \mathsf{ β}}}$ is discussed.

Taking ${\rm{ \mathsf{ α}}}\in \{-4, -2, 0, 2, 4\}$, the tank capacity curve corresponding to different longitudinal inclination angle ${\rm{ \mathsf{ α}}}$ is shown in Figure 7. The influence of longitudinal inclination angle ${\rm{ \mathsf{ α}}}$ on the oil volume function is greater.

Taking ${\rm{ \mathsf{ β}}} = \{-20, -10, 0, 10, 20\}$, the tank capacity curve corresponding to different lateral deflection angle ${\rm{ \mathsf{ β}}}$ is shown in Figure 7. The results show that the influence of lateral deflection angle ${\rm{ \mathsf{ β}}}$ on the oil capacity function has less effect than that of longitudinal inclination angle ${\rm{ \mathsf{ α}}}$, and it has symmetry, the tank capacity curve of ${\rm{ \mathsf{ β}}} = -20, -10$ coincides with that of ${\rm{ \mathsf{ β}}} = 20, 10$ respectively.

3.2.2.   The determination of parameters

Now, based on the actual data "oil output", similar to the least squares data fitting method, the displacement parameters are determined by finding the parameters that minimize the objective function (Formula 10),

where $\mathfrak{R}$ is a subset of more than 300 points in the first set of data, $\left|\mathfrak{R}\right|$ is the number of all elements in the subset, $\mathrm{\Delta }\mathrm{V}({h}_{\mathrm{i}}, {\rm{ \mathsf{ α}}}, {\rm{ \mathsf{ β}}}) = \mathrm{V}({h}_{\mathrm{i}-1}, {\rm{ \mathsf{ α}}}, {\rm{ \mathsf{ β}}})-\mathrm{V}({h}_{\mathrm{i}}, {\rm{ \mathsf{ α}}}, {\rm{ \mathsf{ β}}})$, $\mathrm{\Delta }\mathrm{V}\mathrm{r}\mathrm{e}\mathrm{a}{\mathrm{l}}_{\mathrm{i}}$ is the actual oil output.

Then, the use of alternate progressive contraction of the search method, so that

determines the two displacement parameters.

In the process of determining the displacement parameters, two sets of data are used for calculation respectively, the displacement parameters obtained from the first set of data are ${\rm{ \mathsf{ α}}} = 2$, ${\rm{ \mathsf{ β}}} = 2.9$, and the displacement parameters obtained from the second set of data are ${\rm{ \mathsf{ α}}} = 2$, ${\rm{ \mathsf{ β}}} = 4.9$. These values from the two sets of data are nearly close, so the average value of the two groups is taken to obtain the displacement parameter of the oil storage tank is ${\rm{ \mathsf{ α}}} = 2$, ${\rm{ \mathsf{ β}}} = 3.9$. To test this result, the tank volume table derived from model $\mathrm{V} = \mathrm{V}(h, \mathrm{2, 3.9})$ is used to calculate whether the amount of oil that decreases with the decrease of oil height is more consistent with the measured amount of oil.

The error between the calculated oil output and the actual oil output from the two sets of data is shown in Figure 8. The oil output error of the first set of data is within the range of ± 3.3652, the oil output error of the second set of data is within the range of ± 2.8532, and the maximum relative errors of the two sets are 0.50 and 0.36‰ respectively, which is obviously much more accurate than the original tank capacity table.

Therefore, the calibration value of tank capacity table with oil level height interval of 10cm after the tank displacement can be given, as shown in Table 1.

4.   Conclusions

In this paper, a mathematical model of the tank capacity table for a cylindrical oil tank with spherical crowns at both ends was established using the indicator function integral method. The study was based on the oil input/output process of a given oil storage tank displacement, including the oil input and output volume, the displayed height of the oil level in the tank, and the actual displayed oil volume. The research results showed that errors mainly occur at both ends of the tank, with lower or higher oil heights and obvious systematic error patterns. Based on the measured data, the least squares and alternating progressive contraction search methods were used to determine the displacement parameters (longitudinal inclination angle ${\rm{ \mathsf{ α}}}$ and lateral deflection angle ${\rm{ \mathsf{ β}}}$).

Finally, the accuracy of the model was analyzed and found to meet the national requirements for the error tolerance of tank standard tables, verifying the correctness of the non displacement storage tank capacity table model and indicating that the calculation accuracy of the model can meet the design and requirements. Additionally, a table of oil levels with 10 cm intervals was provided for the oil tank after displacement.

The model avoided the complicated discussion of integral limits in the traditional integral method, simplified the integral calculation, and the calculation method is universal. It can be extended to other types of liquid containers with arbitrary shapes. Therefore, it has great application value for further research on the integral method of indicator function.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors thank all the help from companions of the laboratories.

Conflict of interest

The authors declare there is no conflict of interest.