New research for detecting complex associations between variables with randomness

1.   Introduction

Correlation analysis is particularly important in various fields. The important relationships that may be implied between different variables can be found by measuring the closeness between variables ^[1]. Correlation analysis is widely used in many fields such as finance, medicine, industry and biology. For example, Zhou et al. ^[2] investigated the correlation between the nutritional status and prognosis of COVID-19 patients by using multivariate logistic regression analysis. Xu et al. ^[3] revealed the correlations between the factors and the system status through statistical properties of data, and explored the related factors affecting the operating status of power systems. Liu et al. ^[4] investigated the relationship between intestinal flora content and hypertension, the results showed that the content of intestinal flora has a significant correlation with hypertension.

At present, the correlation analysis methods of variables can be roughly divided into three categories, namely, the correlation measure methods based on statistics, the correlation measure methods based on information theory and the measure methods based on similarity ^[5]. The correlation measure methods based on statistics include Pearson correlation coefficient, Kendell's coefficient and Spearman's coefficient etc. ^[6]. The measure methods based on information theory ^[7] include mutual information, maximum information coefficient (MIC) ^[8] and information gain etc. ^[9]. The similarity measure methods include distance correlation ^[10], Jaccard correlation and cosine similarity, etc. ^[11]. However, the traditional methods of correlation analysis do not comprehensively consider the impact of data uncertainty and distribution ^[12,13], which leads to the neglect of strong regularity information in the variables, so that the correlation coefficient value between variables with strong regularity is too small, and it is believed that there is no correlation or weak correlation between variables. Since the Pearson coefficient can reflect only the degree of linear correlation between variables, and it requires that variables conform to normal distribution. The MIC can capture a variety of functional relationship types, but it is not sensitive to the functional relationships containing specific distributions.

There are many studies on resolving the distribution consistency, uncertainty and randomness in data currently. For example, Gabriela et al. ^[14] use the paraconsistent logic, which can provide a compelling quantitative analysis approach in classification algorithms because it deals directly with inaccurate, inconsistent and incomplete data. Xin et al. ^[15] apply the chance theory to deal with the analysis of indeterminacy, including both uncertainty and randomness, to study two types of linear quadratic (LQ) optimal control models for multistage uncertain random systems. The first model is an LQ model with additive noises, while the second model is an LQ model with both multiplicative noises and additive noises. Yang et al. ^[16] provide a flexible framework for characterizing uncertainty in the outputs of physical systems due to randomness in their inputs or noise in their observations. Ayensa et al. ^[17] consider that data are never uncertainty-free and a suitable approach is needed to face data measurement errors and their intrinsic randomness in problems with well-established physical constraints. Additionally, Villiers et al. ^[18] proposes that if uncertainties in the modeling process are not accounted for, fusion processes may provide under- or overconfident results, or in some cases incorrect results. The authors establish four abstract processes to verify the situation in which uncertainty affects the modeling process. The above literatures all proved that the noise, uncertainty and randomness in data have certain influence on data analysis.

However, for the correlation analysis of data, most of the methods apply some preprocessing methods to alleviate the impact of noise and randomness on the correlation evaluation. For example, Niven et al. ^[19] believe that traditional means of calculating correlation coefficients are known to be adversely affected by outlier data, thus a new method for calculating a robust correlation coefficient is proposed based on a weighted average correlation calculated from different combinations or subsets of the original data, which is more robust than Pearson's or Spearman's correlation coefficients, but the uncertainty and randomness in the data are not analyzed and measured. Johnson et al. ^[20] removed the outliers in the data first and then calculated the correlation from the remaining data, but the outlier data may be reliable data in some case. In addition, the copula function is considered that it contains all the dependent relationships between random variables. Moreover, the copula theory believes that it is unreasonable to analyze the correlation between variables if they conform to different distribution statuses ^[21]. Therefore, in the copula theory, the variables are transformed into same distribution first, and then the correlation between variables is described by constructing the joint distribution of random variables. The copula theory has strong practicability, flexibility and robustness in analyzing the correlation structure of random variables ^[22]. Ma et al. ^[23] study the statistical relationship between random variables from data with association measures, and copula entropy is used to measure the degree of independence between joint distribution and edge distribution for random variables, so as to quantify the dependence of multivariate random variables.

As mentioned above, there are many studies on data noise, uncertainty and randomness indeed, there are few researches that link factors such as data noise, uncertainty and randomness with correlation between variables. Most correlation analysis methods solve the problems of noise and randomness through some pre-processing methods. Furthermore, we find that most correlation analysis methods take the degree that variables conform to certain functional relationship as the only size indicator for correlation. Suppose that the closer the distribution of data points for variables is to the image distribution of a quadratic function, the larger the correlation coefficient of the variable; however, if some data points are added to make the image distribution of data points close to the quadratic function gradually wider, the correlation coefficient will gradually decrease, but the correlation between the variables is strong, so the problem is that the correlation between variables is not weak, but the value of correlation coefficient become smaller. Furthermore, there exist strong correlation and regularity between functional relationship variables with specific distributions according to the scatter plots, so it is necessary to comprehensively evaluate the correlation between variables from multiple perspectives.

Furthermore, in many traditional methods of correlation analysis, it is considered that there exists complete functional relationship between variables when the coefficient value is equal to 1, that is, there exist accurate expression between variables. When the coefficient value is between 0 and 1, it is indicated that there exists dependent relationship between variables. The variables are independent of each other when the correlation value is equal to 0. For correlation relationships, there are no one-to-one functional mapping between the variables, so the tendency of a scatter plot for data can be observed. If there exist regularity between variables, the correlation between variables can be analyzed by regression analysis or correlation analysis methods. Additionally, the correlation between variables needs to be evaluated from multiple perspectives.

The rest of the paper is organized as follows. In Section 2, the related theories applied in this paper are described. In Section 3, the novel correlation analysis framework proposed in this paper is introduced. In Section 4, the proposed correlation analysis framework is applied to various datasets and the correlation of variables are evaluated. In Section 5, we discuss the correlation analysis accuracy compared traditional correlation analysis methods. we provide a summary of this paper in Section 6.

2.   Related theories

2.1.   The approximate fitting based on cubic B-spline

2.1.1.   The cubic B-spline

A spline is a smooth curve through nodes, which is defined by the constraints of control points and nodes. The spline fitting can be regarded as a piecewise fitting, that is, the specific data is divided into multiple segments, and each segment can be fitted to obtain a polynomial. When the basis function of the spline curve is a cubic polynomial, the curve obtained by fitting it is a cubic B-spline ^[24] curve. The definition of the basis function of cubic B-splines is as follows:

$t$ represents the node, $t \in\left[t_{0}, t_{1}, t_{2}, \ldots, t_{m}\right]$, $k = 3$, $j$ represents the number of control points and $m$ represents the number of nodes.

Then, the B-spline curve equation obtained by the basis function of the cubic B-spline is:

where $P_{j}$ represents the control point, and $\cdot$ represents the point multiplication. The process of spline fitting is the process of inversely finding the control points by enumerating the curve equations.

2.1.2.   The approximate based on cubic B-spline

Spline fitting can divide into interpolation fitting and approximate fitting. The difference between the two is whether all data points are passed through by the curve during fitting. The interpolation curve may pass through all data points instead of closely following the data polygon. In order to overcome this problem, approximation techniques are introduced, which relax the strict requirement that the curve must contain all data points.

In global approximation, the curve need not contain every data point except the first and last ones. To measure how well a curve "approximates" to a given data polygon, the concept of error distance is used. The error distance is the distance from the data point to the "corresponding" point on the curve. Therefore, if the sum of these error distances is minimum, the curve should closely follow the shape of the data polygon. Curves obtained in this way are called approximate curves.

2.2.   Information entropy

Information entropy is the measure of reduction degree in the uncertainty of an event, which can be used to measure the uncertainty of information ^[25,26].

According to the information entropy formula proposed by Shannon, for any random variable $X$, suppose the variable X is a discrete variable with n number of values, where the number of unequal values is s, then its information entropy is defined as follows:

where $x \in X$, $x_{i}$ represents the i-th unequal values that belongs to variable X, and $p(x)$ is the probability of something happening, and the unit of entropy is bit.

2.3.   Copula function

Copula function can connect the joint distribution of multidimensional random variables $x_{i}, x_{2}, \ldots, x_{n}$ with their respective marginal distributions $F_{1}\left(x_{1}\right), F_{2}\left(x_{2}\right), \ldots, F_{n}\left(x_{n}\right)$ Sklar's ^[27] theorem has demonstrated that in the general case there exists a multivariate real function $C\left(u_{1}, u_{2}, \ldots u_{n}\right)$, making

This multivariate function C is the copula.

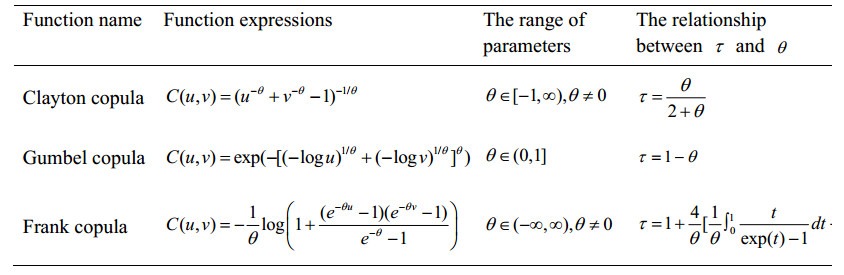
Copula is considered to contain all dependencies between random variables, which can reflect linear relationships and describe nonlinear relationships. Therefore, choosing which copula function to construct the correlation structure of variables is an important subject ^[28]. Copula models can be mainly divided into two categories, which include elliptic copula and Archimedes copula. Archimedes Copula, including three types of functions: Clayton copula, Gumbel copula and Frank copula, which are often used to analyze the correlation structure of binary random variables. We can evaluate the effect of each copula model by calculating the errors of empirical copula and theoretical copula, as well as Akaike information criterion (AIC) and Bayesian Information Criterion (BIC). The calculation formulas of AIC and BIC are shown in Eq (5):

where $m$ represents the number of samples, $k$ represents the number of parameters of the model and the calculation formula of MSE is as follows:

2.4.   Spectral clustering

Spectral clustering ^[29] is a graph-based machine learning algorithm. The graph-based algorithm regards the sample data as the vertices of the graph, constructs edges according to the distances between the data points to form a graph with weights and completes the functions required by the algorithm through processing the graph. For the clustering problem, it is realized by graph cutting, which is to divide the graph into multiple subgraphs. These subgraphs are the clusters. The spectral clustering algorithm constructs an adjacency graph (also known as a similarity graph) of the sample set and obtains the Laplacian matrix of the graph. Next, the matrix is decomposed into eigenvalues, and clusters are constructed by processing the eigenvectors.

2.5.   Analytic hierarchy process

Analytic Hierarchy Process (AHP) ^[30,31] is a systematic and hierarchical analysis method combining qualitative and quantitative, which can assign weights to multiple different indicators. In this paper, we use the largest eigenvalue method in AHP to determine the weight coefficient. The first step is to construct the relative importance matrix of the factors, then to calculate the eigenvector corresponding to the maximum eigenvalue of the matrix, and the eigenvector is normalized to obtain the final weight matrix; The second step is to perform consistency check on the obtained weight matrix, and calculate the consistency index CR. Equation (7) is shown below,

where RI represents the average random consistency, which can be acquired by checking out the table; CR < 0.1, it can be judged that the matrix has consistency, that is, the matrix meets consistency requirements.

3.   The proposed correlation analysis framework

In order to consider the degree of functional relationship between variables, the uncertainty in variables and the degree of dependence on the variables containing distributions, a new correlation analysis framework is proposed in this paper.

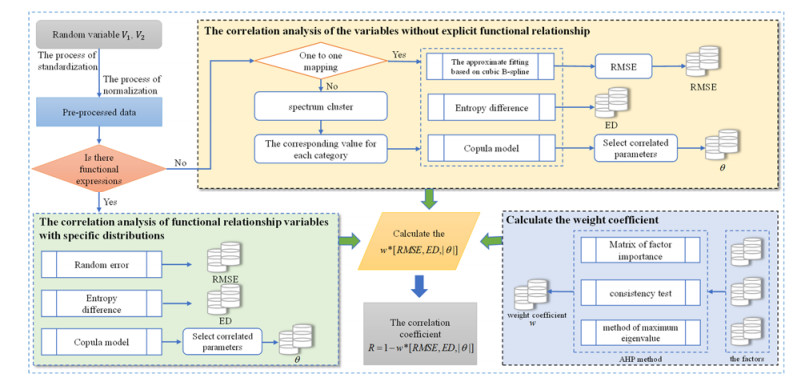
The relationships between variables are divided into the functional relationships with exact expression and the correlation relationships without explicit function expression, so that we will use the proposed analysis framework to analyze the correlation of the two relationship types. The proposed correlation analysis framework is shown in Figure 1, and the correlation analysis framework is specific to continuous bivariate in this paper.

As shown in Figure 1, the correlation analysis framework proposed in this paper is divided into three modules, namely, the correlation analysis module of functional variables with specific distribution, the correlation analysis module of variables without explicit functional relationship, and the calculation module for weight coefficients. For each correlation analysis module, which is also divided into three stages:

1) Measure the degree of functional relationship between variables. Calculating the RMSE of random distribution to evaluate the degree of functional relationship between variables.

2) Measure the degree of uncertainty in the distribution of variables. Calculating the uncertainty information caused by random distribution between variables first, and then the uncertainty degree of random distribution between variables is evaluated according to the information entropy difference between the functional relationship variables and the functional relationship variables containing specific distribution.

3) Measure the degree of dependence on the random distribution of the variables. First, the copula model for random distribution of variables is constructed to represent the correlation structure of variables. Then the optimal copula function is selected according to the error between empirical copula and theoretical copula, AIC and BIC. Finally, the relevant parameter corresponding to the optimal copula is selected to evaluate the degree of dependence on the random distribution of variables.

The stages of calculation module for weight coefficient include construct the factor importance matrix, consistency test and maximum eigenvalue method to generate final weighted coefficients.

3.1.   The description of the correlation analysis framework proposed in this paper

In this section, the correlation analysis framework for the functional relationship variables with distribution and the variables without explicit functional relationship will be introduced, respectively, and the framework is described by flowchart and construction process in detail. The flowchart of correlation analysis framework for functional relationship variables with specific distributions is shown in Figure 2, and the flowchart of correlation analysis framework for variables without explicit function relationship is shown in Figure 3.

3.1.1.   The correlation analysis framework for functional relationship variables with specific distributions

The construction process of the correlation analysis framework for functional relationship variables with specific distributions is as follows:

Assuming random variables $X$ and $Y$, and there is a clear functional relationship between $X$ and $Y$. The function is denoted by $Y = C X+\sigma$, $\sigma$ represents the values that satisfy specific distribution.

Step 1: Standardize and normalize the random variables. The standardized and normalized variables $E_{0}$, $E_{1}$ and $E_{2}$ corresponding to $X$, $Y$ and $Y_{1}$ is obtained. The functional relationship between variables $Y_{1}$ and $X$ is denoted by $Y_{1} = C X$.

Step 2: Calculate the root mean square error (RMSE) between $E_{1}$ and $E_{2}$, then the normalized RMSE is obtained.

Step 3: Calculate the normalized information entropy of variables $X$ and $Y_{1}$. First, we use MIC to obtain the optimal partition interval for the variables $X$ and $Y_{1}$, and enumerating all the partition results. Then, the information entropy of variables $X$ and $Y_{1}$ is calculated after the intervals is divided, and the information entropy is normalized. Finally, the normalized information entropy corresponding to the optimal partition interval is obtained.

Step 4: Construct the copula function. First, the random variables are transformed into the probability distribution function which conforms to the normal distribution. Then, the copula function is constructed on the transformed data.

Step 5: Obtain the correlation parameter $\theta$. Calculate the error between empirical copula and theoretical copula, and obtain the AIC and BIC of the copula model. Then, the correlation parameter corresponding to the best copula function is selected.

Step 6: Obtain the weight $w$. The factor importance matrix is constructed, and the AHP method is applied to obtain the weight matrix $w$. The consistency test is also used to determine whether the factor importance matrix is reasonable.

3.1.2.   The correlation analysis framework for variables without explicit functional relationship

The construction process of the correlation analysis framework for variables without an explicit functional relationship is as follows:

Assuming random variables $X$ and $Y$, and there does not exist specific functional relationship between $X$ and $Y$. The value obtained by the spline fitting is denoted by $Y_{1}$.

Step 1: Standardize and normalize the random variables. The standardized and normalized variables $E_{0}$, $E_{1}$ and $E_{2}$ corresponding to $X$, $Y$ and $Y_{1}$ is obtained. The functional relationship between variables $Y_{1}$ and $X$ is denoted by $Y_{1} = P_{i} \sum_{k = 1}^{m} N_{i, p}\left(t_{k}\right)$.

Step 2: Perform the spectrum cluster. If there doesn't exist one to one mapping between variables, the spectrum cluster is performed to obtain multiple category data.

Step 3: Perform the approximate fitting based on cubic B-spline. The approximation fitting based on cubic B-spline is used to each category data, and the curve expression after fitting is obtained

Step 4: Calculate the root mean square error (RMSE). The final spline RMSE is the sum of the errors of each category.

Step 5: Calculate the normalized information entropy of variables $X$ and $Y_{1}$. First, using MIC to obtain the optimal partition interval for the variables $X$ and $Y_{1}$, and enumerating all the partition results. Then, the information entropy of variables $X$ and $Y_{1}$ is calculated after the intervals is divided, and the information entropy is normalized. Finally, the normalized information entropy corresponding to the optimal partition interval is obtained.

Step 6: Construct the copula function. First, the random variables are transformed into the probability distribution function which conforms to the normal distribution. Then, the copula function is constructed on the transformed data.

Step 7: Obtain the correlation parameter $\theta$. Calculating the error between empirical copula and theoretical copula, the AIC and BIC of the copula model. Then, the correlation parameter corresponding to the best copula function is selected.

Step 8: Obtain the weight $w$. The factor importance matrix is constructed, and the AHP method is applied to obtain the weight matrix $w$. The consistency test is also used to determine whether the factor importance matrix is reasonable.

3.2.   The degree of functional relationship between variables

There may exist functional relationships between correlated variables but subject to some error distributions and randomness. In statistics, regression analysis is often used to explore the relationship between variables. Through regression analysis, the regression equation between variables can be obtained, which can approximately reflect the closeness of the association and the general regulation of changes between variables. Therefore, we can measure the degree of functional relationship between variables by calculating the error between the original values and the fitted values after regression. If the error is equal to 0, it means that there exists perfect functional relationship between variables; the smaller the error, the closer the association between variables, and it indicates that the functional relationship between variables is stronger.

In this paper, the relationship of variables is divided into two cases, which include the explicit functional relationship containing specific distribution and the correlated relationship without explicit function. Algorithm 1 shows the pseudo-code for calculating the RMSE of variables with defined function or undefined function relationship. In order to remove the dimension of data and make the results obtained from the model comparable, so the data are standardized and normalized first, then the preprocessed data are between 0 and 1. The formula of standardization and normalization is shown in Eq (8).

For functional relationship variables with specific distributions, the degree of functional relationship between variables is evaluated by calculating the root mean square error (RMSE) in the distribution of variables. The calculation formula of RMSE is shown in Eq (9).

For the variables without an explicit functional relationship, the function expression between variables was obtained by approximate fitting based on cubic B-spline ^[32,33]. Then, the degree of the functional relationship between variables is evaluated by calculating the RMSE between the original data and the fitted data. First, we divide data into segments, then the approximate fitting based on cubic B-spline is performed on each segment, and the function expression corresponding to each segment is obtained; finally, the function expression function based on spline curve is obtained by summing all the segmented expressions ^[34]. Since the interpolation fitting requires the curve to pass each data point, and the curve obtained by interpolation fitting is complex and irregular, which cannot reflect the shape trend of the original data well. Therefore, the idea of the least square is introduced in an approximate technique ^[35], and the condition of minimizing the error distance between the original value and the functional value is added into the constraints of cubic B-spline fitting. The approximate fitting does not strictly require the curve to pass all data points, and the curve obtained by the fitting follows the shape of the data smoothly and closely, so the method of approximate fitting based on cubic B-spline can better reflect the functional correlation of the original variables. The specific process is as follows:

where $P_{0}, P_{1}, \ldots, P_{h}$ represent $h+1$ numbers of unknown control points. Since the spline will pass the first and last data points, we have $D_{0} = C(0) = P_{0}$ and $D_{n} = C(1) = P_{h}$, so there are only $h-1$ numbers of unknown control points. Taking this into consideration, the curve equation becomes the following:

Introduce the approximation technique, then the sum of all squared error distances between original value and the spline fitting value is as follows:

Our goal is to find those control points $P_{1}, P_{2}, \ldots, P_{h-1}$ such that the function $f(.)$ is minimized.

3.3.   The degree of uncertainty for the distribution of variables

The more cluttered the data distribution, the higher the uncertainty of the information. Therefore, there exist uncertainty difference between the functional relationship variables after regression fitting and the original variables, the uncertainty of variables can adversely affect correlation results, and the degree of uncertainty of variables has an important impact on the correlation analysis of variables. The information entropy can be applied to measure the uncertainty of information, and the degree of uncertainty in the distribution of variables is evaluated by calculating the difference of information entropy between the functional relationship variables and the original variables. The information entropy is calculated by the Eq (3), and the difference entropy (ED) between functional relationship variables and original variables is calculated by

Obviously, the unit of ED is bit, the lower the degree of uncertainty comes the less ED.

The correlation analysis framework is specific to continuous bivariate, and the information entropy is mainly for discrete data. Therefore, the partition idea of MIC is referenced, the partition way corresponding to the maximum mutual information is used as the way of discretization process of the original variables, the probability of data points between variables after discretization is expressed as $p$, and the probability of each part is calculated as the number of data points of the corresponding part divided by the total number of data points. The calculation formula is given in Eq (14), and Figure 4 shows an example of dividing data points between variables, the number of red lines represents the number of dividing intervals. Then, the information entropy of each division is calculated, and in order to facilitate the comparison of the results, the information entropy is normalized so that the value of each information entropy is between 0 and 1. Finally, the normalized information entropy corresponding to the best division can be obtained.

where $m_{ {part }}$ represents the number of data points in a partition, and $m_{ {total }}$ represents the total number of data points in the variable.

3.4.   The degree of dependence on the random distribution of variables

The values of variables studied in this paper are affected by random errors and distributions ^[36], so that there exist uncertainty and randomness in variables, but the probability that these values fall into a certain range is definite. When studying the correlation of variables that are subject to distributions, it is necessary to consider the distribution state of the variables. The copula theory is applied to analyze the correlation of variables affected by distributions.

According to Copula theory, if the distribution status of variables is inconsistent, it is unreasonable to analyze the correlation between variables. Therefore, the random variables are first transformed into probability distribution functions that conform to the same distribution before constructing the correlation structure of random variables, so that the values of random variables are between 0 and 1. Then, the function construction is performed on the transformed data by the copula function, which represents the correlation structure of the random variables. Additionally, all the dependency relationships are contained after constructing the functional relationship, which is the theoretical copula of random variables. The empirical copula is the bridge between the theoretical copula and the actual data. The RMSE between the empirical copula and the theoretical copula, AIC and BIC are used as indicators to evaluate the copula model. Finally, the correlation parameters corresponding to the optimal copula function are selected to measure the dependence on random variables with distributions.

Correlated parameter estimation includes maximum likelihood estimation method and non-parametric estimation method ^[37]. In this paper, the parameters of the function are estimated by non-parametric estimation method, i.e., the parameters are estimated by the relationship between the correlated parameters and the Kendell's coefficients, and the range of parameters corresponding to the Archimedean copula is shown in Table 1.

3.5.   The measure of correlation between variables

The relationship between variables is divided into deterministic relationships and non-deterministic relationships. Deterministic relationships refer to the existence of clear functional relationship between variables, that is, there exists accurate function expression, and the non-deterministic relationship refers to the correlation relationship without clear functional relationship. In many measure methods of correlation, when the correlation value is equal to 1, it is considered that there exists complete functional relationship between variables; when the correlation value is between 0 and 1, there exist correlated relationship between variables; and when the correlation value is equal to 0, the variables are independent. However, many traditional methods do not fully consider the impact of data uncertainty and distribution, which leads to ignoring the strong regularity information in the variables, so that the correlation coefficient value obtained by the variables with strong regularity is too small. Then, it is considered that there exist no correlation or weak correlation between the variables.

Based on the above, in this section, the correlation of the functional relationship variables containing specific distributions and the variables without explicit functional relationships will be analyzed, respectively. By measuring the degree of functional relationship between variables, the degree of uncertainty in the distribution of variables and the dependence on the random distribution of variables, the correlation between the two relationship types is comprehensively analyzed. Additionally, the process of correlation analysis and its rationality are described in detail.

3.5.1.   The measure of correlation for the functional relationship variables with specific distributions

1) The degree of functional relationships between variables

For the functional relationship variables with specific distribution, there exist functional relationships between variables that are subject to some error distributions. The degree of functional relationship between variables is evaluated by calculating the RMSE of random distribution of the functional relationship variables with specific distribution. The smaller the error, the closer the association between variables, and it indicates that the functional relationship between variables is stronger. The larger the error, the sparser the degree of functional relationship between the variables.

2) The degree of uncertainty for the distribution of variables

For the functional relationship variables containing specific distribution, the uncertainty of variables is brought by the distribution of variables. The uncertainty of information is measured by calculating the information entropy in this paper. First, the best partition corresponding to the MIC is calculated for the variables with functional relationships, then enumerating all partition results and calculating the information entropy corresponding to each partition. Finally, the information entropy is normalized to obtain the normalized information entropy corresponding to the best partition. Similarly, the above process was repeated for the functional relationship data containing specific distribution, and the difference of information entropy between the functional relationship variables and the functional relationship variables with distributions is obtained. The uncertainty degree of the functional relationship variable containing specific distribution is evaluated by the difference of normalized information entropy. The greater the difference in the information entropy of the variables, the higher the degree of uncertainty of the variables. Algorithm 2 shows the pseudo-code for computing the entropy difference of variables.

3) The degree of dependence on the random distribution of variables

The function type of Archimedean copula and the construction process of copula function are introduced in Section 3.4. The correlation parameters corresponding to the optimal copula function are used to measure the degree of dependence on variables that subject to distributions. The function expressions of bivariate copulas and the range of parameters corresponding to copula function are shown in Table 1. For the Clayton copula, the range of parameter is $(0, \infty)$, the larger the absolute value of parameter, the greater the correlation of variables containing distributions. Then, when the parameter $|\theta| < 1$, the degree of dependence on variables containing distributions is weak. For Gumbel copula, the range of the parameter is $(0, 1]$, and the closer the correlation parameter is to 0, the more correlated the variables. For Frank copula, the range of the parameter is $(-\infty, \infty)$, and the larger the absolute value of parameter, the greater the correlation of variables containing distributions. Then, when the parameter $|\theta| < 1$, the degree of dependence on variables containing distributions is weak. In order to facilitate the comparison, the reciprocal of the correlation parameters of Clayton copula and Frank copula functions is taken, so that the directions of change of parameter value size and the strength of the correlation is consistent with the Gumbel copula. In addition, in order to compare the correlation values obtained by other methods, and measure the correlation strength of variables more intuitively through the correlation value, and if the absolute value of the parameter that is obtained by constructing the Clayton copula and Frank copula functions of variables is less than 1, it is considered that the correlation between variables is extremely weak. Thus, the inverse of parameter $|\theta| < 1$ is the value of infinity, so the correlation coefficient value $R$ obtained by $1-w^{*}[R M S E, E D, |\theta|]$ is negative. The parameter $|\theta| \geq 1$ corresponding to correlation coefficient values obtained by the new method are between 0 and 1. The closer the correlation value is to 1, the stronger the correlation between variables. Algorithm 3 shows the pseudo-code for measure the correlation of variables with distribution and uncertainty.

3.5.2.   The measure of correlation for the variables without explicit functional relationships

1) The degree of functional relationship between variables

In the actual variables, the functional relationship between variables is not clear, and it is necessary to apply the regression model to obtain the function expression, which can approximately reflect the closeness of the association and the general regulation of changes between variables. The error between the original data and the fitted data will be used to measure the degree of functional relationship between the original variables. In this paper, the approximation fitting based on cubic B-spline is applied to obtain functional relationship expressions between the variables, and then the spline error between the original data and the fitted data is calculated. Due to the idea of minimizing the error distance was adopted by the cubic B-spline. Then, when there exist one-to-many situations in the data or many outliers, the spline function obtained by the spline fitting is complex and does not conform to the shape distribution of the original data. Therefore, before the spline fitting, the data need to be standardized and normalized, and the spectral clustering is performed on the data in the case of one-to-many or many-to-many first. Then, the spline fitting is performed on each category data. Finally, the spline error is the sum of the RMSE after fitting each category data. Algorithm 4 shows the pseudo-code for approximate fitting based on the cubic B-spline.

2) The degree of uncertainty for the distribution of variables

The degree of uncertainty in variables is evaluated by the entropy difference, and the calculated method is as follows: First, the functional expression between variables is obtained by the B-spline approximate fitting, and the MIC between the variables is calculated to obtain the best partition of the data; then the information entropy corresponding to different partitions is calculated, and the information entropy is normalized; finally, the normalized information entropy of the variables after spline fitting corresponding to the best partition is obtained, and the normalized information entropy of the original variables is also derived. The degree of uncertainty for the original data is measured by the difference between the normalized information entropy of the fitting variables and the original variables. The larger the difference, the higher the degree of uncertainty. Similarly, the smaller the difference, the smaller the degree of uncertainty.

3) The degree of dependence on the random distribution of variables

Mentioned in Section 3.4, the correlation of variables with distributions and uncertainty is evaluated by estimating the correlation parameters of the copula function. First, the function of Clayton copula, Gumbel copula and Frank copula in the Archimedes copulas for variables are constructed, and the correlation parameters of the three functions are estimated. Then, the optimal copula function is selected by calculating the fitting error between the empirical copula and theoretical copula, AIC and BIC to represent all dependence structures between variables. Finally, the correlation parameters corresponding to the optimal copula are selected as the measure indicator of correlation for variables containing distributions.

3.6.   The weighted coefficient

Section 3.5 described how to measure the correlation of variables by evaluating the degree of functional relationship, the degree of uncertainty in variables and the degree of dependence on the variables containing distributions. Then, the above three indicators will be integrated into a single correlation value $R$ to evaluate the correlation between variables more intuitively. The weight coefficients of the three indicators will be determined by the maximum eigenvalue method in the AHP method ^[38], and the relative importance matrices for measure indicators are constructed as shown in Table 2. In addition, the constructed importance matrices all pass the consistency test, and the final weight matrix is [0.346, 0.200, 0.454]. The smaller the RMSE, entropy difference and correlated parameter, the closer the association between variables, and the values of three indictors are between 0 and 1, so that the weighted results after integration are transformed to $R = 1-w^{*}[R M S E, B D, |\theta|]$, the larger the correlation value $R$, the more correlated the variables. Where $w$ represents the weight matrix, the $R M S E$ is the root mean square error between the original variable and the variable after constructing a functional relationship, $B E D$ represents the information entropy of variables, and $|\theta|$ represents the absolute values of correlated parameters corresponding to the optimal copula function. Algorithm 5 shows the pseudo-code for AHP method.

4.   The experiment

4.1.   The data description

In order to verify the effectiveness of the method, two types of data were selected for experiments. The first one is the functional relationship variable that contains a specific distribution. Table 3 lists 12 function expressions that contain a specific distribution, where represents the random error that conform to uniform distribution. The expression types include general expressions and parameter expressions. The variable range and distribution data value range are shown in Table 3. The second is to use 4 UCI datasets and 4 artificially synthesized datasets with no explicit functional relationship. The UCI datasets include Iris Data Set, seeds Data Set, Glass Identification Data Set and Wine Data Set. The synthetic datasets include Two_cluster, Twomoons, Five_cluster and Roll. The detailed information of datasets is shown in Table 4.

4.1.1.   Experimental data types that possess specific distribution and functional relationship variables simultaneously

4.1.2.   Datasets with no explicit functional relationship variables

4.2.   Correlation analysis

4.2.1.   Correlation analysis of functional relationship variables containing specific distribution

The first step to carry out the correlation analysis of variables is to draw the scatter plots of the variables to observe the trend of the variable data. Then, the degree of functional relationship between variables is evaluated by the random distribution error of the variables, the entropy difference of the variables with random distribution is calculated to measure the degree of uncertainty of the variables and the copula function models are constructed to measure the degree of dependence on the variables containing distributions. Finally, the strength of correlation of the variables is evaluated integrally.

1) The scatter plots of the variables

For the functional relationship variables containing specific distributions, the scatter plots of the variables are shown in Figure 5, in which the MIC and Pearson coefficient values between the variables are also displayed. It can be seen that all scatter plots have strong regularity from the figure, but the MIC value is relatively small and the Pearson coefficient value is almost equal to 0, which indicates that MIC can measure only the correlation with a specific type of functional relationship but cannot identify the type of variable with distribution, and the Pearson coefficient can evaluate only the type of linear function relationship between variables but the rest of the relationship types cannot be well measured.

2) The degree of functional relationships of the variables

For variables with explicit functional relationship involving specific distributions, the degree of functional relationships that is evaluated by the error brought by the specific distribution. Their distribution errors are expressed by the root mean square error (RMSE) of random distribution of the functional relationship variables with specific distribution. The smaller the error, the higher the degree of functional relationship of the variables. The larger the error, the smaller the degree of functional relationship of the variables. The specific results are shown in the second column of Table 5. Owing to there exists different degree of random distribution between variables, the scatter plots and the results of normalized RMSE for variables are also different, and the greater the degree of random distribution between variables, the larger the value of normalized RMSE for variables, which indicates that the random distribution between variables will affect the degree of functional relationships between variables.

3) Uncertainty measures for distributions between variables

The uncertainty of functional relationship variables containing specific distributions is measured by comparing the information entropy difference brought by variable distribution. First, calculate the MIC value of the specific functional relationship type between the variables, then exhaustively list all the divisions and calculate the information entropy under each division and normalize it. Finally, the normalized information entropy corresponding to the best division is acquired. Furthermore, calculating the normalized information entropy of the optimal division of variables with specific distribution and the difference between the two information entropies is obtained. The experimental results are shown in Table 6, where Normal ED represents the difference of information entropy between functional relationship variables and the variables with specific distributions, Normal Ent represent the normal information entropy of variables. The results show that the distribution of the data will bring a certain degree of information entropy difference.

4) Dependency measures for random distribution of variables

In the experiment of measuring the dependency degree of random distribution of variables, the optimal copula function is selected to construct the correlation structure of variables, and the relevant parameters of the optimal copula are used as the correlation evaluation index of random distribution. The binary copula functions include Clayton copula, Gumbel copula and Frank copula. The fitting errors, AIC and BIC of empirical and theoretical copulas obtained after constructing the function, are used as the index for selecting the optimal copula function. Appendix to Table A1 shows the results of the best copula function, and the best results are shown in bold.

The final results of correlation analysis are shown in Table 5. The correlation of variables is comprehensively evaluated through the degree of functional relationship, degree of uncertainty and degree of random distribution dependence of the variables. Then, the weight coefficients of the three indicators are calculated and summed up. Since the smaller the three indicators, the stronger the correlation, and the value range is between [0, 1], so the weighted sum is subtracted from 1. Finally, the weighted correlation coefficient value is obtained. The larger the value, the stronger the correlation. Likewise, unweighted correlation results can be drawn.

4.2.2.   Correlation analysis of variables without explicit functional relationship

To carry out the correlation analysis of variables, the first step is to draw the scatter plots of the variables to observe the approximate distribution and regularity of the data. Then, the degree of functional relationships between variables is evaluated by the spline error, the entropy difference of the variables is calculated to measure the degree of uncertainty of the data, the copula function model is constructed to measure the degree of dependence of the random distribution of the variables, and the correlation size of the variables is evaluated integrally.

1) The scatter plots of the variables

The scatter plots of variables without explicit functional relationships in the UCI datasets and the artificially synthetic datasets are shown in Figure 6, which also shows the MIC and Pearson coefficient values between partial variables in each dataset. Combining the scatter plots of variables, MIC and Pearson coefficient values, it can be analyzed that Pearson coefficient can well evaluate their linear correlation when there is an obvious monotonic linear correlation shown in the scatter plots, and MIC can do better when the scatter plots show a perfect function image of specific function. However, for the functional relationship variables containing specific distributions, neither can perform well, and the obtained MIC and Pearson coefficient values are small.

2) The degree of functional relationship of the variables

For variables without a clear functional relationship, the degree of functional relationship between the variables was evaluated by the error between the true value and the spline fitting value. The cubic B-spline approximate fitting was performed on the value corresponding to each category. The number of cubic B-spline control points used in this experiment was 4 and the number of nodes was 3. The mean squared errors of the true and fitted values in each category were calculated and summed up. The spline fitting results are shown in Figure 7, and the error are shown in Table 7. Combining the figures and the results in the table, it indicates that the approximate fitting based on cubic B-spline can follow the trend of data points well, and for variables with stronger distribution regularity of data points, the better the fitting effect.

3) The degree of uncertainty for the distribution of variables

For the measurement of uncertainty in variables without explicit functional relationships, the MIC values among variables with spline functional relationships are calculated first, then all divisions are enumerated to derive the best division of variables, the information entropy under each division is calculated and normalized, and finally the normalized information entropy corresponding to the best division is obtained. Furthermore, the normalized information entropy of the original variables corresponding to the best division is also calculated. The degree of uncertainty of the variables without explicit functional relationships was measured by comparing the difference in information entropy between the original data and the spline fitted data, and the results are shown in Table 8. According to the results in the table, the stronger the randomness of distribution for data points of the variables in the datasets, the greater the information entropy obtained and the larger the entropy difference calculated.

4) The degree of dependence on the random distribution of variables

For variables without explicit functional relationships, the correlated parameter corresponding to the optimal copula function is selected to evaluate the correlation degree between variables subject to random distributions. The bivariate copula functions include Clayton copula, Gumbel copula and Frank copula, and the fitting errors of empirical copula and theoretical copula, AIC and BIC are derived after constructing the copula models of variables, and the three indicators are used as evaluation index for selecting the optimal copula function, and the correlation parameter corresponding to the optimal copula is used as an evaluation method for correlation evaluation of random variables. Appendix to Table A2 shows the results of the selection of optimal copula function, and the best results are shown in bold.

The correlation analysis results for the functional relationship variables without clear function are shown in Table 9. The correlation of variables without clear functional relationships is evaluated by the degree of functional relationship between variables, the degree of uncertainty of variables and the degree of dependence on the variables containing distributions. Then, the weight coefficient of the three indicators is calculated, and the weighted sum of the three indicators is performed. Owing to the smaller the three indicators, the stronger the correlation, and the value range is between 0 and 1, so the weighted correlation value is obtained by subtracting the value after weighted summation from 1. The higher the value, the stronger the correlation. Similarly, the unweighted correlation results can be derived. According to the results, the stronger the regularity of the variable, the greater the value of the correlation coefficient.

In addition, in order to compare the performance of correlation analysis methods for the two types of functional relationship variables with specific distribution and the variables without explicit functional relationships, the experimental designs are conducted as follows: First, the correlation analysis performance of the two methods is compared under the same functional expression with specific distribution; second, the performance of the two correlation analysis methods is compared for the same manifold dataset without functional relationships. Combined with the above experiments, the results are analyzed in detail and the reasonable conclusions are drawn below.

According to the experimental results, the performance of the two correlation analysis methods is similar in the case of the same functional relationship expression with specific distribution, and the correlation analysis method aiming at the functional relation variable with specific distribution is slightly better. For manifold datasets without explicit functional relationships, the correlation analysis method without functional relation variables has better performance. However, it is also valid for functional relation variables with specific distributions. According to the experimental results, the performance of the two correlation analysis methods is similar in the case of the same functional relation expression with specific distribution, and the correlation analysis method aiming at the functional relation variable with specific distribution is slightly better. For manifold data sets without explicit functional relations, the correlation analysis method without functional relation variables has better performance. However, it is also valid for functional relation variables with a specific distribution. Moreover, for variables without clear functional relationships, it considers that the correlation analysis method for such variables will fit the function expression between variables first, and then conduct comprehensive analysis to the variables. Therefore, the relationship between the two correlation analysis methods is only for different variable types, and the evaluation methods are actually consistent. When the function expression between variables is wrong, the evaluation method for variables without clear functional relationships can be used to fit the function relationship between variables to get the correct function expression, and then correlation analysis will carry out to get the final correlation coefficient.

5.   Discussion

According to the algorithm theory in this paper, the value range of the correlation value calculated by the method in this paper is between 0 and 1, and the larger the value, the stronger the correlation. In order to verify the effectiveness of the proposed method, the weighted and unweighted correlation coefficients R obtained by the new method are compared with MIC, Pearson coefficient and Mutual Information (MI). The results of the comparison are shown in Table 11, with the best results are shown in bold, and the suboptimal results are marked with the * sign. In addition, for the new method, MIC and Pearson coefficients, the correlation coefficient values of them is equal to 0 when the variables are uncorrelated, while the correlation coefficient value is equal to 1 when the variables containing functional relationship with each other. For MI, the value of MI is close to 0 when the variables are uncorrelated with each other, while the value of MI is close to positive infinity when the variables with functional relationship.

1) According to the results in Table 10, in general, most of the correlation coefficients obtained by the new method are better than MIC and Pearson coefficients, and all are better than mutual information. For the functional relationship variables containing distributions, the MI value is close to 0, and the Pearson coefficient value is almost equal to 0, but there are clear regularities in the scatter plot of the variables, and the correlation coefficient value obtained by the new method and MIC is not equal to 0, which indicates that there exists correlation between the functional relationship variables containing specific distributions, but the MI and Pearson coefficient cannot measure their correlation. Therefore, according to the experimental results, Pearson coefficient can well evaluate the correlation of variables with linear relationship, MIC can better measure the correlation between variables with specific function types, and the new method can measure the functional relationship variables well. In addition, for variables without explicit functional relationship, the values obtained by the MIC and Pearson coefficient are small. However, there exist strong linear or nonlinear correlations between variables in the iris datasets, seeds datasets and the three synthetic datasets according the scatter plots which are shown in Figure 6. This indicates that MIC and the Pearson coefficient cannot evaluate the correlation of variables that subject to distributions and randomness well, but the new method can measure their correlations well

2) For the functional relationship variables containing specific distributions, according to the analysis results of the functional relationship variables that contain specific distribution, the new method has better evaluation ability for variables with obvious regularity in the scatter plots. According to the scatter plots shown in Figure 5, influenced by random error and distribution, the values of variables are non-deterministic, and there exist uncertainty and randomness in variables, but the probability that these values fall into a certain range is definite, and there exist strong regularity between variables. As shown in Table 11, there are 12 numbers of functional relationship variables that contain specific distributions in total, the unweighted results obtained by the new method are all better than MIC and Pearson coefficients, and the weighted correlation coefficient results are better than Pearson coefficients, with 8 numbers of weighted results that are better than MIC, indicating that the correlation analysis framework proposed in this paper can better evaluate the correlation of functional relationship variables that contain distributions.

3) For the experimental results of the variables without explicit functional relationships, there are 16 numbers of variable groups of datasets in total, there are 13 numbers of unweighted results obtained by the new method are better than MIC and Pearson coefficient, and for the weighted results, there are 13 numbers of results are better than MIC and 12 numbers of results are better than Pearson coefficient, respectively. Furthermore, there exist strong linear or nonlinear correlations between variables in the iris dataset, seeds dataset, wine dataset and three synthetic datasets according to the scatter plots, which are shown in Figure 6. For the variables of the iris dataset, seeds dataset, wine dataset, Two_cluster, Twomoons and Five_cluster, the correlation coefficient values of variables obtained in the proposed method are almost larger than MIC, Pearson coefficient and MI, which indicates that the new correlation analysis framework can evaluate not only correlations of variables subject to distributions and randomness, but also can evaluate linear and nonlinear correlations between variables without explicit functional relationships well.

4) The comprehensive analysis shows that MIC can measure only the correlation with specific types of functional relationships but cannot identify the type of variable with distribution, and the Pearson coefficient can evaluate only the type of linear functional relationship between variables but the rest of the relationship types cannot be well measured. However, the proposed correlation analysis framework in this paper cannot only measure the linear or nonlinear correlation of variables containing any functional relationship types, but can also evaluate the relationship of variables with functional relationships involving specific distributions. In addition, the correlation of variables with obvious regularity in the scatter plot and the correlation of variables without clear functional relationship can also be evaluated well. The proposed method comprehensively considers the degree of functional relationship between variables, the degree uncertainty of variables and the degree of dependence on the variables containing distributions, which has a more comprehensive evaluation ability and better evaluation effect.

6.   Conclusions

Most correlation analysis methods do not comprehensively consider the impact of uncertainty and distribution in variables when analyzing the correlation between variables, which leads to the neglect of regularity information in the variables, especially the strong regularity information in variables, so that the correlation coefficient values between variables with regularity calculated by traditional methods are too small, particularly the correlation coefficient values between variables with strong regularity. Moreover, it is believed that there is no correlation or weak correlation between variables. Based on the above problems, a novel correlation analysis framework of variables (RVCR-CA) is proposed in this paper, which considers the degree of functional relationship, the degree of uncertainty for the distribution of variables and the degree of dependence on the variables containing distributions. The correlation analysis framework cannot only evaluates the correlation of variables with obvious regularity in the scatter plots, but can also measure the correlation of variables without regularity in the scatter plots. In addition, for the variables without explicit functional relationships, the framework can analyze the correlation between different variables more comprehensively. In this paper, the experimental design is carried out from the perspective of the functional relationship variables containing specific distribution and the variables without clear functional relationships. Comparing the evaluation methods of correlation, such as MIC, Pearson coefficient and MI, the proposed framework cannot only measure the correlation of variables with any specific functional relationship, but can also evaluate the functional relationship variables containing specific distribution at the same time. For the variables without clear functional relationships, the new method can also better measure the correlation of variables. The proposed correlation analysis framework has a more comprehensive evaluation ability and better evaluation effect.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was supported by the National Natural Science Foundation of China (Grant No 82260849); the National Natural Science Foundation of China (Grant No 61562045); and Jiangxi University of Chinese Medicine Science and Technology Innovation Team Development Program (Grant No CXTD22015).

Conflict of interest

The authors declare that there are no conflicts of interest.

Appendix