Figure 1.
Outlook of the proposed model.
Epilepsy is a common neurological disease characterized by seizures. A person with a seizure onset can lose consciousness which in turn can lead to fatal accidents. Electroencephalogram (EEG) is a recording of the electrical signals from the brain which is used to analyse the epileptic seizures. Physical visual examination of the EEG by trained neurologists is subjective and highly difficult due to the non-linear complex nature of the EEG. This opens a window for automatic detection of epileptic seizures using machine learning methods. In this work, we have used a standard database that consists of five different sets of EEG data including the epileptic EEG. Using this data, we have devised a novel 22 possible clinically significant cases with the combination of binary and multi class type of classification problem to automatically classify epileptic EEG. As the EEG is non-linear, we have devised 11 statistically significant non-linear entropy features to extract from this database. These features are fed to 10 different classifiers of various types for each of the 22 clinically significant cases and their classification accuracy is reported for 10-fold cross validation. Random Forest and Optimized Forest classifiers reported accuracies above 90% for all 22 cases considered in this study. Such vast possible clinically significant 22 cases from the combination of the data from the database considered has not been in the literature with the best of the knowledge of the authors. Comparing with the literature, several studies have presented one or few combinations of these 22 cases in this work. In comparison to similar works, the accuracies obtained by the classifiers were highly competitive. In addition, a novel integrated epilepsy detection index named EpilepIndex (IED) is able to differentiate between epileptic EEG and a normal EEG with 100% accuracy.
Citation: N Arunkumar, B Nagaraj, M Ruth Keziah. EpilepIndex: A novel feature engineering tool to detect epilepsy using EEG signals[J]. Mathematical Biosciences and Engineering, 2023, 20(12): 21670-21691. doi: 10.3934/mbe.2023959
| [1] | Dae Hyeon Kim, Jin-Oh Park, Dae-Young Lee, Young-Seok Choi . Multiscale distribution entropy analysis of short epileptic EEG signals. Mathematical Biosciences and Engineering, 2024, 21(4): 5556-5576. doi: 10.3934/mbe.2024245 |
| [2] | Ning Huang, Zhengtao Xi, Yingying Jiao, Yudong Zhang, Zhuqing Jiao, Xiaona Li . Multi-modal feature fusion with multi-head self-attention for epileptic EEG signals. Mathematical Biosciences and Engineering, 2024, 21(8): 6918-6935. doi: 10.3934/mbe.2024304 |
| [3] | Bei Liu, Hongzi Bai, Wei Chen, Huaquan Chen, Zhen Zhang . Automatic detection method of epileptic seizures based on IRCMDE and PSO-SVM. Mathematical Biosciences and Engineering, 2023, 20(5): 9349-9363. doi: 10.3934/mbe.2023410 |
| [4] | Dominique Duncan, Ronen Talmon, Hitten P. Zaveri, Ronald R. Coifman . Identifying preseizure state in intracranial EEG data using diffusion kernels. Mathematical Biosciences and Engineering, 2013, 10(3): 579-590. doi: 10.3934/mbe.2013.10.579 |
| [5] | Xiaowen Jia, Jingxia Chen, Kexin Liu, Qian Wang, Jialing He . Multimodal depression detection based on an attention graph convolution and transformer. Mathematical Biosciences and Engineering, 2025, 22(3): 652-676. doi: 10.3934/mbe.2025024 |
| [6] | Enas Abdulhay, Maha Alafeef, Hikmat Hadoush, V. Venkataraman, N. Arunkumar . EMD-based analysis of complexity with dissociated EEG amplitude and frequency information: a data-driven robust tool -for Autism diagnosis- compared to multi-scale entropy approach. Mathematical Biosciences and Engineering, 2022, 19(5): 5031-5054. doi: 10.3934/mbe.2022235 |
| [7] | Sakorn Mekruksavanich, Wikanda Phaphan, Anuchit Jitpattanakul . Epileptic seizure detection in EEG signals via an enhanced hybrid CNN with an integrated attention mechanism. Mathematical Biosciences and Engineering, 2025, 22(1): 73-105. doi: 10.3934/mbe.2025004 |
| [8] | Xian Hua, Jing Li, Ting Wang, Junhong Wang, Shaojun Pi, Hangcheng Li, Xugang Xi . Evaluation of movement functional rehabilitation after stroke: A study via graph theory and corticomuscular coupling as potential biomarker. Mathematical Biosciences and Engineering, 2023, 20(6): 10530-10551. doi: 10.3934/mbe.2023465 |
| [9] | Ravichandra Madanu, Farhan Rahman, Maysam F. Abbod, Shou-Zen Fan, Jiann-Shing Shieh . Depth of anesthesia prediction via EEG signals using convolutional neural network and ensemble empirical mode decomposition. Mathematical Biosciences and Engineering, 2021, 18(5): 5047-5068. doi: 10.3934/mbe.2021257 |
| [10] | Ming Meng, Luyang Dai, Qingshan She, Yuliang Ma, Wanzeng Kong . Crossing time windows optimization based on mutual information for hybrid BCI. Mathematical Biosciences and Engineering, 2021, 18(6): 7919-7935. doi: 10.3934/mbe.2021392 |
Epilepsy is a common neurological disease characterized by seizures. A person with a seizure onset can lose consciousness which in turn can lead to fatal accidents. Electroencephalogram (EEG) is a recording of the electrical signals from the brain which is used to analyse the epileptic seizures. Physical visual examination of the EEG by trained neurologists is subjective and highly difficult due to the non-linear complex nature of the EEG. This opens a window for automatic detection of epileptic seizures using machine learning methods. In this work, we have used a standard database that consists of five different sets of EEG data including the epileptic EEG. Using this data, we have devised a novel 22 possible clinically significant cases with the combination of binary and multi class type of classification problem to automatically classify epileptic EEG. As the EEG is non-linear, we have devised 11 statistically significant non-linear entropy features to extract from this database. These features are fed to 10 different classifiers of various types for each of the 22 clinically significant cases and their classification accuracy is reported for 10-fold cross validation. Random Forest and Optimized Forest classifiers reported accuracies above 90% for all 22 cases considered in this study. Such vast possible clinically significant 22 cases from the combination of the data from the database considered has not been in the literature with the best of the knowledge of the authors. Comparing with the literature, several studies have presented one or few combinations of these 22 cases in this work. In comparison to similar works, the accuracies obtained by the classifiers were highly competitive. In addition, a novel integrated epilepsy detection index named EpilepIndex (IED) is able to differentiate between epileptic EEG and a normal EEG with 100% accuracy.
Epilepsy is a tenacious brain disorder that can affect anyone irrespective of their age [1]. Epilepsy occurs due to abnormal or excessive brain discharges of brain nerve cells. There will be a sudden onset of several neurons firing at the same time concurrently. According to the World Health Organization (WHO) report that is updated in February 2023 about 50 million population in the world are suffering from epilepsy [2]. Several of them (80%) are from the countries of low and middle income. WHO also feels that if they are diagnosed at the right time and properly treated 70% of them can live free from epilepsy. The risk of untimely death is three times more for epileptic patients than the normal people [2]. In many places of the world, people with epilepsy are not received well by the general public. Epilepsy has been one of the oldest diseases dating back to 4000 BC with the written records [2]. All these makes it very important to diagnose epilepsy and give the right treatment for the affected people.
The Electroencephalogram (EEG) is a recording of the brain activity which is acquired from the scalp. EEG has been used in the diagnosis of epilepsy since a long time. Recently Magnetic Resonance Imaging (MRI) has also been used in the diagnosis of epilepsy. Predominantly, EEG is being used in epilepsy diagnosis for it is easy to acquire them even for 24-hour recordings.
Much literature is available for automatic classification of epileptic EEG. Generally, the researchers use either the long term EEG recordings or short EEG segments for classification of epileptic EEG. Bonn University data has short term EEG segments [3]. Various literatures have presented binary and multiclass classification problems for this database [4,5,6]. In this study, we have presented 22 different clinically significant cases of Binary and Multiclass classification problems for this database which is not in the literature to the best of knowledge of the authors. A novel IED is also presented for easy identification of epileptic EEG from the normal EEG. A synopsis of the earlier works on Binary and Multiclass problems for this database is discussed as below. Zeng et al used Hurst exponent to classify the three types of EEG from this database [7]. They used support vector machines (SVM), Linear discriminant analysis (LDA) and a decision tree for classification. LDA achieved the highest accuracy of only 76.7%. Wang et al attempted to classify preictal and ictal using discrete wavelet transform and SVM and yielded a result of 99.9% accuracy [8]. Kaleem et al. presented predictive models and used empirical mode decomposition to extract the features and used SVM classifier yielding 88.3% accuracy [9]. Oliva et al. used measurements from bispectrogram, power spectrum and spectrogram as features along with back propagation based multilayer perceptron as a classifier and yielded an accuracy of 100% for the binary class and 98% for the multiclass type classification problem [10]. Like this, there is literature where various methods are presented yielding various ranges of accuracies up to 100% accuracy. Our method presented in this work is novel in terms of using 22 various cases of clinically significant 2–5 class classification problems of epilepsy detection using a combination of 11 unique promising non-linear features across ten different classifiers to yield the best possible accuracy under each respective 22 cases studied. We believe this is the first kind of such a detailed study in the literature for this database. We also devised a novel EpilepIndex IED index which is able to distinguish the epileptic EEG with the normal EEG, which will be a handy tool in a clinical setup.
This paper is organized in the following way. Section 2.1 presents our proposed model of our study and Section 2.2 lists the database that we have considered for our study in this work. The various features proposed to be extracted from the database considered is discussed in Section 3. Section 4 presents the various types of classification problems from binary class to several multiclass classification problem. In this study, we have listed 22 different clinically significant cases of classification problems for this data. This is the first time in the literature such detailed cases are studied for this database to the best of knowledge of the authors. The various classifiers used in this study along with their performance evaluation metrics is presented in the Section 5. The results and discussions from this study forms the Section 6. We present the conclusion in Section 7.
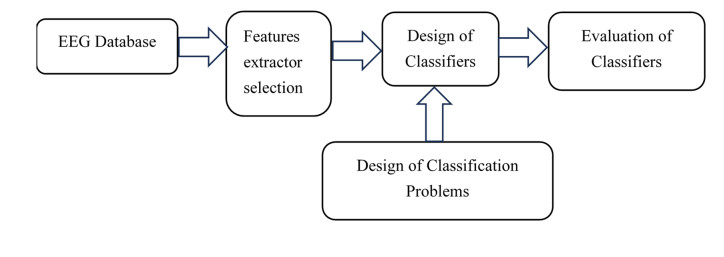
An outlook of our proposed model is shown in the Figure 1. The raw EEG data from the database is supplied to the various non-linear features extractor. The extracted features are evaluated for significance using ANOVA. Then the significant features are feed to various classifiers, which are then evaluated further about the accuracy of the classifiers.
The highly used benchmark database of EEG data is the Bonn University database which is publically available [3]. This data has five sets of EEG data in five categories recorded from 5 patients. We have denoted these five sets as Sets A–E. The specific type of each of these sets are presented in the Table 1. Each set of data contain 100 segments of EEG data, which are sampled at 173.61 Hz with 12-bit A to D resolution. They were filtered using a band pass filter 0.53 to 40 Hz with 12 dB/ octave. Each segment is for a fixed duration of 23.6 seconds, thus yielding 4067 samples in each type. The Figure 2 shows sample data from each category of this dataset. Thus, we have a total of 500 EEG segments each with 4067 samples. Sets A and B are from five healthy volunteers with their eyes open and close respectively following the standard International 10–20 electrode placement system over the scalp. Sets C and D were the recordings of epileptic patients during seizure free intervals with the help of depth electrodes implanted into hippocampal formations (Set C) and from the epileptogenic region (Set D). These were also called as preictal EEG in the literature [4]. Set E is the recordings of EEG when the patient is experiencing seizures from both strip and depth electrodes placed in the neocortex basal and lateral regions. This is also called Ictal EEG [4].
| Type | Description |
| Set A | EEG Segments of healthy volunteers with their eyes open |
| Set B | EEG Segments of healthy volunteers with their eyes closed |
| Set C | EEG Segments from hippocampal formation of the opp. side of the brain |
| Set D | EEG Segments from within epileptogenic zone |
| Set E | EEG Segments during the seizure activity |
DownLoad:
CSV
This database serves as one of the benchmark database for various researches to compare their model with the result of others who have developed other models in the literature. In addition, this dataset is small and yet robust, presenting five different categories of EEG data which is excellent for developing multiclass classification problem. The disadvantage is again as the small size.
The feature extractor extracts 11 different non-linear features from the EEG database. The raw EEG data is fed into the feature extractor. The 11 various non-linear features extracted are Approximate Entropy (ApEn), Sample Entropy (SampEn), Fourth order Cumulant (Cum), Fractal dimension (FD), Hurst Exponent (H), Fuzzy Entropy (Fz), Kolmogorov entropy (K), Kurtosis (Ku), Permutation Entropy (P), Reyni's entropy (Re) and Tsallis entropy (TE). These features are amply available in the literature [4,5,6] for the applications of measures of various kinds of complexities including epilepsy. Hence, we are presenting a short discussion of them here.
Entropy measures the disorderliness in the system. ApEn has been in the literature for a long time to measure the complexity of a system. This has been used in the detection of epilepsy in various literature [4,5,6]. The EEG signal is a complex signal whereas epilepsy signal is mostly repetitive. Hence, measuring the entropy of it gives a unique value and this can be useful as a feature towards automatic detection of the epilepsy signal. Given embedding space BA with samples s(1), s(2), s(3), …, s(S), where S is the total number of sample points, ApEn is defined as
| ApEn(A,b,S)=1S−A+1∑S−A+1k=1 logDmk(b)−1S−A∑S−Ak=1 logDm+1k(b) | (1) |
where
| DAk=2SA(SA−1)∑SAk=1 ∑SAl=1,l≠i Θ(b−∥xk−xl∥) | (2) |
SampEn measures complexity of any time series. Sample entropy is a better form of ApEn entropy where the self matches are not added [6]. Higher measure of SampEn indicates that the signal is more complex and lower measure of it indicates that the signal is less complex. We believe SampEn would be a resourceful feature in our study as well.
In statistics, cumulants provide an alternative to moments. Biomedical signals are highly non-linear in general. EEG as already stated is very random. Epileptic signals are relatively repetitive. Thus, higher order cumulant could be a good feature to discriminate them. The first order cumulant is mean, the second order cumulant is variance and the third order cumulant is the third central moment. The fourth order cumulant is different from the third order. The fourth order cumulant is also used in the literature for EEG [6]. Hence, in this study, we have used the fourth order cumulant as a feature.
Kolmogorov entropy is another form of entropy which calculates the uncertainty of a signal over time. Normal EEG and an epileptic EEG has a lot of variation in the uncertainty. Thus, we propose to use this Kolmogorov entropy as a feature in our study.
Hurst exponent identifies the self-similarity of a time series. It also detects how smooth a time series is in relation to the asymptotic behavior of it. This derives its name from Harlod Edwin Hurst who developed this exponent in relation to hydrology to size a dam. If N is sample data duration, the rescaled range being RS/std, RS being the mean difference between maximum deviation and minimum deviation and std being the standard deviation, Hurst Exponent (H) is defined as
| H=log(Rs/std)log(N) | (3) |
The slope of the above equation gives the Hurst exponent (H). H was applied to various other types of research including epilepsy detection [6]. We have used Hurst exponent in our study, assuming it will be a promising feature for our data.
Fractal geometry is the origin of fractal dimension. FD can detect transients. Hence, it can be used as a feature towards detection of epileptic seizure. A fractal is considered to be a geometric shape that can be divided into smaller shapes, and each of these shapes represent the original in a reduced form. FD can be calculated in various methods for any signal. The standard method used in the literature [6] is considered in this study.
Kurtosis measures the tail details of the distribution of the signal. This is the fourth order of statistical moments. Kurtosis informs about how the data in the distribution is dense in the tails in opposite to the mean. This will be a salient feature as it has the capacity to present the information at the tail of the distribution of the signal.
Fuzzy entropy calculates the unpredictability of any signal. The nature of the EEG signal being highly unpredictable makes Fuzzy entropy a valid choice for extracting the salient features of the signal. Fuzzy entropy has been already used for EEG signal [11,12,13,14]. We have used the same calculations as presented from the literature [11] in this study.
The Reyni's entropy (Re) is yet another wise tool which is used in the literature for EEG signal and other areas. We have used the method devised by Arunkumar et al. for calculating Re in this study [14].
Permutation entropy is there in the literature for long time. This has been applied towards EEG signals as well [11]. Here, we have used the method as presented by Arunkumar et al. [14] to calculate the PE.
TsE has been in the literature for various applications. In this paper, we have devised the method as described by Rajeeva Sharma et al. [11] to calculate the TsE. The non extensivity index is fixed at 2 for calculating the TsE for the EEG data in this study.
This novel combination of these specific 11 cured feature set have not been used in the literature earlier, to the best of our knowledge.
A number of features are generally extracted by the feature extractor. All may not be significantly contributing to discriminating the two sets of the EEG—the epileptic EEG and the normal EEG. Hence, it becomes important to rank the features using their differentiating power between the normal EEG and epileptic EEG. The idea is to feed only the significant features to the classifier, thereby reducing the load on the classifiers which in turn will improve the performance of the classifiers. In order to identify the significant features, we have used students' t test [11]. Then, the significant features are presented to the classifiers for classification.
We have investigated several binary and multiclass classifiers for this database. In essence, we have devised 4 types of classification problems. It should be noted that such type of diversified classification problem definition has not been in the literature for this database to the best knowledge of the authors. They are presented below.
Type I: Binary classification problem—2 classes
Type II: Multiclass classification problem—3 classes
Type III: Multiclass classification problem—4 classes
Type IV: Multiclass classification problem—5 classes
The significance of each case under each type is explained in their respective cases as below.
Binary classification is very common for all learning problems where the machine is trained to distinguish between the two classes. This is a standard benchmark classification tool before going to multi class classification problem. This type of classification problem is an essential type in relation to epilepsy as well. We have to develop an automated system to tell if the EEG considered is epileptic or normal. This forms as a binary type of classification problem for this study. Considering the database that we have taken for this study [3], we have listed all the various possible Binary classification or the 2 class classification problem in Table 2. It can be seen that there are thirteen different scenarios here that are listed from Case 1 to Case 13. The purpose and clinical significance of each of these cases is presented in their respective sections as presented below.
| Type I | Binary Classification (2 Class) |
| Case 1 | Set A vs Set E |
| Case 2 | Set B vs Set E |
| Case 3 | Set A, B vs Set E |
| Case 4 | Set A vs Set C |
| Case 5 | Set A vs Set D |
| Case 6 | Set B vs Set C |
| Case 7 | Set B vs Set D |
| Case 8 | Set C vs Set D |
| Case 9 | Set C vs Set E |
| Case 10 | Set D vs Set E |
| Case 11 | Set A, B vs Set C, D |
| Case 12 | Set C, D vs Set E |
| Case 13 | Set A, B, C, D vs Set E |
DownLoad:
CSV
Case 1 (Set A vs Set E): As we have learned about each set of data for this database [3], we know that Set A is healthy individuals with their eyes open and Set E is from the patients with epilepsy during their seizure. This case presents 2 class classification problem between Sets A and E. This is significant to discriminate between the normal class and the epileptic class to build the classifier for automated diagnosis.
Case 2 (Set B vs Set E): Case 2 is similar to Case 1, but Set B is EEG data with eyes closed verses Set E which is the epileptic EEG. Thus, this case also trains the classifier to detect between the normal and epileptic EEG. This is also essential to develop automated diagnosis of epilepsy.
Case 3 (Set A, B vs Set E): Here, we combine Sets A and B to be in a single class as both these sets are from healthy individuals. Set E belongs to the other class, and we have attempted another type of 2 class classification problem.
Case 4 (Set A vs Set C): In this case, we can see that it is between Sets A and C. As we know Set A is a normal EEG data but Set C is from epileptic patients but data is acquired when they are not experiencing seizures or during the intermittent time of seizures (Inter Ictal). Developing an automatic system to differentiate between Normal and Inter Ictal class is also most necessary as a pre tool towards prediction of the onset of epileptic seizures.
Case 5 (Set A vs Set D): Case 5 is similar to Case 4. Set D is also of the type of Inter Ictal, but from an epileptogenic region of the brain, whereas Set C is from the hippocampal region. Again, a machine learning classifier is supposed to discriminate between a healthy individual and another type of Inter Ictal EEG which comes from the epileptogenic region.
Case 6 (Set B vs Set C): This case gives a 2 class classification problem which will lead to discrimination between healthy eyes open EEG data with the Inter Ictal EEG data.
Case 7 (Set B vs Set D): This is similar to Case 6. The difference is that the automatic detection tool will become robust in its design when learning to differentiate various type of clinical data. It should be noted that such kind of detailed 2 class classification has not been in the literature for this database as far as the knowledge of the authors.
Case 8 (Set C vs Set D): This is an interesting case that we have considered to evaluate our binary classifier to discriminate fine between the two types of Pre Ictal EEG data. This will test the performance of the classifier for these two similar yet different data.
Case 9 (Set C vs Set E): In this case, we have given Inter Ictal and Ictal as 2 class problem to the classifiers. This is another interesting case, as clinically Inter Ictal stage is followed by the Ictal stage. This discrimination will give a way towards building predicting tools for epilepsy. This will be helpful in situations when the epileptic patient is swimming or driving and if they get an onset of a seizure, they will lose consciousness, which can lead to a fatal accident. If the patient can be informed of the oncoming seizure via prediction by identification of Inter Ictal EEG and discriminate it from the Ictal type, it could provide ample time for the patient to get to a safe location.
Case 10 (Set D vs Set E): Again, this case would be similar to the previous Case 9, but this would be another type of Inter Ictal EEG. A robust automatic tool is supposed to get trained well with all aspects of Inter Ictal EEG to discriminate it from the Ictal type of EEG.
Case 11 (Set C, D vs Set E): This case is similar to Case 3. In Case 3, we have combined the healthy data together and contrasted with the Ictal EEG, but we have combined both the Inter Ictal EEG with the Ictal EEG. This is clinically significant to study the onset of epileptic seizures.
Case 12 (Set A, B vs Set C, D): Here, we have combined both Sets A and B to form a single class as normal class. Sets C and D are combined together as they both are typically Inter Ictal EEG and they form Inter Ictal Class forming another nature of a binary classification problem for the dataset considered in our work.
Case 13 (Set A, B, C, D and Set E): This is a peculiar case where Sets A–D are all combined together to form a single class as they all are indirectly normal EEG in comparison to the seizure EEG or Ictal EEG, which is the real epilepsy onset where the person starts to experience convulsions which can lead to loss of consciousness. The system in real time is supposed to have clear discrimination between these two categories and forms the last case in our Binary classification problem.
In general machine learning algorithms are designed for 2 class classification problems, but in reality, mostly multiclass classification problems exist. The database that we have considered have 5 different types of data. The various clinically significant Case 3 class classification problem are listed in Table 3 and discussed as below. As listed in the Table 3, we have 5 different cases of 3 class classification problem for the database considered. A short summary of each of these cases is presented as below with their clinical significance.
| Type II | Multiclass Classification (3 classes) |
| Case 14 | Set A vs Set C vs Set E |
| Case 15 | Set B vs Set D vs Set E |
| Case 16 | Set A vs Set D vs Set E |
| Case 17 | Set B vs Set C vs Set E |
| Case 18 | Set A & Set B vs Set C & Set D vs Set E |
DownLoad:
CSV
Case 14 (Set A vs Set C vs Set E): This case has 3 classes of normal (with eyes closed), Inter Ictal and Ictal from Set A, Set C and Set E. This is the real situation of real-world offline applications where an automatic detection tool is supposed to discriminate for the epilepsy detection.
Case 15 (Set B vs Set D vs Set E): This is another set of 3 classes problem which we have defined with the data where the first class will be from healthy subjects from eyes open (Set B), the second class from another set of Inter Ictal EEG (Set D) and third class is the epileptic EEG (Set E).
Case 16 (Set A vs Set D vs Set E): Here, healthy subjects with their eyes closed is considered as one class, Set D—another type of pre Ictal is considered as the second class and the third class is taken as the epileptic EEG. This is a typical case of a real world scenario where an epileptic person can have normal or pre Ictal or epileptic EEG at any point of time. The device is supposed to identify all the three types correctly avoiding false positives.
Case 17 (Set B vs Set C vs Set E): In this case, using healthy subjects with their eyes open, inter ictal EEG and the epileptic EEG are considered as various 3 classes. This is also a challenge to the machine to detect all the three different classes correctly. All these are essential for building a robust design and identify how various classifiers are going to perform. Hence, we have considered this case also as it is highly relevant to clinical significance.
Case 18 (Set A & Set B vs Set C & Set D vs Set E): This is an interesting case, as all the healthy subjects EEG data (Sets A and B) are considered to be one class. All the inter ictal EEG (Sets C and D) are considered to be together in another class, and in the third class we have the epileptic EEG.
Type III presents various possible clinically significant 4 classes classification problem as listed in Table 4. This is a novel study in our work where we have considered 3 different cases of 4 classes' classification problem. This is referred as Type III of our multiclass classification problem. Cases 19 to 21, as listed in Table 4, encompass 4 classes from the considered database, which have 5 different types of EEG data.
| Type III | Multiclass classification problem (4 classes) |
| Case 19 | Set A vs Set B vs Set C vs Set E |
| Case 20 | Set A vs Set B vs Set D vs Set E |
| Case 21 | Set A vs Set C vs Set D vs Set E |
DownLoad:
CSV
When a neurologist visually examines a patient, they will classify between all these categories of data and tries to locate the epileptic EEG with his intelligence and experience. This is subjective and it will vary between neurologists. The automated tool designed will remove this subjective evaluation and should present concurrent results. Thus, when we are designing an automatic tool for detecting epilepsy, we have to consider the real-world situation (Type III) and attempt to replicate the intelligence and experience of the trained doctor.
Here, we have taken each of the five EEG dataset from the considered database to form five different classes. This also mimics the real-world discrimination of a neurologist doctor who is looking for epileptic patterns in the long-time recordings of the EEG. This is considered as Type IV of multiclass classification problem considering 5 classes which forms the Case 22 in our experiment. This experiment is also a novel case presented in our study.
| Type IV | Multiclass classification problem (5 classes) |
| Case 22 | Set A vs Set B vs Set C vs Set D vs Set E |
DownLoad:
CSV
In this study, we have considered 10 different types of classifiers. They belong to various categories as Bayesian classifier, function-based classifier, meta classifier, rule-based classifier and decision tree-based classifier. The various classifiers considered in this study are Naïve Bayes, Multilayer Perceptron (MLP), Simple Logistic (SL), Radial Basis Function Classifier (RBF), Multiclass Classifier, Multi objective Evolutionary Fuzzy Classifier (MOEF), Non-Nested Generalized Exempler Classifier (NNge), Optimized Forest, J48 Classifier and Random Forest. The type of each of these classifiers is shown in the Table 6.
| Classifier | Nature / Type |
| Naïve Bayes | Bayesian type classifier |
| Multilayer Perceptron (MLP) | Function based classifier |
| Simple Logistic (SL) | Function based classifier |
| Radial Basis Function classifier (RBF) | Function based classifier |
| Multiclass classifier | Meta type classifier |
| Multi Objective Evolutionary Fuzzy classifier (MOEF) | Rule based classifier |
| Non-nested Generalized Exempler (NNge) | Rule based classifier |
| Optimized Forest classifier | Decision Tree type classifier |
| J48 classifier | Decision Tree type classifier |
| Random Forest classifier | Decision Tree type classifier |
DownLoad:
CSV
All these classifiers were used in all the Types I–IV (22 cases) of the classification problems that was presented. All the classifiers considered in this study were executed using the Waikato Environment for Knowledge Analysis (WEKA) tool and computed to their default settings of WEKA [15].
We have used 10-fold cross validation. This gives reliable classification performance for any data. The classifiers are evaluated based on their accuracy in their classification. In the literature there are several other performance metrics such as sensitivity, specificity. Here, we have focused on presenting the accuracy of the classifier as this is most essential towards building an automatic tool for epilepsy detection. Accuracy is defined as the ratio between total numbers of correctly classified EEG segments (TC) with the total number of EEG segments (TNO). Listing all the other performance metrics for all the 22 cases discussed will make the study very detailed and incoherent to the purpose.
| Accuracy = TC/TNO | (4) |
where TNO = TP + TN + FP + FN, TC = TP + TN, TP = True Positives, TN = True Negatives, FP = False Positives and FN = False Negatives.
To make a more meaningful way for easy detection of epileptic EEG, we have developed the EpilepIndex IED index from the features that discriminate between the normal EEG with the epileptic EEG. This concept of Integrated Index is available in the literature for various applications [11]. Here, the most significant features based on its highest p value is considered. With trial and error method, we have devised the following equation for the index IED using the top ranked four features. We have discussed the details of this index in the Section 6.3.
| IED=[100(k∗ApEn)2+10(SampEn+Re2)]475−6 | (5) |
The raw EEG data taken from the database is fed into the feature extractor. As discussed before, the feature extractor extracts all the 11 features (ApEn, SE, FD, Cum4, FzE, K, Kut, H, Pe, Re and TsE) for each of the data in all sets. Table 7 presents the mean and standard deviation of all 11 feature values for the Case 1 (Set A vs Set E). Statistical t test is performed on all these features to identify the p-value which evaluates the significance of these features for discriminating the various category of data. The features are ranked based on its p value, the lowest p value obtaining the rank 1. Re obtains the lowest p value and it is marked in bold. Thus, we can understand that Re has the highest discriminating capacity for this case. It is found that the p value obtained is very less than 0.05 for all features except FzE, which implies that all the features extracted except FzE for this database are statistically significant. All the 22 cases considered in this study are evaluated similarly and only Case 1 is discussed above as a representative.
| Features | Mean (Set A) | Std (Set A) | Mean (Set E) | Std (Set E) | p-value | Rank |
| ApEn | 0.548374 | 0.060308 | 0.651661 | 0.061226 | 3.8 E-22 | 4 |
| SampEn | 1.010935 | 0.163356 | 0.495863 | 0.144952 | 2.04 E-34 | 3 |
| Cum4 | 953423.9 | 1518535 | 1.02E+10 | 3.79E+10 | 0.008 | 8 |
| FD | -1.49284 | 0.073948 | -1.316 | 0.113469 | 1.4 E-12 | 7 |
| H | 0.657052 | 0.061209 | 0.435487 | 0.096808 | 0.016 | 9 |
| FzE | 0.027913 | 0.012109 | 0.021897 | 0.010435 | 0.2 | 11 |
| K | 5.624378 | 0.243047 | 7.120629 | 0.523022 | 2.34 E-37 | 2 |
| Kut | 3.226986 | 0.269942 | 3.428355 | 1.187349 | 0.039 | 10 |
| PE | 1.486605 | 0.05663 | 1.235531 | 0.088102 | 1.39 E-20 | 5 |
| Re | -15.9675 | 0.500365 | -19.5353 | 1.018548 | 1.62 E-43 | 1 |
| TsE | -9759521 | 5089083 | -4.8E+08 | 4.11E+08 | 3.07 E-19 | 6 |
DownLoad:
CSV
These significant features are fed as input to the various classifiers considered. Each classifier is tested with 10-fold cross validation. The classification results for each type of classification problem are presented below.
1) Type I
Type I consists of 13 cases of binary classification problems. All ten proposed classifiers are tested for each of the 13 cases considered. The accuracies achieved by each of the classifiers are presented in the Table 8. The highest accuracy achieved for each case is highlighted in bold.
| Classifiers /Type I |
A vs E (Case 1) |
B vs E (Case 2) |
AB vs E (Case 3) |
A vs C (Case 4) |
A vs D (Case 5) |
B vs C (Case 6) |
B vs D (Case 7) |
C vs D (Case 8) |
C vs E (Case 9) |
D vs E (Case 10) |
CD vs E (Case 11) |
AB vs CD (Case 12) |
ABCD vs E (Case 13) |
| Naïve Bayes | 100 % | 99 % | 99 % | 98 % | 91.5 % | 95.5 % | 87 % | 67.5 % | 99.5 % | 94.5 % | 96.37 % | 78 % | 97 % |
| MLP | 100 % | 99.5 % | 99.67 % | 97.5 % | 97.5 % | 98.5 % | 99.5 % | 86.5 % | 99.5 % | 98 % | 99 % | 97.75 % | 99.4 % |
| Simple Logistic | 100 % | 98.5% | 99.67 % | 98.5 % | 98 % | 98.5 % | 99 % | 83.5 % | 98.5 % | 97.5 % | 98.6 % | 98.75 % | 98.6 % |
| RBF | 100 % | 99.5 % | 99.67 % | 96.5 % | 98 % | 99.5 % | 99.5 % | 83 % | 100 % | 98 % | 99 % | 98.25 % | 97.8 % |
| MultiClass classifier | 99.5 % | 98 % | 100 % | 94.5 % | 97 % | 99.5 % | 99 % | 86.5 % | 99 % | 98 % | 98 % | 97.75 % | 97.6 % |
| Multiobjective evolutionary fuzzy Classifier | 99.5 % | 97 % | 97.67 % | 93.5 % | 96.5 % | 92.5 % | 98.5 % | 77.5 % | 98 % | 96 % | 98 % | 94.75 % | 97.6 % |
| NNge | 100 % | 99 % | 99 % | 95.5 % | 97 % | 97.5 % | 97 % | 83 % | 98 % | 97.5 % | 97.67 % | 96 % | 97.4 % |
| Optimized Forest | 100 % | 98.5 % | 98.67 % | 98 % | 98 % | 97.5 % | 98 % | 86.5 % | 99 % | 98.5 % | 99 % | 97.25 % | 98.4 % |
| J48 | 99.5 % | 97.5 % | 98 % | 97 % | 97 % | 97 % | 94.5 % | 82 % | 99 % | 99.5 % | 99.3 % | 95 % | 98.8 % |
| Random Forest | 100 % | 98.5 % | 98.3 % | 98 % | 98 % | 98 % | 98.5 % | 86 % | 99 % | 98.5 % | 99.3 % | 97.25 % | 98.6 % |
DownLoad:
CSV
Case 1: It can be noted from the table that for case 1, almost all the classifiers have given 100 percent accuracy classifying Set A and Set E correctly. This shows that the feature set that we have considered in this study is extremely suitable in discriminating all the 100 data from each set A and E correctly. A 100 percent accuracy is achieved by various classifiers namely Naïve Bayes, MLP, SL, RBF, NNge and optimized forest classifiers. The other 3 classifiers presented an accuracy with 99.5%. Our investigation finds that all classifiers considered for this case is able to accurately classify between the normal EEG and the epileptic EEG.
Case 2: Case 2 presents another type of normal EEG (with eyes closed) with the epileptic EEG (Set B vs Set E). Here, we can see that the highest accuracy achieved is 99.5% by the MLP and the RBF classifier. The lowest accuracy was achieved by MOEF at 97%. Although 100% accuracy was not achieved by any of the classifier for this case, we can see that all the classifiers considered reported over 97% accuracy.
Case 3: The next interesting case is case 3 where 100% accuracy was obtained by MC Classifier. This proves that our feature combinations possess the ability discriminate all the normal EEG and the epileptic EEG. Five of the other classifiers namely Naïve Bayes, MLP, SL, RBF and NNge all produced accuracies over 99%. The lowest accuracy for case 3 was reported at 97.67% by the MOEF classifier.
Case 4: Here, we move into Set A vs Set C. The highest accuracy was achieved by SL with 98.5%. Generally, to classify a normal EEG with the preictal EEG is very difficult, as can be seen from literature. Our study produced 98.5% with the SL classifier. It can be observed that even the lowest accuracy was reported at 93.5% with the MOEF classifier.
Case 5: This case is similar to case 4 normal vs preictal EEG. Four classifiers, namely SL, RBF, Optimized Forest and Random Forest, gave 98% highest classification accuracy. This demonstrates the robustness of our feature set which was given as input to these classifiers. More than one classifier is able to give the same highest accuracy proving that our selected classifiers are performing well.
Case 6: In this case, we try the binary classification with Normal subjects with their eyes closed with the preictal EEG. 99.5% classification accuracy is reported by RBF and Multiclass classifier proving the versatile nature of our feature set to classify various type of EEG accurately. Even the lowest accuracy stands at 92.5% by the MOEF classifier.
Case 7: This is similar to case 6 but with different preictal EEG as input. MLP and RBF gave the highest accuracy at 99.5% with just one error. On the other hand, Naïve Bayes resulted only in 87%. This lower accuracy of Naïve Bayes cannot be marked because of the feature set, as the same feature set with MLP and RBF produced 99.5% accuracy. All other classifiers result with an accuracy above 97% except J48 classifier with an accuracy of 94.5%. Hence, the accuracy reported by Naïve Bayes is inherent to its own classification algorithm and thus cannot be attributed to the proposed feature set.
Case 8: This is a peculiar case. From the clinical point of view, Sets C and D are preictal type EEG but with different areas of acquisition. This can be seen from the classifier results that none of the classifiers considered were not able to produce accuracy higher than 86.5%. We have considered this case to evaluate the classifier how they behave for almost similar type of data. The failure of the classifiers for this case is evident when the case is seen from the clinical point of view.
Case 9: This is another interesting case - preictal EEG vs Epileptic EEG. Preictal EEG is a kind of EEG which comes before the onset of epileptic seizure. Hence, an automatic tool to detect the epileptic EEG in real time for patients should be made to learn the preictal type of EEG and this automatic detection tool has to discriminate it with the epileptic EEG. RBF achieves 100% accuracy for this case, which is a remarkable achievement for any artificial intelligence (AI) tool for this important case. This can be further experimented and developed towards predicting the onset of epileptic seizures in real time, which is the ultimate aim of the research in automatic detection of epileptic EEG using the AI tools. We are happy to present this result to researchers where this can be further evaluated towards real time detection. All other classifiers considered in this study also reported accuracies above 98%.
Case 10: This is similar to the previous case, where another set of preictal (Set D) vs the epileptic EEG is considered. In this case also, 99.5% accuracy is achieved by the J48 classifier. This again illustrates that the considered feature set is extremely good in providing ability for the classifiers to classify accurately across all types of EEG for the given dataset.
Case 11: This case is considered to further rigorously test our classifiers. Here, we have combined both types of preictal type EEG (Set C and Set D) and tested the classifiers if they can discriminate with the epileptic EEG (Set E). We can see that 99.3% accuracy is obtained by J48 and Random Forest classifiers. The lowest accuracy at 96.37% by the Naïve Bayes classifier. All other classifiers have reported accuracies above 97.6%. Thus, this case further clearly demonstrates the more robustness of the feature set to solving real time detection of epileptic EEG and prediction of the onset of the epileptic EEG.
Case 12: This is another important case where both types of normal EEG are considered to be in a class and both types of preictal EEG are considered to be in another class. The significance of this case is that an AI tool is supposed to ecognizes a normal EEG and a preictal EEG where the patient can be altered about the possibility of the upcoming epileptic seizure onset. If this variation can be detected in real time, then this will give ample time for the patient to move to a safe location if the patient was driving or swimming as the onset of epileptic seizure can lead of loss consciousness. The proper classification that is needed in this case is also important to reduce the false positive alarms. Here, we can see that SL brings out an accuracy of 98.75% which is highly appreciated. Except for Naïve Bayes, all other classifiers resulted in accuracies above 94.75%. The lowest accuracy obtained by Naïve Bayes at 78% needs further evaluation.
Case 13: This case is also very important where all types of EEG from the dataset except the epileptic EEG is considered to be in a class and epileptic EEG in another class. Thus, 400 data (Sets A–D) in one class and 100 data (Set E) in other class. Ultimately, any AI tool has to discriminate correctly between other types of EEG with the epileptic EEG. This particular aspect is evaluated in this case and we can see that the highest accuracy is achieved by the MLP classifier at 99.4% which is excellent. It should be noted that all the other classifiers also resulted in accuracies higher than 97%. All these experiments clearly demonstrates that the feature set considered in this study forms a versatile set in designing an AI based tool for automatic detection of epileptic EEG. An interesting observation about the RBF is worth highlighting here. It can be observed that RBF has attained the highest accuracy for six different cases (cases 1, 2, 5, 6, 7 and 9) among the thirteen presented. Thus, for binary classification, RBF classifier looks a good choice towards design of AI tool for binary classification of epileptic EEG. Naïve Bayes, on the other hand, has produced very low accuracies for Cases 7 and 12. It should also be noted that MOEF classifier although produced accuracies above 92% for all the thirteen cases considered, but did not produce the highest accuracy for any of the considered cases.
2) Type II
Type II is a multiclass classification problem presenting the various possible three class classification problem. The accuracies obtained in each case under Type II is presented in the Table 9.
| Class/Type | A vs C vs E (Case 14) |
A vs D vs E (Case 15) |
B vs C vs E (Case 16) |
B vs D vs E (Case 17) |
AB vs CD vs E (Case 18) |
| Naïve Bayes | 97.6% | 89.6% | 95.3% | 86.6% | 81.2% |
| MLP | 98.6% | 97.3% | 98.6% | 98.6% | 98% |
| Simple Logistic | 97.6% | 97.67% | 98.3% | 98.3% | 98% |
| RBF | 95.33% | 97.33% | 96.33% | 97.33% | 96% |
| Multiclass Classifier | 96.33% | 96% | 97.67% | 95.67% | 96.6% |
| Multiobjective evolutionary fuzzy Classifier | 92.33% | 92.33% | 89.67% | 89.33% | 89.4% |
| NNge | 96.33% | 96.33% | 97.33% | 95.67% | 95.4% |
| Optimized Forest | 98% | 97.67% | 96.33% | 97.67% | 97.2% |
| J48 | 96.6% | 97.3% | 95% | 93.3% | 93.8% |
| Random Forest | 98% | 97.6% | 97% | 97.3% | 97.2% |
DownLoad:
CSV
Case 14: This is a vital case where the classifier is tested for real world situations where there is a normal EEG (Set A), PreIctal EEG (Set C) and Epileptic EEG (Set E). MLP leads all the other classifiers and produces 98.6% accuracy. The lowest accuracy obtained was also above 92.3% by the MOEF Classifier. Thus, we can see that the classifiers are able to discriminate between all these to good accuracies.
Case 15: This is similar to the previous case where another type of preictal EEG is used. The highest accuracy of 97.67% was reported by three classifiers, namely SL, Optimized Forest and Random Forest. The lowest accuracy was reported by Naïve Bayes at 89.6%.
Case 16: This takes another type of normal EEG (Set A) as input in comparison to Case 14. Again, MLP reported a highest accuracy of 98.6%. The lowest accuracy was reported at 89.67% by the MOEF classifier. From Cases 14 and 16 we can deduce that MLP produces an excellent accuracy of 98.6% for all types of available normal EEG class.
Case 17: Here, again the highest accuracy was presented by the MLP classifier at 98.6%. The lowest was by Naïve Bayes with 86.6%.
Case 18: This is an important case where the classifiers are elaborately and rigorously tested for their performance. Here, both normal EEG (Set A and Set B) are considered to be in a single class and both types of preictal EEG (Set C and Set D) forms another class and Set E (Epileptic EEG) forms the other class. We can see that both MLP and SL gives the highest accuracy of 98%. The lowest accuracy was again by the Naïve Bayes.
From the above, we can identify that MLP performs well for the 3 class classification problem across all cases. It was able to consistently produce accuracies above 98.5%. Even in Case 15, the accuracy was above 97%. On the other hand, we find that Naïve Bayes is not a good choice for Type II cases.
3) Type III
Here, we discuss the results obtained from all cases of the Type III, which is a four class type classification problem. The accuracies obtained for this type is shown in Table 10.
| Class/Type | A vs B vs C vs E (Case 19) |
A vs B vs D vs E (Case 20) |
A vs C vs D vs E (Case 21) |
| Naïve Bayes | 87.5% | 79.5% | 79.2% |
| MLP | 98% | 92.75% | 91% |
| Simple Logistic | 90% | 91.5% | 90.2% |
| RBF | 87% | 88.25% | 81.25% |
| Multiclass Classifier | 92.75% | 89.75% | 88.25% |
| Multiobjective evolutionary fuzzy Classifier | 73.25% | 72.75% | 71.25% |
| NNge | 90.5% | 90.5% | 89% |
| Optimized Forest | 92.75% | 91.5% | 91.25% |
| J48 | 90% | 90% | 87% |
| Random Forest | 92.7% | 91.5% | 91.2% |
DownLoad:
CSV
Case 19: Here, Sets A, B, C and E are considered to be of independent classes. Again, we can see that MLP classifier outperforms all other classifiers and yields an accuracy of 98%. The lowest was RBF with 87% and yet Naïve Bayes was at 87.5% denoting that Naïve Bayes in general not a good classifier for multi class classification problem.
Case 20: Here, Sets A, B, D and E are independent classes. MLP gives the highest classification accuracy for this case as well. Although accuracy obtained by the MLP was 92.75%, it was best accuracy in comparison to other classifiers considered in this study. Naïve Bayes yielded only 79.5% and MOEF presented the lowest accuracy at 72.75%.
Case 21: Sets A, C, D and E were considered to be independent classed, forming a four-class classification problem. Optimized Forest gave the highest accuracy of 92.25% and MLP is not too far yielding 92%. The lowest was again from the Naïve bayes classifier at 79.2%. In essence, we can mark that MLP classifier is being a very good choice for the four class classification problem as well for this dataset.
4) Type IV
Type IV is a multiclass classification problem with 5 classes. The accuracy obtained by this Type IV problem is showing in Table 11.
| Class/Type | A vs B vs C vs D vs E (Case 22) |
| Naïve Bayes | 75.2% |
| MLP | 88% |
| Simple logistic | 87.4% |
| RBF | 73.4% |
| Multiclass classifier | 86.6% |
| Multiobjective evolutionary fuzzy classifier | 58% |
| NNge | 85% |
| Optimized forest | 89.4% |
| J48 | 84.2% |
| Random forest | 90% |
DownLoad:
CSV
Case 22: Here, we have considered Sets A–E to be all independent classes, forming a five class classification problem. This will further test the performance of the classifiers. The highest accuracy was obtained by the Random Forest classifier at 90%. MLP is not far away and it produced 88% accuracy. The lowest accuracy was presented by the RBF classifier 73.4%.
The summary of results obtained is presented as follows: From all the types (Types I–IV) problems that has been studied here, we can note that the RBF was a good classifier for Type I cases listed. However, as the number of classes increased from 2 class to 5 class classification problem—RBF performance went down as can be seen from the results. RBF produced only 73.4% for the Type IV problem. It can be noted that MLP always produces accuracies above 97.5% for all cases of Type I problems, above 97.3% for all cases of Type II problems, above 91% for all cases of Type III problems and 88% for the Type IV problem. It should also be noted that Random Forest and Optimized Forest also yielded accuracies higher than 90% for all cases of Type I to Type IV problems, except optimized forest reaching close to 90% (89.4%) for the Type IV (5 class classification problem). Hence, we can declare that the identified feature set was able to produce excellent discrimination for all the 22 cases under all types of problems considered in this study. In summary, MLP classifier has produced, in general, good accuracies, and Random Forest and Optimized Forest classifiers were also equally good with their performance metrics.
A salient comparison of our work with essential and similar type of work in the literature is presented as follows: It should be noted that we have used all ive sets of data from this database in our work, whereas Oliva et al. [10] used only four sets. Set C was ignored by them [10] for the reason mentioned as it could lead to imbalance in their classifier results. In our work, we have clearly included the full set C and designed 22 different clinically significant cases of various binary and multiclass problems and established how our classifier is able to classify all these various sets of data. Oliva et al. [10] also presented their results with error rate of the classifiers whereas we have presented with the accuracies of the classifiers. In general, accuracy is the direct implication of any problem and thus we present it. Khaleem et al. considered only Sets A, B vs E in their study with empirical mode decomposition as feature extraction and SVM classifier [16]. They achieved a highest accuracy of 92.9%. Again, this is just one case among the 22 cases considered in our work. In our study, we have listed this as 3 different cases as Set A vs Set E, Set B vs Set E and Set A, Set B vs Set E (Cases 1–3). In all these cases, we achieve a highest accuracy of 99.5% (Case 2) and 100% (Cases 1 and 3). Even the lowest accuracy was 97%. This shows that our method is superior in terms of yielding higher accuracies. There are several literatures that present one or several combinations of the 22 cases that we have discussed in our study, listing their accuracies obtained, but to the best of our knowledge, none of them have discussed all the possible clinically significant 22 cases for this database.
Although all the features listed in Table 7 expect FzE are statistically significant, we have used the top four ranked features for forming the IED index. The IED index is designed using the top four ranked features (Re, K, SampEn and ApEn) from the t test to identify whether the input given is an epileptic EEG or a normal EEG. This will be easier for a clinical set up in diagnosis of epileptic EEG. Considering this, we have tested the IED index with cases where Set E (Epileptic EEG) is one set and the other combinations as another set (for the binary type—Type I problem). Under this criterion, the following cases are shown: Cases 1–3, 9, 10, 12, 13 and 22 are evaluated to check the robustness of our IED index.
Table 12 shows the mean, standard deviation and p values for the cases considered. We can see clearly that, in each case, the normal EEG mean IED values distinctly low in comparison to the epileptic EEG. The p value for these two classes with shows that IED index being a single measure has the ability to differentiate the normal EEG to the epileptic EEG.
| Cases | Normal EEG | Epileptic EEG | p value |
| Case 1 | 1.42 ± 0.63 | 6.67 ± 1.73 | 2.18 E-56 |
| Case 2 | 2.32 ± 0.72 | 6.67 ± 1.73 | 1.97 E-48 |
| Case 3 | 1.87 ± 0.81 | 6.67 ± 1.73 | 6.98 E-52 |
| Case 9 | 1.80 ± 0.96 | 6.67 ± 1.73 | 3.01 E-55 |
| Case 10 | 3.20 ± 1.71 | 6.67 ± 1.73 | 2.94 E-31 |
| Case 12 | 2.50 ± 1.59 | 6.67 ± 1.73 | 2.02 E-48 |
| Case 13 | 2.18 ± 1.30 | 6.67 ± 1.73 | 1.21 E-49 |
DownLoad:
CSV
Figure 3 shows the box plot for each of these cases. In addition to Table 12, Figure 3 also demonstrates visually how IED has the potential to discriminate the epileptic EEG and the normal EEG. We can see that how for each case, the IED has a distinctive difference for the considered two classes, separating them clearly. In general, for all cases, it can be seen that IED value of less than 4 is a normal EEG and greater than 5 is an epileptic EEG. Box plot of Case 12 is a specific one to be mentioned: It has the preictal type of EEG in one class and the epileptic EEG in another class. IED is able to discriminate this as well with the same index value of 4 between these two classes. This opens the windows towards prediction of the onset of epilepsy. Box plot of Case 13 clearly says that for all the normal EEG in broad sense Sets A–D—the IED is less than 4 and for Set E is above 5. The same can be seen more clearly in case 22 where each of the five types of EEG are kept as independent classes to each other. We can see from the Figure 3 that for Case 22 that expect Set E all other types of EEG has an IED less than 4. Thus, we can deduce that our IED index has the capacity to clearly differentiate the epileptic EEG with all other types of EEG, including the preictal type of EEG with 100% accuracy.
Advantages of this study: 1) To the best of our knowledge, no other study in the literature has elaborately discussed all the possible cases for this database. 2). The features were selected very precisely based on their impact from various literature [6,11,12,13,14,17,18,19,20] and were ranked based on the t test for each case. We have also used ten different classifiers from several categories of the classifier type. Such a vast study on the classifiers for the 22 cases is presented, for first time, by us. 3) In addition, all the features are easy to extract with minimum computation time and thus can give a window towards real time detection of epileptic seizures into the future. We have also tested each of the ten classifiers with 10 fold cross validation for each of the 22 cases listed and identified good classifiers to be MLP, Random forest and Optimized forest for this database. 4) We also devised a novel EpilepIndex IED index which demonstrated its capacity to differentiate the epileptic EEG and the normal EEG with less computation.
Limitations of the study: 1) We focus only on a small database. In general, when the methods that are successful for a small database are taken to a large database or real time applications, it does not present similar accuracies for various reasons such as noise etc. The presented method in this study has to be tested across various other databases for epilepsy. 2) Only EEG segments of fixed duration is considered in this study, but in real time, they are continuous recordings for 24 hours. Only 500 segments of EEG data are available in this database. The method needs to be tested long term EEG to check its proficiency before this can be applied for direct clinical purposes. We have planned to study this method for two or three more large databases on epilepsy and propose to study what variations will be needed when expanded to several databases.
In this work, we have devised four types of binary and multiclass classification problems to detect epileptic EEG. A total of 22 possible clinically significant cases were listed under these four types of classification problems, which is, as far as we know, the first time this is presented in the literature. To achieve this, 11 non-linear features were extracted from the EEG database considered. These statistically significant features were given as input for each of the 10 different classifiers considered in this study. The classifiers were tested for accuracies with 10 fold cross validation. Multilayer Perceptron based classifier presented accuracies higher than 97.3% for Types I and II problem. On the whole, Random Forest and Optimized Forest classifiers presented accuracies higher than 90% for all the 22 cases listed. In addition, a novel EpilepIndex IED index was developed and it was able to differentiate the normal EEG and the epileptic EEG with 100% accuracy. These results need to be evaluated further in large databases to study their performance.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
The authors declare that there are no conflicts of interest.
| [1] |
R. S. Fisher, W. V. E. Boas, W. Blume, C. Elger, P. Genton, P. Lee, et al., Epileptic seizures and epilepsy: definitions proposed by the international league against epilepsy (ILAE) and the international bureau for epilepsy (IBE), Epilepsia, 46 (2005), 470–472. https://doi.org/10.1111/j.0013-9580.2005.66104.x doi: 10.1111/j.0013-9580.2005.66104.x
|
| [2] | World Health Organization, Epilepsy, 2023. Available from: http://www.who.int/news-room/fact-sheets/detail/epilepsy. |
| [3] |
R. G. Andrzejak, G. Widman, K. Lehnertz, C. Rieke, P. David, C. E. Elger, The epileptic process as nonlinear deterministic dynamics in a stochastic environment: an evaluation on mesial temporal lobe epilepsy, Epilepsy Res., 44 (2001), 129–140. https://doi.org/10.1016/S0920-1211(01)00195-4 doi: 10.1016/S0920-1211(01)00195-4
|
| [4] |
U. R. Acharya, F. Molinarib, S. V. Sreec, S. Chattopadhyayd, K. Ng, J. S. Suri, Automated diagnosis of epileptic EEG using entropies, Biomed. Signal Process. Control, 7 (2012), 401–408. https://doi.org/10.1016/j.bspc.2011.07.007 doi: 10.1016/j.bspc.2011.07.007
|
| [5] |
U. R. Acharya, S. V. Sree, J. S. Suri, Use of principal component analysis for automatic detection of epileptic EEG activities, Expert Syst. Appl., 39 (2012), 9072–9078. https://doi.org/10.1016/j.eswa.2012.02.040 doi: 10.1016/j.eswa.2012.02.040
|
| [6] |
U. R. Acharya, S. V. Sree, G. Swapna, R. J. Martis, J. S. Suri, Automated EEG analysis of epilepsy: a review, Knowl.-Based Syst., 45 (2013), 147–165. https://doi.org/10.1016/j.knosys.2013.02.014 doi: 10.1016/j.knosys.2013.02.014
|
| [7] |
K. Zeng, J. Yan, Y. Wang, A. Sik, G. Ouyang, X. Li, Automatic detection of absence seizures with compressive sensing EEG, Neurocomputing, 171 (2016), 497–502. https://doi.org/10.1016/j.neucom.2015.06.076 doi: 10.1016/j.neucom.2015.06.076
|
| [8] |
D. Wang, D. Ren, K. Li, Y. Feng, D. Ma, X. Yan, et al., Epileptic seizure detection in long-term EEG recordings by using wavelet-based directed transfer function, IEEE Trans. Biomed. Eng., 65 (2018), 2591–2599. https://doi.org/10.1109/TBME.2018.2809798 doi: 10.1109/TBME.2018.2809798
|
| [9] |
M. Kaleem, D. Gurve, A. Guergachi, S. Krishnan, Patient-specific seizure detection in long-term EEG using signal-derived empirical mode decomposition (EMD)-based dictionary approach, J. Neural Eng., 15 (2018), 056004. https://doi.org/10.1088/1741-2552/aaceb1 doi: 10.1088/1741-2552/aaceb1
|
| [10] |
J. T. Oliva, J. L. G. Rosa, Binary and multiclass classifiers based on multitaper spectral features for epilepsy detection, Biomed. Signal Process. Control, 66 (2021), 102469. https://doi.org/10.1016/j.bspc.2021.102469 doi: 10.1016/j.bspc.2021.102469
|
| [11] |
R. Sharma, R. B. Pachori, U. R. Acharya, An integrated index for the identification of focal electroencephalogram signals using discrete wavelet transform and entropy measures, Entropy, 17 (2015), 5218–5240. https://doi.org/10.3390/e17085218 doi: 10.3390/e17085218
|
| [12] |
K. P. Noronha, U. R. Acharya, K. P. Nayak, R. J. Martis, S. V. Bhandary, Automated classification of glaucoma stages using higher order cumulant features, Biomed. Signal Process. Control, 10 (2014), 174–183. https://doi.org/10.1016/j.bspc.2013.11.006 doi: 10.1016/j.bspc.2013.11.006
|
| [13] |
N. Arunkumar, K. R. Kumar, V. Venkataraman, Entropy features for focal EEG and non focal EEG, J. Comput. Sci., 27 (2018), 440–444. https://doi.org/10.1016/j.jocs.2018.02.002 doi: 10.1016/j.jocs.2018.02.002
|
| [14] |
N. Arunkumar, K. Ramkumar, V. Venkatraman, E. Abdulhay, S. L. Fernandes, S. Kadry, et al., Classification of focal and non focal EEG using entropies, Pattern Recognit. Lett., 94 (2017), 112–117. https://doi.org/10.1016/j.patrec.2017.05.007 doi: 10.1016/j.patrec.2017.05.007
|
| [15] | Weka Tool, Available from: http://www.cs.waikato.ac.nz/ml/weka/. |
| [16] |
M. Kaleem, D. Gurve, A. Guergachi, S. Krishnan, Patient-specific seizure detection in long-term EEG using signal-derived empirical mode decomposition (EMD)- based dictionary approach, J. Neural Eng., 15 (2018), 056004. https://doi.org/10.1088/1741-2552/aaceb1 doi: 10.1088/1741-2552/aaceb1
|
| [17] |
U. R. Acharya, H. Fujita, V. K. Sudarshan, S. L. Oh, M. Adam, J. E. Koh, et al., Automated detection and localization of myocardial infarction using electrocardiogram: a comparative study of different leads, Knowl.-Based Syst., 99 (2016), 146–156. https://doi.org/10.1016/j.knosys.2016.01.040 doi: 10.1016/j.knosys.2016.01.040
|
| [18] |
N. Arunkumar, K. R. Kumar, V. Venkataraman, Automatic detection of epileptic seizures using permutation entropy, Tsallis entropy and Kolmogorov complexity, J. Med. Imaging Health Inf., 6 (2016), 526–531. https://doi.org/10.1166/jmihi.2016.1710 doi: 10.1166/jmihi.2016.1710
|
| [19] |
N. Arunkumar, K. R. Kumar, V. Venkataraman, Automatic detection of epileptic seizures using new entropy measures, J. Med. Imaging Health Inf., 6 (2016), 724–730. https://doi.org/10.1166/jmihi.2016.1736 doi: 10.1166/jmihi.2016.1736
|
| [20] |
I. Tasci, B. Tasci, P. D. Barua, S. Dogan, T. Tuncer, E. E. Palmer, et al., Epilepsy detection in 121 patient populations using hypercube pattern from EEG signals, Inf. Fusion, 96 (2023), 252–268. https://doi.org/10.1016/j.inffus.2023.03.022 doi: 10.1016/j.inffus.2023.03.022
|
N Arunkumar, B Nagaraj, M Ruth Keziah. EpilepIndex: A novel feature engineering tool to detect epilepsy using EEG signals[J]. Mathematical Biosciences and Engineering, 2023, 20(12): 21670-21691. doi: 10.3934/mbe.2023959
| Type | Description |
| Set A | EEG Segments of healthy volunteers with their eyes open |
| Set B | EEG Segments of healthy volunteers with their eyes closed |
| Set C | EEG Segments from hippocampal formation of the opp. side of the brain |
| Set D | EEG Segments from within epileptogenic zone |
| Set E | EEG Segments during the seizure activity |
DownLoad:
CSV
| Type I | Binary Classification (2 Class) |
| Case 1 | Set A vs Set E |
| Case 2 | Set B vs Set E |
| Case 3 | Set A, B vs Set E |
| Case 4 | Set A vs Set C |
| Case 5 | Set A vs Set D |
| Case 6 | Set B vs Set C |
| Case 7 | Set B vs Set D |
| Case 8 | Set C vs Set D |
| Case 9 | Set C vs Set E |
| Case 10 | Set D vs Set E |
| Case 11 | Set A, B vs Set C, D |
| Case 12 | Set C, D vs Set E |
| Case 13 | Set A, B, C, D vs Set E |
DownLoad:
CSV
| Type II | Multiclass Classification (3 classes) |
| Case 14 | Set A vs Set C vs Set E |
| Case 15 | Set B vs Set D vs Set E |
| Case 16 | Set A vs Set D vs Set E |
| Case 17 | Set B vs Set C vs Set E |
| Case 18 | Set A & Set B vs Set C & Set D vs Set E |
DownLoad:
CSV
| Type III | Multiclass classification problem (4 classes) |
| Case 19 | Set A vs Set B vs Set C vs Set E |
| Case 20 | Set A vs Set B vs Set D vs Set E |
| Case 21 | Set A vs Set C vs Set D vs Set E |
DownLoad:
CSV
| Type IV | Multiclass classification problem (5 classes) |
| Case 22 | Set A vs Set B vs Set C vs Set D vs Set E |
DownLoad:
CSV
| Classifier | Nature / Type |
| Naïve Bayes | Bayesian type classifier |
| Multilayer Perceptron (MLP) | Function based classifier |
| Simple Logistic (SL) | Function based classifier |
| Radial Basis Function classifier (RBF) | Function based classifier |
| Multiclass classifier | Meta type classifier |
| Multi Objective Evolutionary Fuzzy classifier (MOEF) | Rule based classifier |
| Non-nested Generalized Exempler (NNge) | Rule based classifier |
| Optimized Forest classifier | Decision Tree type classifier |
| J48 classifier | Decision Tree type classifier |
| Random Forest classifier | Decision Tree type classifier |
DownLoad:
CSV
| Features | Mean (Set A) | Std (Set A) | Mean (Set E) | Std (Set E) | p-value | Rank |
| ApEn | 0.548374 | 0.060308 | 0.651661 | 0.061226 | 3.8 E-22 | 4 |
| SampEn | 1.010935 | 0.163356 | 0.495863 | 0.144952 | 2.04 E-34 | 3 |
| Cum4 | 953423.9 | 1518535 | 1.02E+10 | 3.79E+10 | 0.008 | 8 |
| FD | -1.49284 | 0.073948 | -1.316 | 0.113469 | 1.4 E-12 | 7 |
| H | 0.657052 | 0.061209 | 0.435487 | 0.096808 | 0.016 | 9 |
| FzE | 0.027913 | 0.012109 | 0.021897 | 0.010435 | 0.2 | 11 |
| K | 5.624378 | 0.243047 | 7.120629 | 0.523022 | 2.34 E-37 | 2 |
| Kut | 3.226986 | 0.269942 | 3.428355 | 1.187349 | 0.039 | 10 |
| PE | 1.486605 | 0.05663 | 1.235531 | 0.088102 | 1.39 E-20 | 5 |
| Re | -15.9675 | 0.500365 | -19.5353 | 1.018548 | 1.62 E-43 | 1 |
| TsE | -9759521 | 5089083 | -4.8E+08 | 4.11E+08 | 3.07 E-19 | 6 |
DownLoad:
CSV
| Classifiers /Type I |
A vs E (Case 1) |
B vs E (Case 2) |
AB vs E (Case 3) |
A vs C (Case 4) |
A vs D (Case 5) |
B vs C (Case 6) |
B vs D (Case 7) |
C vs D (Case 8) |
C vs E (Case 9) |
D vs E (Case 10) |
CD vs E (Case 11) |
AB vs CD (Case 12) |
ABCD vs E (Case 13) |
| Naïve Bayes | 100 % | 99 % | 99 % | 98 % | 91.5 % | 95.5 % | 87 % | 67.5 % | 99.5 % | 94.5 % | 96.37 % | 78 % | 97 % |
| MLP | 100 % | 99.5 % | 99.67 % | 97.5 % | 97.5 % | 98.5 % | 99.5 % | 86.5 % | 99.5 % | 98 % | 99 % | 97.75 % | 99.4 % |
| Simple Logistic | 100 % | 98.5% | 99.67 % | 98.5 % | 98 % | 98.5 % | 99 % | 83.5 % | 98.5 % | 97.5 % | 98.6 % | 98.75 % | 98.6 % |
| RBF | 100 % | 99.5 % | 99.67 % | 96.5 % | 98 % | 99.5 % | 99.5 % | 83 % | 100 % | 98 % | 99 % | 98.25 % | 97.8 % |
| MultiClass classifier | 99.5 % | 98 % | 100 % | 94.5 % | 97 % | 99.5 % | 99 % | 86.5 % | 99 % | 98 % | 98 % | 97.75 % | 97.6 % |
| Multiobjective evolutionary fuzzy Classifier | 99.5 % | 97 % | 97.67 % | 93.5 % | 96.5 % | 92.5 % | 98.5 % | 77.5 % | 98 % | 96 % | 98 % | 94.75 % | 97.6 % |
| NNge | 100 % | 99 % | 99 % | 95.5 % | 97 % | 97.5 % | 97 % | 83 % | 98 % | 97.5 % | 97.67 % | 96 % | 97.4 % |
| Optimized Forest | 100 % | 98.5 % | 98.67 % | 98 % | 98 % | 97.5 % | 98 % | 86.5 % | 99 % | 98.5 % | 99 % | 97.25 % | 98.4 % |
| J48 | 99.5 % | 97.5 % | 98 % | 97 % | 97 % | 97 % | 94.5 % | 82 % | 99 % | 99.5 % | 99.3 % | 95 % | 98.8 % |
| Random Forest | 100 % | 98.5 % | 98.3 % | 98 % | 98 % | 98 % | 98.5 % | 86 % | 99 % | 98.5 % | 99.3 % | 97.25 % | 98.6 % |
DownLoad:
CSV
| Class/Type | A vs C vs E (Case 14) |
A vs D vs E (Case 15) |
B vs C vs E (Case 16) |
B vs D vs E (Case 17) |
AB vs CD vs E (Case 18) |
| Naïve Bayes | 97.6% | 89.6% | 95.3% | 86.6% | 81.2% |
| MLP | 98.6% | 97.3% | 98.6% | 98.6% | 98% |
| Simple Logistic | 97.6% | 97.67% | 98.3% | 98.3% | 98% |
| RBF | 95.33% | 97.33% | 96.33% | 97.33% | 96% |
| Multiclass Classifier | 96.33% | 96% | 97.67% | 95.67% | 96.6% |
| Multiobjective evolutionary fuzzy Classifier | 92.33% | 92.33% | 89.67% | 89.33% | 89.4% |
| NNge | 96.33% | 96.33% | 97.33% | 95.67% | 95.4% |
| Optimized Forest | 98% | 97.67% | 96.33% | 97.67% | 97.2% |
| J48 | 96.6% | 97.3% | 95% | 93.3% | 93.8% |
| Random Forest | 98% | 97.6% | 97% | 97.3% | 97.2% |
DownLoad:
CSV
| Class/Type | A vs B vs C vs E (Case 19) |
A vs B vs D vs E (Case 20) |
A vs C vs D vs E (Case 21) |
| Naïve Bayes | 87.5% | 79.5% | 79.2% |
| MLP | 98% | 92.75% | 91% |
| Simple Logistic | 90% | 91.5% | 90.2% |
| RBF | 87% | 88.25% | 81.25% |
| Multiclass Classifier | 92.75% | 89.75% | 88.25% |
| Multiobjective evolutionary fuzzy Classifier | 73.25% | 72.75% | 71.25% |
| NNge | 90.5% | 90.5% | 89% |
| Optimized Forest | 92.75% | 91.5% | 91.25% |
| J48 | 90% | 90% | 87% |
| Random Forest | 92.7% | 91.5% | 91.2% |
DownLoad:
CSV
| Class/Type | A vs B vs C vs D vs E (Case 22) |
| Naïve Bayes | 75.2% |
| MLP | 88% |
| Simple logistic | 87.4% |
| RBF | 73.4% |
| Multiclass classifier | 86.6% |
| Multiobjective evolutionary fuzzy classifier | 58% |
| NNge | 85% |
| Optimized forest | 89.4% |
| J48 | 84.2% |
| Random forest | 90% |
DownLoad:
CSV
| Cases | Normal EEG | Epileptic EEG | p value |
| Case 1 | 1.42 ± 0.63 | 6.67 ± 1.73 | 2.18 E-56 |
| Case 2 | 2.32 ± 0.72 | 6.67 ± 1.73 | 1.97 E-48 |
| Case 3 | 1.87 ± 0.81 | 6.67 ± 1.73 | 6.98 E-52 |
| Case 9 | 1.80 ± 0.96 | 6.67 ± 1.73 | 3.01 E-55 |
| Case 10 | 3.20 ± 1.71 | 6.67 ± 1.73 | 2.94 E-31 |
| Case 12 | 2.50 ± 1.59 | 6.67 ± 1.73 | 2.02 E-48 |
| Case 13 | 2.18 ± 1.30 | 6.67 ± 1.73 | 1.21 E-49 |
DownLoad:
CSV
| Type | Description |
| Set A | EEG Segments of healthy volunteers with their eyes open |
| Set B | EEG Segments of healthy volunteers with their eyes closed |
| Set C | EEG Segments from hippocampal formation of the opp. side of the brain |
| Set D | EEG Segments from within epileptogenic zone |
| Set E | EEG Segments during the seizure activity |
| Type I | Binary Classification (2 Class) |
| Case 1 | Set A vs Set E |
| Case 2 | Set B vs Set E |
| Case 3 | Set A, B vs Set E |
| Case 4 | Set A vs Set C |
| Case 5 | Set A vs Set D |
| Case 6 | Set B vs Set C |
| Case 7 | Set B vs Set D |
| Case 8 | Set C vs Set D |
| Case 9 | Set C vs Set E |
| Case 10 | Set D vs Set E |
| Case 11 | Set A, B vs Set C, D |
| Case 12 | Set C, D vs Set E |
| Case 13 | Set A, B, C, D vs Set E |
| Type II | Multiclass Classification (3 classes) |
| Case 14 | Set A vs Set C vs Set E |
| Case 15 | Set B vs Set D vs Set E |
| Case 16 | Set A vs Set D vs Set E |
| Case 17 | Set B vs Set C vs Set E |
| Case 18 | Set A & Set B vs Set C & Set D vs Set E |
| Type III | Multiclass classification problem (4 classes) |
| Case 19 | Set A vs Set B vs Set C vs Set E |
| Case 20 | Set A vs Set B vs Set D vs Set E |
| Case 21 | Set A vs Set C vs Set D vs Set E |
| Type IV | Multiclass classification problem (5 classes) |
| Case 22 | Set A vs Set B vs Set C vs Set D vs Set E |
| Classifier | Nature / Type |
| Naïve Bayes | Bayesian type classifier |
| Multilayer Perceptron (MLP) | Function based classifier |
| Simple Logistic (SL) | Function based classifier |
| Radial Basis Function classifier (RBF) | Function based classifier |
| Multiclass classifier | Meta type classifier |
| Multi Objective Evolutionary Fuzzy classifier (MOEF) | Rule based classifier |
| Non-nested Generalized Exempler (NNge) | Rule based classifier |
| Optimized Forest classifier | Decision Tree type classifier |
| J48 classifier | Decision Tree type classifier |
| Random Forest classifier | Decision Tree type classifier |
| Features | Mean (Set A) | Std (Set A) | Mean (Set E) | Std (Set E) | p-value | Rank |
| ApEn | 0.548374 | 0.060308 | 0.651661 | 0.061226 | 3.8 E-22 | 4 |
| SampEn | 1.010935 | 0.163356 | 0.495863 | 0.144952 | 2.04 E-34 | 3 |
| Cum4 | 953423.9 | 1518535 | 1.02E+10 | 3.79E+10 | 0.008 | 8 |
| FD | -1.49284 | 0.073948 | -1.316 | 0.113469 | 1.4 E-12 | 7 |
| H | 0.657052 | 0.061209 | 0.435487 | 0.096808 | 0.016 | 9 |
| FzE | 0.027913 | 0.012109 | 0.021897 | 0.010435 | 0.2 | 11 |
| K | 5.624378 | 0.243047 | 7.120629 | 0.523022 | 2.34 E-37 | 2 |
| Kut | 3.226986 | 0.269942 | 3.428355 | 1.187349 | 0.039 | 10 |
| PE | 1.486605 | 0.05663 | 1.235531 | 0.088102 | 1.39 E-20 | 5 |
| Re | -15.9675 | 0.500365 | -19.5353 | 1.018548 | 1.62 E-43 | 1 |
| TsE | -9759521 | 5089083 | -4.8E+08 | 4.11E+08 | 3.07 E-19 | 6 |
| Classifiers /Type I |
A vs E (Case 1) |
B vs E (Case 2) |
AB vs E (Case 3) |
A vs C (Case 4) |
A vs D (Case 5) |
B vs C (Case 6) |
B vs D (Case 7) |
C vs D (Case 8) |
C vs E (Case 9) |
D vs E (Case 10) |
CD vs E (Case 11) |
AB vs CD (Case 12) |
ABCD vs E (Case 13) |
| Naïve Bayes | 100 % | 99 % | 99 % | 98 % | 91.5 % | 95.5 % | 87 % | 67.5 % | 99.5 % | 94.5 % | 96.37 % | 78 % | 97 % |
| MLP | 100 % | 99.5 % | 99.67 % | 97.5 % | 97.5 % | 98.5 % | 99.5 % | 86.5 % | 99.5 % | 98 % | 99 % | 97.75 % | 99.4 % |
| Simple Logistic | 100 % | 98.5% | 99.67 % | 98.5 % | 98 % | 98.5 % | 99 % | 83.5 % | 98.5 % | 97.5 % | 98.6 % | 98.75 % | 98.6 % |
| RBF | 100 % | 99.5 % | 99.67 % | 96.5 % | 98 % | 99.5 % | 99.5 % | 83 % | 100 % | 98 % | 99 % | 98.25 % | 97.8 % |
| MultiClass classifier | 99.5 % | 98 % | 100 % | 94.5 % | 97 % | 99.5 % | 99 % | 86.5 % | 99 % | 98 % | 98 % | 97.75 % | 97.6 % |
| Multiobjective evolutionary fuzzy Classifier | 99.5 % | 97 % | 97.67 % | 93.5 % | 96.5 % | 92.5 % | 98.5 % | 77.5 % | 98 % | 96 % | 98 % | 94.75 % | 97.6 % |
| NNge | 100 % | 99 % | 99 % | 95.5 % | 97 % | 97.5 % | 97 % | 83 % | 98 % | 97.5 % | 97.67 % | 96 % | 97.4 % |
| Optimized Forest | 100 % | 98.5 % | 98.67 % | 98 % | 98 % | 97.5 % | 98 % | 86.5 % | 99 % | 98.5 % | 99 % | 97.25 % | 98.4 % |
| J48 | 99.5 % | 97.5 % | 98 % | 97 % | 97 % | 97 % | 94.5 % | 82 % | 99 % | 99.5 % | 99.3 % | 95 % | 98.8 % |
| Random Forest | 100 % | 98.5 % | 98.3 % | 98 % | 98 % | 98 % | 98.5 % | 86 % | 99 % | 98.5 % | 99.3 % | 97.25 % | 98.6 % |
| Class/Type | A vs C vs E (Case 14) |
A vs D vs E (Case 15) |
B vs C vs E (Case 16) |
B vs D vs E (Case 17) |
AB vs CD vs E (Case 18) |
| Naïve Bayes | 97.6% | 89.6% | 95.3% | 86.6% | 81.2% |
| MLP | 98.6% | 97.3% | 98.6% | 98.6% | 98% |
| Simple Logistic | 97.6% | 97.67% | 98.3% | 98.3% | 98% |
| RBF | 95.33% | 97.33% | 96.33% | 97.33% | 96% |
| Multiclass Classifier | 96.33% | 96% | 97.67% | 95.67% | 96.6% |
| Multiobjective evolutionary fuzzy Classifier | 92.33% | 92.33% | 89.67% | 89.33% | 89.4% |
| NNge | 96.33% | 96.33% | 97.33% | 95.67% | 95.4% |
| Optimized Forest | 98% | 97.67% | 96.33% | 97.67% | 97.2% |
| J48 | 96.6% | 97.3% | 95% | 93.3% | 93.8% |
| Random Forest | 98% | 97.6% | 97% | 97.3% | 97.2% |
| Class/Type | A vs B vs C vs E (Case 19) |
A vs B vs D vs E (Case 20) |
A vs C vs D vs E (Case 21) |
| Naïve Bayes | 87.5% | 79.5% | 79.2% |
| MLP | 98% | 92.75% | 91% |
| Simple Logistic | 90% | 91.5% | 90.2% |
| RBF | 87% | 88.25% | 81.25% |
| Multiclass Classifier | 92.75% | 89.75% | 88.25% |
| Multiobjective evolutionary fuzzy Classifier | 73.25% | 72.75% | 71.25% |
| NNge | 90.5% | 90.5% | 89% |
| Optimized Forest | 92.75% | 91.5% | 91.25% |
| J48 | 90% | 90% | 87% |
| Random Forest | 92.7% | 91.5% | 91.2% |
| Class/Type | A vs B vs C vs D vs E (Case 22) |
| Naïve Bayes | 75.2% |
| MLP | 88% |
| Simple logistic | 87.4% |
| RBF | 73.4% |
| Multiclass classifier | 86.6% |
| Multiobjective evolutionary fuzzy classifier | 58% |
| NNge | 85% |
| Optimized forest | 89.4% |
| J48 | 84.2% |
| Random forest | 90% |
| Cases | Normal EEG | Epileptic EEG | p value |
| Case 1 | 1.42 ± 0.63 | 6.67 ± 1.73 | 2.18 E-56 |
| Case 2 | 2.32 ± 0.72 | 6.67 ± 1.73 | 1.97 E-48 |
| Case 3 | 1.87 ± 0.81 | 6.67 ± 1.73 | 6.98 E-52 |
| Case 9 | 1.80 ± 0.96 | 6.67 ± 1.73 | 3.01 E-55 |
| Case 10 | 3.20 ± 1.71 | 6.67 ± 1.73 | 2.94 E-31 |
| Case 12 | 2.50 ± 1.59 | 6.67 ± 1.73 | 2.02 E-48 |
| Case 13 | 2.18 ± 1.30 | 6.67 ± 1.73 | 1.21 E-49 |
