Oncology research has focused extensively on estrogen hormones and their function in breast cancer proliferation. Mathematical modeling is essential for the analysis and simulation of breast cancers. This research presents a novel approach to examine the therapeutic and inhibitory effects of hormone and estrogen therapies on the onset of breast cancer. Our proposed mathematical model comprises a nonlinear coupled system of partial differential equations, capturing intricate interactions among estrogen, cytotoxic T lymphocytes, dormant cancer cells, and active cancer cells. The model's parameters are meticulously estimated through experimental studies, and we conduct a comprehensive global sensitivity analysis to assess the uncertainty of these parameter values. Remarkably, our findings underscore the pivotal role of hormone therapy in curtailing breast tumor growth by blocking estrogen's influence on cancer cells. Beyond this crucial insight, our proposed model offers an integrated framework to delve into the complexity of tumor progression and immune response under hormone therapy. We employ diverse experimental datasets encompassing gene expression profiles, spatial tumor morphology, and cellular interactions. Integrating multidimensional experimental data with mathematical models enhances our understanding of breast cancer dynamics and paves the way for personalized treatment strategies. Our study advances our comprehension of estrogen receptor-positive breast cancer and exemplifies a transformative approach that merges experimental data with cutting-edge mathematical modeling. This framework promises to illuminate the complexities of cancer progression and therapy, with broad implications for oncology.
Citation: Abeer S. Alnahdi, Muhammad Idrees. Nonlinear dynamics of estrogen receptor-positive breast cancer integrating experimental data: A novel spatial modeling approach[J]. Mathematical Biosciences and Engineering, 2023, 20(12): 21163-21185. doi: 10.3934/mbe.2023936
| [1] | Hsiu-Chuan Wei . Mathematical modeling of tumor growth: the MCF-7 breast cancer cell line. Mathematical Biosciences and Engineering, 2019, 16(6): 6512-6535. doi: 10.3934/mbe.2019325 |
| [2] | Muhammad Bilal Shoaib Khan, Atta-ur-Rahman, Muhammad Saqib Nawaz, Rashad Ahmed, Muhammad Adnan Khan, Amir Mosavi . Intelligent breast cancer diagnostic system empowered by deep extreme gradient descent optimization. Mathematical Biosciences and Engineering, 2022, 19(8): 7978-8002. doi: 10.3934/mbe.2022373 |
| [3] | Jianqiao Pan, Baoshan Ma, Xiaoyu Hou, Chongyang Li, Tong Xiong, Yi Gong, Fengju Song . The construction of transcriptional risk scores for breast cancer based on lightGBM and multiple omics data. Mathematical Biosciences and Engineering, 2022, 19(12): 12353-12370. doi: 10.3934/mbe.2022576 |
| [4] | Feiyan Ruan, Xiaotong Ding, Huiping Li, Yixuan Wang, Kemin Ye, Houming Kan . Back propagation neural network model for medical expenses in patients with breast cancer. Mathematical Biosciences and Engineering, 2021, 18(4): 3690-3698. doi: 10.3934/mbe.2021185 |
| [5] | Jihong Yang, Hao Xu, Congshu Li, Zhenhao Li, Zhe Hu . An explorative study for leveraging transcriptomic data of embryonic stem cells in mining cancer stemness genes, regulators, and networks. Mathematical Biosciences and Engineering, 2022, 19(12): 13949-13966. doi: 10.3934/mbe.2022650 |
| [6] | Qingqun Huang, Adnan Khalil, Didar Abdulkhaleq Ali, Ali Ahmad, Ricai Luo, Muhammad Azeem . Breast cancer chemical structures and their partition resolvability. Mathematical Biosciences and Engineering, 2023, 20(2): 3838-3853. doi: 10.3934/mbe.2023180 |
| [7] | Sandesh Athni Hiremath, Christina Surulescu, Somayeh Jamali, Samantha Ames, Joachim W. Deitmer, Holger M. Becker . Modeling of pH regulation in tumor cells: Direct interaction between proton-coupled lactate transporters and cancer-associated carbonicanhydrase. Mathematical Biosciences and Engineering, 2019, 16(1): 320-337. doi: 10.3934/mbe.2019016 |
| [8] | Salman Lari, Hossein Rajabzadeh, Mohammad Kohandel, Hyock Ju Kwon . A holistic physics-informed neural network solution for precise destruction of breast tumors using focused ultrasound on a realistic breast model. Mathematical Biosciences and Engineering, 2024, 21(10): 7337-7372. doi: 10.3934/mbe.2024323 |
| [9] | Jian-Di Li, Gang Chen, Mei Wu, Yu Huang, Wei Tang . Downregulation of CDC14B in 5218 breast cancer patients: A novel prognosticator for triple-negative breast cancer. Mathematical Biosciences and Engineering, 2020, 17(6): 8152-8181. doi: 10.3934/mbe.2020414 |
| [10] | Bo An . Construction and application of Chinese breast cancer knowledge graph based on multi-source heterogeneous data. Mathematical Biosciences and Engineering, 2023, 20(4): 6776-6799. doi: 10.3934/mbe.2023292 |
Oncology research has focused extensively on estrogen hormones and their function in breast cancer proliferation. Mathematical modeling is essential for the analysis and simulation of breast cancers. This research presents a novel approach to examine the therapeutic and inhibitory effects of hormone and estrogen therapies on the onset of breast cancer. Our proposed mathematical model comprises a nonlinear coupled system of partial differential equations, capturing intricate interactions among estrogen, cytotoxic T lymphocytes, dormant cancer cells, and active cancer cells. The model's parameters are meticulously estimated through experimental studies, and we conduct a comprehensive global sensitivity analysis to assess the uncertainty of these parameter values. Remarkably, our findings underscore the pivotal role of hormone therapy in curtailing breast tumor growth by blocking estrogen's influence on cancer cells. Beyond this crucial insight, our proposed model offers an integrated framework to delve into the complexity of tumor progression and immune response under hormone therapy. We employ diverse experimental datasets encompassing gene expression profiles, spatial tumor morphology, and cellular interactions. Integrating multidimensional experimental data with mathematical models enhances our understanding of breast cancer dynamics and paves the way for personalized treatment strategies. Our study advances our comprehension of estrogen receptor-positive breast cancer and exemplifies a transformative approach that merges experimental data with cutting-edge mathematical modeling. This framework promises to illuminate the complexities of cancer progression and therapy, with broad implications for oncology.
Breast cancer, the most prevalent disease among women globally, was responsible for over 2.3 million diagnoses and 685,000 fatalities in 2020 [1]. It comprises different kinds that develop in the lobules and ducts of breast tissue [2]. The most common kind is invasive ductal carcinoma, which starts in the ducts and spreads to nearby breast tissue. Other types of breast cancer include inflammatory breast cancer, which is aggressive in nature, and invasive lobular carcinoma, which starts in the lobules [3]. Although the precise etiology of the phenomenon is still unknown, it is widely believed that a combination of genetic and environmental factors influences its manifestation [4]. Risk factors for breast cancer include several characteristics, such as advanced age, familial and personal medical history, breast density and particular genetic abnormalities [5]. Mutations in BRCA1 and BRCA2 genes significantly increase the risk of breast cancer. These genes are responsible for repairing DNA damage, and mutations can impair this function, leading to a higher likelihood of cancer development. A family history of breast cancer, especially in first-degree relatives (mother, sister, daughter), can elevate an individual's risk. Specific genetic mutations passed down through families can be responsible for this predisposition. Prolonged exposure to estrogen, either through early menstruation, late menopause or the use of hormone replacement therapy, can increase the risk of breast cancer. Estrogen can promote cell growth in breast tissue. The symptoms of breast cancer vary depending on the stage of the disease, including manifestations such as the presence of breast tumors, variations in breast form or size, discharge from the nipple and modifications in the skin. The timely identification and intervention of breast cancer afford a considerable likelihood of survival and the attainment of a state of well-being for the majority of women affected by it [6].
Breast cancer is a complex disease that has numerous subtypes, including lobular carcinoma in situ (LCIS), ductal carcinoma in situ (DCIS), inflammatory breast cancer (IBC) and metastatic cancer, each with distinct morphological characteristics, biological behaviors and clinical consequences [7]. LCIS is a precancerous disorder that may develop into invasive cancer, whereas invasive lobular carcinoma spreads beyond breast lobules and may metastasize to other organs [8]. DCIS arises from the breast ducts and remains confined to its original site without invading surrounding tissues [9]. In contrast, IBC, a less common and highly aggressive subtype, is characterized by the infiltration of malignant cells into the skin and lymphatic vessels of the breast [10]. Unlike other forms of breast cancer, IBC often lacks a discernible lump. Consequently, prompt and aggressive treatment is imperative due to its rapid growth and propensity for metastasis. The activation of both innate and adaptive immunity significantly impacts the immune response to breast cancer. In particular, the activation of cytotoxic T lymphocytes (CTLs) and helper T cells plays a critical role in defending against cancer growth [11]. Moreover, antigen-presenting cells play a crucial role in identifying tumors and presenting tumor fragments to T cells. The immune system comprises organs, tissues, cells and molecules that all function together to produce an immune response that protects us from microorganisms, removes toxins and destroys cancer cells [12]. Numerous immunosuppressive chemicals may be found in the microenvironment of tumors with a high burden, which may be responsible for the suppression of the stimulation and activation of immune responses. Tumor-associated macrophages, regulatory T cells and myeloid-derived suppressor cells are significant cells that inhibit the creation of a robust immune response. In addition to increasing the tumor's invasiveness, the production of immunosuppressive cytokines and chemicals, including interleukin-10, transforming growth factor-β and vascular endothelial growth factor, also makes the environment around the tumor more immunosuppressive [13].
The pathogenesis of breast cancer is profoundly influenced by estrogen, an essential hormone that is imperative for the physiological development and functioning of the female reproductive system [14]. Several physiological functions, including the development of the mammary gland, depend critically on estrogen. However, it is important to note that under certain conditions, estrogen may also play a role in the onset and advancement of breast cancer [15]. This involvement primarily occurs through the interaction of estrogen with estrogen receptors located on the surface of breast cancer cells. Upon binding, estrogen activates a cascade of intracellular signaling pathways that can result in the stimulation of key processes such as cell proliferation, survival and migration [16]. Consequently, these cellular events can lead to the formation of breast tumors and their potential dissemination to distant sites within the body. In the clinical management of estrogen-driven breast cancer, a range of therapeutic interventions are employed to mitigate the oncogenic effects of estrogen. These strategies include the use of fulvestrant, tamoxifen, aromatase inhibitors and selective estrogen receptor modulators, all of which either block the actions of estrogen or reduce its production within the body. These interventions represent essential components of breast cancer treatment and prevention strategies, aiming to disrupt the estrogen-driven pathways responsible for the disease's development and progression.
Mathematical modeling is a powerful tool that can be used to understand the complex interactions between estrogen and breast cancer cells. Mathematical models can predict how breast cancer cells will respond to different treatments and identify new targets for drug development. One of the most important factors in the development of breast cancer is the presence of estrogen receptors on the surface of breast cancer cells. Estrogen receptors are proteins that bind to estrogen and transmit signals that stimulate the proliferation of breast cancer cells [17]. Mathematical models can be used to study the effects of estrogen stimulation on breast cancer cells. These models can help researchers to understand how estrogen promotes the growth of breast cancer cells and identify new ways to block the effects of estrogen. Mathematical models can also be used to predict how breast cancer cells will respond to different treatments. For example, mathematical models can predict how breast cancer cells respond to chemotherapy, radiation therapy, or hormone therapy. This information can be used to develop personalized treatment plans for breast cancer patients.
The use of ordinary differential equations has been employed in the study of tumor development and decay, specifically in scenarios involving two or three cell populations consisting of tumor cells and effector cells [18,19]. Complex models, including populations of tumor-related cells and cytokines, have been developed in order to investigate specific aspects of tumor biology [20,21]. Mathematical models focused on the examination of breast cancer development and therapy have introduced innovative perspectives on the dynamics of breast cancer. Jarrett et al. [22] presented a mathematical model to describe the dynamics of HER2-positive breast cancer in the presence of targeted treatment using trastuzumab. According to the proposed mathematical model, the administration of trastuzumab might lead to the stabilization of vasculature and subsequent reduction in tumor development. Wei [23] proposed a theoretical framework for estrogen receptor-positive breast cancer. The numerical simulation results demonstrated that the model had multistability, indicating the presence of three distinct phases in the immunoediting process. The model was subsequently updated to include the incorporation of AZD9496, a novel selective estrogen receptor degrader and palbociclib, a cyclin-dependent kinase 4 and 6 inhibitor [24]. The research posited that using monotherapy with a single medicine may prove futile, but implementing combination treatment might have a synergistic impact. McKenna et al. [25] developed a mathematical model encompassing triple-negative breast cancer and its treatment with doxorubicin chemotherapy. The model was used to examine the response to therapy.
In 2018, Oke et al. developed a deterministic compartmental model with four dimensions to track the progression of breast cancer. The authors found that excess estrogen in the body affected the formation of tumor cells and they emphasized the advantages of breast cancer alleviation policies that combine anti-cancer medications and ketogenic diet techniques [26]. Mufudza et al. examined the impact of estrogen, as a potential risk factor, on breast cancer dynamics [27]. A deterministic mathematical model was developed that incorporates both the immune response and estrogen, aiming to elucidate the general dynamics of breast cancer. Their results showed that a greater likelihood of breast cancer growth was linked to an overabundance of estrogen. Ouifki and Oke have proposed a novel ordinary differential equation-based mathematical model to describe the dynamics of interactions between dormant and active breast cancer cells, estrogen and p53 [28]. The model was designed to consider the association between estrogen and p53, as well as their respective contributions to the activation of dormant breast cancer cells and the apoptosis of active tumor cells. The authors have presented explicit conditions that may prevent paradoxical cancer recurrence as a result of prolonged hormone deprivation therapy.
A comprehensive review of the literature revealed a lack of studies that incorporate mathematical modeling and hormone therapy in estrogen-positive breast cancer. In this study, a mathematical model using partial differential equations was developed to examine valuable insights into the underlying mechanisms that govern tumor growth and the effects of estrogen on tumor cells. This mathematical model can incorporate various factors, such as the diffusion of estrogen in the breast tissue, the proliferation of tumor cells and the response of these cells to estrogen. The developed model allows researchers to investigate the interactions between estrogen and breast cancer cells and predict different treatments' impact on tumor growth. The model can provide insights into breast cancer development and progression mechanisms by incorporating data from multiple sources, such as clinical trials and laboratory experiments. Furthermore, it may help to elucidate hormone therapy's effects and drive the design of personalized treatment strategies for patients with breast cancer. Overall, the proposed mathematical model represents an important step toward improving our understanding of breast cancer and developing more effective treatments for this disease.
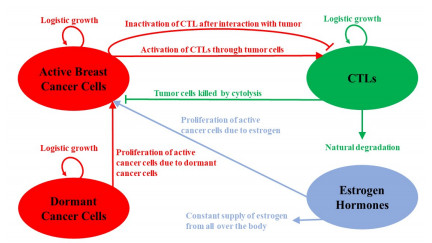
This section aims to develop a mathematical model that provides a framework for analyzing the complicated dynamics underlying estrogen receptor-positive breast cancer. The mathematical model presented herein offers a complete framework for analyzing the complex dynamics underlying estrogen receptor-positive breast cancer. This model is fundamentally based on a carefully designed partial differential equation system that captures the intricate interactions between estrogen, CTLs, dormant cancer cells and active cancer cells within the tumor microenvironment. The progression of breast cancer is significantly influenced by each component of this framework, with estrogen being a crucial factor in cell proliferation and immune responses influencing tumor growth and regression. The objective of this mathematical framework is to elucidate the intricate connections among these elements, providing insights into the effects of hormone treatment and estrogen inhibition on the dynamics of breast tumors. For the reader's convenience, we illustrate the mathematical framework by using a schematic diagram, as shown in Figure 1.
Let y1 denote the compartment of dormant cancer cells, and their logistic growth is defined by the term c1y1(1−y1c2), where c1 is the growth rate and c2 is the carrying capacity of dormant cancer cells. The concept of "carrying capacity" is often used in the context of ecology to describe the maximum population size that a particular environment can sustainably support. However, when discussing dormant breast cancer cells, the term is applied metaphorically and within the framework of cancer biology to describe a similar concept. Dormant breast cancer cells refer to cancer cells that have entered a quiescent or inactive state within the body. These cells are not actively dividing and forming tumors but they are still present in the body. In this context, carrying capacity refers to the limit or threshold of dormant cancer cells that the body can tolerate without becoming actively proliferative and causing disease progression. The growth rate of the dormant cancer cell population may be regulated negatively by a factor c3y1y4, where y4 represents the density of estrogen hormones and c3 is the probability rate for dormant cancer cell transformation into active cancer cells. The equation of dormant cancer cells is given by
| dy1dt=c1y1(1−y1c2)−c3y1y4. | (2.1) |
Cancers of the breast, epidermis and cervix typically give rise to names that reflect the type of tissue in which the DNA is altered. The 145 primary breast cancers that have been found are based on 51 cell lines of malignancy that are divided into two principal strands: one with estrogen receptors, known as the luminal type, and the other without estrogen receptors, which is known as the basal-like type [29]. We use the following equation to describe the dynamics of active breast cancer cells:
| dy2dt=c3y1y4+c4y2(1−y2c5)−c6y2(y3c7+y3)+c8y4. | (2.2) |
The term c3y1y4 defines the growth of active cancer cells due to dormant cancer cells with the aid of estrogen. The logistic growth of active breast cancer cells is defined by the term c4y2(1−y2c5), while the term c6y2(y3c7+y3) represents the degradation of cancer cells due to immune responses. Excessive estrogen-induced DNA mutations will also repopulate active cancer cells by the factor c8y4.
There are different types of immune cells that have different roles in breast cancer. In our model, we only consider the dynamics of CTLs and their role in breast cancer. We model the logistic growth of a comprehensive immune response triggered by cancer cells. To characterize immune cells' stimulation by malignant cells, we introduce the term c9y3(1−y3c10)(y2c11+y2). This term shows the logistic growth of immune cells and its activation by cancer cells in the Michaelis-Menten form. The natural degradation of immune cells is denoted by c13y3 and the term c12y2y3 describes the deterioration of immune cells after interaction with cancer cells. Overall, the equation of CTLs is given by
| dy3dt=c9y3(1−y3c10)(y2c11+y2)−c12y2y3−c13y3. | (2.3) |
Adipocytes are primarily responsible for the production of estrogen. In postmenopausal women with breast cancer, estrogen levels may be higher than the modest quantity. Typically, adipose tissues in the breasts, brain, osteoblasts and numerous other tissues produce estrogen, circulating throughout the body. The volume of estrogen replicated in the body depends on the amount already present. This study entails the use of c14 to model constant estrogen production throughout the body, and natural degradation is represented by c15y4. The equation for estrogen is given by
| dy4dt=c14−c15y4. | (2.4) |
The schematic diagram of the whole modeling process is given in Figure 1.
Combining all of the equations, the proposed zero-dimensional mathematical model is given by
| dy1dt=c1y1(1−y1c2)−c3y1y4, | (2.5) |
| dy2dt=c3y1y4+c4y2(1−y2c5)−c6y2(y3c7+y3)+c8y4, | (2.6) |
| dy3dt=c9y3(1−y3c10)(y2c11+y2)−c12y2y3−c13y3, | (2.7) |
| dy4dt=c14−c15y4, | (2.8) |
where c1,c2,...,c15 are positive constants. The model equations are non-dimensionalized by using
| y1(t)=Y1(τ)k1,y2(t)=Y2(τ)k2,y3(t)=Y3(τ)k3,y4(t)=Y4(τ)k4,τ=k5t, |
where k5=k1c6. The values of k1, k2 and k5 are taken as suggested by [30] while the values of k3 and k4 are taken accordingly. After the simplification and replacement of τ by t, the dimensionless model of the system given by (2.5)–(2.8) is as follows:
| dY1dt=α1Y1(1−Y1α2)−α3Y1Y4, | (2.9) |
| dY2dt=α4Y1Y4+α5Y2(1−Y2α6)−α7Y2(Y3α8+Y3)+α9Y4, | (2.10) |
| dY3dt=α10Y3(1−Y3α11)(Y2α12+Y2)−α13Y2Y3−α14Y3, | (2.11) |
| dY4dt=α15−α16Y4, | (2.12) |
where the values of αi(i=1,2,3,...,16) are given by
| α1=c1k5,α2=c2k1,α3=c3k4k5,α4=c3k2k1k4k5,α5=c4k5,α6=c5k2,α7=c6k5,α8=c7k3,α9=c8k2k4k5,α10=c9k5,α11=c10k3,α12=c11k2,α13=c12k2k5,α14=c13k5,α15=c14k4k5,α16=c15k5. |
We extended the concept of breast tumors to include an implicit spatial dimension under a site on breast tissue. Therefore, we developed a diffusion model in a spatial domain to integrate more aspects of spatial variability. The proposed one-dimensional mathematical model is given by
| ∂Y1(r,t)∂t=σ11r2∂∂r(r2∂Y1(r,t)∂r)+α1Y1(r,t)(1−Y1(r,t)α2)−α3Y1(r,t)Y4(r,t), | (2.13) |
| ∂Y2(r,t)∂t=σ21r2∂∂r(r2∂Y2(r,t)∂r)+α3Y1(r,t)Y4(r,t)+α4Y2(r,t)(1−Y2(r,t)α5)−α6Y2(r,t)(Y3(r,t)α7+Y3(r,t))+α8Y4(r,t), | (2.14) |
| ∂Y3(r,t)∂t=σ31r2∂∂r(r2∂Y3(r,t)∂r)+α9Y3(r,t)(1−Y3(r,t)α10)(Y2α11+Y2)−α12Y2Y3−α13Y3, | (2.15) |
| ∂Y4(r,t)∂t=σ41r2∂∂r(r2∂Y4(r,t)∂r)+α14−α15Y4(r,t), | (2.16) |
where Y1(r,t) is the population of dormant cancer cells in the spatial domain r, Y2(r,t) is the population of active cancer cells in the spatial domain r, Y3(r,t) is the number of immune cells in the spatial domain r and Y4(r,t) is the density of estrogen hormones in the spatial domain r. We consider the radially symmetric case, with the tumor environment being a ball {0≤r<L}.
Hormone therapy may be classified as the primary treatment for estrogen-positive breast cancer, and it functions by inhibiting estrogen's effects on cancer cells. Hormone therapy includes tamoxifen, aromatase inhibitors, fulvestrant and ovarian suppression. In this article, we model the effect of fulvestrant on estrogen and active cancer cells. Fulvestrant is a medication used to treat certain types of breast cancer, including hormone receptor-positive metastatic breast cancer. It works by blocking the estrogen receptor, which is a protein that allows estrogen to bind and activate breast cancer cells. By blocking this receptor, fulvestrant can slow or stop the growth of cancer cells. Fulvestrant is administered as an injection into the muscle. The dosage and frequency of injections depend on the individual patient and the stage of their breast cancer. The administration of the fulvestrant drug can be modeled by the equation given by
| ∂R∂t=σ51r2∂∂r(r2∂R∂r)+f(t)−α16R, | (2.17) |
where f(t) is a function used to describe the intermittent input of fulvestrant injections. The intermittent injections are administered at a fixed dose of 25 mg for several weeks [31]. The effect of hormone therapy is modeled by a term (1−ϵ) and it is added to the dynamics of active cancer cells and estrogen as follows:
| ∂Y2∂t=σ21r2∂∂r(r2∂Y2∂r)+α3Y1Y4+α4Y2(1−Y2α5)−α6Y2(Y3α7+Y3)+α8(1−ϵ)Y4, | (2.18) |
| ∂Y4∂t=σ41r2∂∂r(r2∂Y4∂r)+α14(1−ϵ)−α15Y4. | (2.19) |
The initial and boundary conditions of the one-dimensional model are given by
| {Y1(0,r)=Y01,∂∂rY1(t,0)=0,∂∂rY1(t,1)=0,Y2(0,r)=Y02,∂∂rY2(t,0)=0,∂∂rY2(t,1)=0,Y3(0,r)=Y03,∂∂rY3(t,0)=0,∂∂rY3(t,1)=0,Y4(0,r)=Y04,∂∂rY4(t,0)=0,∂∂rY4(t,1)=0. | (2.20) |
We use several experimental breast cancer studies to quantify the parametric values of the proposed model. An experimental study based on three xenograft models of endocrine therapy-resistant breast cancer [31] has been used to estimate the parametric values for the logistic component involved in active cancer cell dynamics. We use the MATLAB GUI program "GRABIT" to extract the data from [31]; we then used this data for parameter estimation. The experimental data provided in [32] were used to estimate the values of the cytolysis term. Similarly, the parameters of immune cell dynamics were estimated by using clinical data obtained from the analysis of tumor cells and T lymphocytes in breast cancer patients [33]. Complete details of the parametric values are given in Table 1.
| Parameter | Description | Value | Reference |
| α1 | Logistic growth rate of dormant cancer cells | 0.5140 | Extracted from [41] |
| α2 | Carrying capacity of dormant cancer cells | 103 | Assumed |
| α3 | Conversion rate for dormant cancer cells into active cancer cells | 0.08−0.4 | Assumed |
| α4 | Logistic growth rate of active cancer cells | 0.4−0.8 | Estimated from [31] |
| α5 | Carrying capacity of active cancer cells | 103 | Extracted from [42] |
| α6 | Cytolysis rate | 1 | [11] |
| α7 | Michaelis constant of Michaelis–Menten kinetics | 1×101–2×102 | Assumed |
| α8 | Growth of active cancer cells due to estrogen | 0.05–0.2 | Varies |
| α9 | Logistic growth rate of CTLs | 3.7−5.8 | Estimated from [33] |
| α10 | Carrying capacity of CTLs | 103 | [11] |
| α11 | Michaelis constant of Michaelis–Menten kinetics | 1×101−2×102 | [11] |
| α12 | Inactivation rate of CTLs after interaction with active cancer cells | 7.812×10−5 | [11] |
| α13 | Natural degradation rate of CTLs | 0.8729 | [11] |
| α14 | Supply of estrogen | 102−103 | Varies |
| α15 | Natural degradation of estrogen hormones | 0.03−0.07 | Extracted from [43] |
| σ1 | Diffusion coefficient for dormant cancer cells | 1.25×10−3 | [44] |
| σ2 | Diffusion coefficient for active cells | 1.25×10−3 | [44] |
| σ3 | Diffusion coefficient for CTLs | 1.25×10−3 | [44] |
| σ4 | Diffusion coefficient for estrogen hormones | 1.25×10−3 | [44] |
The parameter estimation technique used in this study is summarized in Figure 2. First, a reasonable guess was made to estimate the values of these parameters. Then, the ordinary differential equation system was solved to obtain the estimated values of the tumor dynamics presented by Ypar. We then constructed an error expression (EPar) as the sum of the squared differences between the calculated values (Ypar) and the experimental data (Ydata). The regression approach is the preferred way of finding a local minimum via unconstrained nonlinear optimization methods such as the Nelder-Mead algorithm. This technique minimizes the value of a function by evaluating the function directly without using any derivatives. The process is terminated and the parameter values are chosen as the optimum values if the error EPar does not exceed the user-specified tolerance (TOL). If this is not the case, the parameters' values are changed and the process is repeated. The process is repeated continuously until convergence occurs. The formula for the minimized objective function is as follows
| EPar=N∑i=1(Y(i)par−Y(i)data)2, | (3.1) |
where EPar denotes the difference between the value of active cancer cells (Ypar) estimated from simulations and the observed data (Ydata) over N observations.
The model given by (2.13)–(2.19) constitutes nonlinearly coupled partial differential equations with initial and boundary conditions given by (2.20). We solve these equations by using the forward-time centred-space (FTCS) finite-difference method. We apply forward difference to the time and central difference for the space variable, i.e.,
| {∂Y∂t=Y(i,j+1)−Y(i,j)Δt,∂Y∂r=Y(i+1,j)−Y(i−1,j)2(Δr),∂2Y∂r2=Y(i+1,j)−2Y(i,j)+Y(i−1,j)(Δr)2. | (3.2) |
After discretization, we get the following algebraic equations
| Y(i,j+1)1=[σ1(Δt)(Δr)2+σ1(Δt)ri(Δr)]Y(i+1,j)1+[σ1(Δt)(Δr)2+σ1(Δt)ri(Δr)]Y(i−1,j)1+[1+2σ1(Δt(Δr)2+α1(Δt)(1−Y(i,j)1α2)−α3(Δt)Y(i,j)4]Y(i,j)1, | (3.3) |
| Y(i,j+1)2=[σ2(Δt)(Δr)2+σ2(Δt)ri(Δr)]Y(i+1,j)2+[σ2(Δt)(Δr)2+σ2(Δt)ri(Δr)]Y(i−1,j)2+[1+2σ2(Δt(Δr)2+α4(Δt)(1−Y(i,j)2α5)−α6(Δt)(Y(i,j)3α7+Y(i,j)3)+α8(1−ϵ)(Δt)]Y(i,j)2+α3(Δt)Y(i,j)1Y(i,j)4, | (3.4) |
| Y(i,j+1)3=[σ3(Δt)(Δr)2+σ3(Δt)ri(Δr)]Y(i+1,j)3+[σ3(Δt)(Δr)2+σ3(Δt)ri(Δr)]Y(i−1,j)3+[1+2σ3(Δt(Δr)2−α3(Δt)+α9(Δt)(1−Y(i,j)3α10)(Y(i,j)2α11+Y(i,j)2)−α12(Δt)Y(i,j)2]Y(i,j)3, | (3.5) |
| Y(i,j+1)4=[σ4(Δt)(Δr)2+σ4(Δt)ri(Δr)]Y(i+1,j)4+[σ4(Δt)(Δr)2+σ4(Δt)ri(Δr)]Y(i−1,j)4+[1+2σ4(Δt(Δr)2−α14(1−ϵ)(Δt)−α15(Δt)]Y(i,j)4, | (3.6) |
| R(i,j+1)=[σ5(Δt)(Δr)2+σ5(Δt)ri(Δr)]R(i+1,j)+[σ5(Δt)(Δr)2+σ5(Δt)ri(Δr)]R(i−1,j)+[1+2σ5(Δt(Δr)2−α16(Δt)+f(tj)]R(i,j). | (3.7) |
The stability and convergence of the FTCS scheme completely depend on Δt and Δr [34]. The stability condition for FTCS is given by
| σΔt(Δr)2≤12. | (3.8) |
Thus, we should choose appropriate values of σ, Δt and Δr to satisfy the stability condition of the FTCS scheme.
The finite difference approach is well recognized for its numerical stability and precision, especially in the context of solving partial differential equations that include intricate boundary conditions and irregular geometries. These characteristics distinguish the FTCS scheme from other methods [35,36] and are critical to accurately characterizing the spatial dynamics of breast cancer growth in the tumor microenvironment, which is characterized by variable features and irregular tumor forms. Our study focuses on modeling breast cancer dynamics in a spatially complex environment, requiring an efficient approach that is capable of addressing multiple challenges. The finite difference method readily extends to higher dimensions, making it suitable for our spatial modeling approach.
Global sensitivity analysis is a technique used to analyze the behavior of a mathematical model by considering the impact of varying input parameters simultaneously and uniformly across their full range of possible values [37]. It provides a quantitative measure of how much the model's output changes with variations in the input parameters. This analysis is essential in understanding the behavior of complex models and can help to distinguish key parameters that should be prioritized for further study or optimization. Monte Carlo global sensitivity analysis is a powerful method for assessing input variables' impact on a mathematical model's output. It combines the Monte Carlo method, which involves generating random samples of input values, with global sensitivity analysis, which quantifies the importance of input variables and their interactions with respect to the model output. This approach can provide a comprehensive view of the influence of input variables on the model output, allowing researchers to identify the most critical parameters and prioritize further analysis or optimization. However, it can also be computationally intensive, particularly for models with high-dimensional input spaces.
We performed sensitivity analysis before conducting numerical simulations to determine the impact of various parameters on the dynamics of active tumor cells. We evaluated the uncertainty of six parameters, including α3, α4, α8, α9, α12 and α14. A uniform probability distribution was used to generate a sample of 100 values for each parameter. Results from the sensitivity analysis were included in the numerical simulation to monitor parameter values and enhance the performance and reliability of the model.
The rank correlation coefficients were computed by using the Kendall correlation technique and displayed by using a tornado plot (see Figure 3a). The tornado plot shows that the population of active cancer cells is very sensitive to the parameters α3 and α8. It also shows that four parameters directly impact the population of active cancer cells, while two parameters have an inverse impact. The respective influences of α3 and α8 are plotted separately in Figure 3b and 3c. It can be observed that increasing the α3 and α8 values increases the population of active cancer cells.
Breast cancer is a complex medical disorder distinguished by aberrant cellular proliferation and division within the tissue of the mammary gland. The carrying capacity of the tissue around it may be reached if breast cancer cells continue to proliferate uncontrolled and advance unabatedly. This, in turn, can result in the development of a tumor and the metastasis of cancerous cells to other parts of the body. The present study deals with the dynamics of active cancer cells and CTLs in the presence of estrogen. Figure 4 shows the dynamics of active cancer cells and CTLs without hormone therapy. Notably, the population of both cellular components approaches the carrying capacity limit in the absence of hormone therapy. Breast cancer cells reaching their carrying capacity may develop into tumors, which can be detected by imaging or a physical exam as a palpable mass or lump. Furthermore, when breast cancer cells proliferate beyond their capability, they may become more invasive and spread to nearby lymph nodes or distant organs via the lymphatic or circulatory systems. This process, commonly referred to as metastasis, poses a formidable obstacle to the treatment of breast cancer and significantly diminishes a patient's chances of survival.
Hormone treatment is a well-recognized therapeutic option for breast cancer that works by either inhibiting estrogen's effects or reducing estrogen levels in the body. Cancer cell proliferation may be successfully inhibited or decreased by using this treatment. In this study, we chose to use the pharmacokinetics and pharmacodynamics of fulvestrant to treat estrogen-positive breast cancer. Fulvestrant, a selective estrogen receptor degrader, stops breast cancer cells from signaling with estrogen. We applied intermittent administration of fulvestrant, which entails administering hormone therapy dosage periodically followed by intervals. This strategy is based on the premise that continuous hormone therapy administration can lead to treatment resistance and a diminishing therapeutic response over time. In our simulations, we applied a fixed dose of 25 mg of fulvestrant administered intermittently over 15 weeks. Figure 5 illustrates the dynamics of active cancer cells and CTLs in response to hormone therapy, depicting cyclic behavior in their population.
Breast cancer cells exhibit cyclic behavior in their activity patterns, with periods of rapid growth followed by periods of slow growth or dormancy. This cyclic behavior is known as the cancer cell cycle, characterized by different phases, including the G0, G1, S, G2 and M phases. The G0 phase is considered dormant, as the cells are not actively dividing, allowing them to evade detection and treatment. The G1 phase is the preparatory phase, where the cells prepare for DNA synthesis. The S phase is the phase where DNA replication occurs. The G2 phase is where the cells prepare for mitosis, and the M phase is where cell division occurs. Breast cancer cells can remain in the G0 phase for extended periods of time, allowing them to evade detection and treatment. However, they can also enter a highly proliferative phase, leading to the rapid growth and spread of the tumor. On the other hand, CTLs, i.e., specialized immune cells that target and eliminate cancer cells, exhibit periodic behavior in their activity patterns. This cyclic behavior is likely due to the influence of the body's internal clock, which regulates various physiological processes. In addition to their circadian rhythm, CTLs exhibit periodic behavior in their activity cycles, with periods of activation followed by rest periods. This allows them to conserve energy and maintain their effectiveness in targeting cancer cells over extended periods of time. The cyclic behavior of breast cancer cells and CTLs was studied by using mathematical modeling and phase plane analysis. Understanding the cyclic behavior of cancer cells and CTLs is essential for the development of effective treatments for breast cancer.
The phase-plane dynamics of active cancer cells and CTLs presented in Figure 6 provide insight into the complex interplay between breast tumor cells and the immune system. CTLs have the ability to recognize and eliminate cancer cells, but tumors can evade detection by reducing antigen expression or by upregulating immune checkpoints. This leads to a dynamic balance between tumor cells and CTLs, with periodic fluctuations in the immune response. In addition, the irregular behavior observed may be influenced by the cell cycle of tumor cells. Breast tumor cells can grow and divide at varying rates, resulting in fluctuations in their numbers over time. These fluctuations can significantly impact the immune response, as CTLs may have more or fewer targets to attack depending on the cell cycle phase of the tumor cells. Therefore, understanding the phase-plane dynamics of breast tumor cells and CTLs is crucial for the development of effective treatments for breast cancer.
Phase plane analysis has been recognized as a valuable tool for examining the dynamics of a system under diverse treatment conditions. Specifically, it has been demonstrated that the system's dynamics rely on the immune response's strength and the cells' proliferation rate. When the immune response is vigorous, and hormone therapy is administered, the trajectories in the phase plane tend to converge to a stable equilibrium point, corresponding to the complete elimination of cancer cells, as presented in Figure 6. However, in the case of a typical immune response, the trajectories tend to spiral towards a limited cycle, indicating the system's cyclic behavior and the persistence of cancer cells, as shown in Figure 7a. On the other hand, when the immune response weakens, the trajectories tend to grow exponentially, which results in the cancer cells reaching their maximum carrying capacity, as illustrated in Figure 7b. The proposed mathematical model predicts three distinct states of a breast tumor. With hormone therapy and a robust immune response, a breast tumor can be eradicated entirely or reduced to a minimal size where it poses no harm. According to several studies [38,39,40], a small tumor never develops into an aggressive type and is termed "cancer without disease." With hormone therapy and a typical immune response, a breast tumor can exist to a limited extent and may grow at the end of treatment. Similarly, when the immune response is below average, breast cancer cells grow quickly despite hormone therapy, reaching their maximum carrying capacity. In our proposed model, the immune response is contingent on the growth rate of CTLs. We have chosen a high value of CTL growth rate for a robust immune response, a median value for an average immune response and a low value for a weakened immune response. All values for the CTL growth were taken from the estimated interval as given in Table 1.
The present study presents a mathematical model that elucidates the intricate dynamics of estrogen hormones and their implications in breast cancer progression. The proposed model considers the effects of hormone therapy on reducing the amount of estrogen in the body or inhibiting its impact on breast cancer cells. The graphical representation of estrogen hormones is depicted in Figure 8. Specifically, Figure 8a demonstrates the progression of estrogen without any treatment, while Figure 8b illustrates estrogen dynamics under hormone therapy's influence. The findings suggest that the hormone therapy intervention leads to a decline in the population of estrogen, signifying its potential therapeutic role in breast cancer treatment. Overall, the proposed mathematical model provides a comprehensive understanding of the underlying mechanisms involved in breast tumor progression and the effects of hormone therapy. Furthermore, this model can serve as a valuable tool for identifying novel therapeutic approaches that may be more efficacious than the current therapies.
Breast cancer is the leading cause of death among women worldwide. Inhibiting or decreasing the estrogen production rate is one potential way to increase survival rates and enhance the quality of life for estrogen receptor-positive breast cancer patients. This paper examines the interaction between estrogen and the cancer-immune response in a deterministic setting. We have reviewed recent articles on the mathematical modeling of estrogen and breast cancer cells. We have developed a partial differential equation model based on breast cancer and estrogen pathology to investigate and predict the response to hormone therapy. The key findings of the proposed mathematical model simulation are given below:
● Estrogen increases the growth of cancer cells.
● An intermittent hormone therapy dose controls breast cancer cells' growth rate.
● At early stages, a robust immune response with intermittent hormone therapy can eliminate a breast tumor or reduce it to a minimal size where it poses no harm.
● With hormone therapy and a typical immune response, a breast tumor can exist to a limited extent and may grow at the end of treatment.
● Sometimes, the immune response is not activated or weakens, and this leads to the breast tumor growing rapidly.
The developed model only takes the effects of CTLs and ignores the dynamics of other immune responses. An extension of this model would be to include the dynamics of helper T cells and innate immunity responses. Moreover, the proposed model is limited to only the hormone therapy response. However, in the future, we are interested in upgrading the model to include chemotherapy/immunotherapy or a combination of both. Nevertheless, our research provides new opportunities for understanding the molecular mechanisms underlying estrogen and breast cancer cells, and it will help to analyze personalized therapeutic possibilities.
We may investigate the following options for future developments and uses of our approach as part of our continuing research activities. The spatial modeling methodology used in this work incorporates experimental data and mathematical modeling, which enables its use as a tool to investigate the dynamics of various cancer types within their distinct tumor microenvironments. Further research may be directed towards the application of our developed technique to other subtypes of cancer, taking into account the heterogeneity of the tumor microenvironment and the intricacies of the immune response. Building upon our investigation into hormone therapy for breast cancer, we intend to explore the optimization of treatment strategies in other cancer contexts. This could include the development of personalized treatment regimens and the assessment of therapeutic interventions in diverse cancer types. Our methodology can be extended to assess the efficacy of various drugs and treatment combinations in controlling cancer growth. This may be particularly relevant in the context of precision medicine and the development of targeted therapies. Future directions may involve translating our research findings into clinically relevant applications, potentially informing treatment decisions and strategies in oncology.
The authors declare that they have not used artificial intelligence tools in the creation of this article.
The authors extend their appreciation to the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU). This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) through research project no. IFP-IMSIU-2023053.
The authors declare that there is no conflict of interest.
| [1] |
M. Arnold, E. Morgan, H. Rumgay, A. Mafra, D. Singh, M. Laversanne, et al., Current and future burden of breast cancer: Global statistics for 2020 and 2040, Breast, 66 (2022), 15–23. https://doi.org/10.1016/j.breast.2022.08.010 doi: 10.1016/j.breast.2022.08.010

|
| [2] | G. N. Sharma, R. Dave, J. Sanadya, P. Sharma, K. Sharma, Various types and management of breast cancer: An overview, J. Adv. Pharm. Technol. Res., 1 (2010), 109. |
| [3] |
Y. Feng, M. Spezia, S. Huang, C. Yuan, Z. Zeng, L. Zhang, et al., Breast cancer development and progression: Risk factors, cancer stem cells, signaling pathways, genomics, and molecular pathogenesis, Genes Dis., 5 (2018), 77–106. https://doi.org/10.1016/j.gendis.2018.05.001 doi: 10.1016/j.gendis.2018.05.001

|
| [4] |
C. Urbaniak, G. B. Gloor, M. Brackstone, L. Scott, M. Tangney, G. Reid, The microbiota of breast tissue and its association with breast cancer, Appl. Environ. Microbiol., 82 (2016), 5039–5048. https://doi.org/10.1128/AEM.01235-16 doi: 10.1128/AEM.01235-16

|
| [5] |
D. L. Monticciolo, M. S. Newell, L. Moy, B. Niell, B. Monsees, E. A. Sickles, Breast cancer screening in women at higher-than-average risk: Recommendations from the acr, J. Am. College Radiol., 15 (2018), 408–414. https://doi.org/10.1016/j.jacr.2017.11.034 doi: 10.1016/j.jacr.2017.11.034

|
| [6] |
B. H. Lerner, The breast cancer wars: Hope, fear, and the pursuit of a cure in twentieth-century America, Bull. His. Med., 76 (2002), 179–180. https://doi.org/10.1353/bhm.2002.0039 doi: 10.1353/bhm.2002.0039

|
| [7] |
L. Wiechmann, H. M. Kuerer, The molecular journey from ductal carcinoma in situ to invasive breast cancer, Cancer, 112 (2008), 2130–2142. https://doi.org/10.1002/cncr.23430 doi: 10.1002/cncr.23430

|
| [8] |
R. Benacka, D. Szaboova, Z. Gulasova, Z. Hertelyova, J. Radonak, Classic and new markers in diagnostics and classification of breast cancer, Cancers, 14 (2022), 5444. https://doi.org/10.3390/cancers14215444 doi: 10.3390/cancers14215444

|
| [9] | R. Sumbaly, N. Vishnusri, S. Jeyalatha, Diagnosis of breast cancer using decision tree data mining technique, Int. J. Comput. Appl., 98 (2014). https://doi.org/10.5120/17219-7456 |
| [10] |
B. Lim, W. A. Woodward, X. Wang, J. M. Reuben, N. T. Ueno, Inflammatory breast cancer biology: The tumour microenvironment is key, Nat. Rev. Cancer, 18 (2018), 485–499. ttps://doi.org/10.1038/s41568-018-0010-y doi: 10.1038/s41568-018-0010-y

|
| [11] |
M. Idrees, A. Sohail, Bio-algorithms for the modeling and simulation of cancer cells and the immune response, Bio-Algorithms Med-Syst., 17 (2021), 55–63. https://doi.org/10.1515/bams-2020-0054 doi: 10.1515/bams-2020-0054

|
| [12] | A. K. Abbas, A. H. Lichtman, S. Pillai, Basic Immunology E-Book: Functions And Disorders of The Ommune System, Elsevier Health Sciences, 2019. |
| [13] | Obstacles in the development of therapeutic cancer vaccines, Vaccines Cancer Immunother., (2019), 153–160. https://doi.org/10.1016/B978-0-12-814039-0.00012-6 |
| [14] |
R. A. Hess, D. Bunick, K. H. Lee, J. Bahr, J. A. Taylor, K. S. Korach, et al., A role for oestrogens in the male reproductive system, Nature, 390 (1997), 509–512. https://doi.org/10.1038/37352 doi: 10.1038/37352

|
| [15] |
P. Bhardwaj, C. C. Au, A. Benito-Martin, H. Ladumor, S. Oshchepkova, R. Moges, et al., Estrogens and breast cancer: Mechanisms involved in obesityrelated development, growth and progression, J. Steroid Biochem. Mol. Biol., 189 (2019), 161–170. https://doi.org/10.1016/j.jsbmb.2019.03.002 doi: 10.1016/j.jsbmb.2019.03.002

|
| [16] |
S. S. Skandalis, N. Afratis, G. Smirlaki, D. Nikitovic, A. D. Theocharis, G. N. Tzanakakis, Cross-talk between estradiol receptor and egfr/igfir signaling pathways in estrogen-responsive breast cancers: Focus on the role and impact of proteoglycans, Matrix Biol., 35 (2014), 182–193. https://doi.org/10.1016/j.matbio.2013.09.002 doi: 10.1016/j.matbio.2013.09.002

|
| [17] |
R. X. Song, Z. Zhang, R. J. Santen, Estrogen rapid action via protein complex formation involving ERα and Src, Trends Endocrinol. Metab., 16 (2005), 347–353. https://doi.org/10.1016/j.tem.2005.06.010 doi: 10.1016/j.tem.2005.06.010

|
| [18] |
L. Anderson, S. Jang, J. L. Yu, Qualitative behavior of systems of tumor–cd4+–cytokine interactions with treatments, Math. Methods Appl. Sci., 38 (2015), 4330–4344. https://doi.org/10.1002/mma.3370 doi: 10.1002/mma.3370

|
| [19] |
G. Song, T. Tian, X. Zhang, A mathematical model of cell-mediated immune response to tumor, Math. Biosci. Eng., 18 (2021), 373–385. https://doi.org/10.3934/mbe.2021020 doi: 10.3934/mbe.2021020

|
| [20] |
K. J. Mahasa, R. Ouifki, A. Eladdadi, L. de Pillis, A combination therapy of oncolytic viruses and chimeric antigen receptor t cells: A mathematical model proof of concept, Math. Biosci. Eng., 19 (2022), 4429–4457. https://doi.org/10.3934/mbe.2022205 doi: 10.3934/mbe.2022205

|
| [21] |
K. M. Storey, S. E. Lawler, T. L. Jackson, Modeling oncolytic viral therapy, immune checkpoint inhibition, and the complex dynamics of innate and adaptive immunity in glioblastoma treatment, Front. Physiol., 11 (2020), 151. https://doi.org/10.3389/fphys.2020.00151 doi: 10.3389/fphys.2020.00151

|
| [22] |
A. M. Jarrett, M. J. Bloom, W. Godfrey, A. K. Syed, D. A. Ekrut, L. I. Ehrlich, et al., Mathematical modelling of trastuzumabinduced immune response in an in vivo murine model of her2+ breast cancer, Math. Med. Biol., 36 (2019), 381–410. https://doi.org/10.1093/imammb/dqy014 doi: 10.1093/imammb/dqy014

|
| [23] |
H. C. Wei, Mathematical modeling of tumor growth: The MCF-7 breast cancer cell line, Math. Biosci. Eng., 16 (2019), 6512–6535. https://doi.org/10.3934/mbe.2019325 doi: 10.3934/mbe.2019325

|
| [24] |
H. C. Wei, Mathematical modeling of er-positive breast cancer treatment with azd9496 and palbociclib, AIMS Math., 5 (2020), 3446–3455. https://doi.org/10.3934/math.2020223 doi: 10.3934/math.2020223

|
| [25] |
M. T. McKenna, J. A. Weis, S. L. Barnes, D. R. Tyson, M. I. Miga, V. Quaranta, et al., A predictive mathematical modeling approach for the study of doxorubicin treatment in triple negative breast cancer, Sci. Rep., 7 (2017), 5725. https://doi.org/10.1038/s41598-017-05902-z doi: 10.1038/s41598-017-05902-z

|
| [26] |
S. I. Oke, M. B. Matadi, S. S. Xulu, Optimal control analysis of a mathematical model for breast cancer, Math. Comput. Appl., 23 (2018), 21. https://doi.org/10.3390/mca23020021 doi: 10.3390/mca23020021

|
| [27] | C. Mufudza, W. Sorofa, E. T. Chiyaka, Assessing the effects of estrogen on the dynamics of breast cancer, Comput. Math. Methods Med., 2012 (2012). https://doi.org/10.1155/2012/473572 |
| [28] |
R. Ouifki, S. I. Oke, Mathematical model for the estrogen paradox in breast cancer treatment, J. Math. Biol., 84 (2022), 28. https://doi.org/10.1007/s00285-022-01729-z doi: 10.1007/s00285-022-01729-z

|
| [29] | M. Riaz, M. T. M. van Jaarsveld, A. Hollestelle, W. J. C. Prager-van der Smissen, A. A. J. Heine, A. W. M. Boersma, et al., Mirna expression profiling of 51 human breast cancer cell lines reveals subtype and driver mutation-specific mirnas, Breast Cancer Res., 15 (2013), 33–49. https://doi.org/10.1186/bcr3415 |
| [30] |
V. A. Kuznetsov, I. A. Makalkin, M. A. Taylor, A. S. Perelson, Nonlinear dynamics of immunogenic tumors: Parameter estimation and global bifurcation analysis, Bull. Math. Biol., 56 (1994), 295–321. https://doi.org/10.1016/S0092-8240(05)80260-5 doi: 10.1016/S0092-8240(05)80260-5

|
| [31] |
S. E. Wardell, A. P. Yllanes, C. A. Chao, Y. Bae, K. J. Andreano, T. K. Desautels, et al., Pharmacokinetic and pharmacodynamic analysis of fulvestrant in preclinical models of breast cancer to assess the importance of its estrogen receptor-α degrader activity in antitumor efficacy, Breast Cancer Res. Treatment, 179 (2020), 67–77. https://doi.org/10.1007/s10549-019-05454-y doi: 10.1007/s10549-019-05454-y

|
| [32] |
M. R. Muller, F. Grunebach, A. Nencioni, P. Brossart, Transfection of dendritic cells with rna induces CD4-and CD8-mediated t cell immunity against breast carcinomas and reveals the immunodominance of presented t cell epitopes, J. Immunol., 170 (2003), 5892–5896. https://doi.org/10.4049/jimmunol.170.12.5892 doi: 10.4049/jimmunol.170.12.5892

|
| [33] | I. Gruber, N. Landenberger, A. Staebler, M. Hahn, D. Wallwiener, T. Fehm, Relationship between circulating tumor cells and peripheral T-cells in patients with primary breast cancer, Anticancer Res., 33 (2013), 2233–2238. |
| [34] | G. D. Smith, G. D. Smith, Numerical solution of partial differential equations: Finite difference methods, Oxford university press, 1985. |
| [35] | F. Wang, E. Hou, A direct meshless method for solving two-dimensional secondorder hyperbolic telegraph equations, J. Math., 2020 (2020). https://doi.org/10.1155/2020/8832197 |
| [36] |
F. Wang, E. Hou, S. A. Salama, M. M. A. Khater, Numerical investigation of the nonlinear fractional ostrovsky equation, Fractals, 30 (2022), 2240142. https://doi.org/10.1142/S0218348X22401429 doi: 10.1142/S0218348X22401429

|
| [37] |
K. G. Link, M. T. Stobb, J. D. Paola, K. B. Neeves, A. L. Fogelson, S. S. Sindi, et al., A local and global sensitivity analysis of a mathematical model of coagulation and platelet deposition under flow, PLoS One, 13(2018), e0200917. https://doi.org/10.1371/journal.pone.0200917 doi: 10.1371/journal.pone.0200917

|
| [38] | J. Folkman, R. Kalluri, Cancer without disease, Nature, 427 (2004), 787–787. https://doi.org/10.1038/427787a |
| [39] |
T. Fehm, V. Mueller, R. Marches, G. Klein, B. Gueckel, H. Neubauer, et al., Tumor cell dormancy: Implications for the biology and treatment of breast cancer, Apmis, 116 (2008), 742–753. https://doi.org/10.1111/j.1600-0463.2008.01047.x doi: 10.1111/j.1600-0463.2008.01047.x

|
| [40] |
O. E. Franco, A. K. Shaw, D. W. Strand, S. W. Hayward, Cancer associated fibroblasts in cancer pathogenesis, Semin. Cell Dev. Biol., 21 (2010), 33–39. https://doi.org/10.1016/j.semcdb.2009.10.010 doi: 10.1016/j.semcdb.2009.10.010

|
| [41] |
M. W. Retsky, R. Demicheli, W. J. M. Hrushesky, M. Baum, I. D. Gukas, Dormancy and surgery-driven escape from dormancy help explain some clinical features of breast cancer, Apmis, 116 (2008), 730–741. https://doi.org/10.1111/j.1600-0463.2008.00990.x doi: 10.1111/j.1600-0463.2008.00990.x

|
| [42] | M. Fernandez, M. Zhou, L. Soto-Ortiz, A computational assessment of the robustness of cancer treatments with respect to immune response strength, tumor size and resistance, Int. J. Tumor Ther., 7 (2018), 1–26. |
| [43] |
V. Valayannopoulos, F. Bajolle, J. B. Arnoux, S. Dubois, N. Sannier, C. Baussan, et al., Successful treatment of severe cardiomyopathy in glycogen storage disease type III With D, L-3-hydroxybutyrate, ketogenic and high-protein diet, Pediatr. Res., 70 (2011), 638–641. https://doi.org/10.1203/PDR.0b013e318232154f doi: 10.1203/PDR.0b013e318232154f

|
| [44] |
A. Friedman, K. L. Liao, The role of the cytokines IL-27 and IL-35 in cancer, Math. Biosci. Eng., 12 (2015), 1203. https://doi.org/10.3934/mbe.2015.12.1203 doi: 10.3934/mbe.2015.12.1203

|
| 1. | Zahraa Aamer, Shireen Jawad, Belal Batiha, Ali Hasan Ali, Firas Ghanim, Alina Alb Lupaş, Evaluation of the Dynamics of Psychological Panic Factor, Glucose Risk and Estrogen Effects on Breast Cancer Model, 2024, 12, 2079-3197, 160, 10.3390/computation12080160 | |
| 2. | Aziz Khan, Thabet Abdeljawad, Mahmoud Abdel-Aty, D.K. Almutairi, Digital analysis of discrete fractional order cancer model by artificial intelligence, 2025, 118, 11100168, 115, 10.1016/j.aej.2025.01.036 |
| Parameter | Description | Value | Reference |
| α1 | Logistic growth rate of dormant cancer cells | 0.5140 | Extracted from [41] |
| α2 | Carrying capacity of dormant cancer cells | 103 | Assumed |
| α3 | Conversion rate for dormant cancer cells into active cancer cells | 0.08−0.4 | Assumed |
| α4 | Logistic growth rate of active cancer cells | 0.4−0.8 | Estimated from [31] |
| α5 | Carrying capacity of active cancer cells | 103 | Extracted from [42] |
| α6 | Cytolysis rate | 1 | [11] |
| α7 | Michaelis constant of Michaelis–Menten kinetics | 1×101–2×102 | Assumed |
| α8 | Growth of active cancer cells due to estrogen | 0.05–0.2 | Varies |
| α9 | Logistic growth rate of CTLs | 3.7−5.8 | Estimated from [33] |
| α10 | Carrying capacity of CTLs | 103 | [11] |
| α11 | Michaelis constant of Michaelis–Menten kinetics | 1×101−2×102 | [11] |
| α12 | Inactivation rate of CTLs after interaction with active cancer cells | 7.812×10−5 | [11] |
| α13 | Natural degradation rate of CTLs | 0.8729 | [11] |
| α14 | Supply of estrogen | 102−103 | Varies |
| α15 | Natural degradation of estrogen hormones | 0.03−0.07 | Extracted from [43] |
| σ1 | Diffusion coefficient for dormant cancer cells | 1.25×10−3 | [44] |
| σ2 | Diffusion coefficient for active cells | 1.25×10−3 | [44] |
| σ3 | Diffusion coefficient for CTLs | 1.25×10−3 | [44] |
| σ4 | Diffusion coefficient for estrogen hormones | 1.25×10−3 | [44] |
| Parameter | Description | Value | Reference |
| α1 | Logistic growth rate of dormant cancer cells | 0.5140 | Extracted from [41] |
| α2 | Carrying capacity of dormant cancer cells | 103 | Assumed |
| α3 | Conversion rate for dormant cancer cells into active cancer cells | 0.08−0.4 | Assumed |
| α4 | Logistic growth rate of active cancer cells | 0.4−0.8 | Estimated from [31] |
| α5 | Carrying capacity of active cancer cells | 103 | Extracted from [42] |
| α6 | Cytolysis rate | 1 | [11] |
| α7 | Michaelis constant of Michaelis–Menten kinetics | 1×101–2×102 | Assumed |
| α8 | Growth of active cancer cells due to estrogen | 0.05–0.2 | Varies |
| α9 | Logistic growth rate of CTLs | 3.7−5.8 | Estimated from [33] |
| α10 | Carrying capacity of CTLs | 103 | [11] |
| α11 | Michaelis constant of Michaelis–Menten kinetics | 1×101−2×102 | [11] |
| α12 | Inactivation rate of CTLs after interaction with active cancer cells | 7.812×10−5 | [11] |
| α13 | Natural degradation rate of CTLs | 0.8729 | [11] |
| α14 | Supply of estrogen | 102−103 | Varies |
| α15 | Natural degradation of estrogen hormones | 0.03−0.07 | Extracted from [43] |
| σ1 | Diffusion coefficient for dormant cancer cells | 1.25×10−3 | [44] |
| σ2 | Diffusion coefficient for active cells | 1.25×10−3 | [44] |
| σ3 | Diffusion coefficient for CTLs | 1.25×10−3 | [44] |
| σ4 | Diffusion coefficient for estrogen hormones | 1.25×10−3 | [44] |