MAU-Net: Mixed attention U-Net for MRI brain tumor segmentation

Yuqing Zhang; Yutong Han; Jianxin Zhang; Yuqing Zhang; Yutong Han; Jianxin Zhang

doi:10.3934/mbe.2023907

Mathematical Biosciences and Engineering

2023, Volume 20, Issue 12: 20510-20527. doi: 10.3934/mbe.2023907

Previous Article Next Article

Research article

MAU-Net: Mixed attention U-Net for MRI brain tumor segmentation

1.
School of Computer Science and Engineering, Dalian Minzu University, Dalian 116600, China
2.
Institute of Machine Intelligence and Biocomputing, Dalian Minzu University, Dalian 116600, China
3.
SEAC Key Laboratory of Big Data Applied Technology, Dalian Minzu University, Dalian 116600, China

Received: 25 September 2023 Revised: 02 November 2023 Accepted: 06 November 2023 Published: 13 November 2023

Computer-aided brain tumor segmentation using magnetic resonance imaging (MRI) is of great significance for the clinical diagnosis and treatment of patients. Recently, U-Net has received widespread attention as a milestone in automatic brain tumor segmentation. Following its merits and motivated by the success of the attention mechanism, this work proposed a novel mixed attention U-Net model, i.e., MAU-Net, which integrated the spatial-channel attention and self-attention into a single U-Net architecture for MRI brain tumor segmentation. Specifically, MAU-Net embeds Shuffle Attention using spatial-channel attention after each convolutional block in the encoder stage to enhance local details of brain tumor images. Meanwhile, considering the superior capability of self-attention in modeling long-distance dependencies, an enhanced Transformer module is introduced at the bottleneck to improve the interactive learning ability of global information of brain tumor images. MAU-Net achieves enhancing tumor, whole tumor and tumor core segmentation Dice values of 77.88/77.47, 90.15/90.00 and 81.09/81.63% on the brain tumor segmentation (BraTS) 2019/2020 validation datasets, and it outperforms the baseline by 1.15 and 0.93% on average, respectively. Besides, MAU-Net also demonstrates good competitiveness compared with representative methods.

Keywords:

Citation: Yuqing Zhang, Yutong Han, Jianxin Zhang. MAU-Net: Mixed attention U-Net for MRI brain tumor segmentation[J]. Mathematical Biosciences and Engineering, 2023, 20(12): 20510-20527. doi: 10.3934/mbe.2023907

Related Papers:

[1]	Xiao Wang, Jianbiao Zhang, Ai Zhang, Jinchang Ren . TKRD: Trusted kernel rootkit detection for cybersecurity of VMs based on machine learning and memory forensic analysis. Mathematical Biosciences and Engineering, 2019, 16(4): 2650-2667. doi: 10.3934/mbe.2019132
[2]	Angel Martin-del Rey . A novel model for malware propagation on wireless sensor networks. Mathematical Biosciences and Engineering, 2024, 21(3): 3967-3998. doi: 10.3934/mbe.2024176
[3]	Jing Liao, Jinling Wang, Jiarong Li, Xin Jiang . The dynamics and control of a multi-lingual rumor propagation model with non-smooth inhibition mechanism. Mathematical Biosciences and Engineering, 2024, 21(4): 5068-5091. doi: 10.3934/mbe.2024224
[4]	Tan Gao, Lan Zhao, Xudong Li, Wen Chen . Malware detection based on semi-supervised learning with malware visualization. Mathematical Biosciences and Engineering, 2021, 18(5): 5995-6011. doi: 10.3934/mbe.2021300
[5]	Bin Wang, Fagui Liu . Task arrival based energy efficient optimization in smart-IoT data center. Mathematical Biosciences and Engineering, 2021, 18(3): 2713-2732. doi: 10.3934/mbe.2021138
[6]	Sunmi Lee, Chang Yong Han, Minseok Kim, Yun Kang . Optimal control of a discrete-time plant–herbivore/pest model with bistability in fluctuating environments. Mathematical Biosciences and Engineering, 2022, 19(5): 5075-5103. doi: 10.3934/mbe.2022237
[7]	Agustín Halty, Rodrigo Sánchez, Valentín Vázquez, Víctor Viana, Pedro Piñeyro, Daniel Alejandro Rossit . Scheduling in cloud manufacturing systems: Recent systematic literature review. Mathematical Biosciences and Engineering, 2020, 17(6): 7378-7397. doi: 10.3934/mbe.2020377
[8]	Dengzhi Liu, Zhimin Li, Chen Wang, Yongjun Ren . Enabling secure mutual authentication and storage checking in cloud-assisted IoT. Mathematical Biosciences and Engineering, 2022, 19(11): 11034-11046. doi: 10.3934/mbe.2022514
[9]	Fulian Yin, Xinyi Tang, Tongyu Liang, Yanjing Huang, Jianhong Wu . External intervention model with direct and indirect propagation behaviors on social media platforms. Mathematical Biosciences and Engineering, 2022, 19(11): 11380-11398. doi: 10.3934/mbe.2022530
[10]	Radi P. Romansky, Irina S. Noninska . Challenges of the digital age for privacy and personal data protection. Mathematical Biosciences and Engineering, 2020, 17(5): 5288-5303. doi: 10.3934/mbe.2020286

Abstract

1. Introduction

The construction of energy profiles and their analysis is a new method for studying the physical and functional properties of plasmids. This method came to DNA science from theoretical physics and nonlinear mathematics. In the frameworks of the method, the DNA molecule is considered as a complex dynamic system in which nonlinear conformational perturbations-kinks, can arise and propagate [1]–[4].

Since the work [5], kinks have been actively used to simulate the DNA open states which are small (only a few base pairs long) unwound DNA regions inside which hydrogen bonds between complementary bases are broken. The behavior of the kinks is in many ways similar to that of ordinary particles moving in the DNA potential field. Having calculated the energy profile of the potential field, one can completely solve the problem of the kink dynamics including calculation of time dependence of the kink velocity and construction of the kink trajectory.

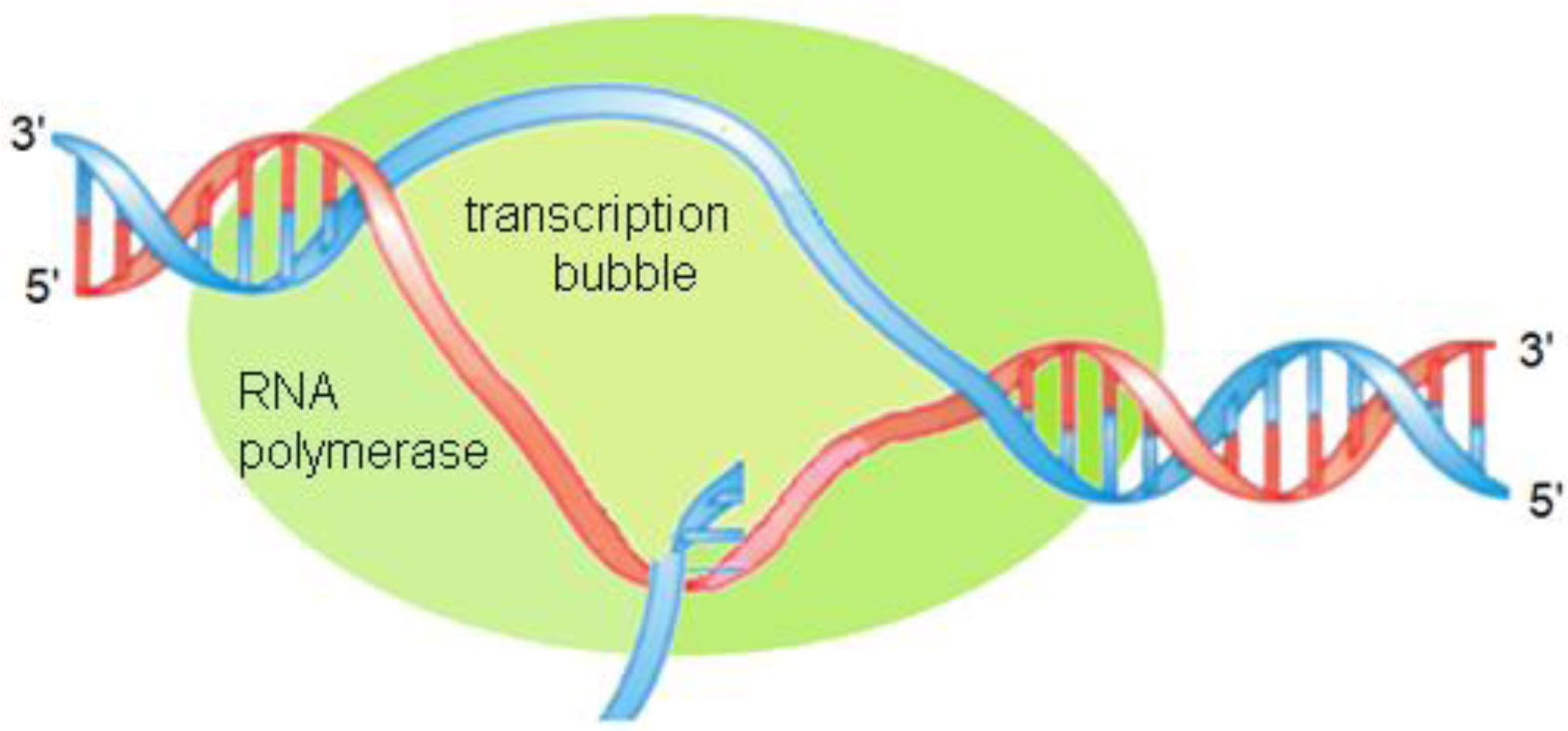
A particular example of the open state is the transcription bubble (Figure 1) which is formed at the initial stage of the transcription process as a result of the interaction of RNA polymerase with DNA promoter region [6],[7]. One of the first attempts to calculate the DNA potential field in which the transcriptional bubble moves was made by Salerno [8]. However, the absence at that time of a complete set of dynamic parameters of DNA, as well as the computer power required for such calculations, forced the author to confine himself to only a small fragment of a DNA molecule, which did not allow to obtain reliable results on the kink dynamics and to relate them with functional properties of the molecule.

Figure 1. Transcription bubble.

DownLoad: Full-Size Img PowerPoint

In this work, we solve this problem on the basis of new data and new approaches to the study of the dynamics of open states in inhomogeneous DNA. In the calculations we use the full set of dynamic parameters of DNA, which was first obtained in [9] and later refined in [10]. The block method and the method of constructing the kinks trajectories are also applied [11],[12]. In contrast to work [12], where only one plasmid profile was calculated, here we use the method of the double profile, which makes it possible to compare the dynamic characteristics of kinks activated in the main and complementary DNA strands. Such a comparison makes it possible to explain in which region of the plasmid the formation of a transcription bubble is most likely, as well to understand in which direction the bubble will move and the transcription process will go.

2. Structure of plasmid pBR322

Plasmid pBR322 [13] is a small circular DNA the sequence of which consists of 4361 bases [14] (Appendix). This sequence contains three coding regions:

CDS-1, encoding tetracycline resistance protein,

CDS-2, encoding ROP protein,

CDS-3, encoding beta-lactamase,

and three promoters: P1, P2 and P3 marked in Appendix by grey. Coordinates of the CDS regions are (86..1276), (1915..2106) and (3293..4153). Coordinates of promoters are (27-33), (43-49) and (4188-4194). The double-stranded scheme of the plasmid is shown in Figure 2a. A linear version of the scheme obtained by cutting at the point Q, is presented in Figure 2b.

Figure 2. Double-stranded scheme of the pBR32 plasmid (a) and its linear analogue (b). Q is the cutting point. S is the starting point. CDS-1, CDS-2 and CDS-3 are coding regions.

DownLoad: Full-Size Img PowerPoint

Table 1. Details of the structure of the main/complementary sequences of the pBR32 plasmid.

Region number	Region coordinates	N_A	N_T	N_G	N_C	N
1	1..85	22/29	29/22	17/17	17/17	85
2 (CDS-1)	86..1276	190/268	268/190	353/381	381/353	1192
3	1277..1914	142/145	145/142	160/191	191/160	638
4 (CDS-2)	1915..2106	54/37	37/54	48/53	53/48	192
5	2107..3292	294/268	268/294	319/305	305/319	1186
6 (CDS-3)	3293..4153	213/223	223/213	203/222	222/203	861
7	4154-4361	67/64	64/67	34/42	42/34	207

| Show Table

DownLoad: CSV

It is convenient to renumber all regions including CDS regions and the regions between them, starting from the point S. A total of 7 regions turned out. Data on their composition are presented in Table 1.

However, the splitting of the sequence into 7 regions does not reflect the circular nature of the plasmid. To take this into account, we combined the 1st and 7th regions into a single region with number (7 + 1). As a result, the total number of regions decreased by one and became equal to six. In what follows, these six regions will be referred to as blocks.

3. Model and methods

To describe angular oscillations of nitrous bases in a separate block of the DNA molecule consisting of N bp, let us use the improved Englander model [5], which is a system of 2N coupled nonlinear differential equations [15]:

$I_{n, 1} \frac{d^{2} φ_{n, 1} (t)}{d t^{2}} - K_{n, 1}^{'} [φ_{n + 1, 1} (t) - 2 φ_{n, 1} (t) + φ_{n - 1, 1} (t)] + k_{n, 1 - 2} R_{n, 1} (R_{n, 1} + R_{n, 2}) \sin φ_{n, 1} - k_{n, 1 - 2} R_{n, 1} R_{n, 2} \sin (φ_{n, 1} - φ_{n, 2}) = - β_{n, 1} \frac{d φ_{n, 1} (t)}{d t},$ (1)

$I_{n, 2} \frac{d^{2} φ_{n, 2} (t)}{d t^{2}} - K_{n, 2}^{'} [φ_{n + 1, 2} (t) - 2 φ_{n, 2} (t) + φ_{n - 1, 2} (t)] + k_{n, 1 - 2} R_{n, 2} (R_{n, 1} + R_{n, 2}) \sin φ_{n, 2} - k_{n, 1 - 2} R_{n, 1} R_{n, 2} \sin (φ_{n, 2} - φ_{n, 1}) = - β_{n, 2} \frac{d φ_{n, 2} (t)}{d t} .$ (2)

Here $φ_{n, i} (t)$ is the angular deviation of the n-th nitrous base of the i-th chain; $I_{n, i}$ is the moment of inertia of the n-th nitrous base of the i-th chain; $R_{n, i}$ is the distance between the center of mass of the n-th nitrous base of the i-th chain and the sugar-phosphate backbone; $K_{n, 1}^{'} = K R_{n, i}^{2}$ ; K is the rigidity (in tension) of the sugar-phosphate backbone; $β_{n, i} = α R_{n, i}^{2}$ , α is the dissipation coefficient; $k_{n, i}$ is a constant characterizing the interaction between bases within pairs; i = 1, 2; n = 1, 2, ... N.

Equations (1)-(2) are simplified if we use the concentration method where the coefficients $I_{n, i}$ , $R_{n, i}$ , $K_{n, i}^{'}$ , $k_{n, 1 - 2}$ and $β_{n, i}$ are averaged according to the following formulas [16]:

$\begin{array}{l} I_{n, i} \to {\bar{I}}_{i} = I_{A} C_{A, i} + I_{T} C_{T, i} + I_{G} C_{G, i} + I_{C} C_{C, i}, \\ R_{n, i} \to {\bar{R}}_{i} = R_{A} C_{A, i} + R_{T} C_{T, i} + R_{G} C_{G, i} + R_{C} C_{C, i}, \\ {K^{'}}_{n, i} \to {\bar{K}}^{'}_{i} = {K^{'}}_{A} C_{A, i} + {K^{'}}_{T} C_{T, i} + {K^{'}}_{G} C_{G, i} + {K^{'}}_{C} C_{C, i}, \\ k_{n, 1 - 2} \to {\bar{k}}_{1 - 2} = k_{A - T} (C_{A, 1} + C_{T, 2}) + k_{G - C} (C_{G, 1} + C_{C, 2}), \\ β_{n, i} \to {\bar{β}}_{i} = β_{A} C_{A, i} + β_{T} C_{T, i} + β_{G} C_{G, i} + β_{C} C_{C, i} . \end{array}$ (3)

where $C_{j . i} = N_{j, i} / N$ is the concentration of bases of the j-th type in the i-th chain; $N_{j, i}$ is the number of the of bases j-th type in the i-th sequence; (j = A, T, G, C); (i = 1, 2).

After the averaging procedure (3), equations (1)–(2) are transformed to the form:

${\bar{I}}_{1} \frac{d^{2} φ_{n, 1} (t)}{d t^{2}} - {\bar{K}}_{1}^{'} [φ_{n + 1, 1} (t) - 2 φ_{n, 1} (t) + φ_{n - 1, 1} (t)] + {\bar{k}}_{1 - 2} {\bar{R}}_{1} ({\bar{R}}_{1} + {\bar{R}}_{2}) \sin φ_{n, 1} - {\bar{k}}_{1 - 2} {\bar{R}}_{1} {\bar{R}}_{2} \sin (φ_{n, 1} - φ_{n, 2}) = - {\bar{β}}_{1} \frac{d φ_{n, 1} (t)}{d t},$ (4)

${\bar{I}}_{2} \frac{d^{2} φ_{n, 2} (t)}{d t^{2}} - {\bar{K}}_{2}^{'} [φ_{n + 1, 2} (t) - 2 φ_{n, 2} (t) + φ_{n - 1, 2} (t)] + {\bar{k}}_{1 - 2} {\bar{R}}_{2} ({\bar{R}}_{1} + {\bar{R}}_{2}) \sin φ_{n, 2} - {\bar{k}}_{1 - 2} {\bar{R}}_{1} {\bar{R}}_{2} \sin (φ_{n, 2} - φ_{n, 1}) = - {\bar{β}}_{2} \frac{d φ_{n, 2} (t)}{d t} .$ (5)

In the continuum approximation, these equations take the following form:

${\bar{I}}_{1} φ_{1 t t} - {\bar{K}}_{1}^{'} a^{2} φ_{1 z z} + {\bar{k}}_{1 - 2} {\bar{R}}_{1} ({\bar{R}}_{1} + {\bar{R}}_{2}) \sin φ_{1} - {\bar{k}}_{1 - 2} {\bar{R}}_{1} {\bar{R}}_{2} \sin (φ_{1} - φ_{2}) = - {\bar{β}}_{1} φ_{1 t},$ (6)

${\bar{I}}_{2} φ_{2 t t} - {\bar{K}}_{2}^{'} a^{2} φ_{2 z z} + {\bar{k}}_{1 - 2} {\bar{R}}_{1} ({\bar{R}}_{1} + {\bar{R}}_{2}) \sin φ_{2} - {\bar{k}}_{1 - 2} {\bar{R}}_{1} {\bar{R}}_{2} \sin (φ_{2} - φ_{1}) = - {\bar{β}}_{2} φ_{2 t} .$ (7)

In the approximation of average field [17], two coupled equations (6) and (7) are transformed into two independent equations:

${\bar{I}}_{1} φ_{1 t t} - {\bar{K}}_{1}^{'} a^{2} φ_{1 z z} + {\bar{k}}_{1 - 2} {\bar{R}}_{1}^{2} \sin φ_{1} = - {\bar{β}}_{1} φ_{1 t},$ (8)

${\bar{I}}_{2} φ_{2 t t} - {\bar{K}}_{2}^{'} a^{2} φ_{2 z z} + {\bar{k}}_{1 - 2} {\bar{R}}_{2}^{2} \sin φ_{1} = - {\bar{β}}_{2} φ_{2 t},$ (9)

where a is the distance between the nearest base pairs. In this approximation, the movement of kinks in the main and complementary chains can be considered separately. The validity of this approximation for DNA was shown in [18], where it was demonstrated numerically that taking into account the interaction between kinks activated in the main and complementary chains leads only to a slight perturbation of the kink shape.

One-soliton solutions of equations (8)–(9), kinks, have then the form :

$\begin{matrix} φ_{k, 1} (z, t) = 4 arctg {exp [(γ_{k, 1} / d_{k, 1}) (z - υ_{k, 1} (t) t - z_{0, 1})]}, \\ φ_{k, 2} (z, t) = 4 arctg {exp [(γ_{k, 2} / d_{k, 2}) (z - υ_{k, 2} (t) t - z_{0, 2})]} . \end{matrix}$ (10)

Here $υ_{k, i}^{} (t)$ is the time dependent kink velocity, $γ_{k, i} (t) = {(1 - υ_{k, i}^{2} (t) / {\bar{C}}_{i}^{2})}^{- \frac{1}{2}}$ is the Lorentz factor, ${\bar{C}}_{i} = {({\bar{K}}_{i}^{'} a^{2} / {\bar{I}}_{i})}^{1 / 2}$ is the sound velocity in the i-th chain, $d_{k, i} = {({\bar{K}}_{i}^{'} a^{2} / {\bar{V}}_{i})}^{1 / 2}$ is the size of the kink in the i-th chain, ${\bar{V}}_{i} = {\bar{k}}_{1 - 2} {\bar{R}}_{i}^{2}$ .

Equation for the kink velocity was obtained by McLaughlin and Scott [19]. In the case of plasmid pBR322, this equation has the form:

$\frac{d υ_{k, i} (t)}{d t} = - \frac{{\bar{β}}_{i}}{{\bar{I}}_{i}} υ_{k, i} (t) [1 - {(\frac{υ_{k, i} (t)}{{\bar{C}}_{i}})}^{2}], (i = 1, 2)$ (11)

The analytical solution of equation (1) found in [20], has the form :

$υ_{k, i} (t) = \frac{υ_{0, i} {\bar{γ}}_{0, i} \exp (- \frac{{\bar{β}}_{i}}{{\bar{I}}_{i}} (t - t_{0}))}{\sqrt{1 + {(\frac{υ_{0, i} {\bar{γ}}_{0, i}}{{\bar{C}}_{i}})}^{2} \exp (- \frac{2 {\bar{β}}_{i}}{{\bar{I}}_{i}} (t - t_{0}))}}$ (12)

where $υ_{0, i}$ is the kink velocity at the initial moment of time $t_{0}, {\bar{γ}}_{0, i} = {(1 - υ_{0, i}^{2} / {\bar{C}}_{i}^{2})}^{- 1 / 2}$ .

The solution for the kink coordinate $z_{k, i} (t)$ determined by the relation $υ_{k, i} (t) = \frac{d z_{k, i} (t)}{d t}$ , was obtained in [12]:

$z_{k, i} = z_{0} - {\bar{C}}_{i} \frac{{\bar{I}}_{i}}{{\bar{β}}_{i}} arcsin (\frac{υ_{0, i}}{{\bar{C}}_{i}} {\bar{γ}}_{0, i} \exp (- \frac{{\bar{β}}_{i}_{i}}{{\bar{I}}_{i}} (t - t_{0}))) + {\bar{C}}_{i} \frac{{\bar{I}}_{i}}{{\bar{β}}_{i}} arcsin (\frac{υ_{0, i}}{{\bar{C}}_{i}} {\bar{γ}}_{0, i})$ (13)

where z₀ is the coordinate of the kink at the initial moment of time t₀.

The total kink energy is determined by the following formula [21]:

$E_{i} = \frac{E_{0, i}}{\sqrt{1 - \frac{υ_{k, i}^{2}}{C_{i}^{2}}}},$ (14)

where $E_{0, i}$ is the rest energy (or the energy of activation) of the kink:

$E_{0, i} = 8 \sqrt{{\bar{K}}_{i}^{'} {\bar{V}}_{i}} (i = 1, 2) .$ (15)

In the case of small velocities ( $υ_{k, i} ≪ С_{i}$ ), formula (11) takes the form:

$E_{i} = \frac{E_{0, i}}{\sqrt{1 - \frac{υ_{k, i}^{2}}{{\bar{C}}_{i}^{2}}}} = E_{0, i} + \frac{m_{k, i} υ_{k, i}^{2}}{2},$ (16)

where ( $m_{k, i} = \frac{E_{0, i}}{2 {\bar{C}}_{i}^{2}}$ ) is the mass of the kink in the i-th chain. Formula (13) confirms that kink can be modeled as a quasiparticle with mass $m_{k, i}$ , velocity $υ_{k, i}$ and potential energy $E_{0, i}$ .

4. Results and discussion

4.1. Energy profile of the main and complementary plasmid sequences

To construct the energy profile, we first calculated the averaged values of the main dynamic parameters of the plasmid: ${\tilde{I}}^{(i)}$ , $\tilde{K}'^{(i)}$ , ${\tilde{V}}^{(i)},$ for each of the six regions:

$\begin{array}{l} {\tilde{I}}^{(i)} = I_{A} C_{A}^{(i)} + I_{T} C_{T}^{(i)} + I_{G} C_{G}^{(i)} + I_{C} C_{C}^{(i)}, \\ {\tilde{K}}^{'}^{(i)} = {K^{'}}_{A} C_{A}^{(i)} + {K^{'}}_{T} C_{T}^{(i)} + {K^{'}}_{G} C_{G}^{(i)} + {K^{'}}_{C} C_{C}^{(i)} \\ {\tilde{V}}^{(i)} = V_{A} C_{A}^{(i)} + V_{T} C_{T}^{(i)} + V_{G} C_{G}^{(i)} + V_{C} C_{C}^{(i)}, \end{array}$ (17)

and also calculated the values of the rest energies of the kinks activated in each of these regions:

${\tilde{E}}_{0}^{(i)} = 8 \sqrt{{\bar{K}}^{'}^{(i)} {\tilde{V}}^{(i)}} .$ (18)

Here ${\tilde{I}}^{(i)}$ is the averaged moment of inertia of the nitrous bases of the i-th region; $\tilde{K}'^{(i)}$ is the torsion rigidity in the i-th region; ${\tilde{V}}^{(i)}$ is a constant characterizing the interaction between complementary bases in the i-th region, i = 1, 2,...6. The calculation results are presented in Table 2.

Table 2. Dynamic characteristics calculated for each of the six regions of the main/complementary sequences of the pBR32 plasmid.

Number of the region	Coordinate of the region	${\tilde{I}}^{(i)}$ ×10⁻⁴⁴ (kg·m²)	$\tilde{K}'^{(i)}$ ×10⁻¹⁸ (N·m)	${\tilde{V}}^{(i)}$ ×10⁻²⁰ (J)	${\tilde{E}}_{0}^{(i)}$ ×10⁻¹⁸ (J)
1+7	(1..85)+(4154..4361)	6.13/6.28	1.94/1.97	2.06/2.10	1.60/1.63
2 (CDS-1)	86..1276	6.05/6.33	1.90/1.97	2.26/2.32	1.66/1.71
3	1277..1914	6.09/6.30	1.92/1.96	2.21/2.26	1.65/1.68
4 (CDS-2)	1915..2106	6.26/6.13	1.97/1.92	2.23/2.19	1.67/1.64
5	2107..3292	6.25/6.14	1.95/1.93	2.22/2.20	1.67/1.65
6 (CDS-3)	3293..4153	6.14/6.25	1.93/1.95	2.17/2.20	1.64/1.66

| Show Table

DownLoad: CSV

With the help of the data from the last column of Table 2 we constructed the double energy profile of the potential field of the plasmid (Figure 3). The energy was calculated not at every point, but for each range into which we divided the plasmid. The coordinates of the bases are plotted in Figure 3 along the horizontal in units of base pairs (bp), 1 bp = 3.4×10^–10 m. The values of the rest energy of kinks are plotted along the vertical.

Figure 3. Double energy profile of the pBR32 plasmid. Solid line corresponds to the main sequence and the dashed line corresponds to complementary sequence. Grey band indicates (7 + 1)-th range.

DownLoad: Full-Size Img PowerPoint

Figure 3 shows that the deepest well in the energy profile of both the main (solid line) and complementary (dashed line) sequences corresponds to the (7 + 1)-th region. This means that the probability of kink activation in this region is the highest. This result is in good agreement with the experimental data summarized in [14]. Indeed. the transcription process usually begins with the binding of RNA polymerase to the promoter region of the DNA sequence, and this event is accompanied by local unwinding double-stranded DNA. According to [14] there are three promoters in the (7 + 1)-th region: the P2 promoter located in the main chain, and the P1 and P3 promoters located in the complementary chain. That saturation of the (7 + 1)-th region with promoters indicates that just in this region with high probability the formation of local unwound regions - kinks, takes place.

It can be seen also that in the (7 + 1)-th region, the rest energy of the kinks activated in the main strand is less than the rest energy of the kinks activated in the complementary strand. This means that the probability of the kink activation in the main strand containing P2 promoter is greater than in the complementary strand containing P1 and P3 promoters. This allows us to suggest that the P1 and P3 promoters are much weaker than the P2 promoter.

4.2. Velocity, coordinate, energy and trajectories of kinks in plasmid pBR322

Using formulas (2)-(4) and the data of Table 2, we plotted the time dependence of the velocity, coordinates and total energy of the plasmid pBR322 kinks (Figures 4–6).

Figure 4. Time dependence of the velocity of kinks activated in the main and complementary sequences of plasmid pBR322. The initial velocity of the kink is 1881 m/s. The dissipation coefficient is 0.126×10⁻¹⁴ J·s/m².

DownLoad: Full-Size Img PowerPoint

Figure 5. Time dependence of the coordinates of kinks activated in the main and complementary sequences of plasmid pBR322. The yellow line corresponds to the main sequence and the red line corresponds to the complementary sequence. The initial velocity of the kink is 1881 m/s. The dissipation coefficient is 0.126×10⁻¹⁴ J·s/m².

DownLoad: Full-Size Img PowerPoint

Figure 6. Time dependence of the total energy of kinks activated in the main and complementary sequences of plasmid pBR322. The yellow line corresponds to the main sequence and the red line corresponds to the complementary sequence. The initial velocity of the kink is 1881 m/s. The dissipation coefficient is 0.126×10⁻¹⁴ J·s/m².

DownLoad: Full-Size Img PowerPoint

Figure 4 shows that the velocity of the kinks activated in both strands decreases with time, which is explained by the effects of dissipation. The velocity of the kink activated in the complementary strand, decreases faster. The zigzags observed on both curves are explained by abrupt changes in the velocity of the kinks when passing the boundaries between the regions.

Figure 5 shows that the coordinate of the kinks grows smoothly and reaches a constant value, which means that the kink movement stops. Kink activated in the main strand stops at the point 2332 bp, and kink activated in the complementary strand stops at 2558 bp.

From Figure 6 it can be seen that at the same value of the initial kink velocity (1881 m/s), the values of the initial total energy of the kinks activated in different strands differ. For kinks activated in the main strand, the initial total energy is 10.42×10⁻¹⁸ (J), and for kinks activated in the complementary strand, the initial total energy is 12.25×10⁻¹⁸ (J). Later both energy curves decreases and reaches the values of the rest energies.

To construct trajectories of kinks in the 3D space, we solved numerically a system of coupled differential equations for the velocity and coordinates of the kinks:

$\frac{d {\tilde{z}}_{k}^{(i)} (t)}{d t} = {\tilde{υ}}_{k}^{(i)} (t),$ (19)

$\frac{d {\tilde{υ}}_{k}^{(i)} (t)}{d t} = - \frac{{\tilde{β}}^{(i)}}{{\tilde{I}}^{(i)}} {\tilde{υ}}_{k}^{(i)} (t) [1 - {(\frac{{\tilde{υ}}_{k}^{(i)} (t)}{{\tilde{C}}^{(i)}})}^{2}] . i = 1, 2, \dots 6$ (20)

The results are presented in the form of trajectories of the kink motion in the space {v, z, t} (Figure 7).

Figure 7. Trajectories of the pBR322 kinks in the 3D space. The yellow line corresponds to the main sequence and the red line corresponds to the complementary sequence. The initial velocity of the kink is 1881 m/s. The dissipation coefficient is 0.126 × 10⁻¹⁴ J·s/m².

DownLoad: Full-Size Img PowerPoint

5. Conclusions

In the present work, we investigated the dynamics of the nonlinear conformation distortions – kinks, activated in the plasmid pBR322. The kinks were considered as quasi particles moving in the potential field of the plasmid. The key moment of the method used is the construction of the double energetic profile the analysis of which gives valuable information about the kink behavior.

To imitate the internal dynamics of the plasmid we used mathematical model consisting of two coupled sine-Gordon equations that in the average field approximation were transformed to two sine-Gordon independent equations with renormalized coefficients. The first equation described angular oscillations of nitrous bases of the main chain in the complementary chain. The second equation described angular oscillations of nitrous bases in the complementary chain. As a result, we obtained two types of kink-like solutions: one type are kinks which were the solutions of the first equation, and the other are kinks which were the solutions of the second equation.

To take into account the circular nature of DNA, we combined the end regions into a single block. Using calculated values of the rest energies of the kinks we constructed two energy profiles: the first for the main sequence, the second for the complementary one.

Analysis of these profiles showed that the deepest well in the energy profiles corresponds to the (7 + 1)-th region. This means that the probability of kink activation in this region is the highest.

Because the kink rest energy in the (7 + 1)-th region of the main sequence is less than in that of the complementary sequence we concluded that the P2 promoter located in the (7 + 1)-th region of the main sequence is stronger than the P1 and P3 promoters located in the (7 + 1)-th region of the complementary sequence. Therefore, it can be assumed that the transcription bubble formed in the (7 + 1)-th region is most likely to start moving in the direction of the CDS-1 region.

We calculated the main characteristics of the kink motion, including the time dependences of the kink velocity, coordinates, and total energy. These calculations were performed at the initial velocity equal to 1881 m/s which was chosen to avoid reflections from energy barriers corresponding to CDS-1 and CDS-2. Despite the fact that here we have considered only one value of the initial kink velocity the proposed approach is applicable to any values of the initial kink velocity. It is necessary only to keep in mind one important condition: the initial values should be less than the sound velocity. This condition arises from the mathematical requirements for the existence and stability of the solution in the form of kink.

It should be noted, also, that these results were obtained under three additional constraints. First, we used a simplified model that took into account angular oscillations of the nitrous bases in only one of the two DNA strands. Second, only one type of internal DNA motions-angular oscillations of the nitrous bases, was taken into accountю. Third, the model used did not take into account the DNA torque. In spite of all these limitations, we can expect that the results of the investigations obtained by simple and convenient method correctly convey the basic laws of the kink dynamic behavior in plasmid pBR322 and can be applied to another DNA sequences.

References

[1]	P. Y. Wen, R. J. Packer, The 2021 WHO classification of tumors of the central nervous system: clinical implications. Neuro-oncology, 21 (2021), 1215–1217. https://doi.org/10.1093/neuonc/noab120 doi: 10.1093/neuonc/noab120
[2]	Z. K. Jiang, X. G. Lyu, J. X. Zhang, Q. Zhang, X. P. Wei, Review of deep learning methods for MRI brain tumor image segmentation, J. Image Graphics, 25 (2020), 215–228.
[3]	S. Pereira, A. Pinto, V. Alves, C. A. Silva, Brain tumor segmentation using convolutional neural networks in MRI images, IEEE Trans. Med. Imaging, 35 (2016), 1240–1251. https://doi.org/10.1109/TMI.2016.2538465 doi: 10.1109/TMI.2016.2538465
[4]	Z. Zhu, X. He, G. Qi, Y. Li, B. Cong, Y. Liu, Brain tumor segmentation based on the fusion of deep semantics and edge information in multimodal MRI, Inf. Fusion, 91 (2023), 376–387. https://doi.org/10.1016/j.inffus.2022.10.022 doi: 10.1016/j.inffus.2022.10.022
[5]	R. Ranjbarzadeh, A. B. Kasgari, S. J. Ghoushchi, S. Anari, M. Naseri, M. Bendechache, Brain tumor segmentation based on deep learning and an attention mechanism using MRI multi‐modalities brain images, Sci. Rep., 11 (2021), 10930.
[6]	R. Ranjbarzadeh, P. Zarbakhsh, A. Caputo, E. B. Tirkolaee, M. Bendechache, Brain tumor segmentation based on an optimized convolutional neural network and an improved chimp optimization algorithm, SSRN, 2022 (2022), forthcoming. https://dx.doi.org/10.2139/ssrn.4295236 doi: 10.2139/ssrn.4295236
[7]	O. Ronneberger, P. Fischer, T. Brox, U-net: Convolutional networks for biomedical image segmentation, in Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, (2015), 234–241. https://doi.org/10.1007/978-3-319-24574-4_28
[8]	Ö. Çiçek, A. Abdulkadir, S. S. Lienkamp, T. Brox, O. Ronneberger, 3D U-Net: learning dense volumetric segmentation from sparse annotation, in Medical Image Computing and Computer-Assisted Intervention–MICCAI 2016: 19th International Conference, Athens, Greece, (2016), 424–432. https://doi.org/10.1007/978-3-319-46723-8_49
[9]	J. K. Sun, R. Zhang, L. J. Guo, Multi-scale feature fusion and additive attention guide brain tumor MR image segmentation, J. Image Graphics, 28 (2023), 1157–1172.
[10]	J. Zhang, Z. Jiang, J. Dong, Y. Hou, B. Liu, Attention gate resU-Net for automatic MRI brain tumor segmentation, IEEE Access, 8 (2020), 58533–58545. https://doi.org/10.1109/ACCESS.2020.2983075 doi: 10.1109/ACCESS.2020.2983075
[11]	A. S. Akbar, C. Fatichah, N. Suciati, Single level UNet3D with multipath residual attention block for brain tumor segmentation, J. King Saud Univ. Comput. Inf. Sci., 34 (2022), 3247–3258. https://doi.org/10.1016/j.jksuci.2022.03.022 doi: 10.1016/j.jksuci.2022.03.022
[12]	D. Liu, N. Sheng, T. He, W. Wang, J. Zhang, J. Zhang, SGEResU-Net for brain tumor segmentation, Math. Biosci. Eng., 19 (2022), 5576–5590. https://doi.org/10.3934/mbe.2022261 doi: 10.3934/mbe.2022261
[13]	D. Liu, N. Sheng, Y. Han, Y. Hou, B. Liu, J. Zhang, et al., SCAU-net: 3D self-calibrated attention U-Net for brain tumor segmentation, Neural Comput. Appl., 35 (2023), 23973–23985.
[14]	A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, et al., Attention is all you need, Adv. Neural Inf. Process. Syst., 30 (2017).
[15]	W. Wang, C. Chen, M. Ding, H. Yu, S. Zha, J. Li, Transbts: Multimodal brain tumor segmentation using transformer, in Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, (2021), 109–119.
[16]	Y. Jiang, Y. Zhang, X. Lin, J. Dong, T. Cheng, J. Liang, SwinBTS: A method for 3D multimodal brain tumor segmentation using swin transformer, Brain Sci., 12 (2022), 797. https://doi.org/10.3390/brainsci12060797 doi: 10.3390/brainsci12060797
[17]	Y. Xu, X. He, G. Xu, G. Qi, K. Yu, L. Yin, et al., A medical image segmentation method based on multi-dimensional statistical features, Front. Neurosci., 16 (2022), 1009581. https://doi.org/10.3389/fnins.2022.1009581 doi: 10.3389/fnins.2022.1009581
[18]	Q. L. Zhang, Y. B. Yang, Sa-net: Shuffle attention for deep convolutional neural networks, in ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), (2021), 2235–2239. https://doi.org/10.1109/ICASSP39728.2021.9414568
[19]	C. Yang, Y. Wang, J. Zhang, H. Zhang, Z. Wei, Z. Lin, et al., Lite vision transformer with enhanced self-attention, in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, (2022), 11998–12008. https://doi.org/10.48550/arXiv.2112.10809
[20]	Y. Cao, J. Xu, S. Lin, F. Wei, H. Hu, Gcnet: Non-local networks meet squeeze-excitation networks and beyond, in Proceedings of the IEEE/CVF international conference on computer vision workshops, (2019), 1971–1980.
[21]	S. Woo, J. Park, J. Lee, Cbam: Convolutional block attention module, in Proceedings of the European conference on computer vision (ECCV), (2018), 3–19.
[22]	X. Li, X. Hu, J. Yang, Spatial group-wise enhance: Improving semantic feature learning in convolutional networks, preprint, arXiv: 1905.09646.
[23]	N. Ma, X. Zhang, H. T. Zheng, J. Sun, Shufflenet v2: Practical guidelines for efficient cnn architecture design, in Proceedings of the European conference on computer vision (ECCV), (2018), 116–131. https://doi.org/10.48550/arXiv.1807.11164
[24]	H. Zhao, J. Shi, X. Qi, Pyramid scene parsing network, in Proceedings of the IEEE conference on computer vision and pattern recognition, (2017), 2881–2890.
[25]	L. C. Chen, G. Papandreou, F. Schroff, H. Adam, Rethinking atrous convolution for semantic image segmentation, preprint, arXiv: 1706.05587.
[26]	D. Hendrycks, K. Gimpel, Gaussian error linear units (gelus), preprint, arXiv: 1606.08415.
[27]	P. Ramachandran, B. Zoph, Q. V. Le, Searching for activation functions, preprint, arXiv: 1710.05941.
[28]	F. Milletari, N. Navab, S. A. Ahmadi, V-net: Fully convolutional neural networks for volumetric medical image segmentation, in 2016 Fourth International Conference on 3D Vision (3DV), (2016), 565–571. https://doi.org/10.1109/3DV.2016.79
[29]	F. Isensee, P. F. Jäger, P. M. Full, P. Vollmuth, K. H. Maier-Hein, nnU-Net for brain tumor segmentation, in Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries: 6th International Workshop, 2021. https://doi.org/10.1007/978-3-030-72087-2_11
[30]	S. Bakas, H. Akbari, A. Sotiras, M. Bilello, M. Rozycki, J. S. Kirby, et al., Advancing the cancer genome atlas glioma MRI collections with expert segmentation labels and radiomic features, Sci. Data, 4 (2017), 1–13.
[31]	S. Bakas, M. Reyes, A. Jakab, S. Bauer, M. Rempfler, A. Crimi, et al., Identifying the best machine learning algorithms for brain tumor segmentation, progression assessment, and overall survival prediction in the BRATS challenge, preprint, arXiv: 1811.02629.
[32]	S. S. Sastry, Advanced Engineering Mathematics, Jones & Bartlett Learning.
[33]	L. R. Dice, Measures of the amount of ecologic association between species, Ecology, 26 (1945), 297–302. https://doi.org/10.2307/1932409 doi: 10.2307/1932409
[34]	O. Oktay, J. Schlemper, L. L. Folgoc, M. Lee, M. Heinrich, K. Misawa, Attention u-net: Learning where to look for the pancreas, preprint, arXiv: 1804.03999.
[35]	J. Tong, C. Wang, A dual tri-path CNN system for brain tumor segmentation, Biomed. Signal Process. Control, 81 (2023), 104411. https://doi.org/10.1016/j.bspc.2022.104411 doi: 10.1016/j.bspc.2022.104411
[36]	Y. Xue, M. Xie, F. G. Farhat, O. Boukrina, A. M. Barrett, J. R. Binder, et al., A multi-path decoder network for brain tumor segmentation, in Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries: 5th International Workshop, BrainLes 2019, Held in Conjunction with MICCAI 2019, Shenzhen, China, (2020), 255–265.
[37]	J. Sun, Y. Peng, D. Li, Y. Guo, Segmentation of the multimodal brain tumor images used Res-U-Net, in Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries: 6th International Workshop, BrainLes 2020, Held in Conjunction with MICCAI 2020, Lima, Peru, (2021), 263–273.
[38]	K. Cheng, C. Hu, P. Yin, Q. Su, G. Zhou, X. Wu, et al., Glioma sub-region segmentation on Multi-parameter MRI with label dropout, in Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries: 6th International Workshop, BrainLes 2020, Held in Conjunction with MICCAI 2020, Lima, Peru, (2021), 420–430.
[39]	Y. Peng, J. Sun, The multimodal MRI brain tumor segmentation based on AD-Net, Biomed. Signal Process. Control, 80 (2023), 104336. https://doi.org/10.1016/j.bspc.2022.104336 doi: 10.1016/j.bspc.2022.104336

This article has been cited by:

L. Krasnobaeva, L. Yakushevich, FEATURES OF THE POTENTIAL FIELD STRUCTURE OF THE PPF1 PLASMID AND THEIR INFLUENCE ON THE CHARACTER OF MOTION OF NONLINEAR CONFORMATIONAL PERTURBATIONS – KINKS, 2022, 7, 2499-9962, 99, 10.29039/rusjbpc.2022.0490

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)