Sparsity enhanced MRF algorithm for automatic object detection in GPR imagery

1.   Introduction

As the basic component, the roadbed is very important to the pavement, which supports the pressure of various vehicles such as cars and the influence of the environment on the surface of the road. It also suffers from the internal composition changes of underground subway, pipeline laying and natural stratigraphic movement, to name a few. If roadbed damage has occurred, it will result in the pavement surface collapsing in urban areas, seriously endangering traffic and personnel safety. As a result, it is imperative to inspect/monitor the roadbed underground status and identify potential damage for maintenance purposes.

In recent years, with the amount of collected data from the roadbed inspection transforming from the TB level to the PB level, how to accurately process and analyze the data is one of the most important topics. On the other hand, with deep network technology, object detection, general item classification, semantic segmentation and other fields have achieved promising results. Among them, the image classification task is a basic task in computer vision. Many other visual recognition tasks benefit from image classification network structure, and ground penetrating radar (GPR) image analysis is one of them. Specifically, GPR is emerging as a viable sensing and imaging tool which makes use of electromagnetic waves to penetrate through the earth surface to illuminate buried objects. The ability of GPR image analysis to detect and analyze subsurface units nondestructively and accurately provides a solid foundation for roadbed monitoring studies. Accordingly, in recent years, we have witnessed an increasing interest in GPR imaging due to its numerous civilian and military applications, including oil and gas exploration, pipe localization, and mine detection, to name a few.

A typical GPR system consists of two main components, i.e., a transmitter and a receiver. In practice, electromagnetic waves with high frequency are first transmitted by the transmitter and propagated through the subsurface. When encountering underground materials (such as metal or concrete), waves will be partially reflected and captured by the receiver. The received signals can be completely different depending on electromagnetic characteristics of underground objects. The subsequent object detection from acquired GPR data is of great practical interest to operators. However, expert assistance is usually required to manually identify buried objects, which can be very labor expensive and time consuming. As such, there is an increasing demand to develop robust (semi)automated object detection techniques for GPR imaging.

In the past decade, researchers have been actively investigating efficient object detection approaches. For instance, in ^[1], target detection was done by using a genetic algorithm to localize the linear/hyperbolic patterns from GPR images. Each candidate solution (chromosome) was manipulated to explore the apex position and the curvature of potential patterns. The fitness function was designed to model the (Hamming) distance between patterns and ground-truth images. Finally, buried objects were revealed by finding chromosomes with highest fitness. Similar work can also be found in ^[2], in which the application of neural networks (NNs) for automatic GPR processing was discussed. This work relied on the high-order statistic features to feed a neural network with radial-basis-function (RBF) structure. Additionally, the detection performance was further enhanced by a multi-objective genetic algorithm. In ^[3], an unsupervised method was proposed. The polynomial expression was first employed in the preprocessing stage as a filter to reduce the data dimension. Second, in the feature extraction stage, polynomial expression was again used for estimating coefficients from Taylor series of the radar pulses' function. Third, those coefficients were utilized for locating objects according to some quality-of-fit criteria. For more on object detection algorithms, interested readers are referred to the survey presented in ^[4], where several computer vision techniques (in particular the feature representation of GPR images) are explored. Furthermore, the capability to reliably discriminate target objects is also investigated.

Furthermore, another popular trend of automatic detection includes the Markov random field (MRF) process, which considers the spatial correlation from adjacent data. In the context of GPR imaging, an 2-D radar image is accordingly modeled as a 2-D random field ^[5]. MRF approach is then used to describe the interdependence of neighborhood pixels and spatial influences. The advantage of MRF in GPR object detection includes utilizing prior information sufficiently, forming a clear boundary and integrating efficiently with other methods. Some preliminary studies of applying MRF on GPR imaging are summarized in Section 2. One typical issue associated with MRF is that some of the key parameters must be tuned manually, which could lead to a serious restriction in practice.

On the other hand, a GPR image is usually subject to electromagnetic noise. As MRF relies on the correlation of adjacent pixels from the neighborhood, corrupted GPR data may lead to over-segmenting objects (or background). Additionally, the standard MRF method does not consider the neighborhood importance, as they are set to have an equal role in determining the center target. In this case, some neighborhoods could have more positive impact, while others could impose noise. To address the aforementioned issues, we would like to introduce some constraints to improve the detection performance by searching for an optimal alternative, i.e., a sparse representation-based MRF model.

Recently, sparse representation has attracted considerable interest, and indicates that a target signal can be decomposed into a linear combination of few elementary signals. In other words, most information from this target signal can be represented using only few nonzero elements. Sparse representation models have therefore become a very popular tool for many optimization applications, such as through-the-wall radar imaging ^[6], algorithm improvement ^[7] and model optimization ^[8], etc.

Following the work mentioned above, in this paper, we propose a novel object detection algorithm, where the traditional MRF model is enhanced using the concept of sparse representation. More precisely, the proposed algorithm integrates the sparse representation technique to obtain a parsimonious MRF model. Additionally, an iterative updating strategy is also employed to optimize key parameters within this sparse MRF model, consequently improving the detection performance.

The rest of the paper is organized as follows. Section 2 gives a brief account of ground penetrating radar imaging, Markov random field and sparse representation, respectively. Section 3 details the proposed algorithm, in which the sparse representation is integrated to improve the standard MRF model. Section 4 discusses the experimental implementation and evaluates the performance of the proposed method, followed by concluding remarks given in Section 5.

2.   Related work

In this section, we provide background information on the study area, focusing on the theory of Markov random field (MRF) and sparse representation, and we also discuss the application of existing MRF work on the field of ground penetrating radar (GPR).

2.1.   Ground penetrating radar (GPR)

Ground-penetrating radar (GPR) is a non-destructive detection technology for detecting underground targets. Specifically, GPR uses antennas to transmit and receive high-frequency electromagnetic waves to detect the characteristics and distribution of materials in the medium. Compared with traditional underground detection technology, GPR has the advantages of fast detection speed, continuous detection process, high resolution, convenient and flexible operation, and low detection cost. At present, ground-penetrating radar is widely used in various fields of ground exploration. The complex underground pipeline system in cities makes urban construction more difficult. Using ground-penetrating radar technology, underground pipeline detection and positioning can be automated, high-speed and reliable ^[9]. Track degradation will be caused by track degradation in use, and high track degradation and poor drainage conditions are the main causes of track degradation. The work from ^[10] analyzed how to determine the degraded track and assist the analysis of degradation causes using ground-penetrating radar, and reliable information is provided for maintenance decisions. Additionally, the study of ^[11] illustrates how ground-penetrating radar can open up the possibility of three-dimensional models of cracks and voids, increasing safety for future assistance in underground engineering. Filippo et al. ^[12] describes the use of ground-penetrating radar on a ship to monitor the seabed topography of frozen and unfrozen water bodies and the application of ground-penetrating radar on a helicopter to monitor ice and snow thickness.

2.2.   Markov random field (MRF)

Markov stochastic process refers to a process where the value of the next point in time is only related to the current value and has no relation to the past; in other words, the future value depends on the present value but not the past one. For example, when a mouse had its brain stem removed, the concept of memory disappeared. Then, if leaving this mouse in an environment of several caves, its behavior, as it moves through those caves, can be seen as a Markov chain, with all of its behavior patterns being determined only based on the current cave. Under the condition of known "present, " the independent property of "future" and "past" is then known as the Markov property. The random process with this property is then termed a Markov process, and its most primitive model is known as the Markov chain.

The Markov random field (MRF), established on top of the Markov stochastic process, is a probabilistic modeling method that involves multiple random variables. It is used to describe a system consisting of a set of random variables that have a certain probability dependence relationship. On the other hand, MRF can be represented by undirected graphs, where each node represents a random variable, and the edges between nodes represent the dependencies between these variables. Each random variable in a MRF satisfies the aforementioned Markov property, indicating that the random variable is related only to its adjacent variables and has no relationship with non-adjacent variables.

Markov random fields are commonly utilized in probabilistic modeling and inference applications such as image processing and natural language processing, due to their ability to effectively handle complex relationships in high-dimensional datasets.

Due to its applicability and flexibility, a large number of Markov random field (MRF)-based approaches have also been proposed for automated object detection in GPR imaging. In ^[13], the radar image was first over-segmented into a large amount of rectangular regions. Then, a Wishart MRF model was used to initialize pixel labels within different regions. The final detection was made by maximizing an iterative Wishart-based likelihood model. In ^[14], the Fuzzy C-Means clustering approach was integrated with MRF for the change detection. Their contribution was to propose a modified MRF energy function, via considering the fuzzy memberships for neighborhood pixels. In ^[15], the MRF model was first utilized to encode the spatial characteristics and correlation among pixels. Later, a mean-field variational Bayesian expectation-maximization method was introduced to jointly estimate parameters and hidden variables within the MRF model. The study conducted in ^[16] introduced a novel mixture model that incorporates a variable determining the equivalent number of looks, which varies across different clusters, unlike the traditional approach that assumes it to be constant for the entire PolSAR image. Additionally, the authors proposed a pioneering supervised classification algorithm that utilizes this new model. In ^[17], a combination of local and global search algorithm was proposed to optimize gray-scale image segmentation based on the MRF model. Specifically, by combining the maximum likelihood of the parameter estimation with the iterative condition model for a local optimization, the optimal solution for those parameters is found, which leads to a better detection accuracy.

2.3.   Sparse representation

Sparse representation is based on the idea that a signal can be decomposed into a linear combination of few elementary signals ^[18]. Considering the target vector $\mathit{\boldsymbol{y}}\in \mathbb{R}^{M}$ and a known dictionary matrix $\mathcal{D}\in \mathbb{R}^{M \times N}$ that contains $N$ columns, the sparse representation aims to minimize the solution sparsity and the reconstruction error:

where $\mathcal{M}\left(\mathit{\boldsymbol{x}}\right)$ is a measure of the vector sparsity, $\|\mathit{\boldsymbol{y}} - \mathcal{D}\mathit{\boldsymbol{x}} \|^2_2$ denotes the reconstruction error, and $\epsilon$ is the bound on the error. One simple strategy for estimating $\mathcal{M}\left(\mathit{\boldsymbol{x}}\right)$ is to consider the $l_{1}$-norm of $\mathit{\boldsymbol{x}}$, which is the sum of the magnitudes of all elements in $\mathit{\boldsymbol{x}}$, i.e., $\mathcal{M}\left(\mathit{\boldsymbol{x}}\right) = \left\|\mathit{\boldsymbol{x}}\right\|_1 = \sum_{i}^N|x_i|$.

The dictionary learning problem, on the other hand, is to optimize the dictionary $\mathcal{D}$ while fixing $\mathit{\boldsymbol{x}}$ and $\mathit{\boldsymbol{y}}$ ^[19]:

Theoretical analysis and empirical results show that the performance of the sparse representation is greatly improved with the dictionary learning method. In other words, with the same sparse representation algorithm, the optimized dictionary leads to a higher-sparsity solution and better reconstruction performance.

{Notably, the sparse representation can also lead to the better predictive performance of the Markov model. This is due to the fact that non-zero elements in the transition matrix represent the most relevant and important information about the system, while the zero elements represent the less relevant-and-important information. By focusing on the non-zero (or important) elements, the model can make more accurate predictions and avoid overfitting. In addition, the sparse representation can also help to identify the most influential factors in the Markov system, which can be useful for decision-making and optimization. Overall, the sparse representation can bring significant benefits to the optimization of Markov models, including storage and computation efficiency, simplification of data structures, and improved predictive performance. As such, it is an important tool for the model development and analysis purposes in a variety of fields.}

In ^[20], it was shown that in the area of object detection, sparse and partial representation has emerged as a novel approach. This technique involves constructing a vocabulary consisting of object parts that contain significant information, based on a set of sample images belonging to the object classes being analyzed. By utilizing the objects' vocabulary and the spatial relationships between them, this method enables the representation of images. It has been demonstrated that this approach achieves high detection accuracy in complex real image test sets and is highly robust in the presence of partial occlusion and background change. In ^[21], sparse representation of search signals on an over-complete dictionary is achieved by optimizing an objective function. This function takes into account both the reconstruction error of measurement signals and their sparsity, resulting in excellent coding and denoising properties. Moreover, a theoretical framework for signal classification based on sparse representation is proposed. By combining the discriminant ability of the classification method with the reconstructive and sparse nature of sparse representation, this framework is effective in handling various types of signal damage, such as noise, missing data and outliers. In ^[22], drawing on sparse coding (Sc) and kernel technique, the development of a novel method for sparse coding was proposed, named KSR-SPM. This technique effectively captures non-linear similarities between features and applies spatial pyramid matching (SPM) to improve performance in diverse areas such as image classification, face recognition and kernel matrix approximation. With its proven success in both computer vision and machine learning tasks, KSR-SPM has established its effectiveness as a valuable tool for researchers and practitioners in the field. In ^[23], to tackle the issue of inaccurate sparse representation resulting from degraded observed images (e.g., noise, blur, and/or under-sampling), the non-local self-similarity of the image was utilized to obtain a reliable estimate of the sparse coding coefficient of the original image. Based on this estimate, the sparse coding coefficient of the observed image is then concentrated, enhancing the performance of sparse representation-based image restoration. By doing so, this approach effectively improves the problem of the original image being unreliably reconstructed, which is common in traditional models. However, the application of the sparse-representation based MRF model is underexplored in the GPR imaging domain, on which this paper focuses.

3.   Sparsity-enhanced MRF model

In this section, we present an improved MRF model for automated object detection. Towards this end, we first formulate the object detection process using a MRF model. Second, the MRF model is enhanced using sparsity regularization. Additionally, we introduce an iterative updating strategy to fine-tune parameters in the proposed sparse model.

Suppose the set of pixels from the observed image is $\mathcal{S} = [s_1, \cdots, s_i, \cdots, s_N] (\forall i\in[1, N])$, where $N$ is the number of pixels. Let $\mathit{\boldsymbol{y}}$ denote the set of pixel labels, i.e., $\mathit{\boldsymbol{y}} = [y_1, \cdots, y_N]$, $y_i \in [1, \cdots, L]$, and $L$ is the number of labels. In this study, we simply categorize the pixel as object or background, consequently casting the detection process as a binary classification (i.e., $L = 2$). In MRF, pixel labels are estimated according to the information acquired from their neighborhoods. Normally, the MRF model is realized by maximizing the a posteriori probability $Pr(\mathit{\boldsymbol{y}}|\mathcal{S})$ (i.e., the MAP process). According to Bayes' theorem, the detection problem can be expressed as

In Eq. (3.1), the distribution $Pr(\mathit{\boldsymbol{y}})$ can be shown to be of a Gibbsian form ^[24]:

where $Z$ is a normalizing constant, and $En(z)$ is the sum of clique energy functions which can be calculated as $En(z) = \sum_{c \in C}V_c(z)$ ($C$ is the set of predefined cliques, and we consider the $1^{st}$ and $2^{nd}$ clique in this study). Furthermore, the cliques function of $V_c(z)$ is computed as

where $s_t$ and $s_a$ represent the target pixel and adjacent pixels from the neighborhood, respectively, and $\gamma$ is a predetermined Gibbsian parameter. In the majority of existing work, this parameter is empirically chosen and fixed during the experiment.

On the other hand, in terms of $Pr(\mathcal{S}|\mathit{\boldsymbol{y}})$, we assume that pixels follow the Gaussian distribution, that is,

where $\mu_s$ and $\sigma_s$ represent the mean and standard deviation of the $s$-th pixel.

There are two main problems with the standard MRF model: (ⅰ) It does not consider the neighborhood importance (alternatively, which neighborhood(s) could be the most influential). Note that in standard MRF, all neighborhoods play an equal role. However, in reality, some neighborhoods can be more important than others, while other neighborhoods could carry more noisy information. As such, the detection outcome can be optimized by searching for a more appropriate range of neighborhoods. (ⅱ) Hyperparameters (i.e., the Gibbsian parameter $\gamma$ in Eq. (3.3) and those of Gaussian distribution ($\mu_s, \sigma_s$) from Eq. (3.4)) could have a significant impact on the detection performance. Nevertheless, in the standard MRF model, $\gamma$ is predetermined empirically and fixed during the detection process. Thus, trial-and-error or cross-validation experiments are often required, which are very time-consuming. Similarly, $\mu_s, \sigma_s$ are estimated using the input image, which is usually with noise. Intuitively, corrupted data could lead to a wrong estimation of hyperparameters, thereby reducing the detection accuracy.

To address the first issue, the sparsity regularization is introduced accordingly. The benefit can be summarized as follows: (ⅰ) The sparsity regularization is widely used in other tasks to improve the generalization ability of the classification result; consequently, by involving the sparsity constraint in GPR imaging, a better detection (i.e., classifying objects from background) performance can be expected. and (ⅱ) The sparsity regularization also has a favorable property of determining effective elements. That is, the sparsity regularization drives weights of insignificant elements towards zero, thus revealing the influential elements (neighborhoods and/or pixels in our case) with non-zero weights. Similarly, to solve the second issue, hyperparameters of ($\gamma$, $\mu_s$, $\sigma_s$) are optimized iteratively, instead of predetermined with cross-validation. The basic idea is to optimize those free parameters in a way that the performance of the sparse representation is enhanced.

Toward this end, we introduce parameters of $(\mathit{\boldsymbol{\alpha}}, \mathit{\boldsymbol{\beta}}, \gamma, \mathit{\boldsymbol{\mu}}, \mathit{\boldsymbol{\sigma}})$, and the objective function for our proposed algorithm is formulated as follows:

where $\|*\|_1$ stands for the $l_1$-norm of a vector, $\mathit{\boldsymbol{\alpha}} = \{\alpha_c|\forall c\in C\}$, $\mathit{\boldsymbol{\beta}} = \{\beta_s|\forall s\in \mathcal{S}\}$, $\mathit{\boldsymbol{\mu}} = \{\mu_s|\forall s\in \mathcal{S}\}$, $\mathit{\boldsymbol{\sigma}} = \{\sigma_s|\forall s\in \mathcal{S}\}$, and $\lambda$ is a penalty term comprising the error and the sparse regularization.

Note that in the standard MRF model, we have $\mathit{\boldsymbol{\alpha}} = \mathit{\boldsymbol{\beta}} = \mathit{\boldsymbol{1}}$. In this case, the proposed algorithm can be cast as an extension of the conventional MRF method. Additionally, when setting the value of the $i$-th element of $\mathit{\boldsymbol{\alpha}}$ (or $\mathit{\boldsymbol{\beta}}$) to zero, that equally implies omitting the $i$-th neighborhood (or pixel) during the optimization, as they are least important. As such, by finding the sparse representation of $[\mathit{\boldsymbol{\alpha}}, \mathit{\boldsymbol{\beta}}]$, we can reveal significant elements (neighborhoods and pixels) that maximize the a posteriori probability $Pr(\mathit{\boldsymbol{y}}|\mathcal{S})$ most.

To solve Eq. (3.5), an iterative technique is employed to fine-tune parameters of $(\mathit{\boldsymbol{\alpha}}, \mathit{\boldsymbol{\beta}}, \gamma, \mathit{\boldsymbol{\mu}}, \mathit{\boldsymbol{\sigma}})$. Specifically, at the $k$-th iteration, we first fix $\gamma^k$, $\mathit{\boldsymbol{\mu}}^k$ and $\mathit{\boldsymbol{\sigma}}^k$ and then update $[\mathit{\boldsymbol{\alpha}}^k, \mathit{\boldsymbol{\beta}}^k]$. Sequentially, we adjust parameters $\gamma^k$, $\mathit{\boldsymbol{\mu}}^k$ and $\mathit{\boldsymbol{\sigma^k}}$ to minimize Eq. (3.5) while fixing $[\mathit{\boldsymbol{\alpha}}^k, \mathit{\boldsymbol{\beta}}^k]$.

Sparse representation stage. To begin with, we consider optimizing $(\mathit{\boldsymbol{\alpha}}, \mathit{\boldsymbol{\beta}})$ with fixed $(\gamma, \mathit{\boldsymbol{\mu}}, \mathit{\boldsymbol{\sigma}})$. Then, $\mathcal{L}(\mathit{\boldsymbol{\alpha}}, \mathit{\boldsymbol{\beta}}, \gamma, \mathit{\boldsymbol{\mu}}, \mathit{\boldsymbol{\sigma}})$ is reformulated as $\mathcal{L}(\mathit{\boldsymbol{\alpha}}, \mathit{\boldsymbol{\beta}})$. Consider its Taylor expansion at the $k$-th iteration value of $(\mathit{\boldsymbol{\alpha}}_k, \mathit{\boldsymbol{\beta}}_k)$ as

where $\mathcal{L}_k'$ and $\mathcal{L}_k''$ denote the first and second derivatives of the function $\mathcal{L}(\mathit{\boldsymbol{\alpha}}, \mathit{\boldsymbol{\beta}})$ evaluated at $(\mathit{\boldsymbol{\alpha}}_k, \mathit{\boldsymbol{\beta}}_k)$. The globally optimal $(\mathit{\boldsymbol{\alpha}}^*, \mathit{\boldsymbol{\beta}}^*)$ that minimizes Eq. (3.6) (or equally Eq. (3.5) with treating $\gamma^k$, $\mathit{\boldsymbol{\mu}}^k$, and $\mathit{\boldsymbol{\sigma^k}}$ as constants) can be analytically computed as $(\mathit{\boldsymbol{\alpha}}^*, \mathit{\boldsymbol{\beta}}^*) = [\mathit{\boldsymbol{\alpha}}_k, \mathit{\boldsymbol{\beta}}_k] - (\mathcal{L}_k'')^{-1}\mathcal{L}_k'$. However, the estimation of $\mathcal{L}_k''$ is not explicitly computed or inverted. We then follow the work in ^[25] by applying the limited-memory quasi-Newton (LMQN) algorithm. More precisely, the update in the gradient $\eta_k = \mathcal{L}_k' - \mathcal{L}_{k-1}'$ and the candidate solution $\xi_k = (\mathit{\boldsymbol{\alpha}}_k, \mathit{\boldsymbol{\beta}}_k) - (\mathit{\boldsymbol{\alpha}}_{k-1}, \mathit{\boldsymbol{\beta}}_{k-1})$ are recorded. Then, both $\eta_k$ and $\xi_k$ are utilized to estimate the $(\mathcal{L}_k'')^{-1}$.

Parameter optimization stage. Next, we adjust parameters $\gamma^k$, $\mathit{\boldsymbol{\mu}}^k$ and $\mathit{\boldsymbol{\sigma^k}}$ to minimize Eq. (3.5) while fixing $[\mathit{\boldsymbol{\alpha}}^k, \mathit{\boldsymbol{\beta}}^k]$. In this study, the stochastic gradient descent technique is employed. Therefore, the updating rule for hyperparameters of ($\gamma^k$, $\mathit{\boldsymbol{\mu}}^k$, $\mathit{\boldsymbol{\sigma}}^k$) can be derived as follows:

where $\Delta$ is the learning step. We repeat the process iteratively until convergence.

Overall, the diagram of the proposed detection algorithm, termed as MRF-L1, is summarized in Algorithm 1. The fundamental improvement of the proposed algorithm is two-fold: The $l_1$ regularization is introduced to search for a sparse representation of the standard MRF model, while an iterative technique is employed to update hyperparameters to enhance the performance of the sparse representation. To halt the proposed algorithm, the termination criterion is set to be if the value of $(\mathcal{L}_{k-1} - \mathcal{L}_k)$ is less than a threshold $\eta$, which is set as $\eta = 10^{-3}$.

At last, we discuss the convergence guarantee of the proposed algorithm by offering the following theorem:

Theorem 1. Using the proposed algorithm, the value from the object function (shown as Eq. (3.5)) decreases with the increase of iterations, and a local minimum can be obtained.

Proof. At each iteration of the proposed algorithm, the sparse solution $[\mathit{\boldsymbol{\alpha}}, \mathit{\boldsymbol{\beta}}]$ and hyperparameters $(\gamma, \mathit{\boldsymbol{\mu}}, \mathit{\boldsymbol{\sigma}})$ take turns being updated while others are fixed. That is, at the $k$-th iteration, we first estimate $[\mathit{\boldsymbol{\alpha}}^k, \mathit{\boldsymbol{\beta}}^k]$ subject to the fixed $(\gamma^{k-1}, \mathit{\boldsymbol{\mu}}^{k-1}, \mathit{\boldsymbol{\sigma}}^{k-1})$. Consequently, the result can be obtained: $\mathcal{L}(\mathit{\boldsymbol{\alpha}}^k, \mathit{\boldsymbol{\beta}}^k, \gamma^{k-1}, \mathit{\boldsymbol{\mu}}^{k-1}, \mathit{\boldsymbol{\sigma}}^{k-1}) < \mathcal{L}(\mathit{\boldsymbol{\alpha}}^{k-1}, \mathit{\boldsymbol{\beta}}^{k-1}, \gamma^{k-1}, \mathit{\boldsymbol{\mu}}^{k-1}, \mathit{\boldsymbol{\sigma}}^{k-1})$.

Then, we then update $(\gamma^{k-1}, \mathit{\boldsymbol{\mu}}^{k-1}, \mathit{\boldsymbol{\sigma}}^{k-1})$ by fixing $[\mathit{\boldsymbol{\alpha}}^k, \mathit{\boldsymbol{\beta}}^k]$. As such, the following inequalities can be obtained: $\mathcal{L}(\mathit{\boldsymbol{\alpha}}^k, \mathit{\boldsymbol{\beta}}^k, \gamma^{k}, \mathit{\boldsymbol{\mu}}^{k}, \mathit{\boldsymbol{\sigma}}^{k}) < \mathcal{L}(\mathit{\boldsymbol{\alpha}}^k, \mathit{\boldsymbol{\beta}}^k, \gamma^{k-1}, \mathit{\boldsymbol{\mu}}^{k-1}, \mathit{\boldsymbol{\sigma}}^{k-1})$. Overall, it is easy to apply a chain rule to have:

Consequently, the objective function value decreases with the increase of iterations, and the convergence of the proposed algorithm is proved. □

4.   Experiments

To investigate the efficiency of the proposed algorithm, we present the experimental results using a real-world dataset. The physical scene (including the radar system) and the evaluation criteria are presented in Section 4.1. The comparison with traditional detection methods is then presented in Section 4.2.

4.1.   Experimental setup

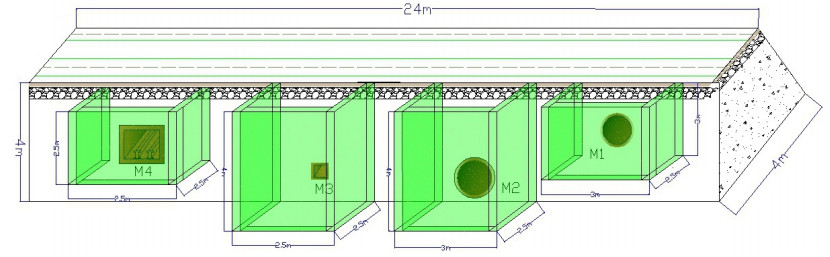
The experimental scene was established according to a physical road (as a concrete cube, see Fig. 1). This physical scene spanned a length of 24 m and a depth of 4 m; the width was equivalent to the depth. Under the ground, there are different types of objects (such as concrete and metals). These objects are placed at different down-range, cross-range and elevation bins. For this paper, we mainly consider the metal objects (labeled as M2) in Fig. 1.

The data acquisition system was manufactured by China University of Mining and Technology (Beijing). This system included two parts, a GPR host and 3 different transmitted frequency GPR antennas, including:

● One GPR host to capture the received signal (see Figure 2 (a));

● An antenna of 50 MHz transmitted frequency (see Figure 2 (b));

● An antenna of 200 MHz transmitted frequency (see Figure 2 (c));

● An antenna of 400 MHz transmitted frequency (see Figure 2 (d)).

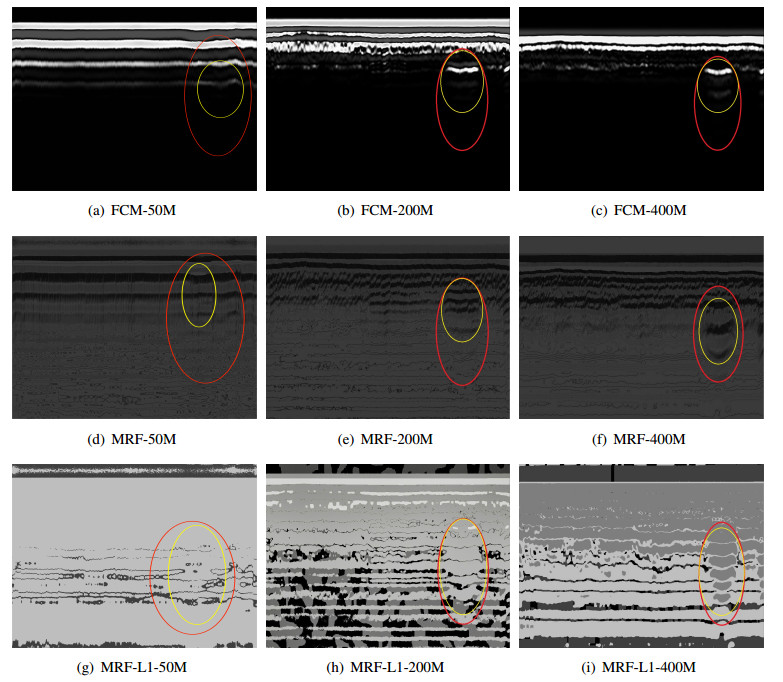
To compare the three antennas, we generate typical imaging examples using each of them. The acquired radar image has 1028 $\times$ 764 pixels and the object highlighted by the red ellipse. In the input image obtained using the 400MHz-antenna (see Figure 3 (c)) we can see that the overall imaging performance is relatively good. Compared to the input image by using the 400 MHz-antenna, the input image produced by the 200 MHz-antenna (see Figure 3 (b)) is blurred and has more noise. As for the image of the 50 MHz-antenna (see Figure 3 (a)), the image is really noisy and blurred. As observed, the lower the frequency of the antenna is, the more noisy the image and more challenging for the detection task.

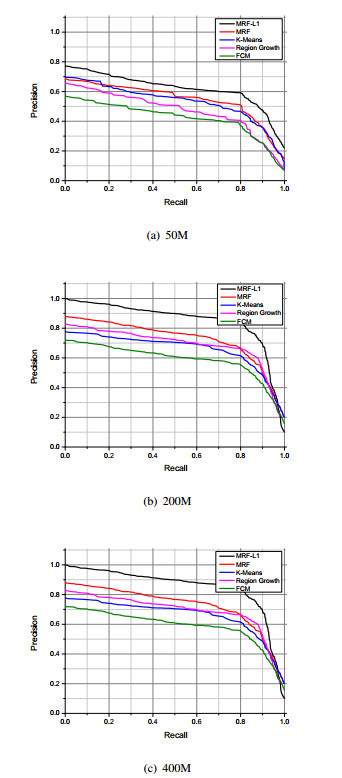
To quantify the performance of detection algorithms, we adopt three performance measures in this study, including precision-recall (P-R) curve, $F_\beta$-measure and mean absolute error (MAE). Among them, the P-R curve emphasizes the ratio between the true positive and predictive positive result, while $F_\beta$-measure considers a weighted average of precision and recall. Therefore, the $F_\beta$-measure takes both false positives and false negatives into account, and it is calculated as follows:

where $\beta = 0.3$ is to emphasize the precision. On the other hand, MAE is defined as the average absolute difference between the ground truth image $I$ and the detection outcome $\widehat{I}$ on the pixel-wise level:

At last, the ground truth image is established using the physical model (estimated by the size of the entire scene and the location of target object).

4.2.   Comparison with existing works

To evaluate our proposed algorithm, in terms of the detection accuracy, conventional detection algorithms are employed, including MRF ^[5], K-Means ^[26], RegionGrowth ^[27], and Fuzzy C-Means (FCM) ^[28]. Interested readers are referred to the original articles and references therein for additional details. Additionally, parameters of reference methods are selected according to the descriptions provided in the respective papers.

Table 1 summarizes the results for the object detection from different methods. Additionally, the P-R curves are also displayed in Figure 4 for quantitative evaluation. As observed, our proposed method performs favorably against traditional methods in terms of the detection accuracy. For instance, in terms of both the $F_\beta$ and MAE measurement, the proposed algorithm achieves the best outcome (on average, 0.7529 for $F_\beta$ and 0.1261 for MAE). A similar conclusion can also be drawn from their P-R curves.

On the other hand, the detection outcomes from methods of FCM, MRF and MRF-L1 are shown in Figure 5. Visual qualities also confirm that the proposed algorithm outperforms other detection methods via identifying buried objects. In particular, for the 50 MHz imagery (with the presence of more noise compared to those of 200M Hz and 400 MHz), our method still achieves a robust detection performance. By contrast, the FCM method only detects a proportion of the object (highlighted with the yellow area), and so did the standard MRF algorithm.

In conclusion, it can be empirically confirmed that the proposed algorithm achieves comparative performance to existing state-of-the-art methods, by achieving robust detection. Again, the proposed approach employs the $l_1$ regularization (or sparse representation) to improve the standard MRF model via maximizing the detection probability. Additionally, the dictionary learning method is further introduced to optimize key parameters within the MRF model, so that the performance of the sparse representation and object detection are improved.

See Table 1 for comparison of run time with GPR acquisition data by using different frequency antennas. Although the accuracy has been improved, the speed has been greatly impaired. This is mainly due to the fact that the algorithms are applied to the difference image to obtain time iteratively.

5.   Conclusion

The automated object detection in ground penetrating radar (GPR) imaging is an active area of research due to its ability to detect buried objects. The Markov random field (MRF) model has been utilized to advance the detection and imaging performance in the past decade, in which spatial relations between adjacent pixels are considered for the detection.

In this paper, we proposed an improved algorithm based on the conventional MRF model. More precisely, a 2-D radar image was first formulated as a standard MRF. Then, the sparse representation technique was introduced to enhance the generalization ability of the MRF model. This was done by searching for the most influential neighborhoods and pixels. Additionally, an iterative updating strategy was also employed for fine-tuning hyperparameters, in a way that a better performance for the sparse representation is achievable. Our work was then evaluated using a real-world GPR dataset, and experimental results show that the proposed algorithm yields competitive detection accuracy compared to traditional approaches.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This article is supported by the National Natural Science Foundation of China (Grant No. 61873004), and the Humanities and Social Sciences Foundation of Anhui Education Department (Grant No. SK2017A0098).

Conflict of interest

The authors declare there is no conflict of interest.