Dynamics of an SEIR model with media coverage mediated nonlinear infectious force

Jingli Xie; Hongli Guo; Meiyang Zhang; Jingli Xie; Hongli Guo; Meiyang Zhang

doi:10.3934/mbe.2023654

Mathematical Biosciences and Engineering

2023, Volume 20, Issue 8: 14616-14633. doi: 10.3934/mbe.2023654

Previous Article Next Article

Research article Special Issues

Dynamics of an SEIR model with media coverage mediated nonlinear infectious force

College of Mathematics and Statistics, Jishou University, Jishou, Hunan 416000, China

Academic Editor: Xiang-Sheng Wang

Received: 10 April 2023 Revised: 04 June 2023 Accepted: 21 June 2023 Published: 05 July 2023

Media coverage can greatly impact the spread of infectious diseases. Taking into consideration the impacts of media coverage, we propose an SEIR model with a media coverage mediated nonlinear infection force. For this novel disease model, we identify the basic reproduction number using the next generation matrix method and establish the global threshold results: If the basic reproduction number $\mathcal{R}_{0} < 1$ , then the disease-free equilibrium $P_{0}$ is stable, and the disease dies out. If $\mathcal{R}_{0} > 1$ , then the endemic equilibrium $P^{*}$ is stable, and the disease persists. Sensitivity analysis indicates that the basic reproduction number $\mathcal{R}_{0}$ is most sensitive to the population recruitment rate $\Lambda$ and the disease transmission rate $\beta _{1}$ .

Keywords:

Citation: Jingli Xie, Hongli Guo, Meiyang Zhang. Dynamics of an SEIR model with media coverage mediated nonlinear infectious force[J]. Mathematical Biosciences and Engineering, 2023, 20(8): 14616-14633. doi: 10.3934/mbe.2023654

Related Papers:

[1]	Elijah B. Baloba, Baba Seidu . A mathematical model of anthrax epidemic with behavioural change. Mathematical Modelling and Control, 2022, 2(4): 243-256. doi: 10.3934/mmc.2022023
[2]	S. Y. Tchoumi, Y. Kouakep-Tchaptchie, D. J. Fotsa-Mbogne, J. C. Kamgang, J. M. Tchuenche . Optimal control of a malaria model with long-lasting insecticide-treated nets. Mathematical Modelling and Control, 2021, 1(4): 188-207. doi: 10.3934/mmc.2021018
[3]	Yaxin Ren, Yakui Xue . Modeling and optimal control of COVID-19 and malaria co-infection based on vaccination. Mathematical Modelling and Control, 2024, 4(3): 316-335. doi: 10.3934/mmc.2024026
[4]	Alexandru Hofman, Radu Precup . On some control problems for Kolmogorov type systems. Mathematical Modelling and Control, 2022, 2(3): 90-99. doi: 10.3934/mmc.2022011
[5]	K. O. Achema, D. Okuonghae, C. J. Alhassan . A mathematical model for assessing the impact of dual-level toxicity on aquatic biospecies and its optimal control analysis. Mathematical Modelling and Control, 2022, 2(3): 100-121. doi: 10.3934/mmc.2022012
[6]	Rashid Jan, Normy Norfiza Abdul Razak, Sania Qureshi, Imtiaz Ahmad, Salma Bahramand . Modeling Rift Valley fever transmission: insights from fractal-fractional dynamics with the Caputo derivative. Mathematical Modelling and Control, 2024, 4(2): 163-177. doi: 10.3934/mmc.2024015
[7]	Chang Luo . Local controllability of complex networks. Mathematical Modelling and Control, 2021, 1(2): 121-133. doi: 10.3934/mmc.2021010
[8]	Iman Malmir . Novel closed-loop controllers for fractional nonlinear quadratic systems. Mathematical Modelling and Control, 2023, 3(4): 345-354. doi: 10.3934/mmc.2023028
[9]	J. O. Akanni, S. Ajao, S. F. Abimbade, Fatmawati . Dynamical analysis of COVID-19 and tuberculosis co-infection using mathematical modelling approach. Mathematical Modelling and Control, 2024, 4(2): 208-229. doi: 10.3934/mmc.2024018
[10]	Mlyashimbi Helikumi, Paride O. Lolika . Dynamics and analysis of COVID-19 disease transmission: The effect of vaccination and quarantine. Mathematical Modelling and Control, 2023, 3(3): 192-209. doi: 10.3934/mmc.2023017

Abstract

1. Introduction

Dengue is an infectious illness that is spread in almost all countries, including in Indonesia ^[1]. Severe dengue is a prominent leader of critical disease and death in some Asian and Latin American countries. Every year, dengue cases occur in East Java province, Indonesia. Based on the Ministry of Health of the Republic of Indonesia, dengue cases in Indonesia until July 2020 reached 71,633. East Java is one of the provinces in Indonesia with high endemic potential from year to year ^[2].

Dengue is a viral infection spread to humans through the bite of infected mosquitoes. Aedes aegypti mosquitoes are the major vectors that transmit the disease. The virus responsible for bringing dengue is called dengue virus (DENV). There are four DENV serotypes, and there is the potential to be infected four times. Currently, there is no particular treatment for dengue/severe dengue. Early detection of dengue disease progression and access to appropriate medical care reduce fatality rates of severe dengue to below 1%. Dengue prevention and regulation depends on effective vector control measures ^[1].

Mathematical modeling can play essential roles in helping understand the complex phenomenon of epidemic spread including the malaria ^[3,4], tuberculosis ^[5,6], measles ^[7], meningitis ^[8], monkeypox ^[9], zika ^[10], and COVID-19 ^[11,12]. With a mathematical model, the relationship between the disease spread and epidemiological parameters can be identified. Several mathematical models of dengue transmission with various types compartments have been studied by researchers ^[13,14]. In ^[15,16], the authors designed mathematical model to study the effect of temperature on the spread of dengue fever. The impact of reinfection with the same serotype on the dynamics of dengue transmission has been studied in ^[17]. Researchers at ^[18,19] developed a fractional order model to understand the dynamics of dengue fever transmission. The authors in ^[20] presented a dynamical model of dengue with hospitalization to analyze the infection in East Java province, Indonesia. Ndii ^[21] formulated a dengue model by incorporating seasonally varying mosquitoes, vaccination, and media. The authors of ^[22] discussed a dengue model that accommodates releasing Wolbachia into wild mosquitoes and vaccination. The authors in ^[23] presented the dengue model by considering the recruitment rate of the human population in terms of logistic growth. The proposed model is more realistic because the growth rate of the human population is not always constant.

This work aims to extend the previous study of ^[23] by formulating a dengue model that captures the control variables, such as fumigation and prevention, by applying the optimal control theory to the model. The model parameters will be estimated based on the dengue data in East Java Province, Indonesia. We employ efficiency and economic methods to examine the most cost-effective strategy among the implemented control scenarios. The remaining part of this paper proceeds as follows. Section 2 explains the model formulation. The analysis of the model is discussed in Section 3. The optimal control problem is studied in Section 4. Section 5 summarizes the main findings of this work.

2. Model formulation

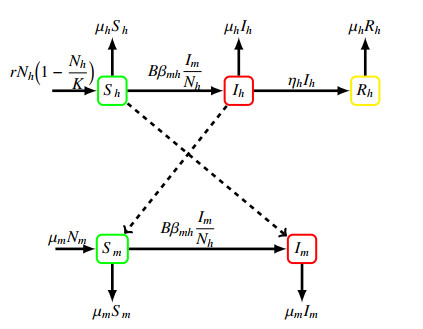
In this study, we consider the dengue transmission model with the assumption that the recruitment rate in the human population is logistic growth as proposed by ^[23]. The total human population $({N {}_{h} })$ is divided into three sub-populations: the susceptible $({S {}_{h} })$ , the infectious $({I {}_{h} })$ , and the recovered $({R {}_{h} })$ . The total mosquitoes population $({N {}_{m} })$ is divided into two sub-populations: the susceptible mosquitoes $({S {}_{m} })$ and the infectious mosquitoes $({I {}_{m} })$ . The flow diagram of the dengue model is displayed in Figure 1. As the diagram in Figure 1 shows, the dengue model is governed by an autonomous system of ODEs as follows:

$\begin{align} \begin{aligned} \begin{split} \frac{d}{dt} S_{h}& = rN_{h} \left(1-\frac{N_{h} }{K} \right)-\left(B\beta _{mh} \frac{I_{m} }{N_{h} } +\mu _{h} \right)S_{h} , \\ \frac{d}{dt} I_{h} & = B\, \beta _{mh} \frac{I_{m} }{N_{h} } S_{h} -\left(\eta _{h} +\mu _{h} \right)I_{h} , \\ \frac{d}{dt} R_{h} & = \eta _{h} I_{h} -\mu _{h} R_{h} , \\ \frac{d}{dt} S_{m} & = \mu _{m} \, N_{m} -\left(B\beta _{hm} \frac{I_{h} }{N_{h} } +\mu _{m} \right)S_{m} , \\ \frac{d}{dt} I_{m} & = B\, \beta _{hm} \frac{I_{h} }{N_{h} } S_{m} -\mu _{m} I_{m} , \end{split} \end{aligned} \end{align}$

(2.1)

with

$N_{h} = S_{h} +I_{h} +R_{h}$

and

$N_{m} = S_{m} +I_{m}.$

Figure 1. Transmission diagram of dengue model.

DownLoad: Full-Size Img PowerPoint

The biologically feasible region of the model (2.1) is set out by

$\begin{equation} \Gamma = \Gamma_h\cup\Gamma_m\subset R_+^3\times R_+^2, \end{equation}$

(2.2)

where

$\begin{equation*} \Gamma_h = \left\{\left(S_h, I_h, R_h\right)\in R_+^3:N_h\le K\right\} \end{equation*}$

and

$\begin{equation*} \Gamma_m = \left\{\left(S_m, I_m\right)\in R_+^2:S_m + I_m \le N_m(0) \right\}. \end{equation*}$

The description of the variables and parameters of the dengue model can be set out in Tables 1 and 2, respectively.

Table 1. Descriptions of the model state variables.

State variables	Biological interpretation
${S}_{h}$	The susceptible of the human population
${I}_{h}$	The infectious of the human population
${R}_{h}$	The recovery of human population
${N}_{h}$	The total number of human population
${S}_{m}$	The susceptible of the mosquito population
${I}_{m}$	The infectious of the mosquito population
${N}_{m}$	The total number of the mosquito population

| Show Table

DownLoad: CSV

Table 2. Descriptions of model parameters.

Symbol	Description
$B$	The biting rate of mosquito
$\beta$ ${}_{mh}$	The transmission probability from $I_m$ to $S_h$
$\beta$ ${}_{hm}$	The transmission probability from $I_h$ to $S_m$
$\mu$ ${}_{h}$	The natural death rate in human
$\eta$ ${}_{h}$	The recovery rate in human
$\mu$ ${}_{m}$	The birth/death rate in the mosquito
$K$	Carrying capacity of the environment
$r$	Intrinsic growth rate

| Show Table

DownLoad: CSV

The change rate of the total human population can be represented by

$\frac{dN_{h} }{dt} = \left[r\left(1-\frac{N_{h} }{K} \right)-\mu _{h} \right]N_{h} .$

The total of the mosquito population is constant. Hence, the system (2.1) can be reduced into the following system:

$\begin{equation} \begin{split} \frac{d}{dt} N_{h}& = \left[r\left(1-\frac{N_{h} }{K} \right)-\mu _{h} \right]N_{h}, \\ \frac{d}{dt} S_{h}& = rN_{h} \left(1-\frac{N_{h} }{K} \right)-\left(B\beta _{mh} \frac{I_{m} }{N_{h} } +\mu _{h} \right)S_{h}, \\ \frac{d}{dt} I_{h} & = B\, \beta _{mh} \frac{I_{m} }{N_{h} } S_{h} -\left(\eta _{h} +\mu _{h} \right)I_{h}, \\ \frac{d}{dt} I_{m} & = B\, \beta _{hm} \frac{I_{h} }{N_{h} } \left(N_{m} -I_{m} \right)-\mu _{m} I_{m}. \end{split} \end{equation}$

(2.3)

2.1. Estimation of the parameters model

In this present section, we devote the parameters estimation of the model (2.3) using the fitting least-squares method ^[24,25]. The monthly cumulative data of dengue in East Java Province, Indonesia, from 2018 until 2020 ^[26] is utilized in this study. The parameters ${\mu }_h$ , ${\mu }_m$ , and $r$ are estimated taking the demographic information. The natural death rate of human $\left({\mu }_h\right)$ is observed from inverse of the average lifespan in East Java Province. The average of lifespan in East Java Province from 2018 until 2020 is 71.15 years. Therefore,

${\mu }_h = \frac{1}{71.15}$

per year ^[27,28]. Next, the death rate of mosquito $\left({\mu }_m\right)$ , is found from the inverse of the average lifespan of Aedes mosquitoes. Based on ^[29], the average of lifespan of Aedes mosquitoes is 25 days, that is

${\mu }_m = \frac{1}{25}$

per day. Furthermore, for the growth rate of human $\left(r\right)$ , is obtained as follows. The average population in East Java Province from 2018 to 2020 is $39,955,059$ ^[30]. Hence,

$\frac{r}{{\mu }_h} = 39,955,059,$

which is the total human population without the disease, so that $r =$ 561,560.91 per year. The other parameters, such as $B, \ \ {\beta }_{mh}, \ \ {\beta }_{hm}, \ \ {\eta }_h, \ \ K,$ and $N_m$ , are estimated with the objective function that minimize

${\mathop{\mathrm{min}}\limits_{B, \ {\beta }_{mh}, \ {\beta }_{hm}, \ {\eta }_h, \ K, \ N_m} \sum^{t_f}\limits_{i = 0}{{\left(I_i-I^{data}_i\right)}^2}\ },$

where $t_f$ is the end time of the cumulative dengue cases data $I^{data}_i$ and $I_i$ , $\left(i = 0, \ 1, \ 2, \dots, \ t_f\right)$ are the cumulative numerical solutions of infected humans from system (2.3). Thus, the initial populations are

$\left({N_h}_0, {S_h}_0, {I_h}_0, I_{m_0}\right) = \left(39,500,851, {N_h}_0-{I_h}_0, I^{data}_0, \ 100\right),$

while the initial parameter values for estimation are

$\begin{equation*} \begin{aligned} \left(B_0, {\beta }_{mh_0}, {\beta }_{hm_0}, {{\eta }_h}_0, K_0, {N_m}_0\right) = \left(0.4, 0.4, 0.4, 0.4, 1.5{N_h}_0, 2.5N_{h_0}\right). \end{aligned} \end{equation*}$

The lower bound parameter values are $\left({10}^{-3}, \ {10}^{-3}, \ {10}^{-3}, \ {10}^{-3}, \ 1.2{N_h}_0, \ 2N_{h_0}\right)$ and upper bound parameter values are $\left(1, \ 1, \ 1, \ 1, \ 2N_{h_0}, \ 3N_{h_0}\right)$ . The result of the estimation and parameter value can be seen in Figure 2 and Table 3.

Figure 2. Comparison of dengue data and the model.

DownLoad: Full-Size Img PowerPoint

Table 3. The parameter value of the model.

Parameter	Value (months)	Source
B	0.3848	Fitted
$\beta {}_{mh}$	0.3632	Fitted
$\beta {}_{hm}$	0.3252	Fitted
$\mu {}_{h}$	$\frac{1}{12*71.15}$	Estimated
$\eta {}_{h}$	0.0198	Fitted
$\mu {}_{m}$	$\frac{1}{\frac{12*25}{365}}$	Estimated
K	59,229,000	Fitted
r	$\frac{39,955,059}{12*71.15}$	Estimated
$N_m$	98,782,000	Fitted

| Show Table

DownLoad: CSV

3. Analysis model

In this section, we present the equilibria and the local stability of the DHF model.

3.1. Equilibria of model

Model (2.3) has the dynamic characteristic of model (2.1), so to understand the dynamics behaviour of the model (2.1), we carry out the analysis of the model (2.3). Likewise, the biological domain in both models is the same. Based on ^[23], two equilibria are obtained, namely the disease-free equilibrium (DFE) and the endemic equilibrium. The DFE of the system (2.3) is provided by

$E_0(N_{h}^* , S_{h}^* , 0 , 0) = \left(K\left(1-\frac{\mu _{h} }{r} \right), K\left(1-\frac{\mu _{h} }{r} \right), 0, 0 \right).$

The DFE $E_0$ is exist if $r > \mu _{h}$ .

Meanwhile, the endemic equilibrium is

$E_{1} (N_{h} , S_{h} , I_{h} , I_{m} ) = (\tilde{N}_{h} , \tilde{S}_{h} , \tilde{I}_{h} , \tilde{I}_{m} )$

with

$\begin{equation*} \begin{split} \tilde{N}_{h} & = K\left(1-\frac{\mu _{h} }{r} \right), \\ \tilde{S}_{h} & = \left(\eta _{h} +\mu _{h} \right)\tilde{N}_{h} \frac{\left(B\, \beta _{hm} \tilde{I}_{h} +\mu _{m} \tilde{N}_{h} \right)}{B^{2} \, \beta _{mh} \, \beta _{hm} N_{m} }, \\ \tilde{I}_{h} & = \frac{\mu _{h} \left(B^{2} \beta _{mh} \beta _{hm} N_{m} -\mu _{m} (\eta _{h} +\mu _{h} )\tilde{N}_{h} \right)}{B\beta _{hm} (\eta _{h} +\mu _{h} )\left(\frac{B\beta _{mh} N_{m} }{\tilde{N}_{h} } +\mu _{h} \right)}, \\ \tilde{I}_{m} & = \frac{B\, \beta _{hm} N_{m} \tilde{I}_{h} }{B\, \beta _{hm} \tilde{I}_{h} +\mu _{m} \tilde{N}_{h} }. \end{split} \end{equation*}$

The endemic equilibrium exists if

$\frac{B^{2} \beta _{mh} \beta _{hm} N_{m} }{\mu _{m} (\eta _{h} +\mu _{h} )\tilde{N}_{h} } > 1$

$\frac{B^{2} \beta _{mh} \beta _{hm} N_{m} }{\mu _{m} (\eta _{h} +\mu _{h} )K\left(1-\frac{\mu _{h} }{r} \right)} > 1, \, \, r > \mu _{h} .$

Using the the next-generation matrix method ^[31], we yield the basic reproduction number as follows:

$\begin{equation} R_{0} = \sqrt{\frac{B^{2} \beta _{hm} \beta _{mh} N_{m} }{\mu _{m} K\left(1-\frac{\mu _{h} }{r} \right)\left(\eta _{h} +\mu _{h} \right)} } , \, \, \, r > \mu _{h} . \end{equation}$

(3.1)

By using the formulation of $R_0$ , the endemic equilibrium exists if

$R^2_0 = \frac{B^2 \beta_{mh}\beta_{hm}N_m}{\mu_m(\eta_h+\mu_h)K\left(1-\frac{\mu_h}{r}\right)} > 1$

or $R_0 > 1$ and $r\mathrm{ > }\mu_h.$

3.2. Local stability analysis

The local stability analysis of dengue model (2.3) can be expressed by the following theorem.

Theorem 3.1. The diseases-free equilibrium $E_{0}\left(N_{h}^{*}, S_{h}^{*}, 0, 0\right)$ of the model (2.3) is locally asymptotically stable if

$R_{0} < 1.$

Proof. The evaluation of Jacobian matrix of the system (2.3) at DFE $E_0$ , we have

$\begin{equation} J_{E_{0} } = \left(\begin{array}{cccc} {\mu _{h} -r} & {0} & {0} & {0} \\ {2\mu _{h} -r} & {-\mu _{h} } & {0} & {-B\beta _{mh} } \\ {0} & {0} & {-(\eta _{h} +\mu _{h} )} & {B\beta _{mh} } \\ {0} & {0} & {\frac{B\beta _{mh} N_{m} }{K\left(1-\frac{\mu _{h} }{r} \right)} } & {-\mu _{m} } \end{array}\right). \end{equation}$

(3.2)

The two eigenvalues of Jacobian matrix (3.2) are $-\mu_h, -\left(r-\mu _{h} \right)$ that are obviously negative. The other two remaining eigenvalues can be found through the following characteristics equation:

$\begin{equation} \lambda ^{2} +a_{1} \lambda +a_{2} = 0 \end{equation}$

(3.3)

for

$a_{1} = \left(\mu _{m} +\eta _{h} +\mu _{h} \right)$

and

$a_{2} = \left(\eta _{h} +\mu _{h} \right)\mu _{m} -\frac{B^{2} \beta _{mh} \beta _{hm} N_{m} }{K\left(1-\frac{\mu _{h} }{r} \right)} .$

Using Routh-Hurwitz criterion, the roots of the Eq (3.3) are negative if $a_{1}, a_{2} > 0\, .$ The coefficient $a_{1} > 0\,$ , while $a_{2} > 0\,$ if

$\frac{B^{2} \beta _{mh} \beta _{hm} N_{m} }{\mu _{m} (\eta _{h} +\mu _{h} )K\left(1-\frac{\mu _{h} }{r} \right)} < 1$

$R_{0} < 1 .$

So, the theorem is proven. □

The endemic equilibrium E ${}_{1}$ in model (2.3) will be asymptotically stable if

${R}_{0} \mathrm{ > }1.$

By Substituting the endemic equilibrium $E_1$ to Jacobian matrix of the system (2.3), we find that the eigenvalue is $-\left(r-\mu _{h} \right)$ and the others are the roots of the equation

$\begin{equation} \begin{aligned} \begin{array}{l} {\lambda ^{3} +\left[\frac{B\beta _{mh} }{\tilde{N}_{h} } \left(\tilde{I}_{m} +\tilde{I}_{h} \right)+2\mu _{h} +\mu _{m} +\eta _{h} \right]\lambda ^{2} } \\ {+\left[\left(\frac{B\beta _{mh} \tilde{I}_{m} }{\tilde{N}_{h} } +\mu _{h} \right)\left(\frac{B\beta _{hm} \tilde{I}_{h} }{\tilde{N}_{h} } +\mu _{m} +\eta _{h} +\mu _{h} \right)\right. } \\ {\left.+\left(\eta _{h} +\mu _{h} \right)\left(\frac{B\beta _{hm} \tilde{I}_{h} }{\tilde{N}_{h} } +\mu _{m} \right)- \frac{B^{2} \beta _{mh} \beta _{hm} \tilde{S}_{h} }{\tilde{N}_{h}^{2} } \left(N_{m} -\tilde{I}_{m} \right)\right]\lambda } \\ {+\left(\frac{B\beta _{mh} \tilde{I}_{m} }{\tilde{N}_{h} } +\mu _{h} \right)\left[\left(\eta _{h} +\mu _{h} \right)\left(\frac{B\beta _{hm} \tilde{I}_{h} }{\tilde{N}_{h} } +\mu _{m} \right)\right. } \\ {\left.- \frac{B^{2} \beta _{mh} \beta _{hm} \tilde{S}_{h} }{\tilde{N}_{h}^{2} } \left(N_{m} -\tilde{I}_{m} \right)\right]+\frac{B^{3} \beta _{mh}^{2} \beta _{hm} \tilde{I}_{h} \tilde{S}_{h} }{\tilde{N}_{h}^{3} } \left(N_{m} -\tilde{I}_{m} \right) = 0.} \end{array}\end{aligned} \end{equation}$

(3.4)

Equation (3.4) can be expressed by

$\lambda ^{3} +b_{1} \lambda ^{2} +b_{2} \lambda +b_{3} = 0$

with

$\begin{equation*} \begin{aligned} \begin{split} b_{1} = &\frac{B\beta _{mh} }{\tilde{N}_{h} } \left(\tilde{I}_{m} +\tilde{I}_{h} \right)+2\mu _{h} +\mu _{m} +\eta _{h}, \\ b_{2} = &\left(\frac{B\beta _{mh} \tilde{I}_{m} }{\tilde{N}_{h} } +\mu _{h} \right)\left(\frac{B\beta _{hm} \tilde{I}_{h} }{\tilde{N}_{h} } +\mu _{m} +\eta _{h} +\mu _{h} \right)\\ &+\left(\eta _{h} +\mu _{h} \right)\left(\frac{B\beta _{hm} \tilde{I}_{h} }{\tilde{N}_{h} } +\mu _{m} \right)-\frac{B^{2} \beta _{mh} \beta _{hm} \tilde{S}_{h} }{\tilde{N}_{h}^{2} } \left(N_{m} -\tilde{I}_{m} \right), \\ b_{3} = &\left(\frac{B\beta _{mh} \tilde{I}_{m} }{\tilde{N}_{h} } +\mu _{h} \right)\left[\left(\eta _{h} +\mu _{h} \right)\left(\frac{B\beta _{hm} \tilde{I}_{h} }{\tilde{N}_{h} } +\mu _{m} \right)\right] \\ &\left[ - \frac{B^{2} \beta _{mh} \beta _{hm} \tilde{S}_{h} }{\tilde{N}_{h}^{2} } \left(N_{m} -\tilde{I}_{m} \right)\right]+\frac{B^{3} \beta _{mh}^{2} \beta _{hm} \tilde{I}_{h} \tilde{S}_{h} }{\tilde{N}_{h}^{3} } \left(N_{m} -\tilde{I}_{m} \right). \end{split}\end{aligned} \end{equation*}$

According to the Ruth-Hurwitz criteria, the roots of the characteristic equation will be negative or have a negative real part if

$b_{1}, b_{2}, b_{3} > 0$

and

$b_{1} b_{2} -b_{3} > 0.$

The coefficients b ${}_{1}$ –b ${}_{3}$ containing $\tilde{N}_{h}, \tilde{S}_{h}, \tilde{I}_{h}, \tilde{I}_{m}$ so showing that the condition for the root must be positive will be difficult to do analytically. Therefore, the numerical simulation is implemented to analyze the stability of the endemic equilibrium. The parameter values used are given in Table 3.

The phase plane graph between the infected mosquito population and the infected human population is presented in Figure 3. Based on , it can be seen that the three graphs converges to the endemic equilibrium E ${}_{1}$ as time evolves when

$R_0 > 1.$

Figure 3. Phase field of

$\left(I_m\right)$ and

$\left(I_h\right)$ .

DownLoad: Full-Size Img PowerPoint

3.3. Sensitivity analysis

In this work, we discuss the sensitivity analysis to recognize the parameter that can influence the threshold $R_0$ . To assign the sensitivity index, we refer to ^[32]. The calculation of the sensitivity index $R_0$ towards to some parameter, say $a$ , is given by

${\mathrm{\Upsilon }}^{R_0}_a = \frac{\partial R_0}{\partial a}\times \frac{a}{R_0}.$

Using the parameter values in , the sensitivity indexes of $R_0$ are summarized in Table 4.

Table 4. Sensitivity index of the parameters.

Parameter	Sensitivity index
B	$1$
$\beta {}_{mh}$	$0.5$
$\beta {}_{hm}$	$0.5$
$\mu {}_{h}$	$-0.028$
$\eta {}_{h}$	$-0.472$
$\mu {}_{m}$	$-0.5$
K	$-0.5$
r	$-1.266\times {10}^{-8}$
$N_m$	$0.5$

| Show Table

DownLoad: CSV

The interpretation of the sensitivity index in can be explained as follows. The positive sign reveals that when the parameter values are raised, the value of $R_0$ will also increase. Conversely, the negative sign reveals that when the parameter's value is raised, the value of $R_0$ will be decreased. For example, for

${\mathrm{\Upsilon }}^{R_0}_B = 1,$

increasing the value of the biting rate of mosquito by $10\%$ , causes $R_0$ to increase by $10\%$ . Thus, for

${\mathrm{\Upsilon }}^{R_0}_K = -0.5,$

increasing the carrying capacity by $10\%$ , causes $R_0$ to decrease by $5\%$ . Likewise, for the other indexes. The highly sensitive parameters should be considered carefully because small variations in these parameters will cause large quantitative changes. shows that the parameter with the greatest influence on the threshold is parameter $B$ . The implication is that an increase in the value of the biting rate of mosquitoes increases the spread of dengue disease in the population. Hence, we can anticipate it with preventive control by using a bed net and mosquito repellent lotion or fumigation control to reduce the mosquito population. Furthermore, the value of the biting rate of mosquitoes will decrease, which implies dengue transmission in the community also decreases.

Based on the contour plot in and , the basic reproduction number $\left(R_0\right)$ will increase in proportion to the results of the sensitivity analysis in . The parameters $B$ and ${\beta }_{mh}$ have a positive relation; however the parameters ${\mu }_m$ and ${\eta }_h$ have a negative relation.

Figure 4. The behaviour of

$R_0$ to the parameters

${\mu }_m$ and

$B$ .

DownLoad: Full-Size Img PowerPoint

Figure 5. The behaviour of

$R_0$ to the parameters

${\beta }_{mh}$ and

${\eta }_h$ .

DownLoad: Full-Size Img PowerPoint

4. Optimal control

In this section, we apply the optimal control (OC) strategy to the dengue model. Based on the sensitivity analysis in the previous section, we can reduce the number of mosquito biting rates with fumigation and prevention efforts. Therefore, we define two control variables, namely $u_1$ as fumigation and $u_2$ as prevention. The dengue model with control variables can be written as follows

$\begin{align*} \frac{dS_h}{dt}& = rN_h\left(1-\frac{N_h}{K}\right)-\left(1-u_2\right)\frac{B{\beta }_{mh}I_m}{N_h}S_h-{\mu }_hS_h, \\ \frac{dI_h}{dt}& = \left(1-u_2\right)\frac{B{\beta }_{mh}I_m}{N_h}S_h-\left({\eta }_h+{\mu }_h\right)I_h, \\ \frac{dR_h}{dt}& = {\eta }_hI_h-{\mu }_hR_h, \\ \frac{dS_m}{dt}& = {\mu }_mN_m-\frac{B{\beta }_{hm}I_h}{N_h}S_m-{\mu }_mS_m-\kappa u_1S_m, \\ \frac{dI_m}{dt}& = \frac{B{\beta }_{hm}I_h}{N_h}S_m-{\mu }_mI_m-\kappa u_1I_m. \end{align*}$

The control variables $u_1$ and $u_2$ are established on interval $\left[0, t_f\right]$ , where

$0\le u_i\left(t\right)\le 1, \ \ \ t\in \left[0, t_f\right], \ \ \ i = 1, 2,$

and $t_f$ represent the final time of the controls. We aim to minimize the number of infected human populations and mosquito populations and keep the cost of employing fumigation and prevention controls as low as possible. For this, we state the objective function

$J\left(u_1, u_2\right) = \int^{t_f}_0{\left(A_1 I_h+ A_2 I_m+\frac{1}{2}c_1u^2_1+\frac{1}{2}c_2u^2_2\right)dt, }$

where $A_1$ and $A_2$ are weights of the objective function for $I_h$ and $I_m$ , respectively, and $c_1$ , and $c_2$ are weight parameters for fumigation and prevention respectively. We utilize the quadratic cost function for $J$ to depict the cost of control efforts. This quadratic function can explain a nonlinear cost increase associated with the performance of control attempts in the field ^[33,34].

Then, to solve this optimal control problem, we assumed that $N_h$ is constant. Using Pontryagin's maximum principle ^[35], the optimal solutions of $u_1$ and $u_2$ are provided by

$\begin{align*} u^*_1& = {\mathrm{min} \left\{1, {max \left(0, \kappa \left(\frac{{\lambda }_4S_m+{\lambda }_5I_m}{c_1}\right)\right)\ }\right\}\ }, \\ u^*_2& = {\mathrm{min} \left\{1, {max \left(0, \left({\lambda }_2-{\lambda }_1\right)\frac{B{\beta }_{mh}I_m}{c_2N_h}S_h\right)\ }\right\}\ }. \end{align*}$

The variables ${\lambda }_i$ , $i = 1, 2, 3, 4, 5$ , are represented as adjoint variables or co-state which satisfies the following equations

$\begin{align*} \frac{d{\lambda }_1}{dt}& = \left({\lambda }_1-{\lambda }_2\right)\left(1-u_2\right)\frac{B{\beta }_{mh}I_m}{N_h}+{\lambda }_1{\mu }_h, \\ \frac{d{\lambda }_2}{dt}& = -A_1+\left({\lambda }_2-{\lambda }_3\right){\eta }_h+\left({\lambda }_4-{\lambda }_5\right)\frac{B{\beta }_{hm}S_m}{N_h}+{\lambda }_2{\mu }_h, \\ \frac{d{\lambda }_3}{dt}& = {\lambda }_3{\mu }_h, \\ \frac{d{\lambda }_4}{dt}& = \left({\lambda }_4-{\lambda }_5\right)\frac{B{\beta }_{hm}I_h}{N_h}+{\lambda }_4\left({\mu }_m+\kappa u_1\right), \\ \frac{d{\lambda }_5}{dt}& = -A_2+\left({\lambda }_1-{\lambda }_2\right)\left(1-u_2\right)\frac{B{\beta }_{mh}S_h}{N_h}+{\lambda }_5\left({\mu }_m+\kappa u_1\right), \end{align*}$

where the transversality conditions

${\lambda }_i\left(t_f\right) = 0, \ \ \ i = 1, 2, 3, 4, 5.$

In this optimal control problem, because $N_h$ is assumed to be constant,

$\frac{dN_h}{dt} = 0\ \Leftrightarrow r = \frac{K}{K-N_h}{\mu }_h,$

as $N_h$ is the population in East Java Province in 2018. We assume that the values of the parameters are given by

$A_1 = A_2 = 1, \ \ c_1 = 15, \ \ c_2 = 10, \ \ \kappa = 0.7$

and

$r = \frac{K}{K-N_h}{\mu }_h$

and the other parameters are referred to Table 3. We solve the numerical optimal control simulation using the backward and forward iteration technique as stated in ^[36]. To determine which strategy or combination provides useful methods of controlling dengue, we addressed the following strategies for our simulation result, as enumerated below.

4.1. Strategy 1. Single intervention: use of fumigation only

The result of the simulation of comparison $I_h$ and $I_m$ without and with control when fumigation usage only is given in . We can observe that using this strategy, the infections of humans and mosquitoes tend to decrease compared to no control. The profile of the optimal control $u_1$ only is presented in Figure 7. It is apparent that fumigation control should be carried out intensively for a maximum of 50 months.

Figure 6. Comparison

$I_h$ and

$I_m$ without and with control.

DownLoad: Full-Size Img PowerPoint

Figure 7. Control profile of

$u_1$ .

DownLoad: Full-Size Img PowerPoint

4.2. Strategy 2. Single intervention: use of prevention only

The result of the simulation of comparison $I_h$ and $I_m$ without and with control when prevention usage only is given in . From , it can be seen that both infection of humans and mosquitoes significantly reduce using this strategy. The profile of the optimal control $u_2$ only is displayed in Figure 9. This figure shows that prevention control should be provided with full effort for almost 50 months.

Figure 8. Comparison

$I_h$ and

$I_m$ without and with control.

DownLoad: Full-Size Img PowerPoint

Figure 9. Control profile of

$u_2$ .

DownLoad: Full-Size Img PowerPoint

4.3. Strategy 3. Double intervention: combination of fumigation and prevention

The result of the simulation of comparison $I_h$ and $I_m$ without and with control when implementing both fumigation and prevention are given in Figure 10.

Figure 10. Comparison

$I_h$ and

$I_m$ without and with controls.

DownLoad: Full-Size Img PowerPoint

Using the last strategy, it is found that both infectious humans and mosquitoes diminish over to compare to without controls. The profile of the optimal control $u_1$ and $u_2$ simultaneously is demonstrated in Figure 11. As depicted in Figure 11, we found that fumigation and preventive control were both maintaining at maximum levels for nearly 50 months before decaying gradually to the lower bound.

Figure 11. Control profiles of

$u_1$ and

$u_2$ simultaneously.

DownLoad: Full-Size Img PowerPoint

Furthermore, to evaluate the most proper strategy, we assess and compare the merit and the costs related to the control measures by adopting the infection averted ratio (IAR), average cost-effectiveness ratio (ACER) and incremental cost-effectiveness ratio (ICER). These economic verify are mathematically established in ^[37,38] as follows:

$\mathrm{IAR = }\frac{\mathrm{Cumulative\ infected\ averted}}{\mathrm{Cumulative\ recovered}}.$

The cumulative infected averted is presented by the sum of the difference between the total infectious individuals without and with control. More explicitly

$\mathrm{I}\mathrm{AR} = \frac{\int^{t_f}_0{\left(I_h\left(t\right)-I^*_h\left(t\right)\right)\ dt}}{\int^{t_f}_0{R^*_h\left(t\right)\ dt}},$

where the symbol with subscript ${}^{*}$ is employed to represent the optimal solutions associated with the corresponding strategy. The most powerful strategy when taking IAR is the strategy with the highest ratio

$\mathrm{ACER = }\frac{\mathrm{Total}\mathrm{\ cost\ invested\ on\ the\ intervention}}{\mathrm{Total\ number\ of\ infectious\ averted}}.$

It proposes a single intervention and evaluates it against its baseline desire. The aim of fumigation control $\left(u_1\right)$ is the reduction of mosquitoes, while prevention control $\left(u_2\right)$ is to protect susceptible humans by diminishing the contact rate. Therefore, we deal with

$\mathrm{ACER = }\frac{\int^{t_f}_0{\left(C_1u^*_1\left(t\right)N^*_m\left(t\right)+C_2u^*_2\left(t\right)S^*_h\left(t\right)\right)\ dt}}{\int^{t_f}_0{\left(I_h\left(t\right)-I^*_h\left(t\right)\right)\ dt}},$

where $C_i$ represents the cost of the 2 possible interventions. The most cost-effective strategy when using ACER is the strategy with the smallest ratio.

$\begin{equation*} \begin{aligned} \mathrm{ICER = }\frac{\mathrm{Difference\ in\ cost\ produced\ by\ strategies\ }i\mathrm{\ and\ }j}{\mathrm{Difference\ in\ the\ total\ of\ infections\ averted\ in\ strategies\ }i\mathrm{\ and\ }j}. \end{aligned} \end{equation*}$

Hence, ICER is utilized to compare two different strategies, namely $i$ and $j$ . We calculate the cost of a strategy as undertaken for ACER. When comparing two or more competing intervention strategies incrementally, one intervention is compared with the next effective alternative in increasing order of total infected averted ^[37]. In computing ACER and ICER, we address the same cost for both interventions

$C_1 = C_2 = 1.$

The result of the calculation of the total infection and total cost is summarised in Table 5, while IAR and ACER is set out in Table 6.

Table 5. Total cost for each intervention strategy.

Strategies	Total Infection averted	Total cost
1	$3.112406\times {10}^4$	$3.1460\times {10}^9$
3	$4.394527\times {10}^4$	$5.0813\times {10}^9$
2	$4.394682\times {10}^4$	$1.9622\times {10}^9$

| Show Table

DownLoad: CSV

Table 6. Comparison of IAR and ACER for each intervention strategy.

Strategies	IAR	ACER
1	$1.2901$	$1.0108\times {10}^5$
3	$2.2588$	$1.1563\times {10}^5$
2	$2.2589$	$4.4650\times {10}^4$

| Show Table

DownLoad: CSV

Based on Table 5, Strategy 2 averts the greatest number of infections and yields the largest ratio

$IAR = 2.2589.$

Hence, it is the most effective. This strategy is also the most cost-effective because it is associated with the smallest average cost-effectiveness ratio

$ACER = 4.4650\times {10}^4.$

Using the total infection and total cost in Table 5, the ICER indexes, as summarised in Table 7, are computed as follows:

$\begin{align*} \mathrm{ICER}\left(\mathrm{1}\right)& = \frac{3.1460\times {10}^9-0}{3.112406\times {10}^4-0}\\& = 1.0108\times {10}^5, \\ \mathrm{ICER}\left(\mathrm{2}\right)& = \frac{1.9622\times {10}^9\mathrm{-}5.0813\times {10}^9}{4.394682\times {10}^4\mathrm{-}4.394527\times {10}^4}\\& = -2.0123\times {\mathrm{10}}^{\mathrm{9}}, \\ \mathrm{ICER}\left(\mathrm{3}\right)& = \frac{5.0813\times {10}^9-3.1460\times {10}^9}{4.394527\times {10}^4-3.112406\times {10}^4}\\& = 1.5095\times {10}^5. \end{align*}$

Table 7. Comparison of ICER for each intervention strategy.

Strategies	ICER	ICER recalculated
1	$1.0108\times {10}^5$	$1.8917\times {10}^4$
3	$1.5095\times {10}^5$	-
2	$\mathrm{-}\mathrm{2.0123\times }{\mathrm{10}}^{\mathrm{9}}$	$-0.9232\times {10}^5$

| Show Table

DownLoad: CSV

Comparing Strategies 1 and 3, the utilization of Strategy 1 is cost-saving over Strategy 3. This means that Strategy 3 is less effective and more costly than the other strategy. Hence, Strategy 3 is eliminated. Furthermore, we recalculate the index of ICER as follows:

Comparing Strategies 1 and 2, the application of Strategy 2 is cost-saving over Strategy 1. This indicates that Strategy 1 is less effective and more costly than the other strategy. Hence, Strategy 1 is removed. Our results recommend that Strategy 2 is the most cost-effective intervention associated with the ICER.

5. Conclusions

This study has investigated the dengue model by incorporating the logistic growth on the recruitment rate in the human population. The model analyses exhibited that the disease-free equilibrium is locally stable when the reproduction number is less than one, while the endemic equilibrium tends to be asymptotically stable when the threshold is greater than one. The parameters of the dengue model are estimated using data on cases of dengue in East Java Province, Indonesia, from 2018 to 2020. The findings indicate that the spread of dengue is persistent in the population.

Next, the sensitivity analysis shows that mosquito biting rate is the most influential parameter in the spread of dengue. Therefore, we carried out the control strategy in the form of fumigation and prevention. Pontryagin's maximum principle was adopted to accomplish the optimal control that minimizes the spread of dengue. The results of the optimal control problem show that the spread of dengue can be controlled by implementing sustainable control over a short period of time, which shows that the optimal control strategy is effective on humans and mosquitoes. Based on the cost-effectiveness evaluation, prevention is the most effective step to reduce dengue transmission using IAR, ACER, and ICER cost analysis.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research has been supported by the Ministry of Research, Technology and Higher Education, Republic of Indonesia, through the PDD 2020.

Conflict of interest

All authors declare that they have no conflicts of interest in this paper.

References

[1]	J. M. Tchuenche, N. Dube, C. P. Bhunu, R. J. Smith, C. T. Bauch, The impact of media coverage on the transmission dynamics of human influenza, BMC Public Health, 11 (2011), 1–14. https://doi.org/10.1186/1471-2458-11-S1-S5 doi: 10.1186/1471-2458-11-S1-S5
[2]	W. K. Zhou, Y. N. Xiao, J. M. Heffernan, Optimal media reporting intensity on mitigating spread of an emerging infectious disease, PLoS One, 14 (2019), e0213898. https://doi.org/10.1371/journal.pone.0213898 doi: 10.1371/journal.pone.0213898
[3]	R. S. Liu, J. H. Wu, H. P. Zhu, Media/psychological impact on multiple outbreaks of emerging infectious diseases, Comput. Math. Methods Med., 8 (2007), 153–164. https://doi.org/10.1080/17486700701425870 doi: 10.1080/17486700701425870
[4]	D. M. Xiao, S. G. Ruan, Global analysis of an epidemic model with nonmonotone incidence rate, Math. Biosci., 208 (2007), 419–429. https://doi.org/10.1016/j.mbs.2006.09.025 doi: 10.1016/j.mbs.2006.09.025
[5]	J. A. Cui, X. Tao, H. P. Zhu, An SIS infection model incorporating media coverage, Rocky Mt. J. Math., 38 (2008), 1323–1334. https://doi.org/10.1216/RMJ-2008-38-5-1323 doi: 10.1216/RMJ-2008-38-5-1323
[6]	J. Cui, Z. Wu, An SIRS model for assessing impact of media coverage, Abstr. Appl. Anal., 2014 (2014). https://doi.org/10.1155/2014/424610
[7]	Y. Wang, J. Cao, Z. Jin, H. Zhang, G. Q. Sun, Impact of media coverage on epidemic spreading in complex networks, Physica A, 392 (2013), 5824–5835. https://doi.org/10.1016/j.physa.2013.07.067 doi: 10.1016/j.physa.2013.07.067
[8]	S. R. Gani, S. V. Halawar, Optimal control for the spread of infectious disease: the role of awareness programs by media and antiviral treatment, Optim. Control Appl. Methods, 39 (2018), 1407–1430. https://doi.org/10.1002/oca.2418 doi: 10.1002/oca.2418
[9]	A. Kumar, P. K. Srivastava, Y. P. Dong, Y. Takeuchi, Optimal control of infectious disease: information-induced vaccination and limited treatment, Physica A, 542 (2020), 123196. https://doi.org/10.1016/j.physa.2019.123196 doi: 10.1016/j.physa.2019.123196
[10]	S. S. Shanta, M. H. A. Biswas, The impact of media awareness in controlling the spread of infectious diseases in terms of SIR model, Math. Modell. Eng. Probl., 7 (2020), 368–376. https://doi.org/10.18280/mmep.070306 doi: 10.18280/mmep.070306
[11]	W. Wang, X. Q. Zhao, Threshold dynamics for compartmental epidemic models in periodic environments, J. Dyn. Differ. Equations, 20 (2008), 699–717. https://doi.org/10.1007/s10884-008-9111-8 doi: 10.1007/s10884-008-9111-8
[12]	W. Xing, J. F. Gao, Q. S. Yan, Q. H. Zhou, Z. H. Yang, An epidemic model with saturated media/psychological impact (in Chinese), J. Northwest Univ. (Nat. Sci. Ed.), 48 (2018), 639–643. Available from: https://kns.cnki.net/kcms/detail/61.1072.N.20181015.1716.006.html.
[13]	Q. L. Yan, S. Y. Tang, S. Gabriele, J. H. Wu, Media coverage and hospital notifications: correlation analysis and optimal media impact duration to manage a pandemic, J. Theor. Biol., 390 (2016), 1–13. https://doi.org/10.1016/j.jtbi.2015.11.002 doi: 10.1016/j.jtbi.2015.11.002
[14]	Q. L. Yan, Y. L. Tang, D. D. Yan, J. Y. Wang, L. Q. Yang, X. P. Yang, et al., Impact of media reports on the early spread of COVID-19 epidemic, J. Theor. Biol., 502 (2020). https://doi.org/10.1016/j.jtbi.2020.110385
[15]	I. Ghosh, P. K. Tiwari, S. Samanta, I. M. Elmojtaba, N. Al-Salti, J. Chattopadhyay, A simple SI-type model for HIV/AIDS with media and self-imposed psychological fear, J. Math. Biosci., 306 (2018), 160–169. https://doi.org/10.1016/j.mbs.2018.09.014 doi: 10.1016/j.mbs.2018.09.014
[16]	S. Latifah, D. Aldila, W. Giyarti, H. Tasman, Mathematical study for an infectious disease with awareness-based SIS-M model, J. Phys. Conf. Ser., 1747 (2021), 012017. https://doi.org/10.1088/1742-6596/1747/1/012017 doi: 10.1088/1742-6596/1747/1/012017
[17]	G. O. Agaba, Y. N. Kyrychko, K. B. Blyuss, Mathematical model for the impact of awareness on the dynamics of infectious diseases, Math. Biosci., 286 (2017), 22–30. https://doi.org/10.1016/j.mbs.2017.01.009 doi: 10.1016/j.mbs.2017.01.009
[18]	P. van den Driessche, J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Math. Biosci., 180 (2002), 29–48. https://doi.org/10.1016/S0025-5564(02)00108-6 doi: 10.1016/S0025-5564(02)00108-6
[19]	C. Castillo-Chaves, H. R. Thieme, Asymptotically autonomous epidemic models, in Mathematical Population Dynamics: Analysis of Heterogeneity. Volume One, Theory of Epidemics, (1995), 33–50. Available from: https://www.researchgate.net/publication/221711274.
[20]	M. Y. Li, H. Smith, L. C. Wang, Global dynamics of an SEIR epidemic model with vertical transmission, SIAM J. Appl. Math., 62 (2001), 58–69. https://doi.org/10.1137/S0036139999359860 doi: 10.1137/S0036139999359860
[21]	N. Chitnis, J. M. Hyman, J. M. Cushing, Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model, Bull. Math. Biol., 70 (2008), 1272–1296. https://doi.org/10.1007/s11538-008-9299-0 doi: 10.1007/s11538-008-9299-0
[22]	Y. N. Sun, Analysis of Several Models on the Infectious Diseases with the Effect of Awareness (in Chinese), Master's thesis, North University of China, 2021. https://doi.org/10.27470/d.cnki.ghbgc.2021.001026
[23]	B. Tang, F. Xia, S. Y. Tang, N. L. Bragazzi, Q. Li, X. D. Sun, et al., The effectiveness of quarantine and isolation determine the trend of the COVID-19 epidemics in the final phase of the current outbreak in China, Int. J. Infect. Dis., 95 (2020), 288–293. https://doi.org/10.1016/j.ijid.2020.03.018 doi: 10.1016/j.ijid.2020.03.018
[24]	M. Mandal, S. Jana, S. K. Nandi, A. Khatua, S. Adak, T. K. Kar, A model based study on the dynamics of COVID-19: prediction and control, Chaos, Solitons Fractals, 136 (2020), 109889. https://doi.org/10.1016/j.chaos.2020.109889 doi: 10.1016/j.chaos.2020.109889
[25]	B. Tang, X. Wang, Q. Li, N. L. Bragazzi, S. Y. Tang, Y. N. Xiao, et al., Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions, J. Clin. Med., 9 (2020), 462. https://doi.org/10.3390/jcm9020462 doi: 10.3390/jcm9020462

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)