Optimal real-time power dispatch of power grid with wind energy forecasting under extreme weather

1.   Introduction

With the overexploitation of fossil energy and uncontrolled carbon emission by humans over the last half-century, the average temperature of the earth has gradually increased, leading to global warming. Extreme weather events associated with climate change, such as hurricanes, typhoons, floods and heat waves, have affected people's lives. At the same time, they also affect and harm the operation and corresponding control of the power system, like generation, transmission and distribution ^[1]. Thanks to advances in the power electronics industry, the stability of new energy generation ^[2] and the ability to rapidly regulate power have improved. Consequently, more and more wind turbines ^[3] and photovoltaics ^[4] are involved in the real-time power balance as the regulation resource. These new sources of energy can be rapidly regulating power by the advanced control systems. At the same time, the new energy generation can also be equipped with appropriate storage devices for excess power storage ^[5,6,7,8].

However, the power generation of these renewable resources poses significant challenges due to their intermittent, unstable and stochastic nature ^[9]. To be specific, the power output of the wind energy is hard to predict accurately, varies quickly in the small control time, and is determined by the weather. Furthermore, extreme weather might cause substantial disruption and damage to turbines, transmission lines and other infrastructure. High wind speeds can force turbines to shut down. Severe rain and hail can damage blades and other components. Furthermore, lightning strikes might result in power disruptions. Hurricanes, tornadoes and severe storms can all have a significant influence on wind power output. Although the engagement of wind energy is able to help reduce the peak load, carbon emission and the coal cost, the wind energy can be subject to a variety of instabilities that can lead to power outages, reduced stability of the system and even power system collapse. Considering the proposed factors, the independent system operators should carefully manage the power command distribution, improve the regulation capacity of the system energy, and utilize the optimal control strategy when integrating the wind energy into the real-time power dispatch.

Real-time power dispatch is a crucial task for ensuring the stability and reliability of power systems, especially with the increasing integration of new energy sources such as wind and solar power. Various techniques have been proposed and applied to solve this problem, such as interior point method ^[10], heuristics-based algorithm ^[11] and predictive-based method ^[12]. These methods are used to determine the optimal scheme of regulation resources' outputs and reach the power balance. However, due to the uncertainty and variability of new energy sources, conventional methods may face challenges in achieving high efficiency and robustness in real-time power dispatch. Therefore, some recent studies have explored novel approaches or advanced control strategies that can better cope with these challenges. Literature ^[13] developed a two objectives optimization framework-based frequency regulation for the optimal requirement of the independent system operators. In addition, a heuristic-based optimal algorithm combined with an ideal point-based decision-making method was designed to effectively and efficiently obtain the Pareto set of the real-time dispatch and select an optimum dispatch scheme for the high penetration of the new energy. Furthermore, for the high utilization of the photovoltaics (PV) energy, ^[14] constructed a two-layer optimal model. To be specific, a swarm reinforcement learning ^[15] was employed to solve the maximum power point ^[16] tracking-based PV array configuration ^[17]. Besides, an interior point was employed to quickly acquire the optimal power dispatch after the previous reconstruction scheme selection. Finally, a reinforcement learning-based method in ^[18] was employed to solve the curse of dimension for the dispatch with the participation of new energy resources.

For wind energy participation, it is important not only to develop optimal strategies to coordinate regulation resources, but also to evaluate power fluctuations in wind energy due to weather changes with more accurate control. There are many references that utilize the effective forecasting method to analyze the extreme weather's influence on the generation of wind energy and the stability of the power system. Literature ^[19] implemented a machine learning-based forecasting method that analyzed the historical series of wind energy using three approaches: gated recurrent unit (GRU), long short-term memory (LSTM) and recurrent neural network (RNN). Through the statistical experiments, this reference compared three machine learning approaches, and the gate reference unit performed best than the long short-term memory and recurrent neural network. The prediction-based method is more suitable for extracting extremely nonlinear and complex data from the input data set in real-time, improving the power system's ability to sense wind energy data, reducing the risk of the system and improving the efficiency of power system operation. In another study ^[20], a wind energy forecasting model based on the wind speed data was conducted to analyze the power output change. Additionally, five machine learning techniques were designed to solve the forecasting process and analyze their performances. In the simulation result, the random forest based method performed best. Literature ^[21] formulated an improved weather research and forecasting model. Besides, a genetic algorithm was employed to execute the optimization of the forecasting model, and a random forest model was trained to select the important parameters of error minimization for the independent system operators. Finally, in literature ^[22], a novel convolution-based LSTM was proposed to extract the spatial and temporal features of the wind power and daily wind speed. Additionally, a support vector machine was combined to process the output of the network and executed the classified task for wind energy.

In addition to forecasting wind power generation, another important aspect of wind energy participation is to develop effective control strategies for coordinating regulation resources and optimizing power dispatch. Some studies have proposed novel methods that combine forecasting techniques and optimization algorithms to achieve this goal. Study ^[23] presented a predictive control framework-based automatic generation control dispatch for the maximum profit of the generating company. Meanwhile, this study effectively evaluated the regulation command at the future time control interval through the adaptive factor-based smoothing spline for the co-optimization between multiple control intervals. In literature ^[24], a transfer learning-based power dispatch scheme forecasting framework for the low economic requirement and high regulation performance. In this reference, an artificial neural network was designed to learn and transfer the optimal knowledge, and a fast interior point method was used to remove the predictive scheme from the infeasible zone to the feasible zone. These studies demonstrated that integrating forecasting methods and optimization techniques could improve the efficiency and reliability of a power system.

In this paper, the problem of optimal power dispatch for wind energy participation under extreme weather conditions is considered. Unlike previous studies that focused on either wind power forecasting or power dispatch optimization separately, a novel integrated model that combines both aspects to achieve higher efficiency and reliability is proposed. The power dispatch model based on wind energy forecasting (PD-WEF) consists of two components: a wind power forecasting component and a power dispatch optimization component. For the wind power forecasting component, literature ^[25] propose an autoregressive integrated moving average model (ARIMA) ^[26] with a power limiter to improve the prediction of the stochastic power output for a noisy wind farm. In ^[27], three models (traditional ARIMA, wavelet-ARIMA and artificial network) are compared for this task. The results show that the artificial network has the best performance, but it requires more historical data and training time than the other models. For power dispatch, the algorithm should optimize the power dispatch scheme to the dispatch units within 4s. Therefore, a fast and simple ARIMA model is used to predict the next time interval's power command for the optimization. Meanwhile, for the power dispatch optimization component, a weighted mean of vectors (INFO) algorithm ^[28] based on two-control interval optimization is designed to optimally allocate the power of the regulation resources in extreme weather. INFO is a heuristic-based algorithm that balances exploration and exploitation in a weighted mean manner to optimize complex problems more accurately and rapidly. INFO has three main steps: updating policy, combination of vectors and improved local search. These steps are based on a novel weighted mean rule using a wavelet function, which can enhance the convergence speed and optimal performance of the algorithm. The following are the main contribution of this work:

1) Compared with previous work, this work presents a two time-control intervals model for PD-WEF. It includes the historical weather experience learning, current time-control interval power scheme optimal and future time-control interval prediction.

2) The ARIMA is employed to learn the historical weather series and predict the next power output of the wind energy at the next time-control interval when suffering weather change. The ARIMA can quickly obtain the forecasting power output of the wind energy for the current optimal operation.

3) The INFO algorithm is employed to rapidly obtain the power dispatch scheme by considering the power deviation between the power input and output of the regulation resource at the current time-control interval and the next time-control interval. The proposed two-control interval optimization with ARIMA can help improve the search ability of the algorithm and the control performance of PD-WEF.

The rest of this work is organized as follows. Section 2 describes the mathematical model of two-control interval optimization for PD-WEF. Section 3 describes the specific implementation of ARIMA-INFO algorithm for PD-WEF. Section 4 performs the simulation experiments and discusses the experimental results. Finally, Section 5 concludes the work.

2.   Mathematical model of PD-WEF

2.1.   Influence of extreme weather on power generation

The energy industry is constantly evolving and new sources of energy are being developed to meet the demand for clean, reliable and cost-effective energy. One of the newest developments in the energy industry is the development of renewable energy sources such as wind, solar and geothermal. These sources of energy are becoming increasingly popular due to their environmental benefits and potential for cost savings. Additionally, these sources of energy are becoming more efficient and cost-effective due to advances in technology. As new sources of energy continue to be developed and refined, they will become more viable options for businesses and consumers.

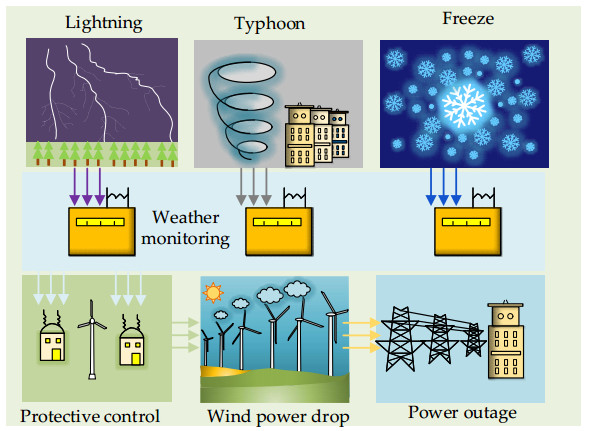
The extreme weather includes heat, cold and wind. The high temperatures can reduce the efficiency of the power system and cause power outages due to the increased demand and the equipment failure. In cold weather, Pipes will freeze and equipment might fail, leading to power outages. Strong winds can cause damage to power lines and other equipment. These influences may cause a variety of problems such as voltage instability, frequency instability and harmonic instability. In this work, the influence of extreme weather on the wind turbine and the impact on the system frequency stability will be analyzed. The following Figure 1 show the influence of extreme weather on wind power generation. If the power of wind turbines can be controlled and collected well, the wind turbines can help reduce the peak load of the power system. While extreme weather events can have a significant effect on the control policy and regulation performance of the wind turbine. In typhoon weather, excessive wind speed may cause displacement of the bearing seat inside or the breakage of the blades. Lighting can cause damage to power lines and other equipment, resulting in outages. When the low temperature or the freeze weather occurs, the blade of the turbine will freeze and the performance of the power regulation will be sharply reduced.

Figure 1.  Influence of extreme weather on wind power generation.

DownLoad: Full-Size Img PowerPoint

2.2.   PD-WEF framework

In this paper, the power outage of wind turbines under extreme is seen as a power disturbance. The other regulation resources (coal-fire, hydro unit, liquefied natural gas (LNG) and photovoltaic (PV)) are employed to balance the load disturbance and the wind power outage disturbance. The control policy and optimal framework of PD-WEF are given in the following Figure 2. The disturbances include the extreme weather influences, load disturbances and other disturbances. It should be noted that the power fluctuations of wind energy and solar power are considered in other disturbances. The influence of extreme weather on solar power is neglected in PD-WEF. When the power system is subjected to the extreme weather, the protective control of the wind turbine will be responded and the power output of the turbine will be dropped. Then, the system should allocate more active power to balance the load disturbance and wind power drop. The controller will collect the tie-line power mismatch and the area frequency deviation, then send the power command to the dispatch center. The algorithm will be employed to distribute the command to each regulation resource. Lastly, the system will continue to execute the above step until the load disturbance is balanced.

Figure 2.  Framework of PD-WEF.

DownLoad: Full-Size Img PowerPoint

2.3.   Constraints

In PD-WEF, to meet the demand of the power generation side and load side, the constraints and objectives should be formulated. The power regulation direction constraint, power balance constraint, regulation capacity constraint and regulation ramp constraint ^[29] should be considered in PD-WEF. The introduced power regulation direction constraint can help reduce the power regulation pressure and power command fluctuation. The power balance constraint can keep the power generation of regulation resource coordinated with the real-time power command. The regulation capacity constraint is the safe range of the regulation resource. Meanwhile, the generation ramp constraint (GRC) defines the power regulation capacity of the regulation resource in one time-control interval. During the power dispatch procedure, these constraints can be formulated as follow:

where $\Delta {P}_{i}^{\mathrm{i}\mathrm{n}}\left(k\right)$ is the power regulation command received by the ith PD-WEF regulation resource at the kth time-control interval and $\Delta {P}_{\mathrm{C}}\left(k\right)$ denotes the total regulation power command generated by the PI controller. ${P}_{i}^{\mathrm{m}\mathrm{i}\mathrm{n}}\left(k\right)$ and ${P}_{i}^{\mathrm{m}\mathrm{a}\mathrm{x}}\left(k\right)$ represent the minimum and maximum of the ith PD-WEF regulation resource at the kth time-control interval. $\Delta {P}_{i}^{\mathrm{o}\mathrm{u}\mathrm{t}}\left(k\right)$ denotes the real power output generated by the ith PD-WEF regulation resource at kth time-control interval, $\Delta T$ represents the optimal time at one time-control interval and $\Delta {R}_{i}$ is the maximum regulation ramp rate of the ith PD-WEF regulation resource.

The following Figure 3 shows the different types of power units with different constraints. The conventional units like coal-fire, hydro unit and LNG have GRC in the dynamic process, while the renewable units with fast regulation of control have no GRC in the dynamic process.

Figure 3.  Dynamic response models of power units. (a) Conventional units. (b) Renewable units.

DownLoad: Full-Size Img PowerPoint

2.4.   Objective function

This paper mainly focuses on the wind power outage when the system is subjected to extreme weather and the real-time power dispatch. After the wind power outage and power command prediction, one potential optimal objective is to reduce the power deviation between the power command and real-time power output generated by regulation resources. The objective optimization with one time-control intervals for the real-time power command can be given as follow:

The objective optimization with two time-control intervals for the real-time power command and prediction power command is considered in this work. This can be given as follow:

where $\Delta \overline{{P}_{\mathrm{C}}}\left(k+1\right)$ is the predicted power regulation command at the ($k+1$)th time-control interval obtained by the predictive method and $\Delta {M}_{i}^{\mathrm{o}\mathrm{u}\mathrm{t}}(k+1)$ is the optimal power scheme at the ($k+1$)th time-control interval computed by the optimal algorithm, ${N}_{\mathrm{S}}$ is the total time control intervals of the system in one service period.

3.   Design of ARIMA-INFO for PD-WEF

3.1.   Framework of two time-control intervals optimization

In Figure 4, the weather influence prediction, optimal operation and dispatch scheme assessment are all included in the PD-WEF. The power command and wind power outage at the subsequent time-control period will be anticipated for the current optimization in the weather impact prediction process. By minimizing the power deviation between the power input command and output command at the two time-control intervals, the INFO will be used to quickly and optimally get the real-time power dispatch scheme. In the forecast procedure, the historical series of power commands and current weather are collected and the ARIMA approach is introduced to forecast the next time power command and wind power drop. The optimal processes of INFO are consisted of updating policy, combination of vectors and improved local search. The power commands received by all regulation resources at the current and future time-control interval will be seen as the optimal variables. Particularly, the optimal power scheme will be the current optimal variables, while the power scheme at the next time-control interval just used to require a higher quality scheme with consistent power deviation.

Figure 4.  Framework of two time-control intervals optimization.

DownLoad: Full-Size Img PowerPoint

3.2.   Design of ARIMA

Most conventional methods only consider how the power is distributed for the current interval and do not consider the effect of the next control interval with the influence of extreme weather. This can lead to sub-optimal dynamic results and insufficient capacity margin. To ensure consistency for the next control interval, it is important to estimate the total power demand for that interval based on previous data. $\mathrm{A}\mathrm{R}\mathrm{I}\mathrm{M}\mathrm{A}(p, D, q)$ ^[26] represents the series is differenced D times, p is the series lag operator and q is the series difference lag operator. The total regulation command at time interval k can be given as follow:

where ${y}_{k}$ is the predicted total power command at the ($k+1$)th control interval, ${\varepsilon }_{k}$ represents the series difference at kth time interval, ${x}_{k}$ is historic series at kth time interval, ${\alpha }_{i}$ and ${\beta }_{i}$ are the corresponding coefficient lag and the corresponding coefficient difference lag of i-order series.

3.3.   Design of INFO

The INFO is a weighted mean-based optimal algorithm. The implementation of INFO includes many random parameters and wavelet functions. It is consisted of five operations, as follows:

1) Parameters and population initialization: Initialize the vector size or the population size ${N}_{\mathrm{P}}$, maximum number of optimal iterations ${N}_{\mathrm{T}}$. Then the initial solution set ${X}_{0}\in {R}^{{N}_{\mathrm{P}}\times 2(n-1)}$, the initial fitness value set ${F}_{0}^{i} = f\left({X}_{0}^{i}\right)(i = \mathrm{1, 2}, ..2n-2)$ are given by the random initialization of the regulation resources power. The number of the optimal variables can be seen as the number of regulation resources removed one of the power balance resources in Eq (1). Lastly, according to the sorting principle, the best, better and worst of the solution set and fitness value set are decided by the initial fitness value and solution set. The most important step is population initialization, it can be given as follows:

where $\Delta \overline{{P}_{\mathrm{C}}}\left(k+1\right)$ represents the predictive power command obtained by the predictive method at the kth time control interval, ${randp}_{i}\in {R}^{1\times n}(\sum _{j = 1}^{n}{randp}_{i}\left(j\right) = 1)$ is a random vector with n dimension, which represents the proportional of the ith regulation resource for the total power command.

For the fitness calculation step, the constraints of the balance regulation resource should be validated. Therefore, the constraints penalty term of the balance resource for fitness calculation should be added as follow:

where $f\left({X}_{i}\right)$ represents the real objective value of the jth population, $F\left({X}_{j}\right)$ represents the calculation value of fitness function for the jth population.

2) Updating policy: First, the updating of the rule stage mainly initializes two random parameters and an exploration function value, as follows:

where ${randc}_{1}$ and ${randc}_{2}$ are two random numbers from 0 to 1, $\delta$ represents the scale rate for the wavelet function, the parameter $\sigma$ is the weighted mean factor and used to regulate the position to the weighted mean of vectors, $g$ is the current iteration of the optimal operation and $\alpha$ is an intermediate parameter.

3) Vector combination: The vector combination is to combine the previous vectors ${z1}_{i}^{g}$ and ${z2}_{i}^{g}$ for the updating of the solution. To improve the search solution quality, a new vector will be generated, as follows:

where ${u}_{i}^{g}$ is the generated vector in the combination process, and $\mu$ is a random number in the range of [0, 0.05].

4) Local search: To improve the exploitation and exploration ability of the proposed method, the combination vector will be updated according to some random operations, as follows:

where $\phi$ and p are the random number in the range of (0, 1).

5) Vector updating: After the proposed (2)–(4) procedure, a new vector ${u}_{i}^{g}$ considering the best, worse and weighted mean rule is created for the new vector updating. Although the new vector considers the above factor, the constraint validation should be included in the optimal iteration, as follow:

Then, the updating rule is executed by the comparison of new vector fitness and current fitness, as follows:

Lastly, until all the vectors in the current iteration are updated, the best, better and worst vector will be updated for the vector optimal updating at the next iteration.

6) Repeat iteration: After a series of iteration processes from (2)–(5), the fitness function value of the best solution will be decreased. Additionally, the optimal process will be terminated when the current iteration goes beyond the maximum iteration. On the basis of the proposed optimal techniques, the optimum of the power dispatch scheme will be obtained. Furthermore, it will be employed for the power scheme evaluation.

3.4.   Calculation flow

The whole optimal process of ARIMA-INFO for PD-WEF is presented in the following Table 1.

Table 1.  The execution process of ARIMA-INFO for PD-WEF.

1: The PD-WEF is subjected to wind power drop or stochastic load disturbance

2: Initialize the system parameters (regulation resources constraints in Eq (1)); 3: FOR1 k:=1 to Ns 4: Input the current power command, weather, constraints and the historical series; 5: Forecast the influence of weather and power command through ARIMA by Eq (4); 6: Initialize the INFO parameters and the population in Eqs (6) and (7); 7: Calculate the initial the best, better and worse fitness function in Eq (8); 8: FOR2 g:=1 to ${N}_{T}$ 9: FOR3 i:=1 to Np 10: Select three random vectors for the weighted mean rule updating; 11: Execute the updating rule by Eqs (9)–(11); 12: Execute the vector combination by Eq (12); 13: Execute the local search by Eqs (13)–(16); 14: If the new solution disobeys Eq (1) 15: Initialize the positions by Eq (17) according to the power capacity; 16: END 17: If $F\left({u}_{i}^{g}\right) > F\left({x}_{i}^{g}\right)$ 18: Execute the vector updating by Eq (18); 19: END 20: END 21: Update the best, better and worse fitness function and solution for the next iteration; 22: END 23: END FOR

---

 | Show Table

DownLoad: CSV

4.   Case studies

4.1.   Parameters settings

In the simulation test, a PD-WEF system with ten regulation resources is implemented for the simulation test in order to validate the effectiveness and efficiency of the INFO. The parameters of the PD-WEF system implemented with four different types of regulation resources ^[13] are shown in below Table 2. Table 3 shows the transfer function of the regulatory resources ^[13]. Additionally, the total time control interval in one service period ${N}_{\mathrm{S}}$ is set to 225, and the time-control interval period T is set to 4 seconds (15 min).

Table 2.  Main Parameters of dispatch regulation resources in PD-WEF system.

Regulation resource No.	Type	Tr (s)	$\Delta {R}_{i}$ (MW/s)	${P}_{i}^{\mathrm{m}\mathrm{a}\mathrm{x}}$(MW)	${P}_{i}^{\mathrm{m}\mathrm{a}\mathrm{x}}$(MW)
G1	Coal-fired	55	0.5	40	−40
G2	Coal-fired	60	0.5	30	−30
G3	Coal-fired	50	0.5	25	−25
G4	LNG	15	0.3	30	−20
G5	LNG	20	0.3	20	−30
G6	LNG	20	0.3	15	−20
G7	Hydro	5	2.5	15	−15
G8	Hydro	5	2.5	10	−10
G9	PV	1	−	5	−10
G10	PV	1	−	10	−5

---

 | Show Table

DownLoad: CSV

Table 3.  Transfer functions of various regulation resources.

Regulation resource No.	Regulation resource type	Transfer function G(s)	Parameters (s)
G1-3	Reheat steam resource	$\frac{1+{T}_{1}s}{(1+{T}_{2}s)(1+{T}_{3}s)(1+{T}_{4}s)}$	T1 = 5, T2 = 0.1, T3 = 10, T4 = 0.3
G4-6			T1 = 0.08, T2 = 10, T3 = 5, T4 = 0.3
G7-8	Hydro resource	$\frac{(1-{T}_{5}s)(1+{T}_{7}s)}{(1+{T}_{6}s)(1+{T}_{8}s)}$	T5 = 1, T6 = 0.5, T7 = 5, T8 = 0.513
G9-10	Non-reheat steam resource, PV	$\frac{1}{1+{T}_{9}s}$	T9 = 0.01

---

 | Show Table

DownLoad: CSV

To select the parameters of INFO, the simulation for different parameter scenarios is conducted. Furthermore, following Figure 5 shows the optimal computation times and the fitness convergence value. It can see that the algorithm acquires an optimum at 50, and just less than 2s. Therefore, for the INFO parameters setting, the number of vectors and maximum iteration are both set to 30 in the statistic test, and both set to 50 in the dynamic test. Additionally, the traditional genetic algorithm (GA) ^[30] is employed to be the comparison algorithm in the test. Meanwhile, the parameters of population and maximum iteration are set the same as INFO for the fair of convergence and performance comparison. Meanwhile, for the two time-control intervals framework, the ARIMA parameters are set to (2, 1, 2). The Lag value is the first parameter, the different order is the second parameter, and the average move size is the last parameter. Two optimal frameworks with one time-control interval and two time-control intervals are given to analyze the combination of predictive method and optimal technique.

Figure 5.  Computation and convergence of INFO at different parameters scenarios. (a) Optimal computation times. (b) Fitness convergence value.

DownLoad: Full-Size Img PowerPoint

4.2.   Statistic test

4.2.1.   Convergence of one time-control interval optimization

In this test, two power commands (${\Delta P}_{\mathrm{C}} = -100\; \mathrm{M}\mathrm{W}$ and ${\Delta P}_{\mathrm{C}} = 100\; \mathrm{M}\mathrm{W}$) are conducted to validate the performance of the proposed algorithm. As shown in Figure 6, the proposed method can require a dispatch scheme with high-quality than GA. In the optimal process of Figure 6(a), the INFO gets the optimum at 14 iterations with a fitness value lower than 520, while the GA obtains the fitness value of about 570 at almost 30 iterations. This indicates that the proposed INFO can help decrease the power deviation between the total power command and the total power output for PD-WEF system. Besides, these two figures show that the proposed method has a better convergence and search ability than GA in the power dispatch optimization.

Figure 6.  Convergence of different algorithms for PD-WEF system at two disturbance scenarios. (a) ${\Delta P}_{\mathrm{C}} = 100\; \mathrm{M}\mathrm{W}$. (b) ${\Delta P}_{\mathrm{C}} = -100\; \mathrm{M}\mathrm{W}$.

DownLoad: Full-Size Img PowerPoint

4.2.2.   Convergence of two time-control intervals optimization

For the two time-control intervals, a power command series is conducted to analyze the convergence and performance of the algorithms. To present the performance of the two algorithms in the power tracking accuracy, the objective function can be revised according to the tracking accuracy, as follow:

The following Figure 7. shows the power command series and optimal process at three consistent time-control intervals. The power command series and predictive command are given in Figure 7(a), (c), (e). These three graphs show that the proposed ARIMA can acquire a predictive power command at the next control interval for the optimization. The Figure 7(b), (d), (f) give the optimal process of the two algorithms with 50 population (or vector) and 50 iterations. The fitness value is the opposite of tracking accuracy. The lower fitness value represents the higher tracking accuracy. It is noticeable that the proposed INFO can acquire the power scheme with higher tracking accuracy based on the forecasting power command of ARIMA. The introduced INFO has the competence of improving the power tracking accuracy, which is about one time higher than that of GA in the three consistent scenarios.

Figure 7.  PD-WEF system at consistent command scenarios based on two time-control intervals optimization. (a), (b) Power command series and convergence at the first time-control interval. (c), (d) Power command series and convergence at the second time-control interval. (e), (f) Power command series and convergence at the third time-control interval.

DownLoad: Full-Size Img PowerPoint

4.3.   Dynamic simulation test

4.3.1.   Load step disturbance with wind power drop

First, the power dispatch process of the two optimal methods and two optimal frameworks for PD-WEF system at ${\Delta P}_{\mathrm{D}} = 50\; \mathrm{M}\mathrm{W}$ and wind power drop ${\Delta P}_{\mathrm{W}\mathrm{G}} = 5\; \mathrm{M}\mathrm{W}$ is shown in Figure 8(a) and its data show that the optimum with a lower amplitude of regulation input command can be required by INFO. This demonstrates that the proposed INFO with two time-control intervals framework can acquire the optimal power scheme with a higher performance than the traditional GA technique or one time-control interval. The following Figure 8(b) shows the dynamic process of power command received by each regulation resource with the two control intervals framework-based INFO. Then, the following Figure 8(c) illustrates the proposed INFO's superiority in reducing the power tracking error between the power input command and real-time power output. At the same time, the real-time power deviation obtained by each algorithm is given in Figure 8(d). It shows that the proposed method can acquire a lower power deviation in the dynamic process of load disturbance or wind power drop. In Figure 8(e), (f), the proposed method can help decrease the peak value of area control error (ACE) and frequency deviation.

Figure 8.  PD-WEF system at dynamic load disturbance ${\Delta P}_{\mathrm{D}} = 50\; \mathrm{M}\mathrm{W}$ and wind power drop ${\Delta P}_{\mathrm{W}\mathrm{G}} = 5\; \mathrm{M}\mathrm{W}$ scenarios based on two time-control intervals optimization and one time-control interval optimization. (a). Load disturbance, wind power drop and real-time power input of different algorithms. (b) Power output of regulation resources obtained by INFO with two time-control intervals. (c) Total power disturbance. (d) Real-time power disturbance. (e) ACE. (f) Frequency deviation.

DownLoad: Full-Size Img PowerPoint

Likewise, the power dispatch process under a load step disturbance ${\Delta P}_{\mathrm{D}} = 50\; \mathrm{M}\mathrm{W}$ and a higher amplitude of wind power drop is illustrated in Figure 9(a). The power output of all ten regulation resources rose from zeros to a maximum value (shown in Figure 9(b)) during the specified optimal procedure produced by INFO. Additionally, the two control intervals framework-based INFO approach can acquire the power schemes with a lower power deviation than one control intervals framework-based method, as illustrated in Figure 9(c). This is partly because the added command of the next time control interval, as opposed to one control interval, is better able to coordinate the numerous regulation resources. As can be seen in the subsequent Figure 9(d), the proposed INFO can track dynamic power more accurately. Figure 9(e), (f) show that the proposed optimization framework and method can similarly help reduce the peak of ACE and frequency deviation.

Figure 9.  PD-WEF system at dynamic load disturbance ${\Delta P}_{\mathrm{D}} = 50\; \mathrm{M}\mathrm{W}$ and wind power drop ${\Delta P}_{\mathrm{W}\mathrm{G}} = 10\; \mathrm{M}\mathrm{W}$ scenarios based on two time-control intervals optimization and one time-control interval optimization. (a). Load disturbance, wind power drop and real-time power input of different algorithms. (b) Power output of regulation resources obtained by INFO with two time-control intervals. (c) Total power disturbance. (d) Real-time power disturbance. (e) ACE. (f) Frequency deviation.

DownLoad: Full-Size Img PowerPoint

Finally, a higher amplitude of wind power drop ${\Delta P}_{\mathrm{W}\mathrm{G}} = 15\; \mathrm{M}\mathrm{W}$ (illustrated in Figure 10(a)) is conducted analysis the influence of the wind power drop. The proposed method can acquire a lower total power deviation (shown in Figure 10(c)) and real-time power deviation (shown in Figure 10(d)). However, the two control intervals framework-based GA technique show the shortcoming in the optimal process when the system is subjected to a higher wind power drop. This means that the ARIMA-based INFO technique can have a good robustness than the GA approach when the system is exposed to more wind power declines. In Figure 10(e), (f), it can be seen that the smaller peak value of ACE and frequency deviation can be obtained by the proposed algorithm.

Figure 10.  PD-WEF system at dynamic load disturbance ${\Delta P}_{\mathrm{D}} = 50\; \mathrm{M}\mathrm{W}$ and wind power drop ${\Delta P}_{\mathrm{W}\mathrm{G}} = 15\; \mathrm{M}\mathrm{W}$ scenarios based on two time-control intervals optimization and one time-control interval optimization. (a). Load disturbance, wind power drop and real-time power input of different algorithms. (b) Power output of regulation resources obtained by INFO with two time-control intervals. (c) Total power disturbance. (d) Real-time power disturbance. (e) ACE. (f) Frequency deviation.

DownLoad: Full-Size Img PowerPoint

4.3.2.   Data analysis at different scenarios

Lastly, twelve load disturbances (−70 to −20MW and 20 to 70 MW) with three amplitude of wind power drop (5MW, 10MW and 15MW) developed to be performed to the PD-WEF system in order to further demonstrate the superiority of the suggested method. The optimal results of online optimization under various disturbance scenarios are given in Table 4. The indexes of the power deviation and tracking accuracy are conductive to exemplifying the high performance of INFO for PD-WF system. According to these statistics, the proposed ARIMA-based ANFO will perform better for the PD-WEF system. In all wind power drop optimization scenarios, the effect is better than other scenarios (except for the −40MW disturbance with 10MW wind power drop, −30MW disturbance with 15MW wind power drop and 20MW disturbance with 5MW wind power drop).

Table 4.  Results comparison of dynamic optimization under different disturbances scenarios.

$\Delta {P}_{\mathrm{D}}$ (MW)	$\Delta {P}_{\mathrm{W}\mathrm{G}}$ (MW)	One time-control interval framework				Two time-control intervals framework
		Power deviation (MW)		Accuracy (%)		Power deviation (MW)		Accuracy (%)
		GA	INFO	GA	INFO	GA	INFO	GA	INFO
−70	5	674.2	1281.9	60.0	57.4	559.8	316.9	61.2	62.8
	10	943.4	1830.7	59.1	55.1	720.8	373.3	60.3	62.5
	15	757.9	2651.6	59.8	52.6	758.2	414.6	60.4	62.2
−60	5	638.4	477.6	60.1	61.4	567.3	246.1	60.5	63.2
	10	798.1	1227.4	58.9	57.0	587.6	296.8	60.6	62.9
	15	674.6	928.1	59.7	59.1	688.2	347.1	60.1	62.4
−50	5	557.6	469.9	60.1	60.9	409.2	229.2	61.2	62.7
	10	534.9	505.2	60.1	60.7	535.5	222.4	60.3	63.0
	15	514.0	1103.5	60.3	57.2	604.2	272.6	60.1	62.6
−40	5	244.3	261.9	61.9	62.3	346.7	167.4	61.1	63.1
	10	438.2	182.7	60.3	62.9	464.9	201.2	59.8	62.9
	15	455.8	344.3	60.5	61.5	529.3	220.0	60.0	62.6
−30	5	306.3	157.5	60.7	62.3	272.0	127.0	60.9	63.0
	10	408.4	261.2	59.7	61.5	333.6	160.2	60.4	62.6
	15	281.2	160.4	61.3	62.7	465.9	187.4	59.6	62.5
−20	5	129.4	129.0	61.6	61.8	205.2	94.7	60.6	62.9
	10	151.0	151.6	61.7	61.8	296.3	117.3	59.7	62.7
	15	163.5	144.9	61.3	62.4	398.8	137.9	58.9	62.6
20	5	125.9	102.7	61.7	62.7	150.0	110.1	61.7	62.5
	10	158.0	149.7	61.2	61.9	193.7	145.4	61.0	62.0
	15	222.5	167.6	60.6	61.8	210.7	139.9	61.2	62.3
30	5	218.3	163.4	61.4	62.4	200.6	150.1	61.8	62.6
	10	217.4	194.2	61.5	62.2	221.1	161.2	61.7	62.8
	15	306.3	251.6	60.7	61.7	279.0	220.2	61.2	62.0
40	5	291.0	171.6	61.3	62.9	267.1	165.9	61.7	63.0
	10	306.1	247.6	61.3	62.0	302.7	201.5	61.4	62.7
	15	329.7	283.2	61.1	62.0	327.7	253.5	61.4	62.4
50	5	353.5	268.8	61.2	62.3	321.2	214.2	61.8	63.0
	10	382.3	323.6	61.2	61.9	377.3	284.3	61.4	62.3
	15	404.7	345.6	61.0	61.8	524.0	311.9	60.7	62.2
60	5	397.1	287.2	61.5	62.6	423.1	258.8	61.6	63.0
	10	456.8	332.9	61.1	62.1	512.1	314.9	61.1	62.6
	15	463.9	371.1	61.4	62.2	519.6	363.1	61.2	62.3
70	5	481.5	326.9	61.4	62.5	509.2	323.5	61.4	62.8
	10	523.3	422.7	61.3	62.0	582.3	382.6	61.1	62.2
	15	576.9	465.4	60.9	61.8	679.5	439.3	60.7	62.1

---

 | Show Table

DownLoad: CSV

Compared with GA, the average power deviation decrease at different load disturbance scenarios with ARIMA-INFO are 52.91, 57.60, 54.76, 45.76, 50.89, 21.61, 19.22, 28.39, 33.43, 29.33, 29.20 and 27.85%. Besides, the average accuracy increase with the ARIMA-INFO at different load disturbance scenarios are 4.64, 5.20, 4.20, 3.10, 3.42, 1.88, 1.72, 2.06, 2.34, 2.16, 2.09 and 1.90%. Without the ARIMA for two time-control intervals framework, the INFO shows a weakness in the decrease of power deviation than GA. With the introduction of ARIMA, the INFO improve the competent of power deviation reduction by about 50.00% and the accuracy increase by about 2.42%, while the GA decrease the competence of power deviation reduction about 2.99%. These demonstrate that the combination of ARIMA and INFO can effectively improve the control performance of PD-WEF system. Furthermore, the two time-control intervals framework is more suitable for INFO than GA algorithm.

5.   Conclusions

In conclusion, three contributions made in this paper are presented as follows:

1) The introduced ARIMA can effectively explore the feature of power command series and quickly acquire the power command at the next control interval for the power dispatch optimization.

2) The introduction of INFO can accelerate the convergence speed and improve the search ability compared with the traditional GA method when solving the PD-WEF with two time-control intervals framework or one time-control interval framework. It can coordinate the regulation resource and reduce the power tracking error. When the system is subjected to more wind power, the ARIMA-based INFO strategy can be more robust than the GA approach.

3) The conducted load disturbance dynamic tests with wind power drop show that the ARIMA-based INFO can effectively and efficiently acquire a high-quality power scheme for PD-WEF system. It can effectively increase the power tracking accuracy, decrease the power tracking error and improve the control performance of the PD-WEF system. Additionally, the ARIMA is more applicable for INFO than the GA algorithm.

Future study will construct the system deployed with more wind regulation resources and more regulation styles. Additionally, more predictive methods will be considered for the improvement of predictive accuracy. Furthermore, the combination of optimization and deep learning technique will be considered to increase power tracking accuracy.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors appreciatively acknowledge the support of the Science and Technology Project of Guangxi Power Grid (Grant No. 046000KK52220007).

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that might influence the work described in this paper.

Appendix

Different from the traditional operation that moves the current solution towards the global optimal solution or local optimal solution, the INFO used three random vectors to compute the weighted mean of vectors for the position updating of the current vector. The mean rule is formulated as follows:

where MR represents the mean rule value, ${X}_{\mathrm{a}}$, ${X}_{\mathrm{b}}$, and ${X}_{\mathrm{c}}$ represents three random vectors, $\varpi$ is the maximum fitness value of the three random vectors, ${X}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}$, ${X}_{\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{r}}$, and ${X}_{\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{e}}$ denotes the best vector, better vector, and worse vector at the current iteration, respectively, $WF1$ and $WF2$ represents the two wavelet functions, r is the random number in the range [0.1, 0.5], $w$ is the wavelet function values that help search the space globally.

Then the mean-based rule can be used to determine two regulate vectors for the following solution updating, as follow:

where randn and rand are the random numbers.