1.
Introduction
Optimization problems are prevalent in a wide range of disciplines and social life tasks, such as resource scheduling, task allocation, path planning, etc. The core idea is to choose the best possible solution from feasible solutions which satisfy the constraints to make the objective sought be as optimal as possible. Most of the engineering research fields need to solve optimization problems with multi-dimensional, complex and large computational loads. Optimization problems have been explored in the pursuit of optimal goals in the long term. To a certain extent, traditional optimization algorithms provide reliable solutions to optimization problems in various fields based on the precise mathematical characteristics of the optimization problem, and they are dedicated to using definite structures and parameters to give optimal solutions. However, for complex optimization problems with non-differential objective and constraint functions and multiple peaks, traditional optimization methods are often complicated to calculate or difficult to yield satisfactory solutions. Swarm intelligence (SI) is an intelligent computing technique, which has been very popular in recent years. The term "swarm intelligence" was introduced by Beni and Wang [1] in the context of cellular robotic systems; Brezočnik et al. [2] consider the advantages of SI to include 1) autonomy, where each agent of the swarm controls its own behavior autonomously, and 2) self-organization, where intelligence appears in the swarm itself, so SI is extremely flexible in solving problems. In actual situations, optimization problems are increasingly characterized by dynamic changes, nonlinearity, uncertainty and high latitude. To effectively solve complex optimization problems in reality, researchers have proposed SI-based optimization algorithms inspired by the behavior of animal groups, such as particle swarm optimization [3], the artificial bee colony algorithm [4], cuckoo search [5], ant colony optimization [6], etc.
The chimp optimization algorithm (ChOA) was proposed by Khishe and Mosavi [7] in 2020; it is a heuristic intelligent optimization algorithm based on the social behavior of chimp populations, and it originates from the simulation of individual chimp intelligence, sexual motivation and predatory behavior in nature; it constructs an effective optimization solution through the processes of driving, chasing, blocking and attacking. For various intelligent optimization algorithms, many improvement strategies have been proposed by numerous scholars. Feng and Song [8] improved the performance of the whale optimization algorithm in the global exploration and local search phases by introducing nonlinear time-variant adaptive weights, introduced a differential mutation perturbation factor in the encircling prey phase of the whale optimization algorithm to avoid premature convergence and improved the logarithmic spiral curve search path for individual whales to improve the algorithm's ability to traverse solutions. Shen et al. [9] adjusted the population diversity through an adaptive multi-scale control factor and designed an assisted swarm in implementing a local search to balance faster convergence and improved solution quality. Tang et al. [10] enhanced the population diversity through an elite ranking strategy, used a nonlinear energy factor adjustment strategy to balance the exploration and exploitation of the algorithm, and used a Gaussian random walk strategy to apply perturbations to the optimal individuals to effectively jump out of the local optimum. Zhang et al. [11] let the gulls choose spiral flight paths in different directions so that the gull flight paths are no longer single, which increased the algorithm diversity and avoided premature convergence of the algorithm by conducting a small search around the target according to the convergence of the algorithm. Deng et al. [12] used the Faure sequence to generate quasi-random numbers to initialize the population to improve the ChOA, approximated the uniform distribution with higher quality, improved the population search speed and solved the Kullback-Leibler problem of stochastic neighbor embedding with better results than the commonly used gradient descent method and stochastic gradient descent method. Xiao et al. [13] used the sine map to initialize the population and modify chaotic vectors to overcome the early convergence problem and applied it to test systems of four cascade reservoirs and three thermal plants with the valve point effect to demonstrate the improvements. Khishe et al. [14] developed weight-based location weighting equations to speed up convergence and improve exploration and exploitation. Mansoor et al. [15] used sine and cosine functions to search for the global optimal solution around the population generated by the ChOA, which was used to train the Fuzzy Neural Network (FNN) model to predict wind power generation for smart grid applications in the short term. Jia et al. [16] used highly destructive polynomial variants to further explore the regions and boundaries of the initial space, used Spearman's rank correlation coefficient to refine the candidate solutions in need of improvement and used the beetle antennae operator to avoid getting trapped in a local optimum to improve the ChOA, and they applied it to train a multilayer perceptron. Dhiman [17] used the sine and cosine functions and the attack strategy from the spotted hyena optimizer [18] to improve the ChOA and increase convergence efficiency. Chen et al. [19] introduced the bubble-net attacking method and the random search mechanism in the whale optimization algorithm [20] into the position updating process of the ChOA in order to improve the local search capability of the ChOA, and they demonstrated the effectiveness of this algorithm for structural damage detection through the validation of a two-story rigid frame model and a simply supported beam model. Kaur et al. [21] used the mathematical equations by a random walk in the cuckoo search algorithm [5] to update the position equations of the ChOA for the optimal design of digital infinite pulse filters. Zhang et al. [22] used Sobol sequences to initialize populations to improve search efficiency, and they used it to enhance the take-off performance of a cruise aircraft.
The motivation of this research is, compared with other intelligent optimization algorithms, to demonstrate that the ChOA has the advantages of no gradient mechanism, few control parameters, being a simple model, easy implementation and high stability, and that it has been successfully applied to various fields and achieved good effects. However, the ChOA is similar to other swarm intelligence optimization algorithms in that it suffers from low solution accuracy, slow convergence speed and the tendency to fall into the local optimum, which needs further improvement in order to achieve better results when applied to practical life. Although the above-mentioned scholars have achieved certain results in the improvement of the algorithm, there are still shortcomings in terms of knowing how to balance the convergence accuracy and convergence speed. Therefore, in order to improve the ChOA's performance and applicability in the optimum search, we propose a chaos somersault foraging ChOA (CSFChOA) on the basis of the ChOA. Simulation experiments were conducted on 23 standard test functions, as well as CEC2019 test functions, to find the best; and, statistical analysis with the Wilcoxon rank sum test was used to verify the superiority of the algorithm. Finally, the feasibility, applicability and superiority of the CSFChOA in practical engineering problems are demonstrated by comparing the test analysis on two complex engineering design problems. The following is a summary of this research's significant contributions.
a) To address the problems of low solution accuracy and slow convergence of the ChOA, the cat chaotic sequence is introduced to generate initial solutions, and opposition-based learning is used to select the better solutions to form the initial population, which can ensure diversity at the initial phase of the algorithm and improve the convergence speed and the accuracy of the algorithm to find the best solution.
b) In order to solve the problem of the ChOA easily falling into a local optimum at the later phase, by taking the optimal solution as the pivot, chimps with better adaptation at the mirror image position replace chimps from the original population using the somersault foraging strategy, which increases the population diversity and expands the search range.
c) The performance of the CSFChOA has been tested by using 23 standard test functions in low dimensions, 13 standard test functions in high dimensions and CEC2019 test functions to find the optimal solution; also, it is statistically analyzed using the Wilcoxon rank sum test and the optimization results are compared with the ChOA and other improved intelligent optimization algorithms.
d) Application of the CSFChOA to two complex engineering designs: the speed reducer design and the three-bar truss design have been tested and analyzed, and the feasibility, applicability and superiority of CSFChOA in practical engineering are verified.
The rest of the paper is organized as follows. After the introduction in Section 1, the CSFChOA is described in detail in Section 2, and a time complexity analysis is performed. Simulations and analysis are given in Section 3. The analysis of the engineering example applications of the CSFChOA is reported in Section 4. Finally, the full work is summarized and discussed in Section 5, which explains the direction of future work.
2.
Chaos somersault foraging chimp optimization algorithm
2.1. Description of CSFChOA
First, the CSFChOA uses cat mapping to generate uniformly distributed populations. Cat mapping features a simple structure, good traversal and is less likely to fall into small loops and unstable periodical points. It traverses all states in the search scope without repeating; a uniformly distributed population can be produced, which can guarantee the quality of the initial solutions and prevent some individuals from being far from the optimal solution due to the uneven distribution of the population; uneven distribution of the population may reduce the speed of the population search, the accuracy of the solution and the diversity of the algorithm. The cat mapping formula is defined as follows.
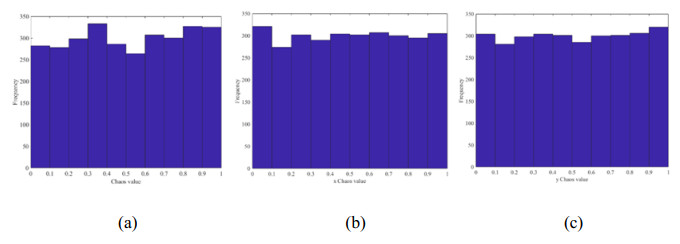
The rand function and cat mapping were used to generate 3000 numbers between [0, 1], as shown in Figure 1; Figure 1(a) shows the frequency histogram generated by the rand function. The cat mapping is a two-dimensional reversible chaotic mapping, and the two histograms in Figure 1(b), (c) are the frequency histograms of the x and y sequences. It can be seen that the cat mapping produces a uniform distribution of chaotic values between [0, 1], and the results are excellent, with the frequency of each unit interval being around 300 for both the x and y sequences. In contrast, the frequency of the rand function per unit interval is uneven, particularly in [0.3, 0.4], where the chaos values is nearly 90 more than in [0.5, 0.6], which is quite different. This shows that the cat mapping is better than the rand function in generating a uniformly distributed population.
In order to increase the speed of convergence of the population and to find the optimal solution faster, opposition-based learning is introduced. If we consider the opposite solution of each individual at the same time with a uniform distribution of the population, the probability of the current individual and the opposite individual being closer to the optimal solution is 50%. Selecting the closer individual as the initial population, i.e., the individuals with higher fitness, means that each individual in the population is one step closer to the optimal individual, which greatly accelerates the algorithm search efficiency and convergence speed.
The cat mapping and opposition-based learning strategy is viewed as a chaotic opposition-based learning strategy. Steps to initialize the population based on this strategy are as follows: first, generate N initial solutions xi using the cat chaotic sequence in the search space [ub, lb]; then, generate the corresponding opposite solutions for each initial solution in the following way.
where k is a random number between [0, 1]; xj is the opposite solution corresponding to each initial solution xi; xdmin and xdmax denote the minimum and maximum values of the dth dimension vector in all initial solutions, respectively. Finally, the initial solutions xi and the opposite solutions xj are combined and sorted in ascending order according to the fitness value, and the top N solutions with the best fitness value are selected as the initial population.
Next, the chimp hunting phase is divided into the exploration phase and the exploitation phase. The exploration phase includes driving, blocking and chasing the prey, and the exploitation phase includes attacking the prey. The population divides chimps into four different roles to perform the division of duties during the hunt, namely, attacker, barrier, driver and chaser, which are the optimal, sub-optimal, third-optimal and fourth-optimal solutions of the chimp group, respectively, with the latter three types of individuals assisting the attacker in the search for prey and other chimps' positions being guided by these four types of chimps for updates. The fitness value of each individual in the population is recalculated at each iteration and compared with the four best fitness values from the previous iteration; the four better individuals are selected as the leaders of the chimp population for this iteration. Each type of chimp has its own independent thinking capability and uses its own search strategy to explore and predict the location of the prey; meanwhile, they have their own individual tasks and will engage in chaotic individual hunting behavior in the final stages of the hunt because of the social motivation from the obtainable behavior and benefits. During the exploration phase, any chimp will change its position depending on the location of its prey, and the mathematical model for driving and chasing the prey is shown in Eqs (3)–(7).
where d is the distance between the chimp and the prey and t is the current number of iterations; xprey is the prey position vector; xchimp is the current chimp position vector; r1 and r2 are random vectors between [0, 1]; f is the convergence factor whose value decreases nonlinearly from 2.5 to 0 with increasing number of iterations (including the exploration phase and the exploitation phase); a is a random vector that determines the distance between the chimp and the prey, and its value is a random number between [-2f, 2f]; when |a| < 1, the position of the chimp tends to approach that of the prey xprey; when |a| > 1, it means that the chimp is forced to be away from the prey position and search for the prey in a wider scope; c is a coefficient that controls the chimp driving and chasing the prey, and it is a random vector in the range of [0, 2]; when c < 1, the impact of the prey position on the chimp position diminishes; otherwise, it increases. m is a chaotic vector calculated from various chaotic mappings, representing the impact of individual motivation on the chimp position during the hunting process.
The mathematical model of chimps attacking the prey during the exploitation phase is shown in Eqs (8)–(16).
where x denotes the position vector of the current chimp, xAttacker denotes the position vector of the attacker, xBarrier denotes the position vector of the barrier, xChaser denotes the position vector of the chaser, xDriver denotes the position vector of the driver, x(t + 1) denotes the updated position vector of the current chimp and c1, c2, c3 and c4 are all random vectors in the range of [0, 1]. It is assumed that the attacker, the driver, the barrier and the chaser have a better knowledge of the location of the potential prey. Thus, the four best solutions obtained so far are stored and other chimps update their position according to the best chimps' positions.
When individuals in the final phase are satisfied with food, the subsequent social motivation will make chimps unleash their natural instincts; individual chimps will attempt to get food in the forced chaotic situation. The chaotic behavior of chimps in the final phase helps to further alleviate the twin problems of local optimum traps and slow convergence when solving high-dimensional problems. The ChOA uses six chaotic mappings [7] of deterministic processes with random behavior. In order to simulate this social behavior, assuming a 50% probability of choosing either the normal update position mechanism or the chaotic model to update the chimps' position, the social stimulus behavior is mathematically modeled as shown in Eq (17).
where μ is a random number taking the value [0, 1] and Chaotic_value is a chaotic mapping used to update the position of the solution.
To avoid falling into the local optimum, inspired by the manta ray foraging optimization algorithm [23], which suddenly flips over to catch plankton, a somersault foraging strategy has been introduced to improve the ability of the ChOA to jump out of the local optimum. In this behavior, the position of the current optimal individual is considered as a pivot. Chimps other than the optimal individual tend to turn around the pivot and then somersault to the mirror image position of their current position. Thus, they always update their position around the best position they have found. The mathematical model is as follows.
where S represents the somersault factor, which determines the somersault range, taken as S = 2; xAttacker(t) is the position of the optimal individual; r1, r2 are two random numbers in the range of [0, 1].
Within the defined somersault range, each chimp has the possibility to move to any position in the new search domain located between the current position and the symmetric position around xAttacker(t). As the distance between a single location and the best location found so far decreases, all individuals gradually approach the optimal solution in the search space. Thus, as the number of iterations increases, the somersault search range adaptively decreases. In each iteration, the current chimp xchimp(t) is compared for fitness with the chimp in the mirror image position, and it is replaced by the chimp in the mirror image position if it has fallen into local optimum. At the same time, it also increases the population diversity for the next iteration and expands the search range. When the iteration is completed, the population has the optimal solution xAttacker in xchimp, which is the final result.
2.2. Implementation of CSFChOA
First, initialize the population through the chaotic opposition-based learning strategy, and then divide the chimps into four different roles to perform the division of duties during the hunt, namely, attacker, barrier, driver and chaser; the positions of other chimps are updated by these four chimp species for guidance. Individuals in the final stages of the hunt are satisfied with food, and subsequent social motivation leads chimps to unleash their natural instincts. Next, the ability of the ChOA to jump out of a local optimum is improved by the somersault foraging strategy. The steps of the CSFChOA implementation proposed in this paper are shown in Figure 2, with rand being a random number of [0, 1].
2.3. Time complexity analysis of CSFChOA
Time complexity is a key indicator to test the operational efficiency and convergence performance of the algorithm. To the ChOA, assuming that the population size is N, the dimension of the search space is d, the time required to initialize the parameters is t1 and the time to generate random numbers is t2, the time complexity of the population initialization phase is
In the iterative phase of the algorithm, the time to calculate the individual fitness value of the population is designed to be f(d), the time to compare the individual fitness values of the population and select the four optimal individual positions is t3, the time to update the convergence factor is t4 and the time to update the position of other chimps in the population to follow the four optimal individual positions is t5; then, the time complexity of this phase is
So, the total time complexity of the ChOA when finding the best solution is
The CSFChOA is derived from the ChOA, so the time to initialize parameters remains the same as the time required by the ChOA. Let the population initialization time to execute the chaotic opposition-based learning strategy be t6 and the time to execute the somersault foraging strategy be t7; then, the time complexity of the CSFChOA is
In summary, the time complexity of the CSFChOA is the same as that of the ChOA, and the improvement strategies proposed in this paper to address the shortcomings of the ChOA do not increase the time complexity.
3.
Simulation experiments and analysis results
3.1. Experimental design and test functions
The simulation environment was set to a 64-bit Windows 10 operating system; the CPU was an Intel(R) Core(TM) i7-10700 with a basic frequency of 2.90 GHz and memory of 16.0 GB; the programming software was MATLAB R2021b. To test the CSFChOA's search performance, 23 reference test functions were taken from the literature [7] to carry out simulation experiments. The expressions, search dimensions, variable boundaries and theoretical optimal values of the reference test functions are given in Table 1. Function denotes the function expression, D denotes the dimension of the problem, fmin is the theoretical optimal value of the function and Range denotes the boundary of the problem search space. F1–F7 are unimodal functions with relatively flat images and only a single extreme value point, mainly used to test the search accuracy and convergence speed of the algorithm. F5 is a Rosenbrock function, which is a single-module function when the dimension is 2 or 3. It has many local extreme value points in the high-dimensional case and belongs to the canyon-type function, which has a narrow and gently changing valley, and its global minimum value appears at the bottom of the valley. This test function is used to test the efficiency of the function search. F8–F13 are multimodal functions; F9 has a number of widely existing minima, and it is regularly distributed and has high requirements for the function to jump out of a local optimum. F14–F23 are fixed-dimension multimodal functions, which are used to test the algorithm's global search ability, local optimum avoidance ability and convergence speed.
3.2. Analysis of the impact of different improved strategies on algorithm performance in low dimensions
To fully validate the effectiveness and superiority of the CSFChOA, the ChOA [7], the ChOA using only the chaotic opposition-based learning strategy for population initialization (CChOA), the ChOA applying only the somersault foraging strategy (SFChOA), the enhanced whale optimization algorithm (EWOA) [8], the multi-scale sine cosine algorithm (MSCA) [9], the multi-directional exploring seagull optimization algorithm based on a chaotic map (MESOA) [11], the multi-strategy ChOA (EOSMICOA) [24] and the CSFChOA were compared through simulation experiments on 23 reference test functions with different optimum finding characteristics. In this research, the parameter values of these algorithms were selected according to the corresponding literature. The general conditions of algorithms were set to be the same: the population size N = 30, the spatial dimension d = 30, the maximum times of iterations tmax = 1000, and each algorithm was run 30 times independently. The performance of each algorithm was evaluated in terms of four performance metrics: the best value, the worst value, the mean value and the standard deviation. The simulation results of the eight algorithms for the 23 reference test functions are shown in Table 2.
As shown in Table 2, the CSFChOA can obtain theoretical optimum convergence when solving the unimodal functions F1–F4, multimodal functions F9, F11 and fixed-dimensional multimodal functions F16, F17, F18 with the standard deviation of 0 on F1–F4, F9, F10, F11. Regarding the mean value, for F1–F13, F15, F17, F18, F19 and F20, the CChOA and SFChOA yielded values smaller than that for the ChOA, which shows the effectiveness of using the chaotic opposition-based learning strategy and the somersault foraging strategy, respectively, both of which can improve the convergence accuracy of the ChOA to some extent. For F16, although the ChOA, CChOA and SFChOA can all converge to the theoretical optimum, the standard deviations of both the CChOA and SFChOA were smaller than the ChOA, which has better robustness. For F1–F4, F7, F9–F11, F13 and F19, the CSFChOA had the highest convergence accuracy compared with the other seven algorithms. For F16 and F18, although other algorithms could find the theoretical optimal solution, the CSFChOA had the smallest standard deviation and demonstrated better robustness. For F5, F8, F12 and F20, the convergence accuracy of the CSFChOA was stronger than that of the other six algorithms, except the EWOA. Although it is weaker than the EWOA, it is more stable. For F15, the CSFChOA was stronger than the other six algorithms, except MESOA. In terms of standard deviation, for F1–F4, F7, F9–F12, F16, F19, F21, F23, the CSFChOA had the smallest standard deviation and the highest stability compared with the other seven algorithms.
3.3. Convergence analysis
To more intuitively reflect the convergence performance of the CSFChOA, the average convergence curve graphs are used to describe the convergence characteristics of the eight algorithms used in Section 3.2 under the conditions of the population size N = 30, the spatial dimension d = 30, the maximum number of iterations tmax = 1000 and 30 times of independent runs of each algorithm. The average convergence curve comparison diagrams of solving the 23 reference test functions F1–F23 of all algorithms are given in Figure 3. In addition, the data for each algorithm run 30 times on each function is plotted as a box plot, which gives a direct indication of how well the different algorithms perform on each function in terms of search performance, as shown in Figure 4.
As can be seen in Figure 3, for F1–F5, F7–F11, F13, F15 and F19, the average convergence curves of the CSFChOA are all located below the ChOA, CChOA, EWOA, MSCA, MESOA and EOSMICOA; it indicates that the CSFChOA has obvious superiority in terms of exploration performance in the early iteration and exploitation performance in the late iteration, both of which are better than the other algorithms, with higher solution accuracy and faster convergence speed for the same times of iterations; it verifies that the CSFChOA can fully guarantee the exploration capability and exploration capability without losing the population diversity and the stability of the search for superiority. In particular, on F1–F4, F9, F11, F16–F18, the CSFChOA can effectively jump out of the local optimum and converge to the theoretical optimum quickly. For functions F5, F8, F10, F13, F18 and F19, although the CSFChOA falls into the local optimum like other algorithms, the optimization-seeking accuracy and the convergence speed of the CSFChOA are much better than those of other algorithms.
The CChOA is below the ChOA for the same times of iterations, which means that the CChOA converges faster than the ChOA. The initialization of the population with the chaotic opposition-based learning strategy can improve the initial population diversity and helps to improve the convergence speed and accuracy of the algorithm. Although this advantage is not obvious, it is more helpful for the introduction of other strategies to find the optimum later. The SFChOA converges significantly faster than the ChOA; it also has a significant improvement in convergence accuracy, and does not stall significantly throughout the iterations. This indicates that the somersault foraging strategy can effectively optimize the globally optimal chimp position, help the population to jump out of the local optimum and make the algorithm less likely to fall into the local optimum so that the theoretical optimal solution can be explored effectively. It can be seen that different improvement strategies have different degrees of improvement on the algorithm's optimality-seeking performance, and that the CSFChOA, which combines the two strategies, shows certain advantages.
As can be seen in Figure 4, for F1–F4, F7, F9–F11, the solution results of the CSFChOA were all around the theoretical optimum, which is both outlier-free and stable compared with the other seven algorithms. For F5, F12, F16, F18, F19, F21 and F23, the boxes of the CSFChOA are close to a line, which indicates high stability. It is very obvious in the figure that, for F5–F13, F15–F20, the convergence accuracies of the CChOA and SFChOA are higher than that of the ChOA, which further proves that using a chaotic opposition-based learning strategy and the somersault foraging strategy both have different degrees of improvement on the convergence ability of the ChOA. The mean value represented by the hollow square inside the box in the figure shows that, compared with the other seven algorithms, the convergence accuracy of the CSFChOA is higher for F5, and that, for F8, the convergence ability of the CSFChOA is only lower than that of the EWOA, but its box is flatter and more stable. For F12, F15, the CSFChOA outperforms the other seven algorithms in terms of box width, outliers and mean value.
The experimental results in Table 2, the average convergence curves in Figure 3 and box plot graphs in Figure 4 verify the effectiveness of the algorithm proposed in this research; its convergence speed is much faster than that of other algorithms, although the convergence accuracy gap is not obvious for some functions. The CSFChOA's solving accuracy is higher and more stable than other algorithms.
3.4. Analysis of the impact of different improvement strategies on algorithm performance in high dimensions
For analysis in this section, the population size N = 30, the spatial dimension d = 1000, the maximum number of iterations tmax = 1000 and each algorithm was run 30 times independently. The performance of each algorithm described in Section 3.2 were evaluated in terms of the best value, the worst value, the mean value and the standard deviation of the four performance metrics. The results of the eight algorithms for solving the F1–F13 functions from the 23 reference test functions are shown in Table 3.
Table 3 shows that the CSFChOA can find convergence to the theoretical optimum with the standard deviation of 0 for F1–F4 and multi-peak functions F9 and F11. Regarding the mean value, for F1–F8, F10, F12 and F13, the CChOA and SFChOA values were smaller than that from the ChOA, which proves that the improvement of the ChOA using chaotic opposition-based learning strategy and the somersault foraging strategy is still effective in high dimensions. For F1–F4, F7, F9 and F11, the CSFChOA had the highest convergence accuracy compared with the other seven algorithms. For the remaining functions, F5, F6, F8, F12 and F13, the CSFChOA had higher convergence accuracy than the other six algorithms, except EWOA. Although weaker than the EWOA, the standard deviation of the CSFChOA was smaller than the EWOA for all five functions, which is more stable than the EWOA. In terms of standard deviation, for F1–F4, F9–F11, the CSFChOA had the smallest standard deviation compared with the other seven algorithms. For F6, F12 and F13, the stability of the CSFChOA was only lower than the MESOA, but its convergence accuracy was higher than the MESOA. For F5, the stability of the CSFChOA was only weaker than the SFChOA and MESOA, but its convergence accuracy was higher than the SFChOA and MESOA. For F7, the stability of the CSFChOA was only weaker than the SFChOA, but its convergence accuracy was higher than that of the SFChOA.
In summary, the improved strategy proposed in this paper has strong performance and robustness in finding the best solution for low-dimensional and high-dimensional problems.
3.5. Wilcoxon rank-sum test
The Wilcoxon rank-sum test is a non-parametric statistical test to fully validate the effectiveness of the improved algorithm; it tested whether the CSFChOA is statistically different from the ChOA [7], arithmetic optimization algorithm (AOA) [25], the chaotic elite Harris hawks optimization algorithm (CEHHO) [10], the EWOA [8], the MSCA [9], the MESOA [11] and the EOSMICOA [24] based on 23 reference test functions at a significance level of p = 5%, 30 dimensions and 30 times of independent runs for each algorithm. In this research, the parameter values of these algorithms were selected according to the corresponding literature. When the p-value is less than 5%, if the H0 hypothesis is rejected, it indicates that there is a significant difference between the two compared algorithms; if the H0 hypothesis is accepted, it indicates that the two algorithms are about identical in terms of their performance in terms of finding the optimum. The p-values of the rank-sum test between the CSFChOA and the seven algorithms on the 23 reference test functions are shown in Table 4. A value marked "NaN" means that it is not applicable, i.e., no significance judgment can be made. The symbols "+", "-" and "=" indicate that the CSFChOA is better, worse or equal compared with the other algorithms, respectively. Most of the p-values were much less than 5%, which indicates that there is a statistical significant difference between the CSFChOA and the other seven algorithms in terms of the effectiveness of the search for the optimum; it verifies that the CSFChOA is significantly superior.
3.6. Experimental analysis of CEC2019 test functions
In order to verify the effectiveness and robustness of the CSFChOA, CEC2019 test functions were used to further verify the performance of the improved algorithm. There are 10 single-objective test functions in CEC2019, each with a theoretical optimum value of 1. These functions are challenging and can test the performance of the algorithm effectively. The introduction of CEC2019 test functions is shown in Table 5. The ChOA [7], AOA [25], CEHHO [10], EWOA [8], MSCA [9], MESOA [11] and EOSMICOA [24] have been compared. In this research, the parameter values of these algorithms were selected according to the corresponding literature. The experimental parameters were taken as the population size N = 30, the maximum times of iterations tmax = 1000, and each algorithm was run 30 times independently to take the worst value, the best value, mean value and standard deviation, as shown in Table 6.
From Table 6, we can see that, for F1, the CSFChOA is the algorithm which can find the theoretical optimum and has the best stability among all of the algorithms. For F2–F10, although the CSFChOA could not find the theoretical optimum like the other algorithms, the convergence accuracy is better than the standard ChOA. For F2–F4, F7, F10, F16–F18, the optimum value obtained by the CSFChOA is much closer to the theoretical optimum than the other seven algorithms. For F6, F8, the convergence ability of the CSFChOA was only worse than the MSCA, but more stable than the MSCA. For F4, F6, the standard deviation of the CSFChOA was lower than those of the other seven algorithms. For F1, F2, F3, F7, the stability of the CSFChOA was in the second place among all of the algorithms. In summary, the CSFChOA has good convergence accuracy and robustness when applied to the challenging CEC2019 test functions.
4.
Application analysis of CSFChOA on engineering examples
To further explore the superiority of the CSFChOA when handling practical engineering application cases, two types of nonlinear constrained optimization problems in engineering were selected: the speed reducer design and the three-bar truss design. The ChOA [7], AOA [25], CEHHO [10], EWOA [8], MSCA [9], MESOA [11] and EOSMICOA [24] were used to solve these two problems respectively. The parameter values of these algorithms were selected according to the corresponding literature. The experimental parameters were taken as the population size N = 30, the maximum times of iterations tmax = 1000, and each algorithm was run 30 times independently.
4.1. Speed reducer design
To a mechanical system, the speed reducer is one of the important components of the gear case, and it can be used for a variety of applications. Design of the speed reducer is optimized to minimize the weight of the speed reducer, which is associated with seven variables, i.e., the tooth width b, modulus of gear m, number of teeth on the pinion z, length of the first shaft between bearings l1, length of the second shaft between bearings l2, diameter of the first shaft d1 and diameter of the second shaft d2. The structure of the speed reducer is schematically shown in Figure 5. The specific mathematical model of the speed reducer is as follows.
Objective function:
Constraint conditions:
Variable range:
The solution results of the eight algorithms are shown in Table 7.
The comparison results in Table 7 show that the CSFChOA performs the best in terms of solving the complex optimization problem of the speed reducer design and can achieve the lowest weight; and, the overall optimization effect was much better than the other seven algorithms. The optimal cost was 64.03 lower than the ChOA, 93.31 lower than the AOA, 2636.45 lower than the CEHHO, 107.67 lower than the EWOA, 20.18 lower than the MSCA, 99,999,394.17 lower than the MESOA and 80.28 lower than the EOSMICOA. The performance of the CSFChOA was 100% better than that of the other algorithms. The comparison results verify the superior performance of the CSFChOA in terms of solving the speed reducer design.
4.2. Three-bar truss design
The three-bar truss design is a structural problem in the field of civil engineering; the objective is to minimize the volume of the truss under hydrostatic pressure while satisfying the stress (σ) constraint on each truss member. A schematic model of a three-bar truss is shown in Figure 6, where H is the height of the truss and P is the concentrated force. The variables for this problem are the optimum cross-sectional areas A1, A2, which is mathematically modeled as follows.
Objective function:
Constraint conditions:
Variable range:
The solution results of the eight algorithms are shown in Table 8.
The comparison results in Table 8 show that the CSFChOA performs the best in terms of solving the complex optimization problem of the three-bar truss design, and that it can achieve the minimum truss volume and the overall optimization effect much better than the other seven algorithms. The optimal cost was 0.0012 lower than the ChOA, 0.4920 lower than the AOA, 0.0001 lower than the CEHHO, 0.0005 lower than the EWOA, 0.0005 lower than the MSCA, 0.0004 lower than the MESOA and 19.1304 lower than the EOSMICOA. The performance of the CSFChOA was 6.77% better than that of the other algorithms. The comparison results verify the superior performance of the CSFChOA in terms of solving the three-bar truss design problem.
In summary, the testing of the above two well-known engineering constraint problems with different levels of complexity fully demonstrates the strong potential and superiority of the CSFChOA on handling different types of engineering optimization problems, and it demonstrates the robustness of the CSFChOA.
5.
Conclusions
To address the problems of slow convergence speed, low accuracy and susceptibility to local optimum traps of the ChOA, a hybrid improvement strategy, i.e., the CSFChOA has been proposed. By combining a chaos initialization method and opposition-based learning initialization strategy, the initial population is generated, which can ensure the diversity of the algorithm at the beginning, as well as improve the convergence speed and optimum searching accuracy. The somersault foraging strategy is used to maintain the population diversity and prevent homogeneity, which can improve ability of the algorithm to jump out of the local optimum. Regarding simulation, the optimization search tests were performed on 23 standard test functions and CEC2019 test functions, and the Wilcoxon rank-sum test was used for statistical analysis. The CSFChOA has been compared with the ChOA and other improved intelligent optimization algorithms. The experimental results show that the CSFChOA was demonstrated to be better than most of the other algorithms in terms of optimum search accuracy, convergence speed and robustness of global optimization in both low-dimensional and high-dimensional experiments. Good results were obtained from the application of the CSFChOA to two complex engineering problems, that is, the design of a three-bar truss and speed reducer; this verifies the feasibility, applicability and superiority of the CSFChOA in practical engineering applications, as well as provides a new idea for solving complex practical engineering problems. However, the CSFChOA has its limitations, like other optimization algorithms, and needs further improvement. It was found during experimental runs that the CSFChOA runs for a long time in high dimensions; we think that this can be solved by introducing a parallel strategy. The research on the human brain has become a hot spot in recent years, and numerous research results have been widely used in clinical diagnosis, artificial intelligence, brain computer interface, etc. After the collection of Electroencephalogram (EEG) signals, frequency components should be extracted, unnecessary components should be removed or noise should be eliminated; therefore, the filtering of EEG signals is very important. The design of the filters can be treated as an optimization problem; we need to find the optimal filter with the most proper specifications, and we are planning to apply the CSFChOA for the optimization of EEG filtering.
Acknowledgments
This work was partially supported by the Shaanxi Key Science and Technology Innovation Team Project (No. 2022TD-26), the Science and Technology Plan of Xi'an city (No. 22GXFW0020), Shaanxi Science and Technology Plan Project (No. 2023YBGY158) and the Fundamental Research Fund for the Central Universities (No. GK202101004).
Conflict of interest
The authors declare that there is no conflict of interest.









 DownLoad:
DownLoad:








