On the variable inverse sum deg index

1.   Introduction

Multi-label learning, specifically used to classify instances that simultaneously relate to multiple class labels, is a popular machine learning paradigm. In real life, an object with multiple labels is common. For instance, a photograph may simultaneously picture mountains, snow, clouds, and the sky, a news article may involve several different topics, and a piece of music may express many emotions. In recent years, multi-label learning was turned into a hotspot in the field of machine learning ^[1]; meanwhile, this technique has also been widely used to retrieve images ^[2,3], classify text ^[4,5], predict drug-induced pathology in multi-organ systems ^[6], study proteins subcellular localization ^[7,8], recognize protein functions ^[9], and construct recommendation systems ^[10].

Many algorithms have been proposed to classify multi-label data; these could be roughly divided into two different groups: problem transformation and algorithm adaption. The former transforms the multi-label learning task into one or more single-label learning tasks ^[11] or label-ranking (LR) tasks ^[12]. Algorithm adaption aims to adapt traditional machine learning algorithms to directly handle multi-label data ^[13,14].

Alternatively, researchers may consider the order of correlations among labels to categorize algorithms, dividing all multi-label learning algorithms into three groups: first-order approaches, which treat each label independently ^[15], second-order methods, which take advantage of pairwise relations between labels to address multi-label learning issues ^[12], and high-order algorithms, which utilize high-order relations among labels to classify multi-label data ^[16,17]. In comparison to first- and second-order approaches, high-order methods can generally yield a better performance, as most real-world applications have high-order relations among their labels ^[1]. The classifier chains (CC) ^[16] and random k-labelsets (RAkEL) ^[17] algorithms are two of the most popular high-order multi-label learning algorithms. The former gradually adds labels into a feature space to train the binary classifier into predicting the next label; the RAkEL randomly divides the label space into multiple k-label subspaces, transforming each to be a multi-class learning task based on the combination of these k-labels. Then, it trains a multi-class classifier on each multi-class task. Specifically, the RAkEL effectively addresses two problems simultaneously: the excessive number of classes being transformed by the label powerset (LP) method, and sparse instances for each class. However, due to the RAkEL always randomly selecting k-label sets, it cannot be guaranteed to focus on the boundaries between labels.

In addition to label correlation, imbalanced data distribution is also an intrinsic characteristic of multi-label data ^[18]. In general, for any one specific label, there are more instances correlated with it than those that are not. For example, in the Google image repository, the number of images containing the mountains label is certainly much lower than the number of images excluding that label. Such an imbalanced class distribution tends to make those traditional multi-label learning models ineffective in recognizing real active labels in a test instance. Therefore, it is necessary to focus on this issue when a multi-label learning algorithm is designed. In single-label learning, there are several techniques dealing with this class imbalance problem, including resampling ^{[19,20,21,22]}, cost-sensitive learning ^[23,24,25], decision output compensation ^[26,27], and ensemble learning ^{[28,29,30,31,32,33]}. However, these single-label class imbalance learning algorithms cannot be directly used on multi-label data due to the existence of complex label correlations. Some recent studies focused on this problem and provided several solutions by borrowing the idea of single-label class imbalance learning techniques, including ML-RUS ^[34], ML-ROS ^[34], ML-SMOTE ^[35], COCOA ^[36], ECCRU ^[37], and LDAML-IMB ^[38]. We note that these emerging multi-label imbalance learning algorithms either fail to properly take advantage of label correlations or require very-high time complexity.

In this study, we propose an improved RAkEL algorithm, called compensation-based correlated k-labelsets (CCkEL), which simultaneously amends the flaw of RAkEL and considers how to address the class imbalance problem. Specifically, the CCkEL first adopts the Jaccard coefficient ^[39] as a similarity metric to find the k-1 strongest correlated labels with each label existing in a label space to create the corresponding k labelset. This replaces the random strategy used by RakEL; by selecting correlated labels, it forces the learning model to pay more attention to the boundary details among k strongly correlated labels. Then, the CCkEL transforms each k-label learning task into a multi-class learning task, in which each class represents a unique label combination. Next, considering that the transformed multi-class datasets might be very skewed, a rapid decision output compensation strategy is designed to enhance the predicted accuracy of active labels during the final decision. The performance of the proposed CCkEL is compared here with several popular multi-label imbalance learning algorithms on 10 benchmark multi-label datasets, and the results show that the proposed CCkEL has excellent classification performance and low time complexity, indicating its effectiveness and superiority.

The key contributions of this study are as follows:

1) A correlated label-selection strategy relying on the Jaccard coefficient is proposed to replace the random label-selection strategy used by the RAkEL algorithm, which makes the learning model focus more on the boundary details among correlated labels;

2) To address the class imbalance issue in the decoded multi-label decision space, a fast decision output compensation strategy relying on the imbalance ratio of labels is designed. It can simultaneously improve the adaption of the learning model to imbalanced data distribution and save running time.

3) A novel multi-label imbalance learning algorithm named CCkEL is presented. Experimental results show that the CCkEL algorithm acquires the lowest average rank in terms of F-micro, HammingLoss, and SubsetAccuracy metrics among all compared algorithms. Meanwhile, it has a moderate running time consumption, which is a little higher than simple baseline algorithms but clearly lower than several other state-of-the-art imbalance multi-label learning algorithms.

The remainder of this paper is organized as follows. Section 2 describes the class imbalance problem in multi-label data, reviews the related work about multi-label imbalance learning algorithms, and illustrates the limitations of the RAkEL algorithm. Section 3 presents the details of the proposed CCkEL algorithm. In Section 4, the experimental results and analysis are presented in detail. Finally, Section 5 concludes the findings of this study.

2.   Problem description and related work

2.1.   Problem description

A multi-label dataset can be represented as $D = \left\{\right({x}_{i}, {y}_{i}\left)\right|1\le i\le N\}$, where N denotes the number of instances, ${x}_{i}\in X$ indicates the feature vector of the ith instance, and ${y}_{i}\subseteq Y = {\{0, 1\}}^{q}$ represents the q-dimensional label vector corresponding to the ith instance. Derived by the multi-label dataset $D$, a multi-label learning model can be induced aiming to $f:X\mapsto Y$, i.e., constructing a mapping between the feature space $X$ and the label space $\text{Y}$.

As indicated in ^[18], for any one label ${l}_{i}$, the number of instances correlated (active) with that label always tends to be lower than the number of instances that are not correlated (inactive) with it. Therefore, each binary classification task corresponding to an independent label existing in the label space is always imbalanced. Here, we use $\left|{D}_{i}^{+}\right|$ and $\left|{D}_{i}^{-}\right|$ to denote the number of active and inactive instances corresponding to the label ${l}_{i}$, respectively. Obviously, we have $\left|{D}_{i}^{+}\right|+\left|{D}_{i}^{-}\right| = N$. Then, several quantized metrics ^[34] to describe the class imbalance level of a multi-label dataset are drawn as follows:

It is clear that the metrics Card, Dens, and MeanIR reflect the imbalance level of the whole multi-label dataset, while ${\mathrm{I}\mathrm{R}}_{i}$ only denotes the imbalance level of the ith label. The smaller Card and Den and the larger $\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{I}\mathrm{R}$ are, the higher is the class imbalance level.

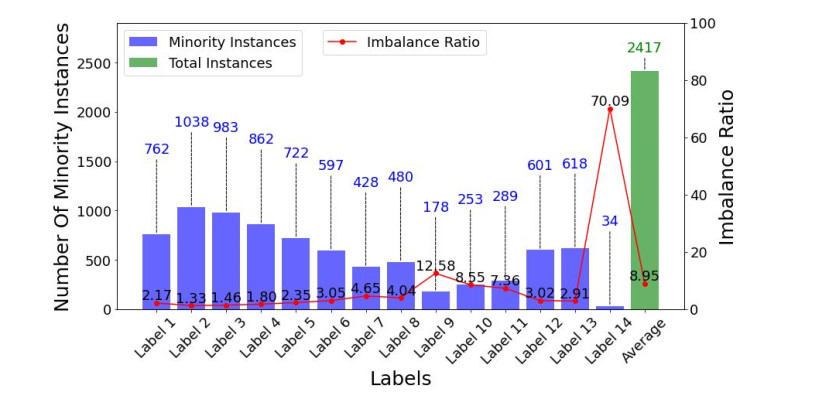
Taking the Yeast dataset as an example, we counted the active instances on each label and further calculated the corresponding ${\mathrm{I}\mathrm{R}}_{i}$ and $\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{I}\mathrm{R}$ (Figure 1). It is noteworthy that, to some extent, there is a class imbalance problem on each class label. Specifically, Label 2 has the lowest IR (1.33), while Label 14 presents the highest IR (70.09); the MeanIR reaches 8.95, indicating that the class imbalance is a non-negligible problem when constructing multi-label learning models.

2.2.   A brief review of related work on multi-label imbalance learning algorithms

In recent years, researchers have focused on the class imbalance problem of multi-label data and tried to propose several solutions considering their characteristics. As indicated in the precious section, there are two differences between single- and multi-label imbalance learning tasks. First, in multi-label data, it is difficult to precisely distinguish majority and minority instances, since each instance simultaneously correlates with multiple class labels. Additionally, that are correlations among labels that cannot be easily isolated.

In the context of sampling, Charte et al. ^[34] proposed the ML-RUS (multi-label random undersampling) and ML-ROS (multi-label random oversampling) algorithms. In their design, only the class label with a lower IR than the MeanIR is considered to be handled. Based on this principle, we either randomly remove the majority instances or copy the minority instances. To promote the robustness of sampling, Charte et al. ^[35] further proposed the ML-SMOTE (multi-label SMOTE) algorithm, which generates synthetic minority instances between two adjacent minority instances. These algorithms alleviate the class imbalance problem to some extent but fail to focus on label correlations. In other words, it is difficult to distinguish minority and majority instances, since a so-called majority instance on one label may be the minority instance on another label. When the instance is removed, it would be beneficial for the first label but harmful for the second label. To address this problem, Liu and Tsoumakas ^[37] integrated the sampling techniques into the framework of the classifier chain ^[16] and proposed the ECC-RU. This algorithm executes random undersampling on each label independently to deal with the class imbalance problem and adopts a classifier chain to address label correlation problems. In comparison with several other multi-label sampling algorithms, the ECC-RU shows significant superiority ^[37].

Besides sampling, the multi-label class imbalance problem can also be addressed in other terms. Zhang et al. ^[36] proposed an ensemble solution named cross-coupling aggregation (COCOA), which uses a pairwise strategy to exploit label correlations and a threshold strategy to deal with class imbalance. Specifically, for each label pair $< {l}_{i}, {l}_{j} >$, it first transforms all instances into one of three classes according to their label values on the label pair: the first class contains all instances belonging to ${l}_{i}$, the second class covers all instances neither belonging to ${l}_{i}$ nor ${l}_{j}$, and the third class includes the remainder instances. Then, a calibrating multi-class learning model is trained on the transformed task, and the corresponding threshold needs to be determined by an optimization procedure. Finally, the predicted label set for a test example is obtained by querying the predictive models of all label pairs. The COCOA algorithm is robust but is also extremely time consuming, as it requires training $K\times q$ triple-class models in total, where $K$ denotes a preset number of correlated labels for each label. In ^[38], Peng et al. proposed an algorithm called LDAML-IMB that adopts the latent Dirichlet allocation (LDA) model to explore label correlations. Specifically, the LDAML-IMB treats each instance as a document and each label as a word in the document. It takes advantage of the LDA to determine the distribution of topics, which reflects the label correlations; then, it integrates the topic information to extend the original feature space and finally decides the predicted set of labels for each instance according to the corresponding topic probabilities. The LDAML-IMB adopts a similar method than COCOA to tackle the class imbalance problem; thus, it is noteworthy that the LDAML-IMB algorithm is relatively time consuming.

2.3.   Random k-labelsets and its limitations

The random k-labelsets (RAkEL) algorithm was initially proposed to overcome the problem of generating an excessive number of classes in the label powerset (LP) algorithm, further improving the robustness of the learning model ^[17]. It firstly randomly extracts multiple k-label subsets from the original label space and then transforms each of them to be a ${2}^{k}$ -class problem according to different combinations of label values. Next, for each transformed multi-class learning task ${D}_{i}$, the RAkEL trains a corresponding learning model ${h}_{i}$. Finally, it adopts the following rule to make a decision for each label ${l}_{i}$ of a test instance $x$.

where $t\in \left[\mathrm{0, 1}\right]$ denotes the decision threshold, which is, in general, set to be 0.5, and

where S denotes the number of k-label subsets that contain the label ${l}_{i}$, i.e., ${l}_{i}\in {D}_{j}$. Figure 2 presents an example to describe the flow path of the RAkEL algorithm.

The RAkEL can be seen as an improved version of the LP algorithm. However, we note that there are still two limitations in the RAkEL algorithm. Although the RAkEL considers the high-order label correlations, the label combinations are random, which may cause the model to only explore a rough boundary while neglecting some details about the classification boundary. Also, the RAkEL fails to solve the class imbalance problem. In this work, we will try to address both problems.

3.   Methods

3.1.   Exploring label correlations

As stated in Section 2.3, the RAkEL algorithm randomly explores label correlations. This tends to generate a rough classification boundary based on the discrepancies among k irrelevant labels, instead of an accurate boundary determined by the differences among k closely correlated labels. In this study, we modified the random fashion adopted by RAkEL and proposed to constitute labelsets among k closely correlated labels. Specifically, considering that a multi-label classification task generally involves a binary label space where each element is labeled either 0 or 1, we decided to use the Jaccard coefficient ^[39] to detect label correlations.

Suppose ${D}^{i}$ and ${D}^{j}$ store the training instances that are active on label ${l}_{i}$ and ${l}_{j}$, respectively; then, the Jaccard coefficient between these two labels can be calculated as follows,

It is obvious that a larger Jaccard coefficient means a closer correlation between two corresponding labels. For example, in an image retrieval task, the images containing sandbeach always include sea but are in general irrelevant to waterfall. When training a learning model, it is more difficult but also useful to explore the difference between the two labels sandbeach and sea than distinguish between sandbeach and waterfall.

For each label ${l}_{i}$ in the label space Y, the k-1 strongest correlated labels with that label can be found by sorting q-1 calculated Jaccard coefficients in descending order. Therefore, it only requires generating q k-labelsets in total.

3.2.   An empirical decision output compensation strategy

In this study, we consider adopting a decision output compensation strategy, i.e., a threshold strategy, to address the imbalanced data classification problem. On the transformed multi-class datasets, the instances belonging to some classes might be extremely sparse, causing their distributions to not being precisely described, which undermines some traditional sampling or cost-sensitive learning methods ^[20].

Although there are several mature decision output compensation algorithms, e.g., SVM-OTHR ^[26] and ODOC-ELM ^[27], they are too complex and time consuming to be used in this scenario. In addition, these methods tend to overfit the learning model, as the optimum solution is always sought out based on the training data.

Based on the considerations above, in this study we developed a fast decision output compensation strategy. Different from the addition compensation strategy adopted by SVM-OTHR and ODOC-ELM, our proposed strategy adopts the multiplication compensation. Specifically, it rewrites the decision output as

where the modified factor $C$ can be calculated by,

where $f$ denotes the modified function, ${\mathrm{I}\mathrm{R}}_{i}$ indicates the class imbalance ratio of label ${l}_{i}$, and ${\lambda }_{1}$ and ${\lambda }_{2}$ are two constants; the former controls the varying gradient of the modified function and the latter indicates the inflection position of the varying curve of the modified function. In this study, we empirically designate ${\lambda }_{1}$ as 0.02 and ${\lambda }_{2}$ as 4. The setting of ${\lambda }_{2}$ satisfies the assumption that the performance of a dataset is impacted by the imbalanced data distribution only when the class imbalance ratio is larger than 4 ^[20]. Similarly, in this study, when and only when the class imbalance ratio of a label is equal to or larger than 4, its decision output is compensated. Specifically, the modified factor C lies in the range (1.5, 2), and its varying curve is drawn in Figure 3.

3.3.   Description of the CCkEL algorithm

Based on the proposed label correlation exploration strategy and the empirical decision output compensation strategy, the flow path of the CCkEL algorithm can be described in detail as follows.

Specifically, $\mathbf{W}$ and $\mathbf{C}$ are two vectors that store the class imbalance ratio and the modified factor of each label, respectively. Q is a matrix to store the Jaccard coefficient between any two labels, while P is the matrix that stores the information about all k-labelsets.

It is noteworthy that several state-of-the-art algorithms, including RAkEL ^[17], COCOA ^[36], ECCRU ^[37], LDAML-IMB ^[38], and our proposed CCkEL, all focus on high-order label correlations. Here, we wish to analyze their differences, further highlighting the rationality of our proposed algorithm. First, both RAkEL and the proposed CCkEL generate q k-labelsets and deal with them by label powerset strategy. However, each k-labelset in the RAkEL is generated randomly, making it possible to involve some irrelevant labels, further lowering the efficiency of each sub-learning model. In addition, the RAkEL fails to consider the potential class imbalance problems in multi-label data. In contrast, the CCkEL improves the efficiency of each sub-learning model, as it constructs each k-labelset among closely correlated labels, and solves the class imbalance issue through a fast threshold strategy. As for COCOA, it only considers pairwise label relations; when there are multiple label correlations, it cannot capture these relations. Meanwhile, it conducts an optimization procedure to seek the optimal threshold, thus being extremely time consuming. In contrast, the CCkEL can rapidly capture high-order label relations and calculate an appropriate threshold. ECCRU explores high-order label correlations by introducing old labels into the feature space and solves the class imbalance problem by adopting random undersampling (RUS) strategy. In contrast to our proposed CCkEL algorithm, the ECCRU tends to introduce more noisy label correlations, which could destroy feature-label mappings, while losing classification information and decreasing the quality of each sub-learning model, as with the adoption of the RUS technique. In comparison to several other algorithms, the LDAML-IMB seems to be more robust, as it can not only capture accurate high-order label correlations but also solve the class imbalance problem in a rational fashion. However, it is extremely time consuming, as both the LDA approach and optimized threshold strategy require high time complexities. This further explains why our proposed CCkEL algorithm may be more effective and efficient than these state-of-the-art algorithms.

Regarding time complexity, the RAkEL algorithm has time complexity $O(q· {F}_{M}(N, d, {2}^{k}\left)\right)$ for training and $O(q· {F}_{M}^{{'}}\left(d, {2}^{k}\right))$ for testing, where N denotes the number of training instances, d represents the dimension of feature space X, ${F}_{M}(N, d, {2}^{k})$ denotes the time complexity of transforming a k-labelset into a multi-class problem and training the corresponding classification model, and ${F}_{M}^{{'}}\left(d, {2}^{k}\right)$ denotes the time complexity for predicting an instance by a trained multi-class learning model and then denoting it into the original k-label space ^[1]. Then, the CCkEL has two more steps than the RAkEL during training. One is calculating the Jaccard coefficients and sorting them with the time complexity $O\left({q}^{2}N\right)$. The other one is calculating the modified factor $C$, which has a time complexity $O\left(1\right)$. Therefore, the training time complexity of the CCkEL is $O(q· {(qN+F}_{M}\left(N, d, {2}^{k}\right)))$, and the testing time complexity of the CCkEL is $O(q· {F}_{M}^{{'}}\left(d, {2}^{k}\right))$.

4.   Experiments and discussion

4.1.   Description of the used datasets

In experiments, we used 10 multi-label datasets collected from two open-source data repositories: OpenML¹ and Mulan². The details about these datasets are presented in Table 1, where #Instances, #Features, and #Labels represent the number of instances, the number of features, and the number of labels contained in the corresponding dataset, respectively. Card, Dens, and MeanIR are three popular multi-label imbalance level metrics, which have been described in Eqs (1), (2), and (4), while IR (min) and IR (max) denote the minimum and maximum imbalance ratios among all labels within the corresponding dataset.

¹ https://www.openml.org

² https://mulan.sourceforge.net/

4.2.   Experimental settings

We compared the proposed CCkEL with the baseline algorithm RAkEL ^[17] and several state-of-the-art imbalanced multi-label learning algorithms, namely ML-RUS ^[34], ML-ROS ^[34], ML-SMOTE ^[35], COCOA ^[36], ECCRU ^[37], and LDAML-IMB ^[38]. All these algorithms were implemented by Python, and they all ran on a hardware environment of Intel(R) Core(TM) i5-11400H @ 2.70GHz.

Specifically, we used five popular performance metrics to evaluate various algorithms, including Micro F-measure (F-micro), Macro F-measure (F-macro), HammingLoss, SubsetAccuracy, and running time. These metrics can be calculated as follows:

where I is an indicator function equal to 1 when the condition is satisfied; otherwise, it is equal to 0. As for several other variables, they can be calculated as follows:

where ${\mathrm{T}\mathrm{P}}_{i}$, ${\mathrm{F}\mathrm{P}}_{i}$, and ${\mathrm{F}\mathrm{N}}_{i}$ represent the true positive rate, false positive rate, and false negative rate on the label ${l}_{i}$, respectively.

To guarantee the impartiality of compared experiments, all algorithms adopted C4.5 decision tree ^[40] as the base level single-label learning model. We selected C4.5 decision tree as it has been widely adopted in experiments of several relevant algorithms ^[17,40]. In practical applications, it could be replaced by any other classifier according to the users' preferences. Except for the CCkEL, all other algorithms used the default settings, which have been suggested in the corresponding references. The CCkEL empirically set $k = \mathrm{m}\mathrm{a}\mathrm{x}(q/3, 3)$. In addition, to truly reflect the performance of each algorithm, we conducted 10 times five-fold cross-validations and then output the average results.

4.3.   Results and discussion

The experimental results of the five performance metrics are presented in Tables 2–6. Additionally, to more intuitively compare the quality of various algorithms, a bar graph depicting the average rankings of each algorithm on five different metrics is also provided in Figure 4.

The results in Tables 2–6 and Figure 4 show that, on the first four performance metrics, the proposed CCkEL is superior to the RAkEL baseline algorithm, indicating that it is necessary to constitute strongly correlated k-labelsets and adopt a compensation strategy to deal with imbalanced data distributions. Clearly, we also note that the CCkEL is more time consuming than the RAkEL as it takes $O\left({q}^{2}N\right)$ more time to calculate Jaccard similarities and sort the corresponding k-labelsets.

In addition, we observe that several complex algorithms, e.g., COCOA, ECCRU, and LDAML-IMB, clearly perform better than those simple-sampling-based algorithms, especially on two specific imbalance performance metrics: F-micro and F-macro. The reason may be that they all focus on complex label correlations. Of course, we also note that these three algorithms are more time consuming than several others.

Regarding the three simple-sampling-based algorithms, i.e., ML-RUS, ML-ROS, and ML-SMOTE, they performed clearly worse than the others. We believe this to be because in multi-label spaces, it is not easy to distinguish which instances are significant or not. Meaning, adding or removing an instance might alleviate the class imbalance level of a label while increasing that of another label. Therefore, although the corresponding references ^[34,35] have stated that these sampling-based algorithms are effective, their performance improvement is not significant enough.

It is obvious that the proposed CCkEL algorithm performs best among all comparative algorithms. In particular, the CCkEL has acquired the lowest average ranking in terms of F-micro, HammingLoss, and SubsetAccuracy metrics, despite being superior in the F-macro metric to the RAkEL baseline algorithm and three sampling-based algorithms. In contrast to three complex ensemble learning algorithms, our proposed CCkEL algorithm is obviously more time saving. The observations above verify the rationality of our algorithm design. We believe that the CCkEL acquires superiority from two aspects: 1) It focuses on how to draw the boundary details by constructing k-labelsets among several closely correlated labels, and 2) it can adaptively amend the negative impact of skewed data distribution for each label by taking advantage of the prior imbalance ratio information of that label.

We also note that the proposed CCkEL algorithm presents particular superiority on those datasets with high MeanIR. Specifically, in terms of the F-micro metric, which mostly reflects the quality of a multi-label imbalance learning algorithm, the CCkEL yielded the best results on three highly imbalanced datasets (i.e., Enron, Medical, and SlashDot) and the second-best results on two moderate imbalanced datasets (i.e., Bibtex and Birds). In contrast, on those datasets with a low imbalance level or few labels, the CCkEL cannot show significant superiority to other algorithms. We consider that, on these types of datasets, there is either a lack of label correlations or invalid compensations for decision thresholds.

4.4.   Significance analysis

In order to further analyze the relative performance of the algorithms involved in this study, the Nemenyi test was adopted as a post-hoc test for the Friedman test ^[41,42]. Here, we focus on the relative performance between our proposed CCkEL algorithm and the other algorithms. If the average rank of the CCkEL and that of another algorithm differs by at least one critical difference (CD) unit, then we consider their performance to be significantly different. Specifically, the CD is calculated as follows

where ${q}_{\alpha }$ denotes the significance level, $L$ indicates the number of compared algorithms in the experiments, and $H$ represents the number of datasets used in the experiments. In a CD diagram, if the average ranks of two algorithms are less than a CD unit, then they would be connected by a thick line to indicate that their difference is not significant at a specific significance level. Figure 5 presents the CD diagrams in terms of five different metrics.

The results in Figure 5 illustrate that the proposed CCkEL algorithm performs best on F-micro, HammingLoss, and SubsetAccuracy metrics, although its superiority is not significant in comparison to several other algorithms. Specifically, on the F-micro metric, the CCkEL is significantly superior to several sampling-based algorithms (i.e., ML-RUS, ML-ROS, and ML-SMOTE). On the HammingLoss metric, the CCkEL performs significantly better than COCOA, ML-ROS, ML-RUS, and LDAML-IMB algorithms. For the SubsetAccuracy metric, the proposed CCkEL algorithm not only significantly outperforms three sampling-based algorithms but also presents a significant superiority in comparison to the LDAML-IMB algorithm. Also, it is noteworthy that on the F-macro metric, the CCkEL algorithm performs worse than three other complex algorithms (ECCRU, COCOA, and LDAML-IMB), but the differences among them are not significant. On the running time metric, we observe that the proposed CCkEL algorithm is significantly more time consuming than the ML-RUS algorithm but more time saving than the LDAML-IMB algorithm. In summary, the statistical results indicate that the proposed CCkEL algorithm is an accurate and stable solution for classifying imbalanced multi-label data.

4.5.   Investigation about the impact of parameters

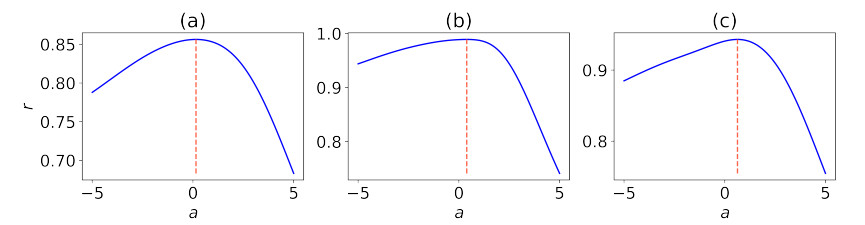
Finally, we investigated the impact of several key parameters used in our proposed algorithms. Figure 6 shows the variation of various performances with gradually increasing k on nine multi-label datasets, where three representative k values, $k = 3$, $k = q/3$, and $k = q/2$ are specifically labeled. Although there are some fluctuations, most curves present a common trend, i.e., the performance first rises with the increase of k value and then gradually declines. This means that the CCkEL algorithm is not appropriate for either designating a too small value or assigning an oversize k value. We believe that a too-small value of k tends to lose some important correlation information, while an oversized k can not only destroy the concentration of the learning model but also greatly add the number of classes in each transformed multi-class learning model to make it more complicated and inaccurate. In addition, with the increment of k, the running time of the CCkEL algorithm also tends to be higher. Further, we observed the CCkEL algorithm to be relatively stable in the context of a specific k value. According to the results from Figure 6, we suggest users to designate $k$ as $\mathrm{m}\mathrm{a}\mathrm{x}(q/3, 3)$ by a rule-of-thumb setting.

Figures 7 and 8 present the performance variance of F-micro and F-macro metrics with a joint change of the parameters ${\lambda }_{1}$ and ${\lambda }_{2}$. Specifically, ${\lambda }_{1}$ varies from 0.01 to 0.20 with an increment of 0.01, and ${\lambda }_{2}$ varies from 1 to 20 with an increment of 1. We randomly conducted 10 experiments on each parameter combination and used the average result to indicate its performance. The results in Figures 7 and 8 present a small performance fluctuation, meaning that although these two parameters can influence classification performance, the influence is not large enough. We consider this to be associated with two reasons. The first one is that the modified factor $C$ varies in a moderate range (1, 2), which can more or less amend the skewed decision threshold, making the worst performance to also be acceptable. The second one is that, in multi-label data, the instances on some labels are easy to be classified, while it may be difficult to distinguish the instances on some other labels; thus, the compensation may effectively improve the classification performance on some labels but destroy that of some other labels. All together, the results reflect that it is relatively safe to designate a small value for the gradient parameter ${\lambda }_{1}$ and a moderate control parameter ${\lambda }_{2}$.

5.   Conclusions and future research

In this paper, we proposed a novel multi-label imbalance learning algorithm named CCkEL, which simultaneously takes advantage of the strong label correlation information existing in the label space and adapts the skewed data distribution in the decision space. It modifies the original RAkEL algorithm by extracting strongly correlated labels to make the learning model focus more on the boundary details. Additionally, a fast compensation-based strategy has been developed to amend the biases caused by skewed data distribution on the learning model trained on each transformed multi-class dataset. The experimental results on ten benchmark multi-label datasets illustrate the superiority of the proposed algorithm in comparison with several state-of-the-art multi-label imbalance learning algorithms. Also, the running time results showed that the CCkEL is a relatively efficient algorithm, especially when compared with several complex ensemble-based multi-label imbalance learning models.

There are two significant limitations in the proposed algorithm. First, the CCkEL is not flexible enough, as it limits the number of correlated labels for any one specific label once k has been designated. That means that if a label has none or only a few correlated labels, some noisy information could be introduced; on the other hand, if a label correlates with a lot of other labels, some useful information could be missed. Second, the compensation is adaptive but not optimum, as we abandon the optimized threshold strategies ^[26,27]. Accordingly, its computational complexity improves tremendously.

In future work, we plan to explore more flexible strategies to get rid of the limitation of the parameter k for further improving the adaption of the algorithm. In addition, the threshold strategy is expected to be replaced by more effective and efficient cost-sensitive learning models to the transformed multi-class learning tasks. Also, we wish to extend the scalability of the experimental data in terms of features, instances, and labels, and adopt more real-world applications containing large-scale multi-label data ^[43,44,45] to further verify the effectiveness and robustness of the proposed CCkEL algorithm.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported in part by the National Natural Science Foundation of China under Grant Nos. 62176107, 62076111, 62076215, and the Open Project of Jiangsu Key Laboratory of Media Design and Software Technology (Jiangnan University).

Conflict of interest

The authors declare there is no conflict of interest.