Figure 1.
Main topology and control structure of LCL inverter.
The regenerative braking in the tram allows the energy to be returned to the power grid through a power inverter. Since the inverter location between the tram and the power grid is not fixed, resulting in a wide variety of impedance networks at grid coupling points, posing a severe threat to the stable operation of the grid-tied inverter (GTI). By independently changing the loop characteristics of the GTI, the adaptive fuzzy PI controller (AFPIC) can adjust according to different impedance network parameters. It is challenging to fulfill the stability margin requirements of GTI under high network impedance since the PI controller has phase lag characteristics. A correction method of series virtual impedance is proposed, which connects the inductive link in a series configuration with the inverter output impedance, correcting the inverter equivalent output impedance from resistance-capacitance to resistance-inductance and improving the system stability margin. Feedforward control is adopted to improve the system's gain in the low-frequency band. Finally, the specific series impedance parameters are obtained by determining the maximum network impedance and setting the minimum phase margin of 45°. The realization of virtual impedance is simulated by conversion to an equivalent control block diagram, and the effectiveness and feasibility of the proposed method are verified by simulation and a 1 kW experimental prototype.
Citation: Sue Wang, Chaohong Zhou, Saleem Riaz, Xuanchen Guo, Haider Zaman, Alsharef Mohammad, Ahmad Aziz Al-Ahmadi, Yasser Mohammed Alharbi, NasimUllah. Adaptive fuzzy-based stability control and series impedance correction for the grid-tied inverter[J]. Mathematical Biosciences and Engineering, 2023, 20(2): 1599-1616. doi: 10.3934/mbe.2023073
| [1] | Sue Wang, Jing Li, Saleem Riaz, Haider Zaman, Pengfei Hao, Yiwen Luo, Alsharef Mohammad, Ahmad Aziz Al-Ahmadi, NasimUllah . Duplex PD inertial damping control paradigm for active power decoupling of grid-tied virtual synchronous generator. Mathematical Biosciences and Engineering, 2022, 19(12): 12031-12057. doi: 10.3934/mbe.2022560 |
| [2] | Tianqi Yu, Lei Liu, Yan-Jun Liu . Observer-based adaptive fuzzy output feedback control for functional constraint systems with dead-zone input. Mathematical Biosciences and Engineering, 2023, 20(2): 2628-2650. doi: 10.3934/mbe.2023123 |
| [3] | Yong Xiong, Lin Pan, Min Xiao, Han Xiao . Motion control and path optimization of intelligent AUV using fuzzy adaptive PID and improved genetic algorithm. Mathematical Biosciences and Engineering, 2023, 20(5): 9208-9245. doi: 10.3934/mbe.2023404 |
| [4] | Yi Zhang, Yue Song, Song Yang . T-S fuzzy observer-based adaptive tracking control for biological system with stage structure. Mathematical Biosciences and Engineering, 2022, 19(10): 9709-9729. doi: 10.3934/mbe.2022451 |
| [5] | Chao Wang, Cheng Zhang, Dan He, Jianliang Xiao, Liyan Liu . Observer-based finite-time adaptive fuzzy back-stepping control for MIMO coupled nonlinear systems. Mathematical Biosciences and Engineering, 2022, 19(10): 10637-10655. doi: 10.3934/mbe.2022497 |
| [6] | Fengyong Li, Meng Sun . EMLP: short-term gas load forecasting based on ensemble multilayer perceptron with adaptive weight correction. Mathematical Biosciences and Engineering, 2021, 18(2): 1590-1608. doi: 10.3934/mbe.2021082 |
| [7] | Siyu Li, Shu Li, Lei Liu . Fuzzy adaptive event-triggered distributed control for a class of nonlinear multi-agent systems. Mathematical Biosciences and Engineering, 2024, 21(1): 474-493. doi: 10.3934/mbe.2024021 |
| [8] | Wouter Huberts, E. Marielle H. Bosboom, Frans N. van de Vosse . A lumped model for blood flow and pressure in the systemic arteries based on an approximate velocity profile function. Mathematical Biosciences and Engineering, 2009, 6(1): 27-40. doi: 10.3934/mbe.2009.6.27 |
| [9] | Yongqiang Yao, Nan Ma, Cheng Wang, Zhixuan Wu, Cheng Xu, Jin Zhang . Research and implementation of variable-domain fuzzy PID intelligent control method based on Q-Learning for self-driving in complex scenarios. Mathematical Biosciences and Engineering, 2023, 20(3): 6016-6029. doi: 10.3934/mbe.2023260 |
| [10] | Peng Guan, Lincoln C. Wood, Jason X. Wang, Linh N. K. Duong . Barriers to blockchain adoption in the seaport industry: A fuzzy DEMATEL analysis. Mathematical Biosciences and Engineering, 2023, 20(12): 20995-21031. doi: 10.3934/mbe.2023929 |
The regenerative braking in the tram allows the energy to be returned to the power grid through a power inverter. Since the inverter location between the tram and the power grid is not fixed, resulting in a wide variety of impedance networks at grid coupling points, posing a severe threat to the stable operation of the grid-tied inverter (GTI). By independently changing the loop characteristics of the GTI, the adaptive fuzzy PI controller (AFPIC) can adjust according to different impedance network parameters. It is challenging to fulfill the stability margin requirements of GTI under high network impedance since the PI controller has phase lag characteristics. A correction method of series virtual impedance is proposed, which connects the inductive link in a series configuration with the inverter output impedance, correcting the inverter equivalent output impedance from resistance-capacitance to resistance-inductance and improving the system stability margin. Feedforward control is adopted to improve the system's gain in the low-frequency band. Finally, the specific series impedance parameters are obtained by determining the maximum network impedance and setting the minimum phase margin of 45°. The realization of virtual impedance is simulated by conversion to an equivalent control block diagram, and the effectiveness and feasibility of the proposed method are verified by simulation and a 1 kW experimental prototype.
A power converter connects the tram to the power grid, facilitating bidirectional power flow [1]. During the normal tram operation, the converter operates as a rectifier. In braking, the converter operates in the inverter mode, feeding back the braking energy to the power grid [2]. However, there is no fixed point for the interface point between the tram and the grid. Therefore, a wide range of impedance networks is possible on the grid side, changing with the connection point [3], especially when the impedance network is large; it seriously affects the control loop gain of the GTI system during tram braking, resulting in system instability [4].
According to [5], in GTI, a significant number of nonlinear equipment is linked to the grid side. When the tram braking energy feeding back to the grid, it is necessary to ensure both the stability of DC side voltage and the good quality of grid current, requiring the GTI to have good steady-state performance. In [6], detecting DC side voltage gives the reference value of the AC side network access current. By controlling the DC side voltage and AC side current, the system has good stability in the braking energy feedback process. In [7], the authors proposed a method using small-signal modeling to analyze the relationship between converter output impedance and DC side line impedance and employing the virtual impedance method to improve the stability of the converter system. Most scholars consider the stability of DC side voltage, reasonable power flow distribution, and power compensation for braking energy feedback to the grid. However, the network impedance at the power grid side changes in real-time due to the different positions of trams connected to the grid while braking. When the network impedance is large, the power grid presents weak inductance, resulting in the decline of the stability margin of the GTI system. Therefore, it is necessary to consider the stability of the GTI system under the condition of a high impedance network.
The combination of fuzzy control and PI control can effectively improve the performance of inverter under strong current network or low network impedance. For example, [8] uses a double fuzzy PI controller to improve the performance of the inverter, in which the input of the main fuzzy controller is the voltage error and the variation of the error, and the output of the main fuzzy controller is used to adjust the parameters of the PI controller; The input of the sub fuzzy controller is the given voltage change on the DC side and the voltage change on the AC side of the inverter, and the output of the sub fuzzy controller is used to assist in adjusting the parameters of the PI controller. This double fuzzy control method effectively reduces the impact on the stability of the inverter system when the DC side voltage changes in a wide range, and also effectively improves the dynamic response speed of the system. [9] Proposed a fuzzy proportional complex integral control (PCI) method to eliminate the control error caused by specific frequency interference signal, suppress the high-order harmonic of grid connected current and improve the quality of grid connected current. [10] introduces an improved ZVS-PWM inverter, which uses fuzzy control to simulate the action mechanism of PID to reduce the complexity of the system. Compared with traditional PID control, PID-like fuzzy controller using fuzzy control to simulate PID working mechanism has better robustness. For islanding solar grid coupled inverters, [11] suggested an adaptive fuzzy control approach. The unmodelled section of a solar grid-connected inverter is simulated using fuzzy control, which decreases the control system's dependency on the model and increases the controller's accuracy. A fuzzy PI composite controller is proposed in [12]. In comparison to classical PI control, fuzzy control updates PI settings live, effectively eliminating DC side voltage overshoot and improving the system's dynamic response speed. [13] combines the fuzzy-logic-based PI controller and the sliding mode controller. The fuzzy controller is connected in series with the PI controller to adjust the PI controller parameters online, which improves the stability of the system. The output of the PI controller is used as the input of the sliding mode controller, which effectively improves the dynamic response speed of the system. Compared with the traditional PI, the proposed method effectively ensures the dynamic performance and steady-state performance of the system, the sensitivity of the system to parameter changes is reduced. In [14], AFPIC is deployed to substitute PI voltage outer loop control, which enhances the robustness of the system and reduces the overshoot of the system. At the same time, the output voltage is feed forward to the input, which effectively weakens the impact of DC side voltage in the start-up stage and increases the anti-disturbance capability of the converter. [15] Designs and implements a GTI based on fuzzy PI control. The parameters of PI controller are adaptively adjusted through control, so that the system can obtain better starting effect and quickly recover to a stable state in case of disturbance.
The above literature shows that AFPIC can effectively improve the stable operation, dynamic response speed, tracking performance and robustness of the inverter. However, under the background of weak grid [16,17], the network impedance of different coupling points is different, resulting in the network impedance of inverter access point is not fixed [18,19], especially the high network impedance will seriously affect the gain of control loop, resulting in the reduction of phase margin, poor stability and poor performance of GTI[20,21]. At the same time, due to the inherent phase lag characteristics of PI controller, it is difficult to take into account the dynamic performance and steady-state performance of the system when adjusting PI controller parameters online[22]. In GTI system, PI controller also has parameter stability range, and fuzzy controller can not adjust PI controller parameters without limit. Therefore, under the condition of high network impedance, it is difficult to meet the stability margin requirements of GTI system only by adjusting PI controller parameters online through fuzzy control. [23]analyzed the impact of phase-locked loop (PLL) and inner loop control bandwidth on the stability margin of MMC system under different short circuit ratio (SCR).Connecting a VSC-HVDC link to a very weak grid (a high-impedance grid) is challenging. [24] Proposes and compares two straightforward solutions, through analysis and comparison, the method to ensure the good stability of the system is obtained.
In order to solve the problem of insufficient stability margin of AFPIC under the condition of high network impedance, a control strategy of fuzzy adaptive PI and series impedance correction is proposed in this paper. The output impedance of the inverter is connected in series with the inductive virtual impedance, so that the output impedance of the inverter is corrected from resistive capacitance to resistive inductance. The relevant series virtual impedance characteristics are determined using bode diagram analysis and the specified line impedance and minimum phase margin. Finally, through the equivalent transformation of the control block diagram, the realization of the virtual impedance is simulated in the control, the phase margin of the output impedance of the inverter under the condition of high network impedance is improved, and the amplitude gain of the low-frequency band of the system is improved through feed forward control. The combination of impedance correction and feed forward control makes the AFPIC have good control performance in all frequency bands.
This research work categorized and divided into five sections. In the second section, the model of GTI under weak current network is established, and the reason for insufficient stability margin of AFPIC under high network impedance is explained. The third section introduces how to use impedance correction method to improve the stability margin of fuzzy adaptive PI control, and how to use feed forward control to improve the amplitude gain of low frequency band. The fifth section verifies the effectiveness of the proposed method through simulation and experiments, and the fourth section summarizes the article.
Fuzzy adaptive PI control is often used to analyze nonlinear systems because of its good dynamic response ability. At present, many scholars have applied fuzzy adaptive PI control to photovoltaic grid connected inverter.
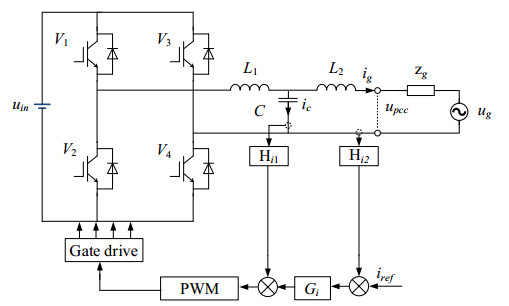
The topology and control structure of the GTI are shown in Figure 1, in which uin is the DC input voltage, V1、V2、V3 and V4 are the switches, L1, C and L2 constitute the LCL filter, zg is the network impedance, ug is the grid voltage, ic is the capacitive current, ig is the grid access current, upcc is the coupling point voltage, iref is the reference current, Hi1 and Hi2 are the feedback coefficients of capacitive current and grid access current respectively. And Figure 2 is the control block diagram of GTI.
| Gi(s)=Kp+Kis | (1) |
where Kp、Ki is as
| {Kp=Kp0+ΔkpKi=Ki0+Δki | (2) |
Kp0 and Ki0 are the initial parameters of PI controller, Δkp and Δki is the adjustment amount of Kp and Ki. The deviation e and deviation change rate ˙e between the reference current iref and the network access current ig are used as the input of the fuzzy controller, Δkp and Δki are used as the output of the fuzzy controller.
The tuning rules are established based on experience, mainly considering the influence of PI controller parameters on stability, dynamic performance and steady-state performance.
The table of fuzzy control rules is shown in Table 1.
| Δkp/Δki | ˙e | |||||||
| NB | NM | NS | ZO | PS | PM | PB | ||
| e | NB | PB|NB | PB|NB | PM|NB | PM|NM | PS|NM | PS|ZO | ZO|ZO |
| NM | PB|NB | PB|NB | PM|NM | PM|NM | PS|NS | ZO|ZO | ZO|ZO | |
| NS | PM|NM | PM|NM | PM|NS | PS|NS | ZO|ZO | NS|PS | NM|PS | |
| ZO | PM|NM | PS|NS | PS|NS | ZO|ZO | NS|PS | NM|PS | NM|PM | |
| PS | PS|NS | PS|NS | ZO|ZO | NS|PS | NS|PS | NM|PM | NM|PM | |
| PM | ZO|ZO | ZO|ZO | NS|PS | NM|PM | NM|PM | NM|PB | NB|PB | |
| PB | ZO|ZO | NS|ZO | NS|PS | NM|PM | NM|PB | NB|PB | NB|PB | |
DownLoad:
CSV
1) When the current error e is large, in order to quickly reduce error and improve the system response speed, Kp takes the larger value and Ki takes the smaller value or zero; With the decrease of deviation e, in order to prevent oscillation caused by excessive overshoot, Kp should be lowered, and Ki should be taken as the smaller value; When the deviation e is very small, Kp value shall continue to decrease, and Ki value shall remain unchanged or be larger to eliminate the static error and avoid the oscillation of the system near the reference value.
2) The larger the change rate of current deviation, the smaller the value of Kp and the larger the value of Ki.
3) When the current deviance e and its rate ˙e both have positive or negative signs, the incoming current changes in the direction of deviation from the reference current, simultaneously, the control function should be strengthened to make the deviation change towards the decreasing trend. We can take smaller Ki which should be taken; When the positive and negative signs of e and ˙e are different, it indicates that the incoming current changes towards the direction close to the reference current. When the current deviation e is large, take a smaller Kp to speed up the transient response. Figure 3 can be obtained by equivalent transformation of Figure 2, Figure 3 is further transformed to Figure 4.
Gx1(s) and Gx2(s) can be expressed as
| Gx1(s)=KPWMs2L1C+sCHi1KPWM+1Gi(s) | (3) |
| Gx2(s)=s2L1C+sCHi1KPWM+1s3L1L2C+s2L2CHi1KPWM+s(L1+L2) | (4) |
L1, L2 and C are LCL filter parameters, and KPWM is modulation coefficient. Inverter loop gain is as follow:
| T(s)=Gx1(s)Gx2(s)Hi2(s) | (5) |
According to the national grid connection standard, the short-circuit ratio (SCR) less than 10 can be called weak network [25], and the calculation of transmission line impedance is:
| Lg=ugSCR×2π×f×ig | (6) |
where f is the grid frequency, ug is the grid voltage and ig is the grid current.
When SCR = 10 and ig = 50A, Lg = 1.4mH. As shown in Figure 5, when SCR > 1 0, although the phase decreases with the increase of inductance, it can still meet the requirement that the phase margin is greater than 45°. However, when Lg = 1.4mH (SCR = 10), the stability margin of GTI decreases to 9°, which is far less than the requirements of GTI for stability margin. We can clearly observe that the AFPIC has limited regulation ability, it can only ensure the good stability of the system under low network impedance. When the network impedance is large, the AFPIC has poor stability or even loses stability.
To raise the stability margin of AFPIC under high network impedance, the method of series virtual impedance is adopted. In order to analyze the output, we should assume that the output impedance of the inverter is equivalent.
According to Figure 3 and Eqs (3)–(5), the network access current can be expressed as
| ig=1Hi2×Γ(s)1+Γ(s)⋅iref(s)−Gx21+Γ(s)⋅upcc(s) | (7) |
with (7), is(s) and Zinv is as follow:
| is(s)=1Hi2×Γ(s)1+Γ(s)⋅iref(s) | (8) |
| Zinv(s)=1+Γ(s)Gx2(s) | (9) |
It can be concluded from Eqs (7)–(9), that the inverter can be represented as a parallel combination of current source is(s) and output impedance Zinv(s), as illustrated in Figure 6.
The grid side current is given by relation
| ig=Zinv(s)Zinv(s)+Zg(s)is(s)−1Zinv(s)+Zg(s)ug(s)=(is(s)−ug(s)Zinv(s))⋅11+Zg(s)Zinv(s) | (10) |
Let H1 and H2 be the following equations respectively:
| H1=is(s)−ug(s)Zinv(s) | (11) |
| H2=11+Zg(s)Zinv(s) | (12) |
The stability of the system depends on H1 and H2. Since H1 is only related to the inverter parameters, the phase margin of H1 can be regarded as a fixed value. Therefore, H2 determines whether the system is stable or not. Following are the two conditions that must be met to ensure the stability of GTI,
1) The GTI is stable when the line impedance Zg = 0
2) 1+Zg/Zinv = 0 is stable.
Condition 1 can be satisfied by the parameter design of the inverter, and condition 2 can be analyzed by using the frequency stability criterion, that is, at the intersection frequency of Zg and Zinv, the phase margin of the system is PM > 0. The calculation formula of system phase margin PM at intersection frequency is as follow:
| PM=180o−[arg(Zg(jω))−argZinv(jω)] | (13) |
ω is the intersection frequency of Zg and Zinv.
We can clearly observe from Eq (13) that the stability margin of the system can be improved by increasing the phase of Zinv, and the series impedance correction can effectively improve the phase margin of Zinv. The equivalent output impedance of inverter after series impedance correction is shown in Figure 7, the equivalent output impedance of the inverter is as follow:
| Z=Zinv + Zo3 | (14) |
The equivalent output impedance of the inverter is resistance capacitance in most frequency bands, as displayed in Figure 8. Therefore, the output impedance can be corrected from resistance capacitance to resistance inductance by connecting the resistance inductance impedance Zo3 in series. After series correction, the phase of equivalent output impedance Z can be greatly improved.
Zo3 is as follow:
| Zo3=L3s+R3 | (15) |
We can clearly observe from Figure 8 that the larger L3, the more obvious the phase increase of Zinv. Therefore, the series pure inductive impedance is most conducive to improve the phase margin. SCR = 3 is chosen, considering the design of the series virtual impedance under the weak power grid. Use iterative method to continuously increase L3 until PM > 45° is met. Take the phase margin PM = 45°, and the corresponding L3 = 750 uH. As seen from Figure 9, using series impedance Zo3, the phase margin at the intersection frequency is increased from PM2 = 12.2° to PM1 = 46.8°, meeting the PM requirements > 45°.
The system control block diagram after series impedance correction is shown in Figure 10.
In order to make the control more convenient, the virtual impedance action point is moved forward to the duty cycle dy.
The series impedance correction may successfully increase the system's stability margin, but the amplitude gain of the system in the low frequency region is dropped just after series impedance correction, according to the assessment in Section 2.2.1 and Figure 9. The feed forward control with high gain at low frequency is used to guarantee that the system has adequate amplitude gain [26,27]. Feed forward control can adopt proportional feed forward, feed forward with filter and other forms. As shown in Figure 12, although proportional feed forward is simple used, it feeds back signals in all frequency bands and has the disadvantage of phase delay. However, feed forward with filter has low-pass characteristics and can effectively reduce the interference of high-frequency signals to the system. Therefore, a filter is introduced in the feed forward link. Since the second-order generalized integrator only has high gain for the signal at 50 Hz and very small gain at other frequency harmonics, the filter of the feed forward link adopts the second-order generalized integrator.
The expression of the second-order generalized integrator is shown in Eq (16).
| Gf(s)=K∗krw0ss2+krw0s+w20 | (16) |
where K denotes the proportional coefficient of feed forward link, kr represent a resonance depth, and w0 is the fundamental frequency.
Figure 13 shows the bode diagram after introducing feedforward, which requires the gain of the system at 50 Hz to be greater than 20 dB. The value of kr is 0.2. We can clearly observe from the Figure 13 that the amplitude gain of the system is 4.7 dB when feedforward control is not introduced. By constantly trying K, when K = 0.2, it meets the requirement that the system amplitude gain is greater than 20dB.
The control block diagram of adding feed forward link and impedance correction link is shown in Figure 14, in which the series impedance correction link is in the solid frame and the feed forward link is in the dotted frame.
From the above analysis, we can clearly observe that fuzzy control is effective in improving the stability of GTI under low network impedance. but under the condition of high network impedance, AFPIC cannot meet the requirements of system stability margin. In contrast, series impedance correction can improve the system stability margin under high network impedance. Feed forward control can effectively improve the amplitude gain of a low-frequency band of the system. The combination of series impedance correction and feed forward control makes the system obtain good phase margin and amplitude gain. It effectively improves the adaptability of AFPIC to the weak power grid.
To check the effectiveness and rationality of the theoretical design in this paper, the simulation model is built using Matlab/Simulink software. The parameters of system under study are listed in Table 2.
| Parameter | Value |
| uin/V | 500 |
| ug/V | 220 |
| L1/uH | 360 |
| L2/uH | 300 |
| C/uF | 10 |
| Hi1 | 1 |
| Hi2 | 0.15 |
DownLoad:
CSV
To validate the theoretical analysis, one groups of experiments are used in the simulation, The experimental value of the other group is SCR = 3, and the calculated Lg = 4.6mH.
Judge whether the system operates stably according to the d-axis current: if the d-axis current fluctuates slightly and is basically a straight line, the system operates stably; If the fluctuation range of d-axis current is large, the system will be unstable.
We can clearly observe from Figure 15(a) that under the independent action of fuzzy adaptive PI, the current of d-axis without line inductance is approximately a straight line, and the amplitude of d-axis current is about 25 A after Lg is input, the system is seriously unstable. Figure 15(b) shows the current waveform. We can clearly observe that after the line inductance is input, the system is unstable and the current is seriously distorted.
Figure 16 shows the current waveform of after impedance correction and feedforward. The GTI system operated under strong current network 0.5 s ago, and the inductance Lg = 4.6 mH was input at 0.5 s. We can clearly observe from Figure 16(a) that even if a large line inductance was input, the d-axis current remained in a straight line after series impedance correction and feedforward control, and the system showed good stability. Moreover, the line inductance of Lg = 4.6 mH does not affect the quality of grid-side current, meeting the standard.
An experimental platform is built to verify the method's correctness further. The control chip adopts TMSF28335, the driving chip adopts HCPL-3120, the isolation chip adopts WRB1205s-3WR2, and the switch tube adopts CSD19535. Figure 17 shows the 1kW experimental platform.
To make the impedance correction effect more intuitive, the DAC function of DSP is used to output the d-axis current. However, because the DAC function cannot directly output the current, the d-axis current is converted into voltage in equal proportion, in which 1 V voltage corresponds to 25 A current.
To verify that the proposed method still has good control effect under high network impedance, the network impedance of Lg = 4.6 mH is input at 0.1 s. We can clearly observe from Figure 18 that after the network impedance is input, the amplitude fluctuation of d-axis current is about 1 V, the corresponding current is 25 A, the system loses stability, and the network current is seriously distorted.
After series impedance correction and feedforward control, the network current waveform is shown in Figure 19. At 0.1 s, the inductance of Lg = 4.6 mH is input. As can be seen from Figure 19(a), after impedance correction, the d-axis current is still a straight line, and the system remains stable. According to the experimental results in Figure 19, the proposed method still has good stability at high network impedance (SCR = 3), and effectively improves the adaptability of AFPIC to weak power grid.
During regenerative braking in a tram, the large network impedance reduces the stability of the inverter. AFPIC can better ensure the system's stable operation under the condition of low network impedance. Still, under high network impedance, AFPIC cannot meet the requirements of system stability margin, resulting in the instability of GTI. Therefore, the series impedance correction method has been adopted in this paper. The simulation and experimental results showed that under high network impedance, that is, when SCR = 3, the oscillation of AFPIC can reach 25 A, and the system is seriously unstable. The proposed method effectively eliminates the oscillations of AFPIC and greatly improves the stability margin of the GTI system. The advantage of this paper is that the impedance parameters in series required by the current system can be designed according to the size of the line impedance and the given stability margin, so that the margin compensation of the system has a theoretical basis, the parameters of the series impedance are more accurate, and the compensation effect is better. In the follow-up study, it is also necessary to consider that when the line impedance changes in real time, the series impedance should be able to be adjusted online to follow the change of line impedance, so that the control system can better adapt to the dynamic changes of the system.
This research work was supported by Taif University Researchers Supporting Project number (TURSP-2020/144), Taif University, Taif, Saudi Arabia.
The authors declare there is no conflict of interest.
| [1] |
Y. He, K. M. Kockelman, K. A. Perrine, Optimal locations of US fast charging stations for long-distance trip completion by battery electric vehicles, J. Cleaner Prod., 214 (2019), 452–461. https://doi.org/10.1016/j.jclepro.2018.12.188 doi: 10.1016/j.jclepro.2018.12.188
|
| [2] |
V. A. Kleftakis, N. D. Hatziargyriou, Optimal control of reversible substations and wayside storage devices for voltage stabilization and energy savings in metro railway networks, IEEE Trans. Transp. Electrif., 5 (2019), 515–523. https://doi.org/10.1109/TTE.2019.2913355 doi: 10.1109/TTE.2019.2913355
|
| [3] |
E. Samavati, H. R. Mohammadi, An improved method for harmonic mitigation and stability improvement of the grid-connected inverters under local load variation and weak grid condition, Int J. Electr. Power Energy Syst., 123 (2020), 106310. https://doi.org/10.1016/j.ijepes.2020.106310 doi: 10.1016/j.ijepes.2020.106310
|
| [4] | S. Fu, X. Zhang, D. Xu, Improved control method of grid-connected converter based on voltage perturbation compensation under weak grid conditions, in 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019-ECCE Asia), (2019), 2586–2591. https://doi.org/10.23919/ICPE2019-ECCEAsia42246.2019.8797350 |
| [5] |
F. Hao, G. Zhang, J. Chen, Z. Liu, D. Xu, Y. Wang, et al., Optimal voltage regulation and power sharing in traction power systems with reversible converters, IEEE Trans. Power Syst., 35 (2020), 2726–2735. https://doi.org/10.1109/TPWRS.2020.2968108 doi: 10.1109/TPWRS.2020.2968108
|
| [6] |
Y. Wang, W. Wen, C. Wang, H. Liu, X. Zhan, X. Xiao, et al., Adaptive voltage droop method of multiterminal VSC-HVDC systems for DC voltage deviation and power sharing, IEEE Trans. Power Del., 34 (2020), 169–176. https://doi.org/10.1109/TPWRD.2018.2844330 doi: 10.1109/TPWRD.2018.2844330
|
| [7] |
B. Liu, H. Ben, Xi. Zhang, T. Meng, X. Wang, Stabilization of a cascaded AC–DC–DC system with small bus capacitance based on small signal analysis, IEEE Trans. Ind. Appl., 54 (2018), 4650–4659. https://doi.org/10.1109/TIA.2018.2837042 doi: 10.1109/TIA.2018.2837042
|
| [8] |
W. Zhang, Y. Fang, R. Ye, Z. Wang, Analysis and design of a double fuzzy PI controller of a voltage outer loop in a reversible three-phase PWM converter, Energies, 13 (2020), 3778. https://doi.org/10.3390/en13153778 doi: 10.3390/en13153778
|
| [9] |
T. Hou, C. Y. Zhang, H. X. Niu, Quasi-Z source inverter control of PV grid-connected based on fuzzy PCI, J. Elect. Sci. Technol., 19 (2021), 100021. https://doi.org/10.1016/j.jnlest.2020.100021 doi: 10.1016/j.jnlest.2020.100021
|
| [10] |
C. W. Tao, C. M. Wang, C. W. Chang, A design of a DC-AC inverter using a modified ZVS-PWM auxiliary commutation pole and a DSP-based PID-like fuzzy control, IEEE Trans. Ind. Electron., 63 (2015), 397–405. https://doi.org/10.1109/TIE.2015.2477061 doi: 10.1109/TIE.2015.2477061
|
| [11] |
Y. Dai, L. Zhang, G. Liu, C. Yang, D. Zhang, X. Huang, Prescribed-performance based finite-time adaptive fuzzy control for PV inverter in islanded systems, Int. J. Electron. Power Energy Syst., 133 (2021), 107254. https://doi.org/10.1016/j.ijepes.2021.107254 doi: 10.1016/j.ijepes.2021.107254
|
| [12] |
Z. Li, W. Cheng, Q. Xiao, W. Liao, Deadbeat predictive power control with fuzzy PI compound controller and power predictive corrector for PWM rectifier under unbalanced grid conditions, Int. J. Fuzzy Syst., 22 (2020), 1277–1288. https://doi.org/10.1007/s40815-020-00847-4 doi: 10.1007/s40815-020-00847-4
|
| [13] |
T. Lei, S. Riaz, N. Zanib, M. Batool, F. Pan, S. Zhang, Performance analysis of grid-connected distributed generation system integrating a hybrid wind-pv farm using UPQC, Complexity, 2022 (2022), 14. https://doi.org/10.1155/2022/4572145 doi: 10.1155/2022/4572145
|
| [14] |
Z. Zheng, N. Wang, Z. Sun, Fuzzy PI compound control of PWM rectifiers with applications to marine vehicle electric propulsion system, Int. J. Fuzzy Syst., 20 (2018), 587–596. https://doi.org/10.1007/s40815-017-0394-y doi: 10.1007/s40815-017-0394-y
|
| [15] |
S. Riaz, L. Hui, M. S. Aldemir, F. Afzal, A future concern of iterative learning control: A survey. journal of statistics and management systems, 24 (2021), 1301–1322. https://doi.org/10.1080/09720510.2020.1856421 doi: 10.1080/09720510.2020.1856421
|
| [16] |
R. Wang, Q. Sun, W. Hu, J. Xiao, H. Zhang, P. Wang, Stability-oriented droop coefficients region identification for inverters within weak grid: an impedance-based approach, IEEE Trans. Syst., 51 (2020), 2258–2268. https://doi.org/10.1109/TSMC.2020.3034243 doi: 10.1109/TSMC.2020.3034243
|
| [17] |
Z. Liu, J. Liu, W. Bao, Y. Zhao, Infinity-norm of impedance-based stability criterion for three-phase AC distributed power systems with constant power loads, IEEE Trans. Power Electron., 30 (2014), 3030–3043. https://doi.org/10.1109/TPEL.2014.2331419 doi: 10.1109/TPEL.2014.2331419
|
| [18] |
J. Xu, S. Xie, LCL-resonance damping strategies for grid-connected inverters with LCL filters: A comprehensive review, J. Mod. Power Syst. Clean Energy, 6 (2018), 292–305. https://doi.org/10.1007/s40565-017-0319-7 doi: 10.1007/s40565-017-0319-7
|
| [19] |
S. Li, X. Li, X. Lee, Weighted average current method for active damping control based on grid voltage feed-forward, J. Cloud Comput., 10 (2021), 1–12. https://doi.org/10.1186/s13677-021-00236-8 doi: 10.1186/s13677-021-00236-8
|
| [20] |
L. Li, W. Chen, Y. Han, Q. Li, Y. Pu, A stability enhancement method based on adaptive virtual resistor for electric-hydrogen hybrid DC microgrid grid-connected inverter under weak grid, Electr. Power Syst. Res., 191 (2021), 106882. https://doi.org/10.1016/j.epsr.2020.106882 doi: 10.1016/j.epsr.2020.106882
|
| [21] |
Z. Lin, X. Ruan, L. Wu, H. Zhang, W. Li, Multi resonant component-based grid-voltage-weighted feedforward scheme for grid-connected inverter to suppress the injected grid current harmonics under weak grid, IEEE Trans. Power Electron., 35 (2020), 9784–9793. https://doi.org/10.1109/TPEL.2020.2970514 doi: 10.1109/TPEL.2020.2970514
|
| [22] | Z. Xu, A. Xu, S. Xie, Dual-loop grid current control technique for grid-connected inverter using an LCL filter, Proc. Chin. Soc. Elect. Eng., 29 (2009), 36–41. |
| [23] | Y. N. Wang, C. Y. Guo, S. Yang, Non-monotonic characteristics of stability margin of MMC system with the change of inner loop current control bandwidth and its mechanism analysis, Proc. Chin. Soc. Elect. Eng., 42 (2022), 3538–3548. |
| [24] |
M. F. M. Arani, Y. A. Mohamed, Analysis and performance enhancement of vector-controlled VSC in HVDC links connected to very weak grids, IEEE Trans. Power Syst., 32 (2017), 684–693. https://doi.org/10.1109/TPWRS.2016.2540959 doi: 10.1109/TPWRS.2016.2540959
|
| [25] |
D. H. Sun, S. Y. Xu, T. Xu, Q. Guo, J. He, B. Zhao, et al., Definition and index of short circuit ratio for multiple renewable energy stations, Proc. Chin. Soc. Elect. Eng., 41 (2021), 497–506. https://doi.org/10.13334/j.0258-8013.pcsee.202112 doi: 10.13334/j.0258-8013.pcsee.202112
|
| [26] |
T. Xue, P. Sun, Z. Xu, Q. Luo, Feedforward phase compensation method of LCL grid-connected inverter based on all-pass filter in weak grid, IET Power Electron., 13 (2020), 4407–4416. https://doi.org/10.1049/iet-pel.2020.0897 doi: 10.1049/iet-pel.2020.0897
|
| [27] |
D. Yang, X. Ruan, H. Wu, A virtual impedance method to improve the performance of LCL-type grid-connected inverters under weak grid conditions, Proc. Chin. Soc. Elect. Eng., 34 (2014), 2327–2335. https://doi.org/10.13334/j.0258-8013.pcsee.2014.15.001 doi: 10.13334/j.0258-8013.pcsee.2014.15.001
|
| 1. | You-Kun Tai, Kuo-Ing Hwu, A Novel ZVS/ZCS Push-Pull LC Resonant DC-DC Converter for Energy Sources, 2023, 16, 1996-1073, 2892, 10.3390/en16062892 | |
| 2. | Mohammed Amine Hoummadi, Manale Bouderbala, Hala Alami Aroussi, Badre Bossoufi, Najib El Ouanjli, Mohammed Karim, Survey of Sustainable Energy Sources for Microgrid Energy Management: A Review, 2023, 16, 1996-1073, 3077, 10.3390/en16073077 | |
| 3. | Jiakang Wang, Hui Liu, Guangji Zheng, Ye Li, Shi Yin, Short-Term Load Forecasting Based on Outlier Correction, Decomposition, and Ensemble Reinforcement Learning, 2023, 16, 1996-1073, 4401, 10.3390/en16114401 | |
| 4. | Leyan Ding, Song Ke, Jun Yang, Xingye Shi, Peixiao Fan, Emanuele Crisostomi, A heuristic-fuzzy improved virtual synchronous generator control strategy for charging station frequency regulation, 2024, 99, 2352152X, 113411, 10.1016/j.est.2024.113411 | |
| 5. | Tobias Graf, Robin Fonk, Christiane Bauer, Josef Kallo, Caroline Willich, Optimal Sizing of Fuel Cell and Battery in a Direct-Hybrid for Electric Aircraft, 2024, 11, 2226-4310, 176, 10.3390/aerospace11030176 | |
| 6. | Yixin Zhuo, Ling Li, Jian Tang, Wenchuan Meng, Zhanhong Huang, Kui Huang, Jiaqiu Hu, Yiming Qin, Houjian Zhan, Zhencheng Liang, Optimal real-time power dispatch of power grid with wind energy forecasting under extreme weather, 2023, 20, 1551-0018, 14353, 10.3934/mbe.2023642 |
Sue Wang, Chaohong Zhou, Saleem Riaz, Xuanchen Guo, Haider Zaman, Alsharef Mohammad, Ahmad Aziz Al-Ahmadi, Yasser Mohammed Alharbi, NasimUllah. Adaptive fuzzy-based stability control and series impedance correction for the grid-tied inverter[J]. Mathematical Biosciences and Engineering, 2023, 20(2): 1599-1616. doi: 10.3934/mbe.2023073
| Δkp/Δki | ˙e | |||||||
| NB | NM | NS | ZO | PS | PM | PB | ||
| e | NB | PB|NB | PB|NB | PM|NB | PM|NM | PS|NM | PS|ZO | ZO|ZO |
| NM | PB|NB | PB|NB | PM|NM | PM|NM | PS|NS | ZO|ZO | ZO|ZO | |
| NS | PM|NM | PM|NM | PM|NS | PS|NS | ZO|ZO | NS|PS | NM|PS | |
| ZO | PM|NM | PS|NS | PS|NS | ZO|ZO | NS|PS | NM|PS | NM|PM | |
| PS | PS|NS | PS|NS | ZO|ZO | NS|PS | NS|PS | NM|PM | NM|PM | |
| PM | ZO|ZO | ZO|ZO | NS|PS | NM|PM | NM|PM | NM|PB | NB|PB | |
| PB | ZO|ZO | NS|ZO | NS|PS | NM|PM | NM|PB | NB|PB | NB|PB | |
DownLoad:
CSV
| Parameter | Value |
| uin/V | 500 |
| ug/V | 220 |
| L1/uH | 360 |
| L2/uH | 300 |
| C/uF | 10 |
| Hi1 | 1 |
| Hi2 | 0.15 |
DownLoad:
CSV
| Δkp/Δki | ˙e | |||||||
| NB | NM | NS | ZO | PS | PM | PB | ||
| e | NB | PB|NB | PB|NB | PM|NB | PM|NM | PS|NM | PS|ZO | ZO|ZO |
| NM | PB|NB | PB|NB | PM|NM | PM|NM | PS|NS | ZO|ZO | ZO|ZO | |
| NS | PM|NM | PM|NM | PM|NS | PS|NS | ZO|ZO | NS|PS | NM|PS | |
| ZO | PM|NM | PS|NS | PS|NS | ZO|ZO | NS|PS | NM|PS | NM|PM | |
| PS | PS|NS | PS|NS | ZO|ZO | NS|PS | NS|PS | NM|PM | NM|PM | |
| PM | ZO|ZO | ZO|ZO | NS|PS | NM|PM | NM|PM | NM|PB | NB|PB | |
| PB | ZO|ZO | NS|ZO | NS|PS | NM|PM | NM|PB | NB|PB | NB|PB | |
| Parameter | Value |
| uin/V | 500 |
| ug/V | 220 |
| L1/uH | 360 |
| L2/uH | 300 |
| C/uF | 10 |
| Hi1 | 1 |
| Hi2 | 0.15 |
