Bifurcation analysis of a sheep brucellosis model with testing and saturated culling rate

Yongbing Nie; Xiangdong Sun; Hongping Hu; Qiang Hou; Yongbing Nie; Xiangdong Sun; Hongping Hu; Qiang Hou

doi:10.3934/mbe.2023069

Mathematical Biosciences and Engineering

2023, Volume 20, Issue 1: 1519-1537. doi: 10.3934/mbe.2023069

Previous Article Next Article

Research article Special Issues

Bifurcation analysis of a sheep brucellosis model with testing and saturated culling rate

1.
School of Mathematics, North University of China, Taiyuan, Shanxi 030051, China
2.
China Animal Health and Epidemiology Center, Qingdao, Shandong 266032, China

Academic Editor: Xichao Duan

Received: 30 July 2022 Revised: 14 October 2022 Accepted: 16 October 2022 Published: 03 November 2022

Testing-culling is a very effective measure for the prevention and control of animal diseases. In this paper, based on sheep brucellosis control policies and animal testing characteristics and considering the limitation of culling resources, a dynamic model is established to study the impact of testing-culling measure. Theoretical analysis reveals that the model may have one or three positive equilibria. The equilibrium in the middle is always unstable, and the model shows saddle-node bifurcation, generalized Hopf bifurcation and Bogdanov-Takens bifurcation. Moreover, the theoretical results are verified via numerical analysis. These results reveal that testing and culling strategies can induce complex transmission dynamics that can help us develop appropriate prevention and control measures for animal brucellosis.

Keywords:

Citation: Yongbing Nie, Xiangdong Sun, Hongping Hu, Qiang Hou. Bifurcation analysis of a sheep brucellosis model with testing and saturated culling rate[J]. Mathematical Biosciences and Engineering, 2023, 20(1): 1519-1537. doi: 10.3934/mbe.2023069

Related Papers:

[1]	Linhua Zhou, Meng Fan, Qiang Hou, Zhen Jin, Xiangdong Sun . Transmission dynamics and optimal control of brucellosis in Inner Mongolia of China. Mathematical Biosciences and Engineering, 2018, 15(2): 543-567. doi: 10.3934/mbe.2018025
[2]	Mingtao Li, Xin Pei, Juan Zhang, Li Li . Asymptotic analysis of endemic equilibrium to a brucellosis model. Mathematical Biosciences and Engineering, 2019, 16(5): 5836-5850. doi: 10.3934/mbe.2019291
[3]	Mingtao Li, Guiquan Sun, Juan Zhang, Zhen Jin, Xiangdong Sun, Youming Wang, Baoxu Huang, Yaohui Zheng . Transmission dynamics and control for a brucellosis model in Hinggan League of Inner Mongolia, China. Mathematical Biosciences and Engineering, 2014, 11(5): 1115-1137. doi: 10.3934/mbe.2014.11.1115
[4]	Qiang Hou, Haiyan Qin . Global dynamics of a multi-stage brucellosis model with distributed delays and indirect transmission. Mathematical Biosciences and Engineering, 2019, 16(4): 3111-3129. doi: 10.3934/mbe.2019154
[5]	Yaoyao Qin, Xin Pei, Mingtao Li, Yuzhen Chai . Transmission dynamics of brucellosis with patch model: Shanxi and Hebei Provinces as cases. Mathematical Biosciences and Engineering, 2022, 19(6): 6396-6414. doi: 10.3934/mbe.2022300
[6]	Yoichi Enatsu, Yukihiko Nakata . Stability and bifurcation analysis of epidemic models with saturated incidence rates: An application to a nonmonotone incidence rate. Mathematical Biosciences and Engineering, 2014, 11(4): 785-805. doi: 10.3934/mbe.2014.11.785
[7]	Fang Zhang, Wenzhe Cui, Yanfei Dai, Yulin Zhao . Bifurcations of an SIRS epidemic model with a general saturated incidence rate. Mathematical Biosciences and Engineering, 2022, 19(11): 10710-10730. doi: 10.3934/mbe.2022501
[8]	Zongmin Yue, Yuanhua Mu, Kekui Yu . Dynamic analysis of sheep Brucellosis model with environmental infection pathways. Mathematical Biosciences and Engineering, 2023, 20(7): 11688-11712. doi: 10.3934/mbe.2023520
[9]	Changyong Xu, Qiang Li, Tonghua Zhang, Sanling Yuan . Stability and Hopf bifurcation for a delayed diffusive competition model with saturation effect. Mathematical Biosciences and Engineering, 2020, 17(6): 8037-8051. doi: 10.3934/mbe.2020407
[10]	Shilian Xu . Saturated lysing efficiency of CD8⁺ cells induced monostable, bistable and oscillatory HIV kinetics. Mathematical Biosciences and Engineering, 2024, 21(10): 7373-7393. doi: 10.3934/mbe.2024324

Abstract

1. Introduction

Brucella is a gram-negative, non-motile coccobacillus that can parasitize various types of livestock and cause brucellosis ^[1]. Brucellosis can be transmitted to susceptible humans and animals mainly through contact with infected animals or ingestion of pathogens from the environment. Brucellosis can cause miscarriage and orchitis in animals and fever, fatigue, joint pain and other symptoms in humans ^[2]. Brucellosis is found all over the world, and nearly 500,000 new cases are recorded every year ^[3]. The brucellosis epidemic not only endangers human health but also affects animal husbandry, which has a large adverse effect on economic development and public health ^[4].

For the prevention and control of animal brucellosis, vaccination, disinfection and testing-culling are the main measures. Many authors have studied the impact of vaccination on the spread of animal brucellosis, and quantitative results have been obtained ^[5,6]. However, a 100% vaccination rate of animals is difficult to achieve, and some vaccines have negative effects. For example, in Korea, vaccination of cattle with RB51 caused side-effects, including abortion, premature birth and a reduced milk yield ^[7]. In other words, brucellosis cannot be eradicated only by vaccination, and other measures should be taken to control animal brucellosis. Although testing and culling measures are difficult to implement in some developing countries because of the high economic cost, they can eliminate animal diseases. For example, bovine brucellosis in New Zealand caused heavy losses to the livestock industry and was eventually eliminated through testing and culling measures ^[8]. Testing and culling measures have been used to prevent and control brucellosis and have significantly reduced the spread of this disease in most Southeast Asian countries ^[9]. Therefore, testing and culling measures are necessary for brucellosis eradication.

Recent studies on the impact of testing and culling measures have contributed to the understanding of the effectiveness of brucellosis control measures ^{[10,11,12,13,14]}. However, these studies mainly focus on the impact of culling measures, and the impact of testing principles and processes on animal brucellosis is still not well researched, which is not conducive to the understanding of the impact of testing behavior and leads to neglect of this risk factor in mathematical modelling. In practice, if an infected animal is found in one place, then all animals in that place will be tested. For example, in Inner Mongolia, China, sheep are numerous, and if an infected sheep is found in one place (a township is treated as a unit), all sheep are tested. Importantly, because of the larger number of sheep, in general, a certain proportion of animals are tested per unit time. In addition, culling resources derived from government supplies may be limited because of the many positive animals. On the basis of these two risk factors and ignoring the contagion of environmental pathogens, a sheep brucellosis model is established:

$\begin{equation} \begin{cases} \frac{dS}{dt} = A-\beta SI-\mu S, \\ \frac{dI}{dt} = \beta SI-(\sigma+\mu)I-m\phi II_d, \\ \frac{dI_d}{dt} = m\phi II_d+\sigma I-\mu I_d-\frac{cI_d}{\alpha+I_d}, \end{cases} \end{equation}$

(1.1)

where $S(t)$ represents the susceptible population, $I(t)$ is the infectious population and $I_d(t)$ is the infectious population with clinical features or found by serological testing. Let $A$ be the constant recruitment rate. $\beta$ and $\mu$ are the infection rate and the natural death rate, respectively. $\sigma$ is the rate of infected animals with clinical features. $m$ is the fraction of positive animals found by testing. $\phi$ is defined as the testing rate, the number of animals tested is $\phi N$ per unit of infectious animals $I_d(t)$ , thus the number of infected animals that have been found through testing is $m\phi N \frac{I}{N} I_{d} = m\phi I I_{d}$ . $c$ represents the maximal supply of culling resources and $\alpha$ is half-saturation constant, measuring the efficiency of the supply of culling resources. The parameters of the model are positive constants.

The motivation for this article is to investigate the impact of restricted culling resources on the dynamics of brucellosis transmission. The rest of this paper is arranged as follows. The basic properties of the model are given in Section 2. In Section 3, the stability of equilibria, saddle-node bifurcation, Hopf bifurcation and Bogdanov-Takens bifurcation of codimension 2 are analyzed. In Section 4, the theoretical results are verified by numerical simulation. Finally, conclusions and discussions are given in Section 5.

2. Basic properties of model

For model (1.1), one can find that

$\begin{align*} \frac{d(S+I+I_d)}{dt} = &A-\mu S-\mu I-\mu I_{d}-\frac{cI_{d}}{\alpha+I_{d}}\\ \leq& A-\mu(S+I+I_d), \end{align*}$

it follows that

$\begin{align*} \lim\limits_{t\rightarrow \infty}\sup (S+I+I_d)\leq \frac{A}{\mu}. \end{align*}$

So the set

$\begin{align*} \Omega = \{(S, I, I_d)\in R^3: S, I, I_d\geq0, S+I+I_d\leq \frac{A}{\mu}\} \end{align*}$

is the positively invariant set of model (1.1).

It is easy to verify that model (1.1) has a disease-free equilibrium $E_0 = (\frac{A}{\mu}, 0, 0)$ . According to the next generation matrix method ^[15], the basic reproduction number is given by

$\begin{align*} R_{0} = \frac{\beta A}{\mu(\sigma+\mu)}. \end{align*}$

For the existence of the endemic equilibrium $E(S^*, I^*, I_d^*)$ of model (1.1), the following equations are given:

$\begin{equation} \begin{cases} A = \beta SI+\mu S, \\ \beta SI = (\mu+\sigma)I+m\phi I_d I, \\ m\phi I_d I+\sigma I = (\mu+\frac{c}{\alpha+I_d})I_d. \end{cases} \end{equation}$

(2.1)

According to the above equations, $S^*$ and $I^*$ can be expressed as functions of $I_d^*$ . That is,

$\begin{align*} S^{*} = \frac{\mu +\sigma +m\phi I_{d}^{*}}{\beta }, \hskip 0.2cm I^{*} = \frac{-m\phi \mu I_{d}^{*}+\mu(\mu+\sigma)(R_{0}-1)}{\beta(m\phi I_{d}^{*}+\mu +\sigma )}, \end{align*}$

where $I_{d}^{*}$ is given by the equation

$\begin{equation} f(I_{d}^{*}) = B_{0}I_{d}^{*{^3}}+B_{1}I_{d}^{*^{2}}+B_{2}I_{d}^{*}+B_{3} = 0, \end{equation}$

(2.2)

where

$\begin{align*} B_{0} = &-m\mu \phi (m\phi +\beta ) < 0, \\ B_{1} = &\mu m\phi (\mu +\sigma )(R_{0}-1)-\mu(\alpha m\phi +\sigma )(m\phi +\beta )-\beta \mu ^{2}-\beta cm\phi , \\ B_{2} = &\mu (\mu +\sigma )(\alpha m\phi +\sigma)(R_{0}-1)-\beta (\mu +\sigma )(\alpha \mu +c)-\alpha m\mu \phi \sigma , \\ B_{3} = &\alpha\sigma \mu (\mu+\sigma)(R_{0}-1). \end{align*}$

Note that $I^{*} > 0$ and $R_{0} > 1$ , then $I_{d}^{*} < I_{c}^{*} = \frac{(\mu+\sigma)(R_{0}-1)}{m\phi}$ .

Let

$\begin{align*} B = B_{1}^{2}-3B_{0}B_{2}, \hskip 0.15cm C = B_{1}B_{2}-9B_{0}B_{3}, \hskip 0.15cm D = B_{2}^{2}-3B_{1}B_{3}, \hskip 0.15cm \Delta = C^{2}-4BD. \end{align*}$

Based on the Descarte's rule of signs, the following cases can be obtained:

Case 1: $B_2 > 0$ or $B_{1} < 0, B_{2} < 0$ . There is a unique positive root of $f(I_{d}^{*}) = 0$ .

Case 2: $B_{1} > 0, B_{2} < 0$ . Similar to the method in ^[16], the following results can be obtained:

(a) $\Delta > 0$ , there is a unique positive root of $f(I_{d}^{*}) = 0$ ;

(b) $\Delta = 0$ , there are two positive roots of $f(I_{d}^{*}) = 0$ ;

To sum up the above results, the following conclusions are derived.

Theorem 1. Assumed that $R_0 > 1$ . If $B_2 > 0$ or $B_{1} < 0, B_{2} < 0$ or $B_{1} > 0, B_{2} < 0, \Delta > 0$ , model (1.1) has a unique endemic equilibrium $E_{1}$ ; if $B_{1} > 0, B_{2} < 0, \Delta = 0$ , model (1.1) has two endemic equilibria $E_{1}$ and $E_{*}$ , $E_{*}$ is an endemic equilibrium of multiplicity 2; if $B_{1} > 0, B_{2} < 0, \Delta < 0$ , model (1.1) has three endemic equilibria $E_{1}, E_{2}$ and $E_{3}$ .

3. Dynamic properties of model

In this section, the stability of equilibria and the local bifurcation of model (1.1) are analyzed, it is of great significance for the prevention and control of brucellosis.

3.1. Stability of equilibria

In this subsection, the global stability of disease-free equilibrium and the local stability of endemic equilibria are analyzed. The following results are first given:

Theorem 2. For model (1.1), if $R_{0}\leq1$ , then $E_{0}$ is globally asymptotically stable.

Proof. The Jacobian matrix of model (1.1) at $E_{0}$ takes the form

$\begin{align*} J_{E_0} = \left(\begin{array}{ccc} -\mu & -\frac{\beta A}{\mu} & 0\\ 0 & \frac{\beta A}{\mu}-\mu-\sigma & 0\\0 & \sigma &-\mu-\frac{c}{\alpha} \end{array} \right), \end{align*}$

then $J_{E_{0}}$ has eigenvalues $\lambda_{1} = -\mu, \lambda_{2} = -(\mu+\frac{c}{\alpha})$ and $\lambda_{3} = (R_{0}-1)(\sigma+\mu)$ . Therefore, $E_{0}$ is locally asymptotically stable if $R_{0} < 1$ and $E_{0}$ is unstable if $R_{0} > 1$ .

Next, when $R_{0}\leq1$ , define the Lyapunov function $L$ as follows:

$\begin{equation*} L = S-S_{0}-S_{0}\ln\frac{S}{S_{0}}+I. \end{equation*}$

It can be concluded that

$\begin{align*} \dot{L}& = (1-\frac{S_{0}}{S})\frac{dS}{dt}+\frac{dI}{dt}\\ & = (1-\frac{S_{0}}{S})(A-\beta SI-\mu S)+\beta SI-(\mu+\sigma)I-m\phi II_{d}\\ &\leq\mu S_{0}(2-\frac{S_{0}}{S}-\frac{S}{S_{0}})+(R_{0}-1)(\mu+\sigma)I. \end{align*}$

Thus, $\dot{L}\leq0$ . Note that the equality $\dot{L} = 0$ means $S = S_{0}$ and $I = 0$ , it implies that $E_{0}$ is the maximum invariant set of model (1.1) in the set $\{\dot{L} = 0\}$ . Therefore, $E_{0}$ is globally asymptotically stable by LaSalle's invariance principle.

The Jacobian matrix at any endemic equilibrium $E(S^{*}, I^{*}, I_{d}^{*})$ is given by

$\begin{align} J_E = \left(\begin{array}{ccc} a & b & 0 \\ d & 0 & f \\ 0 & h & l \\ \end{array} \right), \end{align}$

(3.1)

where

$\begin{align*} a& = -\frac{A}{S^{*}}, \hskip 0.2cm b = -\beta S^{*}, \hskip 0.2cm d = \beta I^{*}, \hskip 0.2cm f = -m\phi I^{*}, \\ h& = \beta S^{*}-\mu, \hskip 0.2cm l = \frac{A-\mu S^{*}-\mu I^{*}-\mu I_{d}^{*}}{\alpha+I_{d}^{*}}-\frac{\sigma I^{*}}{I_{d}^{*}}. \end{align*}$

The characteristic equation can be written as

$\begin{equation} \lambda^{3}+\alpha_{1}\lambda^{2}+\alpha_{2}\lambda+\alpha_{3} = 0, \end{equation}$

(3.2)

where

$\begin{align*} \alpha_{1}& = \frac{1}{(\alpha+I_{d}^{*})S^{*}I_{d}^{*}}((A+\mu S^{*})I_{d}^{*^{2}}+(\mu S^{*^{2}}+(\mu I^{*}+\sigma I^{*}-A)S^{*}+\alpha A)I_{d}^{*}+\alpha\sigma S^{*}I^{*}), \\ \alpha_{2}& = \frac{1}{(\alpha+I_{d}^{*})S^{*}I_{d}^{*}}((S^{*}(\beta (m\phi +\beta )S^{*}-m\mu \phi )I^{*}+\mu A)I_{d}^{*^{2}}+((\beta \alpha (m\phi +\beta )S^{*^{2}}-m\mu\phi \alpha S^{*}\\ &+A(\sigma +\mu ))I^{*}+\mu S^{*}A-A^{2})I_{d}^{*}+\alpha \sigma AI^{*}), \\ \alpha_{3}& = \frac{1}{(\alpha+I_{d}^{*})S^{*}I_{d}^{*}}((\beta m\phi AS^{*}+\beta^{2}\mu S^{*^{2}}-m\mu\phi A)I_{d}^{*^{2}}+(-S^{*^{2}}(-\mu I^{*}-\sigma I^{*}-\mu S^{*}+A)\beta^{2}\\ &+m\phi \alpha \beta AS^{*}-m\mu \phi \alpha A)I_{d}^{*}+\alpha \sigma \beta^{2}I^{*}S^{*^{2}})I^{*}. \end{align*}$

From Eq (2.2), we can represent the coefficient $\alpha_{3}$ as a function on $I_{d}^{*}$ as follows:

$\begin{equation} \alpha_{3}(I_{d}^{*}) = -\beta(m\phi I_{d}^{*}+\mu+\sigma)I^{*}f'(I_{d}^{*}). \end{equation}$

(3.3)

It follows from Eq (2.2) that $f'(I_{d1}^{*}) < 0, f'(I_{d3}^{*}) < 0$ and $f'(I_{d2}^{*}) > 0$ when $E_{1}, E_{2}$ and $E_{3}$ exist. That is, $\alpha_{3}(I_{d1}^{*}) > 0, \alpha_{3}(I_{d3}^{*}) > 0$ and $\alpha_{3}(I_{d2}^{*}) < 0$ . Thus $E_{2}$ is unstable.

Let $\Delta(I_{d}^{*}) = \alpha_{1}(I_{d}^{*})\alpha_{2}(I_{d}^{*})-\alpha_{3}(I_{d}^{*})$ , the following results are derived.

Theorem 3. For model (1.1), the equilibrium $E_{2}$ is unstable when it exists. If $\alpha_{1} > 0, \Delta(I_{d}^{*}) > 0$ , the equilibria $E_{1}$ and $E_{3}$ is locally asymptotically stable when they exist.

Remark. If there is no serological test, the third equation of model (1.1) is independent of the other equations, and a general SI model can be obtained that has a disease-free equilibrium and an endemic equilibrium, both of which are globally asymptotically stable.

3.2. Bifurcation analysis

In this subsection, the conditions for the occurrence of saddle-node, Hopf and Bogdanov-Takens bifurcations are given, which are necessary to understand the impact of testing-culling.

3.2.1. Saddle node bifurcation

Based on the Theorem 1, it is easy to verify that there are two endemic equilibria when $\Delta = 0$ , which implies that the characteristic Eq (3.2) has a simple zero eigenvalue at $E_{*}$ . That is, model (1.1) may undergo a saddle-node bifurcation. In the following pages, a detailed analysis is given by choosing $\sigma$ as the bifurcation parameter.

Let $F_\sigma$ be the derivative of $F$ with respect to $\sigma$ , where $F = (F_1, F_2, F_3)^\mathrm{T}$ is shown as follows:

$\begin{equation*} \begin{cases} F_1\triangleq A-\beta SI-\mu S, \\ F_2\triangleq\beta SI-(\sigma+\mu)I-m\phi II_d, \\ F_3\triangleq m\phi II_d+\sigma I-\mu I_d-\frac{cI_d}{\alpha+I_d}. \end{cases} \end{equation*}$

Let $V$ and $W$ be the eigenvectors corresponding to the eigenvalue $\lambda = 0$ for $J_{E_{*}}$ and $J_{E_{*}}^{T}.$ Then they can be given by

$V = \left( \begin{array}{ccc} V_{1}\\ V_{2} \\ V_{3} \\ \end{array} \right) = \left( \begin{array}{ccc} \frac{-bl}{a}\\ l\\ -h \end{array} \right), W = \left( \begin{array}{ccc} W_{1}\\ W_{2} \\ W_{3} \\ \end{array} \right) = \left( \begin{array}{ccc} \frac{-dl}{a}\\ l\\ -f \end{array} \right),$

where $a, b, d, f, h, l$ are given in (3.1). Furthermore, one can get

$F_{\sigma}(E_{*};\sigma^{*}) = \left( \begin{array}{ccc} 0 \\ -I^{*}\\ I^{*}\\ \end{array} \right)$

and

$D^{2}F(E_{*};\sigma^{*})(V, V) = \left( \begin{array}{ccc} -2\beta V_{1}V_{2}\\ 2\beta V_{1}V_{2}-2m\phi V_{2}V_{3}\\ 2m\phi V_{2}V_{3}+\frac{2c\alpha}{(\alpha+I_{d}^{*})^{3}}V_{3}^{2} \end{array} \right).$

It follows that

$\begin{align*} W^{T}F_{\sigma}(E_{*};\sigma^{*})& = (\mu+\frac{c\alpha}{(\alpha+I_{d}^{*})^{2}})I^{*}\ne0, \\ W^{T}[D^{2}F(E_{*};\sigma^{*})(V, V)]& = -\frac{2\beta^{2}\mu S^{*}}{(\beta I^{*}+\mu)^{2}}(\frac{cI_{d}^{*}}{(\alpha+I_{d}^{*})^{2}}-\frac{\sigma I^{*}}{I_{d}^{*}})^{3}\\ &+2m\phi(m\phi I_{d}^{*}+\sigma)(\frac{cI_{d}^{*}}{(\alpha+I_{d}^{*})^{2}}-\frac{\sigma I^{*}}{I_{d}^{*}}) (\frac{cI_{d}^{*}}{(\alpha+I_{d}^{*})^{2}}\\&-\mu-\frac{c}{\alpha+I_{d}^{*}})+\frac{2cm\alpha\phi I^*(m\phi I_{d}^{*}+\sigma)^{2}}{(\alpha+I_{d}^{*})^{3}}. \end{align*}$

Therefore, when $W^{T}[D^{2}F(E_{*}; \sigma^{*})(V, V)]\ne0,$ model (1.1) undergoes a saddle-node bifurcation at $E_{*}.$

3.2.2. Hopf bifurcation

In this subsection, Hopf and generalized Hopf bifurcations are considered. Let $c$ as the bifurcation parameter, if there exists $c_{1} > 0$ such that $\alpha_{2}(c_{1}) > 0$ and $\alpha_{1}(c_{1})\alpha_{2}(c_{1}) = \alpha_{3}(c_{1})$ , the characteristic Eq (3.2) has a pair of pure imaginary eigenvalues $\pm i\sqrt{\alpha_{2}}$ and a real root $-\alpha_{1}$ . For sufficiently small $\epsilon > 0$ , when $c\in(c_1-\epsilon, c_1+\epsilon)$ , the eigenvalues can be represented as

$\begin{align*} \lambda_{1} = -\alpha_{1}(c), \hskip 0.1cm \lambda_{2} = \omega(c)+iv(c), \hskip 0.1cm \lambda_{3} = \omega(c)-iv(c). \end{align*}$

Substituting $\lambda_{2}$ into Eq (3.2), the transversality condition of Hopf bifurcation can be obtained.

$\begin{align*} \text{sign}\left \{ \frac{\mathrm{d}\omega(c)}{\mathrm{d}c} \right \}_{c = c_{1}} = \text{sign}\left \{\frac{\mathrm{d}(\alpha_{1}(c)\alpha_{2}(c)-\alpha_{3}(c))}{\mathrm{d}c}\big/(2\alpha_{1}^{2}(c)+\alpha_{2}(c))\right\}_{c = c_{1}}\ne0. \end{align*}$

Hence, model (1.1) shows a Hopf bifurcation when $c = c_{1}$ .

Next, we calculate the first and second Lyapunov coefficients by using normal form theory in ^[17]. Let $x = S-S^{*}, y = I-I^{*}, z = I_{d}-I_{d}^{*}$ , then the following system is obtained through the Taylor series about the origin.

$\begin{equation} \begin{cases} \frac{dx}{dt} = ax+by+a_{110}xy, \\ \frac{dy}{dt} = dx+fz+b_{110}xy+b_{011}yz, \\ \frac{dz}{dt} = hy+lz+c_{011}yz+c_{002}z^{2}+c_{003}z^{3}+c_{004}z^{4}+c_{005}z^{5}+\mathcal{O}(\lvert z\rvert ^{6}), \\ \end{cases} \end{equation}$

(3.4)

where $a, b, d, f, h, l$ are given in (3.1), and

$\begin{align*} a_{110} = &-\beta, \hskip 0.1cm b_{110} = \beta, \hskip 0.1cm b_{011} = -m\phi, \hskip 0.1cm c_{011} = m\phi, \hskip 0.1cm c_{002} = \frac{c\alpha}{(\alpha+I_{d}^{*})^{3}}, \hskip 0.1cm\\ c_{003} = &-\frac{c\alpha}{(\alpha+I_{d}^{*})^{4}}, \hskip 0.1cm c_{004} = \frac{c\alpha}{(\alpha+I_{d}^{*})^{5}}, \hskip 0.1cm c_{005} = -\frac{c\alpha}{(\alpha+I_{d}^{*})^{6}}. \end{align*}$

Define $\omega = (x, y, z)^\mathrm{T}$ , note that system (3.4) can be written as

$\begin{equation} \dot{\omega} = J\omega+F(\omega), \end{equation}$

(3.5)

where

$\begin{align*} &J = J_{E}, \\ &F(\omega) = \frac{1}{2}B(\omega, \omega)+\frac{1}{3!}C(\omega, \omega, \omega)+\frac{1}{4!}D(\omega, \omega, \omega, \omega) +\frac{1}{5!}E(\omega, \omega, \omega, \omega, \omega)+\mathcal{O}(\lvert \omega\rvert ^{6}), \end{align*}$

here

$\begin{align*} &B(x, y) = \sum\limits_{j, k = 1}^{3}\frac{\partial^{2}F(\omega)}{\partial \omega_{j}\partial \omega_{k}}\bigg\vert_{\omega = 0}x_{j}y_{k} = \left(\begin{array}{ccc} a_{110}(x_{1}y_{2}+x_{2}y_{1})\\ b_{110}(x_{1}y_{2}+x_{2}y_{1})+b_{011}(x_{2}y_{3}+x_{3}y_{2})\\ c_{011}(x_{2}y_{3}+x_{3}y_{2})+2c_{002}x_{3}y_{3} \end{array}\right), \\ &C(x, y, z) = \sum\limits_{j, k, l = 1}^{3}\frac{\partial^{3}F(\omega)}{\partial \omega_{j}\partial \omega_{k}\partial \omega_{l}}\bigg\vert_{\omega = 0}x_{j}y_{k}z_{l} = \left(\begin{array}{ccc} 0\\ 0\\ -\frac{6c\alpha}{(\alpha+I_{d}^{*})^{4}}x_{3}y_{3}z_{3} \end{array}\right), \\ &D(x, y, z, v) = \sum\limits_{j, k, l, r = 1}^{3}\frac{\partial^{4}F(\omega)}{\partial \omega_{j}\partial \omega_{k}\partial \omega_{l}\partial \omega_{r}}\bigg\vert_{\omega = 0}x_{j}y_{k}z_{l}v_{r} = \left(\begin{array}{ccc} 0\\ 0\\ \frac{24c\alpha}{(\alpha+I_{d}^{*})^{5}}x_{3}y_{3}z_{3}v_{3} \end{array}\right), \\ &E(x, y, z, v, w) = \sum\limits_{j, k, l, r, s = 1}^{3}\frac{\partial^{5}F(\omega)}{\partial \omega_{j}\partial \omega_{k}\partial \omega_{l}\partial \omega_{r}\partial \omega_{s}}\bigg\vert_{\omega = 0}x_{j}y_{k}z_{l}v_{r}w_{s} = \left(\begin{array}{ccc} 0\\ 0\\ -\frac{120c\alpha}{(\alpha+I_{d}^{*})^{6}}x_{3}y_{3}z_{3}v_{3}w_{3} \end{array}\right). \end{align*}$

It is easy to check that

$\begin{align*} Jq = \lambda q, \hskip 0.1cm J^\mathrm{T}p = \overline{\lambda}p, \hskip 0.1cm \langle p, q \rangle = 1, \end{align*}$

where

$\begin{align*} q = \left(\begin{array}{ccc} \frac{b}{i\sqrt{\alpha_{2}}-a}\\ 1\\ \frac{h}{i\sqrt{\alpha_{2}}-l} \end{array}\right), \hskip 0.1cm p = \frac{(a^{2}+\alpha_{2})(l^{2}+\alpha_{2})}{\alpha_{2}^{2}+(a^{2}+bd+fh+l^{2})\alpha_{2}+(fh+l^{2})a^{2}+bdl^{2}} \left(\begin{array}{ccc} \frac{d}{-i\sqrt{\alpha_{2}}-a}\\ 1\\ \frac{f}{-i\sqrt{\alpha_{2}}-l} \end{array}\right). \end{align*}$

By simple calculation

$\begin{align*} l_{11}& = -J^{-1}B(q, \overline{q}) \\& = \frac{2}{(afh+bdl)(a^{2}+\alpha_{2})(l^{2}+\alpha_{2})}(b(h(b_{011}l^{2}+c_{002}fh-c_{011}fl)a^{2}+(a_{110}fh+bb_{110}l)(l^{2} \\&+\alpha_{2})a+\alpha_{2}h(b_{011}l^{2}+c_{002}fh-c_{011}fl)), -a(b(ab_{110}-a_{110}d)l^{3}+hb_{011}(a^{2}+\alpha_{2})l^{2} \\&+(-a^{2}c_{011}fh+\alpha_{2}bb_{110}a-\alpha_{2}(da_{110}b+c_{011}fh))l+c_{002}fh^{2}(a^{2}+\alpha_{2})), (a^{3}b_{011}hl-b( \\&-b_{110}l^{2}+c_{002}dh-c_{011}dl-\alpha_{2}b_{110})a^{2}+a(-da_{110}(l^{2}+\alpha_{2})b+\alpha_{2}hlb_{011})-\alpha_{2}bd(c_{002}h \\&-c_{011}l))h)^{\mathrm{T}}, \\ l_{20}& = (2i\sqrt{\alpha_{2}}I_{3}-J)^{-1}B(q, q)\\ & = \frac{1}{-8i\alpha_{2}^{\frac{3}{2}}+(2al-2bd-2fh)i\sqrt{\alpha_{2}}+(db+4\alpha_{2})l+afh+4\alpha_{2}a}\\&(\frac{2(-2i\sqrt{\alpha_{2}}l-fh -4\alpha_{2})a_{110}b}{i\sqrt{\alpha_{2}}-a} \\&+b(2i\sqrt{\alpha_{2}}-l)(\frac{2b_{110}b}{i\sqrt{\alpha_{2}}-a}+\frac{2b_{011}h}{i\sqrt{\alpha_{2}}-l})+bf(\frac{2c_{011}h} {i\sqrt{\alpha_{2}}-l}+\frac{2c_{002}h^{2}}{(i\sqrt{\alpha_{2}}-l)^{2}}),\\& \frac{2d(2i\sqrt{\alpha_{2}}-l)a_{110}b}{i\sqrt{\alpha_{2}}-a} \\&+(2i\sqrt{\alpha_{2}}-a)(2i\sqrt{\alpha_{2}}-l)(\frac{2b_{110}b}{i\sqrt{\alpha_{2}}-a}+\frac{2b_{011}h}{i\sqrt{\alpha_{2}}-l})+(2i\sqrt{\alpha_{2}}-a) f(\frac{2c_{011}h}{i\sqrt{\alpha_{2}}-l}\\&+\frac{2c_{002}h^{2}}{(i\sqrt{\alpha_{2}}-l)^{2}}), \\&\frac{2dha_{110}b}{i\sqrt{\alpha_{2}}-a}+(2i\sqrt{\alpha_{2}}-a)h(\frac{2b_{110}b}{i\sqrt{\alpha_{2}}-a}+\frac{2b_{011}h}{i\sqrt{\alpha_{2}}-l}) \\&+(-4\alpha_{2}-2i\sqrt{\alpha_{2}}a-db)(\frac{2c_{011}h}{i\sqrt{\alpha_{2}}-l}+\frac{2c_{002}h^{2}}{(i\sqrt{\alpha_{2}}-l)^{2}}))^{\mathrm{T}}, \end{align*}$

where $I_{3}$ is the $3\times 3$ unit matrix, and the first Lyapunov coefficient $l_{1}$ is given by

$\begin{align*} l_{1} = \frac{1}{\sqrt{\alpha_{2}}}\mathrm{Re}(C_{1}), \end{align*}$

where

$\begin{align*} C_{1} = \frac{1}{2}\big\langle p, C(q, q, \overline{q})+B(\overline{q}, l_{20})+2B(q, l_{11}) \big\rangle. \end{align*}$

If $l_{1} = 0$ , the model (1.1) may occur generalized Hopf bifurcation, the second Lyapunov coefficient $l_{2}$ can be calculated by the following form

$\begin{align*} l_{2} = \frac{1}{\sqrt{\alpha_{2}}}\mathrm{Re}(C_{2}), \end{align*}$

where

$\begin{align*} C_{2}& = \frac{1}{12}\big\langle p, E(q, q, q, \overline{q}, \overline{q})+D(q, q, q, \overline{l}_{20})+3D(q, \overline{q}, \overline{q}, l_{20}) +6D(q, q, \overline{q}, l_{11})+C(\overline{q}, \overline{q}, l_{30}) \\&+3C(q, q, \overline{l}_{21})+6C(q, \overline{q}, l_{21})+3C(q, \overline{l}_{20}, l_{20})+6C(q, l_{11}, l_{11})+6C(\overline{q}, l_{20}, l_{11}) \\&+2B(\overline{q}, l_{31})+3B(q, l_{22})+B(\overline{l}_{20}, l_{30})+3B(\overline{l}_{21}, l_{20})+6B(l_{11}, l_{21}) \big\rangle, \end{align*}$

and

$\begin{align*} l_{20}& = (2i\sqrt{\alpha_{2}} I_{3}-J)^{-1}B(q, q), \\ l_{11}& = -J^{-1}B(q, \overline{q}), \\ l_{30}& = (3i\sqrt{\alpha_{2}} I_{3}-J)^{-1}\big[C(q, q, q)+3B(q, l_{20})\big], \\ l_{21}& = (i\sqrt{\alpha_{2}} I_{3}-J)^{-1}\big[C(q, q, \overline{q})+B(\overline{q}, l_{20})+2B(q, l_{11})-2C_{1}q\big], \\ l_{31}& = (2i\sqrt{\alpha_{2}} I_{3}-J)^{-1}\big[D(q, q, q, \overline{q})+3C(q, q, l_{11})+3C(q, \overline{q}, l_{20}) \\&+3B(l_{20}, l_{11})+B(\overline{q}, l_{30})+3B(q, l_{21})-6C_{1}l_{20}\big], \\ l_{22}& = -J^{-1}\big[D(q, q, \overline{q}, \overline{q})+4C(q, \overline{q}, l_{11})+C(\overline{q}, \overline{q}, l_{20})+C(q, q, \overline{l}_{20}) \\&+2B(l_{11}, l_{11})+2B(q, \overline{l}_{21})+2B(\overline{q}, l_{21})+B(\overline{l}_{20}, l_{20})-4l_{11}(C_{1}+\overline{C}_{1})\big], \end{align*}$

where $I_{3}$ is the $3\times 3$ unit matrix, and we do not present the long expressions of $l_{30}, l_{21}, l_{31}, l_{22}$ .

Based on the above theoretical analysis, the following results are derived.

Theorem 4. For model (1.1), if $l_{1} < 0$ $(>0),$ then the bifurcating periodic solutions are asymptotically stable (unstable); if $l_{1} = 0,$ then Hopf bifurcation is generalized.

3.2.3. Bogdanov-Takens bifurcation

According to Theorem 1, model (1.1) has two endemic equilibria $E_{1}$ and $E_{*}$ when $\Delta = 0$ . Furthermore, if $\alpha_{2} = 0$ , the eigenvalues of the Jacobian matrix $J_{E_{*}}$ are $\lambda_{1, 2} = 0$ and $\lambda_{3} = -\alpha_{1}$ , that is to say the model (1.1) may undergo a Bogdanov-Takens bifurcation. Therefore, the following results are given.

Theorem 5. Suppose that $\Delta = 0, \alpha_{2} = 0, M_{20}\neq0$ . If $M_{11}+2L_{20}\neq0$ , then $E_{*}$ is a cusp point of codimension 2; if $M_{11}+2L_{20} = 0$ , $E_{*}$ is at least a cusp point of codimension 3.

Proof. Introducing the following affine transformation

$\begin{equation} \left( \begin{array}{ccc} x\\ y \\ z \\ \end{array} \right) = \left( \begin{array}{ccc} \frac{-bl}{a} &\ -\frac{bl}{a^{2}}+\frac{b}{a} &\ \frac{ba}{l}\\ l& -1 & a\\ -h & 0 & h\\ \end{array} \right)\left( \begin{array}{ccc} u\\ v \\ w \end{array} \right), \end{equation}$

(3.6)

where $a, b, h, l$ are given in (3.1). Then system (3.4) takes the form

$\begin{equation} \begin{cases} \dot{u} = v+L_{20}u^{2}+L_{11}uv+L_{02}v^{2}+w\cdot \mathcal{O}(\lvert u, v\rvert)+\mathcal{O}(\lvert u, v, w\rvert ^{3}), \\ \dot{v} = M_{20}u^{2}+M_{11}uv+M_{02}v^{2}+w\cdot \mathcal{O}(\lvert u, v\rvert)+\mathcal{O}(\lvert u, v, w\rvert ^{3}), \\ \dot{w} = -\alpha_{1}w+K_{20}u^{2}+K_{11}uv+K_{02}v^{2}+w\cdot \mathcal{O}( \lvert u, v\rvert)+\mathcal{O}(\lvert u, v, w\rvert ^{3}), \end{cases} \end{equation}$

(3.7)

where

$\begin{align*} L_{20}& = \frac{-al^{3}a_{110}}{(a-l)(l+a)^{2}}+\frac{l(-b_{011}lh-\frac{b_{110}bl^{2}}{a})}{(l+a)^{2}}-\frac{a(a^{2}+al-l^{2})(c_{002}h^{2}-c_{011}lh)}{h(a-l)(l+a)^{2}}, \\ L_{11}& = \frac{a^{2}l(a_{110}l(\frac{-bl}{a^{2}}+\frac{b}{a})+\frac{a_{110}bl}{a})}{b(a-l)(a+l)^{2}}+\frac{l(b_{011}h+b_{110}l(\frac{-bl}{a^{2}}+\frac{b}{a})+\frac{b_{110}lb}{a})}{(a+l)^{2}}\\ &-\frac{a(a^{2}+al-l^{2})c_{011}}{(a-l)(a+l)^{2}}, \\ L_{02}& = \frac{a^{2}la_{110}(\frac{bl}{a^{2}}-\frac{b}{a})}{b(a-l)(a+l)^{2}}+\frac{lb_{110}(\frac{bl}{a^{2}}-\frac{b}{a})}{(a+l)^{2}}, \\ M_{20}& = -\frac{a_{110}l^{3}a}{(a-l)(a+l)}-\frac{a(-b_{011}lh-\frac{b_{110}bl^{2}}{a})}{a+l}-\frac{a^{2}l(c_{002}h^{2}-c_{011}hl)}{(a-l)(a+l)h}, \\ M_{11}& = \frac{-a^{2}l(a_{110}l(\frac{bl}{a^{2}}-\frac{b}{a})-\frac{a_{110}bl}{a})}{b(a-l)(a+l)}-\frac{a^{2}lc_{011}}{(a-l)(a+l)}\\ &+\frac{a(-b_{011}h+b_{110}l(\frac{bl}{a^{2}}-\frac{b}{a})-\frac{b_{110}bl}{a})}{a+l}, \\ M_{02}& = \frac{a^{2}la_{110}(\frac{bl}{a^{2}}-\frac{b}{a})}{b(a-l)(a+l)}-\frac{ab_{110}(\frac{bl}{a^{2}}-\frac{b}{a})}{a+l}, \\ K_{20}& = L_{20}+c_{002}h-c_{011}l, \\ K_{11}& = L_{11}+c_{011}, \\ K_{02}& = L_{02}. \end{align*}$

Applying the center manifold theorem, system (3.7) becomes

$\begin{equation} \begin{cases} \dot{u} = v+L_{20}u^{2}+L_{11}uv+L_{02}v^{2}+\mathcal{O}(\lvert u, v\rvert ^{3}), \\ \dot{v} = M_{20}u^{2}+M_{11}uv+M_{02}v^{2}+\mathcal{O}(\lvert u, v\rvert ^{3}).\\ \end{cases} \end{equation}$

(3.8)

Using the following transformation

$\begin{align*} u& = \eta_{1}+\frac{1}{2}(L_{11}+M_{02})\eta_{1}^{2}+L_{02}\eta_{1}\eta_{2}+\mathcal{O}(\lvert \eta_1, \eta_2\rvert ^{3}), \\ v& = \eta_{2}-L_{20}\eta_{1}^{2}+M_{02}\eta_{1}\eta_{2}+\mathcal{O}(\lvert \eta_1, \eta_2\rvert ^{3}). \end{align*}$

It can be derived that

$\begin{equation} \begin{cases} \dot{\eta_{1}} = \eta_{2}, \\ \dot{\eta_{2}} = M_{20}\eta_{1}^{2}+(M_{11}+2L_{20})\eta_{1}\eta_{2}+\mathcal{O}(\lvert \eta_1, \eta_2\rvert ^{3}).\\ \end{cases} \end{equation}$

(3.9)

Therefore, assumed that $\Delta = 0, \alpha_{2} = 0, M_{20}\neq0$ . If $M_{11}+2L_{20}\neq0$ , $E_{*}$ is a cusp point of codimension 2, and the codimension of the cusp point is at least 3 if $M_{11}+2L_{20} = 0$ .

In the following analysis, $\phi, c$ are chosen as bifurcation parameters, $\phi = \phi_{0}$ and $c = c_{0}$ satisfy $\Delta = 0$ and $\alpha_{2} = 0$ . The model (1.1) is perturbed with $(\phi, c)$ in a small neighborhood of $(\phi_{0}, c_{0})$ . Let $\phi = \phi_{0}+\epsilon_{1}, c = c_{0}+\epsilon_{2},$ where $\epsilon = (\epsilon_{1}, \epsilon_{2})$ is a parameter vector in a small neighborhood of $(0, 0)$ . By the translation $x = S-S^{*}, y = I-I^{*}, z = I_{d}-I_{d}^{*}$ and using Taylor expansion, model (1.1) is transformed into

$\begin{equation} \begin{cases} \frac{dx}{dt} = ax+by+a_{110}xy, \\ \frac{dy}{dt} = q^{'}+dx+e^{'}y+(f+f^{'})z+b_{110}xy+(b_{011}+b_{011}^{'})yz, \\ \frac{dz}{dt} = c^{'}+(h+h^{'})y+(l+l^{'})z+(c_{011}+c_{011}^{'})yz+(c_{002}+c_{002}^{'})z^{2}+\mathcal{O}(\lvert z\rvert ^{3}), \end{cases} \end{equation}$

(3.10)

where $a, b, a_{110}, d, f, b_{110}, b_{011}, h, l, c_{011}, c_{002}$ are given in system (3.4) and

$\begin{align*} &q^{'} = -m\epsilon_{1}I^{*}I_{d}^{*}, \hskip 0.2cm e^{'} = -m\epsilon_{1}I_{d}^{*}, \hskip 0.2cm f^{'} = -m\epsilon_{1}I^{*}, \hskip 0.2cm b_{011}^{'} = -m\epsilon_{1}, \\ &c^{'} = m\epsilon_{1}I^{*}I_{d}^{*}-\frac{\epsilon_{2}I_{d}^{*}}{\alpha+I_{d}^{*}}, \hskip 0.4cm h^{'} = m\epsilon_{1}I_{d}^{*}, \hskip 0.4cm c_{011}^{'} = m\epsilon_{1}, \\ &l^{'} = \frac{1}{(\alpha+I_{d}^{*})^{2}}(\epsilon_{1}I^{*}m(I_{d}^{*}+\alpha)^{2}-\epsilon_{2}\alpha), \hskip 0.2cm c_{002}^{'} = \frac{\epsilon_{2}\alpha}{(\alpha+I_{d}^{*})^{3}}. \end{align*}$

Applying the transformation (3.6), then system (3.10) restricted on the center manifold is

$\begin{equation} \begin{cases} \dot{u} = v+a_{00}+a_{10}u+a_{01}v+\frac{1}{2}a_{20}u^{2}+a_{11}uv+\frac{1}{2}a_{02}v^{2}+\mathcal{O}(\lvert u, v\rvert ^{3}), \\ \dot{v} = b_{00}+b_{10}u+b_{01}v+\frac{1}{2}b_{20}u^{2}+b_{11}uv+\frac{1}{2}b_{02}v^{2}+\mathcal{O}(\lvert u, v\rvert ^{3}), \end{cases} \end{equation}$

(3.11)

where

$\begin{align*} a_{00}& = \frac{lq^{'}}{(a+l)^{2}}-\frac{a(a^{2}+al-l^{2})c^{'}}{h(a-l)(l+a)^{2}}, \\ a_{10}& = \frac{l(-\frac{dbl}{a}+e^{'}l-fh)}{(a+l)^{2}}-\frac{a(a^{2}+al-l^{2})((h+h^{'})l-(l+l^{'})h)}{h(a-l)(a+l)^{2}}, \\ a_{01}& = -\frac{e^{'}l}{(a+l)^2}+\frac{a(a^2+al-l^2)h^{'}}{h(a-l)(a+l)^2}, \\ a_{20}& = 2L_{20}-2\frac{b_{011}^{'}l^{2}h}{(a+l)^{2}}-2\frac{a(a^{2}+al-l^{2})(c_{002}^{'}h^{2}-c_{011}^{'}lh)}{h(a-l)(a+l)^{2}}, \\ a_{11}& = L_{11}+\frac{l(\frac{blh}{a}+b_{011}^{'}h)}{(a+l)^{2}}-\frac{a(a^{2}+al-l^{2})c_{011}^{'}}{(a-l)(a+l)^{2}}, \\ a_{02}& = 2L_{02}, \\ b_{00}& = -\frac{aq^{'}}{a+l}-\frac{a^{2}lc^{'}}{(a-l)h(a+l)}, \\ b_{10}& = -\frac{a(-\frac{dbl}{a}+e^{'}l-fh)}{a+l}-\frac{a^{2}l((h+h^{'})l-(l+l^{'})h)}{(a-l)(a+l)h}, \\ b_{01}& = -\frac{al^{2}}{(a+l)(a-l)}+\frac{a^{2}e^{'}-bda+bdl}{a(a+l)}+\frac{a^{2}l(h+h^{'})}{(a+l)(a-l)h}, \\ b_{20}& = 2M_{20}+2\frac{a(b_{011}^{'}lh)}{a+l}-2\frac{a^{2}l(-c_{011}^{'}lh+c_{002}^{'}h^{2})}{(a-l)(a+l)h}, \\ b_{11}& = M_{11}+\frac{a(\frac{-blh}{a}-b_{011}^{'}h)}{a+l}-\frac{a^{2}lc_{011}^{'}}{(a+l)(a-l)}, \\ b_{02}& = 2M_{02}. \end{align*}$

Define a nonlinear transformation

$\begin{align*} &x = u, \\ &y = v+a_{00}+a_{10}u+a_{01}v+\frac{1}{2}a_{20}u^{2}+a_{11}uv+\frac{1}{2}a_{02}v^{2}+\mathcal{O}(\lvert u, v\rvert ^{3}). \end{align*}$

It can be derived from system (3.11) that

$\begin{equation} \begin{cases} \dot{x} = y, \\ \dot{y} = g_{00}+g_{10}x+g_{01}y+\frac{1}{2}g_{20}x^{2}+g_{11}xy+\frac{1}{2}g_{02}y^{2}+\mathcal{O}(\lvert x, y\rvert ^{3}), \end{cases} \end{equation}$

(3.12)

where

$\begin{align*} &g_{00} = b_{00}+\mathcal{O}(\epsilon^{2}), \\ &g_{10} = b_{10}+a_{11}b_{00}-b_{11}a_{00}+\mathcal{O}(\epsilon^{2}), \\ &g_{01} = b_{01}+a_{10}+a_{02}b_{00}-(a_{11}+b_{02})a_{00}+\mathcal{O}(\epsilon^{2}), \\ &g_{20} = b_{20}+\mathcal{O}(\epsilon), \\ &g_{11} = a_{20}+b_{11}+\mathcal{O}(\epsilon), \\ &g_{02} = b_{02}+2a_{11}+\mathcal{O}(\epsilon). \end{align*}$

Introducing the transformation

$\begin{align*} x = v_{1}-\frac{g_{01}}{g_{11}}, \hskip 0.1cm \ y = v_{2}. \end{align*}$

One can obtain

$\begin{equation} \begin{cases} \dot{v_{1}} = v_{2}, \\ \dot{v_{2}} = h_{00}+h_{10}v_{1}+\frac{1}{2}h_{20}v_{1}^{2}+h_{11}v_{1}v_{2}+\frac{1}{2}h_{02}v_{2}^{2}+\mathcal{O}(\lvert v_{1}, v_{2}\rvert ^{3}), \end{cases} \end{equation}$

(3.13)

where

$\begin{align*} &h_{00} = g_{00}-\frac{g_{01}}{g_{11}}g_{10}+\mathcal{O}(\epsilon^{2}), \\ &h_{20} = g_{20}+\mathcal{O}(\epsilon), \\ &h_{10} = g_{10}-\frac{g_{01}}{g_{11}}g_{20}+\mathcal{O}(\epsilon^{2}), \\ &h_{11} = g_{11}+\mathcal{O}(\epsilon), \\ &h_{02} = g_{02}+\mathcal{O}(\epsilon). \end{align*}$

Introducing a new time variable $\tau$ by $\mathrm{d}t = (1-\frac{h_{02}}{2}v_{1})\mathrm{d}\tau$ and rewriting $\tau$ as $t$ . Then

$\begin{equation} \begin{cases} \dot{v_{1}} = v_{2}-\frac{h_{02}}{2}v_{1}v_{2}, \\ \dot{v_{2}} = h_{00}+(h_{10}-\frac{h_{02}}{2}h_{00})v_{1}+\frac{1}{2}(h_{20}-h_{02}h_{10})v_{1}^{2}\\ \hskip 0.5cm +\; h_{11}v_{1}v_{2}+\frac{1}{2}h_{02}v_{2}^{2}+\mathcal{O}(\lvert v_{1}, v_{2}\rvert ^{3}). \end{cases} \end{equation}$

(3.14)

Using the transformation

$\begin{align*} \xi_{1} = v_{1}, \hskip 0.1cm \xi_{2} = v_{2}-\frac{h_{02}}{2}v_{1}v_{2}, \end{align*}$

system (3.14) becomes

$\begin{equation} \begin{cases} \dot{\xi_{1}} = \xi_{2}, \\ \dot{\xi_{2}} = \mu_{1}+\mu_{2}\xi_{1}+\mu_{3}\xi_{1}^{2}+\mu_{4}\xi_{1}\xi_{2}+\mathcal{O}(\lvert \xi_{1}, \xi_{2}\rvert ^{3}), \end{cases} \end{equation}$

(3.15)

where

$\begin{align*} \mu_{1} = h_{00}, \hskip 0.1cm \mu_{2} = h_{10}-\frac{1}{2}h_{00}h_{02}, \hskip 0.1cm \mu_{3} = \frac{1}{2}(h_{20}-h_{10}h_{02}), \hskip 0.1cm \mu_{4} = h_{11}. \end{align*}$

Introducing the change of variables and rescaling of time

$\begin{align*} \eta_{1} = \frac{\mu_{4}^{2}}{\mu_{3}}\xi_{1}, \hskip 0.1cm \eta_{2} = \mathrm{sign}(\frac{\mu_{3}}{\mu_{4}})\frac{\mu_{4}^{3}}{\mu_{3}^{2}}\xi_{2}, \hskip 0.1cm t = \left\lvert \frac{\mu_{3}}{\mu_{4}}\right\vert\tau. \end{align*}$

Then system (3.15) takes the required form

$\begin{equation} \begin{cases} \dot{\eta_{1}} = \eta_{2}, \\ \dot{\eta_{2}} = \beta_{1}+\beta_{2}\eta_{1}+\eta_{1}^{2}+s\eta_{1}\eta_{2}+\mathcal{O}(\lvert \eta_{1}, \eta_{2}\rvert ^{3}), \end{cases} \end{equation}$

(3.16)

where

$\begin{align*} \beta_{1} = \frac{\mu_{4}^{4}}{\mu_{3}^{3}}\mu_{1}, \hskip 0.1cm \beta_{2} = \frac{\mu_{4}^{2}}{\mu_{3}^{2}}\mu_{2}, \hskip 0.1cm s = \mathrm{sign}(\frac{\mu_{4}}{\mu_{3}}). \end{align*}$

Next, a numerical example is proposed to show Bogdanov-Takens bifurcation. Taking $\phi = 0.05558, c = 3.69082,$ other parameters are given in (4.1). By simple calculation, it can be obtained that

$\begin{align*} \beta_{1}& = (1.6710\epsilon_{2}-14.134\epsilon_{1})(-0.0011511+0.0030950\epsilon_{1}-9.6342\times10^{-7}\epsilon_{2})^7\\ &\big/(-0.00010783\epsilon_{1}^3+0.000022199\epsilon_{1}^4+1.7360\times10^{-8}\epsilon_{2}-7.3281\times10^{-7}\epsilon_{1}\epsilon_{2}\\ &+0.000042818\epsilon_{1}^2+2.6542\times10^{-6}\epsilon_{1}^2\epsilon_{2}-2.5058\times10^{-6}\epsilon_{1}^3\epsilon_{2}+1.4214\\ &\times10^{-11}\epsilon_{2}^2-5.8151\times10^{-10}\epsilon_{1}\epsilon_{2}^2+1.4172\times10^{-9}\epsilon_{1}^2\epsilon_{2}^2-1.0591\times10^{-6}\epsilon_{1}-1.1977\times10^{-9})^3, \\ \beta_{2}& = (-0.0011511+0.0030950\epsilon_{1}-9.6342\times10^{-7}\epsilon_{2})^4(0.000075528\epsilon_{1}^3-2.9602\\ &\times10^{-5}\epsilon_{2}-0.0045697\epsilon_{1}^2+0.000074794\epsilon_{1}\epsilon_{2}-3.1634\times10^{-6}\epsilon_{1}^2\epsilon_{2}-2.4213\\ &\times10^{-8}\epsilon_{2}^2+3.0469\times10^{-8}\epsilon_{1}\epsilon_{2}^2+0.0018344\epsilon_{1}-2.3246\times10^{-8})\big/(-1.0783\\ &\times10^{-4}\epsilon_{1}^3+0.000022199\epsilon_{1}^4+1.7360\times10^{-8}\epsilon_{2}-7.3281\times10^{-7}\epsilon_{1}\epsilon_{2}+4.2818\\ &\times10^{-5}\epsilon_{1}^2+2.6542\times10^{-6}\epsilon_{1}^2\epsilon_{2}-2.5058\times10^{-6}\epsilon_{1}^3\epsilon_{2}+1.4214\times10^{-11}\epsilon_{2}^2\\ &-5.8151\times10^{-10}\epsilon_{1}\epsilon_{2}^2+1.4172\times10^{-9}\epsilon_{1}^2\epsilon_{2}^2-1.0591\times10^{-6}\epsilon_{1}-1.1977\\ &\times10^{-9})^2\times(-0.0011511+0.0030950\epsilon_{1}-9.6342\times10^{-7}\epsilon_{2}), \end{align*}$

then

$\begin{vmatrix} \dfrac{\partial(\beta_{1}(\epsilon), \beta_{2}(\epsilon))}{\partial(\epsilon_{1}, \epsilon_{2})} \end{vmatrix}_{\epsilon = 0} = 4.4863\times10^{12}.$

Therefore, model (1.1) undergoes a Bogdanov-Takens bifurcation of codimension 2 in a small neighborhood of $(\phi_{0}, c_{0})$ . According to Lemma 8.7 in Kuznetsov ^[17], the following Theorem can be obtained.

Theorem 6. For model (1.1), we take $\phi$ and $c$ as bifurcation parameters, the bifurcation cures are given by the following:

1) Saddle-node bifurcation occurs from the bifurcation curve:

$SN = \left\lbrace (\epsilon_{1}, \epsilon_{2}): 4\beta_{1} = \beta_{2}^{2}\right\rbrace ;$

2) Hopf bifurcation occurs from the bifurcation curve:

$H = \left\lbrace (\epsilon_{1}, \epsilon_{2}): \beta_{1} = 0, \beta_{2} < 0\right\rbrace ;$

3) Homoclinic orbit occurs from the bifurcation curve:

$HL = \left\lbrace (\epsilon_{1}, \epsilon_{2}): 25\beta_{1}+6\beta_{2}^{2}\approx0, \beta_{2} < 0\right\rbrace .$

4. Numerical simulation

In this section, the theoretical conclusions of model (1.1) are validated by the numerical simulation. The following data are used for numerical analysis in the full text.

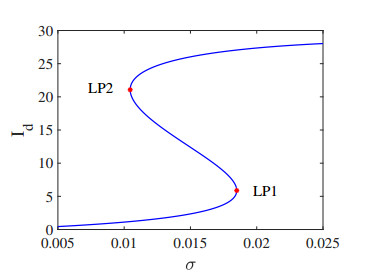
$\begin{equation} A = 5, \hskip 0.1cm \beta = 0.003, \hskip 0.1cm \mu = 0.01, \hskip 0.1cm \sigma = 0.01, \hskip 0.1cm m = 0.02, \hskip 0.1cm \alpha = 0.5. \end{equation}$

(4.1)

In , it is easy to see that the model (1.1) may exist one or three positive equilibria as the change of $\sigma$ . In addition, there are two limit points for model (1.1), that is, the model (1.1) undergoes saddle-node bifurcation.

Figure 1. Existence of saddle-node bifurcation at

$LP1$ and

$LP2$ when

$\sigma = 0.018492(W^{T}[D^{2}$

$F(E_{*}; \sigma^{*})$

$(V, V)] = 2.422\times10^{-6})$ and

$\sigma = 0.010455 (W^{T}[D^{2}F(E_{*}; \sigma^{*})(V, V)] = -8.303\times10^{-7})$ . Where

$A = 5, \beta = 0.003, \mu = 0.01, m = 0.02, \phi = 0.13, c = 4, \alpha = 0.5$ .

DownLoad: Full-Size Img PowerPoint

The bifurcation curve of co-dimension 1 of model (1.1) is given in . Taking c as the bifurcation parameter, there are two Hopf points and two limit points with the change of $c$ . When $c = 3.81680$ , $E_1(\lambda_{1} = -0.6, \lambda_{2, 3} = -0.0003\pm0.08i)$ and $E_3(\lambda_{1, 2} = -0.01\pm0.1i, \lambda_{3} = -0.01)$ are stable foci, $E_2$ is a saddle point and an unstable limit cycle ( $l_1 = 2.1206\times 10^{-5} > 0$ ) emerges from the Hopf point (H1) near the equilibrium $E_{1}$ , which is illustrated in , . If $c = 3.92610$ , $E_1(\lambda_{1} = -0.6, \lambda_{2, 3} = -0.07\pm0.07i)$ and $E_3(\lambda_{1, 2} = -0.01\pm0.1i, \lambda_{3} = -0.01)$ are also stable foci, $E_2$ is a saddle point and an unstable limit cycle ( $l_1 = 3.1916\times 10^{-5} > 0$ ) arises from the Hopf point (H2) near the equilibrium $E_{3}$ , it is shown in Figure 3(c), (d).

Figure 2. Bifurcation diagram of the model (1.1).

DownLoad: Full-Size Img PowerPoint

Figure 3. The phase portraits of model (1.1) with different parameter values.

DownLoad: Full-Size Img PowerPoint

The bifurcation curves of co-dimension 2 are generated from , one of them shows a generalized Hopf bifurcation (GH) and the other is a Bogdanov-Takens bifurcation (BT). In , $E_3(\lambda_{1, 2} = -0.01\pm0.1i, \lambda_{3} = -0.01)$ is locally stable and $E_2$ is a saddle point, the Bautin (generalized Hopf) bifurcation ( $l_1 = 0, l_2 = -6.9961\times 10^{-6} < 0$ ) occurs at $(\phi, c) = (0.13458, 3.84246)$ . There are two limit cycles that appear near equilibrium $E_1$ , and the large limit cycle is stable and the small one is unstable, the phase portrait is illustrated in . In , , $E_1(\lambda_{1} = -0.03, \lambda_{2} = -0.7, \lambda_{3} = -0.4)$ is a stable node and $E_*$ is a BT point of order 2. As shown in Figure 4(c), , , , with the values of $\phi$ and $c$ increase, $E_1$ is still a stable node and $E_3$ is a stable focus, the model first appears an unstable limit cycle around $E_3$ , then the limit cycle disappears, model (1.1) has a homoclinic orbit to the saddle point $E_2$ and it eventually disappears.

Figure 4. The phase portraits near the codimension-2 Bogdanov-Takens bifurcation.

DownLoad: Full-Size Img PowerPoint

5. Conclusions and discussion

Testing-culling is a major prevention and control measure for brucellosis used by the animal disease regulatory authorities of some countries ^[8,18]. Therefore, the impact of testing and culling measures is an interesting research topic. In this paper, on the basis of brucellosis control policies and the characteristics of animal testing and considering the limitation of culling resources, a mathematical model is established to demonstrate the impact of testing and culling measures on the dynamics of brucellosis transmission. The model is found to have a disease-free equilibrium that is globally asymptotically stable if $R_0\leq1$ , and there may be one or three positive equilibria if $R_0 > 1$ , which leads to saddle-node bifurcation, (generalized) Hopf bifurcation and Bogdanov-Takens bifurcation in the model. Biologically speaking, saddle node bifurcation means that the model appears multi-stable; that is, the initial state of each subpopulation may affect the level of brucellosis transmission. The Hopf bifurcation and Bogdanov-Takens bifurcation imply that the model undergoes periodic oscillations. In other words, if the epidemic is at the lowest point of the cycle, it prompts people to think that the disease may disappear, affecting the implementation of prevention and control measures. In addition, the endemic equilibrium of the model is globally asymptotically stable if no testing and culling are conducted, which implies that testing and culling measures can lead to complex dynamics of brucellosis transmission.

Our study has some limitations. Some features of animal culling are still not considered in the model. For example, the disease may spread because of the delayed culling of infected animals. Further, in practice, because of the sensitivity of the test reagents, the test results need to be reconfirmed, and this test process is also not expressed in our model. We need to further consider these aspects.

Acknowledgments

This research is partially supported by the Fundamental Research Program of Shanxi Province (20210302123031, 20210302123019), the National Youth Science Foundation of China (11501528).

Conflict of interest

The authors declare there is no conflict of interest.

References

[1]	T. Barbier, F. Collard, A. Zúñiga-Ripa, I. Moriyón, T. Godard, J. Becker, et al., Erythritol feeds the pentose phosphate pathway via three new isomerases leading to D-erythrose-4-phosphate in Brucella, Proc. Natl. Acad. Sci. U. S. A., 111 (2014), 17815–17820. https://doi.org/10.1073/pnas.1414622111 doi: 10.1073/pnas.1414622111
[2]	P. Andriopoulos, M. Tsironi, S. Deftereos, A. Aessopos, G. Assimakopoulos, Acute brucellosis: Presentation, diagnosis, and treatment of 144 cases, Int. J. Infect. Dis., 11 (2007), 52–57. https://doi.org/10.1016/j.ijid.2005.10.011 doi: 10.1016/j.ijid.2005.10.011
[3]	G. Pappas, P. Papadimitriou, N. Akritidis, L. Christou, E. V. Tsianos, The new global map of human brucellosis, Lancet Infect. Dis., 6 (2006), 91–99. https://doi.org/10.1016/S1473-3099(06)70382-6 doi: 10.1016/S1473-3099(06)70382-6
[4]	H. Zeng, Y. M. Wang, X. D. Sun, P. Liu, Q. G. Xu, D. Huang, et al., Status and influencing factors of farmers' private investment in the prevention and control of sheep brucellosis in China: A cross-sectional study, PLoS Neglected Trop. Dis., 13 (2019), e0007285. https://doi.org/10.1371/journal.pntd.0007285 doi: 10.1371/journal.pntd.0007285
[5]	A. J. S. Alves, F. Rocha, M. Amaku, F. Ferreira, E. O. Telles, J. H. H. Grisi Filho, et al., Economic analysis of vaccination to control bovine brucellosis in the States of Sao Paulo and Mato Grosso, Brazil, Prev. Vet. Med., 118 (2015), 351–358. https://doi.org/10.1016/j.prevetmed.2014.12.010 doi: 10.1016/j.prevetmed.2014.12.010
[6]	Q. Hou, X. D. Sun, J. Zhang, Y. J. Liu, Y. M. Wang, Z. Jin, Modeling the transmission dynamics of sheep brucellosis in Inner Mongolia Autonomous Region, China, Math. Biosci., 242 (2013), 51–58. https://doi.org/10.1016/j.mbs.2012.11.012 doi: 10.1016/j.mbs.2012.11.012
[7]	H. Yoon, O. K. Moon, S. H. Lee, W. C. Lee, M. Her, W. Jeong, et al., Epidemiology of brucellosis among cattle in Korea from 2001 to 2011, J. Vet. Sci., 15 (2014), 537–543. https://doi.org/10.4142/jvs.2014.15.4.537 doi: 10.4142/jvs.2014.15.4.537
[8]	R. M. Davidson, Control and eradication of animal diseases in New Zealand, N. Z. Vet. J., 50 (2002), 6–12. https://doi.org/10.1080/00480169.2002.36259 doi: 10.1080/00480169.2002.36259
[9]	M. Zamri-Saad, M. I. Kamarudin, Control of animal brucellosis: The Malaysian experience, Asian Pac. J. Trop. Med., 9 (2016), 1136–1140. https://doi.org/10.1016/j.apjtm.2016.11.007 doi: 10.1016/j.apjtm.2016.11.007
[10]	N. Zhang, D. S. Huang, W. Wu, J. Liu, F. Liang, B. S. Zhou, et al., Animal brucellosis control or eradication programs worldwide: A systematic review of experiences and lessons learned, Prev. Vet. Med., 160 (2018), 105–115. https://doi.org/10.1016/j.prevetmed.2018.10.002 doi: 10.1016/j.prevetmed.2018.10.002
[11]	P. O. Lolika, C. Modnak, S. Mushayabasa, On the dynamics of brucellosis infection in bison population with vertical transmission and culling, Math. Biosci., 305 (2018), 42–54. https://doi.org/10.1016/j.mbs.2018.08.009 doi: 10.1016/j.mbs.2018.08.009
[12]	L. Bolzoni, R. D. Marca, M. Groppi, A. Gragnani, Dynamics of a metapopulation epidemic model with localized culling, Discrete Cont. Dyn.-B, 25 (2020), 2307–2330. https://doi.org/10.3934/dcdsb.2020036 doi: 10.3934/dcdsb.2020036
[13]	J. Zinsstag, F. Roth, D. Orkhon, G. Chimed-Ochir, M. Nansalmaa, J. Kolar, et al., A model of animal-human brucellosis transmission in Mongolia, Prev. Vet. Med., 69 (2005), 77–95. https://doi.org/10.1016/j.prevetmed.2005.01.017 doi: 10.1016/j.prevetmed.2005.01.017
[14]	M. F. Abakar, H. Yahyaoui Azami, P. Justus Bless, L. Crump, P. Lohmann, M. Laager, et al., Transmission dynamics and elimination potential of zoonotic tuberculosis in morocco, PLoS Neglected Trop. Dis., 11 (2017), e0005214. https://doi.org/10.1371/journal.pntd.0005214 doi: 10.1371/journal.pntd.0005214
[15]	P. van den Driessche, J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Math. Biosci., 180 (2002), 29–48. https://doi.org/10.1016/S0025-5564(02)00108-6 doi: 10.1016/S0025-5564(02)00108-6
[16]	G. H. Li, Y. X. Zhang, Dynamic behaviors of a modified SIR model in epidemic diseases using nonlinear incidence and recovery rates, PLoS One, 12 (2017), e0175789. https://doi.org/10.1371/journal.pone.0175789 doi: 10.1371/journal.pone.0175789
[17]	Y. A. Kuznetsov, Elements of Applied Bifurcation Theory, 3^rd edition, Springer-Verlag, New York, 2004. https://doi.org/10.1007/978-1-4757-3978-7
[18]	D. A. Abernethy, J. Moscard-Costello, E. Dickson, R. Harwood, K. Burns, E. McKillop, et al., Epidemiology and management of a bovine brucellosis cluster in Northern Ireland, Prev. Vet. Med., 98 (2011), 223–229. https://doi.org/10.1016/j.prevetmed.2010.11.002 doi: 10.1016/j.prevetmed.2010.11.002

This article has been cited by:

1.	Zhiguo Liu, Miao Wang, Yingqi Wang, Min Yuan, Zhenjun Li, Retrospective Analysis of the Epidemiological Evolution of Brucellosis in Animals — China, 1951–1989 and 1996–2021, 2024, 6, 2097-3101, 1159, 10.46234/ccdcw2024.235
2.	Shuangjie Bai, Boqiang Cao, Ting Kang, Qingyun Wang, A two-stage sheep-environment coupled brucellosis transmission dynamic model: Stability analysis and optimal control, 2024, 0, 1531-3492, 0, 10.3934/dcdsb.2024126

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

Mathematical Biosciences and Engineering

3.9

Metrics

Article views(2193) PDF downloads(124) Cited by(1)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Mathematical Biosciences and Engineering

Bifurcation analysis of a sheep brucellosis model with testing and saturated culling rate

Related Papers:

Abstract

1. Introduction

2. Basic properties of model

3. Dynamic properties of model

3.1. Stability of equilibria

3.2. Bifurcation analysis

3.2.1. Saddle node bifurcation

3.2.2. Hopf bifurcation

3.2.3. Bogdanov-Takens bifurcation

4. Numerical simulation

5. Conclusions and discussion

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Abstract

1. Introduction

2. Basic properties of model

3. Dynamic properties of model

3.1. Stability of equilibria

3.2. Bifurcation analysis

3.2.1. Saddle node bifurcation

3.2.2. Hopf bifurcation

3.2.3. Bogdanov-Takens bifurcation

4. Numerical simulation

5. Conclusions and discussion

Acknowledgments

Conflict of interest

References

Mathematical Biosciences and Engineering

Bifurcation analysis of a sheep brucellosis model with testing and saturated culling rate

Related Papers:

Abstract

1. Introduction

2. Basic properties of model

3. Dynamic properties of model

3.1. Stability of equilibria

3.2. Bifurcation analysis

3.2.1. Saddle node bifurcation

3.2.2. Hopf bifurcation

3.2.3. Bogdanov-Takens bifurcation

4. Numerical simulation

5. Conclusions and discussion

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. Basic properties of model

3. Dynamic properties of model

3.1. Stability of equilibria

3.2. Bifurcation analysis

3.2.1. Saddle node bifurcation

3.2.2. Hopf bifurcation

3.2.3. Bogdanov-Takens bifurcation

4. Numerical simulation

5. Conclusions and discussion

Acknowledgments

Conflict of interest

References