Expected Value of Multiplicative Degree-Kirchhoff Index in Random Polygonal Chains

1.   Introduction

Throughout this article, all graphs we considered here are finite, undirected and simple connected. We can refer to ^[1,2] for the details of the terminologies and notations mentioned but not defined here. Nowadays, the scholars have done extensive research on chemical compounds by representing vertices as atoms and edges stand for the covalent bonds connecting atoms.

Topological index is one of the most important predicting methods for combining the physicochemical properties with their molecular structures ^[3,4,5,6]. Similar to the other topological indices^[7,8,9], Kirchhoff index is a structure descriptor. The resistance distance is intrinsic to the graph with several physical and purely mathematical explanations ^[10,11]. Meanwhile, the Kirchhoff index has been found useful in assessing cyclicity of polycyclic structures including linear polygonal chains, fullerenes and some other molecular graphs ^[12], such as circulate graphs, distance-regular graphs and so on.

Let $G = (V(G), E(G))$ be a connected graph with $\mid V(G)\mid$ vertices and $\mid E(G)\mid$ edges. For any vertex $m\in V(G)$, denote the degree of $u$ by $d_{G}(u)$(short for d(u)), which is the number of the vertices adjacent to $u$. Klein and Randić^[13] defined the resistance distance based on the power grid theory, and they regarded each edge of the connected graph as a unit resistance, the whole connected graph $G$ is regarded as a power grid $N$. Therefore, the effective resistance of $u$ and $m$ in grid $N$ is the resistance distance between $u$ and $m$, defined as $r(u, m)$. The $r(u, m)$ is the potential difference between $u$ and $m$ of $G$ induced by the particular $u-m$ flow intensity 1 satisfying Kirchhoff's cycle law ^[14]. And the Kirchhoff index of $G$ is denoted by $Kf(G) = \sum_{\{u, m\}\subseteq V_{G}}r(u, m)$.

The multiplicative degree-Kirchhoff index is proposed by Chen and Zhang in 2007 ^[15], which was denoted by

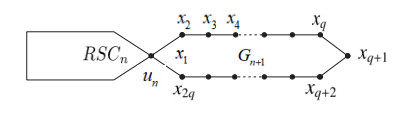
A random polygonal chain $RSC_{n+1}$ with $n+1$ polygons can be considered as a new terminal polygon $G_{n+1}$ has been attached to a polygonal chain $RSC_{n}$ with $n$ polygons through vertex-to-vertex connection, see Figure 1.

For $n\geq 3$, there are $q$ ways to connect the terminal polygon $G_{n+1}$ with front random polygonal chain $RSC_{n}$, which results in the local arrangements, they can be described as $RSC^{1}_{n+1}, RSC^{2}_{n+1}, \cdots, RSC^{q-1}_{n+1}$ and $RSC^{q}_{n+1}$, respectively, see Figure 2.

A random polygonal chain $RSC_{n}$ with $n$ polygons is acquired by adding the terminal polygons step by step. At every step $t( = 3, 4, \ldots, n)$, the connection method is selected from one of the following $q$ possible cases:

● $RSC_{t}\rightarrow RSC_{t+1}^{1}$ with probability $p_{1}$,

● $RSC_{t}\rightarrow RSC_{t+1}^{2}$ with probability $p_{2}$,

● $RSC_{t}\rightarrow RSC_{t+1}^{3}$ with probability $p_{3}$,

$\cdots \cdots$

● $RSC_{t}\rightarrow RSC_{t+1}^{q}$ with probability $p_{q}$,

where $p_{q} = 1-p_{1}-p_{2}-p_{3}-\cdots -p_{q-1}$, and the probabilities $p_{1}, p_{2}, \cdots, p_{q-1}$ and $p_{q}$ are constants, irrelevant to the parameter $t$ We denote by $RSC_{n}(1, 0, \cdots, 0, 0), RSC_{n}(0, 1, \cdots, 0, 0), \cdots, RSC_{n}(0, 0, \cdots, 0, 1), RSC_{n}(0, 0, \cdots, 0, 0)$, the meta-chain $M_{n}$, the orth-chain $O^{1}_{n}$, the orth-chain $O^{2}_{n}$, $\cdots$, the orth-chain $O^{q-2}_{n}$, the para-chain $P_{n}$, respectively.

In ^[16], Huang, Kuang and Deng obtained exact formulas for the expected values of the Kirchhoff indices of the random polyphenyl and spiro chains. Later, Zhang, Li, Li and Zhang ^[17] obtained the expected values for the four indices including Schultz index, Gutman index, multiplicative degree-Kirchhoff index and additive degree-Kirchhoff index of a random polyphenylene chain. Recently, Liu, Zeng, Deng, Tang ^[18], obtained the indices as mentioned above in the random spiro chains, determined the expected values of these indices in the random spiro chain, and the extremal values among all spiro chain with $n$ hexagons.

Motivated by ^[16,18], we consider the expected values of the multiplicative degree-Kirchhoff index of random polygonal chains and explore the property of the multiplicative degree-Kirchhoff index of polygonal chains and determine the expected value of the index $E(Kf^{*}(RSC_{n}))$ in the random polygonal chains with $n$ polygons. This not only proves the correctness of the previous work, but also summarizes the expected value of the multiplicative degree-Kirchhoff index for all polygons containing an even number of edges.

2.   The multiplicative degree-Kirchhoff index of a random polygonal chain

For the random polygonal chain $RSC_{n}$. Denote $RSC_{n+1}$ the graph acquired by connecting a new terminal polygon $G_{n+1}$ to $RSC_{n}$, which is spanned by vertices $x_{1}, x_{2}, \cdots, x_{2q}$ and ${x_{1}}$ is $u_{n}$, (see Figure 1). It is evident that, for all $m\in RSC_{n}$,

Theorem 2.1. The expected value for the multiplicative degree-Kirchhoff index $RSC_{n}(n\geq1)$ of the random polygonal chain is

Proof. Let $Kf^{*}(RSC_{n}) = A+B+C$.

So, $Kf^{*}(RSC_{n+1}) = Kf^{*}(RSC_{n})+4q\sum_{m\in RSC_{n}}d(m)r(m, u_{n})+4q\cdot\frac{4q^{2}-1}{3}n+2q\cdot\frac{4q^{2}-1}{3}$.

For a random polygonal chain $RSC_{n}$, $\sum_{m\in RSC_{n}}d(m)r(m, u_{n})$ is a random variable. Here, we could denote

Thus, a recurrence relation is obtained as follows:

By thinking about the following $q$ possible ways, we can obtain $I_{n}$.

Case 1. $RSC_{n}\longrightarrow RSC_{n+1}^{1}$, then $u_{n}$ coincides with the vertex $x_{2}$ or $x_{2q}$. Hence, $\sum_{m\in V_{RSC_{n}}}r(u_{n}, m)$ is given by $\sum_{m\in V_{RSC_{n}}}r(x_{2}, m)$ or $\sum_{m\in V_{RSC_{n}}}r(x_{2q}, m)$ with probability $p_{1}$.

Case 2. $RSC_{n}\longrightarrow RSC_{n+1}^{2}$, then $u_{n}$ coincides with the vertex $x_{3}$ or $x_{2q-1}$. Hence, $\sum_{m\in V_{RSC_{n}}}r(u_{n}, m)$ is given by $\sum_{m\in V_{RSC_{n}}}r(x_{3}, m)$ or $\sum_{m\in V_{RSC_{n}}}r(x_{2q-1}, m)$ with probability $p_{2}$.

$\cdots \cdots$

Case q-2. $RSC_{n}\longrightarrow RSC_{n+1}^{q-2}$, then $u_{n}$ coincides with the vertex $x_{q-1}$ or $x_{q+3}$. Hence, $\sum_{m\in V_{RSC_{n}}}r(u_{n}, m)$ is given by $\sum_{m\in V_{RSC_{n}}}r(x_{q-1}, m)$ or $\sum_{m\in V_{RSC_{n}}}r(x_{q+3}, m)$ with probability $p_{q-2}$.

Case q-1. $RSC_{n}\longrightarrow RSC_{n+1}^{q-1}$, then $u_{n}$ coincides with the vertex $x_{q}$ or $x_{q+2}$. Hence, $\sum_{m\in V_{RSC_{n}}}r(u_{n}, m)$ is given by $\sum_{m\in V_{RSC_{n}}}r(x_{q}, m)$ or $\sum_{m\in V_{RSC_{n}}}r(x_{q+2}, m)$ with probability $p_{q-1}$.

Case q. $RSC_{n}\longrightarrow RSC_{n+1}^{q}$, then $u_{n}$ coincides with the vertex $x_{q+1}$. Hence, $\sum_{m\in V_{RSC_{n}}}r(u_{n}, m)$ is given by $\sum_{m\in V_{RSC_{n}}}r(x_{q+1}, m)$ with probability $p_{q} = 1-p_{1}-p_{2}-\cdots-p_{q-1}$.

According to the above cases, we have that

And the original value is $I_{1} = \sum_{m\in RSC_{1}}d(m)r(m, u_{1}) = \frac{4q^{2}-1}{3}$. Therefore,

Due to

From the original value,

and the above recurrence relation we may calculate that

The proof is completed.

Specially, if $p_{1} = 1$ which implies $p_{2} = p_{3} = \cdots = p_{q} = 0$, then $RSC_{n}\cong M_{n}$. Similarly, if $p_{2} = 1$ which implies $p_{1} = p_{3} = \cdots = p_{q} = 0$, then $RSC_{n}\cong O^{1}_{n}$; if $p_{3} = 1$ which implies $p_{1} = p_{2} = p_{4} = \cdots = p_{q} = 0$, then $RSC_{n}\cong O^{2}_{n}$ and so on; if $p_{q-1} = 1$ which implies $p_{1} = p_{2} = \cdots = p_{q-2} = p_{q} = 0$, then $RSC_{n}\cong O^{q-2}_{n}$; if $p_{q} = 1$ which implies $p_{1} = p_{2} = \cdots = p_{q-1} = 0$, then $RSC_{n}\cong P_{n}$.

Corollary 2.2. The multiplicative degree-Kirchhoff index of the meta-chain $M_{n}$, the ortho-chains $O^{1}_{n}, O^{2}_{n}, \cdots, O^{q-2}_{n}$, the para-chain $P_{n}$ are

Corollary 2.3. Among the polygonal chains with $n(n\geqslant3)$ polygons, $P_{n}$ realizes the maximum of $E(Kf^{*}(RSC_{n}))$ and $M_{n}$ realizes that of the minimum.

Proof. On the basis of Theorem 2.1, we have

as $n\geq3$, we have that

When $p_{1} = p_{2} = \cdots = p_{q-1} = 0$ (i.e. $p_{q} = 1$), ${P_{n}}$ realizes the maximum of $E[Kf^{*}(RSC_{n})]$, that is $RSC_{n}\cong {P_{n}}$. If $p_{1}+p_{2}+\cdots+p_{q-1} = 1$, let $p_{q-1} = 1-p_{1}-p_{2}-\cdots-p_{q-2} \ (0\leq p_{l}\leq1, l\in[1, q-2])$, we have

Thus,

But $p_{1} = p_{2} = \cdots = p_{q-2} = 0$ (i.e. $p_{q-1} = 1$), $E(Kf^{*}(RSC_{n}))$ can't attain the minimum value. If $p_{1}+p_{2}+\cdots+p_{q-2} = 1$, let $p_{q-2} = 1-p_{1}-p_{2}-\cdots-p_{q-3} \ (0\leq p_{l}\leq1, l\in[1, q-3])$.

Thus,

But $p_{1} = p_{2} = \cdots = p_{q-3} = 0$ (i.e. $p_{q-2} = 1$), $E(Kf^{*}(RSC_{n}))$ can't attain the minimum value. By that analogy, If $p_{1}+p_{2} = 1$, let $p_{1} = 1-p_{2} (0\leq p_{2}\leq1)$.

Thus,

Hence, $E(Kf^{*}(RSC_{n}))$ achieves the minimum value, if $p_{2} = 0 \ (i.e. \ p_{1} = 1)$, that is $RSC_{n}\cong {M_{n}}$. This completes the proof.

3.   Average value of the multiplicative degree-Kirchhoff index

Denote by $\overline{\xi_{n}}$ the set of all polygonal chains with $n$ polygons. In this paragraph, We can characterize the average value of the multiplicative degree-Kirchhoff index with respected to $\overline{\xi_{n}}$.

Theorem 3.1. The average value for the index with respect to $\overline{\xi_{n}}$ is

Proof. In order to obtain the average $Kf^{*}_{avr}(\overline{\xi_{n}})$, it suffices to take $p_{1} = p_{2} = \cdots = p_{q} = \frac{1}{q}$ in the expected value $E(Kf^{*}(RSC_{n}))$. According to Theorem 2.1, we have

After verification, the equation is

4.   Comparative analysis

In contrast to the articles wrote by Zhang, Li, Li and Zhang ^[17] and Liu, Zeng, Deng, and Tang ^[18], we used a similar method to prove the expected value of the index. But here is the difference, the former calculated the expected values for the indices of a random polyphenylene chain which is consist of $n$ hexagons connected by the cut edges randomly. The latter established the expected values of the above-mentioned four indices in a random spiro chain which is consist of $n$ hexagons which connected by squeezing the cut edges so that the two vertices coincide. However, the figure we study consists of $n$ polygons, each has $2q$ edges. That is to say, we can get multiplicative degree-Kirchhoff index of any even polygon by plugging in the number of edges of the polygon.

5.   Concluding remarks

We mainly established the explicit formulas for the expected value of the multiplicative degree-Kirchhoff index of a random polygonal chain, discussed the maximum value and the minimum value of the $E(Kf^{*}(RSC_{n}))$ ^[19,20], meanwhile, obtained the extremal value and average value of the index. All these results will be useful to the study of the topological index of graphs and build some kind of mathematical model from the structure of the chemical, then use that model to predict the activity and the physicochemical properties of more novel compounds, which can provide the microscopic basis for new molecules in synthetic chemistry ^[21,22].

In chemical graph theory, the matter of polygonal chain is being widely studied by researchers ^{[23,24,25,26]}. The molecular structures of polygonal chemicals are various and its physicochemical properties also become more and more important ^{[27,28,29,30]}. It is possible to establish exact formulas for the expected values of some other indices in random polygonal chains with $n$ regular polygons.

Acknowledgments

Valuable, comments and suggestions from the editor and anonymous reviewers are appreciatively acknowledged. This work is partially supported by National Science Foundation of China(Grant No.12171190), Natural Science Foundation of Anhui Province(Grant No.2008085MA01) and Youth fund of Anhui Natural Science Foundation(Grant No.2008085QA01).

Conflict of interest

The authors declare that they have no competing interests.