A data-validated temporary immunity model of COVID-19 spread in Michigan

1.   Introduction

The novel coronavirus SARS-CoV-2 was first identified in Wuhan, China during December 2019 and within months became the deadliest pandemic since the 1918 Spanish flu. Since the beginning of the COVID-19 pandemic, assessing and predicting the epidemiological characteristics, transmission routes, and disease dynamics has been a primary focus of mathematicians, theoretical biologists, and epidemiologists alike ^[1,2]. A common mathematical modeling framework for tracking and forecasting the disease's spread has been that of compartmental models which incorporate at least the susceptible, infectious and recovered individuals ^[3]. Such SIR-type models have been utilized to estimate key epidemiological parameters of SARS-CoV-2, such as the transmission rate and basic reproduction number ^[4,5,6,7]; forecast disease spread under a variety of public policy interventions, including universal face-masking, school closures, and lockdowns ^[8,9,10,11]; and predict the disease burden under a variety of vaccine rollout strategies ^[12,13,14]. Incorporating spatial aspects of disease spread has also been considered in ^[15,16,17]. Despite this significant research attention and the unprecedented haste of vaccine development, however, COVID-19 has continued to spread widely even in regions with relatively high vaccination rates.

A key factor in the persistence of COVID-19 is suspected to be waning immunity, whereby individuals become less protected from infection the further they are away from a previous infection or from their last inoculation ^[18,19]. How to best incorporate waning immunity into SIR-type models of COVID-19 spread, however, remains unsettled. A typical approach has been to incorporate waning immunity through a direct transition back to the susceptible class ^[1,20,21]. This leads to an exponential distribution for the waiting time for loss of immunity which is peaked at time zero. Evidence, however, suggests that previous COVID-19 infection and vaccination provide good protection for most people for several months before waning.

An alternative formulation is to suppose that every individual in the population obtains absolute immunity for the same fixed period of time. This was the approach of Brauer and Castillo-Chavez ^[22] who considered the following system of delay differential equations (DDE) where $S(t)$, $I(t)$ and $R(t)$ are the susceptible, infectious and recovered individuals at time $t$:

where $\beta$ is the transmission rate, $\alpha$ represents the recovery rate and the temporary immunity period of fixed length is $\omega$. In this model, recovered individuals return to the susceptible class after a fixed length of time, $\omega$, so that the immunity period distribution is peaked as a point mass at $\omega$. The model has several drawbacks as a realistic model of disease spread. The authors showed that the endemic equilibrium undergoes a Hopf bifurcation, leading abruptly to the emergence of periodic solutions, which makes it difficult for policy makers to plan healthcare logistics and allocate resources. Furthermore, significant person-to-person variability in the duration of vaccine-induced immunity has been observed, both in longitudinal studies of COVID-19 vaccine antibody responses ^[19] and real-world vaccine efficacy ^[18].

Given the shortcomings of the exponentially and point-mass distributed immunity periods, we propose an intermediate gamma-distributed immunity period. Specifically, we propose a formulation that uses a distributed delay on the immunity periods:

where $g^{p}_{a}(\tau)$ is the gamma distribution

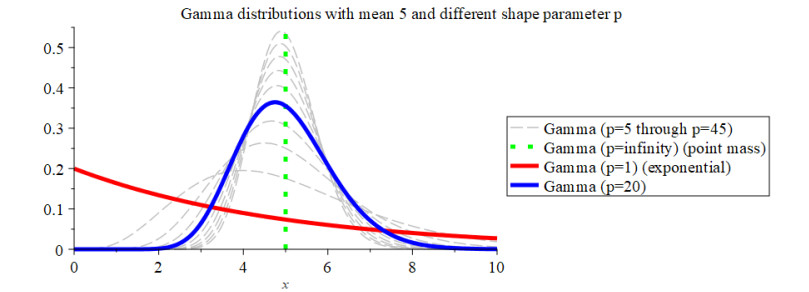
with rate parameter $a > 0$ and shape parameter $p > 0$. The gamma distribution is a natural choice as it provides a bridge between the classical exponential distribution resulting from a direct transition back to susceptibility and the point-mass distribution resulting from a fixed-delay as in (1.1) (see Figure 1).

We note that other approaches have been taken for incorporating waning immunity into disease spread models, including partial differential equation and other delay-differential equation models. In work by Carlsson et al., an age structured model consisting of partial differential equations incorporated waning immunity following natural infection or immunization ^[23]. In a study by Hamami et al., waning immunity was found to be associated with periodic large outbreaks of mumps in Scotland ^[24]. A general framework for modeling SIRS dynamics, while monitoring the immune system status of individuals and including waning immunity and immune system boosting was proposed by Barbarossa ^[25]. Furthermore, under certain assumptions their framework reduces to a delay differential equation model with constant delay that was studied by Taylor et al. in ^[26]. A five-stage loss of immunity model, which is equivalent to a gamma-distributed waning immunity period, has also been recently presented in ^[27].

In this paper, we propose a mathematical model consisting of a system of distributed delay differential equations to assess the effect of temporary immunity from COVID-19 infection and vaccination. The model builds off existing work on COVID-19 modeling by using a more realistic distributed delay for waning immunity, allows for the study of the entwined dynamics of infection-based and vaccination-based immunity and how they influence disease spread and mitigation strategies. We calibrate the model to COVID-19 case and vaccination data from Michigan, show the model's efficacy, and study the sensitivity of the model trajectories with respect to the temporary immunity period and other model parameters. We use the calibrated model to forecast disease burden under different booster shot intervals and population-wide uptake rates.

2.   Mathematical model

In this section, we introduce our mathematical model for incorporating vaccination uptake and temporary immunity, describe our model for vaccination uptake, and conduct basic model analysis, including determining the basic reproduction number of the model.

2.1.   Vaccination with temporary immunity model

We consider a compartmental model where $S(t)$, $I(t)$, $H(t)$, $R(t)$ and $D(t)$ represent the number of susceptible, infectious, hospitalized, recovered, and deceased individuals at time $t$, and $V(t)$ represent the total number of fully vaccinated individuals at time $t$. We introduce the following vaccination with temporary immunity model which incorporates waning immunity from vaccination and previous infection:

where solid arrows $\to$ correspond to direct exponentially-distributed transitions, and squiggly arrows correspond to delayed gamma-distributed transitions. In the model (2.1), susceptible individuals become infectious when they come in contact with infectious individuals at a rate controlled by $\beta(t)$. Infectious individuals can either recover at rate $\gamma$, or become hospitalized at rate $h$. Hospitalized individuals in turn either recover at rate $\gamma$, or become deceased at rate $\delta$. Susceptible individuals vaccinate at a rate $V'(t)$, the time-derivative of the cumulative vaccination uptake curve $V(t)$, and return to susceptibility at a delayed rate. Recovered individuals also return to susceptibility at a delayed rate. Note that, for model simplicity, we have assume infected individuals are immediately infectious (i.e., there is no latency period of exposed class), that infectious and hospitalized individuals recover at the same rate $\gamma$, and that only hospitalized individuals may become deceased.

To build a dynamical model from (2.1), we assume that the transition rates follow the classical mass action law and that the periods of temporary immunity granted by vaccination and infection follow a gamma distribution with the same shape parameter $p$, but different rate parameters $a_x$ and $a_y$, respectively. The system of delay differential equations corresponding to the vaccination with temporary immunity model (2.1) are consequently the following:

Note that we do not include an explicit equation for the recovered class $R(t)$. Rather, individuals are removed from the infectious and hospitalized classes at a rate proportion to $\gamma$ and then return to the susceptible class at a delayed gamma-distributed rate.

Initial conditions are prescribed by:

where $\phi_i$, $i = 1, 2, 3, 4,$ are bounded continuous functions and $s\in\left(-\infty, 0\right]$. See Table 1 for further explanation of the model parameters, their units, and their interpretations. To accommodate the changing transmission dynamics due to changes in public policy and social behavior, we include a time-dependent piecewise-constant transmission rate

This transmission rate function allows the disease's transmission rate in a population to be changed once at a predetermined time $t_{fit}$. Note that both the transmission rates $\beta_1$ and $\beta_2$ and the transition time $t_{fit}$ can be fit to data.

2.2.   Vaccination uptake curve

To model the vaccination uptake curve, we use the Richards' curve ^[28]:

We only consider fully vaccinated individuals so that the curve $V(t)$ corresponds to the cumulative people who have received their second dose of Pfizer-BioNTech or Moderna or their first shot of Johnson & Johnson by time $t$. $M$ represents the maximum number of fully vaccinated individuals, $r$ is the vaccination uptake rate, $a$ represents a vaccination shape parameter, and $t_v$ corresponds to a time shift. The time-derivative of (2.5) is given by:

and gives the number of new vaccinations per day. We elect to use the Richards' curve for its simplicity and quality of fit to the vaccination data (see Figure 2). The Richards' curve was previously used to model the uptake rate of first and second vaccination doses in ^[14]. We point out the nonnegativity of solutions is dependent on the vaccination uptake function, $V(t)$. That is, it's possible that $V(t)$ could drive the susceptible individuals negative if the delay is sufficiently long. However, since we are determining $V(t)$ based on real-world data and not theoretical considerations we leave it as an open problem to determine the theoretical restrictions required on the form of $V(t)$ and its relation to the delays needed for nonnegativity of solutions.

2.3.   Gamma-distributed immunity period

To better understand the delay-distributed terms in (2.2), we note that the substitution $u = t-\tau$ yields:

Therefore, removed individuals revert back to the susceptible class after spending a mean time of $\frac{p}{a_x}$ time units in $R$, given by the gamma distribution. However, instead of a discrete delay as in (1.1), $\tau$ is distributed according to the gamma probability distribution with rate parameter $a_x$ and shape parameter $p$:

where $\Gamma(p) = \int_0^\infty x^{p-1} e^{-x} \; dx$ is the gamma function (see Figure 1). A similar argument shows that vaccinated individuals revert back to the susceptible class $\tau$ units later based on a gamma probability distribution with shape parameters $p$ and $a_y$. We note that we use the same parameter $p$ for both temporary immunity granted from vaccination and infection, but different shape parameters $a_x$ and $a_y$.

If the shape parameter $p$ is an integer (i.e., $p = 1, 2, \ldots, n$) then we may transfer the gamma-distributed delays into a sequence of direct exponentially-distributed delays through a process known as the linear chain trick ^[29,30,31]. This can be seen by noticing that, if $p$ is an integer, then the distribution (2.7) reduces to the Erlang distribution

The functions (2.8) satisfy the initial-value problem

for $j = 2, \ldots, p$. This allows us to transform the integral distributed delays in (2.2) into a system of ordinary differential equations. To accomplish this, we introduce the variables

for $j = 1, 2, \ldots, p$. Differentiating (2.3) and using (2.9) converts the model (2.2) into the following equivalent system of ordinary differential equations:

Initial conditions are calculated using

where $\phi_i$, $i = 1, 2, 3, 4$, are defined above in (2.3) and

where initial histories $\phi_2(s)$ and $\phi_3(s)$ are estimated by interpolation based on the available case data. $\phi_5(s)$ is calculated by interpolating vaccination case data prior to the start date, 20 February 2021. Due to unavailable hospitalization data, $\phi_3(s)$ was set to zero but $\phi_3(0) = 300$. Integration in (2.12) was performed using the trapezoidal rule and its built-in MATLAB implementation $\texttt{trapz}$. $S(0)$ was calculated based on the following formula:

where $R(0)$ and $V(0)$ are the initially recovered and vaccinated individuals, respectively. For simplicity in initial conditions, we assume that there are no reinfections or infected vaccinated individuals by time $t = 0$. This transformation to a system of ordinary differential equations allows one to easily simulate the model using numerical schemes designed for systems of ordinary differential equations.

The linear chain trick corresponds to replacing the gamma-delayed transitions $R$ $S$ and $V$ $S$ in (2.1) with the following sequence of $p$ direct exponentially-delayed transitions:

That is, we break the recovered and vaccinated classes into holding states $X_1, \ldots, X_p$, and $Y_1, \ldots, Y_p$ which delay the conversion from $R$ to $S$ and $V$ to $S$, respectively. Intuitively, this fits well with the understanding of the Erlang distribution as the waiting time for the $p^{th}$ occurrence of an exponentially-distributed event; in this case, it is the waiting time for passing through $p$ exponentially-distributed holding states.

2.4.   Basic and effective reproduction number

The basic reproduction number is the average number of new cases arising from one primary infectious individual in an entirely susceptible population. The reproduction number can be calculated using the next generation matrix method ^[32,33]. For model (2.2) the basic reproduction number takes the form:

where $V(0)$ is the number of individuals vaccinated at the start of the simulation. To account for the dynamics of the spread of the disease over time, we compute the effective reproduction number:

2.5.   Model fitting techniques

We first fit the Richards curve (2.5) to vaccination data to estimate $M$, $a$, $r$ and $t_v$ (see Figure 2) using R Studio ^[34]. We utilize vaccination uptake data from ^[35] which has a live version available at https://github.com/owid/covid-19-data/tree/master/public/data/vaccinations. We consider vaccinated to be fully vaccinated, which at the time of this study corresponded to two vaccine shots of Pfizer-BioNTech or Moderna or one shot of Johnson & Johnson. We use daily cumulative case and death data of COVID-19 from the state of Michigan between 20 February 2021 and 16 October 2021 taken from ^[36].

Using the fitted parameters from the Richards Eq (2.5), we numerically solve model (2.10) using the built-in MATLAB function $\texttt{ode45}$ with $p = 20$ and a given parameter vector $\theta$ (see Table 2 for parameters in $\theta$), and fit the model to Michigan COVID-19 cumulative case and death data from 20 February 2021 to 17 October 2021. Specifically, we let $\hat{x}(t_i, \boldsymbol{\theta})$ be the model solution for the rate of change of the cumulative cases given parameter vector $\boldsymbol{\theta}$ at time point $t_i = 1, \ldots, T$ (in days). We denote the model solution corresponding to the cumulative deaths as $\hat{y}(t_i, \boldsymbol{\theta})$. We let $\textbf{x} = [x_i]$ be the corresponding vector of the rate of change of the cumulative COVID-19 cases and $\textbf{y} = [y_i]$ be the cumulative deaths. The built-in MATLAB functions $\texttt{fminsearch}$ and $\texttt{multistart}$ were used to minimize the following normalized objective function that accounts for daily new cases and cumulative deaths ^[37]:

where $T$ is the total number of data points,

For further reading on estimating parameters in delay differential equations see ^[38].

3.   Main results

In this section, we outline the main results obtained from fitting the vaccination with temporary immunity model (2.2) to vaccination and COVID-19 cases data using the techniques outlined in Section 2.5.

3.1.   Model fitting

We fit the Richards' curve to the cumulative number of daily vaccinations that resulted in an individual becoming fully vaccinated in the state of Michigan. This gave us an estimation for $\frac{dV}{dt}$. We use 20 February 2021 and 17 October 2021 as the starting and ending date, respectively. The best fit curve is shown in Figure 2 where the curve $V(t)$ is represented as a proportion of the entire Michigan population. Parameter estimates are: $M = 5,115,000$, $a = 0.7279$, $r = 0.0323$ and $t_v = 52.82$.

Solution trajectories of model (2.10) corresponding to the fitted model parameters using the procedure discussed in Section 2.5 are shown in Figure 3. Fitted parameters are summarized in Table 2. We find that the mean duration of immunity for vaccination and natural immunity are 350 days and 242 days, respectively.

Model trajectories capture the overall trend of the new observed cases and cumulative cases COVID-19 in Michigan over the simulated time period. However, we note that the model fitting for deceased data is an overestimate near the end of the simulation. We believe this phenomenon can be accounted for by improvements in medical practices and resource availability, which have lowered the disease mortality rate. This is not accounted for in our model.

3.2.   Local sensitivity analysis

Sensitivity analysis is a method for determining which output variables are most sensitive to small parameter perturbations. By observing that small changes to a parameter induce small changes to model dynamics and therefore the output variables, one can feel confident about overall conclusions even if the parameter is unknown in the literature. In contrast, a parameter that when perturbed slightly produces a large change in the model dynamic shows that that parameter is very influential in the model and should be carefully estimated. In addition, sensitivity analysis allows quantitative insights into how model predictions change as parameters are changed. This can be useful in understanding how slight changes in real-world processes can influence the dynamics of COVID-19.

We use the following derivative-based method to calculate local sensitivity functions of model outputs. Let $y(t, \boldsymbol{\theta})$ be the output variable at time $t$ with vector of parameters $\boldsymbol{\theta} = (\theta_1, \theta_2, ..., \theta_k)$ from a model with $k$ parameters. Then the normalized sensitivity function of $y$ with respect to parameter $\theta_i$ is given by ^[39] as:

Notice that the sensitivity function with respect to $\theta_i$ is a function of $t$. Since these are normalized sensitivity functions, we interpret the results of $s_i(t)$ in terms of percent increase or decrease. That is, a $1\%$ increase in $\theta_i$ would result in a $s_i(t)\%$ change in the model output variable $y(t, \boldsymbol{\theta})$ at time $t$. In addition to understanding how parameters influence model dynamics, sensitivities also tell us which parameters have similar effects on model dynamics. We point readers to ^[40] for sensitivity analysis of dynamical systems with time-lags.

We approximated the derivative in (3.1) with a finite difference approximation:

Our analysis shows the model is quite sensitive to vaccination-related parameters (Figure 4) and with intuitive outcomes. In particular, a 1% increase in the maximum vaccination total ($M$), resulted in a 5% decrease in cumulative cases near the end of November. In general, small increases in $M$, result in decreases in cumulative cases. Additionally, an increase in vaccination uptake ($r$) caused a decrease in the number of cumulative cases. We found that a 1% increase in $M$ resulted in a decrease in the effective reproduction number between March and September 2021. After September, the sensitivity index for $R_t$ increased to a maximum of around 2% at the end of November. In a similar fashion, small increases to vaccination uptake ($r$) resulted in a maximum of $0.4\%$ decrease between March and September. After September, the sensitivity index for $R_t$ increased to a maximum of $0.7\%$ near the start of November. See Figure 4 for more details.

In general, hospitalization rate and recovery rate decrease cumulative cases. However, $h$ and $\gamma$ impact the effective reproduction number in a non-trivial way. For example, increases to recovery rate ultimately introduces more susceptible individuals and can increase the effective reproduction number. See Figure 4 for more details.

Lastly, we investigated the cumulative cases and effective reproduction number with respect to the gamma distribution rate parameters $a_x$ and $a_y$. Our findings suggest that cumulative cases are more sensitive with respect to $a_y$ than $a_x$. This is most likely due to the larger number of fully vaccinated individuals when compared to the total number of infected individuals that recovered. We find that, small increases to either $a_x$ or $a_y$ produce increases in cumulative cases. Intuitively, these findings suggest that a decrease in temporary immunity duration (either natural or vaccination induced) have an overall increasing effect on cumulative cases and disease transmission. We note that the effective reproduction number is influenced in a non-trivial way by $a_x$ and $a_y$, but becomes more sensitive later in the simulation when recovered or vaccinated individuals re-enter the susceptible class. See Figure 4 for more details.

3.3.   Perturbations to the mean duration of immunity

Motivated by the sensitivity analysis results, in this section we investigate the model predictions based on changes to the immune duration period that is given by either infection or vaccination. In this spirit, we perturb the rate parameters $a_x$ and $a_y$ by 25% of their fitted values from Table 2. These perturbations result in a mean natural immunity period range of 194 and 323 days. These changes to the mean result in an increase of 223,000 cumulative cases by 25 December 2021 or a decrease in 249,000 cumulative cases, respectively. Similarly, we obtain a mean vaccination immunity period of 280 and 467 days. These changes to the mean result in an increase of 1,666,800 cumulative cases or a decrease in 600,000 cumulative cases, by 25 December 2021, respectively. New observed cases from the model prediction suggest that the model is highly sensitive to changes in $a_y$ and therefore the vaccination immunity period. In contrast, perturbations to the $a_x$ and therefore the immunity period given by natural immunity is not as sensitive. Plots of the model trajectories are displayed in Figure 5.

3.4.   Predictions based on different vaccine strategies

We use the model to simulate different scenarios of vaccination coverage and forecast solutions into the future. Specifically, we introduce a $5$ and $10\%$ increase or decrease to the maximum vaccination total, $M$, after $t = 0$. That is, these simulations use initial conditions based on an unperturbed maximum vaccination total, $M$. Model predictions are presented in Figure 6. We see that with a population that is 10% less vaccinated would have resulted with an additional 300,000 cases of COVID-19 by December 25, 2021. In addition, due to the temporary immunity to the disease we see an earlier increase in cumulative cases roughly starting around the beginning of August. In contrast, the model predicts that a 10% increase in vaccination would have resulted in a 1,361,000 reduction in COVID-19 cases by 25 December 2021. We have also included the model predictions for 5% increase and decreases to $M$ in Figure 6. These changes resulted in a 128,000 increase and 502,500 decrease in cumulative cases by 25 December 2021.

3.5.   Disease burden explorations based on vaccination strategies

We use the calibrated model to make future predictions of disease burden based on different vaccination strategies. We run the model through 1 January 2024 and simulate four scenarios: 1) three vaccination programs that are 280 days apart and with 90% of the original number of vaccinated individuals participating; 2) three vaccination programs that are 280 days apart and with 90% of the previous vaccinated cohort participating; 3) three vaccination programs that are 365 days apart and with 60% of the original number of vaccinated individuals participating; 4) three vaccination programs that are 365 days apart and with 60% of the previous vaccinated cohort participating. We decided to include scenarios 2 and 4 to forecast the disease spread based on waning interest in receiving the vaccine. That is, we model the possibility that social sentiment of the severity of COVID-19 and the need for vaccination shots may change over time. Specifically, we define the number of new vaccinations per day as

where $i = 0, 1, 2, 3,$ correspond to the $i$th vaccination program and $i = 0$ is the original vaccination program. We define $M_0 = M$ and $r_0 = r$ (see (2.6)). In summary, we model each succeeding vaccination program using the Richards' curve from (2.6). We specify parameters used in each vaccination program in Table 3.

Results from the four vaccination scenarios create multiple waves of infection due to loss of immunity and resurgence in the disease (see Figure 7). However, scenarios 1 and 2 provide time periods where the infection is nearly cleared, which realistically could result in stochastic extinction of the disease. In contrast, scenarios 3 and 4 produce endemic situations where the vaccination programs cannot eliminate the disease. Scenarios 2 and 4 (waning interest in vaccination participation) produce two different outcomes based on the percent of individuals previously vaccinated. This suggests that having a high participation rate in the vaccination program is essential to creating scenarios where the disease can be stochastically eliminated.

4.   Discussion

This simulation study used an epidemic compartmental model that included susceptible, infectious, hospitalized, removed and deceased individuals to understand COVID-19 dynamics in Michigan. Our model accounted for temporary immunity of COVID-19 from both vaccination and previous infection by using a distributed DDE framework. Assuming that both the distributed delays follow a gamma distribution, we used the linear chain trick to convert the distributed DDE system into a multi-stage ordinary system of differential equations ^[29,31,42]. We then calibrated the model to Michigan COVID-19 cases, death, and vaccination data from 20 February 2021 to 17 October 2021 to understand and quantify how temporary immunity influences disease dynamics.

Our choice to use a gamma distribution to model the immune duration is based on mathematical simplicity and the fact that it allows the distributed delay differential equation system (2.2) to be converted into a multi-stage system of ordinary differential equations through the linear chain trick. However, recent work has generalized the linear chain trick for other distributions ^[29,43,44].

Our main modeling assumption in this paper is based on studies which suggest that individuals that have received immunity, either from an infection or a vaccine, will lose that immunity over a period of time. However, the cause of this loss of immunity is not specified in our model. In fact, there are many possible reasons why immunity might be lost. One possible reason is the evolution of the virus to a different variant which may reduce the effectiveness of vaccines or natural immunity from a previous strain. For example, the rise of COVID-19 variants such as B.1.1.7 (alpha), B.1.617.2 (delta), and B.1.1.529 (omicron) ^[45]. Another possible reason is the natural decline of COVID-19 antibodies in a vaccinated individual over time ^[46]. In absence of temporary immunity (so that recovered individuals do not return to $S$), we find that the model vastly underestimates the number of daily COVID-19 cases (bottom row, Figure 5), suggesting that temporary immunity is a significant mechanism for understanding the spread of COVID-19 in the future.

Between 1 July 2021 to 1 November 2021 we notice a more linear increase in the number of new observed cases in Michigan (see Figures 3 and 5). Our modeling exercise suggests that immunity duration and the distribution it follows can lead to linear growth in observed cases through the mechanism of gradually reintroducing removed individuals to the susceptible class. We add that, linear and polynomial growth of daily cases for infectious diseases have been observed in multiple case studies with different transmission mechanisms during the initial ascending phase ^[47,48].

Multiple reasons may explain the increase in the transmission rate from 0.39 to 0.71 days$^{-1}$ at the estimated value $t_{fit}\approx 116$ days, which corresponds to July 16, 2021, in the simulation. We find that the timing in the increase of the transmission rate happens around the emergence and rise of B.1.617.2 (delta) in Michigan and may be one explanation for this change in transmission ^[49]. Another reason may be the lifting of face mask requirements and capacity restrictions a month before on June 22 in Michigan ^[50]. Moreover, by including waning immunity, we obtain a better model fit to the data with fewer changes to the transmission rate than what was found in a study of COVID-19 spread in Virginia ^[14].

The mathematical model that we used in this study is subject to limitations. Most importantly, our modeling effort relies heavily on the distribution of the temporary immune period, which we assumed for simplicity follows a gamma distribution. Our model is strictly designed to consider temporary immunity from natural and vaccine-induced immunity, it does not incorporate demographic processes such as birth and natural death processes. In addition, the model does not include mitigating effects that occur from policy changes such as lock-downs or travel restrictions. However, the increase in the piece-wise transmission rate, $\beta(t)$, could be interpreted as an increase in transmission rate due to school openings or decreased social distancing practices (see Table 2). In addition, at the time of this modeling, B.1.617.2 (delta), became the dominant strain in Michigan and our model does not incorporate multiple strains of COVID-19. We believe the above are fruitful directions to consider for future research.

Conflict of interest

The authors declare there is no conflict of interest.