On degree–based topological indices of random polyomino chains

1.   Introduction

Speech problems are linked to negative effects on quality of life, significant indirect costs of speech-related work, short-term demands and projections of costs of primary health care approximately ＄5 billion a year all over the world ^[1]. Dysphony diagnosis may include medical therapy, surgery, and/or speech therapy. Speech therapy can either be used as the primary mode, as an alternative to or as a medium for treatment assistance. Voice therapy in patients with muscles tension dysphony and benign phono-traumatic vocal fold lesions, degeneration of the vocal folds associated with age, disorders of the neurons (incl. Parkinson's disease) and disorders of the voice associated with reflux was shown to be effective. To date, most studies of voice therapy have been carried out in university tertiary voice clinics, whereas further studies on use of speech therapy have been conducted by otolaryngologists who are subject to bias recall ^[1]. In what is perceived as a' normal voice' there is a huge variation. It is problematic to determine its essential properties because a continuum exists between a normal and a disordered voice. A normal voice is essentially in quality unnoticeable and allows sufficient communication and unnecessary effort or inconvenience. Hoarseness is a word that describes an abnormal, harsh, breathy, weak or strained voice quality. A voice problem or dysphony can be defined by structural or functional anomaly of the voice mechanism as any impaired, limited or restricted activity or participation in (world health organization) ^[2]. Vocal production of the voice may be specified by fundamental frequency, intensity, vibration and vocal intonation according to its vocal parameters. The perceptional correlates of frequency are known as pitch or subjective level sensations that are appropriate for age and sex and are known as loudness or subjective noise sensations that are suitable for the environment. ^[3]. A person's voice displays these features as gender, age, emotional state and cultural heritage ^[4]. This represents individual identity and makes it possible to differentiate between individuals. The voice represents different aspects of the individual's physical, social, cultural and psychological development at different stages of life infancy, puberty, adulthood and aging ^[5]. A good voice satisfies the professional and/or personal needs of the individual of full, and is held comfortable in a person's life. Expression quality may be affected by hormonal changes, asthma, disease, blood vessels, neurology and emotional disorders, operations or other general health-related factors ^[3]. There are however no universal criteria to determine the characteristics and limits of a normal voice and certain shifts in voice during a vocalization are anticipated and socially acceptable. But some developments cannot be as indicators of social or emotive expression, despite taking such changes into account. Such changes are then called dysphonia ^[4]. Voice disorders manifest in various ways, including the presence of sensory and auditory symptoms, deviations in vocal quality and functional and/or structural laryngeal changes that may involve behavioral and/or organic factors associated with their genesis and maintenance ^[5]. These disorders can have a negative impact on the patient's quality of life, compromising social, emotional, and work-related situations ^[6,7]. Patients with voice disorders may experience various symptoms, of which hoarseness, sore throat, vocal fatigue, and throat clearing are the most common. These symptoms may be associated with intense voice use, upper respiratory tract infections, stress, and smoking ^[8]. Because manifestation of a voice disorder is multidimensional, its assessment must include a variety of factors, including perceptual voice assessment, visual laryngeal inspection, acoustic analysis, aerodynamic assessment, and vocal self-assessment ^[9]. Voice Pathology disorders can be detected using the classification tools for computer helped voice pathology. Language pathology recently focused on the techniques of machine learning. These tools can early diagnose and offer adequate treatment for voice pathologies. Clinical voice pathology is detected by several procedures, including acoustic analysis. Voice disorder services are available for the study of the auditory behavior of voices suffering from different forms of vocal disabilities in hospitals as much as in electronic voice disorder detection systems. The assessment of pain, such as dysphonia, is an essential factor of the medical evaluation and treatment of man's voice. In addition to larynx and vocal fold endoscopic testing, visual and acoustic measurement techniques are crucial components in the clinical evaluation of dysphonia. It consists of the calculation, in compliance with SIFEL Recommendations ^[10] Edicts and Phoniatrics, following the instructions of the Phoniatrics Committee of the European Society of Laryngology to identify certain modifications to the vocal tract, the relevant parameters obtained from the voice signal. It is, in contrast to other medical tests, a non - invasive clinical trial by direct observation of vocal folds, for example ^[11,12]. For medical diagnosis, the use of classifier systems slowly increases. The development of specialist networks and decision support (DSS) technologies for medical applications has led to the recent advancement in the field of artificial intelligence. Expert systems and various artificial detection intelligence methods had the ability to be good medical devices. Classification systems may contribute to the increase in precision, accuracy and reliability of diagnosis and the reduction of possible errors ^[13].

The first database that is used in this review is Saarbruecken Voice Database (SVD) ^[14]. A collection of voice recordings by over 2000 people. 1) Vocal registration [I a, u] produced at standard, high and low pitches. The truth was recorded in a recording session. 2) Vocal documentation of increasing pitch [I a, u]. 3) Recording of the phrase'' Good morning, how do you like it?''(' How are you, good morning?'). The voice signal and the EGG signal were stored in individual files for the specified components. The database has text file includes all relevant information about the dataset. Those characteristics make it a good choice for experimenters to use. All recorded SVD voices were sampled with a resolution of 16-bit at 50 kHz. There are some recording sessions where not all vowels are included in each version, depending on the quality of their recording. The' Saarbruecken Voice Server' is available via this web interface. It contains multiple internet pages which are used to choose parameters for the database application, to play directly and records and pick the recording session files which are to be exported after chosen desired parameter from SVD database.

The second database that is used in this review is Massachusetts eye and ear infirmary (MEEI) ^[15]. Contains over 1,400 vocal tests of the long vowel / a/ and the first portion of the Rainbow passage, created by MEEI Voice and Speech Lab. It has been sold in two distinct surroundings by Kay Elemetrics ^[16]. The sampling frequency was 50 kHz, while the response frequency for normal samples was 25 kHz or 50 kHz, respectively. It is used in most voice pathology detection and classification experiments although the different conditions and sound levels used to capture normal and pathological voice have many drawbacks. In this collection, some tools, such as stroboscopy, auditory aerodynamics and physical neck and mouth tests, were used to assess speech disorders (this information was provided by Kay Elemetrics).

The third database that is used in this review is Arabic voice pathology database (AVPD) ^[15]. Samples of words and voices were recorded at various sessions in King Abdul Aziz University Hospital in Riyadh, Saudi Arabia, Communication & Swallowing Disorders Unit. In a sound treatment room, a standard recording protocol was used to collect voices of the patient by experienced phoneticists. The database protocol has been developed to prevent specific MEEI data base deficiencies ^[17]. The AVPD provides records of long-standing vowels and voice folding disorders, coupled with the same records of regular speakers. After a laryngeal stroboscope has been clinically checked, pathological vocal folds have been identified. In the case of anatomy, the perceptive degree of voice disorders was calculated at a scale of 1–3, the most severe is 3. The gravity ranking of each sample was focused on the category of three medical experts. The texts are different: (1) three long-lasting vowels with initial details and offset details; (2) single Arabic and several common words; and (3) continuous speech. The chosen text has been specifically selected over all Arabic phonemes. Most speakers have reported three utterances of each vowel: /a/, /u/ and /i/. Just once single words and repetitive speaking were recorded to discourage patients from overloading them. For both normal and disease samples in AVPD, the test frequency is 50 kHz

This paper provides a meta-analysis of the relevant research articles that are directly targeting voice disorders and the databases use for the detection and the machine learning techniques used for the detection as explained in figure 1. This aim of this review is to investigates, summarizes, analyzes and discussions of a series of research articles regarding their details, finding and accuracy. Our research based on research papers from databases such as PubMed, IEEE Xplore and ScienceDirect, till June2020. In this paper, we primarily aim to assess the current efficacy of various methods of machine learning used to detect voice disorders and to explore the development, shortcomings and problems that have been made, as well as future research needs. To the best of our knowledge this is the first literature review that covers all three most popular databases i.e. SVD ^[14], MEEI ^[15] and AVPD ^[15] available for voice disorders. The important contributions of this paper are:

●  Meta-analysis on the detection of voice disorder using SVD ^[14], MEEI ^[15] and AVPD ^[15] databases.

●  Review outcomes and accuracy of 45 relevant articles.

●  Identify the gap for research in this field.

The arrangement of this paper is organized as follows. Section 1 provides a short introduction of voice disorders and databases we have targeted. Section 2 provides the methodology used to conduct this review of the literature. The finding of this systematic assessment is mention in Section 3 of this paper. Section 4 deals with our main research concerns. This conclusion of this whole paper is provided in section 5 with restrictions, research gaps and recommendations for further investigations.

2.   Methodology

2.1.   Search strategy and database information and source

The population, intervention, comparison and outcome bases method (PICO) ^[18] was considered for this meta-analysis. The search strategy was set up according to PICO:

●  P = (Population) = people with voice disorders

●  I = (Intervention) = detection with data given in the form of voices. Here data extraction is done from SVD ^[14], MEEI ^[15] and AVPD ^[15].

●  C = (Comparison) = different Machine learning algorithms

●  O = (Outcome) = report accuracies and compare them.

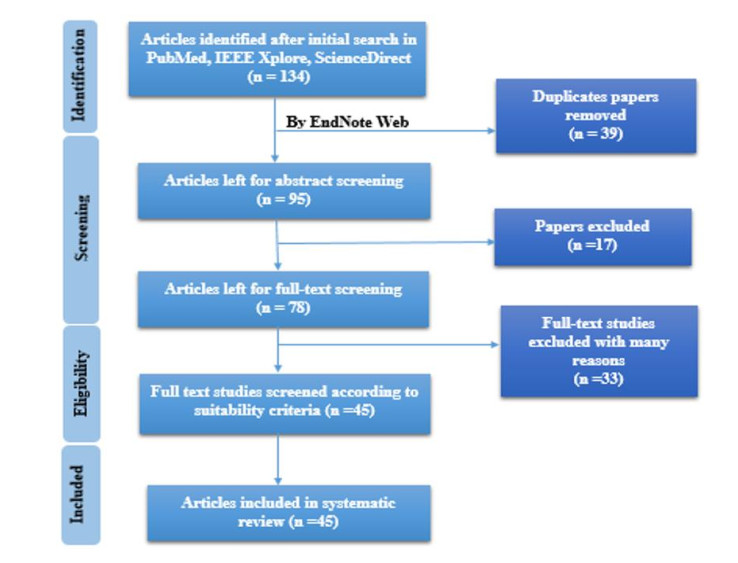
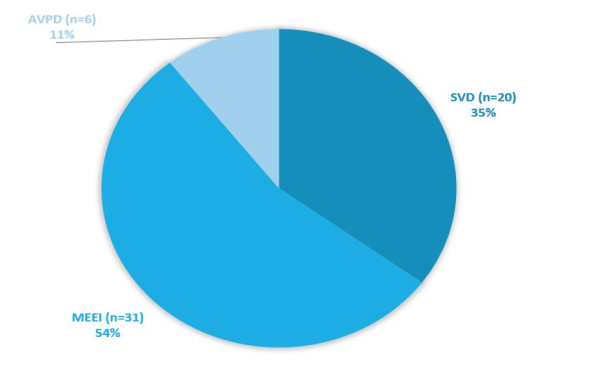
A set of search strings was generated with the Boolean operator combining suitable synonyms and alternate terms: AND restricts and limits the quest and OR expands and extends the search ^[18]. With help of these Boolean operators the search term was formulated as: (voice disorder) AND (SVD/MEEI/AVPD) AND ("computer vision" OR "neural network" OR "artificial intelligence" OR "pattern recognition" OR "machine learning"). Peer-reviewed publications have been searched in 3 big databases: PubMed, IEEE Xplore and ScienceDirect. Search was restricted in ScienceDirect to review articles, research articles, conference abstracts, correspondences, data articles, discussions, case reports. All three databases have been searched till June 2020. The set of keywords were formulated that have been used to perform search in these databases. We searched these three databases three different time for each dataset we have target in our meta-analysis. The search results were in PubMed (n = 12), IEEE Xplore (n = 19) and ScienceDirect (n = 103). The total number of search results were (n = 134) when the initial searched was performed. Total included studies are 45 and this whole process has been explained in the figure 2 flowchart. The total number of each database used is for SVD (n = 20), MEEI (n = 31), AVPD (n = 6) and it has been represented in figure 1. With the help of pie chart. It can be seen from pie chart that MEEI is the most used database for voice pathologies detection.

Using the endnote web system, search results were stored and organized and a table of data extracted from every selected paper was created. For articles deemed to be potentially eligible, full texts were uploaded into the Endnote web (by Clarivate Analytics). The first search applied the search terms for each selected database and included the full document in both journals and conferences. Thousands of irrelevant findings have returned from this procedure, and therefore a decision is made to limit the search on the title and the type of content of the document. Further study is determined by reference to the sources of the related studies found. After collecting primary search studies, we scanned the titles and the abstract for the relevant studies. An ongoing investigation has been carried out with a complete text to assess the relevant studies.

2.2.   Eligibility criteria

This study focused on peer reviewed articles that used machine learning to recognize voice disorders in voice recordings as it’s described in figure 2. In fact, we concentrated mostly on the related research papers with respect to these criteria in order to understand the problem through machine learning or implementation. This only includes articles that solely used voice recordings from SVD ^[14], MEEI ^[15] and AVPD ^[15] database to detect voice disorder. The second criterion is to ensure that the selected research papers use approaches based on machine learning. The criteria eliminated any papers that do not include machine learning or an algorithm in which the disease is defined. This also excludes papers solely based on a qualitative examination and not analyzed on basis of accuracy and quantitative analyzes. The third criterion notes that the research papers chosen also include image detection software for disease. The criteria showed the accuracy of machine learning and its techniques applied in all selected article that are quantitatively reviewed published. In order to report irrelevant research papers, the inclusion and exclusion criteria were used. This examination paper outlines the inclusion and exclusion criteria used:

Inclusion Criteria:

●  Research articles based on voice recordings as a data in order to predict the disorder.

●  Studies that use any of the following: SVD ^[14], MEEI ^[15] and AVPD ^[15] database

●  Research article consisting of machine learning techniques.

●  Articles consists of voice filtering and segmentation techniques or an application or any software in order to detect the disease through voices.

●  All articles are in the language of English.

●  In either a journal or a conference proceeding published story is included.

Exclusion Criteria:

●  Research article that do not include voice recordings as a data were excluded.

●  Studies that didn’t use SVD ^[14], MEEI ^[15] and AVPD ^[51] database.

●  Research articles that do not use any machine learning.

●  Articles that do not use voice filtering and segmentation are excluded.

●  Research which have not been written in English.

●  Research that were not included in any journal or conference proceedings.

3.   Results

3.1.   Identification of studies

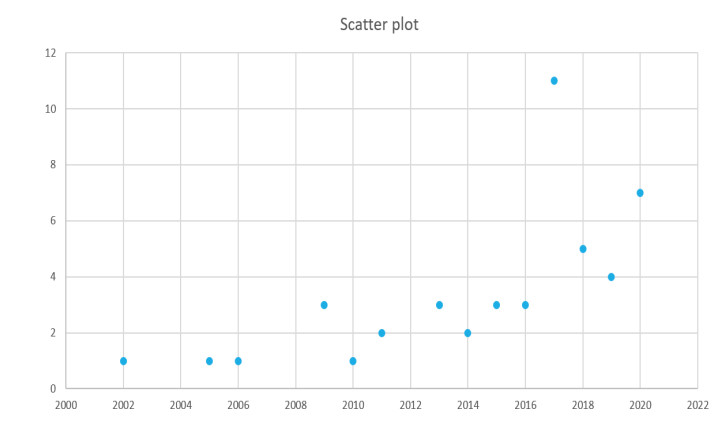
From table 1 we can observe that all the selected and screened stories are in between 2002 to 2020. But most of the publications are from last five years which can be observed in figure 3 which proves that detection of voice disorders through machine learning techniques and to apply them in clinical setting is the area of interest for most of the researchers.

In table 1, it has been observed that SVM is the most used algorithm for the diagnosis of voice disorders in all three datasets. In our lives today the recognition of voice disorders plays an important role. Many of these disorders should therefore be treated until they progress to a critical condition at an early stage of incidence. SVMs have become a popular tool for discriminatory labeling. Speech synthesis is a promising field for recent SVM applications ^[64].

Support Vector Machine (SVM) is an old classification approach and has shown great scientific interest, especially in the fields of machine classification, regression and learning. SVM with the known classes associated. This is defined as filtering or extraction of features. Even if no prediction of unknown samples is necessary, function selection and SVM classification have been used together. They may be used to define main sets that take part in the class differentiation process. The SVM maps the entrance space to a large area. The SVM could determine the border of areas belonging to both classes by calculating an optimal hyperplane separation. The hyperplane is chosen to maximize the distance between the nearest samples of workouts. Initially, SVM models have been defined to categorize linear classes. Because the area of characteristics is large, the function characteristics for finding the separation hyperplane cannot be used directly. The characteristic function is used to compute non-linear mapping using special non-linear functions known as the kernel. The Kernel has the advantage of working in the input area where the weighted sum of the kernel function evaluated by support vectors can be used to solve the classification problem. By using different kernel functions, the SVM algorithm can create a range of learning machines. SVM tends to have a far better accuracy and give promising results then artificial neural network ^[63]. SVM (support vector machines) have become a common tool for classification, regression or novelty recognition machine learning tasks. They demonstrate good performance in general terms on many real questions and the method is logically inspired. The design of the learner machine does not have to be sought through experimentation ^[66]. There are very few free parameters. While SVMs are extremely powerful classifiers utilizing non-linear kernels, there are some downsides to this: 1). To find the best model, various kernel configurations and model parameters must be tested; 2). Training can be very long, particularly if there are many features or examples in the data set; 3). It is difficult to understand their inner workings because the underlying models are based on complex mathematical structures and their findings are difficult to interpret. For eg, the selection of the features with all available data and the subsequent testing of classifier training yield a positive error estimate ^[65].

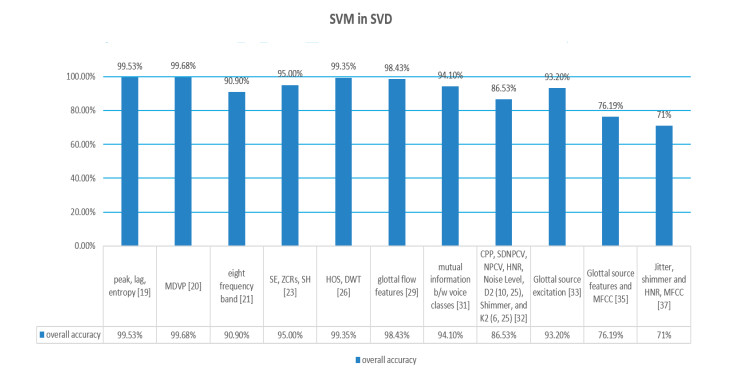
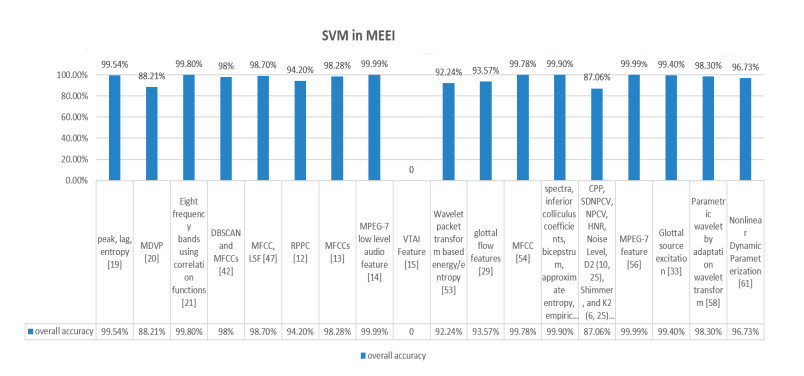
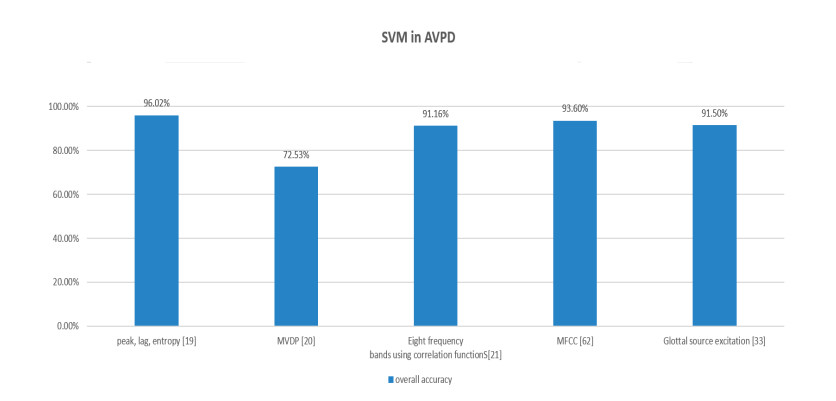
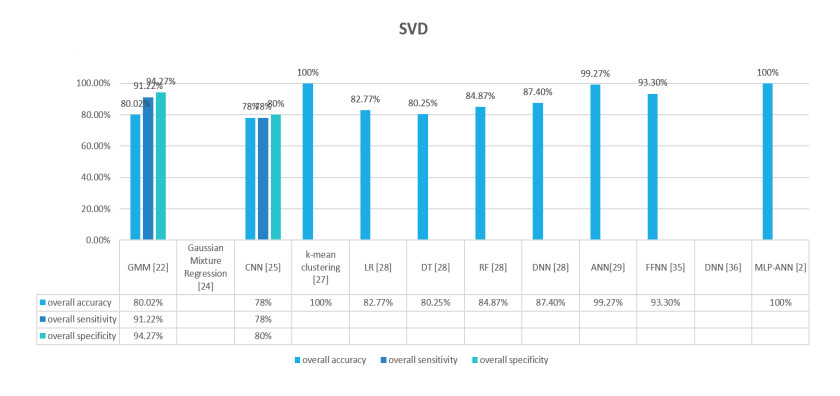
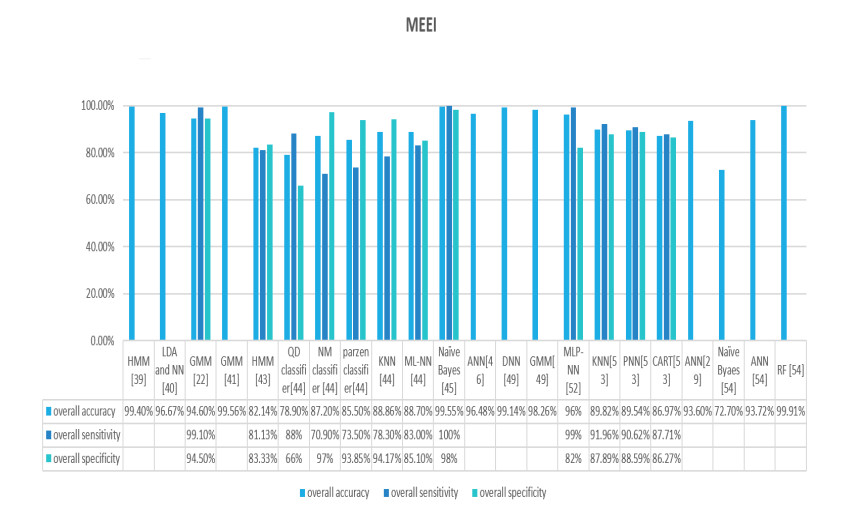
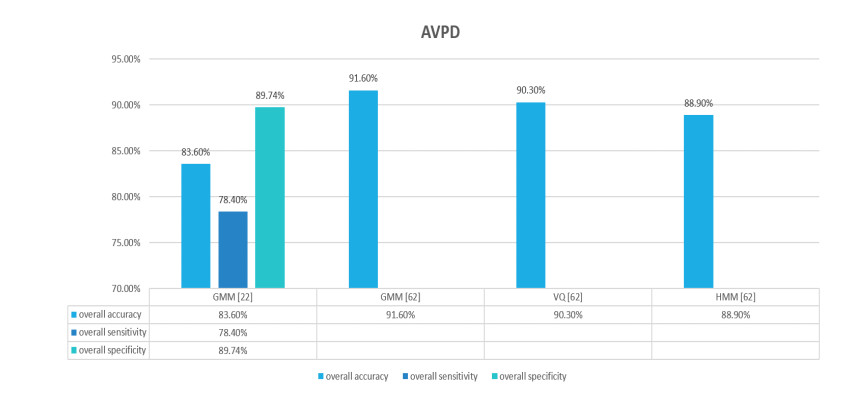
In figure 4, 5, and 6 a quantitative analysis has been carried out that shows that importance of SVM. SVM is the algorithm that has been widely used in the detection of voice disorders. For many years SVM and its application in the area of medical has been the topic of research for many researchers. SVM is the preference of scientist as a machine learning algorithm because of its best accuracy outcomes. In figure 4, 5, and 6 it has been observed that with variation in features different accuracies has been evaluated with SVM as a common algorithm in SVD ^[14], MEEI ^[15] and AVPD ^[15] database.

In figure 7, 8, and 9 a quantitative analysis has been carried out between other algorithms in all selected databases. It has been observed that other than SVM, there are some algorithms that are resulted in good accuracies. For example, in graph 5 of SVD, Zulfiqar Ali et al. ^[22], GMM is used and the resulted accuracy is 80.02% with sensitivity 91.22% and specificity 94.27%. A Gaussian mixture model (GMM), as a weighted sum of Gaussian elements, is a parametric probability density function. GMMs are commonly used as a parametric model to distribute the probability in continuous measurements or characteristics in a biometry system, such as spectral related vocal-tract characteristics in a speech recognition system. The GMM parameters can be estimated from training data based on a well-qualified pre-model iterative EM or Maximum Posteriori (MAP) estimation ^[67]. In Moon et al. ^[28], Random Forest algorithm is used to detect voice disorders and the resulted outcome is 84.87% accuracy however overall sensitivity and specificity were not reported. RF is a series or community of classification trees and regression trees ^[68] which is trained in datasets of the same scale as the training set, called bootstraps. Once a tree is developed, bootstraps are used as test set which do not contain any specific record of the original (out - of-bag (OOB)) samples. The OOB estimate of the generalization error is the error rate of classification in all test sets. In 1996 ^[69] Breiman found that an OOB mistake is correct with a test set of the same size as that for the bagged classifiers. It removes the need for a different test set with the OOB calculation. In SVD, the highest reported accuracy of is 99% ^[20]. After SVM, GMM ^[22,24] and RT ^[29], convolutional neural network used in the detection of voice disorder and resulted in good outcome. A class that is influential in various computer vision tasks, Convolutional neural network (CNN) is attracting interest through a range of domains, including radiology. CNN is designed to learn spatial hierarchies through numerous building blocks, including cooling layers, bonding layers and fully connected layers, automatic and adaptive context propagation. ^[70]. CNN is a deep learning method that is commonly used for solving difficult problems. CNN is a deep learning solution. This overcomes the limitations of traditional machines ^[71]. In ^[25] CNN is used and the reported accuracy is 78%.

In figure 8 of MEEI, Naïve Bayes ^[54] has the lowest reported accuracy which is 72.70%. Other than Naïve Bayes, algorithms like HMM ^[39,43], LDA ^[40], GMM ^[22,41,49], RF ^[54], PNN ^[53], KNN ^[53],

ANN ^[49,29] all have accuracies ranging in between 90% to 100%, which is again considered as the good reported outcome in terms of accuracy.

SVD ^[14], MEEI ^[15] and AVPD ^[15] databases are the center focus of this meta-analysis. Table 2 contain the basic differences in between all three databases which include their language, location, sampling frequency and the text that has been recorded.

In pathology evaluation, perceptual severity has a major role to play, which either in SVD or MEEI repositories is not accessible. A confusion matrix provides information on honestly and incorrect categorized topics in an automated disturbance detection system. The cause for misclassification can be calculated by the perceptual severity of this structure. Automatic systems can at times not differentiate between typical abnormal subjects and relatively severe ones. This is why the perceptive severity in the AVPD is also taken into account in grades 1–3, in which 3 is a highly severe speech disorder. In comparison the typical AVPD participants are reported in the same state as those used for the pathological subjects following the clinical assessment ^[76]. A clinical examination of standard MEEI topics is not conducted although the history of the speech problem is incomplete ^[72]. No such information is provided in the SVD database. In AVPD, according to the MEEI database, all normal and pathological specimens are recorded at a single AVPD sampling frequency. Deliyski et al. concluded that the precision and the efficiency of the acoustic analysis is affected by the frequency of the sampling ^[73]. However, there is a vowel in the MEEI database and three vowels are registered in the AVPD. While three vows are also recorded in the SVD, they are only reported once. In the AVPD, three vowels are repeatedly reported, as some studies have suggested to model the intraspeaker variability for more than one single sample of the same vowel ^[74,75]. The total length of the reported study, that is 60 seconds, is another important feature of the AVPD. By regular as well as disordered individuals any text reported in an AVPD is of the same duration. Between normal and pathologic topics, the recording times in the MEEI database vary. In comparison, the connected language (sentence) duration in the SVD database is only 2 seconds, which is not enough to build an automatic speech detection system. In addition, the SVD database cannot be used for a text-independent system. The AVPD is 18 seconds long on average and comprises seven sentences. The length of Al-Fateha speech is 18 seconds and it is segmented into two components to develop text-independent structures ^[76].

4.   Discussion

After detailed quantitative analysis it has been noticed that only one unsupervised technique is used and that is only in SVD in Panek et al. /2016 ^[27] and its resulted accuracy is up to 99% although resulted sensitivity and specificity is missing. Other than no researcher has used any unsupervised technique for voice pathology detection. The validation of PCA by k-mean clustering and cross validation loses 10% signal (the variance of 90%) from the initial vector of the feature and produces worse results than the analysis by the original 28 vectors of functionality. In comparison with the results for women, the analysis based on kPCA included all the pitches analyzed showed the most accurate evidence of patient's health and condition. The analogous analysis of male recordings showed 100 % accuracy for 28 feature vectors and for the relevant number of key components for each pitch and kPCA result for each vowel. The k-means algorithm provides perfect separation of data for male recordings, which is the opposite of the female analysis using 28 parameters and PCA. This question was coped to and 99% of the classification accuracy from the kPCA analytics, which are non-linear data transformation. This indicates that the isolation of data in linear fashion was not adequate. In addition, k-means algorithm is presented as artifacts allocated by distance to the closest cluster. ^[27], though it is been suggested that researchers should focus more unsupervised techniques and evaluate these databases.

Tissue diseases, systemic changes, mechanical stress, surface discomfort, change in tissue, changes in neurology and muscle, and other factors ^[53] can cause Voice disease. The agility, strength and form of Vocal folds, resulting in abnormal noise and reduced acoustic tone, was affected by the vocal pathology. Subjective and objective evaluations of vocal problems have been approached until now ^[78]. The first group (subjective assessment) is the auditory and visual analysis of vocal folds in a hospital ^[77]. The first is a subjective assessment. The second category (target evaluation) is focused on automatic computer-based processing of acoustic signals to measure and identify the underlying vocal pathology, which may not even be detected by a human ^[62]. Therefore, this type of assessment is inherently non-subjective. Within reality, voices can now easily be captured and stored globally via cloud technologies using many intelligent devices. Many libraries have been commonly used by researchers for the objective assessment of speech pathology. The Massachusetts Eye and Ear Infirmary (MEEI) ^[15], the Saarbrücken Voice Database (SVD) ^[14], and the Arabic Voice Pathology Database (AVPD) ^[15]. In the repositories there are also some pitfalls. For example, certain bases are highly uniformly distributed within stable and unhealthy groups, and datasets provide troubling differences in the number of samples per type of pathology (e.g. there are fewer than 3 as more pathologies in the database). Some repositories do not have details on the severity of disease or on pathology symptoms during phonation, so some of the samples may seem safe, despite being called pathology and vice versa. Not to mention that more than 1 type of pathology is used to label documents and it is particularly challenging to incorporate or delete samples in different language ^[77].

Talking about the limitation of this systematic review, we cannot deny the fact of lower number of included publications. Secondly those articles were selected which were published in English language, which can restrict the portrayal of work from non-English speaking countries and limit the generalizability of the results. Thirdly, there's a big possibility that search strategy for this review may have missed some relevant studies, since the studies which were published in conference proceedings were avoided mostly.

5.   Conclusion

We discussed the strengths and weaknesses of SVD, MEEI and AVPD. After detailed analysis of the studies including the techniques used and outcome measurements, it was also concluded that Support Vector Machine (SVM) is the most common used algorithm for the detection of voice disorders. The amount of work done in this field concluded that clinical diagnosis voice disorders through machine learning algorithms have been the area of interest for most researchers. Other than was also noticed that researchers focus on supervised techniques for the clinical diagnosis of voice disorder rather than using unsupervised techniques. The identified gap that researchers should also focus more on unsupervised techniques in future so the analysis can be made based on their results that which provides the best outcomes and results. The second identified gap is that more work needs to be done on the AVPD database to evaluate its data with more feature extraction.

Conflict of interest

The authors have no conflict of interest in the conducted study.