Vanishing and spreading conditions for a free-boundary epidemic model with subclinical infections and vaccination

1.   Introduction

As a new public health emergency, the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) had infected more than 400,000,000 people worldwide; and the Corona Virus Disease 2019 (COVID-19), had killed more than 5,500,000 people by the end of 2021 ^[1]. The epidemic was accelerated by the transport system used in China during the Chunyun season, which is a mass worker migration in the time of Spring Festival. During Chunyun, many migrant workers had to pass through the whole country regardless of whether heading to north or south. Then the SARS-CoV-2 infection was directly transmitted around China by the well-connected traffic ^[2,3].

In this paper, we will present a COVID-19 epidemiological model with a free boundary to describe the process of change in the region of pathogen transmission equipped with local diffusion process from epicenter to adjacent cities. The local diffusion phenomenon is reflected by introducing Laplace operator, $\Delta f = \frac{\partial^2 f}{\partial x^2}$, with the one-dimensional $x \in {\mathbb{R}}$. In the process of local diffusion, individual movement satisfies the reverse movement rule of Fick's law. Recently, many mathematical models with free boundaries have been developed to study their vanishing and spreading conditions ^[4,5,6,7,8]. For example, reference ^[5] shows that the disease will not spread to the whole area if the basic reproduction number $R_0 < 1$ or the initial infected radius $h_0$ is sufficiently small even that $R_0 > 1$. Reference ^[7] shows that if the spreading domain is high-risk, the disease will spread till the whole area is infected, while if the spreading domain is low-risk, the disease may vanish.

Moreover, in order to get closer to the actual transmission process of the epidemic, we will introduce subclinical infections to the epidemic model, which is an important reason for the COVID-19 transmission globally under strict travel restrictions. The clinical symptoms of coronavirus infection are not identical among the infected individuals, and they can suffer from symptoms associated with the common cold to more severe diseases, such as pneumonia ^[1]. Subclinical infections occur when too few lung cells are infected to cause clinical symptoms. Although subclinically infected individuals do not cause significant physical harm to patients, as observed from the results so far, they still have the ability to transmit coronavirus to others. Moreover, our study found that regardless of whether the free boundary was considered, the presence of subclinically infected persons still increased the basic reproduction number of COVID-19, which increased the difficulty of disease control.

Vaccination worldwide has been playing a crucial role in containing the COVID-19 pandemic. By the end of January 2022, the number of people who had completed the second dose was over 4 billion, which was about 51% of the global population ^[9]. A series of studies had reported on the effectiveness of vaccination ^[10]. Israel's nationwide mass vaccination campaign showed a 92% effectiveness against infection after the second dose ^[11]. In Chile, over the age of 16, the vaccine effectiveness was 16.13% after the first dose and 66.96% after the second dose ^[10]. However, vaccine-induced antibody levels would decline over time. A real-world study of more than 3.43 million people in the United States showed that fully vaccinated people were 88% effective in preventing SARS-CoV-2 infection in the first month and only 47% effective after five months ^[12]. As a result, some countries had proposed a third or even a fourth dose. Whether the COVID-19 vaccination should become or not a periodic schedule similar to the flu vaccination required further practical testing. However, in a mathematical modelling study, we can first propose the model with routine vaccination and predict the possible dynamic behaviour of SARS-CoV-2 transmission.

2.   Model

Inspired by the above discussions, we consider a free-boundary COVID-19 model with subclinical infections and vaccination.

where $\Delta w = w_{rr}$, $r = |x|$ and $x \in {\mathbb{R}}$. It is assumed that the environment is radially symmetric for simplicity.

The initial functions $S_0$, $I_0$, $A_0$ and $R_0$ are nonnegative and satisfy

We divide the population into four compartments: susceptibles $(S)$, infectives with apparent symptoms $(I)$, subclinical infectives without recognizable clinical signs or symptoms $(A)$ and recovered individuals $(R)$. The notation $\Lambda$ and $d$ represent the migration rate and move-out rate, respectively. $e_0$ is the additional mortality rate of COVID-19. The notation $\beta$ represents the per capita incidence rate. $\gamma_1$ and $\gamma_2$ denote the recovery rate of $I$ and $A$. $d_i$, $i = 1, 2, 3, 4$, are the diffusion coefficients for different compartments. $p$ is the proportion of infectives with apparent symptoms, with $0 < p < 1$. $\nu$ is the routine vaccination coverage rate. It is noteworthy that all parameters mentioned above are positive.

3.   Existence and uniqueness

Theorem 3.1. For any given $(S_0, I_0, A_0, R_0)$ satisfying $(2.2)$ and any $\eta \in (0, 1)$, there is a $T > 0$ such that model $(2.1)$ admits a unique bounded solution

Moreover,

Here $C_1$ and $T$ only depend on $h_0$, $\eta$, $||S||_{C^2([0, \infty))}$, $||A||_{C^2([0, h_0])}$, $||I||_{C^2([0, h_0])}$ and $||R||_{C^2([0, h_0])}.$

Proof. At first, we straighten the free boundary as in ^[4]. Let $\xi(s)$ be a function in $C^3[0, \infty)$ satisfying:

Consider the transformation

$\ \ (s, t) \to (r, t) \ \ $ with $\ \ r = s+\xi(s)(h(t)-h_0)$, for $s \in [0, \infty)$,

which is corresponding to

$\ \ (y, t) \to (x, t) \ \ $ with $\ \ x = y+\xi(|y|)(h(t)-\frac{h_0 y}{|y|})$, for $y \in {\mathbb{R}}^n$.

If $t$ is confined to

then the transformation above implies that $x \to y$ is a diffeomorphism from ${\mathbb{R}}^n$ onto ${\mathbb{R}}^n$ and $r \to s$ is a diffeomorphism from $[0, \infty)$ onto $[0, \infty)$. This transformation can change the free boundary $r = h(t)$ to the line $s = h_0$. Then, the rest of the proof is similar to the proof of Theorem 2.1 in ^[5]. We omit the details. This is a common method for dealing with free boundary questions, and more details can be seen in ^[4,5,6,7,8].

Then we consider Theorem 3.2 to extend the local solution in Theorem 3.1 to all $t \geq 0$.

Theorem 3.2. For any given $(S_0, I_0, A_0, R_0)$ satisfying $(2.2)$, the solution of the model $(2.1)$ exists and is unique for all $t \in [0, \infty)$.

Proof. By the uniqueness of solutions in Theorem 3.1, there is a fixed $T$ such that the solution $(S, I, A, R, h)$ is confined to $[0, T)$. If there exist $M_i$, $i = 1, 2, 3$, independent of $T$ such that

Then using the standard parabolic regularity, we can find $M_0$ depending on $\delta \in (0, T)$, $T$ and $M_i$, $i = 1, 2, 3$ such that

$||S(\cdot, t)||_{C^2([0, \infty))}, ||I(\cdot, t)||_{C^2([0, h(t)])}, ||A(\cdot, t)||_{C^2([0, h(t)])}, ||R(\cdot, t)||_{C^2([0, h(t)])} \leq M_0$ for $t \in [\delta, T]$

To repeat the process again by the Theorem 3.1, we can always find a $\tau > 0$ depending on $M_i$, $i = 1, 2, 3$ such that the solution of (2.1) with initial time $T-\frac{\tau}{2}$ can be extended uniquely to the time $T+\frac{\tau}{2}$, then to the time $T+\frac{3\tau}{2}$, ..., then to the infinite time $+\infty$ as long as the solutions remain bounded.

At last, we focus on the existence of $M_i$, $i = 1, 2, 3$, in the proof of Theorem 3.2.

Lemma 3.3. Let $(S, I, A, R, h)$ be a solution to model $(2.1)$ defined for $t \in [0, T)$ for some $T \in (0, \infty)$. Then, there exists constant $M_i$, $i = 1, 2, 3$, independent of $\ T$ satisfying $(3.1)$.

Proof. Since $S(r, t)$ satisfies

we can obtain

by the strong maximum principle. Similarly, let $N = S+I+A+R$, then it is obvious that

Moreover, it is evident to see that $S \geq 0$, $I \geq 0$, $A \geq 0$ and $R \geq 0$ in $[0, \infty) \times [0, T)$ by the strong maximum principle as long as the solution exists. Therefore, $S, I, A, R \leq N$ and we can get $I, A, R \leq M_2$.

Using the Hopf lemma to the equations of $I$ and $A$ implies that

Therefore, $h'(t) > 0$ for $0 < t < T$ by the free boundary conditions.

Then we construct an auxiliary function $w(r, t): = M_2[2C(h(t)-r)-C^2(h(t)-r)^2]$ in order to obtain $w(r, t) \geq I(r, t) + A(r, t)$ in $\Omega$ by choosing appropriate $C$, where $\Omega = \{(r, t):h(t)-C^{-1} < r < h(t), 0 < t < T\}$.

Direct calculations show that,

and

If we choose

then we can get

in $\Omega$, with $D = \min \{d_2, d_3\}$, $\gamma = \max \{e_0+\gamma_1 +d, \gamma_2+d\}$,

and then

due to $w(h_0, 0) = I_0(h_0)+A_0(h_0) = 0.$

By the maximum principle, we can obtain

4.   Disease vanishing and spreading

At first, we define the basic reproduction number $R_0$ without spatial heterogeneity as the corresponding ODE model (4.1) by the method in ^[13].

The Jacobian matrix of $(I, A)$ is

Let $J = F-V$, $F$ be the rate of appearance of new infections in compartment $I$, $V$ be the rate of transfer of individuals out of compartment $I$. Then, we get

We call $FV^{-1}$ be the next generation matrix for the model (4.1) and set $R_s = \rho (FV^{-1} \big|_{E_0} )$, where $E_0 = (\frac{(1-\nu)\Lambda}{d}, 0, 0, 0)$ is the disease-free equilibrium of model (4.1) and $\rho(A$) denotes the spectral radius of a matrix $A$.

Then we get

As indicates above, the first term $\frac{(1-\nu) p \beta \Lambda }{d(e_0+\gamma_1+d)}$ is the contribution to the basic reproduction number by the clinical infections; the second term $\frac{(1-\nu) (1-p) \beta \Lambda }{d(\gamma_2+d)}$ is the contribution by the subclinical infections.

We prove in Theorem 4.1 that $R_0 < 1$ is the sufficient condition for disease vanishing. However, $R_0 > 1$ is not the sufficient condition for disease spreading. Reference ^[5] shows that the disease will also not spread to the whole area if the initial infected radius $h_0$ is sufficiently small even that $R_0 > 1$.

If the free boundary condition is transformed into a fixed boundary $h_0$, then the system (2.1) is transformed to (4.2).

We consider the eigenvalue problems of $I$ and $A$ in system (4.2) at disease-free equilibirum $E_0$, respectively. For $I$, let $\lambda_1$ be the first eigenvalue of the following eigenvalue problem

and the eigenfunction $\psi_1$ with respect to $\lambda_1$ be positive on $(0, h_0)$, then $\lambda_1$ can be represented by the following variational form

For $A$, let $\lambda_2$ be the first eigenvalue of the following eigenvalue problem

and the eigenfunction $\psi_2$ with respect to $\lambda_2$ be positive on $(0, h_0)$, then $\lambda_2$ can be represented by the following variational form

Therefore, the basic reproduction number of system (4.2) can be defined as

Furthermore, we define another basic reproduction number $R^F_0(t)$ of model (2.1) with free boundary condition $h(t)$ as in ^[7].

In view of Lemma 3.3, we can observe that $h(t)$ is monotone increasing. Therefore, $R^F_0(t)$ is also monotone increasing with $t$. It is clear to see that $R_0 \geq R^F_0(t)$. Moreover, it follows that $R_0$ and $R^F_0(0)$ would decrease with routine vaccination by their definitions.

Theorem 4.1. If $R_0 < 1$, then $\lim\limits_{t \to \infty} ||I(\cdot, t)||_{C([0, h(t)])} = 0$, $\lim\limits_{t \to \infty}||A(\cdot, t)||_{C([0, h(t)])} = 0$, $h_\infty < \infty$, which implies that the disease is vanishing; If $R^F_0(0) > 1$, then $\ \lim \limits_{t \to \infty } \inf ||I(\cdot, t)||_{C([0, h(t)])} > 0$, $\lim\limits_{t \to \infty} \inf ||A(\cdot, t)||_{C([0, h(t)])} > 0$, $h_\infty = \infty$, which implies that the disease is spreading.

Proof. According to the comparison principle, we can obtain $S(r, t) \leq u(t)$ for $r \geq 0$ and $t \in (0, \infty)$, where

which is the solution of

Since $\lim\limits_{t \to \infty} u(t) = \frac{(1-\nu) \Lambda}{d}$, we deduce that $\lim\limits_{t \to \infty} \sup S(r, t) \leq \frac{(1-\nu)\Lambda}{d}$ uniformly for $r \in [0, \infty)$.

If $R_0 < 1$, there exists $T_0$ such $S(r, t) \leq \frac{(1-\nu)(1+R_0)\Lambda}{2dR_0}$ in $[0, \infty) \times [T_0, \infty)$. Then $I(r, t)$ satisfies

Therefore $\lim\limits_{t \to \infty} ||I(\cdot, t)||_{C([0, h(t)])}|| = 0$ due to $\frac{(1-\nu) (1+R_0) p \beta \Lambda }{2dR_0(e_0+\gamma_1+d)} < R_0 < 1$. Similarly, we can obtain $\lim\limits_{t \to \infty}||A(\cdot, t)||_{C([0, h(t)])} = 0$.

Next, we show that $h_\infty < \infty$ if $R_0 < 1$. Direct calculation shows that

Then integrating it from $T_0$ to $t$, $t > T_0$, we can obtain

which implies that $h_\infty < \infty$. Moreover, it follows from the first equation of (2.1) that $\lim\limits_{t \to \infty} S(r, t) = \frac{(1-\nu)\Lambda}{d}$ uniformly in any bounded subset of $[0, \infty)$

We now use proof by contradiction to show the results when $R_0^F(0) > 1$. Suppose that $h_\infty < \infty$. For some $\delta > 0$, there exists a $T_1 > 0$ such that $S(r, t) \geq \frac{(1-\nu)\Lambda}{d}-\delta$ when $t > T_1, r \in [0, \infty)$, and then $I(r, t)$ satisfies that

Then it is obvious that the $I(r, t)$ has a lower solution $\underline{I}(r, t)$, which satisfies that

Since $R^F_0(0) > 1$, there exists sufficiently small $\delta$ such that

Without loss of generality, we suppose that $\frac{(1-\nu) p \beta \Lambda }{d(d_2(\frac{\pi}{h_0})^2+ e_0+\gamma_1+d)} > \frac{(1-\nu) (1-p) \beta \Lambda }{d(d_3(\frac{\pi}{h_0})^2 +\gamma_2+d)}$. Therefore, $\underline{I}(r, t)$ is unbounded in $[0, h(t)) \times [T_1, \infty)$. Then we can obtain $\lim\limits_{t \to \infty} ||I(\cdot, t)||_{C([0, h(t)])} = \infty$.

However, if $\lim\limits_{t \to \infty} ||I(\cdot, t)||_{C([0, h(t)])} = \infty$, then there exists a sequence $(r_k, t_k)$ in $[0, h(t)) \times (0, \infty)$ such that $I(r_k, t_k) \geq \frac{\delta}{2}$ for all $k \in {\mathbb{N}}$, and $t_k \to \infty$ as $k \to \infty$. Since that $0 \leq r_k < h(t) < h_\infty < \infty$, we then have a subsequence of $\{r_{k_n}\}$ converges to $r_0 \in [0, h_\infty)$. Assume ${r_{n}: = r_{k_n}}$, then we obtain a new sequence $\{r_n\}$, $r_n \to r_0$ as $n \to \infty$ such that $I(r_n, t_n) \geq \frac{\delta}{2}$.

Define $S_n(r, t) = S(r, t_n + t)$, $I_n(r, t) = I(r, t_n + t)$, $A_n(r, t) = A(r, t_n + t)$ and $R_n(r, t) = R(r, t_n + t)$ for $(r, t) \in (0, h(t_n + t))\times (t_n, \infty)$. It follows from the parabolic regularity that $\{ (S_n, I_n, A_n, R_n) \}$ has a subsequence $\{ (S_{n_i}, I_{n_i}, A_{n_i}, R_{n_i}) \}$ converges to $(\widetilde{S}, \widetilde{I}, \widetilde{A}, \widetilde{R})$ as $i \to \infty$, which satisfies

Since $\widetilde{I}(r_0, 0) \geq \frac{\delta}{2}$, we have $\widetilde{I} > 0$ in $[0, h_\infty) \times (0, \infty)$. Using the Hopf lemma, there exists $\sigma > 0$ such that $\widetilde{I}_r(h_\infty, 0) \leq -\sigma$. Moreover, $h(t)$ is increasing and bounded by Theorem 3.1. By the $L^p$ estimates and the Sobolev's embedding theorem, there exists a constant $C_0$, which depends on $\eta$, $h_0$, $h_\infty$ and $||I_0||_{C([0, h_0])}$, for any $0 < \eta < 1$, such that

Therefore, $h'(t) \to 0$ as $t \to \infty$. According to the definition of $h'(t)$, we can obtain $I_r (h(t_n), t_n) \to 0$, which implies $\widetilde{I}_r(h_\infty, 0) = 0$. It leads to a contradiction to the fact $\widetilde{I}_r(h_\infty, 0) \leq -\sigma$ depending on $h_\infty < \infty$.

Furthermore, by the definition of $I$ and $A$, we can obtain the result about $A$, which is similar to the proof above.

5.   Numerical results

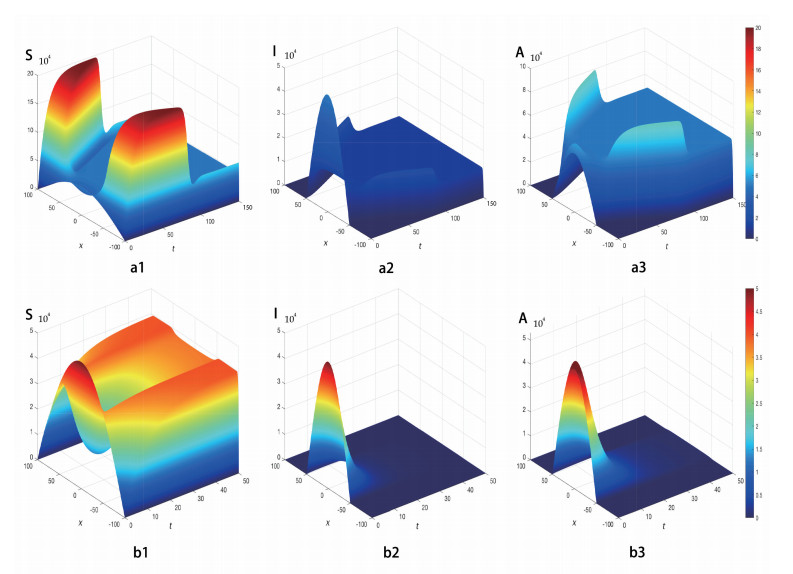
Assume that $\Lambda = 2 \ day^{-1}$, $p = 20\%$, $d_2 = d_3 = 4 \ day^{-1}$, $S_0(x) = 5\cos{\frac{\pi x}{4h_0}}$, $x \in {\mathbb{R}}$, $I_0(x) = A_0(x) = 5\cos{\frac{\pi x}{2h_0}}$, $x \in [-h_0, h_0]$, $h_0 = 50 \ km$. a1, a2 and a3 in Figure 1 show the long time behaviors of $S$, $I$ and $A$ when $R^F_0(0) = 3.29 > 1$ with $\nu = 0$. And Figure 1(b1)–(b3) show the long time behaviors of $S$, $I$ and $A$ when $R_0 = 0.82 < 1$ with $\nu = 80 \%$. The numerical simulations show that routine vaccination would decrease the basic reproduction number, and then change the disease from spreading to vanishing. Moreover, if $R^F_0(0) > 1$, then the number of infections would expand from hotspots area $x \in [-50, 50]$ to free areas without confirmed cases, $x \in [-100, -50) \cup (50,100]$, and the local diffusion would make such expansion continuous as shown in Figuer 1(a2), (a3). If $R_0 < 1$, then the diseases would vanish in hotspots area as shown in Figure 1(b2), (b3).

The consideration of subclinical infection increases the difficulty of disease control since we have got a more complicated expression of the basic reproduction numbers $R_0$ and $R_0^F(0)$. The parameter sensitivity analysis is shown in Figure 2, which is consistent with the theoretical analysis results that $R^F_0(0) < R^F_0(\infty) < R_0$. We further obtain that the difficulty of disease control is lower than that of infinite boundary diffusion for a limited area. With the free boundary $h(t)$ increase, the basic reproduction number would also increase. This conclusion theoretically verifies the significance of epicenter being in lockdown for COVID-19 control in China at the beginning of 2020. Limiting spatial population migration could theoretically reduce the threshold conditions for disease outbreaks. Furthermore, there were significant differences in the same amount of vaccination effects. As shown in the Figure 2, vaccine demand of $R_0^F(0) < 1$ was significantly smaller than that of $R_0 < 1$. These analyses were crucial for the real-time adjustments of disease control and prevention responses.

6.   Discussion

This paper presented a free-boundary epidemic model with subclinical infections and vaccination. Then, we gave sufficient conditions for the disease vanishing or spreading. Although $R_0 < 1$ is the sufficient condition for disease vanishing, $R_0 > 1$ is not the sufficient condition for disease spreading. Therefore, we used another basic reproduction number $R^F_0(t)$ to discuss the sufficient condition for disease spreading. Under the condition $R^F_0(0) < 1 < R_0$, if $h_\infty < \infty$, then the disease is vanishing; if $h_\infty = \infty$, then the disease is spreading. The disease will spread to the whole area if $R^F_0(0) > 1$. In order to emphasize the effect of basic reproduction number on the disease vanishing and spreading, we omitted the confine by the initially infected radius $h_0$. The participation of subclinical infections increase the numerical value of $R_0$ and $R^F_0(0)$, and then magnify the difficulty to control the disease. A higher routine vaccination rate might be needed to reduce to $R_0 < 1$.

The global pandemic has provided more considerations on spatial heterogeneity for studying the COVID-19 dynamics model. In the classical infectious disease compartment model, it is generally assumed that the individuals in the population are uniformly mixed and homogeneous. However, the population structure shows heterogeneity characteristics of non-uniform mixing in the real world. The uneven flow of people between regions affects the transmission dynamics of COVID-19. In this paper, we described the local spread of COVID-19 from the hot spot city of Wuhan to neighboring cities in the early stages of the outbreak in China. The local diffusion phenomenon was reflected by introducing the Laplace operator. Since it was difficult to observe the numerical simulation in two-dimensional space, this study simulated the local spatial diffusion of disease through one-dimensional and time-varying scenarios. Our hot spot area was a 100 km straight line, evenly distributed among 200,000 people, with a birth rate of 2 people per day. The diffusion coefficient was 4 people per day. Then the infected population would unconsciously expand from hot spots into a larger space of 200 km at the beginning of the epidemic. Figure 2 showed that the specific results of the numerical simulation. Through these simulation results and mathematical theory, we obtained the influence of the participation of subclinical infection on the spread of disease and analyzed the suppression effect of vaccination.

However, the local free boundary conditions are not accurate enough to describe the global prevalence of COVID-19 for long-distance population movements by airplanes or high-speed trains, which is the part of this article that we have not considered. In addition, because there are many parameters in the COVID-19 model, we cannot know the specific parameter estimates, and even if we did get them, they would not be very accurate. More extensive epidemiological investigation and more accurate parameter range are conducive to further studying mathematical models of infectious diseases such as COVID-19.

Acknowledgments

This study was supported by funding from Chinese Academy of Medical Sciences (CAMS) Innovation Fund for Medical Sciences (2020-I2M-1-001).

Conflict of interest

The authors declare there is no conflict of interest.