1.
Introduction and mathematical model
The management of infectious diseases is a major challenge for public health systems globally, especially in the era of global pandemics such as COVID-19. The speed of epidemic spread, the mutations of pathogens, and the socioeconomic challenges related to their management present complex issues for health authorities. In light of these challenges, optimizing intervention strategies is crucial to minimize the health and economic impacts of epidemics [1,2,3,4,5,6].
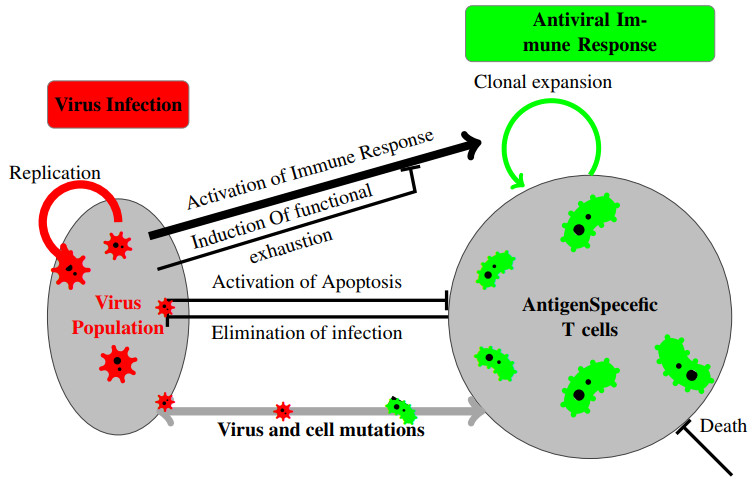
The immune system's ability to control virus infections is based on various critical aspects of the virus-host interaction, including in situ reactions (such as virus replication within cells, cell activation, proliferation, differentiation, and death) and spatial transport mechanisms (such as virus spread between cells and tissues, immune cell trafficking, and migration) [7]. It has been recognized, particularly in the case of systemically spreading virus infections like human immunodeficiency virus (HIV), that an integrated understanding of virus propagation and T cell surveillance in infected tissues is crucial for comprehending disease pathogenesis and the progression to AIDS (Acquired immunodeficiency syndrome) [8,9].
The concept of quasi-species offers a suitable framework for understanding virus evolution [10,11]. Various models have been developed to describe the evolution of a discrete set of virus variants through systems of differential equations [12,13]. The study of virus evolution within a continuous genotype space has been addressed in previous works [14,15,16,17,18]. Infection spreading in cell culture or tissue has been studied in [7,19,20].
This study extends the investigation initiated by previous research by further examining virus density evolution within the genotype space, particularly in its interaction with the immune response. Understanding these dynamics is crucial, as it can provide insights into how viruses adapt and potentially evade immune detection, which has significant implications for vaccine development and therapeutic strategies. By elucidating the relationship between virus density and immune response, this work aims to inform public health interventions and enhance our overall understanding of viral pathogenesis. We analyze the distribution of virus density, denoted as V(x,t), within the genotype space represented by the variable x at time t, alongside the concentration of virus-specific T lymphocytes, denoted as C(x,t).
The model describes how the number of viruses and the strength of the immune response change as the infection develops over time, and is given by the following system of reaction-diffusion equations:
To simplify mathematical computations, the genotype variable x is considered on the whole axis. The model is shown graphically in Figure 1 and explained as follows: Diffusion terms in both equations account for the small, random mutations that occur in both viruses and cells. The second term in Eq (1.1) depicts the process of virus replication within host cells. It is proportional to the virus density V and to the dimensionless quantity of uninfected cells (K−k1H(V)). Here, K=1 corresponds to the dimensionless total number of cells, and the number of infected cells is directly proportional to the total amount of virus H(V), which competes for host cells. This assumption is valid if we assume that infected host cells do not undergo mortality. We will examine two distinct scenarios. In the first scenario, viruses compete for host cells independently of their genotype, known as global competition [18], where
In the second scenario, this competition depends on the genetic distance between genotypes [18], denoted as
where the kernel ϕ(x−y) determines the effectiveness of this competition. It will be convenient henceforth to employ distinct notation for these integrals. The final two terms in this equation represent virus elimination by immune cells and the virus mortality rate, which is independent of the immune response but may depend on the virus genotype, with the rate σ(x). The parameter D is a positive constant that represents the half-saturation.
The second term on the righthand side of Eq (1.2) depicts the clonal expansion of immune cells induced by the presence of the antigen (virus). The function p(V) is positive when V>0.
The function p(V) may exhibit various behaviors: it can be linear, increase with saturation, or grow initially for small V and then decay for large V. The mortality rate q(V) of immune cells can either depend on the virus density or remain independent of it, taking a positive constant value. We assume that p(0)<q(0). This condition implies that in the absence of viral load, the birth rate of cells is lower than their mortality rate, resulting in a decline in cell concentration. We do not account for memory cells that persist in the organism after the infection is eradicated. When the viral load V surpasses a certain threshold, p(V) exceeds q(V), triggering the initiation of the immune response against the pathogens. Otherwise, the concentration of immune cells diminishes, and the immune response does not impact the progression of infection in the organism. It's worth noting that a high virus concentration can suppress the proliferation rate of immune cells, but we do not consider this effect here (see [7,19]).
The functions H(V), p(V), and q(V) are biologically grounded and supported by previous studies on viral evolution and immune dynamics. They provide a realistic framework for modeling the dynamic interactions between virus populations and immune cells, particularly T cells (see [7,14,17] and the references therein).
In Section 2, we investigate the existence of positive stationary solutions for the system described by Eqs (1.1) and (1.2) that decay at infinity. Such solutions correspond to virus quasi-species. The presence of these solutions is determined by the viability intervals within the genotype space, where the rate of birth surpasses the rate of death. Section 3 provides a concise overview of the temporal model, highlighting its key features and dynamics. In Section 4, we focus on the local reaction–diffusion model, presenting its formulation and key characteristics. Section 5 introduces the nonlocal reaction–diffusion model, discussing the inclusion of nonlocal interactions and their impact on the system. In Section 6, we explore the conditions for instability and the mechanisms of pattern formation, including criteria for both Turing and spatial Hopf bifurcations. Finally, Section 7 provides a discussion summarizing the main results and outlining potential directions for future research.
2.
Existence of positive stationary solution
In this section, we study the existence of positive stationary solutions for the system (1.1)–(1.2) under the condition that the virus mortality rate σ(x) is lower than the virus replication rate within a specific range of genotypes. Our analysis suggests that this genotype-dependent virus mortality rate plays a crucial role in enabling the persistence of virus quasi-species.
2.1. Global competition
The equations governing the stationary solutions of the system (1.1)–(1.2) over the entire axis are as follows:
We simplify the notation by assuming that d1=d2=D=k1=k=a=b=1. Here, we examine the scenario of global competition among viruses for host cells, where H(V)=I(V). Our goal is to find positive solutions to this system of equations that approach zero as x→±∞.
The existence of these solutions is determined by the function σ(x), which sets the virus mortality rate. A typical example is given by σ(x)=0 for |x|≤x0 and σ(x)=σ0>1 for |x|≥x1, where x0 and x1>x0. The functions σ(x), p(V), and q(V) are assumed to be nonnegative and sufficiently smooth. Additional conditions will be formulated below. We will prove the existence of a solution using the topological degree method. Initially, we will establish some preliminary estimates for potential solutions to this problem.
Lemma 1. Suppose (V(x),C(x)) constitutes a positive solution to Eqs (2.1) and (2.2), with V(±∞)=0 and C(±∞)=0. Then, it follows that I(V)<1.
Proof. Assuming that the statement of the lemma does not hold, that is I(V)≥1, we conclude that V(x) satisfies the inequality:
Since q(x)≤0 and q(x)≢, from the strong maximum principle [21], we deduce that V(x) cannot attain a positive maximum or a negative minimum. Therefore, V(x)\equiv 0 , which contradicts the hypothesis V(x) > 0 . □
Consider (V(x), C(x)) as a positive solution to (2.1) and (2.2). The following lemma provides some properties of this solution.
Lemma 2. 1) There exists a positive constant K such that 0 < V(x) < K for all x \in \mathbb{R} .
2) If \frac{p(V)}{q(V)} is bounded for all V \geq 0 , then there exists a constant M > 0 such that 0 < C(x) < M for all x \in \mathbb{R} .
Proof. Suppose there exists a point x_0 such that V(x_0) is the global maximum of V(x) over the entire domain. From Eq (2.1), we deduce:
Utilizing Taylor's expansion around x_0 , we obtain the following lower bound for V(x) :
where \chi lies between x and x_0, and g(x) = 1 - \frac{(x - x_0)^2}{2}. Let \Omega represent the interval where g(x) is positive. Hence, we have
From Lemma 1, it follows that
Thus, we conclude the first part of the lemma.
Let us now prove the second part of the lemma. If C achieves a positive maximum at some point y_0, then C''(y_0) < 0. This implies:
Consequently,
which completes the proof of the lemma.
To ensure the existence of solutions for our nonlinear system, we use the Leray-Schauder method, which is based on the concept of topological degree and a continuation technique. This method involves introducing a continuation parameter \tau \in [0, 1] in a family of parameterized equations of the form H(u, \tau) = \tau F(u) + (1 - \tau) G(u) = 0 , where F(u) is the nonlinear operator of the original equation and G(u) is a simpler operator, often linear. The idea is to first solve the simplified equation G(u) for \tau = 0 , and then continuously track the solutions as \tau increases until \tau = 1 , where the original equation is recovered. The parameter \tau thus establishes a homotopy between these two operators. If the operator H(u, \tau) satisfies compactness and continuity conditions, and the topological degree remains constant and nonzero throughout the deformation, the existence of solutions for \tau = 1 is guaranteed. This process is central to our proof of the existence of solutions in this study.
The preliminary estimates of solutions are provided by Lemma 2 above. Let U : = (V, C) and consider the operator
Let A_\tau(U) be defined as a mapping from the weighted Hölder space (C_\mu^{2+\alpha} (\mathbb{R}))^2 to the space (C_\mu^\alpha (\mathbb{R}))^2 , where 0 < \alpha < 1 and \tau \in [0, 1] serves as a parameter. Here, the space C_\mu^\alpha (\mathbb{R}) consists of functions u(x) such that u(x)\mu(x) \in C_\mu^{2+\alpha} (\mathbb{R}) , with \mu(x) = 1+x^2 . This weight function grows polynomially at infinity. The introduction of weighted spaces is crucial for defining the topological degree for elliptic operators in unbounded domains, as discussed in works such as [21]. Furthermore, the incorporation of weighted spaces ensures the well-definedness of the integral I(V) , preserving the integrity of the essential spectrum.
We will assume, for simplicity, that \sigma_\tau(x) is infinitely differentiable with respect to both x and \tau, with additional conditions to be specified later. Let L_\tau be the operator obtained by linearizing the operator A_\tau about U = 0, defined as:
Recall the assumption:
Lemma 3. If the principal eigenvalue of the differential operator
is positive for \tau_0 \leq \tau\leq \tau_1 , where \tau_0, \tau_1 are fixed, then there exists a positive constant \epsilon such that for any positive solution of the equation A_\tau(U) = 0 with \tau_0 \leq \tau\leq \tau_1 , we have
Proof. It follows from condition (2.11) that the unique solution of the equation
is identically zero. Suppose for the sake of contradiction that the statement of the lemma does not hold. This implies the existence of a sequence of solutions U_k(x) for \tau = \tau_k such that U_{m_k} \to 0 . Without loss of generality, we can assume that \tau_k \to \tau_* for some \tau_*\in [\tau_0, \tau_1] . Then, we have:
Let w_k = U_k/\|U_k\| . Then, L_{\tau_k} w_k = o(1) . Using the property that operators L_{\tau_k} are proper with respect to w and \tau (see [21]), we can deduce that the sequence w_k is compact. Consequently, there exists a subsequence, which we denote also as w_k , converging to some function w_0 . Therefore, L_{\tau_*}w_0 = 0 .
Since the functions w_k(x) are positive, the limit function w_0(x) is also nonnegative. Thus, w_0(x) \geq 0 for all x . This implies that L_{\tau_*} has a zero eigenvalue with a positive eigenfunction. However, the only positive eigenfunction of L_{\tau_*} corresponds to the principal eigenvalue [22]. This leads to a contradiction. Hence, the assertion of the lemma holds. □
Theorem 1. Let p(V) , q(V) , and \sigma(x) be nonnegative infinitely differentiable functions. Assume p(V)/q(V) is bounded for V \geq 0 , \sigma(x) = \sigma > 1 for |x|\geq x_1 with positive constants \sigma, \ x_1 , and condition (2.11) is satisfied. Suppose the principal eigenvalue of the problem
is positive. Then, the system (2.1)–(2.2) admits a positive solution converging to 0 at infinity.
Proof. To establish the theorem, we define \sigma_\tau(x) = (1 - \tau)\sigma(x) + \tau \sigma, and consider U = (V, C) as the solution of problem (2.1)–(2.2). Given that \sigma > 1, the spectrum of the operator L_1 is situated in the left half-plane. Notably, the essential spectrum S_e(L_\tau) of the operator L_\tau remains constant for all \tau, with \text{Re}(L_\tau) \leq -\delta < 0 for some positive \delta. Let \lambda_0(\tau) denote the principal eigenvalue of L_\tau. According to the lemma assumption, we have \lambda_0(0) > 0.
The principal eigenvalue \lambda_0(\tau) is a decreasing function with respect to \tau \in [0, 1]. There exists a value \tau_0 \in [0, 1] such that \lambda_0(\tau_0) = 0. For 0 < \tau < \tau_0, we have \lambda_0(\tau) > 0, and for \tau_0 < \tau < \tau_1, where \tau_1 lies within the interval (\tau_0, 1], \lambda_0(\tau) < 0. However, it is important to note that ensuring the existence of the eigenvalue for all values of \tau in the interval, [0, 1] remains challenging due to the possibility of its proximity to the essential spectrum.
Let us examine the equation A_\tau(U) = 0 in a small neighborhood of the bifurcation point \tau = \tau_0 . As the parameter approaches this threshold, the previously stable trivial solution U = 0 becomes unstable, leading to the emergence of another solution U_\tau(x) . This newfound solution is characterized by its positivity, attributed to the positivity of the principal eigenfunction w_0(x) , as detailed in Lemma 3. Furthermore, the index of this solution, that is, the value of the degree with respect to a small ball containing this solution, equals 1. Indeed, from the homotopy invariance of the degree, it follows that
for all \tau > \tau_0 and sufficiently close to \tau_0 . Here, \tilde U_\tau denotes a negative solution emerging from the trivial solution and converging to -U_0(x) . Given that ind(0) = -1 , matching (-1)^\nu with \nu = 1 , representing the count of positive eigenvalues of the linearized operator, leads to the conclusion that ind(U_\tau) = ind(\tilde U_\tau) = 1 .
Lemma 2 implies the existence of a positive constant M_0 , ensuring that |U|_{E_1} < M_0 for any positive solution u of the equation A_\tau(U) = 0 . Moreover, by employing Lemma 3, we deduce the existence of a positive value \delta(\tau) such that |U|_{E_1} > \delta(\tau) for \tau < \tau_0 .
Let us consider the domain
for some \delta_0 > 0 sufficiently small. Choose \tau_2 < \tau_0 such that \delta(\tau) > \delta_0 for 0\leq \tau\leq \tau_2.
As A_\tau(U)\neq 0 for U\in \partial \Omega , it follows that the degree \gamma(A_\tau, \Omega) remains unchanged over \tau \in [0, \tau_2] . Thus, we can deduce that \gamma(A_0, \Omega) = \gamma(A_{\tau_2}, \Omega) = ind(U_{\tau_2}) = 1 . This indicates that the equation A_0(U) = 0 possesses a solution within \Omega . This conclusion establishes the validity of the theorem.
2.2. Nonlocal competition
In the context of nonlocal competition, our analysis centers on the integral J(V) rather than I(V) .
Furthermore, we assume the kernel \phi(x) to be bounded and integrable. Specific examples will be explored subsequently. The proof of solution existence mirrors the previous case, albeit with some differences related to a priori estimates of solutions provided in the following lemma.
Lemma 4. Suppose (V(x), C(x)) represents a positive solution of Eqs (2.18) and (2.19). Then, the following assertions hold:
1). There exists a positive constant K_1 such that 0 < V(x) < K_1 .
2). If \frac{p(V)}{q(V)} is bounded for all V\geq 0 , then there exists a constant M_1 such that 0 < C(x) < M_1 .
Proof. We will divide the proof of the lemma into two cases: J(V) < 1 and J(V) \geq 1 . In the first case, we can conclude that V''(x) \geq -aV(x) for all x \in \mathbb{R} . In the second case, we observe that V''(x) > 0 > -aV(x) for all x \in \mathbb{R} , as V(x) \geq 0 . Let x_0 denote the global maximum of V(x) , which exists since the function is positive and decays at infinity. Our aim is to demonstrate that J(V(x_0)) < 1 . Suppose to the contrary that J(V(x_0)) \geq 1 . This would result in a contradiction of signs in (2.18) at x = x_0 . Expanding V(x) in a Taylor series about x_0 , we obtain the following lower bound:
where a_2 = V''(\chi)/2 and g(x) = 1-a(x-x_0)^2/2 . Since the function g(x) is positive in the interval x_0-\sqrt{\frac{2}{a}} < x < x_0+\sqrt{\frac{2}{a}} and equals zero at its boundaries, we can find x_1 in this interval such that g(x)\geq k > 0 and \phi(x) > 1/2 for all x\in [x_0, x_1] . Consequently,
This estimate establishes the first part of the lemma. The proof of the second part follows a similar approach to that of Lemma 2.
The remaining part of the proof for the existence of a solution follows a similar approach to that used in the case of global competition; hence, we omit the details here.
3.
The temporal model
We begin the examination of the interaction between viral infection and the immune response with the model that does not incorporate diffusion:
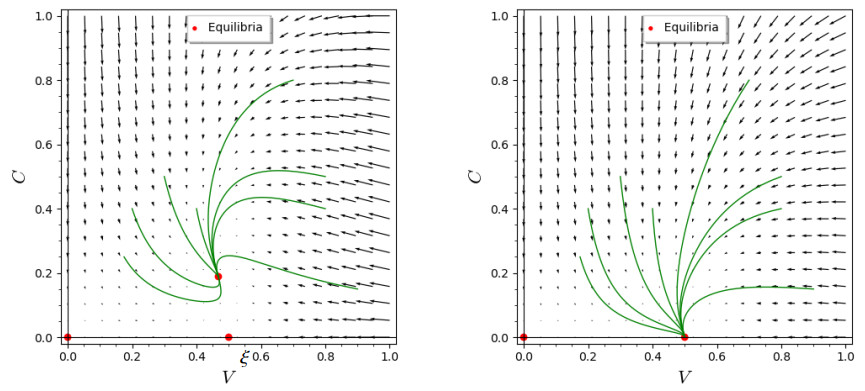
where we set p(V) = pV and q(V) = qV+\sigma_2 , assuming that a > \sigma_1, p > q . This model possesses three stationary solutions, E_0(0, 0) , E_1(1-\frac{\sigma_1}{a}, 0) , and the coexistence (positive) equilibrium E^*(V^*, C^*) , where
and V^* is a positive root of the following cubic equation:
Let us note that C^* is positive if the following inequality holds:
To determine the number of equilibrium points of system (3.1)–(3.2), one needs to count the number of positive real roots of Eq (3.4) that lie in the interval (0, 1) . Since F(0) = -\sigma_2(a-\sigma_1+k) < 0 , and
according to Descartes's rule of signs [23], F has exactly one positive root in (0, 1) . Taking into account (3.5), the nontrivial equilibrium exists if
It can be shown that the trivial equilibrium point E_0 is a saddle point regardless of the parameter values. On the other hand, if \sigma_2 > (p-q)(1-\frac{\sigma_1}{a}) , the coexistence (positive) point does not exist and the virus-only equilibrium E_1 is stable. In the case when the opposite inequality holds \sigma_2 < (p-q)(1-\frac{\sigma_1}{a}) , the point E_1 becomes unstable. In this case, the coexistence equilibrium point E^* is stable. Indeed, linearizing system (3.1)–(3.2) around E^* , we obtain the associated characteristic equation.
where
and
Because
and
then, E^* is locally asymptotically stable whenever it exists. An illustrative representation of the population dynamics of viruses and immune cells is presented in Figure 2.
4.
Local reaction–diffusion model
In this section, we extend the temporal model (3.1)–(3.2) presented in the preceding section by incorporating the random dispersal of the virus and immune cell populations. The corresponding spatiotemporal model is given by
subjected to a nonnegative initial condition and the periodic boundary condition. The parameters d_1 and d_2 , respectively, denote the diffusion coefficients representing the mutation rates of the virus and immune cell populations. For simplicity, we restrict ourselves to one-dimensional spatial domain \mathbb{R} .
The equilibrium points found in the temporal model (3.1)–(3.2) also serve as equilibrium points in system (4.1)–(4.2). We now examine the Turing instability of the nontrivial equilibrium solution E^*(V^*, C^*) in system (4.1)–(4.2), which is locally asymptotically stable in absence of diffusion. Turing instability occurs when the corresponding non-diffusive system is stable, and destabilization occurs by some unstable mode of spatial perturbations caused by diffusion.
The following inequalities define the conditions for Turing instability [24]:
where
Two conditions (4.3) and (4.5) cannot be satisfied simultaneously due to the fact that a_{11} < 0 and a_{22} < 0 . Consequently, the local spatiotemporal model fails to satisfy the criteria for Turing instability.
5.
Nonlocal reaction–diffusion model
We extend the spatiotemporal local model (4.1)–(4.2) by introducing a nonlocal term, leading to the following nonlocal spatiotemporal model:
We note that the equilibrium points found in the temporal model (3.1)–(3.2) are also equilibrium points in the system (5.1)–(5.2). We will derive the instability criteria for the positive homogeneous steady-state E(V^*, C^*) . The associated eigenvalue problem takes the following form:
where z(x) , and w(x) are spatial perturbations and
Utilizing the Fourier transform on Eqs (5.3) and (5.4), we obtain:
Here, \bar{z} , \bar{w} , and \bar{\phi} represent the Fourier transforms of the functions z(x) , w(x) , and \phi(z) , respectively (see [21]). It is important to note that the Fourier transform is understood in the sense of distributions (see, e.g., [25]), which broadens its application to functions that are not necessarily integrable in the traditional sense. Thus, the existence of space-homogeneous solutions on an infinite domain is compatible with the use of the Fourier transform, allowing for effective analysis of the behaviors of these solutions.
The characteristic equation associated with the system (5.5)–(5.6) can be formulated as follows:
where
The homogeneous steady-state remains stable under space dependent perturbations if the following two conditions are met:
For any positive real values of \xi and M , the homogeneous steady-state experiences instability through Turing bifurcation if \Gamma(\xi, M) < 0 for all \xi and \Delta(\xi_T, M) = 0 for a specific \xi_T . It undergoes spatial Hopf bifurcation if \Gamma(\xi_H, M) = 0 for a certain \xi_H and \Delta(\xi, M) > 0 for all \xi .
The characteristic equation for the local reaction-diffusion equation model (4.1)–(4.2) can be obtained from (5.7) by substituting \bar{\phi} = 1 . As mentioned earlier, when \bar{\phi} = 1 , it is impossible to contravene the inequalities stated in (5.10). In the numerical simulations presented below, we examine the solution behavior when the kernel function \phi(x) is a step function
Here, we assumed that the kernel function \phi(x) is a nonnegative even function with compact support of length 2M . Therefore, when its support tends to zero (i.e., M \to 0 ), the nonlocal model (1.1)–(1.2) becomes the local model (4.1)–(4.2) [26].
In this case, the Fourier transform of \phi(\xi) is
5.1. Stationary patterns
First, let us delve into the condition for Turing instability, which can be determined by solving the system of equations:
It follows from the second equation of (5.13) that
Let \xi M = z , and from (5.14) we get
We claim that Eq (5.15) has countable positive roots 0 < z_1 < z_2 < z_3 < \dots . Set \mu_i = \sin z_i/z_i , i \in \mathbb{Z}^+ , and
From equality \Delta(\xi, M) = 0 , we get
and the corresponding values of M_j are determined by the following equality:
Based on the parameter values, we can compute the threshold values \xi_j and M_j . Noting that Q_0 > 0 , we need either of the following conditions to be met:
1). Q_{1i}^2 > 4Q_0 Q_{2i} , Q_{1i} < 0 , and Q_{2i} > 0 or
2). Q_{2i} < 0 .
5.2. Time oscillations
To determine the threshold for spatial Hopf-bifurcation, we need to find positive values of \xi and M such that the condition \Gamma(\xi, M) = 0 is met. By differentiating \Gamma(\xi, M) = 0 with respect to M , we find:
and thus we can define \mu_j, j\in \mathbb{Z} , as above. Therefore, \xi_j and M_j are determined by the following equalities:
Similarly, the following conditions need to be satisfied: a_1-b_2-aV^*\mu_i > 0 .
6.
Instability and pattern formation
In this section, we will examine the instability conditions outlined above and identify the parameter regions associated with stable and unstable solutions. Additionally, we will depict the resulting patterns through direct numerical simulations. Without loss of generality, we choose d_1 as the bifurcation parameter. Then, we can calculate threshold values of parameter d_1 .
6.1. Spatial patterns for the nonlocal model
Assume that \lim\limits _{M \rightarrow 0+} \Gamma(\xi, M) < 0 and \lim\limits _{M \rightarrow 0+} \Delta(\xi, M) > 0 . These criteria guarantee the stability of the homogeneous steady-state under space-independent perturbations. The critical wave number and the corresponding Turing bifurcation threshold in terms of d_1 can be established by solving the following two equations:
From \Delta(k, M) = 0 , we get
When we substitute this expression into the second equation in (6.1), we get:
We solve Eq (6.3) numerically for the wave number \xi , and we fix all parameter values except for \xi . This equation might possess multiple positive roots. Substituting these solutions \xi_T in Eq (3.7), we obtain corresponding diffusion coefficients d_1 . The minimum among all positive values of d_{1} is the critical value d_1 = d_{1T} .
Consider, as example, the following values of parameters:
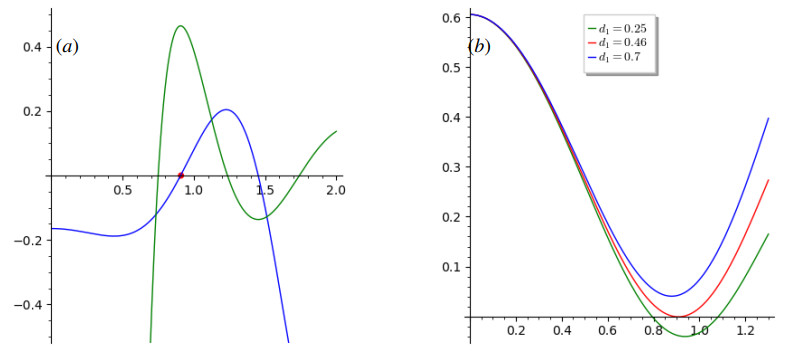
Then V^* = 0.48, C^* = 0.39. To illustrate the formation of patterns driven by nonlocal interactions, we plot in Figure 3(a), the graph of the function defined by Eq (6.3) with respect to \xi (in blue) and located the roots of this function. Furthermore, in Figure 3(b) we plot the curve of d_1 with respect to \xi (in green). We identify \xi_{T} = 0.91 in red on the Figure 3(a), along with the bifurcation threshold d_{1T} = 0.46 . As is illustrated in Figure 3(b), when d_1 exceeds its critical value d_{1T} , the function \Delta(\xi, M) is negative for a certain range of \xi . This implies that the characteristic Eq (5.7) has at least one positive root, which indicates that Turing instability occurs and spatiotemporal pattern emerges for d_1 < d_{1T}.
6.2. Spatial Hopf bifurcation
We determine the spatial Hopf bifurcation threshold relative to the parameter d_1 . For a suitable M , if one can identify a unique value \xi = \xi_H such that \Gamma(\xi_H, M) = 0 , then \xi_H represents the critical wave number for the spatial Hopf bifurcation. This critical wave number can be obtained by solving the following two equations simultaneously:
We derive the value of d_1 from the equation \Gamma(\xi, M) = 0 :
By replacing the expression for d_1(\xi) from Eq (6.5) into the second equation of (6.4), we derive:
Equation (6.6) can possess multiple positive real roots depending on the parameter values. It is essential to verify that the corresponding values of d_1(\xi) are positive. We choose the root \xi_H such that d_1(\xi_H) is the smallest positive number, satisfying \Delta(\xi_H, M) > 0 .
For illustrative purposes, let's consider the following set of parameter values:
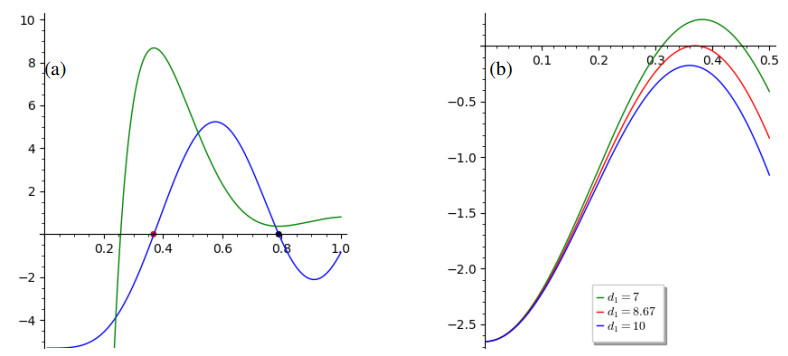
Then V^* = 0.48, C^* = 0.39 . For M = 10 , in Figure 4(a), we plot the graph of the function defined by Eq (6.6) in blue with respect to \xi , and mark the roots of this function. Additionally, we plot the curve of d_1 with respect to \xi in green. On the graph, we identify \xi_T = 0.37 in red, along with the bifurcation threshold d_{2T} = 8.67 . As illustrated in Figure 4(b), for d_1 < d_{1H} , we have \Gamma(\xi, 21) > 0 for a certain range of values of \xi . Therefore, the spatial Hopf bifurcation occurs as d_{1} crosses the critical threshold d_{1H} from higher to lower values.
6.3. Turing-Hopf bifurcation
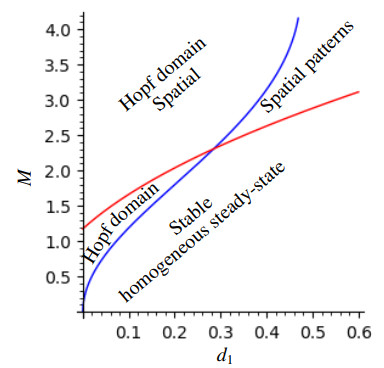
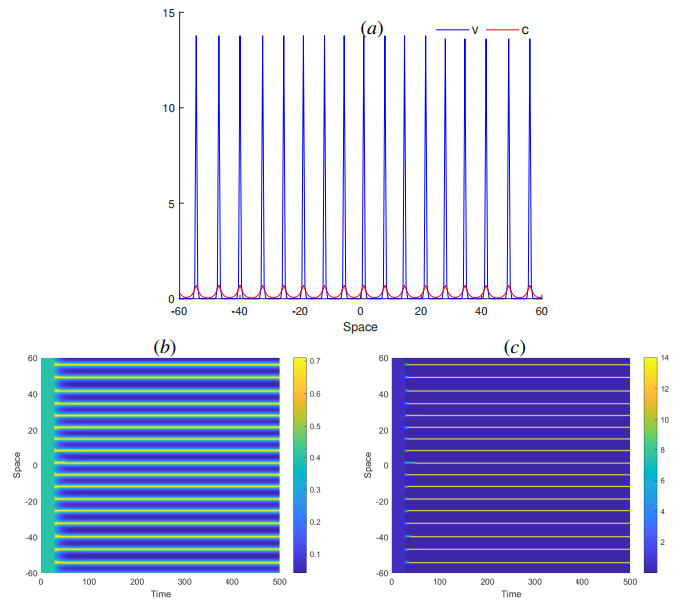
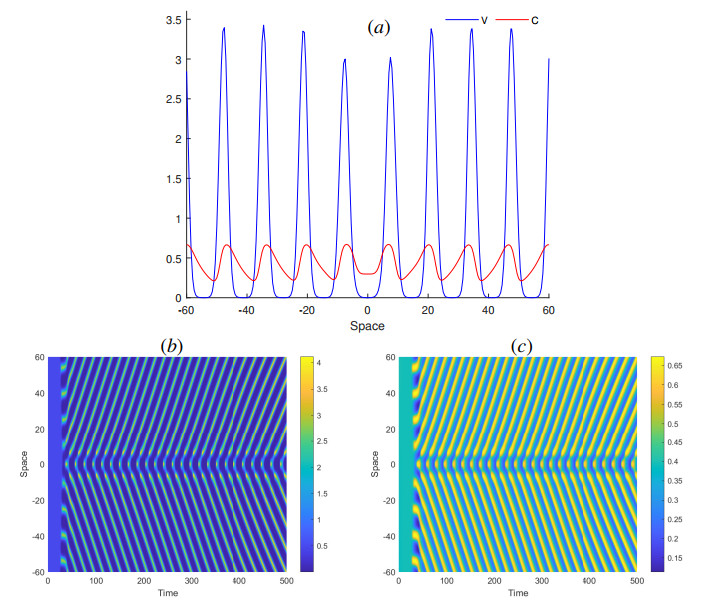
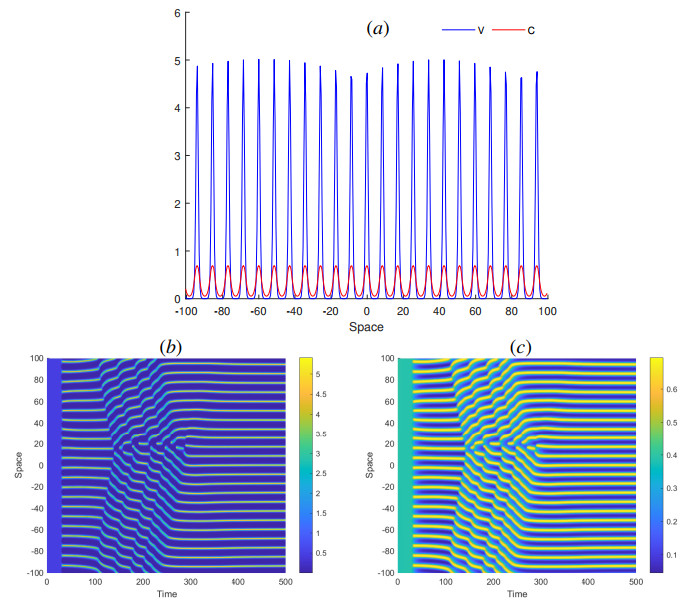
In many dynamic systems, Hopf bifurcation breaks the temporal symmetry of the system and induces periodic oscillations which are uniform in space and periodic in time, while the Turing instability breaks the spatial symmetry leading to the pattern formation that is stationary in time and oscillatory in space. In this subsection, we consider Eqs (1.1) and (1.2) in a bounded interval 0 < x < L with periodic boundary conditions, using a small random perturbation to the homogeneous steady state of the system as the initial condition. We study the coupling between the two different instabilities, i.e., Turing-Hopf bifurcation in the (d_1, M) parameter space, which is represented in Figure 5. There exists a region where stable stationary solutions, which are spatially homogeneous, are present. These solutions can lose their stability through two primary mechanisms. In the first scenario, a real eigenvalue crosses the origin, leading to the emergence of stable stationary solutions that exhibit periodicity in space (as shown in Figure 6). In the second scenario, a pair of complex conjugate eigenvalues intersects the imaginary axis, resulting in time-periodic oscillations of a solution that remains constant in space (not represented). As we delve deeper into the instability region, both instabilities can occur concurrently, giving rise to complex spatiotemporal dynamics. Consequently, Figure 7 illustrates periodic oscillations over time in the spatial structure, where amplitude waves propagate from the center of the interval toward its boundaries. Meanwhile, Figure 8 depicts the scenario of a Turing-Hopf bifurcation, resulting in the existence of a branch of spatially heterogeneous and time periodic solutions.
7.
Discussion
The virus within a host organism undergoes frequent mutations, resulting in the emergence of new variants that compete, persist, or vanish during this ongoing competition. This population of viruses, characterized by closely related genotypes, is referred to as a virus quasi-species. From a modeling perspective, these variants can be conceptualized as a distribution of virus densities across genotype space, centered around an average genotype. The existence of such quasi species is influenced by the interplay between virus replication within host cells and its genotype dependent mortality, which may occur independently of immune responses. The results obtained demonstrate that the model (1.1)–(1.2) illustrates the complexity of viral dynamics and immune responses. For instance, Figure 6 shows a stationary solution with a certain number of spikes representing different virus variants and the corresponding immune cells involved in the adaptive immune response. In contrast, the viral dynamics observed in Figure 7 differ significantly: new virus variants emerge at the center of the interval and move toward the boundary of the domain. This motion occurs due to the genetic pressure from the antigen-specific immune response. Immune cells eliminate virus with the corresponding antigens and lead to the virus evolution trying to avoid the immune response.
Problem (1.1)–(1.2) can have different stationary solutions for the same values of parameters. These different solutions are similar to the solution shown in Figure 6 but they have different numbers of spikes. As such, in the beginning of simulations in Figure 8, there are 22 spikes. The choice of initial condition means that the time-dependent solution of system (1.1)–(1.2) approaches this stationary solution, but after some time we observe transition to another stationary solution with a different number of spikes. This transition occurs due to the emergence of new virus variants manifested by the splitting of the existing variant into two new variants for x = 20 and t = 150 . Then such emergence of new variants occurs several times leading to the convergence to the stationary solution with 26 spikes. Emerging new virus variants push away the existing variants resulting in consecutive waves of their displacement. This new solution is stable, and it does not change any more for large time. Spatial localization of new emerging variants can be determined by the choice of initial conditions and small perturbations of solutions.
The presence of viability intervals confers a fitness advantage, predisposing the emergence of virus quasi-species with specific genotypes. Alternatively, virus quasi-species may emerge without any assumed fitness advantage for certain genotypes. From a modeling standpoint, this mechanism bears resemblance to the emergence of biological species through intraspecific competition and natural selection (sympatric speciation) [19,27,28].
Nonlocal competition for host cells, coupled with interactions with the immune response, leads to the emergence of genotype-dependent virus distributions, without any inherent advantage for particular genotypes. Numerical simulations demonstrate that these distributions can be either stationary or time-dependent, with fluctuations in the sizes of virus subpopulations and the emergence of new variants. Unlike scenarios involving global competition or no competition (where H(u) = u ), the emergence of virus quasi-species occurs exclusively in cases of nonlocal competition. Additionally, a low virus mutation rate (diffusion coefficient) fosters the emergence of virus quasi-species, while a high mutation rate can lead to their extinction. Notably, while previous work [29] only identified stationary patterns, our study also observes temporal dynamics (using a different model).
In summary, this study explores two mechanisms for the emergence of virus quasi-species using simplified yet biologically realistic models of virus replication and immune response. More comprehensive models of immune response could provide further insights into the roles of innate and adaptive immune responses, as well as other factors influencing viral infections.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This study was supported by PHC-Maghreb 22MAG22 and DGRSDT-Algeria. The second author was supported through the RUDN University Strategic Academic Leadership Program.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: