Global stability of age-of-infection multiscale HCV model with therapy

1.   Introduction

In medicine, hepatitis C (HC) is generally divided into acute and chronic HC. It is worth noting that the commonality of the two is that their early symptoms are not obvious, so it is easy to be ignored by most people in the early stage of the disease. According to medical research, the root of HC is the highly contagious hepatitis C virus (HCV), and once infected by this virus, it is difficult to be cured. What is worrying is that if early HC patients are not treated promptly, they may develop cirrhosis and liver cancer. Nowadays, there is neither an effective vaccine against HC nor a suitable treatment option. And people infected with the virus can only use some antiviral drugs for intervention treatment, such as ribavirin.

For decades, interferon (IFN)-based treatment ^[1,2] is the standard treatment method for chronic HCV infection, and about 50% to 60% of patients can obtain sustained virological response (SVR). The SVR of the IFN inducer can reduce the incidence of hepatocellular carcinoma (HCC) by about four times ^[3,4]. During the past several years, major breakthrough has been made about the treatment of HC. The use of new direct-acting antiviral agent (DAA) ^[5,6] can effectively remove HCV in a short time (generally 12 weeks) with an efficiency of up to 95%–99%. Above results has been basically verified in a number of clinical trials. With more and more breakthroughs in the research and development of new antiviral drugs, the cure of chronic HC has become within reach. In that case, we have sufficient reasons to speculate that the number of people whose disease caused by HC has deteriorated to liver cirrhosis and liver cancer will considerably be reduced.

Theoretical research on HCV with treatment has been focused on. In 1998, Neumannd et al. ^[7] was utilized a mathematical model to illustrate the viral decline of patients under the antiviral effect of IFN-$\alpha$-$2b$. And they have used the model to show that the main initial function of IFN was to prevent the production or drop of virus particles. It also proved that the early monitor of the virus can help guide the treatment. In 2013, Guedj and Rong et al.were inspired by the HCV model ^[7] and used the multi-scale age-structured model ^[8,9,10], combined with related dynamics knowledge, to reasonably explain the changes of HCV virus under DAA, regardless of whether the patient has been treated or not. In 2017, Goyal et al. ^[11] were regarded HCV-RNA as an infectious virus, and a model was established to predict the time required for cure. The model has been successful in explaining the effects of short-term drug interventions and is consistent with actual data. In the same year, Quintela et al. ^[12] were considered the age structure of both the positive and negative strands of HCV-RNA. They studied the earlier multiscale model and discovered that HCV-RNA cells can effectively prevent the production and release of new viruses.

In the study of the treatment of HC, we found a key point worthy of attention. We cannot prevent the re-infection with HC, and then the vaccine plays a role in terms of the prevention and treatment of the disease. Echevarria et al. and Lombardo et al. ^[13,14] combined the immune response and the production of alanine-aminotransferase together. In particular, they took into account the treatment of HCV and the status of antibodies, to illustrated the importance of post-treatment vaccines.

In existing research, most HCV multiscale models are expressed in the form of a partial differential equation (PDE). But its disadvantages such as time-consuming numerical calculation and poor convergence cannot be ignored. In order to solve the above problems, Kitagawa and Nakaoka et al. ^[15] considered "the problem of model agammaegation" and converted the PDE model into an ordinary differential equation (ODE) model, which greatly improved computational efficiency.

2.   Preliminaries

In this paper, we mainly study the multiscale age-structured model of the treatment stage of HCV infection. Let us first briefly review the following theorems, which will help to understand the proof process and results of the theorem present in this article.

Theorem 1. (Theorem 2.33 in ^[16]) The following statements are equivalent:

(ⅰ) There exists a compact attractor of bounded sets (which is unique and contains every bounded backward invariant set).

(ⅱ) $\Phi$ is point-dissipative, asymptotically smooth, and eventually bounded on every bounded set in $X$.

Theorem 2. (Theorem 2.39 in ^[16]) Let the semiflow $\Phi$ be state-continuous, uniformly in finite time, and $A$ be a compact forward invariant subset of $X$ that attracts all compact subsets of a neighborhood of itself (e.g a local compact attractor of compact sets). Then $A$ is locally asymptotically stable.

Theorem 3. (Theorem 2.46 in ^[16])

Let $X$ be a closed subset of a Banach space $E, \; J$ a time set and $\Phi:\; J\times X\rightarrow X$ a state-continuous semiflow. Then $\Phi$ is asymptotically smooth if there are maps $\Psi$, $\Theta:\; J\times X\rightarrow X$ such that

and the following hold for any bounded closed set $C$ that is forward invariant under $\Phi$:

(ⅰ) $\mathop {\lim \inf }\limits_{J \owns t \to \infty }$ diam${\theta _t}(C) = 0$,

(ⅱ) there is some $r_{C} \in J$ such that $\Psi_{t}(C)$ has compact closure for all $t \in J, \; t \geq r_{C}$.

Theorem 4. (Theorem 5.2 in ^[16]) If $X_{0} \ne \emptyset$, $\rho \circ \Phi$ is continuous, and $\Phi$ is uniformly weakly $\rho$-persistent, then $\Phi$ is uniformly $\rho$-persistent.

Theorem 5. (Theorem 5.7 in ^[16])

Assume that $X_{0} \ne \emptyset$, $\Phi$ is uniformly weakly $\rho$-persistent, $\rho \circ \Phi$ is continuous, and

(H1) there exists no total $\Phi$-trajectory with range in A such that

Then the attractor A is the disjoint union

of three invariant sets $A_0$, $C$, $A_1$. $A_0$ and $A_1$ are compact and the following hold.

(ⅰ) ${A_0} = A \cap {X_0}$ is compact attractor of comparct subsets of $X_0$; more strongly, every compact subset $K$ of $X_0$ has a neighborhood in $X_0$ that is attracted by $A_0$. Further, $A_0$ attracts every subset of $X_0$ that is attracted by $A$.

(ⅱ) $A_1$ is uniformly $\rho$-persistent and is the compact attractor of neighborhoods of compact sets in $X \backslash {X_0}$. It also attracts all sets that are attracted by $A$ and on which $\Phi$ is eventually uniformly $\rho$-persistent. In particular, $A_1$ is stable.

(ⅲ) If $x \in X \backslash {A_1}$ and $\phi$ is a total $\Phi$-trajectory through $x$ with pre-compact range, then $\phi(t) \rightarrow {A_0}$ for $t \rightarrow -\infty$.

If $x \in X \backslash {A_0}$ and $\phi$ is a total $\Phi$-trajectory through $x$ with pre-compact range, then $\phi(t) \rightarrow {A_1}$ for $t \rightarrow \infty$.

In particular, the set $C$ consists of those points $x \in A$ through which there exists a total trajectory $\phi$ with $\phi(-t) \rightarrow {A_0}$ and $\phi(t) \rightarrow {A_1}$ as $t \rightarrow \infty$.

Corollary 1. (Corollary B.6 in ^[16]) Let $w, r$ and $g$ be nonnegative and locally integrable,

Assume that $k$ is not zero a.e. Then there exists some $b > 0$, which only depends on $k$ and not on $g$, such that $w(t) > 0$ for all $t > b$ with $\int_0^{t - b} {g(s){\rm d}s} > 0.$

In particular, if $g$ is continuous at $0$ and $g(0) > 0$, then $w(t) > 0$ for all $t > b$.

Theorem 6. (Theorem 3.1 in ^[17]) Let $K$ be a subset of $L^1(\mathbb{R}^+)$. Then $K$ has compact closure if and only if the following conditions hold:

(ⅰ) $\mathop {\sup }\limits_{f \in K} \int\limits_0^\infty {\left| {f(a)} \right|{\rm d}a} < \infty$ ,

(ⅱ) $\mathop {\lim }\limits_{r \to \infty } \int\limits_r^\infty {\left| {f(a)} \right|{\rm d}a} = 0$ uniformly in $f \in K$,

(ⅲ) $\mathop {\lim }\limits_{h \to {0^ + }} \int\limits_0^\infty {\left| {f(a + h) - f(a)} \right|{\rm d}a} = 0$ uniformly in $f \in K$,

(ⅳ) $\mathop {\lim }\limits_{h \to {0^ + }} \int\limits_0^h {\left| {f(a)} \right|{\rm d}a} = 0$ uniformly in $f \in K$.

Lemma 1. (Lemma 5.6 in ^[18]) The following alternative holds: either $B$ is $0$ everywhere on $\mathbb{R}$ or $B$ is positive everywhere on $\mathbb{R}$.

3.   The model

In order to study the problem that HCV decreases rapidly in the early stage but slowly in the later treatment with IFN, the following model ^[7] has been constructed

The intracellular viral dynamics were incorporated into the multi-scale model and another variable $R$ ^[9] was introduced, which is expressed by the following formula:

$R$ represents the quantity of intracellular genomic RNA (i.e., positive-strand HCV RNA) within an infected cell.

Combining Eqs (1) and (2), the multi-scale model was obtained that include the dynamics of intracellular viral RNA replication and extracellular viral infection, which were described by the following partial differential equations (PDEs).

The detailed parameters of the model are explained as follows:

(1) The amount of uninfected target cells at time $t$ within unit volume is denoted by $T(t)$; $V(t)$ is the number of free virus.

(2) $i(t, \; a)$ and $r(t, \; a)$ are numbers of infected cells and positive-strand HCV RNA at time $t$ with infection age $a$.

(3) $s$ presents the production rate, $d$ is per capita death rate of target cells, in addition, $\beta V(t)T(t)$ is the viral infection rate.

(4) $a$ is the age of infection, and $a\rightarrow\delta(a)$ is assumed to be the mortality of infected cells at the infection age of $a$. We take the second equation of (3.1) as an example to explain the influence of infection age on infected cells. The fourth equation can be obtained similarly. Let $a_+$ be the upper limit of the age of infection and it is reasonable to consider $i(t, \; a_+) = 0$. Obviously,

can respectively represent the population number in the interval $[a_1, \; a_2]$ of infection age at time $t$ and total population number. If $\triangle a$ is small, then

respectively represent the approximate values of the population number and the number of deaths in the interval $[a, \; a+\triangle a]$ of infection age at time $t$. Given a small time interval $\triangle t$, the population with infection age $a$ at time $t$ becomes that with infection age $a+\triangle t$ at time $t+\triangle t$. Therefore, $i(t, \; a)\triangle a$ becomes

after $\triangle t$. Combined the mortality rate in $\triangle t$, an equation can be established

Divide $\triangle a\triangle t$ on both sides of the above formula, and let $\triangle t\rightarrow 0$, we can get our equation.

$\; a\rightarrow\alpha(a), a\rightarrow\mu(a)$ are assumed to be age-dependent rates of intracellular viral RNA production and degradation at $a$, respectively. And $\rho(a)$ represents the rate with infection age $a$ at which RNA is assembled/secreted.

The age-dependent relationship of $\delta(a), \; \alpha(a), \; \mu(a)$ and $\rho(a)$ can be given by data fitting (such as least squares regression) of experimental data.

(5) Virus increases by $\int_0^{\infty}\rho(a)r(t, \; a)i(t, \; a){\rm d}a$ and disappears at rate $c$.

(6) $\epsilon_{\alpha}, \; \epsilon_s, \; \kappa$ are assumed to be the effects of inhibiting intracellular viral RNA production, blocking assembly/ secretion as virus into plasma, and enhancing RNA degradation, respectively, and $0\leq\epsilon_{\alpha}, \; \epsilon_s\leq1, \; \kappa\geq1$.

(7) $i_0(a)$ and $r_0(a)$ stand for the initial distributions of infected cells and intracellular viral RNA; "$r(t, \; 0) = 1$" declares that the infected cell has one viral RNA at the beginning.

In the beginning, we need the following assumption to analyze the model (3.1).

Assumption 1. $a\rightarrow\delta(a), \; a\rightarrow\alpha(a)$ as well as $a\rightarrow\mu(a)$ belong to $L_+^{\infty}(0, \; +\infty)$ and $\varsigma(a) = \min\{\delta(a), \; c\}\geq d$ for almost every $a\geq0$.

Taking $m(t, \; a) = i(t, a)r(t, \; a)$, the model (3.1) is transformed into

where $\gamma(a) = (1-\epsilon_s)\rho(a)+\kappa\mu(a)+\delta(a)$.

Define $X: = \mathbb{R}\times L^1(\mathbb{R}^+)\times L^1(\mathbb{R}^+)\times \mathbb{R}$ to be a functional space holding norm

and $X_+ = \mathbb{R^+}\times L_+^1(\mathbb{R}^+)\times L_+^1(\mathbb{R}^+)\times \mathbb{R^+}$ is the positive cone of $X$.

According to the results from Theorem 1.1 in ^[19], we draw the following conclusion.

Theorem 7. The problem (3.4) has a unique non-negative solution $(T, \; i, \; m,$ $V)\in C^1(\mathbb{R^+})\times C(\mathbb{R^+}, \; L_+^1(\mathbb{R}^+))\times C(\mathbb{R^+}, \; L_+^1(\mathbb{R}^+))\times C^1(\mathbb{R^+}, \; \mathbb{R^+})$ for the initial condition in $X_+$.

Utilizing the method in section 8.2.1 in ^[20], add $R(t)$ satisfying

into (3.4). $R(0)\geq0$ gives $R(t)\geq0\; (\forall\; t\geq0)$ by Assumption 1. Denote $N(t): = T(t)+\int_0^{\infty}i(t, \; a){\rm d}a+\int_0^{\infty}m(t, \; a){\rm d}a+V(t)+R(t)$ and

Therefore, it is followed that

Theorem 8. $N(t)\leq M: = \max\{N(0), \; s/d\}$ for $t > 0$ and $\lim_{t\rightarrow\infty}N(t) = s/d$. We also have

4.   Existence of equilibria

The equilibrium $(\bar{T}, \; \bar{i}(a), \; \bar{m}(a), \; \bar{V})$ of (3.4) satisfies

The solutions of initial value problem for $\bar{i}(a)$ and $\bar{m}(a)$ are as follows:

where $\tau(a) = \pi(a)[1+(1-\epsilon_{\alpha})\int_0^a \frac{\alpha(s)\omega(s)}{\pi(s)}{\rm d}s], \; \omega(a) = e^{-\int_0^a\delta(l){\rm d}l}, \; \pi(a) = e^{-\int_0^a\gamma(l){\rm d}l}$.

Let $K = (1-\epsilon_{s})\int_0^{+\infty}\rho(a)\tau(a){\rm d}a$, then we have

leading to $\bar{T} = \frac{c}{\beta K}$ and $\bar{V} = \frac{s-d\bar{T}}{\beta\bar{T}} = \frac{\beta sK-dc}{\beta c}$.

As a result, define

then $E^*(\bar{T}, \; \bar{i}(a), \; \bar{m}(a), \; \bar{V})$ is the unique positive equilibrium of (3.4) when $\mathcal{R} > 1$, and there always exists an infection-free equilibrium marked by $E_0(s/d, \; 0, \; 0, \; 0)$.

5.   Global stability about infection-free equilibrium

The linearized system of (3.4) at $E_0$ is

leading to the characteristic equation

that is,

Obviously, one eigenvalue marks $\lambda = -d$ and others are produced by

therefore

When $\mathcal{R} < 1$, if there is an eigenvalue $\lambda_0$ such that ${\rm Re}\lambda_0\geq0$, then

i.e. $\mathcal{R}\geq1$. This means a contradiction. It is declared that all eigenvalues of (5.1) at $E_0$ are negative while $\mathcal{R} < 1$.

Theorem 9. When $\mathcal{R} < 1$, the infection-free equilibrium $E_0$ is locally asymptotically stable.

Next, we study the global stability of $E_0$. By using Volterra integral formulation, we get

Thus, it is obtained that

where $B_1(t): = i(t, \; 0)$.

That is,

where $B_2(t): = m(t, \; 0)$. In fact, $B_1(t) = B_2(t): = B(t)$ gives that

and

From Theorem 8 and fluctuation method Proposition A.14 in ^[16], there exist sequences $t_n, \; s_n, \; r_n, \; \vartheta_n\rightarrow\infty\; (n\rightarrow\infty)$ such that as $n\rightarrow\infty$

where

Plugging $\vartheta_n$ into (5.7) and letting $n\rightarrow\infty$, we deduce that

Theorem 2 produces that

so $V^{\infty} = 0$ when $\mathcal{R} < 1$. Furthermore, it is also proved that $B^{\infty} = 0$ and $T(t)$ as $t\rightarrow\infty$ obeys the equation $\frac{{\rm d}}{{\rm d}t}T(t) = s-dT(t)$, implying that $T(t)\rightarrow s/d\; (t\rightarrow\infty)$. As a result, it is received that

Theorem 10. Provided that $\mathcal{R} < 1$, the infection-free equilibrium $E_0$ exhibits global asymptotic stability.

6.   The semiflow and global attractor

In this part, we focus on a compact attractor of all bounded subset of $X^+$. The unique solution of (3.4) can generate the semiflow $\Phi:\; \mathbb{R}^+\times X^+\rightarrow X^+$ with

Indeed, the semiflow is continuous.

Theorem 11. There exists a compact attractor $\bf{A}$ of bounded subsets of $X^{+}$ of the semiflow $\Phi$.

Proof. In order to prove this conclusion, we need to get that $\Phi$ is eventually bounded, point-dissipative on every bounded set of $X^{+}$ and asymptotically smooth followed by Theorem 1 (Theorem 2.33 in ^[16]). The first two parts hold from Theorem 7. We only prove that $\Phi$ is asymptotically smooth applying Theorem 3 (Theorem 2.46 in ^[16]). Denote

with

where

Let $C$ be a bounded closed set that is forward invariant under $\Phi$.

as a result, $\Phi_1\rightarrow0$ as $t\rightarrow\infty$ uniformly for $(T_0, \; i_0, \; m_0, \; V_0)\in C$. Next, it is necessary to show that $\Phi_2$ has a compact closure. Thus, we have to check assertions of Theorem 6 (Theorem 3.1 in ^[17]). Obviously, it is easy to check (ⅰ), (ⅱ) and (ⅳ) and let us prove (ⅲ). Set

and $\int_{t-h}^t|\omega(a)B(t-a)|{\rm d}a\rightarrow0$ as $h\rightarrow0$. The first term of $I_h$ satisfies

Referring to Theorem 8, it is observed that

Let

and

Then

Hence, $I_h$ goes to $0$ uniformly in $C$ as $h\rightarrow0^+$.

Let $\phi:\; \mathbb{R}\rightarrow X^+$ be the total $\Phi$-trajectories, $\phi(t) = (T(t), \; i(t, \; \cdot), \; m(t, \; \cdot),$ $V(t))$ and $\phi(t+r) = \Phi(t, \; \phi(r)), \; t\geq0, \; r\in\mathbb{R}$. Following the discussions in ^[16,17], the trajectory is illustrated by

for $t\in\mathbb{R}$.

We can give the estimates on total trajectories.

Lemma 2. For all $(T_0, \; i_0(\cdot), \; m_0(\cdot), \; V_0)\in\bf{A}$, the estimates hold for all $t\in \mathbb{R}$

where $\mu_1 = \min\{d, \; \inf_{a\in\mathbb{R}}\{\delta(a)\}\}, \; \mu_2 = \min\{d, \; \inf_{a\in\mathbb{R}}\{\gamma(a)\}\}$.

Proof. Consider

and we have

Then

where $\mu_1 = \min\{d, \; \inf_{a\in\mathbb{R}}\{\delta(a)\}\}$. By comparison theorem,

Similarly, in terms of $m(t, \; a)$, calculation leads to

and

where $\mu_2 = \min\{d, \; \inf_{a\in\mathbb{R}}\{\gamma(a)\}\}$.

By integrating from $r$ to $t$ and letting $r\rightarrow-\infty$,

with $C_0 = \frac{s\mu_1+s(1-\epsilon_{\alpha})\|\alpha\|_{\infty}}{\mu_1\mu_2}$.

gives us

Furthermore, adopting conclusions above, the following facts are correct

From (6.2), we also have

producing

7.   Global stability of infected equilibrium with therapy

Our main purpose is to discuss the global stability of $E^*$. Firstly, according to Theorem 4 (Theorem 5.2 in ^[16]), the uniform persistence of the disease is investigated.

Set the subset $X_0$ of $X^+$ defined by

with $\bar{\pi}(\sigma) = (1-\epsilon_{s})\int_0^{\infty}\frac{\rho(\sigma+s)\pi(\sigma+s)}{\pi(\sigma)}{\rm d}s, \; \bar{\omega}(\sigma) = (1-\epsilon_{s})(1-\epsilon_{\alpha})\int_0^{\infty}\frac{\rho(\sigma+s)\pi(\sigma+s)}{\omega(\sigma)}$ $(\int_{0}^{\sigma+s}\frac{\alpha(l)\omega(l)}{\pi(l)}{\rm d}l){\rm d}s$. Clearly, we have the lemma as follows:

Lemma 3. If $(T_0, \; i_0(\cdot), \; m_0(\cdot), \; V_0)\in X_0$, then there exists $t_0 > 0$ such that $B(t) > 0$ for all $t > t_0$. If $(T_0, \; i_0(\cdot), \; m_0(\cdot), \; V_0)\in X^+\setminus X_0$, then $B(t) = 0$ for all $t\geq0$.

Proof. Solving the last equation in (3.4) gives us

implying

If $V_0 > 0$, then $B(t) > 0$ for all $t\geq0$. Set

Suppose $(T_0, \; i_0(\cdot), \; m_0(\cdot), \; V_0)\in X_0$, and then integrating $I_0$ yields

Moreover, by Theorem 8, we have

Using Corollary 1 (Corollary B.6 in ^[16]),

and

demonstrate $t_0 > 0$ such that $B(t) > 0$ for any $t > t_0$ provided that $T_0 > 0$.

If $(T_0, \; i_0(\cdot), \; m_0(\cdot), \; V_0)\in X^+\setminus X_0$, then it is demonstrated that

Fubini's Theorem leads to

Applying Gronwall's inequality, it is declared that $B(t) = 0$ for all $t\geq0$.

Denote the persistence function by $\rho:\; X^+\rightarrow\mathbb{R}^+$, that is,

Theorem 4 (Theorem 5.2 in ^[16]) gives information that weakly uniform persistence produces strongly uniformly persistence.

Lemma 4. Suppose that $x\in X_0$, then there is some $\varepsilon > 0$ such that

for each solution of (3.4) while $\mathcal{R} > 1$.

Proof. It is assumed that $\Phi$ is not weakly uniformly persistent. In other words, there is an arbitrarily small $\varepsilon_0 > 0$ giving

Denote $T_{\infty} = \liminf_{t\rightarrow\infty}T(t)$, and $t_k\rightarrow\infty\; (k\rightarrow+\infty)$ is a sequence satisfying $T(t_k)\rightarrow T_{\infty}$ together with $T'(t_k)\rightarrow0$. Thus,

Owing to $\mathcal{R} > 1$, there is a small positive constant $\varepsilon_1$ giving

On the other hand, for any $t\geq0$,

For $\lambda > 0$, Laplace transform to the above inequality leads to

where

Now, we obtain

Because $B(t) = \beta V(t)T(t)\geq\frac{\beta(s-\varepsilon_0)}{d}V(t)$, it is deduced that

causing

Choosing $\lambda = \varepsilon_0$, we have

which contradicts (7.3).

Based on Lemma 4, we need another hypothesis ($H_1$) of Theorem 4 (Theorem 5.2 in ^[16]). It is quite easy to check the following result.

Lemma 5. If $\rho(\phi(t)) = 0$ for any $t\leq0$, it holds that $\rho(\phi(t)) = 0$ for all $t > 0$.

Referring to the proving method of Lemma 1 (Lemma 5.6 in ^[18]), we can also show that

Lemma 6. Either $B(t) = 0$ or $B(t) > 0$ for all $t\in\mathbb{R}$ holds.

On account of Lemmas 4–6, Theorem 4 (Theorem 5.2 in ^[16]) produces the strong uniform persistence of the disease.

Theorem 12. Provided that $\mathcal{R} > 1$, each solution of (3.4) is strongly uniformly persistent for $(T_0, \; i_0(\cdot), \; m_0(\cdot), \; V_0)\in X_0$.

Furthermore, we obtain the result in view of Theorem 5 (Theorem 5.7 in ^[16]).

Theorem 13. There is a compact invariant set $\bf{A_1}$ that is uniformly $\rho$-positive. In other words, there exists some $\delta > 0$ such that

attracting every solution as $(T_0, \; i_0(\cdot), \; m_0(\cdot), \; V_0)\in X_0$.

The next part is devote to the main conclusion about the global asymptotic stability of $E^*$.

Theorem 14. If $\mathcal{R} > 1$, then it is demonstrated that $E^*$ of (6.2) has globally asymptotical stability in $X_0$.

Proof. Let $\Psi:\; \mathbb{R}\rightarrow\bf{A_1}$ be a total $\Phi$-trajectory, where $\Psi(t) = (T(t), \; i(t, \; \cdot), \; m(t,$ $\cdot), \; V(t))$ is the solution of (6.2) with initial value $(T_0, \; i_0(\cdot), \; m_0(\cdot), \; V_0)$. Denote the function $H(y) = y-1-\ln y$, $\Omega = \frac{\beta\bar{V}\bar{T}}{c}$, and for $a\geq0$,

For $\Psi(t) = (T(t), \; i(t, \; \cdot), \; m(t, \; \cdot), \; V(t))\in\bf{A_1}$, define Lyapunov functional $V(\Psi(t)) = V_1(\Psi(t))+V_2(\Psi(t))+V_3(\Psi(t))+V_4(\Psi(t))$ where

and

Using the initial equation of (6.2), we have

After a process of Lemma 9.18 in ^[16], it is obtained that

and

Next, the last equation of (6.2) gives us

Finally, we have

Noticing that $\int_0^{\infty}\rho(a)\bar{m}(a){\rm d}a = c\bar{V}$,

and some simple calculation to $\phi'(a), \; \psi'(a)$, then $V'(\Psi(t))$ becomes

Based on $-\ln(1/x)-x+1\leq0$ and $H(b)-H(a)+(a-b)H'(b)\leq0$, it is derived that

Obviously, $V'(\Psi(t)) = 0$ implies $\Psi = E^*$. LaSalle's Invariance Principle tells us that the largest invariant set satisfying $V'(\Psi(t)) = 0$ is $\{E^*\}$. In that $\bf{A_1}$ is compact, $\alpha$ and $\omega$-limit sets are compact, invariant, non-empty and attract $\Psi(t)$ as $t\rightarrow\pm\infty$, respectively. $V'(\Psi(t))\leq0$, as a consequence, $V = 0$ on $\omega$ and $\alpha$-limit sets that includes only $E^*$. Therefore, $\Psi(t)\rightarrow E^*$ as $t\rightarrow\pm\infty$, that is,

Due to

$V(\Psi(t)) = V(E^*)$ for any $t\in\mathbb{R}$ meaning $\Psi(t) = E^*$. Then, $\bf{A_1}$ is $E^*$ in reality, linked to the local asymptotical stability of $\bf{A_1}$ of Theorem 2 (Theorem 2.39 in ^[16]), consequently, $E^*$ is globally asymptotically stable.

8.   Numerical simulation

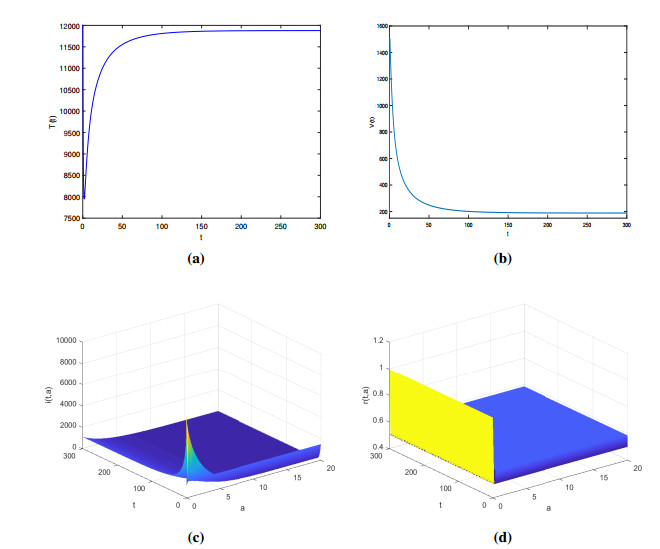
In this part, we choose a set of parameters to display the theoretical part above. $s = 1.3\times10^4$ cells/mL, $d = 1$ day$^{-1}$, $\beta = 5\times10^{-5}$ mL day$^{-1}$ virion$^{-1}$, $c = 22.3$ day$^{-1}$, $\epsilon_{\alpha} = 0.5$, $\epsilon_{s} = 0.01$, $\kappa = 4$ and $\rho(a), \; \delta(a), \; \mu$ $(a), \; \alpha(a)$ are seen as constants $\rho = 2$ day$^{-1}$, $\delta = 0.3$ day$^{-1}$, $\mu = 1$ day$^{-1}$, $\alpha = 7$ day$^{-1}$. Calculations gives that $\mathcal{R} = 0.1164 < 1$, $s/d = 1.3\times10^4$ and $\bar{r}(a) = 0.5853+0.4147e^{-5.98a}$. Transfer (3.1) into an ODE system by discretizing $a$ and MATLAB ODE solver provides the solutions in Figure 1. At this time, the equilibrium $(s/d, \; 0, \; \bar{r}(a), \; 0)$ of (3.1) corresponding to $E_0$ in system (3.4) is globally asymptotically stable, where $\bar{r}(a) = \frac{\tau(a)}{\omega(a)}$.

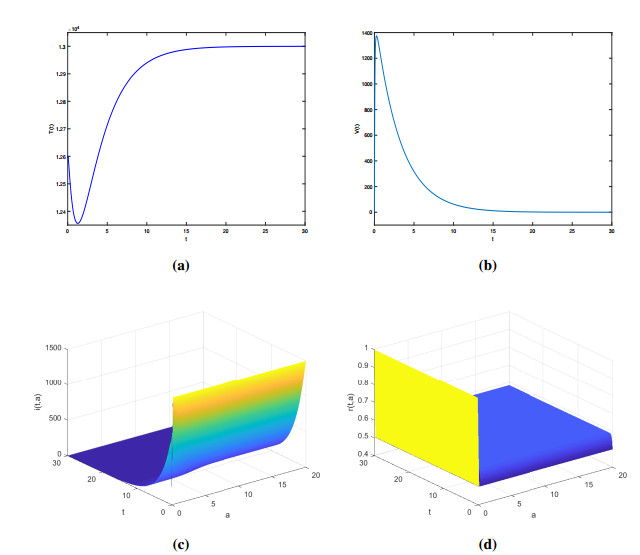
Setting $\beta = 5\times10^{-4}$ mL day$^{-1}$ virion$^{-1}$ and unchanged other parameters leads to $\mathcal{R} = 1.1641 > 1, \; \bar{T} = 1.188\times10^4, \; \bar{i}(a) = 1.8322\times10^3e^{-0.3a}, \; \bar{r}(a) = 0.5853+0.4147e^{-5.98a}, \; \bar{V} = 189$. Considering the case of model (3.1) without therapy, i.e., $\epsilon_{\alpha} = \epsilon_s = 0$ and $\kappa = 1$, we have $\mathcal{R} = 4.2986 > 1$ under the parameters above. At this time, there exists an infected equilibrium $(\tilde{T}, \; \tilde{i}(a), \; \tilde{r}(a), \; \tilde{V})$, where $\tilde{T} = 3.0242\times10^3, \; \tilde{i}(a) = 9.9758\times10^3e^{-0.3a}, \; \tilde{r}(a) = 2.3333-1.3333e^{-3a}, \; \tilde{V} = 6.5972\times10^3$. In order to observe the effect of treatment, we choose $(\tilde{T}, \; \tilde{i}(a), \; \tilde{r}(a), \; \tilde{V})$ as the initial value in our simulation. According to both the theory above and Figure 2, we obtain a globally asymptotically stable infected equilibrium $(\bar{T}, \; \bar{i}(a), \; \bar{r}(a), \; \bar{V})$ of (3.1). Also, it is clear that the quantity of HCV RNA, viruses and infected cells are all decreasing, and the treatment is effective.

9.   Conclusions

In the present paper, the global stability of an age-dependent HCV model under the treatment with multiscale structure is explored. Two equilibria including infection-free $E_0$ and infected ones $E^*$ of this model are obtained initially for the deformed model (3.4). Subsequently, we define a quantity $\mathcal{R}$ to separate the existence of infected equilibrium or not. Provided that $\mathcal{R} < 1$, $E_0$ is locally and globally asymptotically stable by means of the eigenvalue analysis and Volterra integral formulation. Furthermore, the existence, uniqueness and positivity of solutions of (3.4) are able to be proved, based on that we construct a Lyapunov functional declaring the globally asymptotical stability of infected equilibrium $E^*$ under therapy.

Our results demonstrate that virus is extinct with $\mathcal{R} < 1$, on the contrary, it continues to exist with $\mathcal{R} > 1$. However, from the numerical simulation, it can be seen that the amount of virus significantly reduces after the treatment.

Acknowledgments

This work was supported by the National Natural Science Foundation of China [grant numbers 11301263, 11701306, 11701275]; the China Postdoctoral Science Foundation [grant number 2018M630547]; the Natural Science Fund Development Project by Nanjing Tech University; the Second Batch of High Level Demonstration Project for Sino-foreign Cooperative Education in Jiangsu; and the China Scholarship Council.

Conflict of interest

The authors declare that they have no competing interests.