1.
Introduction
Symmetry reduction plays a central role in the field of geometric mechanics [1,4,23], and it involves expressing the dynamics of a mechanical system with symmetry in terms of the equivalence classes of group orbits on the space of solutions. This allows one to derive reduced equations of motion on a lower-dimensional reduced space which is obtained by quotienting the phase space by the symmetry action. The modern approach to symmetry reduction was introduced in [3,26,28,33], but the notion of symmetry reduction arises in earlier work of Lagrange, Poisson, Jacobi, and Noether.
Discrete variational mechanics [12,17,27] provides a discrete (in time) notion of Lagrangian dynamics, based on a discrete Hamilton's principle. This leads to discrete flow maps that are symplectic, and exhibit a discrete Noether's theorem. In turn, this naturally raises the question of whether one can develop a corresponding theory of symmetry reduction for discrete variational mechanics. Interest in this direction was motivated in part by attempts to understand the integrable discretization of the Euler top due to [29]. Prior work on discrete symmetry reduction includes a constrained variational formulation of discrete Euler–Poincaré reduction [7,21], the associated reduced discrete Poisson structure [22], discrete Euler–Poincaré reduction for field theories [36] and discrete fluids [30,32], discrete Lie–Poisson integrators [5,18], discrete higher-order Lagrange–Poincaré reduction [6], and a discrete notion of Routh reduction for abelian groups [11]. The resulting symplectic and Poisson integrators can be viewed as geometric structure-preserving numerical integrators, and this is an active area of study that is surveyed in [10]. In addition, discrete reduction theory can also be expressed in terms of composable groupoid sequences, which was the approach introduced in [39], and explored further in [19], and extended to field theories in [37].
The goal of this paper is to develop a discrete analogue of Dirac cotangent bundle reduction [42] for Lagrangian systems, that is to say, a discrete Dirac reduction theory for implicit Lagrangian systems. The relevance of this type of reduction lies in the fact that it allows for treating a wide variety of systems with symmetry from a unifying viewpoint, including degenerate systems. Therefore, our discrete analogue allows us to construct geometric integrators for those systems. The theory presented here is limited to systems with abelian symmetry groups, but we expect to extend it to nonabelian groups in the future. Moreover, our work here is the first step in the construction of a category containing discrete Dirac structures that is closed under quotients, as proposed in [16], which is fundamental for the study of discrete Dirac reduction by stages.
In addition, framing the discrete reduction theory in the context of discrete Dirac mechanics is significant, as it is the natural setting for studying discrete Hamiltonian mechanics on manifolds, particularly when expressed in terms of the discrete generalized energy. This is because the notion of discrete Hamiltonians [12,17], which are Type 2 and 3 generating functions, does not make intrinsic sense on a nonlinear manifold, since it is not possible to specify a covector on a nonlinear manifold without also specifying a base point. In contrast, the discrete generalized energy does make intrinsic sense, and is a more promising foundation on which to construct a discrete analogue of Hamiltonian mechanics on manifolds. Discrete Dirac mechanics is also the basis of a discrete theory of interconnections [31], which allows one to construct discretizations of complex multiphysics systems by interconnecting simpler subsystems, which provides a framework for geometric structure-preserving discretization of port-Hamiltonian systems [35].
Reduction theory can be addressed either in terms of the reduction of geometric structures like the symplectic or Poisson structures, or in terms of the reduction of variational principles. In this work, we will start with the discrete Lagrange–Dirac mechanics that was developed in [16], which can be viewed as a discrete analogue of Lagrange–Dirac mechanics, that can be formulated both in terms of Dirac structures [40] and the Hamilton–Pontryagin variational principle [41]. In order to coordinatize the reduced spaces arising in the reduction that we will perform, we rely on the notion of discrete principal connections that was introduced in [14] and further developed in [9].
Overview
In Section 2, we will recall the notion of discrete principal connection [9,14] and discrete Dirac mechanics [15,16]. Initially, we will consider the case where the configuration space Q is a vector space, and the symmetry group G is a vector subspace acting on Q by addition, and show how the discrete Dirac structure is group-invariant, descends to a discrete Dirac structure on the quotient space in Section 3. In Section 4, we will show how the reduced discrete Dirac structure can be used to derive the reduced discrete equations of motion, after we derive the reduced discrete Dirac differential, which is a map arising in the reduced discrete Tulczyjew triple. In Section 5, we also show that the discrete variational principle can be expressed in terms of a discrete generalized energy, and that if the discrete Lagrangian is group-invariant, then so is the discrete generalized energy. This induces a reduced discrete variational principle, which yields the same reduced discrete equations of motion. Then, in Section 6, we show that, in the nonlinear setting, we can use the notion of retractions [2] and an atlas of retraction compatible charts [16] to develop a global discrete theory, whose local representatives recover the vector space theory that we considered in the earlier part of the paper. This is significant, because that implies that with respect to an atlas of retraction compatible charts, the local theory that we initially constructed on each chart is compatible on overlapping domains, and induces a well-defined global theory on a manifold endowed with a semi-global retraction map. In Section 7, we will illustrate the proposed discrete reduction theory by applying it to simulate the charged particle in a magnetic field, and the double spherical pendulum. Finally, we will summarize our contributions in the conclusion, and discuss future research directions.
2.
Preliminaries
2.1. Group actions
Let Q be a smooth manifold, G be a Lie group, and ΦQ:G×Q→Q a free and proper left action of G on Q. We will denote ΦQ(g,q)=g⋅q for each q∈Q and g∈G. For a fixed g∈G, we define the map ΦQg:Q→Q as q↦q⋅g. Likewise, for a fixed q∈Q, we define the map ΦQq:G→Q as g↦q⋅g. The action being free and proper yields a principal bundle πQ,Σ:Q→Σ, where Σ=Q/G. We denote the equivalence class of q∈Q by [q]∈Σ. In general, we use a superscript to denote the space where G acts, and brackets [⋅] to denote the corresponding equivalence classes.
The diagonal action on Q×Q is given by
Likewise, the lift of the action to the cotangent bundle is given by
where the superscript ∗ denotes the adjoint map. In other words, for each vg⋅q∈Tg⋅qQ we have
The infinitesimal generators (or fundamental vector fields) of the action ΦQ are denoted by ξQ∈X(Q) for each ξ∈g, where g is the Lie algebra of G, and analogously for the actions defined on the other spaces. In the same fashion, the momentum map J:T∗Q→g∗ of the action is defined by ⟨J(pq),ξ⟩=⟨pq,ξQ(q)⟩ for each pq∈T∗Q and ξ∈g.
2.1.1. Group actions on vector spaces
Now we suppose that Q is a vector space, which allows us to identify
In addition, assume that G⊂Q is a vector subspace* acting by addition, i.e., g⋅q=g+q for each g∈G and q∈Q. In this case, we have g−1=−g and the action on T∗Q reduces to,
*Recall that any vector space can be regarded as a Lie group with the additive structure.
To conclude, note that g=G and g∗=G∗, and that the exponential map is the identity. Hence, ξQ(q)=ξ for each ξ∈g and q∈Q. Subsequently, the momentum map is given by ⟨J(q0,p0),ξ⟩=⟨p0,ξ⟩ for each (q0,p0)∈T∗Q and ξ∈g.
2.2. Discrete principal connections
Discrete principal connections were first introduced in [14] and further studied in [9]. Let Q be a smooth manifold and G be a Lie group acting freely and properly on Q.
Definition 2.1. A discrete principal connection on the principal bundle πQ,Σ:Q→Σ is a (smooth) function ωd:Q×Q→G such that
1. ωd(q0,q0)=e, the identity element, for each q0∈Q.
2. ωd(g0⋅q0,g1⋅q1)=g1ωd(q0,q1)g−10 for each (q0,q1)∈Q×Q and g0,g1∈G.
Discrete principal connections are not generally defined globally on Q×Q, as its global existence implies a global trivialization of TQ. Instead, it is only semi-globally defined on a G-invariant open subset U⊂Q×Q containing the diagonal, i.e., (q0,q0)∈U for each q0∈Q. Nevertheless, in the following we assume that they are globally defined in order to simplify the notation.
A discrete principal connection ωd enables us to define the discrete horizontal bundle as
In addition, ωd induces a discrete horizontal lift, i.e., a map hd:Q×Σ→Q×Q that is the inverse of the diffeomorphism (idQ×πQ,Σ)|Hd:Hd→Q×Σ. We denote ¯hd=π2∘hd:Q×Σ→Q, where π2 denotes the projection onto the second component.
2.2.1. Local expression of discrete connections on vector spaces
Suppose that Q is a vector space and G⊂Q is a vector subspace acting by addition. Therefore, Σ=Q/G is a vector space and the projection πQ,Σ:Q→Σ is linear. In this case, we assume that the horizontal lift, hd:Q×Σ→Q×Q, is a linear map (where the vector structure on the product is given by the direct sum). This, in turn, ensures that ¯hd:Q×Σ→Q is also linear.
Working in a trivialization of πQ,Σ, i.e., supposing that Q=Σ×G with πQ,Σ=π1 and the vector structure given by the direct sum, then the horizontal lift of the discrete connection is determined by a map hd:Q×Σ→G defined by hd=π2∘¯hd, i.e.,
Of course, hd is also linear and, from [9, Equation (4.2)], it satisfies
In particular, hd(q0,x0)=g0 and hd(g+q0,x1)=g+hd(q0,x1), for each g∈G (to obtain this second equation we have used the equivariance of ωd).
On the other hand, the dual of Q is given by Q∗=Σ∗×G∗, and the adjoint of hd can be written as h∗d=(h∗d,Q,h∗d,Σ):G∗→Q∗×Σ∗ for some linear maps h∗d,Q:G∗→Q∗ and h∗d,Σ:G∗→Σ∗. They are related to the adjoint of ¯hd as follows
Similarly, we denote by hd,Q:Σ→G the adjoint map of h∗d,Q, and analogously for hd,Σ:Σ→G. In fact, we have hd,Q(q0)=hd(q0,0) and hd,Σ(x1)=hd(0,x1). Hence,
For the sake of simplicity, we introduce the map h0d:Σ×Σ→G, where h0d(x0,x1)=hd((x0,0),x1). Lastly, observe that hd:Q×Σ→G may be regarded locally as a map defined on (Σ×G)×Σ. For this reason, we denote its partial derivatives by
for each (q0,x1)=((x0,g0),x1)∈(Σ×G)×Σ. Due to the linearity of hd, they are given by
We conclude with the following straightforward result.
Lemma 2.2. Let Q=Σ×G be a trivialization of πQ,Σ. Then for each q0=(x0,g0)∈Q and p0=(w0,r0)∈Q∗ we have J(q0,p0)=r0.
2.3. Discrete Dirac mechanics
Let us briefly recall the formulation of discrete Dirac mechanics introduced in [15,16]. Here, we present only the unconstrained case. In the following, let Q be a vector space.
2.3.1. Generating functions and discrete Tulczyjew triple
The Tulczyjew triple consists of three diffeomorphisms defined between the iterated tangent and cotangent bundles of a smooth manifold (cf. [40]).
If ΘT∗(T∗Q)∈Ω1(T∗(T∗Q)) and ΘT∗(TQ)∈Ω1(T∗(TQ)) denote the tautological 1-forms on T∗(T∗Q) and T∗(TQ), respectively, then the Tulczyjew triple induce a symplectic form on T(T∗Q),
Remark 2.3. Given a continuous Lagrangian, L:TQ→R, the Tulczyjew [34] and the Dirac [40] approaches of mechanics make use of the Tulczyjew triple to define the induced Dirac structure on T∗Q,
and the Dirac differential,
Then, the Lagrange–Dirac equations for the vector field X:T∗Q→T(T∗Q) are given by
where FL:TQ→T∗Q is the Legendre transform of the Lagrangian. The key idea of discrete Dirac mechanics is to build a discrete analogue of the Tulczyjew triple that retains the symplecticity of the maps involved. In turn, the discrete Tulczyjew triple will be used to construct the discrete analogue of the induced Dirac structure. To that end, generating functions are utilized to construct the symplectic maps.
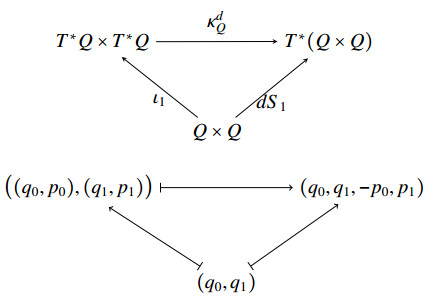
By means of the Poincaré Lemma (see [16, § 3.2] for details), it can be shown that a map F:T∗Q→T∗Q, given by (q0,p0)↦(q1,p1) is symplectic if and only if there exists a function S1:Q×Q→R, known as the Type 1 generating function, such that p0=−D1S1(q0,q1) and p1=D2S1(q0,q1) for each (q0,q1)∈Q×Q. We denote by ι1:Q×Q→T∗Q×T∗Q the map defined as (q0,q1)↦((q0,p0),(q1,p1)), and arrive at the following commutative diagram.
An analogous conclusion may be reached by using a function S2:Q×Q∗→R, known as Type 2 generating function. In such case, we obtain a map
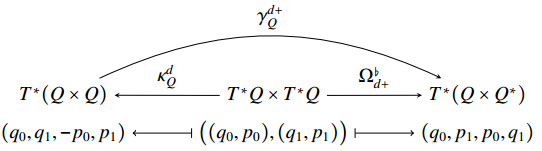
This way, we define the (+)-discrete Tulczyjew triple as follows,
The discrete triple preserve the symplecticity of the continuous triple in the sense that the following is a natural symplectic form on T∗Q×T∗Q,
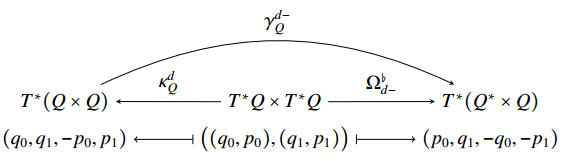
On the other hand, a function S3:Q∗×Q→R, known as Type 3 generating function, may be used to get a map
By using Ω♭d− instead of Ω♭d+, we arrive to an analogous diagram called the (−)-discrete Tulczyjew triple, which also inherits the symplecticity properties of the continuous triple.
2.3.2. Discrete implicit Lagrangian systems
Definition 2.4. The (+)-discrete induced Dirac structure is defined as
where z=(q,p)∈T∗Q≃Q×Q∗. Similarly, the (−)-discrete induced Dirac structure is defined as
Remark 2.5. A Dirac structure on a smooth manifold M is a maximally isotropic subbundle of its Pontryagin bundle, TM⊕T∗M (see, for example, [40]). Recall that the Whitney sum is a fibered sum over M, i.e., its elements are of the form (vx,αx)∈TxM×T∗xM for each x∈M. Note that π1(z0,z1)=z0≠z+=π1(αz+), where π1 denotes the projection onto the first component. Subsequently, (z0,z1,αz+) are not elements of the Pontryagin bundle of M=T∗Q and, hence, the (+)-discrete induced Dirac structure Dd+ defined above is not a Dirac structure on T∗Q in the sense of Dirac structures on manifolds. The same holds for the (−)-discrete induced Dirac structure. Despite this, we refer to these objects as discrete induced Dirac structures, in order to be consistent with the existing literature on discrete Dirac mechanics [16,31].
Although these discrete structures are not Dirac structures themselves, the discrete Tulczyjew structure is still present. Therefore, the maps involved are symplectic and, hence, they can be used to construct variational integrators.
Remark 2.6. It is worth noting that a new approach to discrete Dirac mechanics has been introduced in [8]. In this proposed approach, the discrete structures are actual Dirac structures, which allows one to apply the previous results found in the literature for Dirac mechanics. It would be interesting to explore a reduction theory for this new discrete Dirac mechanics and to compare it with the one given in the present paper. We leave this for future work.
Given a (possibly degenerate) discrete Lagrangian Ld:Q×Q→R, its derivative is the map dLd:Q×Q→T∗(Q×Q) given by
where Di denotes the partial derivative with respect to the i-th component, i=1,2. The (+)-discrete Dirac differential is the map
Analogously, the (−)-discrete Dirac differential is the map
At last, a discrete vector field on T∗Q is a sequence
Definition 2.7 ((+)-discrete implicit Lagrangian system). A (+)-discrete implicit Lagrangian system, also called a (+)-discrete Lagrange–Dirac system, is a pair (Ld,Xd), where Ld is a discrete Lagrangian on Q and Xd is a discrete vector field on T∗Q, satisfying the (+)-discrete Lagrange–Dirac equations, i.e.,
The equations are locally given by
Definition 2.8 ((−)-discrete implicit Lagrangian system). A (−)-discrete implicit Lagrangian system, also called a (−)-discrete Lagrange–Dirac system, is a pair (Ld,Xd), where Ld is a discrete Lagrangian on Q and Xd is a discrete vector field on T∗Q, satisfying the (−)-discrete Lagrange–Dirac equations, i.e.,
The equations are locally given by
Since we are considering the unconstrained case, both the (+) and (−)-discrete Lagrange–Dirac equations are equivalent to the discrete Euler–Lagrange equations [27].
2.3.3. Variational structure for discrete implicit Lagrangian systems
The discrete Lagrange–Dirac equations may also be obtained from a variational principle, as shown in [16]. As above, there exist two possible choices when performing discretization. Firstly, the (+)-discrete Pontryagin bundle is the (vector) bundle over Q given by
Given a discrete Lagrangian Ld:Q×Q→R, the (+)-discrete Lagrange–Pontryagin action is the discrete augmented action defined as
The (+)-discrete Lagrange–Pontryagin principle,
is obtained by enforcing free variations {(δqk,δq+k,δpk+1)∈Q×Q×Q∗∣0≤k≤N} that vanish at the endpoints, i.e., δq0=δqN=0.
Theorem 2.9. The (+)-discrete Lagrange–Pontryagin principle is equivalent to the (+)-discrete Lagrange–Dirac equations.
On the other hand, the (−)-discrete Pontryagin bundle is given by
The (−)-discrete Lagrange–Pontryagin action is defined as
The (−)-discrete Lagrange–Pontryagin principle,
is obtained by enforcing free variations {(δq−k+1,δpk,δqk+1)∈Q×Q×Q∗∣0≤k≤N} that vanish at the endpoints, i.e., δq0=δqN=0.
Theorem 2.10. The (−)-discrete Lagrange–Pontryagin principle is equivalent to the (−)-discrete Lagrange–Dirac equations.
3.
Reduction of the discrete Dirac structure
Let Q be a vector space and G⊂Q be a vector subspace acting by addition on Q. In this section we will show that the discrete induced Dirac structure on Q is G-invariant and we will reduce it to the corresponding quotient.
3.1. Trivializations of the tangent bundle and cotangent bundles
Let ωd:Q×Q→G be a discrete connection form on πQ,Σ. We define a right trivialization of TQ=Q×Q as
Observe that it is a linear map with the vector structure of Q×Q given by the direct sum. Using [9, Remark 4.3] it is straightforward to check that λd is an isomorphism (of bundles over TΣ=Σ×Σ) with inverse given by
The action of G on Q×Q induces an action on Q×(Σ×G) by means of λd. Using the equivariance of ωd, such an action is given by
By construction, λd is equivariant, i.e., λd∘ΦQ×Qg=ΦQ×(Σ×G)g∘λd for each g∈G. Subsequently, it descends to a left trivialization of (Q×Q)/G, i.e., an isomorphism of the corresponding quotients,
Furthermore, note that (Q×(Σ×G))/G≃Σ×(Σ×G) via the isomorphism
Remark 3.1. For the (−)-case, it will be useful to trivialize the first factor instead, i.e., we consider the map
Of course, all the computations performed for λd are also valid for ˜λd by exchanging the order of the factors.
On the other hand, we define a right trivialization of T∗Q≃Q×Q∗ as
Again, this trivialization is a linear map with the vector structure on Q×Q∗ given by the direct sum.
Remark 3.2. Observe that the adjoint of the projection πQ,Σ:Q→Σ yields a canonical embedding of Σ∗ into Q∗. However, there is not a canonical linear projection of Q∗ onto Σ∗. The discrete principal connection gives a choice of this projection via the adjoint of the horizontal lift, thus yielding the following split
In addition, ⟨π∗Q,Σ(w),ξQ(q0)⟩=0 for every w∈Σ∗ and ξ∈g, so we have
where the superscript 0 denotes the annihilator.
Using the previous remark, it can be seen that the inverse of ˆλd is given by
where (μ0)Q(q0)∈Q∗ is implicitly defined by the relations ⟨(μ0)Q(q0),ξQ(q0)⟩=⟨μ0,ξ⟩ for each ξ∈g and (π2∘¯h∗d)((μ0)Q(q0))=0.
It is easy to check that the action of G on Q×(Σ∗×g∗) induced by ˆλd is given by
Remark 3.3. For the (−)-case, it will be useful to trivialize the first factor instead. To that end, we consider the map
As for ˜λd, all the computations performed for ˆλd are also valid for ˇλd by exchanging the order of the factors.
Since Q×Q, Q×(Σ×G), Q×Q∗ and Q×(Σ∗×g∗) are vector spaces, we may identify their tangent and cotangent bundles as in (2.2), e.g., T∗(Q×Q)=Q×Q×Q∗×Q∗. Furthermore, we may consider the diagonal actions of G on T(Q×Q) and T(Q×Q∗), as in (2.1). Likewise, on T∗(Q×Q) and T∗(Q×Q∗) we consider the cotangent lift of the action, as in (2.3). In turn, these actions may be transferred to the corresponding (co)tangent bundles of Q×(Σ×G) and Q×(Σ∗×g∗) using the maps λd and ˆλd, and their adjoint maps, accordingly. Note that since these maps are linear, their derivatives are the maps themselves. This can be done because λd and ˆλd are linear isomorphisms. For instance, the action of G on T∗(Q×(Σ∗×g∗)) is induced from the action on T∗(Q×Q∗) using the map ˆλd and its adjoint, as well as their inverses.
3.2. Local expressions of the trivializations and quotients
In order to study the explicit expression of the maps introduced above, we choose a trivialization Q=Σ×G of πQ,Σ as in Section 2.2.1. Using the local expression of the discrete connection, we have
Hence,
Its adjoint is given by
for each (p0,w1,r1)∈Q∗×(Σ∗×G∗). Hence,
for each (p0,p1)∈Q∗×Q∗. Now we perform analogous computations for ˆλd, where we used (2.4) and Lemma 2.2,
The inverse is given by
Likewise, its adjoint is given by
At last, we have
On the other hand, observe that the group action is locally given by
where we identify G≃{0}×G⊂Q. Using the local expression for the trivializations and their adjoints, we obtain the local expression for the actions of G on the (co)tangent bundles of Q×(Σ×G) and Q×(Σ∗×g∗).
Proposition 3.4. The action of G on T∗(Q×(Σ∗×g∗)) is locally given by
for each g∈G, (q0,w0,μ0)∈Q×(Σ∗×g∗) and (p1,x1,ξ1)∈Q∗×(Σ×g).
Analogously, the action on T(Q×(Σ∗×g∗)) is locally given by
for each g∈G and (q0,w0,μ0),(q1,w1,μ1)∈Q×(Σ∗×g∗).
Proof. As explained at the end of the previous section, the action of G on T∗(Q×(Σ∗×g∗)) is induced from the action on T∗(Q×Q∗). Namely,
The computation for T(Q×(Σ∗×g∗)) is analogous.
To conclude, by the previous proposition, we may define the following local isomorphisms,
and
Remark 3.5. By using ˇλd instead of ˆλd (recall Remark 3.3), we arrive at analogous results. In particular, we have the isomorphisms
and
3.3. Invariance of the discrete induced Dirac structure
The definition of invariance for (continuum) Dirac structures [42] can be extended to the discrete setting. More specifically, Dd+ is said to be G-invariant if for each g∈G and (z0,z1,αz+)∈Dd+ we have
Similarly, Dd− is said to be G-invariant if for each g∈G and (z0,z1,αz−)∈Dd− we have
Proposition 3.6. The discrete induced Dirac structures Dd+ and Dd− are G-invariant.
Proof. Let g∈G and (z0,z1,αz+)∈Dd+. By definition, we have
Recall that the actions are given by
and
respectively. Hence,
and
where ˜z+=(g+q0,p1). It immediately follows that Ω♭d+(˜z0,˜z1)=˜α˜z+, which establishes the desired result. The computation for Dd− is analogous.
On the other hand, the right trivialization ˆλd allows Dd+ to induce a (+)-discrete Dirac structure on Q×(Σ∗×g∗),
where, for the sake of simplicity, we let ˆz=ˆλd(z) for each z=(q,p)∈Q×Q∗. Equivalently, Ω♭d+ induces a map ˆΩ♭d+ between the trivialized spaces by imposing the commutativity of the following diagram,
This way, ˆDd+ can be regarded as the (+)-discrete Dirac structure induced by ˆΩ♭d+, i.e.,
Of course, the G-invariance of Dd+ implies the G-invariance of ˆDd+, since we have constructed the actions on the trivialized space so that ˆλd is equivariant.
The same stands for the (−)-discrete Dirac structure. Namely, we have the following diagram,
Hence, we define
3.4. Reduced discrete Dirac structure
The G-invariance of ˆDd+ ensures that it descends to a discrete Dirac structure on the quotient space. Since Ω♭d+ and ˆλd are equivariant, so is ˆΩ♭d+, which induces a well-defined map between the quotient spaces,
Then, the reduced (+)-discrete Dirac structure is the structure induced by this map, i.e.,
Locally, identifications (3.10) and (3.11) enable us to regard [ˆΩ♭d+] as a map between the trivializations,
Lemma 3.7. Working in a trivialization and using the above identification, we have
for each (x0,w0,μ0,q1,w1,μ1)∈Σ×(Σ∗×g∗)×Q×(Σ∗×g∗).
Proof. We employ the explicit local expression computed in the previous sections,
Observe that [ˆΩ♭d+] is a bundle morphism covering the identity if we regard the previous maps as bundles over Σ with the projection onto the first component.
Proposition 3.8. Locally, the reduced (+)-discrete Dirac structure is given by
In the same fashion, we may define the reduced (−)-discrete Dirac structure as
By analogous computations using Remark 3.5, we arrive at the local expressions.
Lemma 3.9. Locally, we have
for each (q0,w0,μ0,x1,w1,μ1)∈Q×(Σ∗×g∗)×Σ×(Σ∗×g∗).
Proposition 3.10. Locally, the reduced (−)-discrete Dirac structure is given by
4.
Discrete Lagrange–Poincaré–Dirac reduction
Making use of the reduced discrete Dirac structure, we will compute the the reduced equations corresponding to a discrete Lagrange–Dirac system. Let Q be a vector space and G⊂Q be a vector subspace acting by addition on Q, and Ld:Q×Q→R be a (possibly degenerate) G-invariant discrete Lagrangian, i.e.,
The invariance of the discrete Lagrangian leads to the invariance of its partial derivatives.
Lemma 4.1. If Ld is G-invariant, then so are its partial derivatives DiLd:Q×Q→Q∗, i=1,2, i.e.,
Proof. For each q∈Q we have
An analogous computation establishes the result for D2Ld.
Remark 4.2. Working on a trivialization Q=Σ×G of πQ,Σ, we may regard Ld as a function defined on (Σ×G)×(Σ×G). This way, its partial derivatives can be written as
for each (q0,q1)=(x0,g0,x1,g1)∈(Σ×G)×(Σ×G), and analogous for D2Ld(q0,q1).
We may regard a discrete vector field, Xd+, that is a solution of the (+)-discrete Lagrange–Dirac equations, as a map
It follows from Lemma 4.1 that this map is G-equivariant. Similarly to Ω♭d+, this induces a map between the trivialized spaces by imposing the commutativity of the following diagram,
Since ˆXd+ is G-equivariant, it descends to a (+)-discrete reduced vector field,
As above, locally we may regard it as [ˆXd+]:Σ×(Σ×G)→Σ×(Σ∗×g∗)×Q×(Σ∗×g∗).
Similarly, if Xd− is a solution of the (−)-discrete Lagrange–Dirac equations, we may trivialize it as follows,
This way, we obtain the (−)-discrete reduced vector field,
Locally, we may regard it as a map [ˆXd−]:(Σ×G)×Σ→Q×(Σ∗×g∗)×Σ×(Σ∗×g∗).
4.1. Reduced discrete Dirac differential
The next step is to trivialize γd+Q and the exterior derivative of the discrete Lagrangian. To that end, we impose the commutativity of the following diagram,
Furthermore, since γd+Q, λd and ˆλd are G-equivariant, so is ˆγd+Q, by construction. The same holds for ^dLd, by Lemma 4.1. By composing the previous maps, we induce the (+)-discrete Dirac differential on the trivialized spaces,
Due to G-equivariance, it descends to the corresponding quotients, yielding the reduced (+)-discrete Dirac differential,
Proposition 4.3. Locally, the reduced (+)-discrete Dirac differential is given by a map [ˆD+Ld]:Σ×(Σ×G)→Σ×(Σ∗×g∗)×Q∗×(Σ×g). Furthermore, for each (x0,x1,g1)∈Σ×(Σ×G), it is given by
where the partial derivatives of Ld are evaluated at (x0,0,x1,g1+h0d(x0,x1)).
Proof. Once again, we use the explicit local expressions computed in the previous sections,
where the partial derivatives are evaluated at (x0,0,x1,g1+h0d(x0,x1)) and we used (2.5) in the last step.
For the (−)-case, we consider the diagram
Subsequently, we arrive at the reduced (−)-discrete Dirac differential,
Proposition 4.4. Locally, the reduced (−)-discrete Dirac differential is given by a map [ˆD−Ld]:(Σ×G)×Σ→(Σ∗×g∗)×Σ×(Σ×g)×Q∗. Furthermore, for each (x0,g0,x1)∈(Σ×G)×Σ, it is given by
where the partial derivatives of Ld are evaluated at (x0,g0+h0d(x1,x0),x1,0).
4.2. (+)-discrete Lagrange–Poincaré–Dirac equations
Define ˆLd+:Q×(Σ×G)→R by the condition ˆLd+∘λd=Ld. Clearly, it is G-invariant, thus inducing the (+)-discrete reduced Lagrangian,
Locally, we may regard it as ld+:Σ×Σ×G→R. It is easy to check that
Lemma 4.5. Locally, for each (x0,x1,g1)∈Σ×Σ×G we have
where the partial derivatives of Ld and ld+ are evaluated at (x0,0,x1,g1+h0d(x0,x1)) and (x0,x1,g1), respectively.
Proof. Let (x0,g0,x1,g′1)∈(Σ×G)×(Σ×G). Using (3.2), we obtain
Recall that the partial derivatives of hd are given by (2.6). Using this fact, as well as the chain rule and the relation above, we obtain
In the above expressions, the partial derivatives of Ld and ld+ are evaluated at (x0,g0,x1,g′1) and (x0,x1,g′1−hd((x0,g0),x1)), respectively. To conclude, we choose g0=0 and g′1=g1+h0d(x0,x1).
Gathering the results of the previous sections, we arrive at the main result of this paper.
Theorem 4.6. ((+)-discrete Lagrange–Poincaré–Dirac equations). Let (Ld,Xd+) be a (+)-discrete Lagrange–Dirac system and suppose that Ld is G-invariant. Let [ˆDd+], [ˆXd+] and [ˆD+Ld] be the reduced (+)-discrete Dirac structure, the (+)-discrete reduced vector field and the reduced (+)-discrete Dirac differential defined in (3.12), (4.1) and (4.3), respectively. Then, they satisfy the (+)-discrete Lagrange–Poincaré–Dirac equations, i.e., for each 0≤k≤N−1, we have
In order to obtain its local expression, we write the discrete vector field as
Subsequently, the reduced equations read as
Making use of Proposition 3.8, Proposition 4.3 and Lemma 4.5 we arrive at the local expression for the reduced discrete equations of motion,
In the above equations, partial derivatives of ld+ are evaluated at (xk,x+k,g+k).
4.3. (–)-discrete Lagrange–Poincaré–Dirac equations
As in the previous case, we define ˆLd−:(Σ×G)×Q→R by the condition ˆLd−∘˜λd=Ld, which induces (−)-discrete reduced Lagrangian,
Locally, it is given by ld−:Σ×G×Σ→R. It is easy to check that
Lemma 4.7. Locally, for each (x0,x1,g1)∈Σ×Σ×G we have
where the partial derivatives of Ld and ld− are evaluated at (x0,g0+h0d(x1,x0),x1,0) and (x0,g0,x1), respectively.
Theorem 4.8 ((−)-discrete Lagrange–Poincaré–Dirac equations). Let (Ld,Xd−) be a (−)-discrete Lagrange–Dirac system and suppose that Ld is G-invariant. Let [ˆDd−], [ˆXd−] and [ˆD−Ld] be the reduced (−)-discrete Dirac structure, the (−)-discrete reduced vector field and the reduced (−)-discrete Dirac differential defined in (3.13), (4.2) and (4.4), respectively. Then, they satisfy the (−)-discrete Lagrange–Poincaré–Dirac equations, i.e., for each 0≤k≤N−1, we have
Locally, the equations are given by
Making use of Proposition 3.10, Proposition 4.4 and Lemma 4.7 we arrive at the local expression for the reduced discrete equations of motion,
In the above equations, partial derivatives of ld− are evaluated at (x−k+1,g−k+1,xk+1).
5.
Reduction of the discrete variational principle
In this section, we perform reduction of discrete Lagrange–Dirac systems from the variational point of view. As expected, we will recover the discrete Lagrange–Poincaré–Dirac equations obtained from the geometric reduction of the discrete Dirac structure. Let Q be a vector space and G⊂Q be a vector subspace acting by addition on Q.
5.1. Trivialization of the (+)-discrete Pontryagin bundle
Let ωd:Q×Q→G be a discrete connection form. Using the trivializations defined in Section 3.1, we define the following map
Again, the G-action on Q×Q×Q×Q∗ given by
induces an action on the trivialized space via Λd+.
Let Q=Σ×G be a trivialization of πQ,Σ, as in Section 2.2.1. For each q0=(x0,g0),q+0=(x+0,g+0),q1=(x1,g1)∈Q=Σ×G and p1=(w1,r1)∈Q∗=Σ∗×G∗, the local expression of Λd+ is
Similarly, for each q0=(x0,g0),q1=(x1,g1)∈Q, (x+0,g+0)∈Σ×G and (w1,μ1)∈Σ∗×g∗ we have
At last, locally we may identify the quotient spaces as
and
5.2. Trivialization of the (-)-discrete Pontryagin bundle
In the same vein as in the previous section, we trivialize the (−)-discrete Pontryagin bundle. Namely, we define
Again, the G-action on Q×Q×Q∗×Q may be transferred to the trivialized space via Λd−.
Let Q=Σ×G be a trivialization of πQ,Σ, as in Section 2.2.1. For each q0=(x0,g0),q−1=(x−1,g−1),q1=(x1,g1)∈Q=Σ×G and p0=(w0,r0)∈Q∗=Σ∗×G∗, the local expression of Λd+ is
Similarly, for each q0=(x0,g0),q1=(x1,g1)∈Q, (x−1,g−1)∈Σ×G and (w0,μ0)∈Σ∗×g∗ we have
At last, locally we may identify the quotient spaces as
and
5.3. (+)-discrete reduced variational principle
Let Ld:Q×Q→R be a (possibly degenerate) G-invariant discrete Lagrangian and consider the corresponding (+)-discrete reduced Lagrangian ld+:(Q×(Σ×G))/G→R. The (+)-discrete generalized energy is the map
Since Ld is G-invariant, so is Ed+. Analogous to the discrete Lagrangian, we consider the trivialized energy, i.e., ˆEd+:Q×(Σ×G)×Q×(Σ∗×g∗)→R, which is defined by the condition ˆEd+∘Λd+=Ed+. Again, ˆEd+ is G-invariant, what enables us define the reduced (+)-discrete generalized energy,
Lemma 5.1. Locally, the reduced (+)-discrete generalized energy is a map ed+:Σ×(Σ×G)×Q×(Σ∗×g∗)→R. Furthermore, for each (x0,x+0,g+0,q1,w1,μ1)∈Σ×(Σ×G)×Q×(Σ∗×g∗) we have
Proof. It is a straightforward computation, making use of the local expressions of the maps and actions that we have computed previously,
The following result relates the variational principles in both the original and the reduced spaces.
Theorem 5.2 (Reduced variational principle). Let Ld:Q×Q→R be a G-invariant discrete Lagrangian and {(qk,q+k,pk+1)∈Q×Q×Q∗∣0≤k≤N} be a trajectory on the (+)-discrete Pontryagin bundle. Consider the reduced trajectory, i.e.,
where (ˆqk,ˆx+k,ˆg+k,ˆqk+1,ˆwk+1,ˆμk+1)=Λd+(qk,q+k,qk+1,pk+1) for 0≤k≤N−1. Then the (+)-discrete Lagrange–Pontryagin principle (2.11) is satisfied if and only if the reduced (+)-discrete Lagrange–Pontryagin principle is satisfied, i.e.,
for free variations
with fixed endpoints, i.e., δˆq0=δˆqN=0.
Proof. By construction, we have
To arrive at our conclusion, note that the free variations of the Lagrange–Pontryagin principle yield free variations on the trivialized space (with fixed endpoints), since Λd+ is a linear isomorphism.
Lastly, we show that the reduced variational equations agree with the reduced geometric equations obtained in the previous section from the reduced discrete Dirac structure.
Proposition 5.3. The variational equations obtained from the reduced (+)-discrete Lagrange–Pontryagin principle are the (+)-discrete Lagrange–Poincaré–Dirac equations.
Proof. Since the equations are local, we may work in a trivialization Q≃Σ×G of πQ,Σ. Observe that locally, (5.8) reads as
for free variations
with fixed endpoints, i.e., δx0=δxN=0 and δg0=δgN=0. Making use of Lemma 5.1 and taking variations δxk, 1≤k≤N−1, with fixed endpoints, we get
Analogously, taking variations δgk, 1≤k≤N−1, with fixed endpoints, yield
Now, we consider variations δx+k, 0≤k≤N−1,
Similarly, for variations δg+k, 0≤k≤N−1,
Next, for variations δwk+1, 0≤k≤N−1,
In the end, for variations δμk+1, 0≤k≤N−1,
In the above equations, partial derivatives of ld+ are evaluated at (xk,x+k,g+k). By gathering all the equations and rearranging terms, it is easy to check that these equations are exactly (4.6).
5.4. (-)-discrete reduced variational principle
Last of all, we carry out the same procedure, but using the (−)-discrete reduced Lagrangian ld−:((Σ×G)×Q)/G→R. The (−)-discrete generalized energy is the map
The trivialized energy, ˆEd−∘Λd−=Ed−, gives rise to the reduced (−)-discrete generalized energy,
Lemma 5.4. Locally, the reduced (−)-discrete generalized energy is a map ed−:(Σ×G)×Σ×(Σ∗×g∗)×Q→R. Furthermore, for each (x−1,g−1,x1,w0,μ0,q0)∈(Σ×G)×Σ×(Σ∗×g∗)×Q we have
Theorem 5.5 (Reduced variational principle). Let Ld:Q×Q→R be a G-invariant discrete Lagrangian and {(q−k+1,pk,qk+1)∈Q×Q∗×Q∣0≤k≤N} be a trajectory on the (−)-discrete Pontryagin bundle. Consider the reduced trajectory, i.e.,
where (ˆx−k+1,ˆg−k+1,ˆqk+1,ˆwk,ˆμk,ˆqk)=Λd−(q−k+1,qk+1,pk,qk) for 0≤k≤N−1. Then the (−)-discrete Lagrange–Pontryagin principle (2.13) is satisfied if and only if the reduced (−)-discrete Lagrange–Pontryagin principle is satisfied, i.e.,
for free variations
with fixed endpoints, i.e., δˆq0=δˆqN=0.
Proposition 5.6. The variational equations obtained from the reduced (−)-discrete Lagrange–Pontryagin principle are the (−)-discrete Lagrange–Poincaré–Dirac equations.
6.
Nonlinear theory
The previous reduction theory has been developed for the linear setting, i.e., when Q is a vector space and G⊂Q is a vector subspace acting by addition on Q. Nevertheless, it can be applied when Q is an arbitrary smooth manifold and G is an abelian Lie group acting freely and properly on Q. In order to see this, we use retractions and retraction compatible charts (see, for example, [2,16]).
Definition 6.1. A retraction of a smooth manifold M is a smooth map R:TM→M such that for each m∈M we have Rm(0m)=m and (dRm)0m=idTmM, where Rm=R|TmM and we make the identification T0m(TmM)≃TmM.
Observe that the second condition ensures that Rm:TmM→M is invertible around 0m.
Definition 6.2. Let M be an n-dimensional smooth manifold and R:TM→M be a retraction of M. A coordinate chart (U,ϕ) on M is said to be compatible at m∈M with R if ϕ(m)=0 and R(vm)=ϕ−1((dϕ)m(vm)) for each vm∈TmM, where we identify TmRn≃Rn using the standard coordinates in Rn.
For the particular case of a Lie group G and g∈G, it was shown in [16, §9] that the canonical coordinates of the first kind at g∈G (cf. [21,38]) are a coordinate chart compatible with the retraction defined by RGg=Lg∘exp∘(dLg−1)g, where Lg:G→G denotes the left multiplication by g.
Proposition 6.3. Let R:TM→M be a retraction of an n-dimensional smooth manifold M and (U,ϕ) be a compatible coordinate chart on M at m∈M. Then for each† r∈U and pm∈T∗mM we have
†We will assume that the inverse of Rm is defined on the whole of U by choosing a smaller coordinate domain if necessary.
where R−1m(r)≃ri∂i and pm≃pidqi in this chart.
In other words, the previous result says that the dual pairing of TmM and T∗mM reduces to the usual Euclidean inner product on Rn when using retraction compatible charts.
6.1. Retractions and abelian Lie group actions
In what follows, let Q be a smooth manifold and G be a connected, abelian Lie group acting freely and properly (on the left) on Q, thus yielding a principal bundle πQ,Σ:Q→Σ=Q/G. Consider retractions RΣ:TΣ→Σ and RG:TG→G of Σ and G, respectively, and a trivializing set U⊂Σ of πQ,Σ. For simplicity, we write U=Σ, so we have an identification Q≃Σ×G. Under this identification, a straightforward check shows that the map
is a retraction of Q. We may use it to define (at least locally) a discrete Lagrange–Pontryagin action. Namely, given a (possibly degenerate) discrete Lagrangian Ld:Q×Q→R, the (+)-discrete Lagrange–Pontryagin action is defined as
where qk,q+k∈Q and pk+1∈T∗qk+1Q. The (+)-discrete Lagrange–Pontryagin principle is obtained by enforcing free variations vanishing at the endpoints. In order for the previous expression to be well-defined, q+k must be in the neighborhood of qk+1 where Rqk+1 is invertible for each 0≤k≤N−1. This can always be achieved for bounded initial conditions by reducing the size of the time step. Furthermore, Proposition 6.3 ensures that using retraction compatible coordinate charts, this discrete action reduces to the one considered in the linear case (2.10).
In the same vein, the (−)-discrete Lagrange–Pontryagin action is defined as
where q−k+1,qk+1∈Q and pk∈Q∗. Once again, Proposition 6.3 ensures that, in a retraction compatible chart, the discrete action reads as in the linear case (2.12).
On the other hand, recall that the G action on the trivialized principal bundle is given by the left multiplication, i.e., g⋅q0=(x,gg0) for each g∈G and q0=(x0,g0)∈Q≃Σ×G. Furthermore, suppose that the retraction on G is given by RGg0=Lg0∘exp∘(dLg−10)g0, as mentioned when describing the canonical coordinates of the first kind. Since G is abelian and connected, the exponential map is surjective and, hence, the inverse of RGg0 exists locally around every element of the group. As a result, when q0=(x0,g0) is fixed, an action of Tg0G on Tq0Q=Tx0Σ⊕Tg0G may be built as follows
for each vx0∈Tx0Σ, and ug0,vg0∈Tg0G. When g0=0, this action has a very simple expression,
where we have used that G is abelian. This is the case considered in the previous sections, a vector subspace acting by addition. Note that if g0≠0, we obtain the same result by using the left translation.
In summary, the linear theory developed above is the coordinate representation of a general system with abelian group of symmetries when retraction compatible charts are used. This allows us to use the linear theory at least locally on a coordinate chart. Furthermore, if Σ and G both admit retraction compatible atlases, then a retraction compatible atlas for Q can be built such that each coordinate domain is a trivializing set for πQ,Σ. Hence, we can make computations on the whole Q by starting from a specific compatible chart and changing to another one whenever it is necessary. Since the variational principle, as well as the group action, have the same expressions in each compatible chart, the local preservation of geometric properties extends to the global setting. This is an important feature of retraction compatible atlases, since computation on local charts might otherwise lead to dynamics that is not globally well-defined. The discrete analogue of Tulczyjew dynamics (see, [34]) appears to be the discrete Dirac mechanics of [16] that we based our construction upon, so the analogous reduced discrete geometric structures for discrete Tulczyjew dynamics can be obtained from our construction.
7.
Examples
We present two examples to illustrate the reduction theory developed above. In both of them, we employ the (+)-discrete equations.
7.1. Charged particle in a magnetic field
We analyze the dynamics of a charged particle moving in a magnetic field, as presented in [25] for the continuous case. To account for gauge symmetry, we consider the Kaluza-Klein configuration space,
with coordinates (q,θ), where q=(q1,q2,q3)∈R3 and θ≃eiθ∈S1. The Kaluza-Klein Lagrangian is defined as
where m∈R+ is the mass of the particle, A∈Ω1(R3) is the magnetic potential, and ⟨⟨⋅,⋅⟩⟩ denotes the Euclidean inner product in R3. The conjugate momenta are given by
It is clear that this Lagrangian is invariant under the tangent lifted action of S1 on QK given by θ′⋅(q,θ)=(q,θ′+θ) for each (q,θ)∈QK and θ′∈S1. Note that using these coordinates, the action is linear. The corresponding quotient is Σ=QK/S1≃R3. Choosing the principal connection ω=A+dθ∈Ω1(QK) on QK→R3, the corresponding reduced equations are the Lorentz force law together with the conservation of the momentum corresponding to θ, i.e.,
where B∈X(R3) is the magnetic field corresponding to‡ B=dA∈Ω2(R3), and e=cpθ is the electric charge of the particle.
‡Recall that we can associate to each 2-form α=αiι∂i(d3q)∈Ω2(R3) a vector field \boldsymbol\alpha = \alpha^i\partial_i\in\mathfrak X(\mathbb R^3) , which is known as proxy field, where \iota_U denotes the left interior product by U\in\mathfrak X(\mathbb R^3) .
7.1.1. Discrete equations
Given h > 0 , consider the following discrete Lagrangian
It is easy to check from Definition 2.1 that the following is a discrete principal connection,
Subsequently, the local map \text{h}_d: Q_K\times\mathbb R^3\to\mathbb S^1 is given by \text{h}_d((q_0, \theta_0), q_0^+) = \theta_0 and \text{h}_{d, \Sigma}\equiv0 . The reduced discrete Lagrangian (4.5) is
Consider an interval [0, T]\subset\mathbb R and divide it into N = T/h subintervals [t_k, t_{k+1}] , with t_k = kh , 0\leq k\leq N-1 . As usual, we let q_k = q(t_k) , 0\leq k\leq N , and analogously for the other quantities. Similarly, we express the discrete vector field as [\hat X_d^k] = (q_k, w_k, \mu_k, q_{k+1}, \theta_{k+1}, w_{k+1}, \mu_{k+1}) . By computing the partial derivatives of the reduced discrete Lagrangian, we obtain the reduced discrete equations
7.1.2. Numerical computations
In order to implement the above equations, we need to make a particular choice of the particle mass and charge, time interval, magnetic field and initial conditions. We express all of the magnitudes in natural units, i.e., c = 1 . We choose m = 1 , e = 1 and T = 20 . For each q = (q^1, q^2, q^3)\in\mathbb R^3 , we write q = q^i\partial_i\in T_q\mathbb R^3\simeq\mathbb R^3 when regarded as a vector. Hence, \left\langle {\left\langle { q, \cdot} \right\rangle } \right\rangle = q^i dq^i . On the other hand, we suppose that the magnetic field is constant, i.e., \text{B}(q) = B_0\partial_z for some fixed B_0\in\mathbb R . The corresponding magnetic potential is
We suppose that the initial position is the origin, q_0 = 0 , and the initial velocity is \dot q_0 = \partial_1+\partial_3 . Likewise, we choose \theta_0 = 0 . Since A(q_0) = A(0) = 0 , the corresponding initial momenta are
and (p_\theta)_0 = e = 1 . Likewise, we have \dot\theta_0 = (p_\theta)_0-\langle A(q_0), \dot q_0\rangle = 1 . The initial position and momenta may be trivialized using (3.6),
On the other hand, it is easy to check that the exact solution of (7.1) for B_0 = 1 is
After working out the approximate solution for different values of N and comparing it to the exact solution, we can see that the error decreases with the number of steps at a second-order rate of convergence, as shown in Table 1. In addition, Figure 1 compares both the exact and numerical trajectories for N = 100 , i.e., h = 0.2 .
7.2. Double spherical pendulum
In this example, we investigate the double spherical pendulum. We assume that there is no friction and that the system is under a uniform gravitational field. The dynamics of the double spherical pendulum has been investigated in [20,24] and variational integrators from different perspectives have been proposed in [11,13].
For i = 1, 2 , we denote by m_i\in\mathbb R^+ , l_i\in\mathbb R^+ and r_i\in\mathbb R^3 the particle mass, the link length and the position of the i -th pendulum, respectively. Furthermore, we use standard coordinates r_i = (r_i^1, r_i^2, r_i^3)\in\mathbb R^3 with the coordinate origin at the fixed pivot, and we suppose that the gravitational acceleration is given by \boldsymbol{g} = (0, 0, -g) for some fixed g\in\mathbb R^+ . This way, the Lagrangian is
where \left\langle {\left\langle {\cdot, \cdot} \right\rangle } \right\rangle denotes the Euclidean inner product in \mathbb R^3 . In addition, the links connecting the particles yield the following constraints,
To avoid the need for constraints, we use spherical coordinates for each particle, r_i = (\rho_i, \theta_i, \varphi_i) , i = 1, 2 , where the origin of the first sphere is at the pivot and the origin of the second one is at the first particle, as shown in Figure 2. As such, the constraints become \rho_i = l_i , i = 1, 2 , and may be imposed explicitly in the Lagrangian. Then, the configuration space is given by
with angular coordinates (\theta_1, \varphi_1, \theta_2, \varphi_2) . After the change of coordinates, the Lagrangian reads
where T_2 is the kinetic energy of the second pendulum,
Observe that the system is invariant by simultaneous rotation of both pendula around the Z -axis, i.e., the group of symmetries is G = \mathbb S^1 with the action on \mathbb S^2\times\mathbb S^2 given locally by
for each (\theta_1, \varphi_1, \theta_2, \varphi_2)\in\mathbb S^2\times\mathbb S^2 and \theta\in\mathbb S^1 . As usual, we denote the quotient by \Sigma = (\mathbb S^2\times\mathbb S^2)/\mathbb S^1 .
Remark 7.1. Observe that this action is not free. Indeed, it leaves invariant configurations with \varphi_1 = k_1\pi and \varphi_2 = k_2\pi for some k_1, k_2\in\mathbb Z . Therefore, the following is only valid for trajectories not passing through those configurations.
At last, we perform another change of coordinates,
with \varphi_1 and \varphi_2 remaining the same. Observe that the inverse is given by \theta_1 = \vartheta_1-\vartheta_2 and \theta_2 = \vartheta_1+\vartheta_2 . In these coordinates, the action reads
for each (\vartheta_1, \varphi_1, \vartheta_2, \varphi_2)\in\mathbb S^2\times\mathbb S^2 and \theta\in\mathbb S^1 .
7.2.1. Discrete equations
For the sake of simplicity, we will let q_0 = (\vartheta_1, \varphi_1, \vartheta_2, \varphi_2)\in\mathbb S^2\times\mathbb S^2 and x_0 = (\varphi_1, \vartheta_2, \varphi_2)\in(\mathbb S^2\times\mathbb S^2)/\mathbb S^1 , and analogous for q_0^+ and x_0^+ . Given h > 0 , we define the discrete Lagrangian as
Likewise, we choose the following discrete principal connection
In particular, the map \text{h}_d: Q\times\Sigma\to G is given by \text{h}_d\left(q_0, x_0^+\right) = \vartheta_1 . Thus, \text{h}_{d, \Sigma}\equiv0 , \text{h}_{d, \Sigma}^*\equiv0 and \text{h}_d^0\equiv0 . The reduced discrete Lagrangian is
for each x_0, x_0^+\in\Sigma and \vartheta_1^+\in\mathbb S^1 . Given the interval [0, T]\subset\mathbb R , we divide it into N = T/h subintervals [t_k, t_{k+1}] , with t_k = kh , 0\leq k\leq N-1 . We denote the discrete vector field by [\hat X_d^k] = (x_k, w_k, \mu_k, q_{k+1}, w_{k+1}, \mu_{k+1}) , 0\leq k\leq N-1 . Observe that w_k = (w_k^1, w_k^2, w_k^3)\in\Sigma^*\simeq\mathbb R^3 and \mu_k\in G^*\simeq\mathbb R . Since \text{h}_d((\vartheta_1, 0), 0) = \vartheta_1 and \text{h}_{d, Q}(x_0, 0) = 0 , the reduced discrete equations read
where (\varphi_1, \vartheta_2, \varphi_2) , \mu_0 and w_0 are the initial conditions, and (\vartheta_1^+, \varphi_1^+, \vartheta_2^+, \varphi_2^+) , \mu_1 and w_1 are the unknowns. As in the previous example, by using (3.6), the momentum is given by p_0 = (\mu_0, w_0) .
7.2.2. Numerical computations
For the numerical simulation, we need to fix the parameters of the system, as well as the initial conditions. Using SI units, we pick T = 100 , N = 10^4 , m_1 = 20 , m_2 = 35 , l_1 = 500 , l_2 = 800 , g = 9.8 , q_0 = (0, 9/4, 2, 3) and (\mu_0, w_0) = (0, 0, 1, 1) . Recall that the (+) -discrete generalized energy of the system is given by (5.7), i.e., (E_d)_k = L_d(q_k, q_k^+) , where we have used that q_{k+1} = q_k^+ , 0\leq k\leq N-1 . The evolution of the energy is plotted in Figure 4. Observe that it exhibits good near energy conservation, since it oscillates around a fixed value instead of exhibiting a spurious drift. This is typical of symplectic, and in particular, variational integrators, but is not generally true of standard integrators. Moreover, we have simulated the system by using the (+) -discrete Euler–Lagrange equations. The difference between the energies obtained from our reduced equations and the energy obtained from the Euler–Lagrange equations is also plotted in Figure 4. As can be seen, both methods give almost the same values for the discrete energy. However, we have observed that our method was about 75% faster than the usual discrete Euler–Lagrange equations, which suggests that the reduced integrator could be significantly faster than the unreduced one.
8.
Conclusions
In this paper, we developed the theory of discrete Dirac reduction of discrete Lagrange–Dirac systems with an abelian symmetry group acting on a linear configuration space. This involves using the notion of discrete principal connections to coordinatize the quotient spaces, which allows us to study the reduction of the Dirac structure and the discrete variational principle expressed in terms of the discrete generalized energy. Both the reduced discrete Dirac structure and the reduced discrete variational principle lead to the same reduced discrete equations of motion. We also discussed the role of retractions and the atlas of retraction compatible charts in allowing us to generalize the local theory that was discussed to a discrete reduction theory that is globally well-defined on a manifold.
For future work, we will extend this to the setting of nonabelian symmetry groups, and to discrete analogues of Routh reduction, where the discrete dynamics is also restricted to the level sets of the discrete momentum. In the same vein, it would be interesting to explore discrete Dirac reduction by stages. To that end, a category containing discrete Dirac structures that is closed under quotients must be constructed and the reduction procedure must be defined on the whole category.
Acknowledgments
The first author was supported by Ministerio de Universidades, Spain, under an FPU grant and partially supported by Ministerio de Ciencia e Innovación, Spain, under grant PID2021-126124NB-I00. The second author was supported in part by the NSF under grants DMS-1411792, DMS-1345013, DMS-1813635, CCF-2112665, by AFOSR under grant FA9550-18-1-0288, and by the DoD under grant HQ00342010023 (Newton Award for Transformative Ideas during the COVID-19 Pandemic).
Conflict of interest
The authors declare there is no conflict of interest.










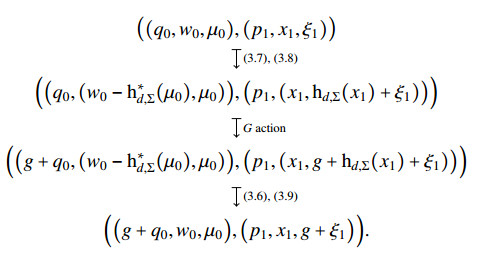

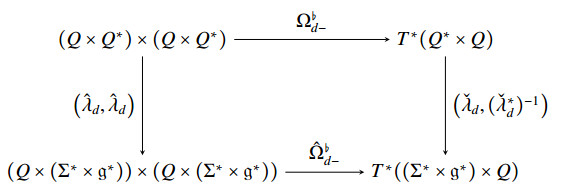
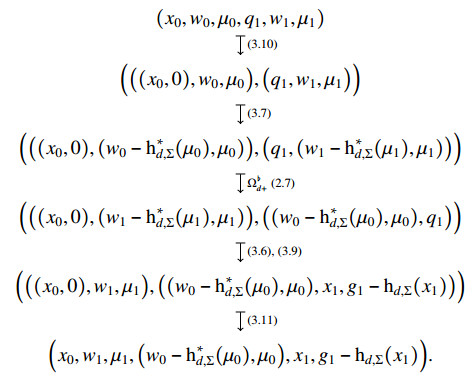
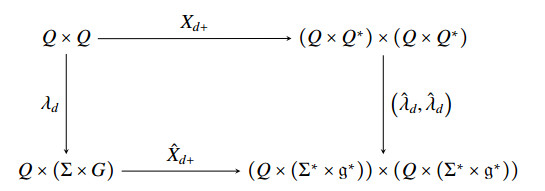
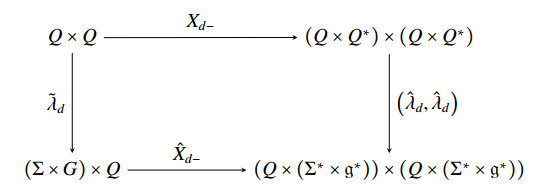
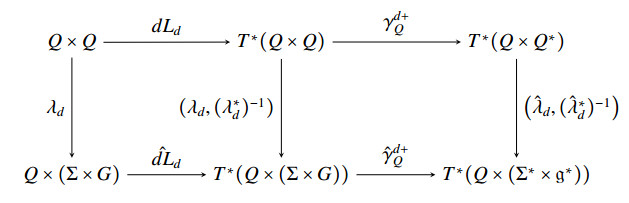
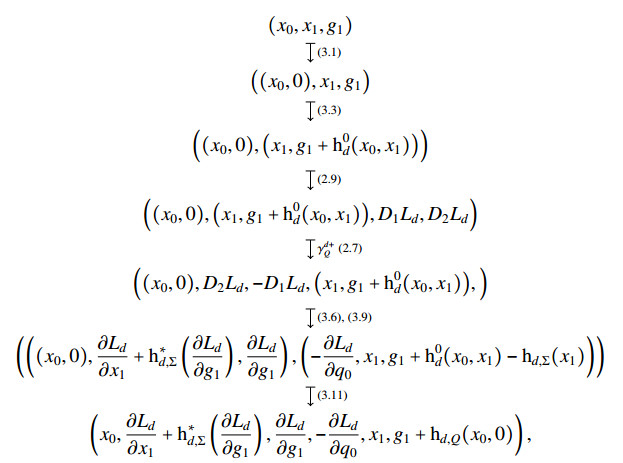
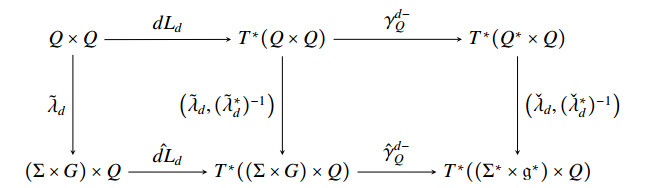
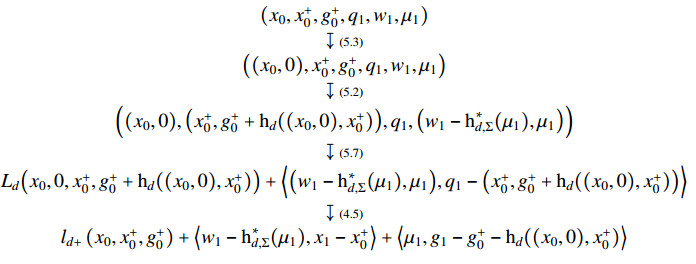
 DownLoad:
DownLoad: