A reaction-diffusion predator-prey model with pursuit, evasion, and nonlocal sensing

1.   Introduction

The mathematical modeling of predator-prey interactions has a long and rich history. The basic dynamics are given by the system of Lotka–Volterra (here in nondimensional form)

where $u(t)\ge 0$ represents the predator and $w(t)\ge 0$ the prey at time $t\ge0$. According to system (1.1), the predator population decreases exponentially in the absence of prey, while the prey follows a logistic growth law. Interactions between predators and prey are modeled by a mass-action law benefitting the predator and depleting the prey. The system's main feature is the global asymptotic stability of its only nontrivial steady state $(u, w) = (\frac{\alpha-1}\alpha, \frac1\alpha)$, which, for $\alpha > 1$, expresses a balance between predation, prey reproduction, and predators' natural death rate.

When spatial movement is expected to influence the dynamics, it is natural to consider predator and prey densities $u(t, x)$ and $w(t, x)$ depending on a spatial variable $x$ in some physical domain $\Omega \subset \mathbb{R}^2$. Then, one can introduce spatial diffusion and advection to model foraging movement, the spreading of the population in a territory, and/or movement in a preferred direction.

In particular, besides spatial diffusion, a reasonable assumption is that the prey tries to evade the predator, while the predator tries to chase the prey. This can be modeled by introducing advection terms into the equations. Thus, the predators advect towards regions of higher prey density, while prey advects away from regions of higher predator density. Variants of this idea have been considered, for instance, in ^{[1,2,3,4,5,6,7,8,9,10,11,12,13,14]}.

Recently, indirect prey- and predator-taxis have been introduced as a mechanism allowing pursuit and evasion ^[3,4,10,15]. This supposes that the advection velocities are mediated by some indirect signal, which may be an odor, a chemical, a field of visual detection, or seen as a potential. In this spirit, following ^[3,4,10,15], we consider the predator-prey system with pursuit, evasion and non-local sensing (already written in a non-dimensional form)

for $t > 0$, $x$ in a bounded, open $\Omega\subset \mathbb{R}^2$, supplemented with boundary conditions

and initial data $u_0(x), w_0(x)$. Here, $u(t, x)$ is the predator density, $w(t, x)$ is the prey density, $p(t, x)$ is the odor produced by the prey, $q(t, x)$ is the odor produced by the predator, and $\alpha, \beta, D_w, D_p, D_q, \delta_p, \delta_q$ are non-negative non-dimensional constants --- see the Appendix for the physical meaning of the constants and details on the non-dimensionalisation procedure. System (1.2) states that the predator is attracted to the odor $p$ of the prey $w$, which solves a (steady-state) diffusion equation with source proportional to $w$, while the prey is repelled by the odor $q$ produced by the predator.

Notice that the equations for the odors of the prey and predator are elliptic, rather than parabolic. This is justified in cases where the diffusion of the odor happens in a much faster time scale than the movement of individuals, which is reasonable on a variety of ecological settings.

Note also that we refer to $p$ and $q$ as "odors" but these quantities do not necessarily model chemical odors. They may be more generally interpreted as potentials representing the chance of an animal being detected at a distance by, e.g., visual means.

We remark on the Neumann boundary conditions (1.3). They model the fact that in the time evolution of system (1.2) there is no flow of individuals across the border of the physical domain. Depending on the particular application, this may be a natural assumption, modeling for instance an enclosed area. However, different boundary conditions could be envisaged (e.g., Dirichlet or mixed-type) reflecting distinct natural settings. Here we limit ourselves to the analisys with (1.3). Still, in the numerical experiments presented below, we show an example with Dirichlet boundary conditions.

1.1.   Main contributions and outline of the paper

In light of the recent mathematical results in ^[4,15], our main contributions are the introduction of the predator-prey Lotka-Volterra dynamics and the numerical simulations. As we will see, the interaction terms on the right-hand side make the analysis more involved, in particular with respect to the derivation of $L^\infty$ estimates. Indeed, while it is shown in the above-mentioned works that the system with no population or interaction dynamics does not originate finite time blow-up of the solutions, the predator equation dynamics introduces a quadratic term $uw$ so it is not obvious that the boundedness property remains valid. We shall see that the attractive-repulsive nature of the advection terms continues to ensure boundedness of the solutions. Moreover, the property of instantaneous boundedness of the solution even for unbounded initial data, observed already in ^[4], remains valid in this setting.

An outline of the paper follows. In Section 2, we present our main well-posedness result. Next, in Section 3 we derive our main a priori estimates in $L^\gamma$ spaces, for $\gamma\in [1, \infty]$. This will allow us, in Section 4, to construct strong and then weak solutions to the system (1.2), completing the proof of our well-posedness result. Finally, in Section 5 we detail an implicit-explicit two-step finite volume method for the approximation of system (1.2) and present some numerical experiments.

2.   Main Results

The main results of this paper are concerned with the well-posedness and Lebesgue integrability of weak solutions of the system (1.2). We follow a strategy similar to ^[4,16], making use of fine a priori estimates in Lebesgue spaces, and a De Giorgi level-set method ^[17] to obtain boundedness of the solutions. Still, the character of the present system introduces several changes in the analysis with respect to the results in ^[4,16].

The system (1.2) is, mathematically, of chemotaxis type ^[18,19]. As is well known, such systems may exhibit blow-up of solutions in finite time, see for example the review ^[20]. Therefore, it is not obvious at first glance whether solutions might also possess blow-up behavior. As we shall see in the following analysis, the indirect nature of the sensing, as well as the attraction-repulsion behavior, prevent the densities from becoming infinite in finite time.

We say that the quadruple $(u, w, p, q)$ is a weak solution of the system (1.2) if it satisfies:

1. $(u, w)\in L^2(0, T; H^1(\Omega))$ and $(\partial_t u, \partial_t w) \in L^2(0, T, [H^1(\Omega)]^{*})$, and

2. For any test function $\xi \in C^\infty ([0, \infty)\times \Omega)$ compactly supported in $[0, T)\times \overline{\Omega}$, we have

and

Note that while the biologically relevant regime is when $\alpha > 1$, the value of $\alpha > 0$ does not change the results, so we present most of our analysis with $\alpha$, as well as all the remaining constants in system (1.2), set to 1.

We will suppose throughout the paper that the initial data $(u_0, w_0)$ is non-negative and has finite mass

and that $\Omega\subset \mathbb{R}^2$ is a bounded domain of class $C^2$. The main results regarding the system (1.2) are collected here:

Theorem 2.1. Let the initial data $u_0, w_0$ be in $L^{\alpha}(\Omega)$ for some $\alpha > 2$. Then, the system (1.2) has a unique non-negative weak solution. The following estimates are satisfied by the solutions for any $0\leq t \leq T < \infty$,

(ⅰ) For any $\gamma\in[1, \alpha]$, it holds

In particular, if $u_0, w_0 \in L^\infty(\Omega)$, then

(ⅱ) $L^\gamma-$integrability: for any $\gamma\in (\alpha, \infty]$, it holds

In particular, we have the $L^\infty$-integrability property

for some $C$ independent of $t > 0$.

3.   Analysis of the system (1.2)

In this section we provide a priori estimates which will be used in the well-posedness results. To establish the existence of a weak solution, we must first prove that strong, or classical, solutions exist. We say that $(u, w, p, q)$ is a classical solution of the system (1.2) if it satisfies:

1. $(u, w, p, q) \in C([0, T]; L^2(\Omega))$ and each of the terms in the system (1.2) are well defined functions in $L^2((0, T)\times \Omega)$,

2. The equations on (1.2) are satisfied almost everywhere, and

3. The initial data $(u, w)|_{t = 0} = (u_0, w_0)$ and boundary conditions (1.3) are satisfied almost everywhere.

An essential feature of solutions of (1.2) is the following mass estimate:

Proposition 3.1 (Mass estimate). Let $(u, w, p, q)$ be sufficiently smooth non-negative solutions of the system (1.2) with the boundary conditions (1.3). Then there exists a constant $\mathcal{M}$ depending on $\|u_0\|_1$, $\|w_0\|_1$, $\alpha$, $\beta$ and $|\Omega|$, but not on $t$, such that for all $t > 0$,

Proof. Integrating the first and second equations of (1.2) and using the Neumann boundary conditions (1.3), we find

From $\beta(w - w^2) \le \frac{(\beta+1)^2}{4\beta} - w$ we get, with $\zeta(t) : = \int_{\Omega} w + \frac\beta\alpha u \, dx$,

The conclusion of the proposition readily follows.

3.1.   A priori estimates in $L^{\gamma}$

In this section we prove that data $(u_0, w_0) \in L^1 (\Omega)$ generate instantaneous $L^\gamma$-integrability, with $\gamma > 1,$ for classical non-negative solutions of (1.2).

Proposition 3.2 (A priori estimates in $L^{\gamma}$). Let $(u, w, p, q)$ be sufficiently smooth nonnegative solutions of the system (1.2) with boundary condition (1.3) and integrable initial data, and let $t > 0$ be arbitrary. Then, for any $\gamma\in (1, \infty)$, $\epsilon > 0$, we have the estimate

Moreover, if $u_0, w_0 \in L^\gamma(\Omega)$, then actually

for some $C > 0$ depending on $\mathcal{M}$ and $L^\gamma-$norms of the data, but independent of $t$.

Proof. We will frequently use the Gagliardo–Nirenberg–Sobolev (GNS) inequality in two dimensions (see e.g. ^[21]), holding for any $\alpha\geq 1$,

as well as the interpolation inequality

We start by multiplying the second equation of (1.2) by $w^{\gamma-1}$ and integrating, to find (discarding a nonpositive term)

Now multiply the fourth equation of (1.2) by $w^\gamma$ and integrate by parts to get

Also using

we find, discarding nonpositive terms,

Let us consider the terms on the right-hand side of the previous inequality. Take a small $\epsilon > 0$ to be specified later. We use the following consequence of Young's inequality, $q w^{\gamma} \le \epsilon w^{\gamma+1} + \epsilon^{-\gamma} q^{\gamma+1}$, and also the inequality

which is obtained from Young's inequality, the mass estimate (3.1), and the interpolation inequality (3.5). Therefore, for some constant $C$ depending on $\gamma$, $\mathcal{M}$, and $\epsilon$,

This way, we find

and from the GNS inequality (3.4) and $\epsilon$ sufficiently small,

Again, from $\int_{\Omega} w^{\gamma} \, dx \le C + \varepsilon\int_{\Omega} w^{\gamma+1} \, dx$, we get

for some $C$ depending on $\gamma$, $\mathcal{M}$, the GNS constant, and the parameters of the system.

To deal with the last term on the right-hand side of (3.8), multiply the fourth equation of (1.2) by $q^{\gamma-1}$ to get

From the GNS inequality (3.4) we deduce that

Choosing $\epsilon$ small, we find

In view of (3.9), the estimate (3.8) becomes

Note that the gain from $w$ being the prey population, and thus having a repulsive behavior, is reflected in the lower power $u^\gamma$.

In contrast, performing very similar computations using the first and third equations of the system (1.2), so that instead of (3.6) only

is valid, we find that for $\alpha \ge 2$

Adding (3.10) and (3.11) gives

It is clear that to conveniently bound the terms on the right-hand side using the left-hand side, we should take $\alpha < \gamma < \alpha+1$.

Now, we make use of the interpolation inequalities

Recalling the mass estimate (3.1), we get

for $C$ depending on $\gamma, \alpha$, and $\mathcal{M}$. Now, $\theta_2(\alpha+1) < \gamma+1$ and $\theta_1\gamma < \alpha+1$, so using Young's inequality with a sufficiently small $\epsilon$ allows the terms on the right-hand side to be absorbed into the left-hand side. This gives

for $C$ depending on $\gamma, \alpha$, and $\mathcal{M}$. Next, use the inequality (3.5) to find

and so, from $\big(\| u\|_\alpha^\alpha \big)^{\frac{\alpha}{\alpha-1}} \le \big(\| u\|_\alpha^\alpha \big)^{\frac{\gamma}{\gamma-1}}$ and convexity of the power function, we find, setting

that

Now use the ODE comparison result from [16, Corollary A.2] to conclude

In view of the definition of $\eta$, one finds

and, taking $\gamma = \alpha+\epsilon$,

for $C$ depending on $\gamma, \alpha$, and $\mathcal{M}$. This proves the estimate (3.2). The uniform estimate (3.3) follows from the afore-mentioned ODE comparison results in ^[16]. This concludes the proof of Proposition 3.2.

3.2.   $L^\infty$ estimates

In this section we prove two boundedness results adopting De Giorgi's energy method (see ^[17] and ^{[4,16,22,23,24]} for related applications of the method). Throughout this section, we will use the notation $\gamma^+$ to denote an arbitrary fixed number in $(\gamma, +\infty)$.

First, we consider initial data $u_0$ and $w_0$ only in $L^1(\Omega)$, and obtain an estimate of the type

for some constant $C > 0$ depending on $\mathcal{M}$, but not on $T > 0$. Then, we will suppose that the initial data $u_0$ and $w_0$ are in $L^\infty(\Omega)$. Then we can upgrade the estimates above to

where $C$ now depends also on the $L^\infty$ norms of initial data.

To further clarify the notation, let us spell out that, for instance, the estimate (3.12) precisely means that for any $\epsilon > 0$, it holds

with a constant $C$ that may, however, depend on $\epsilon$.

3.2.1.   Initial data in $L^1$

The main result in this section is the following:

Proposition 3.3. Let $(u, w, p, q)$ be a sufficiently smooth non-negative solution of the system (1.2) with boundary conditions (1.3) and integrable, nonnegative initial data, and let $T > 0$ be arbitrary. Then, for all $t \in (0, T]$, we have the estimate

where the constant $C$ is independent of $T > 0$.

Let us begin by recording here the following $L^\infty$ estimates, which are a consequence of elliptic regularity for the last two equations of the system (1.2) and Proposition 3.2.

and

The first step in the proof of Proposition 3.3 is a boundedness result valid on each interval $(t_*, T)$ with $t_* > 0$.

Lemma 3.4. Let $(u, w, p, q)$ be as in Proposition 3.3, and let $t_* > 0$. Then, there exist constants $M, N > 0$ depending on $t_*, T,$ and $u(t_*), w(t_*)$ such that $0 \leq u(t, x) \leq M$ and $0 \leq w(t, x) \leq N$ almost everywhere on $(t_*, T) \times \Omega$.

Proof. Although the structure of the proof is the similar to corresponding results in ^[4,16], we show the details since the rather involved calculations depend heavily on the structure of the system. Consider $(u, p)$ a non-negative, sufficiently smooth solution to the general problem

in $[0, T] \times \Omega$ with the boundary conditions

where ${\mathbf{n}}$ is the outward unit normal vector to $\partial \Omega$, $f$ and $w$ are known, and $w$ satisfies

Similarly, take a non-negative solution $(w, q)$ to the problem

$[0, T] \times \Omega$ with boundary conditions

$g$ and $u$ given and $u$ satisfying

We denote $V_\lambda = \{(t, x) \in \Omega \times [0, T], \; u(t, x) > \lambda \}$ and define

Multiplying the first equation of (3.15) by $u_\lambda$, integrating in space and using (3.16), we obtain

For the first term on the right-hand side note that using Young's inequality, we find

Thus,

Let $M > 0$ be a constant to be defined later, let $t_* > 0$, and set

for $k = 0, 1, 2, \dots$. Define the energy functional

where we use the notation $u_k = u_{\lambda_k}$. Similarly, we define for $w$ the energy functional

with the same definitions of $\lambda_k$ (with $N$ instead $M$) and $t_k$, for some $N > 0$ to be chosen later.

With $\lambda = \lambda_k$ on (3.19), integrating over $[s, t]$, we obtain

We use this relation with $t_{k-1} \leq s \leq t_k \leq t \leq T$ to check that

Integrating with respect to $s$ over $[t_{k-1}, t_k]$, bearing in mind that $t_k-t_{k-1} = t_*/2^k$ and only the first term on the right-hand side of this inequality depends on $s$, we obtain

Now, we are going to introduce a series of estimates for $I_1$, $I_2$ and $I_3$. For this, we will use the Gagliardo-Nirenberg interpolation inequality in $\mathbb{R}^n$ (see e.g. ^[25]) and a key estimate for ${\bf 1}_{V_k}$. Note that we are temporarily performing the analysis in $n$ dimensions. We have

which holds for any $\alpha \in [0, 1]$ and $1 \leq p \leq \infty$. Choosing the parameter $\alpha \in [0, 1]$ such that $\alpha p = 2$, it follows that $p = 2\frac{n+2}{n}$ and

Observe also that $u_k > 0$ implies $u > \lambda_k$, therefore $u-\lambda_{k-1} > \lambda_k-\lambda_{k-1} = \frac{M}{2^k}$. We also have $u-\lambda_k < u-\lambda_{k-1}$, thus, which a simple computation,

holds for all $a \geq 0$.

● Estimate for $I_1$

First, note that for $a \geq 0$ we have

We choose $a$ in (3.24) such that $2+a = p = 2\frac{n+2}{n}$, so $a = \frac{4}{n}$. Thus,

Note that $\int_{t_{k-1}}^T (\|u_{k-1}\|_2^2 +\|\nabla u_{k-1}\|_2^2) \; ds \leq (T+1) U_{k-1}$, which leads to

● Estimate for $I_2$

We have that

Now, choosing $a = p$ in (3.24), we obtain

where we need $q > 1$. Thus,

where we used (3.23) with the relation (3.22). We choose $\alpha \in (0, 1)$ satisfying $\frac{\alpha p}{q} = 2$ to find

Observe that $\alpha = \frac{2q}{p}$ implies $\alpha = \dfrac{qn}{n+2q}$, then

where $q$ is such that $1 < q < \frac{n}{n-2}$. Thus,

where in this last step we proceeded as in the estimate for $I_1$. Therefore

● Estimates for $I_3$

Proceeding as we did for the estimate of $I_2$, using that $u_k \leq u {\bf 1}_{V_k}$, we have

where $\alpha$, $p$ and $q$ are the same of the estimate for $I_2$. Since $\underset{t \geq \frac{t_*}{2}}{\sup} \; \|f_+ u\|_{q'} \leq \underset{t \geq \frac{t_*}{2}}{\sup} \; \{ \|f_+\|_{2q'} \|u\|_{2q'} \}$, we find

Combining (3.25), (3.26) e (3.27), we obtain

Now we are going to restrict our reasoning to the case $n = 2$, where we have $\alpha = \frac{q}{q+1}$ and the advantage that we can take $1 < q < \infty$, since $1 < q < \frac{n}{n-2} = \infty$. Using Proposition 3.2, we have

Likewise,

and particularizing to $f_+ = uw$,

Therefore,

Now, substituting these results in (3.28), we obtain

We are going to prove that there exists a constant $a \in (0, 1)$ depending only on $q$ such that $U_k \leq a^k U_0$ for all $k \in \mathbb{N}$. First, set $V_k = a^k U_0$. Then applying the recurrence relation defined by the right-hand side of (3.31) to $V_k$ gives

Now we choose $a$ such that $\max\{2^3 a, \; 2^{\frac{2(q+1)}{q}} a^{\frac{1}{q}} \} < 1$. So, the last line of (3.32) is bounded by

Now, choosing $M$ so that

we find that

In other words, $V_k$ is a supersolution of the recurrence relation defined by (3.31). By a comparison principle, we have $U_k \leq a^k U_0 \underset{k \to +\infty}{\longrightarrow} 0$. Thus, we obtain

Fatou's lemma implies

which in turn implies $0 \leq u(t, x) \leq M$ almost everywhere on $({t_*/2}, T) \times \Omega$. For ${t_*/2} < 1$ we can determine $M$ explicitly via

Taking $q \searrow 1$, we have

A very similar computation using (3.17), (3.21), particularizing to $g_+ = w$ gives

Then, we obtain $N > 0$ as before so that $0\leq w(t, x) \leq N$ almost everywhere on $({t_*/2}, T) \times \Omega$ and when $0 < {t_*/2} < 1$, $N$ can be estimated by

Renaming $t_*/2$ as $t_*$ concludes the proof of Lemma 3.4.

Proof of Proposition 3.3. In Lemma 3.4 we found $M, N > 0$ such that $0 \leq u(t, x) \leq M$ and $0 \leq w(t, x) \leq N$ almost everywhere on $(t_*, T) \times \Omega$. From (3.33) and (3.34) we see that $M$ and $N$ depend directly on $U_0$ and $W_0$, respectively. First, we are going to obtain appropriate estimates for these terms, from which the $L^\infty-$bound for $w$ and $u$ in the time interval $(t_*, 1)$ follows. After this, we will extend the estimate for general large intervals. Proceeding as we did in (3.19) for the particular case $f_+ = uw$, we have

where, in the last step, we used

which follows from the first equation of (3.15). Observe that

Substituting this in (3.35), we obtain

Integrating over $[s, t]$, we find

Observe that from this inequality we conclude

Now, via (3.33), using the estimates made previously, we get for $t\ge t_*$

where we remember that $0 < t_* < 1$. For $W_0$, a similar computation with (3.17) and particularizing $g = w$ leads to

Now, via (3.34), we conclude for $t\ge t_*$

where we recall that $0 < t_* < 1$.

These estimates are valid whenever $0 < t_* \leq t \leq T = 1$, but the same reasoning can be applied for any $T > 0$ and it would provide a bound depending on $T$. In order to justify that the same $L^\infty$-estimate can be made uniform with respect to $T$, we proceeding by extending this estimate in a similar way as was done in ^[16]: let $t_1 \in (t_*, T-t_*)$ and note that the shifted functions $w_{t_1}(t, x) = w(t+t_1, x)$ and $u_{t_1}(t, x) = u(t+t_1, x)$ are still solutions of the same problem with initial data $w_{t_1}(0, x) = w(t_1, x)$ and $u_{t_1}(0, x) = u(t_1, x)$, and the appropriate right-hand side. Since the constant $C$ doesn't change due to the Proposition 3.1, we pick $t_1 \in (0, T)$ and repeat the same arguments to $w_{t_1}$ and $u_{t_1}$, which leads the same $L^\infty$-bounds (3.37) and (3.38) for $w$ and $u$ on the interval $[t_*, T]$. It means that (3.37) and (3.38) happen for $[t_*+t_1, T+t_1]$, that is, we extend (3.37) and (3.38) over $[t_*, T+t_1]$. We can repeat this procedure, completing the proof of Proposition 3.3.

3.2.2.   Initial data in $L^\alpha,$ $\alpha > 2$

We suppose now we have initial data $u_0$ and $w_0$ in $L^\alpha(\Omega)$, for some $\alpha > 2$. We will slightly modify the previous analysis in order to obtain better versions of the estimates in Propositions 3.2 and 3.3, as well as a uniform estimate in $L^\infty$ in the case of bounded initial data.

Proposition 3.5. Let $u_0$ and $w_0$ be initial data in $L^{\alpha}(\Omega)$, for some $\alpha\in(2, \infty]$. The estimates (3.2) of Propositions 3.2 and 3.3 can be upgraded by adding to the constant $C$ the dependence of $L^{\alpha}$-norms on the initial data: for any $\gamma > \alpha$, we have

and, in particular,

If $u_0, w_0 \in L^\infty(\Omega)$, then we have the uniform estimate

where the constant $C > 0$ is independent of $T > 0$.

Proof. First of all, by Proposition 3.2, there exist a constant $A > 0$ such that

We change the definition $t_k = (1-1/2^k)t_*$, and observe now that $t_0 = 0$. Note first that (3.30) becomes

since $\|\nabla p(t)\|_\infty \leq \|u(t)\|_{\alpha} \leq A < \infty$. In this way, (3.31) becomes

with a constant $C$ depending on $\mathcal{M}$, $A$ and $T$, but independent of $t_*$ and $k$. We are going to proceed as we did after (3.31), but now with (3.42), relying on the fact that here we have

where the constant $\tilde{C}$ depends on $\mathcal{M}$, $A$ and $T$. Let us now see that there exist $a \in (0, 1)$, $M > 0$, so that $U_k \leq a^k U_0$, for all $k$. So, taking the right-hand side of (3.42) applied to $V_k : = a^k U_0$, we find

Then, taking $a$ so that $2^3a < 1$,

Choosing $M > 0$ so that

we get that $V_k$ is a supersolution of the recurrence defined by (3.42), and so $U_k \leq a^k U_0 \underset{k \to +\infty}{\longrightarrow} 0$. Observe also that for $t < 1$

Thus, we have $0 \leq u(t, x) \leq M$, whence it follows that

We get the same estimate for $w$ proceeding exactly in the same way for $W_k$, which leads to

This proves (3.40). Estimate (3.39) follows by Lebesgue interpolation between estimates (3.44) and (3.45) and mass conservation.} From this point, the deduction of the uniform estimate of Proposition 3.5 using (3.44) and (3.45) is very similar to [16,Prop.3.2], so we refer the reader to that work for details.

4.   Construction of classical and weak solutions

The a priori estimates of the previous sections will now allow us to prove the global well-posedness of the system (1.2). The first step is to prove existence and uniqueness of classical solutions with smooth initial data. For this, we will use the Banach fixed-point theorem. A stability result for such solutions will be obtained and the existence of a weak solution follows as a consequence.

4.1.   Construction of classical solutions

Let $w_0 \in C_c^\infty(\Omega)$ and define the set

equipped with the norm

Note that $\Upsilon$ with the metric induced by $\|\cdot \|_\Upsilon$ is a complete metric space. In this section we prove the following theorem:

Theorem 4.1. Let $u_0$ and $w_0 \in C_c^\infty(\Omega)$ be non-negative initial dada. Then, for all $T > 0$ the system (1.2) supplemented with the boundary condition (1.3) admits a unique non-negative classical solution. This solution satisfies the estimates obtained in Propositions 3.2, 3.3 and 3.5.

The main step to prove this theorem is the use of the following lemma, whose proof is standard and can be found in [16,Thm. 3.1].:

Lemma 4.2. Let $\psi$ be a smooth solution of

with $b, B, \nabla \cdot B\in L^\infty$. Then,

Now let $\phi \in {\Upsilon}$ and let $p = p[\phi]$ be the solution of

Linear theory guarantees that there exists a unique solution $p \in H^1(\Omega)$, and, since $\phi(t) \in L^\infty(\Omega)$ and $\Omega$ is smooth, we have $p(t) \in H^2(\Omega)$ with $\|p(t)\|_{H^2} \leq C \|\phi(t)\|_{L^2}$ almost everywhere in time. Therefore we have $p(t), \nabla p(t)$ and $\Delta p(t) \in L^\infty(\Omega)$. Now we associate $u = u[\phi]$ the solution of

By linear theory, $u$ is unique and such that $u \in L^2(0, T; H^1(\Omega)) \cap C([0, T], L^2(\Omega))$. Linear theory still guarantees that there exists some constant $C > 0$ depending on $T$ and $\Omega$ such that $\|u\|_{L^\infty(0, T; H^1(\Omega))} \leq C\|u_0\|_{{H^1}(\Omega)}$. Now, we associate $q = q[\phi]$ the solution of

The same arguments lead to the existence of a unique solution $q \in H^1(\Omega)$, which satisfies $q(t) \in H^2(\Omega)$ with $\|q(t)\|_{H^2} \leq C \|u(t)\|_{L^2}$, then $q(t), \nabla q(t), \Delta q(t) \in L^\infty(\Omega)$. Finally, we associate $w = w[\phi]$ the solution of

where $w[\phi]$ is the only weak solution and such that $w \in L^2(0, T; H^1(\Omega)) \cap C([0, T], L^2(\Omega))$.

Lemma 4.3. For $T > 0$ small enough, $w[\phi] \in \Upsilon$.

Proof. Applying Lemma 4.2 for $w[\phi]$,

Note that all terms in the exponential can be bounded by $C\|\phi\|_\infty$, with $C > 0$ depending on the data of the problem. Thus, for $T > 0$ small enough we have $0 \leq w(t, x) \leq 2 \|w_0\|_\infty$, which means $w[\phi] \in \Upsilon$.

Lemma 4.4. $\Phi: \phi \in \Upsilon \mapsto w[\phi] \in \Upsilon$ is a contraction on $[0, T]$ for some $T > 0$.

Proof. Let $\phi_1, \phi_2 \in \Upsilon$ and define $\overline{w} = w_1-w_2$, where $w_1$ and $w_2$ are the respective associated solutions, and so forth. It's easy to check that

Multiplying by $\overline{w}$ and integrating in space, we obtain

where we used the estimates for $w_i$, $u_i$ and $\phi_i$ guaranteed by Lemma 4.2 and by the definition of $\Upsilon$, respectively. Substituting

and

in (4.3), we find

By Gronwall's lemma, it follows that

for some constant $K > 0$ which may change from line to line. Likewise, for $\overline{u} = u_1-u_2$, we get

Note that

Combining (4.5) and (4.6) with (4.4), we conclude that

for all $t \in [0, T]$. Thus, for $T > 0$ small enough, $\Phi$ is a contraction.

This is enough to prove Theorem 4.1. We take $\tilde{T} > 0$ being the smallest guaranteed by Lemma 4.3 and Lemma 4.4. By the fixed point theorem, the result follows for small time. Extension to $[0, T]$ is done in a standard way.

Let $\alpha > 2$. We say that the system of equations (1.2) is stable on $L^\infty(0, T; L^{\alpha} (\Omega))$ when, given two pairs of initial data $u_{0, i}, w_{0, i} \in L^{\alpha}(\Omega)$, the respective classical solutions $u_i$ and $w_i$ admit $C > 0$ depending only on $\mathcal{M}$ and on $L^{\alpha}-$norms of the data such that

Proposition 4.5. Let $\alpha > 2$. The system (1.2) is stable (in the sense of (4.7)) on $L^\infty(0, T; L^{\alpha} (\Omega))$.

Proof. Let $\overline{u} = u_1-u_2$ and similarly for the other differences. The system for the differences reads

Multiplying (4.8) by $\overline{u}$ and integrating in space, we get

It is easy to check using (3.40) that

Hölder inequality guarantees that

Observe that using

for $q \in (1, \infty)$, with $\|\nabla \overline{p}(t)\|_{2q}^2 \leq C\|\overline{p}(t)\|_{H^2}^2 \leq C\|\overline{w}(t)\|_2^2$ and $\|u_2(t)\|_{2q'}^2 \leq \|u_2(t)\|_\infty^{1+\frac{1}{q}} \|u_2(t)\|_1^{\frac{1}{q'}}$ and (3.40), we find

Then,

Choosing $q$ big enough, we have from (4.9) and the previous estimates that

for some small $\epsilon.$ A similar result is obtained for $\overline{w}$ using the same arguments, where we get

Defining $Z(t) = \|\overline{u}\|_2^2 + \|\overline{w}\|_2^2$, we have

Integration of this differential equation leads to the result.

4.2.   Global well-posedness of weak solutions

Now we are ready to state and prove a well-posedness result for weak solutions:

Theorem 4.6. Fix an arbitrary $T > 0$ and assume non-negative initial data $u_0, w_0 \in L^{\alpha}(\Omega)$, for some $\alpha > 2$. Then, there exists a unique non-negative weak solution for the system (1.2). This solution satisfies the estimates of Proposition 3.2 and 3.3–3.5.

Proof. Take a sequence of non-negative initial data $u_{0, k}, w_{0, k} \in C_c^\infty(\Omega)$ with $u_{0, k} \to u_0$ and $w_{0, k} \to w_0$ both strongly in $L^{\alpha}(\Omega)$. Theorem 4.1 guarantees sequences $u_k, w_k, p_k$ and $q_k$ in $C([0, T], L^2(\Omega))$ strong solutions of the system (1.2) for each pair of data $u_{0, k}, w_{0, k} \in C_c^\infty(\Omega)$,

$k \in \mathbb{N}$. The following convergence properties hold:

ⅰ) $u_k \to u$ and $w_k \to w$ strongly in $L^\infty(0, T; L^2(\Omega))$.

ⅱ) $p_k \to p$ and $q_k \to q$ strongly in $L^\infty(0, T; H^1(\Omega))$.

ⅲ) $u_k \rightharpoonup u$ and $w_k \rightharpoonup w$ weakly in $L^2(0, T; H^1(\Omega))$.

ⅳ) $\partial_t u_k \to \partial_t u$ and $\partial_t w_k \to \partial_t w$ weakly in $L^2(0, T; [H^1(\Omega)]^*)$.

ⅴ) $u_k \nabla p_k \to u\nabla p$ and $w_k \nabla q_k \to w\nabla q$ strongly in $L^1((0, T)\times \Omega)$.

In fact, estimate (3.3) guarantees that $u_k$ and $w_k$ are uniformly bounded in $L^\infty(0, T; L^{\alpha}(\Omega))$ with respect to $k \geq 1$. Therefore, Proposition 4.5 applied to the Cauchy differences $u_k-u_l$, $w_k-w_l$, $k, l \in \mathbb{N}$ guarantees that $u_k$ and $w_k$ are Cauchy sequences in $L^\infty(0, T; L^2(\Omega))$, giving ⅰ). Now, let $\overline{p} = p_k-p_l$ with $k, l \in \mathbb{N}$, and denote $\overline{w} = w_k-w_l$. Multiplying by $\overline{p}$ the difference of the third equations of (1.2) and integrating in space, we get

Similarly, with the fourth equation we compute

Thus, using Proposition 4.5, we have

This means that $p^k$ and $q^k$ are Cauchy sequences in $L^\infty(0, T; H^1(\Omega))$, so we get ii). Next, multiply the first and second lines of (1.2) by $u_k$ and $w_k$, respectively, and integrate in space. Using (3.13), (3.14), we find

Integrating in time gives that $\nabla u_k, \nabla w_k$ are in $L^2(0, T; L^2(\Omega))$ uniformly in $k$. From this we find iii).

It is classical to check that $\partial_t u_k(t) = \nabla \cdot (\nabla u_k -u_k \nabla p_k) +u_k w_k -u_k \in (H^{1})^*$ and $\partial_t w_k(t) = \nabla \cdot (\nabla w_k + w_k \nabla q_k) +w_k-w_k^2 -u_k w_k \in (H^{1})^*$. For instance, if $\varphi \in L^2(0, T; H^1)$, then we find (to take just the term involving $\nabla u_k$, and using that $\nabla u_k$ is in $L^2(0, T; L^2(\Omega))$ uniformly in $k$)

Treating the other terms similarly, we get that $\partial_t u_k$ and $\partial_t w_k$ are bounded in $L^2(0, T; [H^1(\Omega)]^*)$, so iv) holds. The last convergence follows from the previous ones.

Thus, we can pass to the limit $k\to \infty$ in (4.10) to find that $(u, w, p, q)$ is a weak solution of (1.2). The condition $(u(0), w(0)) = (u_0, w_0)$ is satisfied by continuity at $t = 0$ which follows from the estimate on the time derivatives. Finally, using the approximating by classical solutions we can check that the stability result from Proposition 4.5 and estimate (4.11) hold for weak solutions. This can be used to prove uniqueness: using the notations in Proposition 4.5, if $(u_i, w_i, p_i, q_i)$, $i = 1, 2$ are two weak solutions associated to the same initial data, then (4.7) proves that $(u_1, w_1) = (u_2, w_2)$ a.e. on $[0, T]\times \Omega$. In turn, the estimate (4.11) (which, since it is a direct consequence of Proposition 4.5, also holds for weak solutions) gives uniqueness of $p$ and $q$.

5.   Numerical experiments

In order to show some of the relevant features of the system, we provide in this section the details of a numerical simulation of (1.2). Our goal is to present an implicit-explicit finite volume scheme and showcase some numerical results exhibiting the system's main features, namely, evasive behavior of the prey, and chasing by the predator.

We consider the system (1.2) in a rectangular domain $\Omega = [0, L_{x}]\times[0, L_{y}]$, where we introduce a cartesian mesh consisting of the cells $I_{i, j}: = [x_{i-\frac12}, x_{i+\frac12}]\times[y_{j-\frac12}, y_{j+\frac12}],$ which for the sake of simplicity, are assumed square with uniform size, so $|I_{i, j}|: = h^{2}$ for all $i$ and $j$. Consider a step size $\Delta t > 0$ to discretize the time interval $(0, T)$. Let $N > 0$ the smallest integer such that $N\Delta t\leq T$ and set $t^{n}: = n\Delta t$ for $n\in\{0, N\}$. The cell average of a quantity $v$ at time $t$ is defined by

and define $\overline{v}_{i, j}^{n}: = \overline{v}_{i, j}(t^{n})$. Note that in this section we use $\mathbf{x} = (x, y)$ to denote the spatial variable. Let $f_k(u, w)$, $k = 1, 2$, be the reactive terms in the right-hand side of the first two equations in (1.2). Then, the terms

are approximated by $f_{k, i, j}: = f_{k}(\overline{u}_{i, j}, \overline{w}_{i, j}), k = 1, 2.$ The Laplacian on a Cartesian grid is discretized via

The numerical fluxes in the $x$- and $y$- directions are respectively

and

and in a similar way for $\mathcal{F}^{2}_{i+\frac12, j}(\mathbf{q})$ and $\mathcal{F}^{2}_{i, j+\frac12}(\mathbf{q})$. Finally we incorporate a first-order Euler time integration for the $u$ and $w$ components. The diffusive terms are treated in an implicit form and an explicit form is used for the convective and reactive terms. The initial data are approximated by their cell averages,

To advance the numerical solution from $t^n$ to $t^{n+1} = t^{n} + \Delta t$, we use the following finite volume scheme: given ${\mathbf{u}}^{n} = (\overline{u}_{i, j}^{n})$ and ${\mathbf{w}}^{n} = (\overline{w}_{i, j}^{n})$ for all cells $I_{i, j}$ at time $t = t^{n}$, the unknown values ${\mathbf{u}}^{n+1}$ and ${\mathbf{w}}^{n+1}$ are determined by the following two steps implicit-explicit scheme:

Step 1 solve for $\mathbf{p} = (\overline{p}_{i, j})$ and $\mathbf{q} = (\overline{q}_{i, j})$

Step 2 solve for $\mathbf{u}^{n+1} = (\overline{u}^{n+1}_{i, j})$ and $\mathbf{w}^{n+1} = (\overline{w}^{n+1}_{i, j})$

where we have used the notation $\Delta_{h} = (\Delta_{i, j})$ to indicate the matrix of the discrete Laplacian operator, and $\mathcal{I}$ is the identity matrix.

Theorem 5.1. Suposse that $f_{1}(u, w) = u(\alpha w-1)$ and $f_{2}(u, w) = \beta w(1-u-w)$ Then the solutions $\overline{p}_{i, j}$, $\overline{q}_{i, j}$ and $\overline{u}_{i, j}^{n+1}$, $\overline{w}_{i, j}^{n+1}$ of the finite volume scheme (5.3a)–(5.3b) and (5.4a)–(5.4b) respectively, are nonnegatives for all $i, j$ provided $\overline{u}_{i, j}^{n}$, $\overline{w}_{i, j}^{n}$ are nonnegative for all $i, j$, and the following CFL-like condition is satisfied:

where

Proof. In (5.3a)–(5.3b), we have a linear system of algebraic equations for $\overline{p}_{i, j}$ and $\overline{q}_{i, j}$ which need to be solve in each time step $t^{n}$. However, observe that the matrix of these linear systems are diagonally dominant, which guarantee the existence of solution and the positivity of ${p}_{i, j}$ and $q_{i, j}$. Each system of equations (5.4a)–(5.4b) can be seen as a linear system for $\overline{u}^{n+1}_{i, j}$ and $\overline{w}^{n+1}_{i, j}$ respectively, where the right side is positive according with the CFL condition (5.5) (see ^[26,27,28]) which guarantees the positivity of $\overline{u}^{n+1}_{i, j}$ and $\overline{w}^{n+1}_{i, j}$.

Each system of linear algebraic equations for $\overline{p}_{i, j}$, $\overline{q}_{i, j}$ and $\overline{u}_{i, j}^{n+1}$, $\overline{w}_{i, j}^{n+1}$ can be solved by using an accurate and efficient linear algebraic solver.

5.1.   Test 1: chasing and evasion

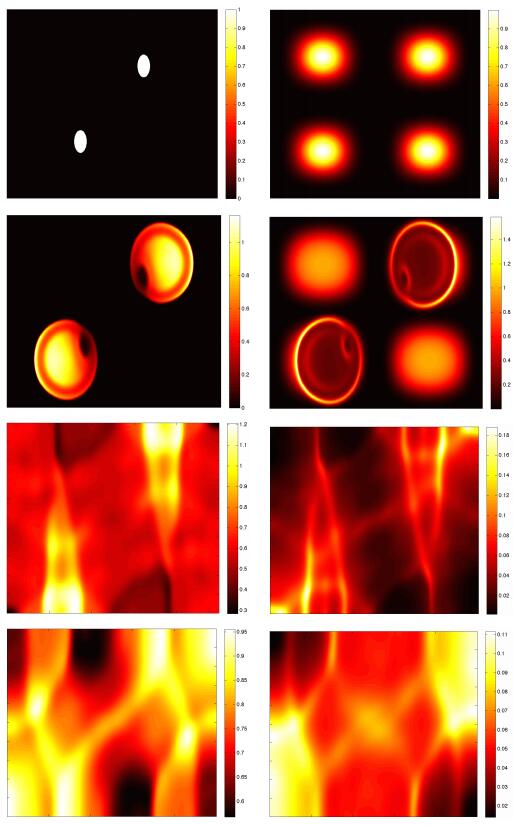
In this numerical test, shown in Figure 1, we suppress the terms on the right-hand side of (1.2), to ignore the population dynamics and emphasize the effect of the pursuit and evasion. We can see that the predator starts to chase the prey even though at first any direct contact with it would be very small (due to diffusion only). The prey takes evasive action immediately. Note that by choosing large $\delta_u, \delta_w$ in this example, we see from Tables 1 and 2 that this may be interpreted as saying that the chemical sensitivity of the predator and prey are large compared to their diffusion rates. Therefore, we expect that the movement observed in Figure 1 is due to the attraction and repulsion terms and not so much to the diffusion. The numerical parameters are a 400 by 400 spatial cell grid, and a time step of 0.01.

5.2.   Test 2: full dynamics

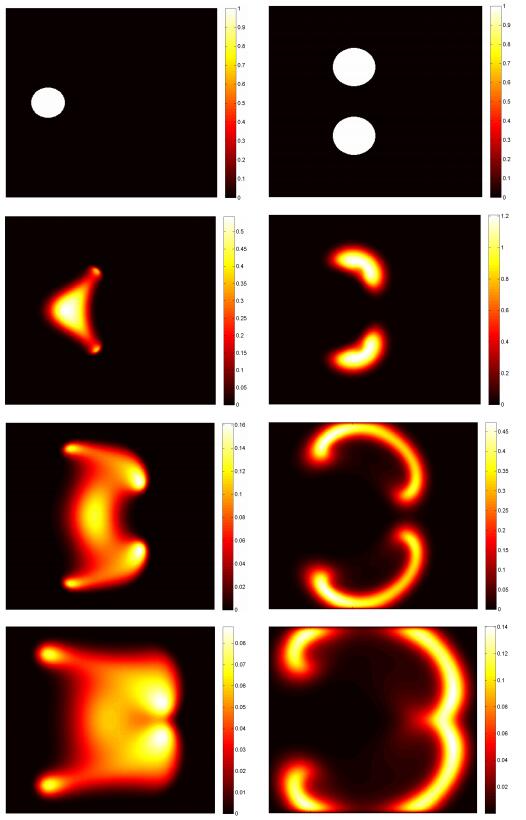
In this test, shown in Figure 2, we set some generic parameters in the system (1.2) in order to observe the full behavior. We can see now the predator-prey interaction taking place, as the densities of the two species fluctuate more widely in relation to the previous example, due to the predator's population growth from predation. After some time, the solution seems to exhibit wave-like interaction patterns with decreasing amplitudes, stabilizing around the values predicted by the equilibrium point $(\frac{\alpha-1}\alpha, \frac1\alpha) = (0.9, 0.1)$. Although here we show the solution only until $t = 10$, computation up to larger times, not shown here, confirm this behavior. The numerical parameters are a 400 by 400 spatial cell grid, and a time step of 0.01.

5.3.   Test 3: Dirichlet boundary conditions

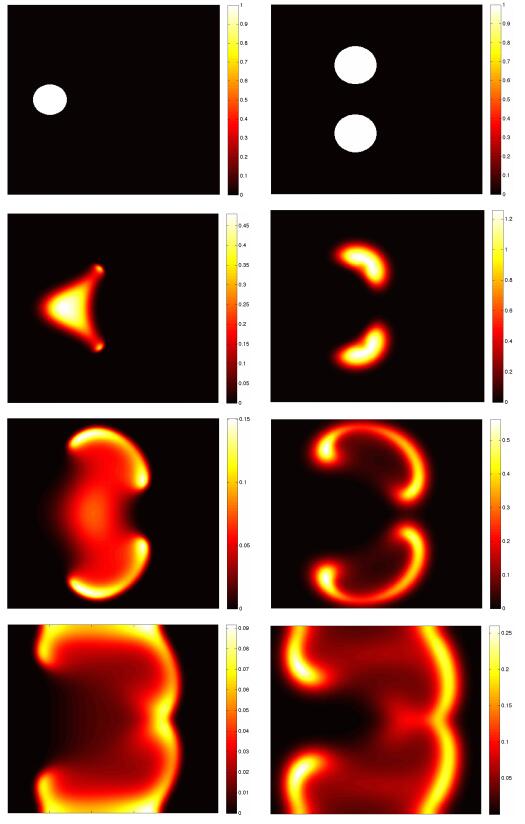
This test, which we show in Figure 3, implements a variant of the proposed method for system (1.2) with Dirichlet boundary conditions instead of the conditions (1.3). The parameters are the same as in Test 1. We can see that although the general dynamics remains similar, the boundary behavior affects the solution, in particular making the maximum density smaller. This in natural, since a Dirichlet condition corresponds, physically, to an absorption, or death, at the boundary.

One can also see, especially on the prey column, the formation of steep gradients along the border (boundary layers). This, again, is natural, since with the parameters of the simulation, the evasion dynamics of the prey should be dominant. Since evasion corresponds in (1.2) to an advection term, the formation of boundary layers when considering Dirichlet conditions is to be expected.

6.   Conclusions and outlook

In this work, we have studied analytically and numerically a system of parabolic-elliptic PDEs modeling predator-prey dynamics including prey- and predator-taxis, indirect detection by means of a "potential" or odor, diffusion, and Lotka–Volterra dynamics. We have seen that the system is well posed and established boundedness properties of the solution in Lebesgue spaces. Although these purely mathematical properties may not be of immediate biological relevancy, the reasonings and results establish that the model does not lead to non-biological phenomena such as blow-up in finite time – this being by no means a given property of systems of parabolic equations.

The Lotka–Volterra dynamics with logistic term featured in the right-hand side of our system was chosen since it is the simplest model not leading to unrealistic population explosions. Therefore, possible extensions of our work include the question of whether the results still hold for more realistic population dynamics, namely Holling-type, or after the inclusion of Allee effects, prey handling time, etc.

One other obvious extension to the system (1.2) would be to consider a fully parabolic system where the odor diffusion time scale is of the same order than the population diffusion time scale. In that case, the analysis is more involved. We plan to address this question in future work.

Acknowledgements

P.A. was partially supported by Faperj "Jovem Cientista do Nosso Estado" grant no. 202.867/2015, Capes by PRONEX, and CNPq grant no. 442960/2014-0. B.T. acknowledges the support from Capes via a doctoral grant from the Institute of Mathematics of UFRJ. L.M.V. was supported by CONICYT/PIA/Concurso Apoyo a Centros Científicos y Tecnológicos de Excelencia con Financiamiento Basal AFB170001. The authors would also like to thank the anonymous referee for their insightful comments.

Conflict of interest

The authors declare there is no confict of interest.

Appendix

The dimensional version of system (1.2) reads as follows:

supplemented with appropriate no-flux boundary conditions similar to (1.3).

In Table 1 we present the physical meaning of the parameters appearing in (6.1), and in Table 2 we show the dimensionless parameters appearing in system (1.2), obtained after a standard non-dimensionalization procedure applied to the system (6.1).