Transmission dynamics of cholera with hyperinfectious and hypoinfectious vibrios: mathematical modelling and control strategies

1.   Introduction

Cholera is an acute disease caused by Vibrio cholerae O-group 1 or O-group 139, which can give rise to diarrhea and vomit. The World Health Organization (WHO) estimates that there are 1.3 to 4 million cholera cases per year with about 21,000 to 143,000 deaths all over the world ^[1]. Beginning in April 2017, a major cholera epidemic occurred in Yemen, with about 500,000 reported cases and 2,000 deaths. Due to the deterioration of health systems and associated infrastructures, cholera spreads more seriously. The WHO has announced that as many as 30,000 health care workers are devoted to the treatment in Yemen. At present, the epidemic situation of major cities including Sanaa, Hajja, and Amran, is under control ^[1]. In order to better understand the transmission dynamics of cholera and provide some valuable insights on the prevention and control, some cholera models have been proposed (see, for example, ^[2,3,4,5,6]). In ^[2], Tien and Earn considered the following cholera model with both human-to-human and environment-to-human transmissions:

where $S(t)$, $I(t)$ and $R(t)$ denote the densities of susceptible, infected and recovered individuals, respectively; $B(t)$ denotes the concentration of V. cholerae in contaminated water; $\mu$ is the birth and natural death rate; ${\beta_h}$ and $\beta$ are the human-to-human transmission rate and environment-to-human transmission rate, respectively; $\gamma$ is the recovery rate of infected individuals; $\xi$ is the contribution rate of each infected individual to the concentration of V. cholerae; $\delta$ is the net death rate of V. cholerae.

In ^[7], Hartley et al. found that short-lived, hyperinfectious state of vibrios decays in a matter of hours into a state of lower infectiousness, and incorporated this hyperinfectious state into a cholera model to provide a much better fit with the observed epidemic pattern. Besides, Neilan et al. ^[8] formulated a mathematical model to include two classes of bacterial concentrations, one is hyperinfectious and another is less-infectious. Furthermore, in ^[9], Mukandavire et al. indicated that human-to-human transmission is a very fast transmission process with a lower infectious dose as a result of immediate water or food contamination by hyperinfectious vibrios from freshly passed human stool. Besides, Mukandavire et al. pointed out that if vibrios have been in the environment for a sufficiently long period (anywhere from 5 to 18 hours), they are no longer hyperinfectious, namely, in a hypoinfectious state.

Note that the incidence rate in system (1.1) is bilinear, which regards the infection rate per density of infected individuals or per concentration of vibrios as a constant. Actually, the incidence rate is influenced by the inhibition effect from behavioral change of susceptible individuals and the crowding effect of vibrios. In ^[10], experimental studies indicated that the probability of infection depends on the concentration of vibrios in the contaminated water and only enough inoculum of vibrios can lead to cholera. In ^[11], Codeço introduced a new form ${\beta}B/(k+B)$ to measure the effect of saturation, where ${\beta}$ measures the infection force of vibrios and $B/(k+B)$ measures the inhibition effect and crowding effect. There have been several works on cholera models with saturation incidence in the literature (see, for example, ^[3,4,6,12]).

Motivated by the works of Tien and Earn ^[2], Mukandavire et al. ^[9], and Codeço ^[11], in the present paper, we are concerned with the effects of hyperinfectious and hypoinfectious vibrios, both human-to-human and environment-to-human transmissions on the global dynamics of cholera. Besides, vaccination is widely used to prevent and control cholera, thus some susceptible individuals become vaccinated individuals. In ^[13], A.P. Lemos-Pai$\tilde{a}$o et al. proposed a cholera model including vaccination and illustrated the importance of vaccination campaigns on the control and eradication of a cholera outbreak. To this end, we consider the following differential equations:

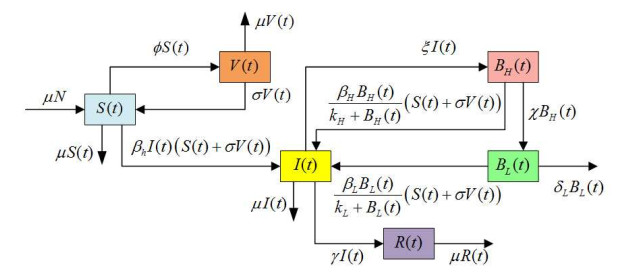
where $S(t)$, $V(t)$, $I(t)$, $R(t)$, ${B_H}(t)$, ${B_L}(t)$ and other parameters are described in Table 1. Corresponding flowchart of cholera transmission in system (1.2) is depicted in Figure 1.

The initial condition for system (1.2) takes the form

where constants $S^0, \; V^0, \; I^0, \; R^0, \; B_H^0, \; B_L^0$ are defined on $[0, \infty)$. It can be proved by the fundamental theory of functional differential equations ^[14] that system (1.2) has a unique solution $(S(t), V(t), I(t), R(t), B_H(t), B_L(t))$ satisfying the initial condition (1.3). It is easy to show that all solutions of system (1.2) with initial condition (1.3) are defined on $[0, + \infty)$ and remain positive for all $t\ge0$, while, ${\bf\Omega}$ is a positively invariant set for system (1.2), where

which implies that $S(t), V(t), I(t), R(t), B_H(t)$ and $B_L(t)$ are bounded in the invariant set ${\bf\Omega}$.

This paper is organized as follows. In Section 2, we calculate the basic reproduction number to system (1.2) and establish the existence of disease-free and endemic equilibria. In Section 3, the local asymptotic stability of each of the equilibria is studied. In Section 4, we investigate the global asymptotic stability of each of the equilibria. In Section 5, we carry out a study of optimal control to seek cost-effective solutions of control strategies for cholera. In Section 6, we present numerical simulations to illustrate the theoretical results and describe the cholera outbreak in Haiti. Furthermore, we obtain the optimal control solution by the Forward-Backward Sweep Method. The paper ends with a conclusion in Section 7.

2.   Basic reproduction number and feasible equilibria

System (1.2) always has a disease-free equilibrium ${E_0}(S_0, V_0, 0, 0, 0, 0) = (\mu N/(\mu+\phi), \phi N/(\mu+\phi), 0, 0, 0, 0)$. By the method of van den Driessche and Watmough ^[15], the associated next generation matrices are given by

and

Then, the basic reproduction number is determined by the spectral radius of $FV^{-1}$, namely,

which represents the average number of new infections generated by a single newly infectious individual during the full infectious period. It can be shown that system (1.2) has an endemic equilibrium ${E^*}({S^*}, {V^*}, {I^*}, {R^*}, {B_H^*}, {B_L^*})$ if ${{\cal R}_0} > 1$, which satisfies that

and $I^*$ is the positive real root of the following equation:

where

Denote the left side of (2.2) by $P(I^*)$. Note that $\mathop{\lim}\limits_{{I^*}\to+\infty}P(I^*) = +\infty$ and $P(0) = {s_7} < 0$ if ${{\cal R}_0} > 1$, thus system (1.2) has a positive equilibrium $E^*$.

3.   Local asymptotic stability

In this section, we are concerned with the local asymptotic stability of disease-free and endemic equilibria. The approach of proofs is to analyze the distribution of roots for corresponding characteristic equations.

Theorem 3.1. If ${{\cal R}_0} < 1$, the disease-free equilibrium ${E_0}$ of system (1.2) is locally asymptotically stable; if ${{\cal R}_0} > 1$, ${E_0}$ is unstable.

Proof. The characteristic equation of system (1.2) at $E_0$ is

It is clear that (3.1) has negative real roots ${\lambda} = -\mu, {\lambda} = - (\mu+\phi)$ and other roots are determined by the following equation:

Denote ${{\cal R}_0} = {{\cal R}_{01}} + {{\cal R}_{02}} + {{\cal R}_{03}}$, where

Substituting ${{\cal R}_{0}}$, ${{\cal R}_{01}}$, ${{\cal R}_{02}}$ into (3.2) yields

Now, we claim that all roots of (3.3) have negative real parts. Otherwise, system (1.2) has a root $\lambda_1 = x_1 + iy_1$ with $x_1 \ge 0$. In this case, if ${{\cal R}_{0}} < 1$, it is easy to see that

It follows that

which contradicts to (3.3). Therefore, if ${{\cal R}_{0}} < 1$, all roots of (3.1) have negative real parts and $E_0$ is locally asymptotically stable. If ${{\cal R}_{0}} > 1$, we denote the left side of (3.1) by $G(\lambda)$:

where $G(0) = {\delta _L}\chi\mu^2(\mu+\phi)(\gamma + \mu)(1 - {{\cal R}_{0}}) < 0$ and $G(\lambda) \to \infty$ as $\lambda \to \infty$. Noting that $G(\lambda)$ is a continuous function with respect to $\lambda$, if ${{\cal R}_{0}} > 1$, Eq. (3.1) has a positive real root, then $E_0$ is unstable.

Theorem 3.2. If ${{\cal R}_0} > 1$, the endemic equilibrium ${E^*}$ of system (1.2) is locally asymptotically stable.

Proof. The characteristic equation of system (1.2) at $E^*$ is

where

It is obvious that (3.4) has a negative real root ${\lambda} = -\mu$ and other roots are determined by the following equation:

For the sake of contradiction, let $\lambda_2 = x_2 + iy_2$ with $x_2 \ge 0$. Noting that $X\left({{S^*} + \sigma {V^*}} \right) = \mu+\gamma$ and $\sigma < 1$, we have

Hence, we obtain that

which contradicts to (3.5). Therefore, if ${{\cal R}_{0}} > 1$, all roots of (3.4) have negative real parts and $E^*$ is locally asymptotically stable.

4.   Global asymptotic stability

In this section, we study the global stability of each of the equilibria to system (1.2). The approach of proofs is to use suitable Lyapunov functionals and LaSalle's invariance principle. Since the variable $R(t)$ does not appear explicitly in the first three and last two equations in system (1.2), we don't need to consider it in later analysis.

Theorem 4.1. If ${{\cal R}_{0}} < 1$, the disease-free equilibrium ${E_0}$ of system (1.2) is globally asymptotically stable.

Proof. Let $(S(t), V(t), I(t), B_H(t), B_L(t))$ be any positive solution of system (1.2) with initial condition (1.3). Define

where constants $c_1$ and $c_2$ will be determined later. Calculating the derivative of $V_1(t)$ along positive solutions of system (1.2) yields

Substituting $S_0 = \mu N/(\mu+\phi), V_0 = \phi N/(\mu+\phi)$ into (4.1), we obtain that

Choose

From (4.2), we have

It follows from the inequality of arithmetic and geometric means that $\dot V_1(t) \le 0$ with equality holding if and only if $S = {S_0}, V = {V_0}, I = B_H = B_L = 0$. It can be verified that ${M_0} = \{ {E_0}\} \subset {\bf\Omega}$ is the largest invariant subset of $\{(S(t), V(t), I(t), B_H(t), B_L(t)):\dot V_1(t) = 0\}$. Noting that if ${{\cal R}_{0}} < 1$, $E_0$ is locally asymptotically stable, thus we obtain the global asymptotic stability of $E_0$ from LaSalle's invariance principle.

Theorem 4.2. If ${{\cal R}_{0}} > 1$, the endemic equilibrium ${E^*}$ of system (1.2) is globally asymptotically stable.

Proof. Let $(S(t), V(t), I(t), B_H(t), B_L(t))$ be any positive solution of system (1.2) with initial condition (1.3). Define

where constants $l_1$ and $l_2$ will be determined later. Calculating the derivative of $V_2(t)$ along positive solutions of system (1.2) yields

Substituting (2.1) into (4.3) yields

Choose

Direct calculation shows that

Thus, it follows from the inequality of arithmetic and geometric means that $\dot V_2(t) \le 0$ with equality holding if and only if $S = {S^*}, V = {V^*}, I = {I^*}, B_H = {B_H^*}, B_L = {B_L^*}$. It can be proved that ${M^*} = \{{E^*}\} \subset {\bf\Omega}$ is the largest invariant subset of $\{(S(t), V(t), I(t), B_H(t), B_L(t)):\dot V_2(t) = 0\}$. Noting that if ${{\cal R}_{0}} > 1$, $E^*$ is locally asymptotically stable, we therefore obtain the global asymptotic stability of $E^*$ from LaSalle's invariance principle.

5.   Optimal control strategies

Optimal control methods help us find cost-effective strategies to control various kinds of diseases. We aim to minimize the number of infected individuals and the corresponding cost of the strategies during the course of an epidemic. Control strategies, such as quarantine, vaccination, treatment, and sanitation, can realize the control of cholera at different cost.

Let $X = (S, V, I, R, B_H, B_L)$. Define a control function set as $U = \{u_i|i = 1, 2, 3, 4\}$, where the meanings of $u_i$ are listed as follows:

(1) $u_1$ is a quarantine strategy which is used to reduce the contact between susceptible individuals and infected individuals;

(2) $u_2$ is a vaccination strategy that can improve the immunocompetence of susceptible individuals;

(3) $u_3$ is a treatment strategy that aims at increasing the recovery rate of infected individuals;

(4) $u_4$ is a sanitation strategy that aims at killing vibrios in contaminated water.

Due to the limitation of medical technology or cost, each of control strategies $u_i$ has upper bound $u_{imax}$. The model with control strategies is given by the following system of nonlinear ordinary differential equations:

The set $\mathcal{X}$ of admissible trajectories is given by

and the admissible control set $\mathcal{U}$ is given by

From ^[16,17], we consider the objective functional

Thereinto, $A$ denotes the weight constant of the infected individuals, while, $B_1$, $B_2$, $B_3$ and $B_4$ are the weight constants for the control strategies. ${B_1}{u_1}^2/{2}$, ${B_2}{u_2}^2/{2}$, ${B_3}{u_3}^2/{2}$ and ${B_4}{u_4}^2/{2}$ describe the cost associated with quarantine, vaccination, treatment, and sanitation strategies, respectively. The square of the control variables shows the severity of the side effects of the four strategies ^[17]. Our aim is to minimize the number of infected individuals and corresponding cost of the strategies. The optimal control problem consists of determining the vector function ${X^\diamond}(\cdot) = \left({{S^\diamond}(\cdot), {V^\diamond}(\cdot), {I^\diamond}(\cdot), {R^\diamond}(\cdot), {B_H}^\diamond(\cdot), {B_L}^\diamond(\cdot)} \right) \in {\cal X}$ associated with an admissible control $U^\diamond(\cdot) \in \mathcal{U}$ on the time interval $[0, T]$, minimizing the objective functional $J$, i.e.,

The existence of an optimal control $U(\cdot)$ comes from the convexity of the objective functional $J$ with respect to the controls and the regularity of the system (5.1): see, e.g., ^[18,19].

According to the Pontryagin Maximum Principle ^[20], if $U(\cdot)\in \mathcal{X}$ is optimal for problem (5.2) with fixed final time $T$, then there exists a nontrivial absolutely continuous mapping $\lambda :[0, T] \to {\mathbb{R}^6}$, $\lambda (t) = \left({{\lambda _1}(t), {\lambda _2}(t), {\lambda _3}(t), {\lambda _4}(t), {\lambda _5}(t), {\lambda _6}(t)} \right)$, called the adjoint vector, such that

(1) the control system:

(2) the adjoint system:

(3) the minimization condition:

(4) hold for almost all $t \in [0, T]$, where the function $H$, defined by

is called the Hamiltonian.

(5) Moreover, the following transversality conditions also hold:

From ^{[18,19,20,21]}, it is not difficult to show the following theorem.

Theorem 5.1. The optimal control problem (5.2) with fixed final time $T$ admits a unique optimal solution $\left({{S^\diamond}(\cdot), {V^\diamond}(\cdot), {I^\diamond}(\cdot), {R^\diamond}(\cdot), {B_H}^\diamond(\cdot), {B_L}^\diamond(\cdot)} \right)$ associated with an optimal control $U(t)$ for $t \in [0, T]$. Moreover, there exist adjoint functions ${\lambda _i}^\diamond(\cdot)$ $(i = 1, \ldots, 6)$ such that

with transversality conditions

Furthermore,

where

In the next section, we solve $u_i^\diamond$ by a numerical method. Numerical techniques for optimal control problems can often be classified as either direct or indirect. In terms of disease control, indirect methods, such as the Forward-Backward Sweep Method, approximate solutions to optimal control problems by numerically solving the boundary value problem for the differential-algebraic system generated by the Maximum Principle ^[22].

6.   Numerical simulations

In this section, we want to illustrate the theoretical results for system (1.2) by numerical simulations. Besides, we transform system (1.2) to simulate the cholera outbreak in Haiti. Furthermore, by Forward-backward Sweep Method, we obtain the optimal control strategies and show the graph trajectories of infected individuals as well as hyperinfectious and hypoinfectious vibrios with optimal control and without optimal control.

6.1.   Dynamical behaviors of the model

Following ^{[8,11,24,25,26]}, we choose appropriate parameter values and simulate each of the equilibria, respectively.

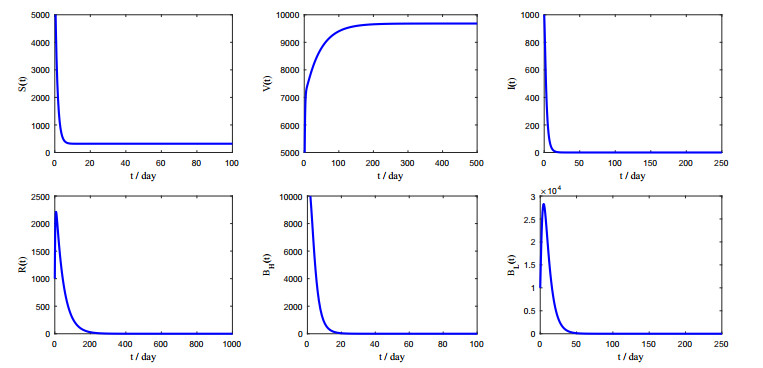
Case 1: By simple computing, we obtain that ${\cal R}_{0} = 0.4335 < 1$. From Theorem 3.1, we derive that disease-free equilibrium $E_0(318.12, 9681.88, 0, 0, 0, 0)$ is locally asymptotically stable. Figure 2 shows the results of simulations using parameters from Case 1 in Table 2. The six figures plot the time evolution of the six variables $S(t), V(t), I(t), R(t), B_H(t)$ and $B_L(t)$, respectively. In fact, we can observe in Figure 2 that infected and recovered individuals, as well as hyperinfectious and hypoinfectious vibrios, die out.

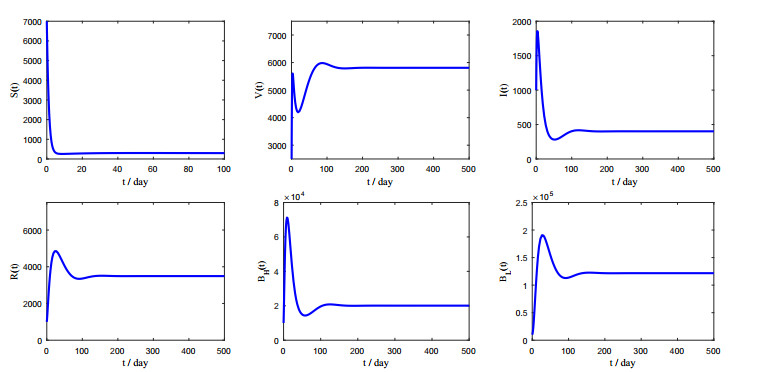
Case 2: Similarly, we derive that ${\cal R}_{0} = 4.5718 > 1$. From Theorem 3.2, we obtain that endemic equilibrium $E^*(297.01,$ $5809.58,401.57, 3491.84, 20078.04, 121685.53)$ is locally asymptotically stable. Figure 3 shows the results of simulations using parameters from Case 2 in Table 2. Each figure plots the time evolution of the corresponding variable, too. From Figure 3, we see that infected and recovered individuals, as well as hyperinfectious and hypoinfectious vibrios, persist at the endemic level.

6.2.   Simulations of the cholera outbreak in Haiti

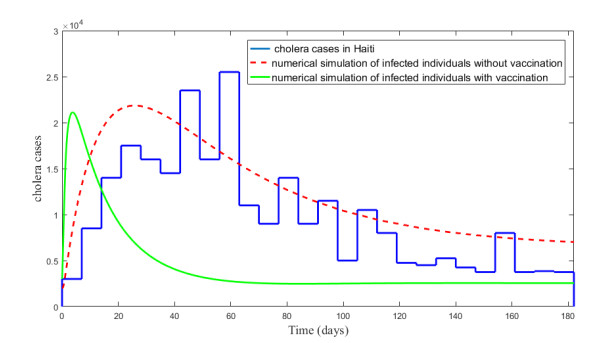
The first cholera cases in Haiti started to be reported on 14 October 2010 in the department of Artibonite from where the outbreak rapidly spread along the Artibonite river affecting several departments. In the beginning of November 2010, the overall case fatality rate (CFR) in hospitals was $3.8\%$. This high CFR reflects the lack of experience of the healthcare system to deal with case management as well as the fact that patients reached the health facilities too late ^[28]. In Figure 4, weekly reported cholera cases in Haiti from 1 November 2010 to 1 May 2011 are plotted in blue line. To simulate this cholera outbreak, we remove the vaccinated individuals from system (1.2) and carry out the following subsystem without vaccination:

Meanwhile, considering the medical treatment and public health of Haiti, we decrease the recovery rate of infected individuals from $0.2$/day to $0.05$/day. The constant of total population $N$ is adjusted to $50000$. From Figure 4, we observe that the numerical simulation of infected individuals in subsystem (6.1) (red dashed curve) is approximately in accord with the real cholera cases in Haiti (blue line). Once taking the vaccination control strategy, as we can see, the numerical simulation of infected individuals in system (1.2) (green curve) decreases quickly to a lower level.

6.3.   Optimal control solution

The idea exploited by Forward-Backward Sweep Method is that the initial value problem of the state equation is solved forward in time, using an estimate for the control and costate variables, then the costate final value problem is solved backward in time (see, for example, ^[12,17,23]). In ^[27], Lenhart and Workman employed the Forward-Backward Sweep Method combined with progressive-regressive Runge-Kutta fourth-order schemes to get the optimal solution. Based on Lenhart and Workman's method, our numerical simulations are performed by using a MATLAB code. The MATLAB function linspace creates $n+1 = 101$ equally spaced nodes between $0$ and $1$, including $0$ and $1$. Here, $\vec x = ({x_1}, \ldots, {x_{n + 1}})$ and $\vec \lambda = ({\lambda _1}, \ldots, {\lambda _{n + 1}})$ are the vector approximations for the state and adjoint. The related parameter values in systems (5.1) and (5.3) are the same as Case 1 in Table 2. A rough outline of the algorithm is given below.

(1) Make an initial guess for $\vec u$ over the interval;

(2) Using the initial condition $x(0)$ and the values for $\vec u$, solve $\vec x$ forward in time according to system (5.1). Specifically, given a step size $h$ and an ODE $x'(t) = f(t, x(t))$, the approximation of $x(t + h)$ given $x(t)$ is

where

(3) Using the transversality condition $\lambda_{n+1} = \lambda(T) = 0$ and the values for $\vec u$ and $\vec x$, solve $\vec \lambda$ backward in time according to system (5.3) by a similar way as (6.2);

(4) Update $\vec u$ by entering the new $\vec x$ and $\vec \lambda$ values into the characterization of the optimal control (5.4);

(5) Check convergence. If variable values in this iteration and the last iteration are negligibly close, output the current values as solutions. If values are not close, return to Step 2.

When all steps are complete, we obtain the optimal control strategies, which can be seen in Figure 5a. On account of medical technology and cost, each of control strategies has limitation, thus we set ${u_{1\max }} = 0.8$, ${u_{2\max }} = 0.7$, ${u_{3\max }} = 0.6$ and ${u_{4\max }} = 0.9$. We observe that $u_2(t)$, namely, vaccination strategy, could be reduced 82 days later from the beginning of the cholera outbreak, which saves much cost of vaccination. Similarly, After 27 days, $u_4(t)$, namely, sanitation strategy, is not much necessary and could be canceled gradually. In Figure 5b–Figure 5d, we compare the graph trajectories of infected individuals as well as hyperinfectious and hypoinfectious vibrios with optimal control and without optimal control. It is clear that infected individuals, as well as hyperinfectious and hypoinfectious vibrios, have been reduced due to the control strategies. From Figure 5, we suggest that taking control strategies at the very beginning of cholera outbreaks can reduce the number of infected individuals remarkably, which are also cost-effective optimal strategies.

7.   Discussion

In this paper, we have considered a cholera model including hyperinfectious and hypoinfectious vibrios, both human-to-human and environment-to-human transmissions. By a complete mathematical analysis, the threshold dynamics of the model was established and it can be fully determined by the basic reproduction number. If ${{\cal R}_{0}} < 1$, the disease-free equilibrium $E_0$ is locally and globally asymptotically stable; if ${{\cal R}_{0}} > 1$, the endemic equilibrium $E^*$ is locally and globally asymptotically stable. Numerical simulations vividly illustrate our main results of stability analysis for system (1.2). Besides, we simulated the cholera outbreak in Haiti. Furthermore, we obtained the optimal solution by the Forward-Backward Sweep Method.

At the beginning of cholera epidemic, hyperinfectious vibrios freshly-shed from infected individuals play an important role in cholera transmission, due to that they are likely to come into contact with other individuals ^[7]. Therefore, the strategies of quarantine and sanitation can effectively control the cholera epidemic. Besides, vaccination strategy is still the most efficient control strategy to prevent, control and eradicate cholera. As for treatment strategy, it is an essential method to fight cholera and reduce the death rate due to the disease. In contrast to the control strategies in ^[12,29], Modnak or Lemos-Pai$\tilde{a}$o et al. only considered a single control method, vaccination or quarantine. In a word, a combination with all the above strategies could yield the best control effect of cholera.

With the development of economy and society, the rate of population movement has accelerated in recent years. In view of this, considering the heterogeneity of each individual is an important factor in constructing more realistic models, that is, spatially heterogeneous epidemic models. The theoretical analysis of these models may be more complicated and we leave it for further investigation.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Nos. 11871316, 11801340, 11371368), the Natural Science Foundation of Shanxi Province (Nos. 201801D121006, 201801D221007).

Conflict of interest

The authors declare that they have no competing interests.