Citation: Erin N. Bodine, Connor Cook, Mikayla Shorten. The potential impact of a prophylactic vaccine for Ebola in Sierra Leone[J]. Mathematical Biosciences and Engineering, 2018, 15(2): 337-359. doi: 10.3934/mbe.2018015
| [1] | Majid Jaberi-Douraki, Seyed M. Moghadas . Optimal control of vaccination dynamics during an influenza epidemic. Mathematical Biosciences and Engineering, 2014, 11(5): 1045-1063. doi: 10.3934/mbe.2014.11.1045 |
| [2] | Stephen Tully, Monica-Gabriela Cojocaru, Chris T. Bauch . Multiplayer games and HIV transmission via casual encounters. Mathematical Biosciences and Engineering, 2017, 14(2): 359-376. doi: 10.3934/mbe.2017023 |
| [3] | Eunha Shim, Beth Kochin, Alison Galvani . Insights from epidemiological game theory into gender-specific vaccination against rubella. Mathematical Biosciences and Engineering, 2009, 6(4): 839-854. doi: 10.3934/mbe.2009.6.839 |
| [4] | Charles Wiseman, M.D. . Questions from the fourth son: A clinician reflects on immunomonitoring, surrogate markers and systems biology. Mathematical Biosciences and Engineering, 2011, 8(2): 279-287. doi: 10.3934/mbe.2011.8.279 |
| [5] | Xiaojing Wang, Yu Liang, Jiahui Li, Maoxing Liu . Modeling COVID-19 transmission dynamics incorporating media coverage and vaccination. Mathematical Biosciences and Engineering, 2023, 20(6): 10392-10403. doi: 10.3934/mbe.2023456 |
| [6] | Beatriz Machado, Liliana Antunes, Constantino Caetano, João F. Pereira, Baltazar Nunes, Paula Patrício, M. Luísa Morgado . The impact of vaccination on the evolution of COVID-19 in Portugal. Mathematical Biosciences and Engineering, 2022, 19(1): 936-952. doi: 10.3934/mbe.2022043 |
| [7] | Amira Bouhali, Walid Ben Aribi, Slimane Ben Miled, Amira Kebir . Impact of immunity loss on the optimal vaccination strategy for an age-structured epidemiological model. Mathematical Biosciences and Engineering, 2024, 21(6): 6372-6392. doi: 10.3934/mbe.2024278 |
| [8] | Giulia Luebben, Gilberto González-Parra, Bishop Cervantes . Study of optimal vaccination strategies for early COVID-19 pandemic using an age-structured mathematical model: A case study of the USA. Mathematical Biosciences and Engineering, 2023, 20(6): 10828-10865. doi: 10.3934/mbe.2023481 |
| [9] | Zuzana Chladná . Optimal time to intervene: The case of measles child immunization. Mathematical Biosciences and Engineering, 2018, 15(1): 323-335. doi: 10.3934/mbe.2018014 |
| [10] | Antonella Lupica, Piero Manfredi, Vitaly Volpert, Annunziata Palumbo, Alberto d'Onofrio . Spatio-temporal games of voluntary vaccination in the absence of the infection: the interplay of local versus non-local information about vaccine adverse events. Mathematical Biosciences and Engineering, 2020, 17(2): 1090-1131. doi: 10.3934/mbe.2020058 |
Since its discovery in 1976 in the country of Zaire (now the Democratic Republic of the Congo), four primary strains of the Ebola virus disease (EVD) have been identified: Zaire ebolavirus, Sudan ebolavirus, Reston ebolavirus, and Côte d'Ivoire ebolavirus [19]. The Zaire ebolavirus is the strain of the 2014 West Africa outbreak and the strain that has caused the deadliest recorded EVD outbreaks [41]. Figure 1 classifies the 19 outbreaks of EVD with more than 5 reported cases (excluding the 2014 West Africa Outbreak) by mortality rate [12]. Zaire ebolavirus is the strain responsible for all of the outbreaks in the highest mortality rate category (80-100%) and four out of five of the outbreaks in the second highest mortality rate category (60-79%).
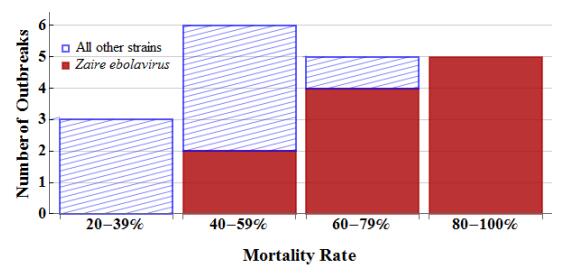 Figure 1. Histogram of mortality rates for the 19 outbreaks of EVD that have had more than 5 reported cases (excluding the 2014 West Africa Outbreak); outbreaks of Zaire ebolavirus are shown in solid red while all other outbreaks are shown in cross-hatched blue. Data taken from [12].
Figure 1. Histogram of mortality rates for the 19 outbreaks of EVD that have had more than 5 reported cases (excluding the 2014 West Africa Outbreak); outbreaks of Zaire ebolavirus are shown in solid red while all other outbreaks are shown in cross-hatched blue. Data taken from [12].Ebolavirus can only be transmitted through direct contact with the bodily fluids of an infectious individual or body [22]. An individual infected with ebolavirus will not become infectious or show symptoms for several days (range: 2-21 days, mean
While the 2014 West Africa EVD outbreak originated in the country of Guinea during December of 2013 [8], Sierra Leone and Liberia were also greatly affected [20,9,67]. A timeline of major outbreak response plan implementations during the 2014 West Africa EVD outbreak is shown in Figure 2.
 Figure 2. Timeline showing the implementation of different control strategies over the course of the outbreak. The date for time
Figure 2. Timeline showing the implementation of different control strategies over the course of the outbreak. The date for time The timeline in Figure 2 divides the outbreak into five disjoint segments according to the response plans implemented over the course of the epidemic. At the beginning of the outbreak, there was no response plan in place because the World Health Organization (WHO) did not declare the outbreak severe enough to require immediate support until mid July of 2014. The initial response plan (WHO Phase 1), implemented July 31,2014, by the WHO, was intended to stop the transmission of EVD in the most affected countries (Sierra Leone, Liberia, and Guinea), as well as provide neighboring countries with support to prevent further spread of the disease [66,65,63]. Following this first-response plan, the United Nations (UN) created the UN Mission for Ebola Emergency Response (UNMEER) plan on September 19,2014 [58,63]. The UNMEER plan added to the efforts of the WHO plan already under way and was intended to isolate EVD cases, ensure safe burials for as many EVD deaths as possible, assist in facilitating case management, and educate individuals in identifying EVD symptoms and going to hospitals when infected [58]. By mid November 2014, the implementation of UNMEER was underway [58,63]. In January of 2015, the WHO shifted the focus of their plan to increasing their capacity for identifying and tracing cases and their contacts; this shift in focus has been termed ''Phase 2'' of the WHO Ebola Response Plan [63]. The UNMEER response plan continued in conjunction with Phase 2 of the WHO response plan. In July 2015, the UNMEER response plan ended [58], and the WHO Ebola Response Plan shifted to Phase 3. This phase focused on stopping all remaining sources of EVD transmission by working in conjunction with international, national, and community partners to improve the speed of case identification, establish and maintain health facilities, and improve Ebola survivor support [63].
Several mathematical and computational models simulating the spread of EVD through a population have been proposed. These models have been used to explore a variety of questions about EVD outbreaks and to estimate rates of transmission and the basic reproduction number of particular outbreaks. Previously proposed models have noted the importance of EVD outbreak models including features like modes of transmission from deceased infectious [59,52,50,21,53], explicitly defining distinct susceptible groups for both high and low risk of exposure to EVD [35], differentiating the infectious in hospitals from the infectious not in hospitals [7,52,50,60], and defining healthcare workers as distinct from other susceptible individuals [50]. However, none of these previous models have included all four of these features. Several models simulate the effects of possible intervention strategies and control measures such as isolation, quarantine, and social intervention to reduce transmission rates during an outbreak [52,35,2,50,40,21,53]. However, the 2014 EVD outbreak hastened the development of a prophylactic vaccine [32] the impact of which has yet to be fully explored.
The clinical trials of the recently developed EVD vaccine used a ring vaccination strategy [31]. The ring vaccination strategy identifies and vaccinates contacts of infectious individuals, as well as contacts of contacts. Recent studies have used a network-based transmission agent-based model [14] and spatially explicit agent-based models [1,46] to examine the impact of ring vaccination of EVD outbreaks using data from the 2014 West Africa Outbreak. The explicit inclusion of space within the model follows the modeling approach of ring vaccination models for foot and mouth disease [47,37].
Many of the previous EVD models are used to estimate the basic reproduction number (
We have developed an ordinary differential equations model that simulates an Ebola epidemic within a population and takes into account: (1) transmission through contact with infectious EVD individuals and deceased EVD bodies, (2) the heterogeneity of the risk of becoming infected with EVD, and (3) the increased survival rate of infected EVD patients due to greater access to trained healthcare providers via an increase in healthcare workers within the population. We apply this model to the population of Sierra Leone during the 2014 EVD outbreak.
The total population is divided into 12 states (see Figure 3). There are three classes of susceptible individuals: healthcare workers who have a high risk of exposure (
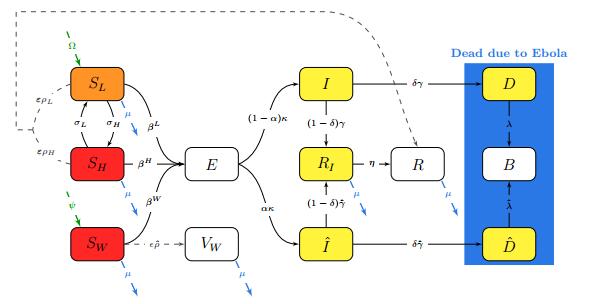 Figure 3. Flow diagram of the model given in System (1). Shaded compartments indicate high risk of exposure (red), low risk of exposure (orange), and ability to transmit EVD (yellow). Green arrows indicate movement into the population, blue arrows indicate background death, and dashed line arrows indicate vaccination.
Figure 3. Flow diagram of the model given in System (1). Shaded compartments indicate high risk of exposure (red), low risk of exposure (orange), and ability to transmit EVD (yellow). Green arrows indicate movement into the population, blue arrows indicate background death, and dashed line arrows indicate vaccination.Once an individual becomes infected, they move to the exposed class (
Given the availability of a prophylactic vaccine, our model allows for the vaccination of susceptible individuals, effectively moving them to the recovered and non-infectious class (
Background death due to natural causes occurs in all three susceptible classes (
The model equations are given in System (1). See Table 1 for a description of each of the model's parameters.
| Parameter | Units | Value | Description | Source | |
| Fitted Parameters | |
See Table 3 | transmission rate from infectious individuals to high risk susceptible individuals | ||
| |
See Table 3 | transmission rate from infectious individuals to low risk susceptible individuals | |||
| |
See Table 3 | transmission rate from infectious individuals to susceptible healthcare workers | |||
| See Table 3 | transmission rate from deceased individuals to high risk susceptible individuals | ||||
| See Table 3 | transmission rate from deceased individuals to low risk susceptible individuals | ||||
| See Table 3 | transmission rate from deceased individuals to susceptible healthcare workers | ||||
| See Table 3 | transmission rate from recovering, still infectious individuals to low risk individuals | ||||
| -- | See Table 3 | proportion of symptomatic individuals who go to hospitals | |||
| -- | See Table 3 | scaling constant where |
|||
| Vax | -- | |
proportion of individuals in whom the vaccine is effective | [31] | |
| -- | See Section 5 | proportion of low susceptible population ( |
|||
| -- | See Section 5 | proportion of high susceptible population ( |
|||
| -- | See Section 5 | proportion of healthcare workers ( |
|||
| See section 3 | migration rate of healthcare workers into the population | ||||
| |
natural death rate per day per 1,000 individuals | [16] | |||
| |
natural birth rate per day per 1,000 individuals | [16] | |||
| |
rate at which individuals become symptomatic and infectious | [45] | |||
| |
infectious period of individuals who are not in hospitals | [50] | |||
| |
infectious period of individuals who are in hospitals | ||||
| -- | |
proportion of individuals who die from Ebola | [12] | ||
| |
number of healthcare workers in the population prior to outbreak | [16] | |||
| |
burial rate of deceased individuals who were not in hospitals | ||||
| |
burial rate of deceased individuals who were in hospitals | [50] | |||
| |
rate at which recovering and still infectious individuals become non-infectious | [18,15] | |||
| |
rate at which individuals move from low risk to high risk susceptible populations | ||||
| rate at which individuals move from high risk to low risk susceptible populations | |||||
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
| S′L(t)=Ω−βL1I+βL2D+β3RINSL−ερLSL+σLSH−σHI+ˆI+D+ˆDNSL−μSL | (1.1) |
| S′H(t)=−βH1I+βH2DNSH−ερHSH+σHI+ˆI+D+ˆDNSL−σLSH−μSH | (1.2) |
| S′W(t)=ψ(ϕ+I+ˆI+D+ˆD)−βW1ˆI+βW2ˆDNSW−εˆρSW−μSW | (1.3) |
| E′(t)=(βH1I+βH2D)SH+(βL1I+βL2D+β3RI)SL+(βW1ˆI+βW2ˆD)SWN−κE | (1.4) |
| I′(t)=κ(1−α)E−γI | (1.5) |
| ˆI′(t)=καE−ˆγˆI | (1.6) |
| R′I(t)=γ(1−δ)I+ˆγ(1−δνϕϕ+SW+VW)ˆI−ηRI−μRI | (1.7) |
| R′(t)=ε(ρHSH+ρLSL)+ηRI−μR | (1.8) |
| D′(t)=γδI−λD | (1.9) |
| ˆD′(t)=ˆγ(δνϕϕ+SW+VW)ˆI−ˆλˆD | (1.10) |
| B′(t)=λD+ˆλˆD | (1.11) |
| V′W(t)=εˆρSW−μVW | (1.12) |
In System (1),
| N(t)=SH(t)+SL(t)+SW(t)+E(t)+I(t)+ˆI(t)+RI(t)+R(t)+D(t)+ˆD(t)+B(t)+VW(t). |
Since transmission of the Ebola virus requires direct contact with bodily fluids, we assume transmission is frequency dependent; see Equations (1.1, 1.2, 1.3, and 1.4). In response to the increasing severity of the epidemic in West Africa, many countries around the world sent doctors and healthcare workers to help treat EVD patients [48]. Additionally, during the WHO's initial response, one of the primary objectives was to train individuals to care for EVD patients and attend to those who had died of EVD [63]. Thus, our model assumes that the migration rate of new healthcare workers into the population depends on the number of currently infectious live individuals and dead bodies at time
The initial time
The values for parameters
The infectious period of individuals who go to hospitals with Ebola symptoms (
The parameters
The migration rate of healthcare workers into the population due to the outbreak (
The transmission rates within our model are a product of the rate at which susceptible individuals come into contact with infectious individuals and the probability that a single infectious contact will transmit the virus to a susceptible individual. Unique transmission rates are used for each susceptible class and for each mode of transmission (i.e., from infectious individuals and infectious dead bodies). See Table 1 for the definition of each transmission rate and Table 3 for transmission rate values used. The implementation of the response plans resulted in behavioral changes that altered contact rates and thus transmission rates. Using incidence data from the CDC [9] and System (1), we have estimated the transmission rates
For each response period,
| CIi(t)=∫t0κE(u)duandCDi(t)=∫t0γδI(u)+ˆγδνϕϕ+SW(u)+VW(u)du. |
The parameter set that best describes the outbreak over this time period minimizes the weighted error
| hi=∑t∈τ√w(t)[(CDi(t)−CD∗t)2+(CIi(t)−CI∗t)2], | (2) |
where
| w(t)=1−0.5e−a(t−b), |
where the values of
| |
|
|
|
|
|
| |
0.015 | 0.030 | 0.060 | 0.013 | 0.013 |
| |
40 | 20 | 10 | 50 | 45 |
Next, for each parameter set for the second response period,
The process is repeated for response periods
The results in Table 3 show that the proportion of infected individuals who seek medical treatment (
Figure 4 shows the cumulative number of infections and deaths over time as reported by the CDC (points) and as predicted by the model (solid curve) simulated over
Epidemic reproduction numbers provide a measure of the severity of an outbreak of an infectious disease. The most commonly calculated reproduction number is the basic reproduction number,
An expression for
| S∗H=E∗=I∗=ˆI∗=R∗I=D∗=ˆD∗=B∗=0 |
| S∗L=ΩϵρL+μ,S∗W=ψϕϵˆρ+μ,R∗=ΩϵρLμ(ϵρL+μ),V∗W=ϵˆρψϕμ(ϵˆρ+μ), |
and the expression for
| R0=[μ(ˆγˆλ(βL2γδ(η+μ)+λ(−β3γ(δ−1)+βL1(η+μ)))(μ+ϵρW)(μ+ψ)Ω+α(γλ(η+μ)(μ+ϵρL)ϕψ(βW2ˆγδμν+βW1ˆλ(μ+ψ))−ˆγˆλ(μ+ϵρW)(βL2γδ(η+μ)(μ+ψ)+λ(β3γδ(μ(ν−1)−ψ)+βL1(η+μ)(μ+ψ)))Ω))]/[γˆγλˆλ(η+μ)(μ+ϵρL)(μ+ϵρW)(μ+ψ)(ϕψ+Ω)]. |
Evaluating
The actual reproduction number for an outbreak,
| p(t)=I(t)+ˆI(t)+RI(t)+D(t)+ˆD(t). |
The incidence at time
| j(t)=∫tt−1κE(s)ds. |
Give the incidence and prevalence, the actual reproduction number is defined as
| RA(t)=ξj(t)p(t), |
where
| ξ=(1−α)1γ+α1ˆγ+δ((1−α)1γ+α1ˆγ)+(1−δ)1η. |
Figure 5 shows
 Figure 5.
Figure 5. The average actual reproduction number for the
| ˉRiA=1ti+1−ti∫ti+1t=tiRA(s)ds, |
where
| Response period | |
| |
3.31 |
| |
1.88 |
| |
0.90 |
| |
0.27 |
| |
0.16 |
The effective reproduction number,
| RE(t)=R0(SH(t)+SL(t)+SW(t)N(t)). | (3) |
It should be noted that
The magnitude of the 2014 EVD outbreak in West Africa hastened the development of a vaccine against Ebola. In July 2015, it was reported that the rVSV-ZEBOV vaccine showed 100% (95% CI 74.7-100.0;
Though a prophylactic vaccine is designed to be administered to individuals prior to exposure in order to prevent an outbreak, if a prophylactic vaccine against ebolavirus had existed during the beginning of the 2014 EVD outbreak in West Africa, it likely would have been administered to individuals not yet exposed to the virus (the susceptible population). To determine what impact this would have had on the outbreak, using System (1), we calculated the cumulative number of infections and deaths that would have occurred in Sierra Leone if a vaccination campaign had started at
We consider four different vaccination strategies. In each case, we assume that the vaccine has 100% efficacy (
Table 5 shows the cumulative number of infections and deaths prevented if the vaccination campaign had been introduced at the beginning of each of the intervention periods. If the moderate vaccination campaign (the first strategy discussed above and in Table 5) had begun with the first intervention response (WHO Phase 1 starting at
| Cumulative Infections | Cumulative Deaths | |||||
| at tf | Prevented | at tf | Prevented | |||
| Baseline |
14436 | 0 | 4416 | 0 | ||
| Start vax at | 8863 | 5573 | 2738 | 1678 | ||
| 12583 | 1853 | 3837 | 579 | |||
| 13225 | 1211 | 4050 | 366 | |||
| 14325 | 111 | 4392 | 24 | |||
| Start vax at | 5138 | 9298 | 1656 | 2760 | ||
| 11075 | 3361 | 3343 | 1073 | |||
| 12168 | 2268 | 3708 | 708 | |||
| 14173 | 263 | 4357 | 59 | |||
| Start vax at | 13999 | 437 | 4283 | 133 | ||
| 14285 | 151 | 4369 | 47 | |||
| 14351 | 85 | 4391 | 25 | |||
| 14429 | 7 | 4415 | 1 | |||
| Start vax at | 8821 | 5615 | 2726 | 1690 | ||
| 12553 | 1883 | 3827 | 589 | |||
| 13211 | 1225 | 4046 | 370 | |||
| 14323 | 113 | 4391 | 25 | |||
A prophylactic vaccine is designed to be administered prior to exposure in order to prevent an outbreak. Thus we determined the proportion of the population that would have needed to have been vaccinated prior to the 2014 EVD outbreak in Sierra Leone in order to prevent that outbreak from occurring; we refer to this proportion as the vaccination threshold.
The vaccination threshold is determined by simulating System (1) assuming no intervention and with the same initial conditions as described in Section 3 (but with only one initially infected individual). Additionally, at time
Given that healthcare workers are at a greater risk of exposure during an outbreak, we assume that any efforts to vaccinate a population against ebolavirus prior to an outbreak would preferentially vaccinate healthcare workers. Thus, if
Table 6 shows the effect of vaccination prior to an initial outbreak given various levels of vaccination coverage (
| Vaccination strategy for |
||||||||
| CI | CI | CI | CI | |||||
| 0 | 4156370 | 495 | 3743965 | 516 | 650846 | 492 | 2643460 | 492 |
| 0.10 | 3064971 | 648 | 2506362 | 694 | 1853742 | 644 | 1845334 | 644 |
| 0.20 | 1866043 | 974 | 1026659 | 1138 | 1040091 | 987 | 1030788 | 988 |
| 0.29 | 764174 | 1990 | 37 | 103 | 188898 | 2267 | 188898 | 2267 |
| 0.30 | 646329 | 2270 | 33 | 0 | 82717 | 2546 | 82717 | 2546 |
| 0.31 | 529673 | 2657 | 29 | 0 | 19911 | 2502 | 19911 | 2502 |
| 0.32 | 414210 | 3213 | 25 | 0 | 3866 | 2091 | 3866 | 2091 |
| 0.33 | 300060 | 4090 | 23 | 0 | 954 | 1570 | 954 | 1570 |
| 0.34 | 171811 | 5697 | 20 | 0 | 325 | 1023 | 325 | 1023 |
| 0.35 | 13195 | 7300 | 18 | 0 | 147 | 0 | 147 | 0 |
| 0.36 | 431 | 0 | 16 | 0 | 81 | 0 | 81 | 0 |
| 0.40 | 26 | 0 | 20 | 0 | 23 | 0 | 23 | 0 |
| 0.50 | 7 | 0 | 7 | 0 | 7 | 0 | 7 | 0 |
| 0.60 | 4 | 0 | 4 | 0 | 4 | 0 | 4 | 0 |
| 0.70 | 2 | 0 | 2 | 0 | 2 | 0 | 2 | 0 |
| 0.80 | 2 | 0 | 2 | 0 | 2 | 0 | 2 | 0 |
| 0.90 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
In the first scenario, where vaccination only occurs prior to
In all four scenarios in Table 6, the proportion of the individuals in the
 Figure 6. Matrix plots displaying the sensitivity of the parameters
Figure 6. Matrix plots displaying the sensitivity of the parameters We have proposed a model that simulates the temporal dynamics of an EVD outbreak. We used this model, along with cumulative infections and death data from the CDC, to determine subpopulation-specific transmission rates (
We also used our model to show that, even if there had been an ambitious rVSV-ZEBOV vaccination campaign during the 2014 EVD outbreak, it would not have been enough to halt the epidemic. This is due to the fact that rVSV-ZEBOV is a prophylactic vaccine designed to prevent infection and does not treat those already infected. To determine the effectiveness of the rVSV-ZEBOV vaccine in preventing an outbreak we calculated the vaccination threshold. Based on our findings we recommend that the Sierra Leone government aim to vaccinate at least 95% of their healthcare workers and 40% of the general population. Compared to vaccination thresholds needed to achieve herd immunity [30] in other diseases (
Since the waning of the 2014 EVD outbreak, there have been flare-ups. For example, in late February and early March 2016, there were eight EVD cases in Guinea after the outbreak had been declared over on December 29,2015 [61]. These flare-ups are due to the virus remaining present in individuals who are recovering and show the importance of the inclusion of the
In light of the 2014 EVD outbreak in West Africa, ebolavirus has become a disease of much greater concern than it historically has been. To aid in understanding the dynamics of the disease, many mathematical models have been proposed. The novel model we propose adds another tool for understanding EVD dynamics, and our analysis of this novel model shows the impact of the implemented response strategies on transmission rates and other parameters in Sierra Leone. Lastly, and most importantly, our analysis provides a vaccination threshold for the new rVSV-ZEBOV vaccine in Sierra Leone. Furthermore, the ability of our model in predicting the outcome of an array of vaccination coverages makes our model a useful tool for determining future vaccination policy.
| [1] | [ M. Ajelli, S. Merler, L. Fumanelli, A. Pastore, Y. Piontti, N. E. Dean, I. M. Longini Jr. , M. E. Halloran and A. Vespignani, Spatiotemporal dynamics of the Ebola epidemic in Guinea and implications for vaccination and disease elimination: A computational modeling analysis BMC Medicine 14(2016), p130. |
| [2] | [ C. L. Althaus, Estimating the reproduction number of ebola virus (EBOV) during the 2014 outbreak in West Africa PLOS Currents Outbreaks (2014), Edition 1. |
| [3] | [ E. J. Amundsen,H. Stigum,J. A. Rottingen,O. O. Aalen, Definition and estimation of an actual reproduction number describing past infectious disease transmission: application to HIV epidemics among homosexual men in Denmark, Norway, and Sweden, Epidemiol Infect, 132 (2004): 1139-1149. |
| [4] | [ D. Bernoulli,S. Blower, An attempt at a new analysis of the mortality caused by smallpox and of the advantages of inoculation to prevent it, Reviews in Medical Virology, 14 (2004): 275-288. |
| [5] | [ S. M. Blower,E. N. Bodine,K. Grovit-Ferbas, Predicting the potential public health impact of Disease-Modifying HIV Vaccines in South Africa: The problem of subtypes, Curr Drug Targets Infect Disord, 5 (2005): 179-192. |
| [6] | [ S. M. Blower,H. Dowlatabadi, Sensitivity and uncertainty analysis of complex models of disease transmission: An HIV model, as an example, Int Stat Rev, 62 (1994): 229-243. |
| [7] | [ C. Browne,H. Gulbudak,G. Webb, Modeling contact tracing in outbreaks with application to Ebola, J Theor Biol, 384 (2015): 33-49. |
| [8] | [ S. Calvignac-Spencer, J. M. Schulze, F. Zickmann and B. Y. Renard, Clock rooting further demonstrates that Guinea 2014 EBOV is a member of the Zaïre Lineage, PLOS Currents Outbreaks (2014), Edition 1. |
| [9] | [ CDC, 2014 Ebola outbreak in West Africa -Case Counts, Centers for Disease Control and Prevention (2016), http://www.cdc.gov/vhf/ebola/outbreaks/2014-west-africa/case-counts.html. |
| [10] | [ CDC, Ebola survivors, Centers for Disease Control (2016), http://www.cdc.gov/vhf/ebola/outbreaks/2014-west-africa/survivors.html. |
| [11] | [ CDC, Ebola virus disease -signs and symptoms, Centers for Disease Control (2015), http://www.cdc.gov/vhf/ebola/symptoms/index.html. |
| [12] | [ CDC, Outbreak chronology: Ebola virus disease, Centers for Disease Control (2015), http://www.cdc.gov/vhf/ebola/outbreaks/history/chronology.html. |
| [13] | [ G. Chowell,N. W. Hengartner,C. Castillo-Chavez,P. W. Fenimore,J. M. Hyman, The basic reproductive number of Ebola and the effects of public health measures: The cases of Congo and Uganda, J Theor Biol, 229 (2004): 119-126. |
| [14] | [ G. Chowell,M. Kiskowski, Modeling ring-vaccination strategies to control ebola virus disease epidemics, Mathematical and Statistical Modeling for Emerging and Re-emerging Infectious Diseases, null (2016): 71-87. |
| [15] | [ A. Christie,G. J. Daview-Wayne,T. Cordier-Lasalle,D. J. Blackley,A. S. Laney,D. E. Williams,S. A. Shinde,M. Badio,T. Lo,S. E. Mate,J. T. Ladner,M. R. Wiley,J .R. Kugelman,G. Palacios,M. R. Holbrook,K. B. Janosko,E . de Wit,N. van Doremalen,V. J. Munster,J. Pettitt,R. J. Schoepp,L. Verhenne,I. Evlampidou,K. K. Kollie,S. B. Sieh,A. Gasasira,F. Bolay,F. N. Kateh,T. G. Nyenswah,K. M. De Cock, Possible sexual transmission of Ebola virus-Liberia, 2015, MMWR Morb Mortal Wkly Rep, 64 (2015): 479-481. |
| [16] | [ CIA, The CIA World Factbook, Central Intelligence Agency, United States (2015), https://www.cia.gov/library/publications/resources/the-world-factbook/. |
| [17] | [ A. Cintrón-Arias,C. Castillo-Chávez,L. M. A. Bettencourt,A. L. Lloyd,H. T. Banks, The estimation of the effective reproduction number from disease outbreak data, Math Biosci Eng, 6 (2009): 261-282. |
| [18] | [ G. F. Deen,B. Knust,N. Broutet,F. R. Sesay,P. Formenty,C. Ross,A. E. Thorson,T. A. Massaquoi,J. E. Marrinan,E. Ervin,A. Jambai,S. L. R. McDonald,K. Bernstein,A. H. Wurie,M. S. Dumbuya,N. Abad,B. Idriss,T. Wi,S. D. Bennett,T. Davies,F. K. Ebrahim,E. Meites,D. Naidoo,S. Smith,A. Banerjee,B. R. Erickson,A. Brault,K. N. Durski,J. Winter,T. Sealy,S. T. Nichol,M. Lamunu,U. Ströher,O. Morgan,F. Sahr, Ebola RNA Persistence in Semen of Ebola Virus Disease Survivors --Preliminary Report, N Engl J Med, null (2015). |
| [19] | [ E. de Wit, H. Feldmann and V. J. Munsters, Tackling Ebola: New insights into prophylactic and therapeutic intervention strategies, Genome Med 3(2011). |
| [20] | [ M. G. Dixon,I. J. Schafer, Ebola Viral disease outbreak --West Africa, 2014, MMRW Morb Mortal Wkly Rep, 63 (2014): 548-551. |
| [21] | [ T. S. Do,Y. S. Lee, Modeling the spread of Ebola, Osong Public Health and Research Perspectives, 7 (2016): 43-48. |
| [22] | [ S. F. Dowell,R. Mukunu,T. G. Ksiazek,A. S. Khan,P. E. Rollin,C. J. Peters, Transmission of Ebola hemorrhagic fever: A study of risk factors in family members, Kikwit, Democratic Republic of the Congo, 1995, J Infect Dis, 179 (1999): S87-S91. |
| [23] | [ P. van den Driessche,J. Watmough, Reproduction number and sub-threshold endemic equilibria for compartmental models of disease transmission, Math Biosci, 180 (2002): 29-48. |
| [24] | [ M. Eichner,K. Dietz, Transmission potential of smallpox: Estimates based on detailed data from an outbreak, Amer Journal of Epidem, 158 (2003): 110-117. |
| [25] | [ M. Eichner,S. F. Dowell,N. Firese, Incubation period of ebola hemorrhagic virus subtype zaire, Osong Public Heath Res Perspect, 2 (2011): 3-7. |
| [26] | [ D. Fisman, E. Khoo and A. Tuite, Early epidemic dynamics of the West African 2014 Ebola outbreak: Estimates derived with a simple two-parameter model PLOS Currents Outbreaks (2014), Edition 1. |
| [27] | [ T. C. Germann, K. Kadau, I. M. Longini Jr. and C. A. Macken, Mitigation strategies for pandemic influenza in the United States PNAS (2006). |
| [28] | [ R. F. Grais,M. J. Ferrari,C. Dubray,O. N. Bjornstad,G. T. Grenfell,A. Djibo,F. Fermon,P. J. Guerin, Estimating transmission intensity for a measles epidemic in Niamey, Niger: Lessons for intervention, Transactions of the Royal Society of Tropical Medicine and Hygiene, 100 (2006): 867-873. |
| [29] | [ J. M. Heffernan,R. J. Smith,L. M. Wahl, Perspectives on the basic reproductive ratio, J Roy Soc Interface, 2 (2005): 281-293. |
| [30] | [ J. M. Heffernan,M. J. Keeling, Implications of vaccination and waning immunity, Proc R Soc B, 276 (2009): 2071-2080. |
| [31] | [ A. M. Henao-Restrepo,A. Camacho,I. M. Longini,C. H. Watson,W. J. Edmunds,M. Egger,M. W. Carroll,N. E. Dean,I. Diatta,M. Doumbia,B. Draguez,S. Duraffour,G. Enwere,R. Grais,S. Gunther,P.-S. Gsell,S. Hossmann,S. V. Watle,M. K. Kondé,S. Kéïta,S. Kone,E. Kuisma,M. M. Levine,S. Mandal,T. Mauget,G. Norheim,X. Riveros,A. Soumah,S. Trelle,A. S. Vicari,J.-A. Rottingen,M.-P. Kieny, Efficacy and effectiveness of an rVSV-vectored vaccine in preventing Ebola virus disease: Final results from the Guinea ring vaccination, open-label, cluster-randomised trial (Ebola Ça Suffit!), The Lancet, 389 (2017): 505-518. |
| [32] | [ A. M. Henao-Restrepo,I. M. Longini,M. Egger,N. E. Dean,W. J. Edmunds,A. Camacho,M. W. Carroll,M. Doumbia,B. Draguez,S. Duraffour,G. Enwere,R. Grais,S. Gunther,S. Hossmann,M. K. Kondé,S. Kone,E. Kuisma,M. M. Levine,S. Mandal,G. Norheim,X. Riveros,A. Soumah,S. Trelle,A. S. Vicari,C. H. Watson,S. Kéïta,M. P. Kieny,J.-A. Rottingen, Efficacy and effectiveness of an rVSV-vectored vaccine expressing Ebola surface glycoprotein: Interim results from the Guinea ring vaccination cluster-randomised trial, The Lancet, 386 (2015): 857-866. |
| [33] | [ B. S. Hewlett,R. P. Amola, Cultural contexts of Ebola in Northern Uganda, Emerg Infect Dis, 9 (2003): 1242-1248. |
| [34] | [ M. Ibrahim,L. Alexander,C. Shy,S. Farr, UNC Department of Epidemiology: Incidence vs. Prevalence, Epidemiologic Research & Information Center Notebook, null (1999): 1-5. |
| [35] | [ A. Kahn, M. Naveed, M. Dur-e-Ahmad and M. Imran, Estimating the basic reproductive ratio for the Ebola outbreak in Liberia and Sierra Leone Infect Dis Poverty 4(2015), p13. |
| [36] | [ M. J. Keeling and P. Rohani, Modeling Infectious Diseases in Humans and Animals Princeton University Press, 2008. |
| [37] | [ M. J. Keeling,M. E. J. Woolhouse,R. M. May,G. Davies,B. T. Grenfell, Modelling vaccination strategies against foot-and-mouth disease, Nature, 421 (2003): 136-142. |
| [38] | [ Y. Kinfu,M. R. Dal Poz,H. Mercer,D. B. Evans, The health worker shortage in Africa: Are enough physicians and nurses being trained?, Bull World Health Organ, 87 (2009): 225-230. |
| [39] | [ N. M. Kudoyarova-Zubavichene,N. N. Sergeyev,A. A. Chepurnov,S. V. Netesov, Preparation and Use of Hyperimmune Serum for Prophylaxis and Therapy of Ebola Virus Infections, J Infect Dis, 179 (1999): 218-223. |
| [40] | [ J. Legrand,R. F. Brais,P. Y. Boelle,A. J. Valleron,A. Flahault, Understanding the dynamics of Ebola epidemics, Epidemiol Infect, 135 (2007): 610-621. |
| [41] | [ E. M. Leroy,P. Rouquet,P. Formenty,S. Souquiere,A. Kilbourne,J.-M. Froment,M. Bermejo,S. Smit,W. Karesh,R. Swanepoel,S. R. Zaki,P. E. Rollin, Multiple Ebola virus transmission events and rapid decline of Central African wildlife, Science, 303 (2004): 387-390. |
| [42] | [ Y. Liu,J. Wang,S. Liu,J. Du,L. Wang,W. Gu,Y. Xu,S. Zuo,E. Xu,Z. An, Introduction of inactivated poliovirus vaccine leading into the polio eradication endgame strategic plan; Hangzhou, China, 2010-2014, Vaccine, 35 (2017): 1281-1286. |
| [43] | [ S. Marino,I. B. Hogue,C. J. Ray,D. E. Kirschner, A methodology for performing global uncertainty and sensitivity analysis in systems biology, J Theor Biol, 254 (2008): 178-196. |
| [44] | [ M. D. McKay,R. J. Beckman,W. J. Conover, A comparison of three methods for selecting values of input variables in the analysis of output from a computer code, Technometrics, 21 (1979): 239-245. |
| [45] | [ M. I. Meltzer,C. Y. Atkins,S. Santibanez,B. Knust,B. W. Petersen,E. D. Ervin,S. T. Nichol,I. K. Damon,M. L. Washington, Estimating the future number of cases in the Ebola Epidemic --Liberia and Sierra Leone, 2014-2015, MMWR Morb Mortal Wkly Rep, null (2014). |
| [46] | [ S. Merler, M. Ajelli, L. Fumanelli, S. Parlamento, A. Pastore y Piontti, N. E. Dean, G. Putoto, D. Carraro, I. M. Longini Jr. , M. E. Halloran and A. Vespignani, Containing Ebola at the source with ring vaccination PLOS Neglected Tropical Diseases 10(2016), e0005093. |
| [47] | [ J. Müller,B. Schönfisch,M. Kirkilionis, Ring vaccination, Journal of Mathematical Biology, 41 (2000): 143-171. |
| [48] | [ Medicins Sans Frontieres/Doctors Without Borders, Ebola (2015), http://www.doctorswithoutborders.org/our-work/medical-issues/ebola. |
| [49] | [ H. Nishiura, Correcting the actual reproduction number: A simple method to estimate R_0 from early epidemic growth data, Int J Environ Res Public Health, 7 (2010): 291-302. |
| [50] | [ A. Pandey,K. E. Atkins,J. Medlock,N. Wenzel,J. P. Townsend,J. E. Childs,T. G. Nyenswah,M. L. Ndeffo-Mbah,A. P. Galvani, Strategies for containing Ebola in West Africa, Science, 346 (2014): 991-995. |
| [51] | [ J. Prescott,T. Bushmaker,R. Fischer,K. Miazgowicz,S. Judson,V. J. Munster, Postmortem stability of Ebola virus, Emerg Infect Dis, 21 (2015): 856-859. |
| [52] | [ C. M. Rivers, E. T. Lofgren, M. Marathe, S. Eubank and B. L. Lewis, Modeling the impact of interventions on an epidemic of Ebola in sierra leone and liberia PLOS Currents Outbreaks (2014), Edition 2. |
| [53] | [ D. Salem,R. Smith?, A mathematical model of ebola virus disease: Using sensitivity analysis to determine effective intervention targets, Proceedings of SummerSim-SCSC, null (2016): 16-23. |
| [54] | [ E. E. Salpeter,S. R. Salpeter, Mathematical mode for the epidemiology of tuberculosis, with estimates of the reproductive number and infection-delay function, Am J Epidemiol, 142 (1998): 398-406. |
| [55] | [ R. Smith?, Modelling Disease Ecology with Mathematics American Institute of Mathematical Sciences, 2008. |
| [56] | [ L. R. Stanberry, Clinical trials of prophylactic and therapeutic herpes simplex virus vaccines, Herpes, null (2004): 161A-169A. |
| [57] | [ United Nations, Making A Difference the Global Ebola Response: Outlook 2015 United Nations, (2015), http://ebolaresponse.un.org/outlook-2015. |
| [58] | [ United Nations Global Ebola Response, UN Mission for Ebola Emergency Response (UNMEER) United Nations, (2015), http://ebolaresponse.un.org/un-mission-ebola-emergency-response-unmeer. |
| [59] | [ G. Webb, C. Browne, X. Huo, O. Seydi, M. Seydi and P. Magal, A model of the 2014 Ebola epidemic in West Africa with contact tracing PLoS Currents Outbreaks (2015), Edition 1. |
| [60] | [ G. Webb,C. Browne, A model of the Ebola epidemics in West Africa incorporating age of infection, J Biol Dyn, 10 (2016): 18-30. |
| [61] | [ WHO, WHO coordinating vaccination of contacts to contain Ebola flare-up in Guinea, World Health Organization, (2016), http://www.who.int/features/2016/ebola-contacts-vaccination/en/. |
| [62] | [ WHO, One year into the Ebola epidemic: A deadly tenacious and unforgiving virus, World Health Organization, (2015), http://www.who.int/csr/disease/ebola/one-year-report/introduction/en/. |
| [63] | [ WHO, Ebola outbreak 2014 -present: How the outbreak and WHO's response unfolded, World Health Organization, (2016), http://who.int/csr/disease/ebola/response/phases/en/. |
| [64] | [ WHO, Ebola virus disease, World Health Organization, (2015), http://www.who.int/mediacentre/factsheets/fs103/en/. |
| [65] | [ WHO, WHO: Ebola Response Roadmap World Health Organization, (2014), http://www.who.int/csr/resources/publications/ebola/response-roadmap/en/. |
| [66] | [ WHO, Ebola Virus Disease Outbreak Response Plan in West Africa World Health Organization, (2014), http://www.who.int/mediacentre/factsheets/fs103/en/. |
| [67] | [ WHO Ebola Response Team, Ebola Virus Disease in West Africa -The First 9 Months of the Epidemic and Forward Projections, N Engl J Med, 371 (2014): 1481-1495. |
| 1. | A. Mhlanga, Dynamical analysis and control strategies in modelling Ebola virus disease, 2019, 2019, 1687-1847, 10.1186/s13662-019-2392-x | |
| 2. | Debkusum Mukhopadhyay, Samares Pal, Efficacy of Isolation as a Control Strategy for Ebola Outbreaks in Combination with Vaccination, 2019, 14, 1793-0480, 115, 10.1142/S179304801950005X | |
| 3. | Berge Tsanou, Jean Mbaro Saman Lubuma, Arsène Jaurès Ouemba Tassé, Hervé Michel Tenkam, Dynamics of host-reservoir transmission of Ebola with spillover potential to humans, 2018, 14173875, 1, 10.14232/ejqtde.2018.1.14 | |
| 4. | Karima Kabli, Soumia El Moujaddid, Khadija Niri, Abdessamad Tridane, Cooperative system analysis of the Ebola virus epidemic model, 2018, 3, 24680427, 145, 10.1016/j.idm.2018.09.004 | |
| 5. | Lee Worden, Rae Wannier, Nicole A. Hoff, Kamy Musene, Bernice Selo, Mathias Mossoko, Emile Okitolonda-Wemakoy, Jean Jacques Muyembe Tamfum, George W. Rutherford, Thomas M. Lietman, Anne W. Rimoin, Travis C. Porco, J. Daniel Kelly, Townsend Peterson, Projections of epidemic transmission and estimation of vaccination impact during an ongoing Ebola virus disease outbreak in Northeastern Democratic Republic of Congo, as of Feb. 25, 2019, 2019, 13, 1935-2735, e0007512, 10.1371/journal.pntd.0007512 | |
| 6. | T. Berge, A. J. Ouemba Tassé, H. M. Tenkam, J. Lubuma, Mathematical modeling of contact tracing as a control strategy of Ebola virus disease, 2018, 11, 1793-5245, 1850093, 10.1142/S1793524518500936 | |
| 7. | Ravi Potluri, Amit Kumar, Vikalp Maheshwari, Charlie Smith, Valerie Oriol Mathieu, Kerstin Luhn, Benoit Callendret, Hitesh Bhandari, Malaya Kumar Sahoo, Impact of prophylactic vaccination strategies on Ebola virus transmission: A modeling analysis, 2020, 15, 1932-6203, e0230406, 10.1371/journal.pone.0230406 | |
| 8. | Hamed Agahi, A control approach for monotone systems with multi-valued characteristics: Application to an Ebola Virus model, 2020, 56, 09473580, 265, 10.1016/j.ejcon.2020.02.011 | |
| 9. | Calvin Tadmon, Jacques Ndé Kengne, Mathematical modelling and nonstandard finite scheme analysis for an Ebola model transmission with information and voluntary isolation, 2022, 28, 1023-6198, 299, 10.1080/10236198.2022.2042524 | |
| 10. | Peiyu Chen, Wenhui Fan, Xudong Guo, Constantinos Siettos, A hybrid simulation model to study the impact of combined interventions on Ebola epidemic, 2021, 16, 1932-6203, e0254044, 10.1371/journal.pone.0254044 | |
| 11. | Mavis Obeng-Kusi, Magdiel A. Habila, Denise J. Roe, Brian Erstad, Ivo Abraham, Economic evaluation using dynamic transition modeling of ebola virus vaccination in lower-and-middle-income countries, 2021, 24, 1369-6998, 1, 10.1080/13696998.2021.2002092 | |
| 12. | Ravi Potluri, Amit Kumar, Valérie Oriol-mathieu, Thierry Van Effelterre, Laurent Metz, Hitesh Bhandari, Model-based evaluation of the impact of prophylactic vaccination applied to Ebola epidemics in Sierra Leone and Democratic Republic of Congo, 2022, 22, 1471-2334, 10.1186/s12879-022-07723-6 | |
| 13. | Tahira Sumbal Shaikh, Ali Akgül, Muhammad Aziz ur Rehman, Nauman Ahmed, Muhammad Sajid Iqbal, Naveed Shahid, Muhammad Rafiq, Manuel De la Sen, Analysis of a Modified System of Infectious Disease in a Closed and Convex Subset of a Function Space with Numerical Study, 2023, 12, 2075-1680, 79, 10.3390/axioms12010079 | |
| 14. | Donal Bisanzio, Ashley E. Davis, Sandra E. Talbird, Thierry Van Effelterre, Laurent Metz, Maren Gaudig, Valérie Oriol Mathieu, Anita J. Brogan, Targeted preventive vaccination campaigns to reduce Ebola outbreaks: An individual-based modeling study, 2023, 41, 0264410X, 684, 10.1016/j.vaccine.2022.11.036 | |
| 15. | Suliman Jamiel M. Abdalla, Faraimunashe Chirove, Keshlan S. Govinder, A systematic review of mathematical models of the Ebola virus disease, 2022, 42, 0228-6203, 814, 10.1080/02286203.2021.1983745 | |
| 16. | A. J. OUEMBA TASSÉ, B. TSANOU, J. LUBUMA, JEAN LOUIS WOUKENG, FRANCIS SIGNING, EBOLA VIRUS DISEASE DYNAMICS WITH SOME PREVENTIVE MEASURES: A CASE STUDY OF THE 2018–2020 KIVU OUTBREAK, 2022, 30, 0218-3390, 113, 10.1142/S0218339022500048 | |
| 17. | Huarong Ren, Rui Xu, Prevention and control of Ebola virus transmission: mathematical modelling and data fitting, 2024, 89, 0303-6812, 10.1007/s00285-024-02122-8 | |
| 18. | Manjari Shankar, Anna-Maria Hartner, Callum R. K. Arnold, Ezra Gayawan, Hyolim Kang, Jong-Hoon Kim, Gemma Nedjati Gilani, Anne Cori, Han Fu, Mark Jit, Rudzani Muloiwa, Allison Portnoy, Caroline Trotter, Katy A. M. Gaythorpe, How mathematical modelling can inform outbreak response vaccination, 2024, 24, 1471-2334, 10.1186/s12879-024-10243-0 | |
| 19. | Suliman Jamiel M. Abdalla, Keshlan S. Govinder, Faraimunashe Chirove, The impact of geographically-targeted vaccinations during the 2018-2020 Kivu Ebola outbreak, 2025, 142, 0307904X, 115972, 10.1016/j.apm.2025.115972 |
| Parameter | Units | Value | Description | Source | |
| Fitted Parameters | |
See Table 3 | transmission rate from infectious individuals to high risk susceptible individuals | ||
| |
See Table 3 | transmission rate from infectious individuals to low risk susceptible individuals | |||
| |
See Table 3 | transmission rate from infectious individuals to susceptible healthcare workers | |||
| See Table 3 | transmission rate from deceased individuals to high risk susceptible individuals | ||||
| See Table 3 | transmission rate from deceased individuals to low risk susceptible individuals | ||||
| See Table 3 | transmission rate from deceased individuals to susceptible healthcare workers | ||||
| See Table 3 | transmission rate from recovering, still infectious individuals to low risk individuals | ||||
| -- | See Table 3 | proportion of symptomatic individuals who go to hospitals | |||
| -- | See Table 3 | scaling constant where |
|||
| Vax | -- | |
proportion of individuals in whom the vaccine is effective | [31] | |
| -- | See Section 5 | proportion of low susceptible population ( |
|||
| -- | See Section 5 | proportion of high susceptible population ( |
|||
| -- | See Section 5 | proportion of healthcare workers ( |
|||
| See section 3 | migration rate of healthcare workers into the population | ||||
| |
natural death rate per day per 1,000 individuals | [16] | |||
| |
natural birth rate per day per 1,000 individuals | [16] | |||
| |
rate at which individuals become symptomatic and infectious | [45] | |||
| |
infectious period of individuals who are not in hospitals | [50] | |||
| |
infectious period of individuals who are in hospitals | ||||
| -- | |
proportion of individuals who die from Ebola | [12] | ||
| |
number of healthcare workers in the population prior to outbreak | [16] | |||
| |
burial rate of deceased individuals who were not in hospitals | ||||
| |
burial rate of deceased individuals who were in hospitals | [50] | |||
| |
rate at which recovering and still infectious individuals become non-infectious | [18,15] | |||
| |
rate at which individuals move from low risk to high risk susceptible populations | ||||
| rate at which individuals move from high risk to low risk susceptible populations | |||||
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|
| |
0.015 | 0.030 | 0.060 | 0.013 | 0.013 |
| |
40 | 20 | 10 | 50 | 45 |
| Response period | |
| |
3.31 |
| |
1.88 |
| |
0.90 |
| |
0.27 |
| |
0.16 |
| Cumulative Infections | Cumulative Deaths | |||||
| at tf | Prevented | at tf | Prevented | |||
| Baseline |
14436 | 0 | 4416 | 0 | ||
| Start vax at | 8863 | 5573 | 2738 | 1678 | ||
| 12583 | 1853 | 3837 | 579 | |||
| 13225 | 1211 | 4050 | 366 | |||
| 14325 | 111 | 4392 | 24 | |||
| Start vax at | 5138 | 9298 | 1656 | 2760 | ||
| 11075 | 3361 | 3343 | 1073 | |||
| 12168 | 2268 | 3708 | 708 | |||
| 14173 | 263 | 4357 | 59 | |||
| Start vax at | 13999 | 437 | 4283 | 133 | ||
| 14285 | 151 | 4369 | 47 | |||
| 14351 | 85 | 4391 | 25 | |||
| 14429 | 7 | 4415 | 1 | |||
| Start vax at | 8821 | 5615 | 2726 | 1690 | ||
| 12553 | 1883 | 3827 | 589 | |||
| 13211 | 1225 | 4046 | 370 | |||
| 14323 | 113 | 4391 | 25 | |||
| Vaccination strategy for |
||||||||
| CI | CI | CI | CI | |||||
| 0 | 4156370 | 495 | 3743965 | 516 | 650846 | 492 | 2643460 | 492 |
| 0.10 | 3064971 | 648 | 2506362 | 694 | 1853742 | 644 | 1845334 | 644 |
| 0.20 | 1866043 | 974 | 1026659 | 1138 | 1040091 | 987 | 1030788 | 988 |
| 0.29 | 764174 | 1990 | 37 | 103 | 188898 | 2267 | 188898 | 2267 |
| 0.30 | 646329 | 2270 | 33 | 0 | 82717 | 2546 | 82717 | 2546 |
| 0.31 | 529673 | 2657 | 29 | 0 | 19911 | 2502 | 19911 | 2502 |
| 0.32 | 414210 | 3213 | 25 | 0 | 3866 | 2091 | 3866 | 2091 |
| 0.33 | 300060 | 4090 | 23 | 0 | 954 | 1570 | 954 | 1570 |
| 0.34 | 171811 | 5697 | 20 | 0 | 325 | 1023 | 325 | 1023 |
| 0.35 | 13195 | 7300 | 18 | 0 | 147 | 0 | 147 | 0 |
| 0.36 | 431 | 0 | 16 | 0 | 81 | 0 | 81 | 0 |
| 0.40 | 26 | 0 | 20 | 0 | 23 | 0 | 23 | 0 |
| 0.50 | 7 | 0 | 7 | 0 | 7 | 0 | 7 | 0 |
| 0.60 | 4 | 0 | 4 | 0 | 4 | 0 | 4 | 0 |
| 0.70 | 2 | 0 | 2 | 0 | 2 | 0 | 2 | 0 |
| 0.80 | 2 | 0 | 2 | 0 | 2 | 0 | 2 | 0 |
| 0.90 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| Parameter | Units | Value | Description | Source | |
| Fitted Parameters | |
See Table 3 | transmission rate from infectious individuals to high risk susceptible individuals | ||
| |
See Table 3 | transmission rate from infectious individuals to low risk susceptible individuals | |||
| |
See Table 3 | transmission rate from infectious individuals to susceptible healthcare workers | |||
| See Table 3 | transmission rate from deceased individuals to high risk susceptible individuals | ||||
| See Table 3 | transmission rate from deceased individuals to low risk susceptible individuals | ||||
| See Table 3 | transmission rate from deceased individuals to susceptible healthcare workers | ||||
| See Table 3 | transmission rate from recovering, still infectious individuals to low risk individuals | ||||
| -- | See Table 3 | proportion of symptomatic individuals who go to hospitals | |||
| -- | See Table 3 | scaling constant where |
|||
| Vax | -- | |
proportion of individuals in whom the vaccine is effective | [31] | |
| -- | See Section 5 | proportion of low susceptible population ( |
|||
| -- | See Section 5 | proportion of high susceptible population ( |
|||
| -- | See Section 5 | proportion of healthcare workers ( |
|||
| See section 3 | migration rate of healthcare workers into the population | ||||
| |
natural death rate per day per 1,000 individuals | [16] | |||
| |
natural birth rate per day per 1,000 individuals | [16] | |||
| |
rate at which individuals become symptomatic and infectious | [45] | |||
| |
infectious period of individuals who are not in hospitals | [50] | |||
| |
infectious period of individuals who are in hospitals | ||||
| -- | |
proportion of individuals who die from Ebola | [12] | ||
| |
number of healthcare workers in the population prior to outbreak | [16] | |||
| |
burial rate of deceased individuals who were not in hospitals | ||||
| |
burial rate of deceased individuals who were in hospitals | [50] | |||
| |
rate at which recovering and still infectious individuals become non-infectious | [18,15] | |||
| |
rate at which individuals move from low risk to high risk susceptible populations | ||||
| rate at which individuals move from high risk to low risk susceptible populations | |||||
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|
| |
0.015 | 0.030 | 0.060 | 0.013 | 0.013 |
| |
40 | 20 | 10 | 50 | 45 |
| Response period | |
| |
3.31 |
| |
1.88 |
| |
0.90 |
| |
0.27 |
| |
0.16 |
| Cumulative Infections | Cumulative Deaths | |||||
| at tf | Prevented | at tf | Prevented | |||
| Baseline |
14436 | 0 | 4416 | 0 | ||
| Start vax at | 8863 | 5573 | 2738 | 1678 | ||
| 12583 | 1853 | 3837 | 579 | |||
| 13225 | 1211 | 4050 | 366 | |||
| 14325 | 111 | 4392 | 24 | |||
| Start vax at | 5138 | 9298 | 1656 | 2760 | ||
| 11075 | 3361 | 3343 | 1073 | |||
| 12168 | 2268 | 3708 | 708 | |||
| 14173 | 263 | 4357 | 59 | |||
| Start vax at | 13999 | 437 | 4283 | 133 | ||
| 14285 | 151 | 4369 | 47 | |||
| 14351 | 85 | 4391 | 25 | |||
| 14429 | 7 | 4415 | 1 | |||
| Start vax at | 8821 | 5615 | 2726 | 1690 | ||
| 12553 | 1883 | 3827 | 589 | |||
| 13211 | 1225 | 4046 | 370 | |||
| 14323 | 113 | 4391 | 25 | |||
| Vaccination strategy for |
||||||||
| CI | CI | CI | CI | |||||
| 0 | 4156370 | 495 | 3743965 | 516 | 650846 | 492 | 2643460 | 492 |
| 0.10 | 3064971 | 648 | 2506362 | 694 | 1853742 | 644 | 1845334 | 644 |
| 0.20 | 1866043 | 974 | 1026659 | 1138 | 1040091 | 987 | 1030788 | 988 |
| 0.29 | 764174 | 1990 | 37 | 103 | 188898 | 2267 | 188898 | 2267 |
| 0.30 | 646329 | 2270 | 33 | 0 | 82717 | 2546 | 82717 | 2546 |
| 0.31 | 529673 | 2657 | 29 | 0 | 19911 | 2502 | 19911 | 2502 |
| 0.32 | 414210 | 3213 | 25 | 0 | 3866 | 2091 | 3866 | 2091 |
| 0.33 | 300060 | 4090 | 23 | 0 | 954 | 1570 | 954 | 1570 |
| 0.34 | 171811 | 5697 | 20 | 0 | 325 | 1023 | 325 | 1023 |
| 0.35 | 13195 | 7300 | 18 | 0 | 147 | 0 | 147 | 0 |
| 0.36 | 431 | 0 | 16 | 0 | 81 | 0 | 81 | 0 |
| 0.40 | 26 | 0 | 20 | 0 | 23 | 0 | 23 | 0 |
| 0.50 | 7 | 0 | 7 | 0 | 7 | 0 | 7 | 0 |
| 0.60 | 4 | 0 | 4 | 0 | 4 | 0 | 4 | 0 |
| 0.70 | 2 | 0 | 2 | 0 | 2 | 0 | 2 | 0 |
| 0.80 | 2 | 0 | 2 | 0 | 2 | 0 | 2 | 0 |
| 0.90 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |