1. Introduction

Complex networks are good models for describing and studying complex systems [6,1,21]. It ignores many properties that are not related to the study, and describes the system as a graph containing only nodes and edges, in which nodes represent the elements of the system and edges represent the interactions between them. Some real world networks include the WWW(World Wide Web) networks [8], Internet networks, collaboration networks, citation networks, metabolism networks etc, and some constructed networks include Euler graph, 'small world' network [25], BA network [3], etc.

To study complex networks and their properties, we should first study some basic special quantities characterizing the topology structure of the networks. Traditionally, these characteristic quantities are borrowed from graph theory, such as degree distribution $p(k)$, average degree $\langle k\rangle$, joint degree distribution $p(k_1, k_2)$, average path length $l$, clustering coefficient $C$, and degree-degree correlation coefficient $C_{k_1, k_2}$, etc. Among them, the degree distribution is the most important topological quantity of the network. Its calculation method mainly includes: the Mean-field method [2], the master equation method [4], the rate equation method [13], and Markov chain-based numerical method [23], etc [5]. The Mean-field method considers degree as continuously changing, and obtains continuous rate of change of $k_i$ [2]. Inspired by this idea, here we also use the continuous degree method (CDM). It will transform the network evolution model into a partial differential equation, which can be analysed easily. Using the CDM, we establish a partial differential equation on the cumulative distribution function $F(k, t)$ with the growing network, analytical results of the cumulative distribution function $F(k, t)$ and the degree distribution $p(k, t)$ are obtained. In addition to the degree distribution, the joint degree distribution $p(k_1, k_2)$ is also another important topology quantity of a network. It is defined as the fraction of directed edges whose nodes have degrees $k_1$ and $k_2$. So far the calculation method of joint degree distribution is mainly the rate equation [14]. In this paper, we calculate the joint degree distribution of BA model by also applying the CDM. As a consequence, we calculate the conditional degree distribution $p(k_1|k_2)$ and the degree correlation of the networks.

Transmission dynamics on complex networks is another focus of network research. Its dynamical behavior is often influenced by the network topology. Regarding the spread of epidemic, for example, different network topologies often have different threshold and propagation behavior. The main existing epidemic models are node-based model [22,26,0], pairwise models [11,12], effective degree models [15], and edge-based models [20,19,18,24]. Although these models have different styles, they all divide the nodes and edges into different classes according to the node degree. Here we also consider the node degree as a continuous variable, and apply the CDM to establish a continuous degree SIS epidemic model on static BA network. Simultaneously, we also take into account the evolution of the network, and build a continuous degree SIS epidemic model on a BA growing network.

The rest of this paper is organized as follows. In Section 2, applying the CDM, we calculate the degree distribution of three different growing models, which are the BA growing model, the preferential attachment accelerating growing model and the random attachment growing model. In Section 3, we calculate the joint degree distribution of the BA model also using the CDM, and study its degree correlation. In Section 4, we establish a continuous degree SIS model on a static degree uncorrelated network and a BA growing network, respectively. Finally, in Section 5, we conclude the paper.

---

2. Some calculations of the degree distribution of growing networks with CDM

In this section, we use CDM to calculate the degree distribution of the following three growing models: the BA growing model, the preferential attachment accelerating growing model and the random attachment growing model. The main notations are defined in Table 1.

---

2.1. Calculation of the degree distribution of the BA growing model with CDM

First, we recall the BA model, whose evolution mechanism contains two aspects:

H1: Growth: Starting with a small number ($m_0$) of nodes, we add a new node with $m(\leq m_0)$ edges at every time step. The node added at $i^{th}$ time step is marked as $i$.

H2: Preferential attachment: the probability $\Pi_i$ that node $i$ connects to a new node is proportional to its degree $k_i$, i.e., $\Pi _i=\frac{k_i}{\sum_j k_j}$.

We consider that the time $t$ and the node degree $k$ change continuously. Let $N(t)$ represent the total number of nodes at time $t$, $\hat{N}(k, t)$ represent the number of nodes with degree less than or equal to $k$ at time $t$. Let $F(k, t)$ represent the cumulative distribution function of network (or the proportion of nodes with degree less than or equal to $k$) at time $t$, and let the derivative of $F(k, t)$ with respect to $k$ represent the degree distribution $p(k, t)$, in fact the probability density, at time $t$. In the continuous degree case, obviously, we have the following relation:

$\hat{N}(k, t) = N(t)F(k, t) = N(t)\int_0^k p(x, t)\, dx.$

(1)

It's not difficult to find that the growth of the BA model satisfies the Markov property. That is to say, the network structure at time $t+\Delta t$ depends only on the structure at the most recent time $t$ and does not depend on the history of the evolution. Based on this we can establish the evolution equation for $F(k, t)$.

For a node with degree $k(>m)$ at time $t$, say node A, because of the addition of the new node and new edges, the degree of node A will become $k+\theta_t^k$ at time $t+\Delta t$ in the continuous degree cases, where $\theta_t^k = m\Delta t\frac{k}{\Sigma k}$ is the increased degree of node A. Meanwhile, for those nodes with degree less than node A's degree (equal to $k$) at time $t$, their degree is still less than A's degree ($k+\theta_t^k$) at time $t+\Delta t$ due to the co-evolution of nodes. Taking into account the adding of new nodes, $\hat{N}(k+\theta_t^k, t+\Delta t)$ includes two parts, the old nodes $\hat{N}(k, t)$ and the newly added nodes $\Delta \hat{N}(k, t)$, so we have the following relation:

$\hat{N}(k, t) + \Delta \hat{N}(k, t) = \hat{N} (k+\theta_t^k, t+\Delta t).$

(2)

(2) presents the quantitative relation between $\hat{N}(k, t)$ and $\hat{N}(k+\theta_t^k, t+\Delta t)$ at time $t$ and time $t+\Delta t$. $\Delta \hat{N}(k, t)$ is the newly added nodes with degree less than or equal to $k$ in time $\Delta t$. We have $\Delta \hat{N}(k, t)=\Delta t$, $\Sigma k=2(l_0+mt)$ ($l_0$ see Table 1). Substituting these and (1) into (2), we obtain

$N(t)F(k, t) + \Delta t = N(t+\Delta t)F\left(k+\frac{m\Delta t k }{2(l_0+mt)}, t+\Delta t\right).$

(3)

According to the evolution mechanism of the model, we have $N(t) = m_0 + t$. Substituting it into (3), we obtain

$(m_0+t)F(k, t) + \Delta t=(m_0+t+\Delta t)F\left(k+\frac{m\Delta t k}{2(l_0+mt)}, t+\Delta t\right).$

(4)

Taking the Taylor expansion for $F(k+\frac{m\Delta t k}{2(l_0+mt)}, t+\Delta t)$, retaining only the first order terms of $\Delta t$ and simplifying, we have

$\frac{m\Delta tk }{2(l_0+mt)}\frac{\partial F(k, t)}{\partial k} + \Delta t\frac{\partial F(k, t)}{\partial t} + \frac{\Delta t(F(k, t)-1)}{m_0+t}=o(\Delta t).$

(5)

Dividing by $\Delta t$ on both sides of the above equation, and letting $\Delta t \rightarrow 0$, we get the following partial differential equation on $F(k, t)$:

$\frac{mk}{2(l_0+mt)}\frac{\partial F(k, t)}{\partial k} +\frac{\partial F(k, t)}{\partial t}+\frac{F(k, t)-1}{m_0+t}=0,$

(6)

in the feasible region $D = \{(k, t)|k\geq m, t\geq 0\}$. We know that the degree of the new node added at time $t$ is the minimum degree at that moment, and that the new node is attached with $m$ edges when it is added to the network at time $t$, so the minimum degree of the nodes is $m$ at that time. Thereby we have following initial and boundary conditions:

$\begin{cases} F(k, 0)=\Psi(k), \\ F(m, t)=0, \forall t> 0, \end{cases}$

(7)

where, $\Psi(k)$ is the cumulative distribution function of the initial network. Note that this boundary condition defaults the degree $k$ of initial nodes is greater than $m$. In this way, the calculation of the cumulative distribution function $F(k, t)$ reduces to solving an initial-boundary value problem, which is easier to deal with mathematically. Using the characteristic line method to solve (6), and substituting (7) into the general solution, we can get

$F(k, t)=\left\{\begin{array}{ll} 1-\frac{1}{m_0+t}\left(m_0+\frac{ml_0+m^2 t}{k^2}-\frac{l_0}{m} \right), &\mbox{ if }m\leq k\leq m(1+\frac{mt}{l_0})^{\frac{1}{2}};\\ \frac{t}{m_0+t}+\frac{m_0}{m_0+t} \Psi\left(\frac{k}{(1+\frac{mt}{l_0})^{\frac{1}{2}}}\right), &\mbox{ if } k > m(1+\frac{mt}{l_0})^{\frac{1}{2}}. \end{array}\right.$

(8)

This equation means that, for given time $t>0$, the nodes with degree $m\leq k\leq m(1+\frac{mt}{l_0})^\frac{1}{2}$ are the newly added $t$ nodes from time 0 to time $t$, whose degree change depending on the boundary condition, and the nodes with degree $k>m(1+\frac{mt}{l_0})^\frac{1}{2}$ are the initial $m_0$ nodes, whose degree change depending on the initial condition.

Assuming that the derivative of cumulative distribution function $\Psi (k)$ with respect to $k$ is the probability density function $p(k, 0)$, then differentiating (8) with respect to $k$, we get the degree distribution:

$\begin{split} p(k, t)&=\frac{\partial F(k, t)}{\partial k} \\ &=\left\{\begin{array}{ll} \frac{2ml_0+2m^2t}{m_0+t}k^{-3}, &\mbox{ if }m\leq k\leq m(1+\frac{mt}{l_0})^{\frac{1}{2}};\\ \frac{m_0}{(m_0+t)(1+\frac{mt}{l_0})^\frac{1}{2}} p\left(\frac{k}{(1+\frac{mt}{l_0})^\frac{1}{2}}, 0\right), &\mbox{ if } k > m(1+\frac{mt}{l_0})^{\frac{1}{2}}. \end{array}\right. \end{split}$

(9)

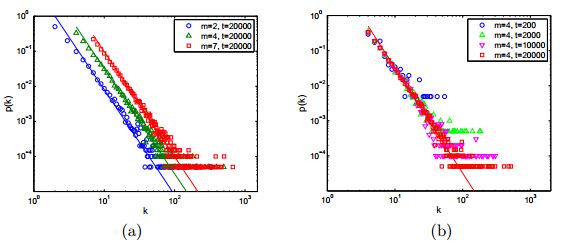
As we can see, $m_0$ is a very small number when time $t$ is large enough. If we don't consider the initial $m_0$ nodes this result is very close to $\frac{2m^2t}{m_0+t} \frac{1}{k^3}$ in [2], and both are asymptotically equal to the stationary state $2m^2k^{-3}$ when time $t$ is large enough. In Figure 1, we show the simulation results and corresponding analytical results with different parameter $m$ and time $t$, respectively.

We assume $p(k, 0)$ satisfies $\int_m^\infty kp(k, 0)\, dk=\frac{2l_0}{m_0}$, then with the degree distribution (9), we can calculate the average degree

$\langle k_t \rangle = \int_m ^\infty kp(k, t)\, dk=\frac{2(l_0+mt)}{m_0+t}.$

From this expression, we can easily understand that the average degree $\langle k_t\rangle$ is equal to the ratio of two times the actual number of edges and the total number of nodes. Furthermore, the average degree $\langle k_t\rangle$ is approximately equal to $2m$ when time is large enough.

---

2.2. Calculation of the degree distribution of the preferential attachment accelerating growing model with $m$-varying with CDM

Different from BA model, many real networks exhibit accelerating growth, such as the Internet and WWW [8,23,5,9], where the edge number grows faster than the nodes numbers. Here we use the CDM to calculate the degree distribution of one preferential attachment accelerating growing model with $m$-varying.

Let $mt^\alpha$ be the new edge number attached with the new node added at time $t$, $0\leq \alpha < 1$. That means the new node added at time $t$ will connect to $mt^\alpha$ different existing nodes. The rest of the evolution mechanism remains the same as the BA model described in Section 2.1. Similar to the analysis in Section 2.1, the cumulative distribution function $F(k, t)$ satisfies the following relation from time $t$ to $t+\Delta t$:

$N(t)F(k, t) + \Delta t = N(t+\Delta t)F\left(k+\theta_t^k, t+\Delta t\right),$

(10)

where $\theta_t^k=\int_t^{t+\Delta t}mx^\alpha \, dx\frac{k}{\Sigma k} \simeq\frac{(\alpha+1)k\Delta t}{2t}$. Substituting this into (10) and taking the Taylor expansion, we get

$\frac{(\alpha +1)k}{2t}\frac{\partial F(k, t)}{\partial k} +\frac{\partial F(k, t)}{\partial t}+\frac{F(k, t)-1}{m_0+t}=0,$

(11)

in the feasible region $D =\{(k, t)|k>mt^{\alpha}, t>0\}$. For degree $k$($>mt^\alpha$) nodes, the coefficient $\frac{(\alpha +1)k}{2t}$ in (11) can be regarded as the changing rate of degree over time $t$. And this rate of change is larger than the add rate of new node $(mt^\alpha)' = \alpha mt^{\alpha-1}$, since $0\leq \alpha < 1$. So the minimum degree of the nodes is $mt^\alpha$ which is the degree of new added node at time $t$. Thus, the boundary condition will be

$F(mt^\alpha, t)=0, \forall t> 0.$

(12)

Solving this boundary problem, we obtain

$F(k, t)=1-\frac{1}{m_0+t}\left(m_0+\left(\frac{k}{m} \right)^{\frac{2}{\alpha-1}} t^{\frac{1+\alpha}{1-\alpha}} \right).$

(13)

Consequently, the degree distribution is

$\begin{split} p(k, t)=\frac{\partial F(k, t)}{\partial k}&=\frac{2}{(m_0+t) (1-\alpha)}m^{\frac{2}{1-\alpha}} t^{\frac{1+\alpha}{1-\alpha}} k^{-\frac{3-\alpha}{1-\alpha}} \\ &\approx \frac{2}{1-\alpha}m^{\frac{2}{1-\alpha}} t^{\frac{2\alpha} {1-\alpha}} k^{-\frac{3-\alpha}{1-\alpha}}. \end{split}$

(14)

This result is completely equivalent to (24) in [23]. The simulation results and analytical results are showed in Figure 2.

---

2.3. Calculation of the degree distribution of the random attachment growing model with CDM

In this subsection, we will calculate the degree distribution of random attachment growing model using CDM. Same as the BA model, the random attachment growing model also starts with a small number ($m_0$) of nodes, and add a new node with $m(\leq m_0)$ edges at every time step. But the difference is that the newly added node in this model is randomly connected with the old ones. That is to say, for one edge the probability each old node be chosen to connect is the same, equal to $\frac{1}{N(t)}$.

Similar to the BA growing model, we also have the following relationship on cumulative distribution function $F(k, t)$

$N(t)F(k, t) + \Delta t = N(t+\Delta t)F\left(k+\theta_t^k, t+\Delta t\right),$

(15)

where $\theta_t^k=m\Delta t\frac{1}{N(t)} = \frac{m\Delta t}{m_0+t}$. Substituting this into (15) and dealing with it using the same processing method as Section 2.1 and 2.2, we get

$\frac{m}{m_0+t}\frac{\partial F(k, t)}{\partial k} +\frac{\partial F(k, t)}{\partial t}+\frac{F(k, t)-1}{m_0+t}=0,$

(16)

also in the feasible region $D = \{ (k, t) | k>m, t>0\}$. As the same with BA model, this partial differential equation has the initial and boundary conditions (7).

Solving (16), and substituting (7) into the general solution, we get

$F(k, t)=\left\{\begin{array}{ll} 1-e^{1-\frac{k}{m}}, & m < k \leq m+\ln{(\frac{m_0+t}{m_0})^m};\\ \frac{t}{m_0+t}+\frac{m_0}{m_0+t}\Psi\left(k+\ln{(\frac{m_0}{m_0+t})^m}\right), &k > m+\ln{(\frac{m_0+t}{m_0})^m}. \end{array}\right.$

(17)

If we ignore the initial $m_0$ nodes, the degree distribution is

$p(k, t)=\frac{\partial F(k, t)}{\partial k}=\frac{1}{m}e^{1-\frac{k}{m}}, m < k \leq m+\ln{(\frac{m_0+t}{m_0})^m}.$

(18)

This result is the same as the (17) in [2], which verifies the accuracy of CDM again. In Figure 3, we show the simulation results as well as analytical results.

---

3. Calculation of the joint degree distribution of the BA growing model with CDM

In Section 2, we have shown that the CDM can be used to calculate the degree distribution of some growing models. In this section, with the help of the CDM, we will calculate the joint degree distribution of BA model.

Assume that the edges have direction, so the total number of directed edges, written as $L(t)=2(l_0+mt)$, is twice the number of actual edges. The joint degree distribution $p(k_1, k_2)$ here we study is the fraction of directed edges that connect nodes of degree $k_1$ and degree $k_2$.

In the continuous degree case, let $\hat{L}(k_1, k_2, t)$ represent the total number of directed edges whose degrees are sequentially not larger than $k_1$ and $k_2$ at time $t$, let $F(k_1, k_2, t)$ represent the joint cumulative distribution function at time $t$, namely, the proportion of directed edges whose degrees are sequentially not larger than $k_1$ and $k_2$ at time $t$. It is well known that the second order partial derivative $p(k_1, k_2, t)$ of joint cumulative distribution function sequentially with respect to $k_1$ and $k_2$ represents the joint degree distribution, actually the joint probability density. So we have the following relations:

$\hat{L}(k_1, k_2, t)=L(t)F(k_1, k_2, t),$

(19)

$F(k_1, k_2, t)=\int_0^{k_1}\int_0^{k_2}p(x_1, x_2, t)\, dx_1\, dx_2.$

(20)

For a directed edge which from one node with degree $k_1$ point to another node with degree $k_2$ at time $t$, due to the addition of new nodes and new edges, the degrees of its two nodes sequentially will be $k_1+\theta_t^{k_1}$ and $k_2+\theta_t^{k_2}$ at time $t+\Delta t$. Therefore, similar to the thought of degree distribution, the $\hat{L}(k_1+\theta_t^{k_1}, k_2+\theta_t^{k_2}, t+\Delta t)$ consists of the old directed edges $\hat{L}(k_1, k_2, t)$ and some newly added directed edges $\Delta \hat{L}(k_1, k_2, t)$ whose degrees are sequentially not larger than $k_1$ and $k_2$, namely,

$\hat{L}(k_1, k_2, t) + \Delta \hat{L}(k_1, k_2, t) = \hat{L}(k_1+\theta_t^{k_1}, k_2+\theta_t^{k_2}, t+\Delta t).$

(21)

Substituting (19) into (21), we have

$L(t)F(k_1, k_2, t) + \Delta \hat{L}(k_1, k_2, t) = L(t+\Delta t)F(k_1+\theta_t^{k_1}, k_2+\theta_t^{k_2}, t+\Delta t),$

(22)

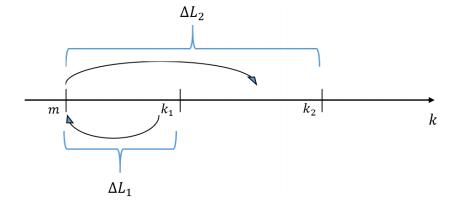
where, $\theta_t^k$, as described in Section 2, is the increased degree of the node at time $t+\Delta t$ whose degree is $k$ at time $t$. $\Delta \hat{L}(k_1, k_2, t)$ is consists of two parts, shown in Figure 4, one part is the directed edges which point to the new node, denoted as $\Delta L_1$. $\Delta L_1$ is equal to the accumulation number of new edges connected nodes with degree from $m$ to $k_1$. The other part is the directed edges emitted by the new node, denoted as $\Delta L_2$. Similar to $\Delta L_1$, $\Delta L_2$ is equal to the accumulation number of new edges connected nodes with degree from $m$ to $k_2$. So we have the expression $\Delta \hat{L}(k_1, k_2, t)=\Delta L_1+\Delta L_2$. Where

$\Delta L_1=m\Delta t\frac{\int_{m}^{k_1}kN(t)p(k, t)\, dk} {\int_{m}^{\infty}kp(k, t)N(t)\, dk},$

(23)

and

$\Delta L_2=m\Delta t\frac{\int_{m}^{k_2}kN(t)p(k, t)\, dk} {\int_{m}^{\infty}kp(k, t)N(t)\, dk}.$

(24)

In the above two equations, $m\Delta t$ represents the number of added directed edges which are point to or emitted by the new node. $\Delta L_1$ and $\Delta L_2$ are piecewise functions due to the $p(k, t)$ is a piecewise function. Now we only calculate the directed edges between the young nodes, $m < k_1, k_2 \leq m\left( 1+\frac{mt}{l_0}\right)^{\frac{1}{2}}$, which are added in the process of the evolution of the network not the initial nodes.

Substituting $L(t)=2(l_0+mt)$, $N(t)=m_0+t$, (9), (23) and (24) into (22), we have

$\begin{split} 2(l_0+mt)F(k_1, k_2, t)&+m\Delta t\left(2-\frac{m}{k_1}-\frac{m}{k_2}\right) \\ &= 2(l_0+mt+m\Delta t)F(k_1+\theta_t^{k_1}, k_2+\theta_t^{k_2}, t+\Delta t), \end{split}$

(25)

where $\theta _t^{k_i }= m\Delta t\frac{k_i }{2(l_0+mt)}$, $i\in 1, 2$. Taking the Taylor expansion for the right side of (25), both sides divided by $\Delta t$, and let $\Delta t \rightarrow 0$, finishing

$\begin{split} \frac{mk_1}{2(l_0+mt)}\frac{\partial F(k_1, k_2, t)}{\partial k_1} &+\frac{mk_2}{2(l_0+mt)}\frac{\partial F(k_1, k_2, t)}{\partial k_2} +\frac{\partial F(k_1, k_2, t)}{\partial t} \\ &+\frac{m}{l_0+mt}\left(F(k_1, k_2, t) +\frac{m}{2k_1}+\frac{m}{2k_2}-1\right)=0, \end{split}$

(26)

in the feasible region $D = \{(k_1, k_2, t)|m < k_1, k_2 \leq m\left( 1+\frac{mt}{l_0}\right)^{\frac{1}{2}}, t>0\}$. And the boundary conditions is

$\left\{\begin{array}{ll} F(k_1, m, t)=0, & \forall t> 0, m < k_1\leq m\left( 1+\frac{mt}{l_0}\right)^{\frac{1}{2}}, \\ F(m, k_2, t)=0, & \forall t> 0, m < k_2\leq m\left( 1+\frac{mt}{l_0}\right)^{\frac{1}{2}}. \end{array}\right.$

(27)

Using the characteristic line method to solve this boundary value problems, we get

$F(k_1, k_2, t)=1-\frac{m}{k_1} -\frac{m}{k_2} +\frac{m^2}{k_1k_2}.$

(28)

This joint cumulative distribution function applies only to the directed edges between the young nodes. The proportion of these directed edges to the total directed edges is $F\left(m\left(1+\frac{mt}{l_0}\right)^{\frac{1}{2}}, m\left(1+\frac{mt}{l_0}\right)^{\frac{1}{2}}, t\right)$, which is equal to $\left(1-\left(\frac{l_0}{l_0+mt}\right)^{\frac{1}{2}}\right)^2$, and this result tends to 1 when the time $t$ is large enough. So (28) can be seen as the joint cumulative distribution function of the total directed edges on the steady state.

Differentiating the (28) sequentially with respect to $k_1$ and $k_2$, we obtain the joint degree distribution

$p(k_1, k_2, t)=\frac{\partial^2F}{\partial k_2\partial k_1}=\frac{m^2}{k_1^2k_2^2}.$

(29)

From (29) we can see that the joint degree distribution $p(k_1, k_2, t)$ does not contain the time variable $t$, that is to say, the joint degree distribution does not vary over time $t$. So we denote $p(k_1, k_2, t)$ as $p (k_1, k_2)$.

For the joint degree distribution in (29), it is easy to verify that $p(k_1, k_2)$ satisfies the following three properties:

1. Symmetry, namely

$p(k_1, k_2)=p(k_2, k_1), \forall k_1, k_2 \geq m,$

(30)

2. Normalization, namely

$\int_m^\infty \int_m^\infty p(k_1, k_2)\, dk_2\, dk_1=1,$

(31)

3. Marginal distribution, namely

$q(k_2)=\int_m^\infty p(k_1, k_2)\, dk_1= \frac{m}{k_2^2},$

(32)

where $m$ denotes the minimum of node degrees. The marginal distribution $q(k)$ can be defined as the probability that a randomly chosen neighbor of a randomly chosen node will have degree $k$. $q(k)$ can be also regarded as the fraction of directed edges which send out by nodes of degree $k$. In general, the marginal distribution $q(k)$ is different from the degree distribution $p(k)$.

Now, we consider the conditional degree distribution $p(k_2|k_1, t)$, which is defined as the probability that a randomly chosen neighbor of a node of degree $k_1$ have degree $k_2$. From (9) and (29), we have

$p(k_2|k_1, t)=\frac{\langle k_t\rangle p(k_1, k_2, t)}{k_1p(k_1, t)} =\frac{m}{k_2^2} .$

(33)

From (33), we know that in BA growing network the conditional degree distribution $p(k_2|k_1)$ does not depend on the start nodes of degree $k_1$, only relates to the point nodes of degree $k_2$, and is equal to the marginal distribution of degree $k_2$ node $q(k_2)$. So we say the BA model has no degree correlations.

Next, we study the degree correlation of BA model by using the assortativity coefficient $C_{k_1, k_2}=\frac{\langle k\rangle N[k_1k_2]}{k_1[k_1]k_2[k_2]}$ in [10], which compares the true number of pairs of a given degree with the expected number of pairs connected at random. In the case of continuous degree, $[k_1k_2]$ represents the true density of pairs of $k_1$ -$k_2$ node, which equals to $L(t)p(k_1, k_2)$. $[k]$ represents the node density of degree $k$, which equals to $N(t)p(k, t)$. Substituting these into $C_{k_1, k_2}$, we have

$C_{k_1, k_2}=\frac{\langle k\rangle N[k_1k_2]}{k_1[k_1]k_2[k_2]}=1.$

(34)

From (34) we can get that the edge number of $k_1$ -$k_2$ pairs connected at random is equal to the actual number of edges. In other words, the BA networks have no degree correlations, which is of great significance in the study of network spreading dynamics.

---

4. The SIS model on degree uncorrelated networks based on the CDM

In addition to the structure of the network, we will use the CDM to study the epidemic spreading on static and growing networks, respectively.

---

4.1. The SIS model on static network

In order to establish a continuous degree SIS model on a static degree uncorrelated network, first, let each node exist only in two discrete states, susceptible or infected. We use $\hat{N}_{S}(k, t)$ and $\hat{N}_{I}(k, t)$ to represent the number of susceptible nodes and infected nodes whose degree is less than or equal to $k$ at time $t$. We use $F_S(k, t)$ and $F_I(k, t)$ to represent the cumulative distribution functions of susceptible nodes or infected nodes at time $t$. Thus their partial derivatives with respect to variable $k$, $p_S(k, t)$ and $p_I(k, t)$, represent the probability density of susceptible nodes or infected nodes at time $t$, respectively, namely the degree distribution. $p_S(k, t)$ or $p_I(k, t)$ can be regarded as the probability that a node randomly selected with degree $k$ and is susceptible or infected. They satisfy the following relations:

$\hat{N}(k, t)=\hat{N}_{S}(k, t) + \hat{N}_{I}(k, t),$

(35)

$\hat{N}_{S}(k, t)=N(t)F_S(k, t),$

(36)

$\hat{N}_{I}(k, t)=N(t)F_I(k, t),$

(37)

$F_S(k, t)=\int_0^k p_S(x, t)\, dx,$

(38)

$F_I(k, t)=\int_0^k p_I(x, t)\, dx.$

(39)

Then we consider the spread mechanism. At each time step, one susceptible node becomes infected node due to the contact with the infected neighbors, and the probability of each contact and infection with infected nodes is $\lambda$. At the same time, each infected node is cured and becomes susceptible state again with probability $\gamma$.

The epidemic spreading also satisfies the Markov property. So from time $t$ to time $t+\Delta t$, the state transition of $p_S(k, t)$ and $p_I(k, t)$ can be expressed as follows:

$\begin{cases} p_S(k, t+\Delta t) = \gamma \Delta t p_I(k, t) + (1-\lambda k \Theta_k \Delta t)p_S(k, t), \\ p_I(k, t+\Delta t) = (1-\gamma \Delta t) p_I(k, t) + \lambda k \Theta_k \Delta t p_S(k, t), \end{cases}$

(40)

where, $\gamma \Delta t$ is the recovery rate of infected nodes in time $\Delta t$, and $(1-\lambda k \Theta_k \Delta t)$ is the rate of not being infected of susceptible nodes in time $\Delta t$. $\Theta_k= \int_0^\infty p(x|k, t) \frac{p_I(x, t)}{p(x, t)}\, dx$ is the probability that an edge emitted by degree $k$ node points to an infected node. In a degree uncorrelated network, say, the BA network, the $\Theta_k$ will be $\Theta= \frac{1}{\langle k\rangle} \int_0^\infty xp_I(x, t)\, dx$. Transforming (40) and dividing by $\Delta t$ both sides, then let $\Delta t \rightarrow 0$, we get

$\begin{cases}\label{equ-41} \frac{\partial p_S(k, t)}{\partial t}= -\lambda k\Theta p_S(k, t) +\gamma p_I(k, t), \\ \frac{\partial p_I(k, t)}{\partial t}= \lambda k\Theta p_S(k, t) -\gamma p_I(k, t). \end{cases}$

(41)

This is the continuous degree SIS model on degree uncorrelated static networks. This model is corresponding to the discrete degree SIS model established by R. Pastor-Satorras and A. Vespignani in [22]. The essential difference is that the variable $k$ in this model is a continuous variable, but in other model variable $k$ is a discrete variable. So the range of variable $k$ in this model is the positive real numbers, not only positive integers.

Similar to the discrete degree SIS model, the spread threshold of epidemic is also equal to $c=\frac{\lambda \langle k^2\rangle}{\gamma \langle k\rangle}$. This means that if $c < 1$, the disease dies out, otherwise the disease spreads. On the BA static network this threshold is infinite, i.e., small amount of infected nodes can cause the outbreak of epidemics.

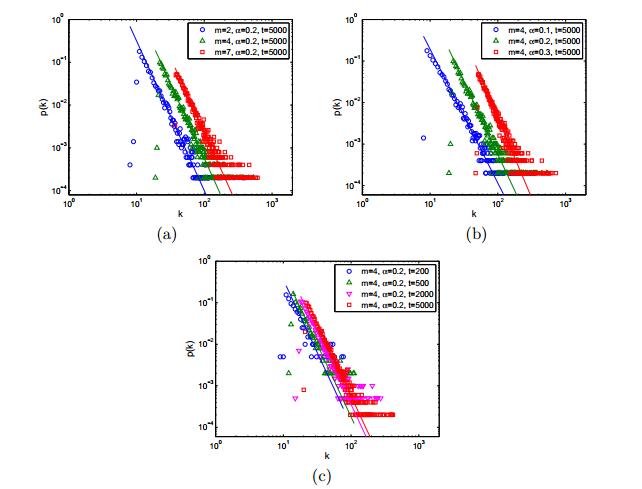
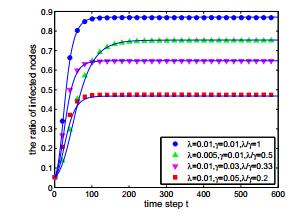
It is very difficult to obtain the analytical solution of (41). Take the BA static network as an example, we perform the simulations. As depicted in Figure 5, the stochastic simulations are in good accord with the numerical simulations. In Figure 5, We can also see that the smaller the ratio $\frac{\lambda}{\gamma}$, the smaller the infected proportion at steady state. This is obvious because both the small infected rate $\lambda$ and the big recovery rate $\gamma$ can prevent the spread of epidemic.

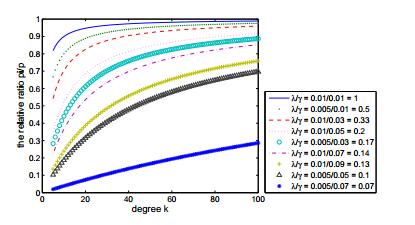
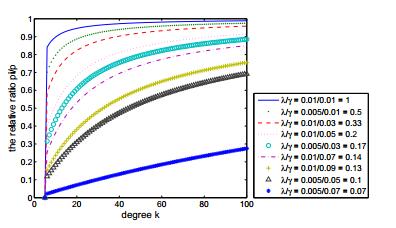
It is shown in Figure 6 that for a node the greater the degree, the greater the probability of being infected. This is easy to understand that the big degree nodes have more neighbors, so the infected neighbors are more, thus the ratio of infected will increase.

---

4.2. The SIS model on BA growing network

It is well known that many networks in reality are evolving constantly, not in the static state, such as the WWW and friends networks, which exist the addition or extinction of nodes and the disconnection or rewiring of edges. At the same time, the spread of epidemic is entangled with the network evolution. And the spread is also influenced by the network evolution. In this subsection we use the CDM to study the special BA growing network whose growth along simultaneously with the spread of epidemic, and establish the continuous degree SIS model on a BA growing network.

The evolution mechanism of growing network consists of three parts: the H1 H2 in Section 2.1 and the following H3. Note that the nodes before the time step $t_0$ are the susceptible, and the new nodes added at every time step are also the susceptible.

H3: Epidemic Spread: at time step $t_0$, there appears infected nodes. From this time on, the epidemic is propagated. namely there not only have the addition of new node to the network, but also have the epidemic spread. And the spread mechanism of epidemic is the same as the Section 4.1.

From the above evolution mechanism, we can know that before the time step $t_0$ this network is the same as the BA network. But after time step $t_0$, there appears the spread of epidemic. Therefore, we only study the network after time step $t_0$.

The notation $\hat{N}_{S}(k, t)$ and $\hat{N}_{I}(k, t)$ are the same as the Section 4.1. Let $\hat{L}_k^S(t)$ represent the number of directed edges which from susceptible $\hat{N}_{S}(k, t)$ nodes point to infected nodes at time $t$, $\hat{L}_k^S(t)=N(t)\int_m^k p_S(x, t) x \Theta \, dx$ where $\Theta$ is as described in Section 4.1. Based on (2), we consider the node state and the spread of epidemic, and exist

$\begin{cases} \hat{N}_{S}(k, t) - \Delta t \lambda \hat{L}_k^S(t) + \Delta t\gamma \hat{N}_{I}(k, t) + \Delta t = \hat{N}_{S}(k+\theta_t^k, t+\Delta t), \\ \hat{N}_{I}(k, t) + \Delta t \lambda \hat{L}_k^S(t) - \Delta t\gamma \hat{N}_{I}(k, t) = \hat{N}_{I}(k+\theta_t^k, t+\Delta t). \end{cases}$

(42)

Substituting (36), (37), and $\hat{L}_k^S(t)=N(t)\int_m^k p_S(x, t) x \Theta \, dx$ into (42), we get

$\begin{cases} \begin{split} N(t)F_S(k, t) &- \Delta t \lambda N(t)\int_m^k p_S(x, t) x \Theta \, dx \\ &+ \Delta t\gamma N(t)F_I(k, t) + \Delta t = N(t+\Delta t)F_S(k+\theta_t^k, t+\Delta t), \\ N(t)F_I(k, t) &+ \Delta t \lambda N(t)\int_m^k p_S(x, t) x \Theta \, dx \\ &- \Delta t\gamma N(t)F_I(k, t) = N(t+\Delta t)F_I(k+\theta_t^k, t+\Delta t). \end{split} \end{cases}$

(43)

Taking the Taylor expansion for the right-hand side of this equations, both sides of equations divided by $\Delta tN(t)$, then let $\Delta t \rightarrow 0$, we obtain

$\left\{ \begin{align} &\frac{mk}{2({{l}_{0}}+mt)}\frac{\partial {{F}_{S}}(k,t)}{\partial k}+\frac{\partial {{F}_{S}}(k,t)}{\partial t}+\frac{{{F}_{S}}(k,t)-1}{{{m}_{0}}+t} \\ &+\lambda \int_{m}^{k}{x}{{p}_{s}}(x,t)\Theta dx-\gamma {{F}_{I}}(k,t)=0, \\ &\frac{mk}{2({{l}_{0}}+mt)}\frac{\partial {{F}_{I}}(k,t)}{\partial k}+\frac{\partial {{F}_{I}}(k,t)}{\partial t}+\frac{{{F}_{I}}(k,t)}{{{m}_{0}}+t} \\ &-\lambda \int_{m}^{k}{x}{{p}_{s}}(x,t)\Theta dx+\gamma {{F}_{I}}(k,t)=0. \\ \end{align} \right.$

(44)

The sum of two equations in (44) is

$\frac{mk}{2(l_0+mt)}\frac{\partial (F_S+F_I)}{\partial k} + \frac{\partial (F_S+F_I)}{\partial t} + \frac{(F_S+ F_I)-1}{m_0+t}=0.$

(45)

Where $F_S$ is short for $F_S(k, t)$, and $F_I$ is the same. This equation is the same as (6) of BA growth without considering the nodes states. So we can know that $p(k, t)$ is the sum of $p_S(k, t)$ and $p_I(k, t)$ according to Section 2.

(44) contains the variables $p_S(k, t), p_I(k, t), F_S(k, t), F_I(k, t)$. In order to close the equations, we differentiate the equations both sides with respect to $k$, and get

$\begin{cases} \begin{split} \frac{mk}{2(l_0+mt)}\frac{\partial p_S(k, t)}{\partial k} + \frac{\partial p_S(k, t)}{\partial t} =&-\lambda \Theta k p_S(k, t) + \gamma p_I(k, t) \\ &-\left(\frac{m}{2(l_0+mt)}+\frac{1}{m_0+t}\right)p_S(k, t), \\ \frac{mk}{2(l_0+mt)}\frac{\partial p_I(k, t)}{\partial k} + \frac{\partial p_I(k, t)}{\partial t} =& \lambda \Theta k p_S(k, t) - \gamma p_I(k, t) \\ &- \left( \frac{m}{2(l_0+mt)}+\frac{1}{m_0+t}\right)p_I(k, t), \end{split} \end{cases}$

(46)

where $\Theta= \frac{1}{\langle k\rangle} \int_m^\infty xp_I(x, t)\, dx$. These differential-integral equations are the continuous degree SIS model on the BA growing network, they describe the evolution of degree distribution of susceptible and infected, respectively. According to the evolution mechanism of the network, we can know that the newly added node is susceptible, not the infected. Therefore, we have the following initial-boundary value conditions:

$\begin{cases} p_I(k, t_0)=p_I^\ast(k), \\ p_S(k, t_0)=p(k, t)-p_I^\ast(k), \\ p_I(m, t)=0, &\forall t>t_0, \\ p_S(m, t)=p(m, t), &\forall t>t_0 . \end{cases}$

(47)

As described in Section 4.1, the spread threshold of epidemic on static BA network is infinite, so the spread threshold of epidemic on BA growing network is also infinite if the growth is not very fast, namely, small amount of infected nodes can also cause the outbreak of epidemic.

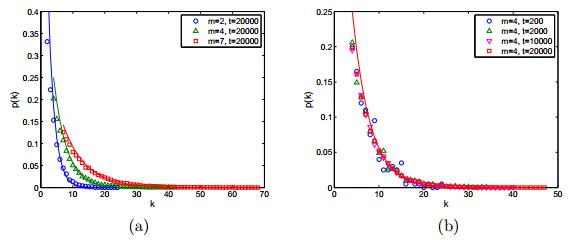
Solving analytically these equations is difficult, so we perform the following simulation. In Figure 7, we find that the big degree nodes have a relatively high probability of being infected, $\frac{p_I(k, t)}{p(k, t)}$, this is the same as the epidemic spread on static BA network.

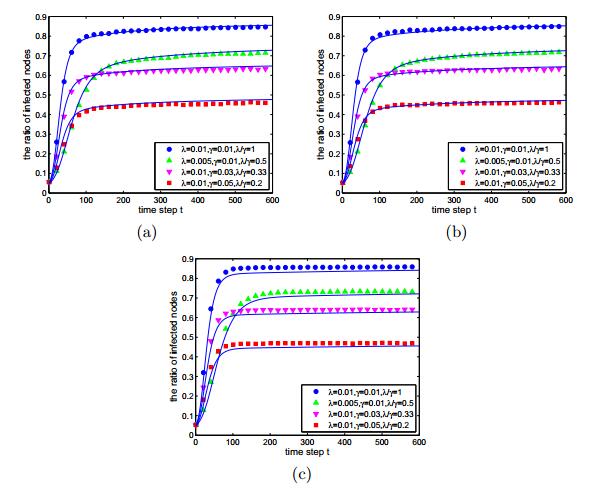
As depicted in Figure 8, the newly added health nodes can slightly reduce the ratio of infected nodes, but the final ratio of infected nodes will gradually tend to the final ratio of infected nodes of SIS model on static network. This result can also be obtained from (46), because that when time $t$ tends to infinity the autonomous system (46) will become non-autonomous system (41). In Figure 8(a) and 8(b), we can see after about 100 time steps that infected ratio will slowly rise, but in Figure 8 (c) the rise is not obvious. Hence, the larger the epidemic occurrence time $t_0$, the smaller the influence of network growth to the epidemic spread.

---

5. Conclusion

When a network reaches certain size, the node degree can be considered as a continuous variable, so we put forward the CDM to calculate the degree distribution. Using the CDM we calculate the degree distribution of the three growing models, which are the BA growing model, the preferential attachment accelerating growing model with $m$-varying and the random attachment growing model. Moreover, we also use CDM to calculate the joint degree distribution $p(k_1, k_2)$ of the BA growing model, the result reveals that the BA model has no degree correlations. In addition, the continuous degree SIS models on the static and growing networks are established via CDM.

Although the analytical solution of PDEs is usually difficult to obtain, there is some advantages of CDM, i.e., we can transform the evolution of network into a partial differential equation(s) on cumulative distribution function or probability density function, thus we can study analytically the structure of networks and the spread of epidemic on them.

In this paper, we use the CDM to calculate the topology structure of networks and establish the epidemic models on these networks. However, the evolution mechanism of networks in reality is very complicated. For example, a network may exist the addition or extinction of nodes, the disconnection or rewiring of edges, or even the both. When considering the state of nodes, the evolution of the nodes and edges may depend on the state of nodes, which are likely to occur in a real social network. E. g., the susceptible individuals may break the connection with infected, or rewire with other susceptible. Thus, with the CDM we will consider the following problems: (1) which topological structure can also be studied; (2) When we consider the state of nodes and the evolution mechanism of networks, how should we build the model in this case.

---

Acknowledgments

It is a pleasure to thank professor Zhenchao Han of Rutgers University for modification and guidance. This work was supported by National Natural Science Foundation of China under Grant Nos.11331009,11171314, TianYuan Special Foundation of the National Natural Science Foundation of China (11226259), Research Project supported by Shanxi Scholarship Council of China (2013-3), outstanding creative team of colleges and universities in Shanxi Province No. 232548901001, and sci-tech innovation team in Shanxi Province "The spread of infectious diseases prevention and control" No. 2015013001-06.

---