1. Motivation and preliminaries

Insulin secretion from electrically coupled $\beta$-cells is governed by bursting electrical activity. Pancreatic $\beta$-cells are a well-known example of emergent oscillations in interacting cell populations. The $\beta$-cells are organized into functional units of thousands of endocrine cells, called islets of Langerhans. There are recent works in the literature that support the $\beta$-cell behavior predicted by different models. In the context of $\beta$-cells organization in the islets, the reader is referred to [41], [31] and [43] and regarding the individual $\beta$-cell activity, the works [5] and [17] represent a particularly relevant combination between experiments and theory.

The membrane potential of these cells may experience a transition from bursting-spiking oscillations to continuous spiking oscillations, in the presence of a stimulatory level of glucose. The bursting behavior, firstly identified by Rinzel, consists of alternating active phases of spiking and quiescence whose particular form seen in $\beta$-cells is essentially of 'square wave' [40]. The bursting dynamics has been studied in the literature in a biophysical context (please see for instance [3], [4] and [24]). The electrical activity is of vital importance for the biophysical function of the cells since it governs oscillations in the intracellular calcium concentration, in particular it is the trigger for the release of the insulin hormone.

One of the first models for bursting dynamics was proposed by Atwater et al. [2]. It was based on extensive experimental data, incorporating the important cellular mechanisms that were thought to underlie bursting. Following this experimental work, Chay and Keizer developed a mathematical model for the ionic and electrical behavior of the pancreatic $\beta$-cells [6]. This model was reduced to a system of three variables and studied in terms of chaotic dynamics by Chay [7].

In a purely deterministic context and with the purpose of studying a geometrical mechanism for chaos generation, Bo Deng introduced a system that reproduces phenomenologically the glucose-induced electrical activity on the pancreatic $\beta$-cells [9]. The data were obtained experimentally by the technique of microelectrode recording and were regenerated mathematically by recording six time series taken from the work carried out in [42]. The researchers impaled a $\beta$-cell within an islet of Langerhans and measure the collective glucose-induced electrical activity of around 1000 cells.

A great deal of nonlinear systems, in particular the Deng bursting-spiking model, display different dynamical regimes depending on the systems parameters or external inputs. An important result in the field of nonlinear dynamics and chaos has been the discovery of different routes to chaos ([30] and [36]). These are periodic-chaos transitions which have received major attention in the literature. They make chaotic a non-chaotic system when a control parameter is changed and they may include: periodic-doubling cascades (taking place the Feigenbaum phenomenon), intermittency, the transition to chaos through a torus breakdown [35], among other dynamical regimes. Despite their importance, less attention has been devoted to the so-called chaos-chaos transitions in which relevant dynamical features of a chaotic attractor suddenly change with the variation of a control parameter. Specifically, when the changes on the control parameter occur in the neighborhood of a critical transition point, an abrupt qualitative change (or transition) in the dynamics may take place within the chaotic regime. This particular dynamical phenomenon has been identified as a type of interior crisis. In this context, the term 'crisis' means sudden increase or decrease in the size of a chaotic attractor as a system's control parameter passes through a certain threshold value. A remarkable study of crisis transitions in excitable cell models has been carried out by Fan and Chay in [15]. The analyzed dynamical systems represent the oscillatory behavior of membrane potentials observed in excitable cells such as pancreatic $\beta$-cells, neuronal cells and cardiac cells. The authors Fan and Chay examined the occurrence of the interior crisis in these systems, in particular the bursting-spiking transition in the Hindmarsh-Rose neuron model, by two means: (ⅰ) constructing bifurcation diagrams by numerically integrating the systems of differential equations and (ⅱ) computing the number of unstable periodic orbits embedded within the chaotic attractors, which suddenly increases or decreases at the crisis. Following this work, Fan and Chay showed in [16] that the topological entropy changes discontinuously when an interior crisis occurs in certain dissipative dynamical systems. In the context of chaos-chaos transitions, the bursting-spiking behavior of the Hindmarsh-Rose neuron model was also described by J. M. González-Miranda in [18] using different dynamical systems techniques.

After the mentioned work of J. M. González-Miranda [18], a similar transition was studied in a stochastic model of the electrophysiological behavior of the pancreatic $\beta$-cell [1], using similar methods and techniques of the theory of nonlinear dynamics and chaos, namely return maps, Poincaré maps, Lyapunov exponents and time series. Several results, related to the continuous interior crisis, have also been reported in the study of complex bifurcation structures in different types of excitable cells (in this context, please see [19], [20], [21], [45], [46] and [14]). It has been shown that the existence and extent of those complex bifurcation structures might be useful to understand the mechanisms used by neurons to encode information and give rapid responses to external stimuli. In particular, the dynamics of meaningful mathematical systems, when studied as a function of significant control parameters, can exhibit the continuous interior crisis [18], which provides a potential mechanism for quick responses by switching between different dynamical behaviors. The complexity of dynamical transitions, predicted by specific theoretical models of excitable systems, has also been demonstrated using experimental evidences (please see [22], [44], [38] and [23]). The experimental observations not only reveal the nonlinear dynamics of the complex firing patterns, of particular excitable biological systems, but also provide an experimental demonstration of the existence of bifurcations from bursting to spiking. This experimental approach represents a significant effort that contributes for the validation of the models, giving realism and significance to the obtained theoretical results. Indeed, the useful background information provided in the literature previously described, helps the progress of the research on excitable physiological systems, where abrupt changes of the dynamics, such as the interior crisis [18], can occur in response to a small system parameter modification.

Without doubt, the exploratory studies that have been conducted are important for the description of different dynamical behaviors. However, and to the best of our knowledge, no systematic integrated approach, involving simultaneously numerical algorithms and effective analytical methods for highly nonlinear problems like the Homotopy Analysis Method, has been adopted to explore the effect of key control parameters on abrupt qualitative changes (transitions) in the dynamics.

Inspired by the previously mentioned studies on the chaotic interior transitions, particularly by the work carried out by J. M. González-Miranda in [18], the goal of this article is to provide a contribution to the detailed analysis of a chaotic interior crisis of the Deng model [9], which is cast as a singularly perturbed system of ordinary differential equations. We will see that the abrupt change of the attractor size, when the system control parameters vary, is a key feature of the dynamics in the vicinity of the transition point. More precisely, in this work we present a description of the interior crisis, that corresponds to the transition between the bursting and the spiking dynamics in the chaotic regime, through a systematic and comprehensive study based simultaneously on: (ⅰ) time series variations within the crisis; (ⅱ) return maps, symbolic dynamics, invariant intervals; (ⅲ) topological invariants in the crisis regime and (ⅳ) analytical solutions triggering the bursting-spiking transition.

Starting with the study of time series variations, we continue with the analysis of appropriate return maps ([10] and [11]). The joined use of symbolic dynamics and amplitudes of invariant intervals associated to the mentioned return maps, becomes a new and elegant procedure to identify accurately the crisis transition point. The chaotic behavior characterizing the crisis is quantified with the computation of the topological entropy and the maximum Lyapunov exponent. A novel approach complements our study and deserves to be emphasized -the newly developed analytical solutions for the Deng bursting-spiking model [12] are particularly interesting and allow the construction process of a solution triggering the bursting-spiking transition. It is well-known that numerical algorithms allow us to analyze the dynamics at discrete points only and, in general, exact/closed-form solutions of nonlinear equations are extremely difficult to obtain. As a consequence, in recent years there has been a growing interest of many researchers in obtaining continuous solutions to dynamical systems by means of analytical techniques. One such general analytical technique used to get convergent series solutions of strongly nonlinear problems is the so-called Homotopy Analysis Method (HAM), developed by Shijun Liao (see, for instance, [27], [28] and [29]), with contributions of other researchers in theory and applications. The existence of the transition, here studied for the Deng bursting-spiking model, is of particular interest in biophysics, since it provides a mechanism that allows rapid switching between different relevant dynamical behaviors.

For the sake of clarity we briefly describe in the following subsection the main aspects of the studied Deng model.

---

1.1. Description of the Deng bursting-spiking model

The phenomenological Deng model, that mimics the glucose-induced electrical activity on pancreatic $\beta$-cells, is given by the following differential system

$\begin{array}{l} \frac{dC}{dt}=\epsilon \left( V-\rho \right) , \\ \\ \xi \frac{dN}{dt}=-r_{1}N^{3}+\Gamma _{1}N^{2}+\Gamma _{2}N+\Gamma _{3}NV-N^{2}V+ \\ ~~~~~~~~+\Gamma _{4}V+\Gamma _{5}, \\ \\ \frac{dV}{dt}=N_{\max }V^{2}+\Gamma _{6}V+r_{3}CVN-NV^{2}+\Gamma _{7}CV+ \\ ~~~~~~~~+\Gamma _{8}NV+\Gamma _{9}CN+\Gamma _{10}C+\Gamma _{11}N+\Gamma _{12} \end{array} \label{System}$

(1)

with

$\begin{align*} \Gamma _{1}& =N_{\max }r_{1}+V_{\max }+2r_{1}N_{\min }, \\ \Gamma _{2}& =-N_{\max }V_{\max }-2r_{1}N_{\max }N_{\min }-N_{\min }V_{\max }- \\ & ~~~~~-r_{1}N_{\min }^{2}-\eta _{1}, \end{align*}$

$\begin{align*}\Gamma _{3}& =N_{\min }+N_{\max }, \\ \Gamma _{4}& =-N_{\min }N_{\max }, \\ \Gamma _{5}& =N_{\min }N_{\max }V_{\max }+r_{1}N_{\min }^{2}N_{\max }\eta _{1}r_{2}, \\ \Gamma _{6}& =-2N_{\max }V_{\min }+r_{3}C_{\min }N_{\max }, \\ \Gamma _{7}& =-r_{3}N_{\max }, \\ \Gamma _{8}& =-r_{3}C_{\min }+2V_{\min }, \\ \Gamma _{9}& =-r_{3}V_{\min }, \\ \Gamma _{10}& =r_{3}V_{\min }N_{\max }, \\ \Gamma _{11}& =-V_{\min }^{2}+r_{3}C_{\min }V_{\min }-\eta _{2}-w, \\ \Gamma _{12}& =N_{\max }V_{\min }^{2}-r_{3}C_{\min }V_{\min }N_{\max }+\eta _{2}N_{\max }+ \\ & ~~~~+wN_{\min }, \end{align*}$

and

$r_{1}=\frac{V_{\max}-V_{spk}}{N_{\max}-N_{\min}},~\ r_{2}=\frac{N_{\max }+N_{\min}}{2},~r_{3}=\frac{V_{spk}-V_{\min}}{C_{\ast}-C_{\min}}.$

(2)

The three dynamical variables are:

(1):  the variable $C$ that corresponds to the intracellular calcium $Ca^{2+}$ concentration gradient;

(2):  the variable $N$ that measures the fraction of open potassium channels;

(3):  the variable $V$ that corresponds to the membrane voltage.

In a physiological context, the membrane voltage (also called transmembrane potential or membrane potential) is the difference in electric potential between the interior and the exterior of biological cells. In particular, the membranes of excitable cells are polarized or, in other words, exhibit a resting membrane potential. This means that there is an unequal distribution of ions on the two sides of the excitable cell membrane. The sign minus of a negative resting potential means that the inside is negative relative to (or compared to) the outside of the cell. A resting potential occurs when a membrane is not being stimulated. This resting state will be maintained until the membrane is disturbed or stimulated. The dynamic changes in the membrane potential in response to a sufficiently strong stimulus is called an action potential. The voltage arises from specific changes in membrane permeabilities for potassium, sodium, calcium, and chloride ions.

In the context of $\beta$-cells, voltage gated calcium ion channels and ATP-sensitive potassium ion channels are embedded in each cell surface membrane. These ATP-sensitive potassium ion channels are normally open and the calcium ion channels are normally closed. Potassium ions diffuse out of the cell, down their concentration gradient, making the inside of the cell more negative with respect to the outside (as potassium ions carry a positive charge). At rest, this creates a potential difference across the cell surface membrane of -70 mV (millivolts). When the potential difference across the membrane becomes more positive (as potassium ions accumulate inside the cell), this change opens the voltage-gated calcium channels, which allows calcium ions from outside the cell to diffuse in and down their concentration gradient. In physiology, a concentration gradient (particularly, the concentration gradient of the dynamical variable $C$) results from an unequal distribution of ions across the cell membrane. The sign minus of a negative concentration gradient means that the inside is negative relative to (or compared to) the outside of the cell. Membrane voltage and concentration gradients are noteworthy and eye-catching features of the excitable cells behavior.

The parameters are: $w$, $N_{\min}$, $N_{\max}$, $V_{\min}$, $V_{\max}$, $V_{spk}$, $C_{\min}$, $C_{\ast}$, $\eta_{1}$, $\eta_{2}$, $\xi$, $\epsilon$ and $\rho$. The parameters $\eta_{1},$ $\eta_{2}$, $\xi$ and $\epsilon$ are non-negative small parameters, which control the singular perturbation processes of the model.

The particular parameter $\rho$ is central in our study and it represents the glucose concentration of the system. For further information concerning the biophysical significance and meaning of the variables and parameters, the reader is referred to the papers [9] and [10]. Later on, in the interpretation of the obtained results, we will devote special attention to the $\beta$-cells activity in the production of insulin and to the role of glucose level in the bloodstream.

---

1.2. Numerical simulations. The bursting and spiking regimes

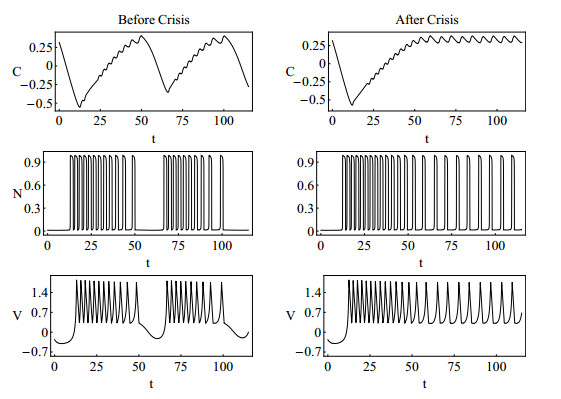
At this moment of our study, we can gain some insights about the geometry of the trajectories in the long run by numerically integrating the Deng system (1). Using the StiffnessSwitching NDSolve method from MATHEMATICA 10.0, which is regarded as one of the powerful techniques for numerically computing highly accurate solutions of differential equations, a structure emerges when the solution $\left(C(t),N(t),V(t)\right)$ is visualized as a trajectory in three-dimensional space (see an example of the chaotic attractor in Figure 1(a)). Depending on the value of parameter $\rho,$ the wave forms of the temporal behavior of variable $V$ demonstrates two qualitatively different regimes, namely bursting oscillations and spiking oscillations. These two types of behaviors are respectively displayed in Figure 1(b) and in Figure 1(c).

The bursting oscillations alternates between the silent phase and the active phase and occurs for lower values of $\rho$. The spiking oscillations correlate well with insulin secretion and we expect that the higher the glucose concentration, the longer the period of time a typical trajectory spends in the active phase, therefore giving way to continuous spiking [2]. This regime occurs for higher values of $\rho$ near $V_{\max }$.

In our study we will use throughout standard values of the parameters suggested in [10], $w=1.0,$ $N_{\min }=0.0,$ $N_{\max }=1.0,$ $V_{\min }=-0.5,$ $V_{\max }=2.0,$ $V_{spk}=0.0,$ $C_{\min }=-0.5,$ $C_{\ast }=0.0,$ $\eta _{1}=0.05,$ $\eta _{2}=0.05,$ $\xi =0.005,$ and we will consider $\rho$ and $\epsilon$ as the control parameters. The dynamics is studied for these particular values of the parameters due to the fact that the time series of the membrane voltage match very well with the experimental membrane records in the literature ([9] and [10]). As we stated earlier, the parameter $\rho$ is the glucose concentration and $\epsilon$ is one of the parameters that controls the singular perturbation processes of the model. In our analysis we consider $0.42\leq \rho \leq 0.642$ and $0.05\leq \epsilon <1$, since the interior glucose-induced crisis can be clearly observed for these ranges of the control parameters.

After the previous considerations, we are able to provide a description of the interior crisis. In Figure 2, we exhibit the time series of the three model variables before and after the studied interior glucose-induced crisis that we are going to analyze.

---

2. Interior crisis in the Deng bursting-spiking system

At this moment, particularly inspired by the work carried out by González-Miranda in [18], we are able to present in this section numerical evidences and theoretical reasoning which show that the Deng system for pancreatic $\beta$-cells is able to undergo a continuous interior crisis when the transition from bursting to spiking dynamics occurs. The detailed description of the crisis mechanism at the transition point is provided by means of: (ⅰ) time series ranges of variations; (ⅱ) amplitudes of invariant intervals and symbolic dynamics associated to a family of unimodal iterated Poincaré return maps (making possible a more accurate identification of the crisis transition point); (ⅲ) computation of topological invariants (namely, the topological entropy and the maximum Lyapunov exponent).

For a bursting-spiking system in general, and in particular for the Deng system, it is convenient to study the dependence of the intracellular calcium concentration gradient, $C(t)$, on the control parameters since to each relative maximum of $C(t)$ corresponds a spike (a peak) in the time series of the membrane voltage $V(t)$. As a consequence, the study of $C(t)$ is simultaneously elegant and representative of the noteworthy and eye-catching features of the dynamics.

---

2.1. Time series variations within the crisis

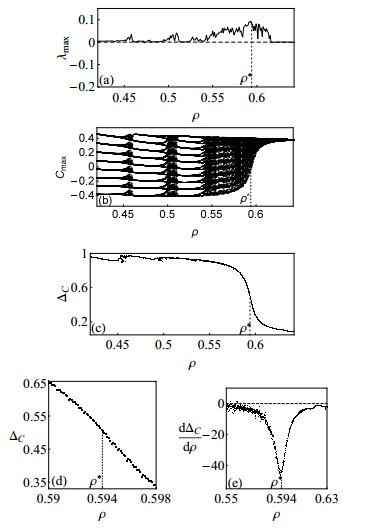
To start with, we present in Figure 3(a) numerical results for the maximum Lyapunov exponent (according to the procedure explained in a following subsection dedicated to topological invariants) and in Figure 3(b) the bifurcation diagram given from the consecutive relative maxima, $C_{\max }$, reached by $C(t)$ when $\epsilon =0.08$ and $0.42\leq \rho \leq 0.642$. As we are about to realize, the displayed results of Figure 3 provide clear evidence of a key dynamical feature -the Deng system's attractor undergoes a sudden change around $\mathit{\rho =\rho }^{\ast }\mathit{ \approx 0.594}$. By coincidence, the largest Lyapunov exponent attains a maximum $\lambda _{\max }\approx 0.1$ for $\rho ^{\ast }\approx 0.594$. In fact, the abrupt qualitative transition around $\rho ^{\ast }\approx 0.594$ when $\rho$ increases, as seen in the bifurcation diagram, bears a fast decrease of the size of the three-dimensional attractor and does affects the nature of the dynamics. As far as this aspect is concerned, Figure 3(c) is particularly insightful, where the values of range of variation of $C(t)$, $\Delta _{C}=C_{Max}-C_{Min}$ (difference between the absolute maximum ($C_{Max}$) and absolute minimum ($C_{Min}$) of $C$), appear as a function of $\rho$ (similar results (not shown) have also been obtained for $N(t)$ and $V(t)$).

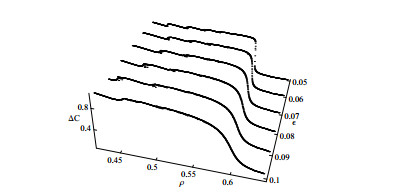
As also described in [18] for the Hindmarsh-Rose neuron model, the three-dimensional attractor decreases in size along a curve which displays a inflection point (in our case at $\rho =\rho ^{\ast }\approx 0.594$), which is identified as the transition point for $\rho .$ This sudden continuous change is called continuous interior crisis. In order to get a more complete characterization of the chaos-chaos transition, the function $\Delta _{C}(\rho )$ and its derivative $d\Delta _{C}(\rho )/d\rho$, have been displayed in a narrow interval $[0.590,0.598]$, a close neighborhood around the transition point (Figure 3(d) and Figure 3(e)). In all situations, we have found a value for the transition point around $\rho ^{\ast }\approx 0.594$. This detailed study of the time series of $C(t)$ suggests that the crisis implies deep and significant variations in the dynamical properties before and after the crisis transition. A 3D-representation of functions $\Delta _{C}(\rho )$ for different values of $\epsilon$ is depicted in Figure 4. Naturally, to each curve corresponds a particular transition pair $\left( \rho ^{\ast },\epsilon ^{\ast }\right)$ of control parameters.

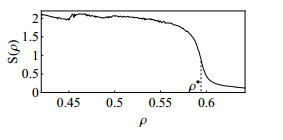
After the previous considerations, let us establish a dynamical measure $S(\rho)$ given by the product

$S(\rho)=\Delta_{C}(\rho).\Delta_{N}(\rho).\Delta_{V}(\rho)\text{,}$

where $\Delta_{C}(\rho)=C_{Max}(\rho)-C_{Min}(\rho)$, $\Delta_{N}( \rho)=N_{Max}(\rho)-N_{Min}(\rho)$ and $\Delta_{V}(\rho)=V_{Max}( \rho)-V_{Min}(\rho)$. The quantity $S(\rho)$ represents the volume of a rectangular parallelepiped whose boundary surfaces enclose a 3D set where the attractor could be placed in. This volume provides us direct quantitative insights about the system's trajectories in the three-dimensional space. This strategy allows us to work with dynamical features, such as shrinking and enlargement of the attractor, which represent different states of the informally called 'size of the attractor'. In Figure 5, we represent the variation of $S$ with the parameter $\rho$. As expected, the function $S(\rho)$ has the same key dynamical features of $\Delta_{C}(\rho)$, depicted in Figure 3(c). In particular, with the curve corresponding to $S(\rho)$, we are also able to find the approximation for the crisis transition point, $\rho=\rho^{\ast}\approx0.594...$.

---

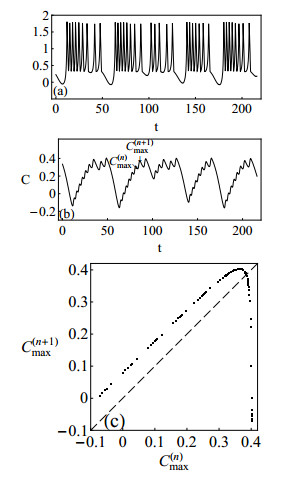
2.2. Return maps, symbolic dynamics and invariant intervals. The crisis transition point

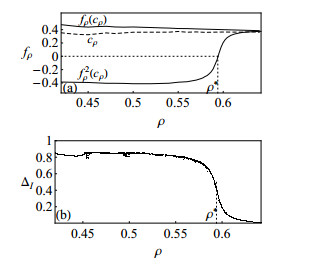
In order to gain more significant qualitative insights into the principles and mechanisms underlying the interior crisis, we analyze in this paragraph a family of unimodal maps which are low-dimensional maps that incorporate representative dynamical properties of the phenomenon (logistic-like maps presented in [10] and [11]). These maps are constructed by recording the successive relative (local) maxima of the numerical solution $C(t)$ and by considering pairs $(C_{\max}^{(n)},C_{ \max}^{(n+1)})$, where $C_{\max}^{(n)}$ denotes the $n^{th}$ local maximum. As mentioned previously, each local maxima corresponds to a peak in the membrane voltage time series. (please see Figures 6(a) and 6(b)). As shown in Figure 6(c), the data from the chaotic time series appear to fall on a logistic curve. Indeed, treating the graph as a function $C_{\max}^{(n+1)}=f(C_{\max}^{(n)})$ allow us to reveal particularly interesting features about the dynamics on the attractor. The obtained iterated maps dynamically behave like unimodal maps, which have found significant applications on symbolic dynamics theory. In this context, a unimodal map $f$ on the interval $I=\left[ a,b\right]$ is a two-piecewise monotone map with one turning point $c_{\rho}.$ The interval $I$ is then subdivided into the sets:

$I_{L}=[a,c_{\rho}[\text{, }I_{C_{\rho}^{\ast}}=\{c_{\rho}\} \text{,} I_{R}=]c_{\rho},b]\text{,}$

in such way that the restriction of $f$ to interval $I_{L}$ is strictly increasing and the restriction of $f$ to interval $I_{R}$ is strictly decreasing (see Figure 6(c)). Beginning with the turning point of $f$, $c_{\rho}$ (relative extremum), we obtain the orbit

$O\left( c_{\rho}\right) =\left \{ x_{i}:x_{i}=f^{i}\left( c_{\rho}\right) , \text{ }i\in \mathbb{N}\right \} .$

The turning point $c_{\rho }$ plays an important role. The dynamics of the interval is completely characterized by a symbolic sequence associated to the turning point orbit. The ordered sequence of elements $x_{i}\ $of $O\left( c_{\rho }\right)$ determines the dynamical invariant interval $I=\left[ f^{2}(c_{\rho }),f(c_{\rho })\right] =\left[ x_{2},x_{1} \right]$. The variation of the extrema of these invariant intervals (leftmost and rightmost points), for $\rho \in \lbrack 0.42,0.642]$, are depicted in Figure 7(a).

Now, let us take the previous considerations in the context of the interior crisis. Interestingly, the graph of the amplitudes of the invariant intervals $I$ as a function of $\rho$, $\Delta _{I}\left( \rho \right)$, represented in Figure 7(b), has the same key features of $\Delta _{C}(\rho )$, depicted in Figure 3(c). In particular, with the curve corresponding to $\Delta _{I}\left( \rho \right)$, we are also able to obtain the approximation for the transition point $\rho =\rho ^{\ast }\approx 0.594$, within the interior crisis. This detailed characterization of the invariant intervals of the form $I=\left[ f^{2}(c),f(c)\right]$, constructed using the return maps, also suggests that the crisis implies deep and significant variations in the attractor dynamical properties along the crisis transition. Each curve corresponding to $\Delta _{I}\left( \rho \right)$ provides us with precisely the same transition pairs of control parameters $\left( \rho ^{\ast },\epsilon ^{\ast }\right)$ obtained with the curves $\Delta _{C}(\rho )$. Given the importance of the transition points, it is crucial to focus our attention on a procedure for their computation. Remarkably, the transition occurs for $\rho$ and $\epsilon$ corresponding to $f^{2}(c_{\rho })=0$ (please see the dotted line represented in Figure 7(a)). Having stated this, an elegant, effective and accurate method of solving the equation $f^{2}(c_{\rho })=0$, i.e., a way of determining a transition point, arrives with the use of symbolic dynamics theory. Specifically, taking a return map (Figure 6(c)), we associate to the orbit $O\left( c_{\rho }\right)$ a sequence of symbols, $S=S_{1}S_{2}$, where $S_{j}\in \mathcal{A}=\{L,O,R\}$ and

$\begin{array}{c} S_{j}=L\;\;\;\text{if}\;\;\;f^{j}\left( x\right) <0 \\ S_{j}=O\;\;\;\text{if}\;\;\;f^{j}\left( x\right) =0 \\ S_{j}=R\;\;\;\text{if}\;\;\;f^{j}\left( x\right) >0\text{.} \end{array}$

Naturally, $S_{1}$ is associated to the iterate $f(c_{\rho })$ and $S_{2}$ is associated to the iterate $f^{2}(c_{\rho })$. The symbolic sequences $S$ are always of the form $S=RS_{2}$. Given a particular return map, the solution of $f^{2}(c_{\rho })=0$, in terms of $\rho$ and $\epsilon$, is obtained recording the sequences $S=RS_{2}$, varying $\rho$ (or $\epsilon$), and picking up the value of $\rho$ (or $\epsilon$) corresponding theoretically to the sequence $S=RO$ (which in practice occurs after $S=RL$ and before $S=RR$) with a desired precision for $\rho$ (or $\epsilon$).

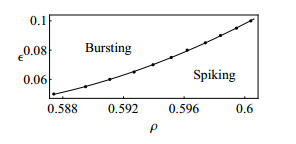
Using the previous procedure of symbolic dynamics theory, we are now able to provide a more accurate value for $\rho ^{\ast }$ (or $\epsilon ^{\ast }$) in the context of the chosen characterization of the interior crisis ($\epsilon =0.08$ and $\rho \in \lbrack 0.42,0.642]$). As a result, for $\epsilon =0.08$ we obtain the transition point $\rho ^{\ast }=0.59439...$. In Figure 8, we exhibit the transition phase diagram of the interior crisis for $\rho \in \lbrack 0.580,0.6004]$ and $\epsilon \in \lbrack 0.05,0.1]$. It is displayed a set of critical points in the $(\rho ,\epsilon )$-plane separating bursting from spiking dynamics. Interestingly, we have found out that the critical points follow the function $\epsilon (\rho )=120.19887\rho ^{2}-138.89324\rho +40.16240$. This identification allow us to establish a clear crisis transition between the two key dynamical behaviors of the Deng model -bursting and spiking regimes.

The outlined methodology for the description of the crisis provides us another illustration of the powerful and insightful use of low-dimensional maps incorporating representative dynamical properties of the phenomenon, in the context of symbolic dynamics theory.

---

2.3. Topological invariants in the crisis regime

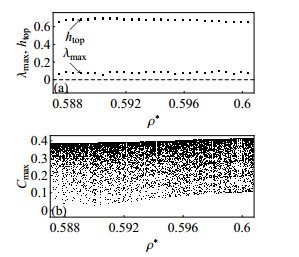
In this paragraph, we examine the degree of chaoticity of the Deng model, along the curve of critical points identified previously in Figure 8, by means of topological invariants with the computation of the topological entropy and the maximum Lyapunov exponent.

We start with by taking up the generalized problem of characterizing the chaoticity of the dynamics with symbolic dynamics theory considering an accurate estimate of the topological entropy, a central measure related to orbit growth.

Let us consider again the unimodal family of maps $f$ and the interval $I$ subdivided into the sets $I_{L}=[a,c_{\rho}[$, $I_{C_{\rho}^{\ast}}=\{c_{ \rho }\}$ and $I_{R}=]c_{\rho},b]$. As mentioned before, the function $f$ is monotonically increasing for $x\in I_{L}$ and monotonically decreasing for $x\in I_{R}$ (Figure 6(c)). We call a lap of $f$ each of such maximal intervals where the map $f$ is strictly increasing or strictly decreasing. The total number of distinct laps is called the lap number of The growth number$f$ and it is usually denoted by $\ell=\ell \left( f\right)$. The left and the right subintervals are labeled by the letters $L$ and $R$, respectively and the set $I_{C_{\rho}^{\ast}}$ will be denoted by $C^{\ast}$. The symbolic sequence starting from $f(c_{\rho})$ plays an important role in the symbolic dynamics of one-dimensional maps and it is called kneading sequence. Consequently, let us consider the orbit of the critical point of $f$, $O\left( c_{\rho}\right)$, obtained by iterating the map, that is, $O\left( c_{\rho}\right) =\left \{ x_{i}:x_{i}=f^{i}\left( c_{\rho}\right) ,\text{ } i\in \mathbb{N}\right \} .$ From this numerical orbit, $O\left( c_{\rho}\right) ,$ we get a symbolic sequence (symbolic orbit)

$S = {S_1}{S_2}...{S_j}...{\rm{, where }}\left\{ {\begin{array}{*{20}{l}} {{S_j} = L\;\;\;\;{\rm{if}}\;\;\;{f^j}\left( x \right) < {c_\rho }{\rm{,}}}\\ {{S_j} = {C^ * }\;\;\;{\rm{if}}\;\;\;{f^j}\left( x \right) = {c_\rho }}\\ {{S_j} = R\;\;\;{\rm{if}}\;\;\;{f^j}\left( x \right) > {c_\rho }} \end{array}} \right.,$

that characterizes the dynamics. When $O(c_{\rho})$ is a $k$-periodic orbit, we obtain a sequence of symbols that can be characterized by a block of length $k$, the kneading sequence $S^{(k)}=S_{1}S_{2}...S_{k-1}C^{\ast}$. The orbit $O\left( c_{\rho}\right)$, which is made of ordered points $x_{i}$, determines a partition $\mathcal{P}^{(k-1)}$ of the invariant range $I= \left[ f^{2}(c_{\rho}),f(c_{\rho})\right] =\left[ x_{2},x_{1}\right]$ into a finite number of subintervals labeled by $I_{1}$, $I_{2}$, ..., $I_{k-1}$. This partition is associated to a $(k-1)\times(k-1)$ transition matrix $M=[a_{ij}]$, where the rows and columns are labeled by the subscript of subintervals and the matrix elements are defined as $a_{ij}=1$ if $I_{j}\subset f\left( I_{i}\right)$ and $a_{ij}=0$ if $I_{j}\varsubsetneq f\left( I_{i}\right)$.

The topological entropy represents the exponential growth rate for the number of orbit segments distinguishable with arbitrarily fine but finite precision. This numerical invariant describes in a suggestive way the exponential complexity of the orbit structure with a single nonnegative real number [25]. For a system given by an iterated function, the topological entropy represents the exponential growth rate of the number of distinguishable orbits of the iterates. More precisely, the growth rate of the lap number of $f^{k}$ ($k^{th}$-iterate of $f$) is

$s\left( f\right) =\lim\limits_{k\rightarrow \infty}\sqrt[k]{\ell(f^{k})}$

and the topological entropy of a unimodal interval map $f$, denoted by $h_{top}\left( f\right)$, is given by

$h_{top}\left( f\right) =\log s\left( f\right) =\log \lambda_{\max}(M\left( f\right) ),$

where $\lambda_{\max}(M\left( f\right) )$ is the spectral radius of the transition matrix $M\left( f\right)$ ([33], [26] and [34]). The following example illustrates the computation of the topological entropy using the established procedure.

Example.   Let us consider the orbit of a turning point defined by the period-6 kneading sequence $(RLLLLC)^{\infty}.$ Putting the orbital points in order we obtain

${x_2} < {x_3} < {x_4} < {x_5} < {x_0} < {x_1}{\rm{ }}{\rm{.}}$

The corresponding transition matrix is

$M\mathcal{(}f\mathcal{)}=\left[ \begin{array}{ccccc} 0&1&0&0&0 \\ 0&0&1&0&0 \\ 0&0&0&1&0 \\ 0&0&0&0&1 \\ 1&1&1&1&1 \end{array} \right]$

which has the characteristic polynomial

$p(\lambda)=\det(M\mathcal{(}f\mathcal{)-}\lambda I)=1+\lambda+\lambda ^{2}+\lambda^{3}+\lambda^{4}-\lambda^{5}.$

The growth number $s(f)$(the spectral radius of matrix $M(f)$)is $1.96595...$. Therefore, the value of the topological entropy can be given by

$h_{top}\left( f\right) =\log s\left( f\right) =0.675975...\text{ .}$

The maximum Lyapunov exponent is a convenient indicator of the exponential divergence of initially close points, characteristic of the chaotic attractors ([32], [8] and [39]. A discussion about the Lyapunov exponents as a quantitative measure of the rate of separation of infinitesimally close trajectories, as well as a computation method, can be found in [37]. In the next lines, we will briefly explain the procedure used to compute the Lyapunov exponents. The characteristic Lyapunov exponents measure the typical rate of exponential divergence of nearby trajectories in the phase space, i. e., they give us information on the rate of growth of a very small perturbation of the initial state of the system.

Let us consider a set of nonlinear evolution equations of the form

$\frac{d\mathbf{x}}{dt}=\mathbf{F}\left( \mathbf{x},t\right) \label{SystemLyaps}$

(3)

where $\mathbf{x}=\left( x_{1},x_{2},...,x_{n}\right) \in \mathbb{R}^{n}$ $\left( n\geq 3\right)$ and $\mathbf{F}=\left( F_{1},F_{2},...,F_{n}\right)$ is a differentiable function. Assuming that the motion takes place in a bounded region of the phase space, we study the infinitesimal distance between two trajectories, $\delta \mathbf{x}(t)=\mathbf{x}(t)-\mathbf{x} ^{\ast }(t)$, which is regarded as a vector, $\mathbf{\eta }(t)=\left( \eta _{1}(t),\eta _{2}(t),...,\eta _{n}(t)\right) ^{T}$, satisfying the linear equation $\frac{d\mathbf{\eta }}{dt}=\mathbf{J}~\mathbf{\eta .}$ Solving this linear law over the time range $t_{0}\leq t\leq t_{f}$, we obtain a solution of vectors $\mathbf{\nu }_{i}(t)\in \mathbb{R}^{n}$ $\left( i=1,2,...,n\right)$. Now, let us consider orthogonal vectors to $\mathbf{ \nu }_{i}(t),$ with norm represented by $\mathcal{N}_{i}(j)$, for every time step $\tau =t_{j+1}-t_{j}$, $j=0,1,...,m$ and $m=\frac{t_{f}-t_{0}}{\tau }$. The Lyapunov exponents for the nonlinear system of differential equations are given by

$\lambda _{i}=\underset{m\longrightarrow +\infty }{\lim }\frac{\sum \limits_{j=1}^{m}\ln \mathcal{N}_{i}(j)}{m\tau }\;\;\;\;\;\left( i=1,2,...,n\right) . \label{Lyaps}$

(4)

In order to gain insights about the degree of chaoticity of the Deng model, along the curve of critical points identified previously in Figure 8, we display in Figure 9(a)the maximum Lyapunov exponent and the topological entropy, along the crisis transition curve. The positivity of the largest Lyapunov exponent and the positivity of the topological entropy are an indication that the system stays chaotic along this curve, i.e., a signature of chaos along the interior crisis transition between bursting and spiking regimes. Indeed, this fact justifies the designation 'chaos-chaos crisis'. As far as the computation of the topological entropy and the largest Lyapunov exponent are concerned, the reader is referred to additional illustrative examples provided in [11] and in [13].

The characterization of the crisis transition in the $(\rho,\epsilon)$-plane is complemented with the presentation in Figure 9(b) of a typical bifurcation diagram along the curve of critical points.

---

2.4. Interpretation of the results

As mentioned previously, parameter $\rho$ represents the glucose concentration of the system. Glucose is an important source of energy for the cells in our bodies, but it's too big to simply diffuse into the cells by itself. Instead, it needs to be transported into the cells. By facilitating glucose transport into cells from the bloodstream, insulin lowers blood glucose levels. When blood glucose levels start to rise, pancreatic $\beta -$cells quickly respond by producing and by secreting insulin. Therefore, the hormone insulin is responsible for regulating level of glucose in the blood.

A damage to the $\beta -$cells, can lead to increased levels of blood glucose. This can be due to insulin not being produced at all, or not in quantities sufficient to be able to reduce the blood glucose level. As important as insulin is to preventing too high of a blood glucose level, it is just as important that there not be too much insulin. Lower levels of glucose are associated to hypoglycemia and higher levels of glucose are a signature of hyperglycemia.

Glucose levels in the blood are usually measured in terms of milligrams per deciliter (mg/dl). The range of $\approx$70 to $\approx$105 mg/dl is commonly considered as normal. When the system is functioning properly, the pancreas continually monitors blood glucose levels and responds accordingly. The importance of insulin is juxtaposed with that of glucose. Both are required for life.

In the context of the interior glucose-induced crisis, the electrical activity of pancreatic $\beta -$cells exhibits a transition from a bursting regime to spiking regime.

As far as the Deng model is concerned, the glucose concentration $\rho$ is a value in the interval [0, 1], which can also be interpreted as a percentage of glucose in the bloodstream related to a particular threshold. A crisis critical value $\rho$*=0.59439... (obtained in the previous Subsection B) means that a concentration of glucose higher than 59, 439...% of the considered threshold represents a build-up of glucose in the blood and a situation of hyperglycemia. Taking into account that, for certain patients, a sustained concentration of 180 mg/dl is considered chronic hyperglycemia associated with damage to the blood vessels, heart attacks and death, a concentration of 59.439...% of this dangerous level of glucose (the threshold 180 mg/dl), corresponds, in fact, to a glucose concentration of 106, 9902... mg/dl, which can be taken as a starting concentration level of hyperglycemia (a concentration higher than the rightmost value of the considered normal range $\approx$70 to $\approx$105 mg/dl). The crisis can represent a failure in the production of insulin.

---

3. Analytical solutions triggering the bursting-spiking transition

Based on the newly developed analytical results for the Deng equations [12], we exhibit in this section explicit series solutions, focusing our attention on the membrane voltage $V(t)$, triggering the transition from bursting to spiking behaviors along the critical points within the interior crisis. In [12], the authors give all the details concerning the use of the homotopy analysis method (HAM) to construct the analytical solutions of the Deng equations (1). Here, for clarity reasons, we just provide the very last results of the HAM application to the Deng model.

According to the notations and definitions provided in [12], a $M^{th}$-order approximate analytic solution of the Deng equations (which corresponds to a series solution with $M+1$ terms) of practical interest is given by

$C_{M}(t)=C_{0}(t)+\sum \limits_{m=1}^{M}C_{m}(t), \label{approximationX1}$

(5)

$N_{M}(t)=N_{0}(t)+\sum \limits_{m=1}^{M}N_{m}(t), \label{approximationX2}$

(6)

$V_{M}(t)=V_{0}(t)+\sum \limits_{m=1}^{M}V_{m}(t), \label{approximationX3}$

(7)

where

$C_{m}(t)=\chi_{m}~C_{m-1}(t)+h~e^{-t}\int \limits_{0}^{t}e^{\tau}R_{1,m} \left[ \overrightarrow{u}_{m-1}\right] d\tau, \label{SolX1m}$

(8)

$N_{m}(t)=\chi_{m}~N_{m-1}(t)+h~e^{-t}\int \limits_{0}^{t}e^{\tau}R_{2,m} \left[ \overrightarrow{u}_{m-1}\right] d\tau, \label{SolX2m}$

(9)

and

$V_{m}(t)=\chi _{m}~V_{m-1}(t)+h~e^{-t}\int \limits_{0}^{t}e^{\tau }R_{3,m} \left[ \overrightarrow{u}_{m-1}\right] d\tau . \label{SolX3m}$

(10)

Defining the vector$\overrightarrow{u}_{m-1}=\left( C_{m-1}(t),N_{m-1}(t),V_{m-1}(t)\right) ,$ we have

$\begin{array}{c} R_{1,m}\left[ \overrightarrow{u}_{m-1}\right] =\frac{dC_{m-1}(t)}{dt} -\epsilon V_{m-1}(t)+\left( 1-\chi _{m}\right) \epsilon \rho , \\ \\ R_{2,m}\left[ \overrightarrow{u}_{m-1}\right] =\xi \frac{dN_{m-1}(t)}{dt}+ \\ \\ +r_{1}\sum \limits_{k=0}^{m-1}\left[ \left( \sum \limits_{j=0}^{k}N_{k-j}(t)~N_{j}(t)\right) N_{m-1-k}(t)\right] - \\ \\ -\Gamma _{1}\sum \limits_{k=0}^{m-1}\left( N_{m-1-k}(t)~N_{k}(t)\right) -\Gamma _{2}N_{m-1}(t)- \\ \\ -\Gamma _{3}\sum \limits_{k=0}^{m-1}\left( V_{m-1-k}(t)~N_{k}(t)\right) + \\ \\ +\sum \limits_{k=0}^{m-1}\left[ \left( \sum \limits_{j=0}^{k}N_{k-j}(t)~N_{j}(t)\right) V_{m-1-k}\right] - \\ \\ -\Gamma _{4}V_{m-1}(t)-\left( 1-\chi _{m}\right) \Gamma _{5} \end{array}$

and

$\begin{array}{c} R_{3,m}\left[ \overrightarrow{u}_{m-1}\right] =\frac{dV_{m-1}(t)}{dt}- \\ \\ -N_{\max }\sum \limits_{k=0}^{m-1}\left( V_{m-1-k}(t)~V_{k}(t)\right) -\Gamma _{6}V_{m-1}(t)- \\ \\ -r_{3}\sum \limits_{k=0}^{m-1}\left[ \left( \sum \limits_{j=0}^{k}N_{k-j}(t)~C_{j}(t)\right) V_{m-1-k}(t)\right] + \\ \\ +\sum \limits_{k=0}^{m-1}\left[ \left( \sum \limits_{j=0}^{k}V_{k-j}(t)~V_{j}(t)\right) N_{m-1-k}(t)\right] - \\ \\ -\Gamma _{7}\sum \limits_{k=0}^{m-1}\left( V_{m-1-k}(t)~C_{k}(t)\right) - \\ \\ -\Gamma _{8}\sum \limits_{k=0}^{m-1}\left( V_{m-1-k}(t)~N_{k}(t)\right) - \\ \\ -\Gamma _{9}\sum \limits_{k=0}^{m-1}\left( N_{m-1-k}(t)~C_{k}(t)\right) - \\ \\ -\Gamma _{10}C_{m-1}(t)-\Gamma _{11}N_{m-1}(t)- \\ \\ -\left( 1-\chi _{m}\right) \Gamma _{12}. \\ \end{array}$

In order to have an effective analytical approach of Eqs. (1) for higher values of $t$, we use the step homotopy analysis method (SHAM), in a sequence of subintervals of time step $\Delta t$, and we consider the $6$ -term SHAM series solutions ($5^{th}$-order approximations)

$C(t)=C(t^{\ast})+\sum \limits_{m=1}^{5}C_{m}(t-t^{\ast}), \label{SubApproximX1}$

(11)

$N(t)=N(t^{\ast})+\sum \limits_{m=1}^{5}C_{m}(t-t^{\ast}), \label{SubApproximX2}$

(12)

$V(t)=V(t^{\ast})+\sum \limits_{m=1}^{5}V_{m}(t-t^{\ast}). \label{SubApproximX3}$

(13)

at each subinterval. As an example, the SHAM initial terms of the series corresponding to $m=1$ and $m=2$, take the form

$\begin{align*} C_{1}(t)&=0.26625\epsilon h-0.26625\epsilon he^{-(t-t^{\ast})}+\epsilon \rho h- \\ & -\epsilon \rho he^{-(t-t^{\ast})}, \\ N_{1}(t)&=1.92621\ast10^{-6}h-1.92621\ast10^{-6}he^{-(t-t^{\ast})}, \\ V_{1}(t)&=0.0964916h-0.0964916e^{-(t-t^{\ast})}h, \end{align*}$

and

$\begin{align*} C_{2}(t)&=0.26625\epsilon h-0.26625\epsilon he^{-(t-t^{\ast})}-0.0964916\epsilon h^{2}+ \\ & +0.0964916\epsilon h^{2}e^{-(t-t^{\ast})}+\epsilon h\rho-\epsilon h\rho e^{-(t-t^{\ast})}+ \\ & +0.362742\epsilon h^{2}(t-t^{\ast})e^{-(t-t^{\ast})}+ \\ & +\epsilon h^{2}\rho(t-t^{\ast})e^{-(t-t^{\ast})} \\ N_{2}(t)&=1.92621\ast10^{-6}h-1.92621\ast10^{-6}he^{-(t-t^{\ast})}- \\ & -0.00104701h^{2}+0.00104701h^{2}e^{-(t-t^{\ast})}+ \\ & +0.00104702h^{2}(t-t^{\ast})e^{-(t-t^{\ast})} \\ V_{2}(t)&=0.0964916h-0.0964916he^{-(t-t^{\ast})}+0.033392h^{2}- \\ & -0.033392h^{2}e^{-(t-t^{\ast})}+0.0615503\epsilon h^{2}- \\ & -0.0615503\epsilon h^{2}e^{-(t-t^{\ast})}+0.231175\epsilon \rho h^{2}- \\ & -0.231175\epsilon \rho h^{2}e^{-(t-t^{\ast})}+ \\ & +0.0630997h^{2}(t-t^{\ast})e^{-(t-t^{\ast})}- \\ & -0.0615503\epsilon h^{2}(t-t^{\ast})e^{-(t-t^{\ast})}- \\ & -0.231175\epsilon \rho h^{2}e^{-(t-t^{\ast})}, \end{align*}$

with $t^{\ast}$ the time corresponding to the beginning of each interval. Identical changes occur naturally for the other terms. It's important to emphasize that in the explicit series solutions, the parameters $\epsilon$ and $\rho$ are our control parameters and $h$ is an artificial parameter that can be freely chosen to adjust and control the solution convergence region. This parameter $h$ has a key role on the homotopy analysis methodology. For additional explanations concerning the detailed construction of the analytical solution of the Deng model by means of HAM/SHAM, the reader is referred to [12] and references therein.

Let us consider again the glucose induced interior crisis. In order to obtain solutions triggering the chaotic bursting-spiking transition in the pancreatic $\beta$-cells system, along the curve corresponding to $\epsilon (\rho )$ of Figure 8, we establish a new function, called triggering function,

$T(\rho ,\delta )=\epsilon (\rho )+\delta \text{,}$

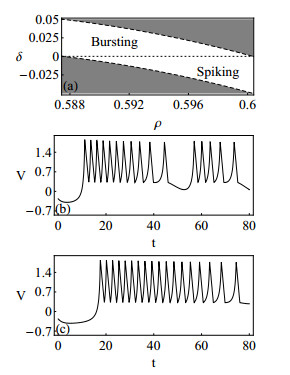
where $\delta$ is a switching parameter such that $\delta \in J_{\rho }=\left[ 0.05-\epsilon (\rho ),0.1-\epsilon (\rho )\right]$. According to Figure 10(a), which illustrates the variation of the interval $J_{\rho }$ with $\rho$ within the crisis, we obtain:

(ⅰ) the bursting regime for a positive value of $\delta$, such that $\delta \in \left] 0,0.1-\epsilon(\rho)\right]$;

(ⅱ) the spiking regime for a negative value of $\delta$, such that $\delta \in \left[ 0.05-\epsilon(\rho),0\right[$.

Now, considering the Solutions (11)-(13), we replace $\epsilon$ by the triggering function $T(\rho,\delta)$. This procedure allows us to obtain the derived analytical membrane voltage solution $V(t)$ for different values of $\delta$, in the established neighborhood of the crisis transition points. The bursting behavior is depicted in Figure 10(b) and the spiking behavior is shown in Figure 10(c). We emphasize that the triggering function, $T(\rho ,\delta),$ represents an elegant and effective context to perform the bursting-spiking transition, where simply positive values of $\delta \in J_{\rho}$ correspond to bursting behavior and negative values of $\delta \in J_{\rho}$ correspond to spiking behavior.

---

4. Final considerations

Phenomenological models developed to reproduce the behavior of excitable cell membranes have provided many nontrivial examples of dynamical behavior.

A chaotic transition from bursting to spiking behaviors has been identified as a crisis and analyzed by Fan and Chay in [15] and by González-Miranda for the Hindmarsh-Rose neuron model in [18]. Following the identification criteria of the bursting-spiking transition provided in [18], i.e. the existence of a drop in the size of the three-dimensional attractor, we presented in this article the observation of an interior glucose-induced crisis in the Deng model, which mimics the electrical activity of pancreatic $\beta$-cells. The description of the interior crisis in the Deng bursting-spiking equations presented here stands out to be relevant for the theory of chaotic nonlinear systems, particularly for the analysis of biophysical models. Indeed, the Deng model addresses interesting mathematical and physical questions. In the literature, the sharp chaos-chaos transitions, characterized by an abrupt reduction of the attractor size, are less represented. However, they are extremely important in the context of the theory of excitable systems. The existence of an interior crisis in the Deng model for pancreatic $\beta$-cells has potential applications in biophysics because it provides a switching mechanism by which a tiny change on a system's control parameter can toggle the dynamics between two significantly different dynamic regimes.

Our characterization of the chaotic bursting-spiking transition in the Deng model started with the study of the time series variations. This procedure allowed us to gain the first insights into the principles and mechanisms underlying the interior crisis, namely: the critical point and the narrow critical interval region around it. The largest Lyapunov exponent does not provide convincing and conclusive evidence for the occurrence of some interior crisis transitions (please see [15] and [16]). However, there are models for which the largest Lyapunov exponent attains a peak within the interior crisis. this coincidence does happen in the work of J. M. González-Miranda ([18]) and also in our study of the Deng bursting-spiking model. The introduction of iterated one-dimensional maps, related to the calcium dynamics, became extremely effective for the analysis of the crisis in terms of symbolic dynamics and invariant intervals. In particular, we were able to accurately identify a curve of critical points in a biophysically meaningful parameter space of $\rho$ (the glucose concentration) and of $\epsilon$ (a singular perturbation parameter). Interestingly, we found out that each transition point occurs when the second iterate of the map's turning point is equal to zero ($f^{2}(c_{\rho })=0$). The degree of chaoticity of the Deng system along the curve of critical points was characterized based on the computation of the topological entropy and the maximum Lyapunov exponent. The positivity of these numerical invariants are a signature of chaos along the interior crisis transition between bursting and spiking behaviors.

By means of explicit series solutions of the Deng equations presented in [12], we have created a triggering function, that tuned the system close the continuous interior crisis, with the property -small changes on this function produce very rapid changes in the temporal pattern of membrane voltage.

Given the nature of our work, using different tools for the characterization of the chaotic glucose-induced crisis in the Deng pancreatic β-cells system, we are lead to restate the natural applications of our study in different fields, namely: in biophysics, where bursting-spiking chaotic systems are common, or in chemistry, where chaos-chaos transitions frequently occur. Our systematic integrated approach, involving simultaneously numerical methods and analytical solutions given by effective methods for highly nonlinear problems like the HAM, brings novelty to our study and it is likely to inspire applications of the HAM analytical procedure for studying abrupt qualitative changes in nonlinear problems arising in theoretical biology, as well as in other fields of science. An exhaustive study into the dynamics essence of abrupt qualitative transitions, considering multiple parameter variation, together with an analytical methodology, is an avenue of future research.

---