An application of heuristic optimization algorithm for demand response in smart grids with renewable energy

Nomenclature

1.   Introduction

The escalating demand for electricity has been accompanied by a concerning rise in carbon and greenhouse gas emissions, posing significant environmental challenges and the potential for climate change ^[1]. In response to these pressing issues, regulatory bodies and policymakers have increasingly turned to renewable energy generation (REG) and demand response programs (DRP) to meet consumer needs while minimizing pollution emissions ^[2]. This shift has catalyzed the development of smart power grids (SPGs), which serve as platforms for the large-scale deployment of REG and DRP solutions. DRP initiatives come in various forms, with incentive-based and price-based programs being two prominent categories ^[3]. Incentive-based DRP entails direct load control by utility companies, while price-based programs incentivize consumers to adjust their energy consumption patterns in response to dynamic pricing signals ^[4,5]. Both approaches offer a range of benefits, including enhanced user comfort, reduced electricity bills, and decreased environmental impact.

Thus, in the literature, researchers have implemented DRP of SPG to achieve these benefits. For example, in ^[4], the authors used price-based DRP to schedule domestic appliances. Authors in ^[5] used various pricing DRP signals like critical peak pricing, time-of-use (ToU) scheme, real-time pricing (RTP), day-night, and combined RTP and inclining block tariff (RTP-IBT) to achieve objectives of power usage scheduling. ToU is a pricing scheme where energy price fluctuates according to the day time horizon and the associated demand levels. Typically, there are different rates for the peak, off-peak, and shoulder periods. Day-night is a pricing scheme that involves different electricity rates for day and night periods, encouraging consumers to shift energy-intensive activities to off-peak hours. RTP is a dynamic pricing scheme in which electricity rates are set based on actual market conditions in real time. Prices can fluctuate throughout the day based on factors such as supply and demand. This paper presents an RTP for the energy scheduler (ES) to effectively control the operation of household appliances, aiming to achieve an optimal operation schedule ^[6]. The ES aims to achieve the desired comfort level (refers to the shortest amount of time that an appliance may be delayed in its operation as part of a load scheduling) for residential users. A two-fold mechanism achieves the desired comfort level by operating appliances during their preferred operation hours and avoiding energy peaks and rebound peak formation on the load curve. Authors developed an energy management system (EMS) with hybrid energy sources and intelligent algorithms for optimal appliance operation scheduling using DRP to alleviate and curtail peaks in load demand via household load shifting ^[7].

Researchers programmed ES using a metaheuristic algorithm for scheduling load and energy under the DRP to achieve desired objectives. As an illustration, the particle swarm optimization (PSO) technique is developed in ^[8], which is used for community microgrids to minimize operation costs. However, one objective operational cost is addressed, and other interdependent objectives, such as pollution emissions and peak to average demand ratio (PADR), are ignored. In ^[9], PSO is developed to solve load scheduling and service microgrid on-site photovoltaic (PV) integration using batteries. Some authors have developed evolutionary algorithms to address power usage scheduling problems ^[10,11]. The authors developed an evolutionary algorithm to solve load-scheduling problems and achieve economic cost minimization, pollution minimization, peak curtailment, and user discomfort minimization ^[12]. A fuzzy inference system is developed in conjunction with a genetic optimization algorithm (GOA) to program the ES to maximize profit under the ToU pricing scheme within grid-connected microgrids ^[13]. In ^[14], authors defined a multi-objective optimization problem considering Pareto optimality. Stochastic search methods are implemented to drive viable potential solutions for decision variables. The evaluation demonstrates these methods' effectiveness in generating and preserving viable points during the solution determination, which is challenging for comparable methods. A multi-objective evolutionary algorithm is employed to address the formulated problem, resulting in the creation of a Pareto optimal DRP. Simulations indicate that the proposed method surpasses comparable approaches in terms of energy costs while achieving a satisfactory load factor. The authors in ^[15] developed a multi-objective home EMS with battery energy storage system (BESS), investigated the relationship between utility costs and the load elasticity index, and analyzed a few case studies. The results illustrate the correlation between load responsiveness/load elasticity and utility cost of homes. In addition, uncertainty/variability analysis is included to demonstrate robustness of the proposed control scheme. A GOA and its variants are utilized for energy cost and PADR reduction by optimal power usage scheduling of the residential load ^[16,17,18]. This study, with the support of SPG, adjusts generation and load, measures and monitors data, and transmits and distributes power for optimal energy management. The work ^[19] used a multi-objective genetic algorithm to address the load scheduling problem and explicitly considered the economic, technical, quality of service, and comfort aspects, focusing on multi-objective optimization in SPG. A home EMS utilizes the GOA to optimize household appliance load scheduling. The goal is to realize substantial cost savings while preserving user comfort through efficient operations ^[20]. In ^[21], an enhanced differential evolutionary algorithm (EDE) is developed for DRP between users and aggregators. The authors developed a combined PSO-Binary PSO algorithm in ^[22] for optimal demand-side management in SPG. In ^[23], the authors adapted the cuckoo search algorithm to maintain a balanced load curve by considering user preferences and constraints. In ^[24], the authors developed a hybrid heuristic algorithm to solve the multi-objective load scheduling problem to achieve economic and environmental benefits. The grey wolf and crow search optimization algorithm and grey wolf optimization algorithm are proposed for smart home appliances controlling, monitoring, and scheduling in ^[25,26], respectively. The aim is to reduce energy costs, increase savings and comfort, and reduce the PADR. In ^[27], Harris Hawk's algorithm-based ES is developed to solve the power scheduling problem of home appliances considering REGs and pricing DRP. The aim is to minimize the electricity bill, operation delay time, and PADR. However, the stated models cannot cater to the complexity and large-size load scheduling problems in a timely manner. Metaheuristic algorithms are most suitable for solving the load scheduling problem because they can handle the complexity and large size of the problem and can provide near-optimal solutions in a reasonable amount of time. However, they cannot guarantee the best solution's determination because of the dependence on the choice of parameters and quality of the initial solutions. Thus, to solve the above issues, the heuristic algorithm wind driven optimization (WDO) is improved, namely, crossover mutated enhanced wind-driven optimization (CMEWDO) algorithm, and ES is developed to solve the residential load scheduling problem in SPG.

The related work provides a solid foundation for comprehending the theme, offering various methods to tackle the power usage scheduling problem through DRP integrated with EMS in SPG. However, the existing literature on EMS primarily focuses on minimizing electricity bills from an economic perspective or reducing PADR from a load stability standpoint through DRP. The economic objective, specifically minimizing the electricity bill through load shifting, often results in rebound peaks and consumer discomfort. Conversely, the load stability objective, that is, PADR minimization, causes discomfort without addressing economic concerns. Many studies consider the variability of electricity prices, concentrating on economic objectives; few delve into the impact of household consumer behavior attributes to achieve load stability objectives. The literature is limited in addressing dual objectives involving both economic and peak load stability; notably, the tri-objective scenario still needs to be explored. The tradeoff between objectives and the issue of conflicting parameters in addressing load scheduling problems still needs to be solved. Merely considering one aspect, such as energy cost or PADR, and neglecting their conflicting aspects, such as rebound peaks and user discomfort, is inadequate. Therefore, a comprehensive model is imperative to address the load scheduling problem, demonstrating the capability of managing conflicting objectives simultaneously. Motivated by a commitment to resolve scheduling problems and tackle conflicting objectives, the ES is developed. The ES is programmed using the CMEWDO algorithm, aiming to provide an effective solution. The rationale behind the CMEWDO algorithm selection is due to its suitability for addressing the specific optimization challenges and objectives outlined in the research problem. Its enhanced exploration and exploitation capabilities, adaptability to complex problems, and previous success in similar applications make it a suitable choice for optimizing the operation of smart EMS in the context of load scheduling using DRP and solar PV to achieve desired objectives. The ES is based on the CMEWDO engages users in DRP facilitated by the utility, and ES offers dual benefits to both power suppliers and consumers: minimization of users' electricity bills and alleviation of peaks in the load-demand curve. The originality and primary technical contributions are highlighted below.

● According to the energy consumption characteristics, loads are modeled in three categories: time-regulating appliances (TRAs), power-regulating appliances (PRAs), and critical appliances (CAs), while considering consumer and utility constraints. This research indicates that enhancing the load flexibility in terms of both time and power to a certain extent facilitates peak load adjustment, load shifting, and load scheduling in the developed model.

● A generic energy management system is developed, where probability density function (PDF) is employed to predict solar irradiation to estimate REG accurately. The CMEWDO algorithm is proposed for ES to optimize the operation of REG, BESS, and load.

● The optimization problem is modeled as a minimization problem targeting economic objective, PADR, and user discomfort with simultaneous minimization for 2 scenarios both with and without REG.

The structure of this work is as follows: Section 2 introduces the methodology of this work, Section 3 showcases the simulations, and Section 4 presents the conclusion.

2.   Methodology

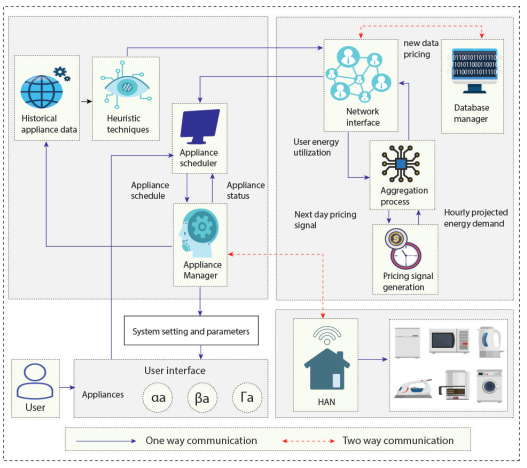
A framework for power usage scheduling is proposed to address the load scheduling challenge in SPG, aimed at mitigating PADR and reducing electricity bills while ensuring consumer comfort remains uncompromised. The developed framework includes ES, smart meters, advanced metering infrastructure (AMI), BESS, REGs, appliances, and controlling and monitoring displays, which is an adapted version of ^[28]. Illustrated in Figure 1, the framework's operation involves home users inputting appliance parameters and constraints through the user interface, which are then transmitted to the scheduling unit via the network interface. The ES, utilizing the CMEWDO algorithm, receives ToU-DRP signals along with appliance parameters and constraints from the network interface. Subsequently, the ES generates an optimized operation schedule for home appliances under ToU-DRP, considering both utility and user constraints. This operation schedule is then communicated to home appliances via the home area network. The management unit can facilitate monitoring and control throughout the scheduling process.

2.1.   AMI

AMI is a key technology of SPG, enabling consumers and utilities to actively participate in addressing load scheduling challenges within the electricity market. AMI is a comprehensive system with advanced metering devices, data management systems, and communication networks that facilitate bidirectional communication between the power supplier and power consumers. AMI performs main functions such as accurate and timely metering, real-time communication, data analytics, and load control while participating in SPG to solve load scheduling problems. It enables the utility to obtain energy consumption and other parameters and to communicate with consumers load management programs, incentives, and pricing in real-time. Furthermore, utility with AMI remotely controls and manages consumer load using DRP to balance supply and demand. In short, AMI plays a vital role in enabling the utility to monitor and manage energy consumption at the consumer level and enable the consumers to proactively engage in the energy market to resolve load scheduling and improve grid reliability, which benefits users and utility.

2.2.   Demand response program

DRP refers to the practice of adjusting electricity usage in response to variations in price or by offering incentives. This study considers a price-based DRP, encompassing various types, including RTP, day-ahead pricing (DAP), critical peak pricing (CPP), and ToU, as defined in ^[29]. Among these schemes, ToU is adopted in this work owing to its flexibility and dependence on the time of use. The daytime span, i.e., twenty-four hours, is divided into three levels: peak, mid, and low. The ToU is modeled and defined in Eq (2.1), which is obtained from ^[28].

where $\varphi_1$, $\varphi_2$, and $\varphi_3$ are tariffs for three defined levels, and ${T_1}, {T_2}, \& {T_3}$ are three periods against three levels, that is, low, high, and mid-price periods, respectively. The ES receives ToU-DRP, power operation pattern of appliances, and generation from REGs and power grid for generating power usage schedule.

2.3.   Solar PV energy generation

Among the renewable sources, solar energy is plentiful, easily available, and free. Thus, this study considered solar PV as an REG. The aim is to use solar energy to reduce electricity bills, PADR, etc. Solar energy is modeled and defined in (2.2) ^[30]. The symbols used in (2.2) defined as $\mathop E\nolimits^{pv}$ are generated output power, $\mathop \partial \nolimits^{pv}$ denotes solar system efficiency, and $\mathop A\nolimits^{pv}$ shows solar panel area. $rad\left(t \right)$ and ${Tp\left(t \right)}$ illustrate irradiation and temperature, respectively, and the temperature correction factor is constant and equal to 0.005. The PV is modeled in Eq (2.2), as in ^[30].

The utilization of the Weibull PDF for modeling solar irradiation is demonstrated in Eq (2.3), as referenced in ^[30]. The symbols used in Eq (2.3) are defined as follows: $\theta 1$ and $\theta 2$ illustrate the shape factors, $0 < rad(t) < \infty$, $\omega$ indicates the weight factor, and $\lambda 1$ and $\lambda 2$ represent the scale factors.

The ES uses the maximum available solar energy during high-price hours, and low-price hours charges BESS to minimize electricity bills.

2.4.   Battery as energy storage

BESS plays a vital role in modern energy systems, helps balance the power grid, improves reliability and resilience, and enables REG integration. Power usage scheduling with BESS involves charging batteries during periods of low demand, such as at night when many businesses are closed, and electricity usage is lower. The charged energy can then be discharged during periods of high demand, such as during hot afternoons when many people are running air conditioning units. By doing this, the BESS minimizes the peak electricity demand and alleviates the burden on the electrical grid, resulting in a more dependable and robust electric supply. The BESS is used to provide backup power during a power outage situation. For example, if a hospital has a BESS installed, it can use the charged energy to power critical systems during an outage, such as life support equipment, until the power is restored. In addition to load scheduling and backup power, BESS can also help integrate REGs, such as solar power, into the power grid. REGs are variable and intermittent. BESS is charged with excess energy during periods of high production and then discharged during periods of low production, providing a more stable and reliable source of energy. Thus, BESS remarkably curtails pollution emissions and notably alleviates electricity bills. In addition, the BESS exchanges power with the utility when the load demand is at its peak with the highest hours. The BESS is modeled and defined in Eq (2.4). The symbols used are defined as $BESS$, ${\mu ^{BESS}}$, $\eta$, ${E^{SOC}}$, representing the charged energy, efficiency, time duration, solar power supplied to BESS, and power discharged from BESS to load, respectively. The BESS is modeled in Eq (2.4), as in ^[30].

where ${E^{SOC}}$ is the state of charge (SOC) that defines BESS charging/discharging operations, which is modeled as follows:

Limits designed to resolve overcharging/deep discharging are presented as follows, likewise in ^[30].

The ES based on the CMEWDO algorithm receives the ToU-DRP, REGs, utility generation signal, user appliance operation pattern, and utility/user constraints for generating the appliance operation schedule.

2.5.   Residential load/appliances

The load is classified into three types based on operational behavior and demand requirements: TRAs, PRAs, and CAs. TRAs have two further categories: interruptible appliances (IAs) and uninterruptible appliances (NIA). IAs can have their operations delayed or interrupted by the ES, if necessary. They operate in separate time intervals, and interruptions do not affect task completion. Examples of IAs include washing machines (WM), clothing dryers (CD), and dishwashers (DW). Consumers operate WMs such that they can complete their tasks before the CD deadline or the DW may finish dishwashing before a certain time. NIAs can only be interrupted, shifted, or shut down once their operation is completed; only delays are possible prior to starting the operation.

PRAs is a category of smart appliances that possess adjustable power capabilities. They are designed to operate with minimum rated power during on-peak hours for electricity bills and PADR minimization while maintaining consumer comfort. These appliances are assigned a secondary priority.

PRAs, such as refrigerators, air conditioners, and dispensers, are time-inelastic because they operate continuously throughout the day. The PRAs are power elastic, whose operation is power regulating between the minimum, maximum, and rated power as per the constraints. CAs such as electric toasters (ET), electric kettles (EK), and microwave ovens (MO) are critical and cannot be interrupted in any condition. Table 1 presents the considered appliance parameters and specifications, which is adopted from ^[28].

For each appliance $i \in P, NIA, IA, \& CA$, we define the position $S_t^i = (r_t^i, w_t^i)$ at time slot t for power regulating, time regulating, and critical. Here, $r_t^i$ represents the remaining operation time slots for appliance $i \in P, NIA, IA, \& CA$, and $w_t^i$ represents the waiting time slots of appliance $i \in P, IA, NIA, \& c$. We define $X_t = { 0, 1}$ as an indicator that signifies the appliance's status, that is, whether the appliance is in the on/off state $(X_t = 1/0)$. By considering the current position $S_t^i$, the type of the appliance, and its status $X_t$, we can determine the status of the appliances in coming hours, denoted as $S_{t+1}^i$. The current and next status of PRAs, TRAs, and CAs are modeled one by one as follows, similarly in ^[28].

In the case of PRAs, the current and next status can be mathematically represented as follows, similarly as in ^[28]:

For IAs, there is flexibility to delay, interrupt, or shut down their operation as needed. This can be represented by the initial and subsequent statuses, similar to those described in ^[28].

An NIA can only tolerate delays and cannot be interrupted once their operation has begun until it is finished. The initial and subsequent time slot positions for NIAs can be illustrated similarly to those described in ^[28].

Continuous operation is required for CAs throughout the day. The positional evolution of both the initial and subsequent status for CAs is as follows, likewise in ^[28].

In the developed scheduling framework based on the CMEWDO algorithm, smart appliances interact with the ES based on the CMEWDO algorithm. The ES schedules the power usage pattern of appliances under ToU-DRP, REGs, and utility, subject to consumer and utility constraints. At the start of the scheduling period frame, each appliance $i$ submits a request to the ES-based CMEWDO algorithm. This request includes information about the appliance type (IAs, NIAs, PRAs, or CAs), along with the desired start and end times of its operation.

To calculate energy consumption, we assume that the collection of appliances is represented by $A$, which can be expressed as the union of four subsets: $A = { A^{IA} \cup A^{NIA} \cup A^{PRA} \cup A^{CA} }$. Here, $A^{IA}$ represents a set of appliances that can be interrupted, $A^{NIA}$ represents a set of appliances that cannot be interrupted, and $A^{CA}$ represents a set of appliances that are critical and must consistently operate. The time span denoted as $T_h$, ranging from 1 to 24, is the time frame in which all appliances are scheduled and subjected to constraints. The energy consumption of each appliance is calculated as follows:

The total consumed energy is determined by aggregating the individual energy consumption of all appliances, and the calculation is performed as follows:

where $\varepsilon_T$ denotes the net energy consumption.

The electricity bill refers to the payment that users need to submit to the utility company for utilizing electrical energy over a designated period. In this study, the electricity bill is calculated by considering ToU-DRP provided by the utility company. The formulation for the electricity bill that users pay to the utility company for the energy consumed using ToU-DRP is as follows:

The net electricity bill denoted as $\sigma$ and the ToU-DRP signal represented as $\varphi(t)$ are used to calculate the electricity bill. The electricity bill with REGs and BESS is determined as follows:

The ES is programmed using the CMEWDO algorithm to generate load operation schedules under the ToU-DRP, REGs, utility generation, utility and consumer constraints, and power usage patterns. The ES based on the CMEWDO algorithm shares created load operation schedules in real time with participating appliances using AMI.

2.6.   Proposed CMEWDO algorithm

This section covers the description of the developed CMEWDO algorithm. The ES is programmed using the CMEWDO algorithm to solve load scheduling problems to achieve desired objectives: electricity bill and PADR minimization without compromising comfort. The ES is programmed using the CMEWDO algorithm, aiming to provide an effective solution. The rationale behind the CMEWDO algorithm selection is due to its suitability for addressing the specific optimization challenges and objectives outlined in the research problem. Its enhanced exploration and exploitation capabilities, adaptability to complex problems, and previous success in similar applications make it a suitable choice for optimizing the operation of smart EMS in the context of load scheduling using DRP and solar PV to achieve desired objectives. The CMEWDO algorithm hyperparameters are summarized in Table 2. The CMEWDO algorithm is developed by improving the WDO algorithm via applying crossover and mutation rates on the global best result obtained from WDO. The inspiration for developing the CMEWDO algorithm is to achieve the desired objectives simultaneously: electricity bill and PADR minimization without compromising consumers' comfort. A detailed description of the CMEWDO is provided below. The WDO is a population-based stochastic optimization algorithm that solves load scheduling problems in SPG. The load scheduling problem involves determining the optimal scheduling of loads in the SPG to minimize electricity bills and PADR without compromising consumers' comfort. Step-wise details of WDO to solve the load scheduling problem are presented as follows:

Step 1: First, the power usage scheduling problem is defined, including the objective function, decision variables, constraints, and search space. The objective is to minimize the utility bill and PADR while ensuring that consumers' comfort remains uncompromised. The decision variables are the scheduling of loads over some time, while the constraints include the demand and supply balance, minimum and maximum limits on loads and generators, and ramping constraints.

Step 2: In the WDO, a population of wind parcels represents the candidate solutions to the optimization problem. The wind parcels are initialized with random positions and velocities within the search space. The parcel position shows a potential solution, while its velocity represents the direction and magnitude of the wind parcel's movement.

Step 3: The fitness of each wind parcel is evaluated using an objective function. In load scheduling, fitness is the system's electricity bill and PADR for a given parcel's position. The initial velocity is formulated using Eq (2.21).

Step 4: The velocity and position of each parcel are updated (see Eq (2.22) and Algorithm 1) based on its good position and the best-known position among all parcels in the swarm. This process fosters both the exploitation and exploration of the search space and promising regions. The updated position represents a new scheduling of loads over the period.

where $\alpha$ is the friction coefficient, $\nu_{old}$ is velocity in the previous iteration, $g$ is gravitational acceleration, $x_{old}$ is air parcel position in previous iteration, ${P_{max}}$ is maximum pressure, ${P_{old}}$ is air pressure in the previous iteration, $c = -2RT$ $R$ signifies the universal gas constant, and $T$ is temperature.

Step 5: The optimization process continues until a termination criterion is met, such as a maximum number of iterations or a satisfactory level of convergence. Convergence can be checked by monitoring the fitness of the best parcel in the swarm over time.

Step 6: Once the optimization is completed, the optimal solution is identified as the parcel with the best fitness value. The scheduling of loads and generation obtained from the best parcel represents the optimal solution to the load scheduling problem.

Step 7: The crossover and mutation operation (see Algorithm 2) are applied to the global result obtained from WDO to achieve the solution that satisfies all the constraints and consequences in the lowest electricity bill and PADR while maintaining consumers' comfort.

In summary, CMEWDO is used to solve load scheduling problems by initializing a population of parcels with random positions and velocities, evaluating fitness as per the objective function of all parcels, and updating the position and velocity of each parcel based on its own best-known position. Finally, the best solution found by the swarm is selected as the optimal generator schedule for the load-scheduling problem. This solution should satisfy all constraints, resulting in the lowest electricity bill and PADR while maintaining consumer comfort. The implementation of the developed CMEWDO algorithm is shown in Figure 3.

2.7.   Power usage scheduling problem formulation

This study aims to optimize electricity bills and PADR by power usage scheduling without compromising consumer comfort. Initially, each objective is formulated separately, after which the power usage scheduling problem is formulated as an optimization problem. The electricity bill pertains to the charges imposed by the utility company on consumer for energy utilized within a specific timeframe. The developed model computes electricity bills for both interruptible and uninterruptible appliances. The electricity bill in aspects of the cost of all appliances is modeled in Eq (2.20). In the subsequent equation, the notation is clarified as follows:

PADR is a metric that represents the ratio of peak to average demand within defined time periods. A decrease in PADR is advantageous for consumers and utilities since it minimizes the gap between electricity demand and generation. PADR is denoted by the symbol $\gamma$. The mathematical expression for PADR is given in Eq (2.25), as presented in ^[28], where $\varepsilon_{(t)}$ denotes the power consumed by the appliance.

The level of comfort experienced by consumers is influenced by various factors such as power consumption, delay, temperature, air quality, lighting, humidity, sound, and resident characteristics ^[28]. This study focuses on the consumer comfort associated with waiting time, specifically the delay users face when shifting their appliance usage from high to low-price hours. The appliance operation pattern differs pre- and post-scheduling because devices are operated during low-price time slots instead of high-price ones. Consequently, users may experience frustration, which is measured by waiting time/delay. As a tradeoff between electricity bills and waiting time, users who can afford to wait longer will incur lower bills, whereas those who cannot wait as long will pay higher electricity bills. Because there is a tradeoff between the utility bill and delay/waiting time, users who can wait longer will have lower bills, whereas those who cannot wait as long will have higher bills. Appliances with adjustable power settings have zero waiting time because they operate continuously within predefined 24-hours timeframes, contributing to scheduling via power flexibility. The consumer comfort related to waiting time is modeled below, similarly as in ^[28].

In the given context, the variable ${\kappa}$ represents the waiting time that each appliance $a$ may experience owing to the shifting of appliances. ${T_{a, t}^{o, unsch}}$ represents the operational status of the appliances before scheduling, whereas $T_{a, t}^{o, sch}$ represents the operational status of the appliances after scheduling. ${T_a^{lo}}$ refers to the total duration of the appliance's operation. The ES based on the CMEWDO adjusts and shifts the appliances from high to low price hours, considering ToU-DRP and consumer priorities. The determination of a maximum delay acceptable to a user is computed using the following formulation.

In the given equation, $\kappa^d$ represents the maximum acceptable delay that an appliance may face when transitioning its operation from high to low price hours, while $T_a^t$ represents the overall time interval for the appliance.

The consumer comfort is compromised as the maximum delay $\kappa^d$ increases. The discomfort experienced by the consumers reaches its peak when the actual waiting time $\kappa$ equals the maximum allowable delay $\kappa^d$. This represents the worst-case scenario, although it is not a common occurrence. The consumer discomfort, expressed as a percentage, is formulated as follows:

Load scheduling balances generation and demand to reduce electricity bills and PADR without compromising consumer comfort. To achieve these objectives, the power usage scheduling problem is formulated as an optimization problem, where the objective function is a weighted sum of the electricity bill, consumer comfort, and PADR.

The power usage scheduling problem presented in Eq (2.29) is subject to the following set of constraints.

The following constraints are imposed on the minimization problem described by Eq (2.29): Constraint (2.30a) ensures that the total PADR of the energy consumption must not exceed the capacity of the power grid, denoted by ${{\rm P}_c}$. This helps to prevent power shortages or blackouts. Constraint (2.30b) specifies a scheduling interval for the energy consumption. Constraint (2.30c) imposes a constraint on the load, ensuring that the power consumption with and without scheduling remains equal. Constraint (2.30d) imposes an appliance status to ensure the ON/OFF status of appliances must be equal in number with and without scheduling, but not be prior and post scheduling. Similarly, constraint (2.30e) ensures that appliance hours of operation with and without scheduling must be equal.

3.   Results and discussions

The developed framework with ES based on the CMEWDO technique simulation is conducted in MATLAB 2017b. Installed on a laptop, it has specifications: 12th Gen Intel(R) Core(TM) i5-1240P with processor 1.70 GHz and RAM 16GB. The ES of the developed framework is based on the CMEWDO compared with existing whale optimization algorithm (WOA), EDE, and WDO to validate the applicability of the developed framework. The developed framework solves the power usage scheduling problem in electricity bills and minimizes PADR while maintaining consumer comfort. The developed framework utilizes REGs and BESS to provide power to the utility during high price hours. The developed framework based on the CMEWDO algorithm with REGs and BESS is implemented for two scenarios: REGs and BESS integration without scheduling and REGs and BESS integration with scheduling for performance evaluation. The developed framework includes power sources (such as utility power grid, REGs, and BESS), ToU-DRP, and home appliances to generate a power usage scheduling pattern for users. The exogenous input signals, such as ToU-DRP received from the utility taken from ^[28], ambient temperature and solar irradiance used in REGs, and charging level of BESS, are shown in Figures 3–5, respectively, which are used by the developed algorithm for creating operation schedule for appliances.

Figure 3 presents the A1-category ToU-DRP pricing signal/tariff, which is provided by the Islamabad Electric Supply Company (IESCO) for the winter season of 17th January 2020. This tariff data, obtained from the National Electric Power Regulatory Authority (NEPRA) of Pakistan, offers a more representative and region-specific pricing signal for our simulations.

The solar irradiance and temperature data presented in Figures 4 and 5, are sourced from METEONORM 6.1, a reputable software package recognized for providing reliable meteorological data. The selection of the Islamabad region in Pakistan emphasizes the specific geographical context for our research. Islamabad, the capital city of Pakistan, represents a distinct geographical location with unique climatic conditions covering all four seasons: spring, autumn, winter, and summer. The choice of this region allows us to tailor our analysis to the characteristics and challenges associated with the local climate. The solar irradiance and temperature data obtained from METEONORM are crucial inputs for the simulation of renewable energy systems, particularly solar PV installations. This data enables a realistic representation of the local climate and its impact on the performance of energy generation components.

The solar PV energy system is considered an REG, which is dependent on solar radiation and temperature. Figure 6 depicts the REGs estimated generation, and the BESS charging level is illustrated in Figure 7.

The developed CMEWDO algorithm-based ES actively engages users in ToU-DRP to create a power usage schedule under REGs and utility generation for two scenarios: REGs and BESS integration without scheduling, and REGs and BESS. The results obtained for both scenarios are discussed below.

3.1.   Case Ⅰ: REGs and BESS integration without scheduling

Case 1 unfolds REGs and BESS integration potentials without scheduling in aspects of the electricity bill and PADR. The load distribution among REGs, BESS, and utility is depicted in Figure 8. It illustrates a portion load shifted from the power grid to REGs, and that REGs and BESS serve the load during peak hours. Each objective evaluation is discussed as follows:

The power usage pattern of the load with REGs and BESS without scheduling is shown in Figure 9. It is obvious from Figure 9 that case 1 (load without scheduling, REGs, and BESS) has a high power consumption of 430 W at hours 1, 19–24, moderate power consumption of 350 W at hours 13–15, and low power consumption of 101 Wh at hours 3–5. Case 2 (load without scheduling and with REGs) shows the highest power consumption at hours 10 and 11 and the lowest at hours 12, 13, 15, and 16. In contrast, case 2 has moderate power consumption during the remaining hours. The findings reveal that in case 3 (load without scheduling and with REGs and BESS integration), the power consumption has the highest peak of 600 Wh, 480 Wh, and 360 Wh at hours 1, 4, and 22, respectively. In contrast, the lowest power consumption behavior is observed at hours 11, 12, 15, and 16, and the remaining hours have moderate energy consumption. After including the BESS, the power consumption becomes higher than that in case 1 and case 2. This rise in power consumption is due to the use of 30% REG energy for charging the BESS. On the other hand, at hours 9, BESS discharged, and load on the utility is reduced by 65.5% and 60.2% than case 1 and case 2, respectively.

The hourly electricity bill against the consumed energy is depicted in Figure 10. Results illustrate that at hours 19–21 without REGs and BESS integration, the electricity bill is high, that is, 100 cents. On the other hand, the hourly electricity bill is lower than at all hours compared to without REGs and BESS integration, except hours 9. When REGs and BESS are integrated, the electricity bill is further reduced compared with the case without REGs and BESS integration. Thus, integrating REGs and BESS significantly contributes to electricity bill reductions.

The net electricity bill for case 1 is illustrated in Figure 11. Findings reveal that with the integration of REGs, the electricity bill is reduced by 11.53%. Further, if BESS is integrated with the system, the reduction in bill payment is increased by 20.8%. Thus, this huge reduction in electricity bills is possible only by investing a small capital cost on REGs and BESS integration.

Thus, with REGs and BESS integration, electricity bills will be reduced per hours and net basis compared to without REGs and BESS.

The assessment of the PADR without scheduling and with/without REGs and BESS integration is depicted in Figure 12. Results illustrate that the integration of REGs alleviates PADR by 17.3%. On the other hand, when both REGs and BESS are integrated with the system, the curtailment in PADR is 25.58%. Thus, the integration of REGs and BESS reduces PADR, which is beneficial for utility in terms of reliability improvement of power systems and for consumers in terms of electricity bills.

The comprehensive evaluation of Case 1, considering aspects such as the electricity bill and PADR minimization, is summarized in Table 3.

3.2.   Case Ⅱ: REGs and BESS integration with scheduling

In case Ⅱ, the developed framework based on the CMEWDO algorithm is compared with other algorithms in aspects of power usage scheduling with REGs and BESS integration, and the obtained results are discussed as follows: Scheduled and without scheduled power usage pattern with/without REGs and BESS integration is depicted in Figure 13. The power usage pattern without load scheduling and with REGs and BESS has the highest peak of 60 kWh at hours 1, followed by a peak power usage of 48 kW at hours 22. The moderate power usage pattern is recorded in time slots 4–7, 13–15, and 19–21, and the lowest power consumption in the remaining hours. The maximum power consumption of WOA is 50.87 kWh at hours 1, that of EDE is 49.12 kWh at hours 1-6, that of WDO is 54.02 kWh at hours 21–24, that of CMEWDO is 43.14 kWh at hours 3 and 4. It is obvious from the results presented in Figure 13 that the power usage pattern of the developed CMEWDO algorithm is moderate and balanced compared with existing algorithms. The developed CMEWDO algorithm shifted the load from peak hours 9–17 to off-peak hours 1–8 and 19–24 optimally and uniformly distributed during the scheduling time horizon compared to existing algorithms. In contrast, the load distribution of the other algorithms is nonuniform; either the load is shifted to off-peak hours or a heavy load is operated during on-peak hours. Consequently, the developed CMEWDO algorithm returned optimal power usage patterns that highly contribute to electricity bills and PADR reduction.

The hourly electricity bill of consumed energy pre- and post-scheduling with REGs and BESS is illustrated in Figure 14. The highest electricity bill of WOA is 102.87 cents at hours 1, that of EDE is 100.59 cents at hours 1–6, that of WDO is 103.02 cents at hours 21–24, that of CMEWDO is 87.14 cents at hours 3 and 4. The net electricity bill for 24 hours is illustrated in Figure 15. The net electricity bill without scheduling is 1300 cents compared to WOA, EDE, WDO, and the CMEWDO algorithm with 1250, 1190, 1220, and 1030 cents, respectively. The findings reveal that the net electricity bill of the developed CMEWDO algorithm is less than that without scheduling and other algorithms. Thus, findings validate that the developed CMEWDO algorithm outperforms in terms of hourly and net electricity bill reduction.

The PADR evaluation of load scheduling with REGs and BESS is depicted in Figure 16. The PADR of unscheduled, WOA, EDE, WDO, and the proposed CMEWDO algorithm is 3.7, 2.7, 2.9, 3.1, and 2.1, respectively.

The developed CMEWDO algorithm and other algorithms WOA, EDE, and WDO reduced PADR by 37.7%, 20.35%, 16.26%, and 14.56%, respectively. This outstanding reduction of the developed CMEWDO algorithm is because the load is uniformly distributed in both peak and off-peak hours, and the rebound peak formation issue is resolved. In contrast, other algorithms redistribute the load unevenly from in off-peak and peak hours, consequently creating rebound peaks that cause reliability issues at the utility end. The findings validate that the developed CMEWDO algorithm effectively shifts the load from high to low-price hours. Consequently, the PADR is reduced, which benefits users and the utility end.

The schedule generated by CMEWDO is compared with schedules produced by other algorithms (WOA, EDE, and WDO) to assess the waiting time that consumers experience. Consumer comfort in aspects of waiting time evaluation of the CMEWDO and comparative algorithms like WOA, EDE, and WDO are shown in Figure 17. The ES based on the WOA created schedule poses average delays of 4, 2, 4.5, 2, and 1.5 hours by TRAs (IAs and NIAs) such as WM, CD, DW, EWH, and VC, respectively. On the other hand, PRAs (DP, RF, and AC) and CAs (ET, EK, and MO) face zero delays because they are PRAs and CAs. The ES based on EDE created schedule poses average delays of 3, 3.5, 3, 2.5, and 2 hours by TRAs (IAs and NIAs) such as WM, CD, DW, electric water heater (EWH), and vaccume cleaner (VC), respectively. On the other hand, PRAs (dispenser (DP), refrigerator (RF), and air conditioner (AC)) and CAs (ET, EK, and MO) face zero delays because they are PRAs and CAs, which are illustrated in Figure 17. The ES generated schedule using the WDO algorithm results in average delays of 2.8, 2, 2.6, 2.1, and 1.3 hours by TRAs (IAs and NIAs) such as WM, CD, DW, EWH, and VC, respectively. On the other hand, PRAs (DP, RF, and AC) and CAs (ET, EK, and MO) face zero delays because they are power regulating and critical appliances, as shown in Figure 17. The ES based on the CMEWDO created schedule poses average delays of 2.1, 1, 1.5, 1.8, and 1.1 hours by TRAs (IAs and NIAs) such as WM, CD, DW, EWH, and VC, respectively. On the other hand, PRAs (DP, RF, and AC) and CAs (ET, EK, and MO) face zero delays because they are PRAs and CAs. This behavior is illustrated in Figure 17. This evaluation concludes that the developed CMEWDO algorithm outperforms comparative algorithms in aspects of average waiting time, i.e., consumer comfort. Evaluation of the developed framework based on the CMEWDO compared with other schemes in aspects of the electricity bill, PADR, and consumer discomfort reduction is listed in Table 4. Results show that the developed algorithm outperforms existing algorithms in terms of the desired objectives.

4.   Conclusions

This study introduces a framework for scheduling the operation of home appliances through ToU-DRP under the integration of REGs, BESS, and utility supply. Subsequently, the CMEWDO algorithm is devised to tackle the load scheduling problem in two scenarios: REGs and BESS integration without scheduling and REGs and BESS integration with scheduling. The primary goal of this study is to encourage residential users to actively participate in ToU-DRPs and adopt REGs and BESS solutions to address power usage problems. The developed framework, powered by the CMEWDO algorithm, aims to reduce electricity bills and PADR while ensuring consumer comfort. The evaluation highlights the efficacy of the CMEWDO algorithm in significantly reducing electricity bills by 26.21% and PADR by 37.7%. Additionally, the average waiting time is reduced to 1.5, demonstrating the proposed approach's practical applicability and superior performance. Moving forward, future research could explore the scalability and robustness of the framework across larger and more diverse datasets. Moreover, investigating the integration of emerging technologies, such as internet of things (IoT) devices and machine learning algorithms, could further enhance the efficiency and adaptability of the proposed framework. Overall, this study lays the groundwork for advancing smart energy management systems and promoting sustainable practices in residential settings.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors are thankful to the Deanship of Scientific Research at Najran University for funding this work under the Research Priorities and Najran Research Funding Program grant code (NU/NRP/SERC/12/12). The authors also extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number "NBU-FPEJ-2024-2200-01".

Funding

The authors are thankful to the Deanship of Scientific Research at Najran University for funding this work under the Research Priorities and Najran Research Funding Program grant code (NU/NRP/SERC/12/12). The authors also extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number "NBU-FPEJ-2024-2200-01".

Conflict of interest

The authors declare no conflict of interest.