Asymptotic behavior of a stochastic hybrid SIQRS model with vertical transmission and nonlinear incidence

1.   Introduction

Hepatitis B is a life-threatening viral infection that presents a significant global public health challenge. It is associated with severe chronic conditions, including cirrhosis and hepatocellular carcinoma, which are major contributors to mortality among affected individuals. Beyond the immediate health impacts, chronic Hepatitis B infection can lead to long-term disabilities due to liver damage and related complications. The hepatitis B virus (HBV) targets liver cells, where it establishes infection, replicates extensively, and releases large quantities of viral particles into the bloodstream. The infection manifests in two forms: Acute and chronic. Acute hepatitis B often resolves within six months, with the immune system effectively clearing the virus and leading to full recovery. However, if the infection persists beyond six months, it progresses to a chronic state, which is where many disability-related complications arise. Chronic Hepatitis B, especially in those infected during childhood, increases the risk of progressive liver disease and complications that severely impair daily functioning. Common symptoms in advanced stages, such as hepatic encephalopathy, cause cognitive impairments, while fatigue and pain limit physical activity and mobility, leading to functional disabilities. Children infected with HBV between the ages of 1 and 8 years are at significant risk of developing chronic, often asymptomatic infection, yet they remain carriers capable of transmitting the virus to others. Globally, an estimated 240 million people live with chronic HBV-related liver infections, with around 600,000 deaths annually from both acute and chronic forms of the disease ^[1,2]. HBV transmission primarily occurs through contact with infected blood or bodily fluids, including through sexual contact, blood transfusions, and perinatal transmission from mother to child. Age at infection is a critical factor in disease progression and the potential for disability. Infants and young children, particularly those under six, are more likely to develop chronic hepatitis B, leading to an 80-90% likelihood of chronic infection in those infected within the first year of life and 30-35% in those infected between ages 1 and 6. By contrast, less than 5% of adults who acquire HBV progress to chronic symptoms. Nevertheless, 15-25% of individuals who contract HBV early in life experience HBV-related complications, including liver cancer, cirrhosis, and associated disabilities due to extensive liver damage ^[3,4].

Chronic carriers of the hepatitis B virus (HBV) typically do not exhibit a history of acute illness; however, they are at risk for developing cirrhosis, which involves scarring of the liver and can potentially lead to liver failure or hepatocellular carcinoma. A small percentage (1%–6%) of chronic carriers are able to clear the virus naturally. Some individuals infected with HBV may present symptoms similar to those caused by other viral infections, while many remain asymptomatic until serious complications, such as liver damage, emerge. In some cases, it can take 2 to 5 months for symptoms of hepatitis B to appear ^[5,6]. However, for others, symptoms may be minimal or completely absent, despite the potential for severe disease progression. Asymptomatic individuals, although not manifesting symptoms, can still transmit the virus and may develop chronic HBV infection later in life. Additionally, certain individuals may act as carriers of the virus without being infected ^[7]. Prophylactic administration of the HBV vaccine and hepatitis B immune globulin within 12 hours of birth can significantly reduce the risk of mother-to-child transmission of HBV, lowering it from 20-90% to 5-10%. Subsequent doses of the vaccine are typically given at 1–2 months and again at 6 months of age, but not beyond that ^[8,9]. In many adult cases, treatment is not required as spontaneous immunity often develops ^[10]. In any case, antiviral treatment might be vital in the beginning phases for people with compromised resistant frameworks or those encountering a forceful beginning of contamination. For those with ongoing HBV disease, therapy is vital to decrease the gamble of serious intricacies like liver malignant growth or cirrhosis. The span and way to deal with treatment are impacted by the HBV genotype and the particular antiviral routine utilized, which might go from a half year to a year ^[11].

One of the primary concerns in the study of hepatitis B virus (HBV) infection is developing strategies to control the infection rate and eradicate the virus from the population. Mathematical models are valuable tools for optimizing resources and implementing control measures more effectively ^[12,13]. Anderson and May used a simple mathematical model to illustrate the effect of carriers on HBV transmission ^[14]. A mathematical model was also developed to control HBV infection, which was later employed to formulate a strategy for eliminating HBV ^[7,15]. An age-structured model was proposed by Zheo et al. ^[16] for predicting HBV transmission and evaluating the effectiveness of vaccination programs in China. A model developed by Wang et al. ^[17] was used to analyze the impact of vaccination on a population and to assess other control measures for HBV infection, with further analysis and applications provided by Zhang and Zhou ^[18]. Khan et al. proposed a mathematical model aimed at controlling the spread of both chronic and acute HBV transmission ^[19]. Pulse vaccination epidemic models ^[20,21] have demonstrated that pulse vaccination can maintain the epidemic in a stable state by optimizing the quantity of vaccines administered and the intervals between vaccinations. However, the costs associated with vaccination and treatment strategies can be significant and may not always be feasible. Therefore, it is crucial to predict and implement vaccination and treatment strategies that are well-suited to the specific context. In this regard, Khan and Zaman developed a model for HBV transmission and vaccination ^[21], while Jaouade Danane and Karam Allali conducted mathematical analysis on the delayed treatment of HBV infection, considering the immune response and the role of DNA-containing capsids in the host's body ^[22].

Over the last decade, the study of mathematical models for biological systems has gained considerable attention within the scientific community, as highlighted in studies ^[23,24]. These models often incorporate state variables that are inherently nonnegative, such as physical attributes, chemical concentrations, population densities, and other measurable properties. Diffusion significantly impacts the spatial and temporal variation of these variables within a system. It represents the movement of particles such as molecules or individuals in a population from areas of higher concentration to areas of lower concentration. These models are generally built upon systems of differential equations. However, obtaining exact solutions to such systems is often challenging and complex, necessitating the use of approximation techniques. We aim to investigate the influence of diffusion on these models by employing numerical methods.

2.   Model formulation

Hepatitis B, a viral infection instigated by the Hepatitis B Virus (HBV), predominantly targets and inflicts damage on the liver. A detailed mathematical model addressing HBV dynamics was recently introduced by Zada et al. ^[25]. This model categorizes the total population $N(t)$ at any time $t$ into five distinct compartments: the susceptible individuals $S(t)$, those in the latent stage $L(t)$, the acutely infectious group $I(t)$, chronic HBV carriers $C(t)$, and those who have recovered $R(t)$. The total population at any time can thus be expressed as:

This equation captures the overall flow of individuals through different stages of the disease, describing how HBV transmission and progression occur across these compartments. The model is governed by the following set of nonlinear ordinary differential equations (ODEs):

The parameters in the given system of equations represent various aspects of the hepatitis B virus (HBV) dynamics. The parameter $\mu$ represents the birth rate, and $\omega$ denotes the proportion of the population without vaccination. The term $\nu$ is the proportion of children born to chronically infected mothers who are unvaccinated. The parameter $v$ is related to the effect of treatment or intervention on the susceptible population, $S(t)$. The rate $\mu_0$ represents the natural mortality rate, while $\beta$ is the transmission rate of the virus from acutely infected individuals, $I(t)$, to susceptible individuals. Similarly, $\epsilon \beta$ indicates the transmission rate from chronically infected individuals, $C(t)$, to susceptibles. The vaccination rate is represented by $\gamma_3$, and $\sigma$ is the rate at which latently infected individuals, $L(t)$, progress to the acute infection stage. The parameter $\gamma_1$ denotes the rate at which acutely infected individuals either recover or progress to chronic infection, with $q$ being the proportion that progresses to chronic infection. The chronic infection-related mortality rate is denoted by $\mu_1$, and $\gamma_2$ is the rate at which chronically infected individuals recover.

The chronically infected compartment $C(t)$ is of particular importance because individuals in this class are at high risk of developing severe, long-term health complications, such as cirrhosis and hepatocellular carcinoma. These complications are associated with significant functional impairment, leading to long-term disability and reduced quality of life. Studying the dynamics of the chronically infected class helps in understanding the progression from acute infection to chronic disease and the subsequent disability burden, emphasizing the need for effective intervention strategies. Consequently, the model captures the dynamics of susceptible ($S(t)$), latent ($L(t)$), acutely infected ($I(t)$), chronically infected ($C(t)$), and recovered ($R(t)$) populations over time, providing insights into both transmission and the long-term impact of HBV on population health.

Most of the HBV models available in the literature are non-spatial and assume that the population is well-mixed. However, this assumption can lead to inaccuracies, as the transmission dynamics of HBV are often influenced by spatial factors. To address this limitation, a spatially independent model introduced by Zada et al. ^[25] has been expanded to include spatial dynamics by incorporating a diffusion term, thereby creating a reaction-diffusion model. This model accounts for the movement of individuals and the consequent spatial variation in infection spread. The revised model is presented as follows:

The model is initialized with the following conditions:

where $f_1(x, y)$, $f_2(x, y)$, $f_3(x, y)$, $f_4(x, y)$, and $f_5(x, y)$ define the initial spatial distributions of the various groups within the population, categorized by their disease status, respectively.

The boundary conditions for the reaction-diffusion model (2.2) are specified as homogeneous Neumann boundary conditions, which represent no flux across the boundaries. These conditions ensure that the spatial derivatives of the variables with respect to the boundary normals are zero. Mathematically, they are expressed as follows:

where $\frac{\partial}{\partial n}$ denotes the derivative in the direction normal to the boundary $\partial \Omega$, and $\Omega$ is the spatial domain. These boundary conditions indicate that there is no movement of individuals across the boundaries of the spatial domain, which is biologically reasonable for modeling the dynamics of populations within a confined area.

In this formulation, $S = S(x, y, t)$, $L = L(x, y, t)$, $I = I(x, y, t)$, $C = C(x, y, t)$, and $R = R(x, y, t)$ represent the spatially and temporally dependent compartments of the population. Since $R(t)$ is not directly involved in the first four equations, it is convenient to consider the system (2.2) as:

Subject to the initial conditions (2.3) and boundary conditions (2.4).

3.   Steady states of the model

The hepatitis B epidemic model exhibits two primary equilibrium states: the disease-free equilibrium (DFE) and the endemic equilibrium (EE) ^[25]. The disease-free equilibrium occurs when the population is uninfected, represented mathematically as:

In contrast, the endemic equilibrium corresponds to a steady state where the disease persists within the population. This state can be expressed as:

where

with the parameters defined as:

3.1.   Basic reproduction number

The basic reproduction number, represented as $R_0^{HBV}$, is determined here. This metric quantifies the average number of secondary infections caused by a single infection in a completely susceptible population. To calculate $R_0^{HBV}$, it is essential to distinguish infected and noninfected populations, employing the next-generation matrix approach ^[26,27]. The variables $L, I, C$, and $S$ represent the respective infected and noninfected cell populations. By isolating the infection terms, the infection-free equilibrium model is expressed using a matrix representation to account for infection terms $F$ and $V$. The $F$ matrix specifically captures the terms driving the infection, while $V$ includes the remaining components of the system and $D$ represents the diffusion coefficients, as defined below:

By calculating the Jacobian matrix of the system using $R_0^{HBV}$, the matrices $F^*$ and $V^*$ are obtained as follows:

At equilibrium, the transition and infection rates are described by $F^*$ and $V^*$. The time spent in each state is determined by the inverse of $V^*$, denoted as $V^{*-1}$. During an outbreak, the number of new infections is derived from the product $F^* V^{*-1}$. The dominant eigenvalue of $F^* V^{*-1}$ represents the basic reproduction number, which can be expressed as:

The model predicts a disease-free state, whereas $R_0 > 1$ indicates the persistence of the disease, leading to the endemic equilibrium.

4.   Stability of endemic equilibrium point

In this section, the stability of the two-dimensional diffusive epidemic model is examined. The system represented by Eq (2.5) tends to converge toward the equilibrium values $(S^{\ast}, L^{\ast}, I^{\ast}, C^{\ast})$. To assess the stability of these equilibrium points, the system is linearized around the steady state, employing the methodology outlined in ^[28] and ^[29].

Theorem 4.1. For the system (2.5), the endemic equilibrium is locally asymptotically stable if and only if $R_0^{HBV} > 1$ and the following condition is satisfied:

Proof. Let the perturbed variables of $S(x, y, t)$, $L(x, y, t)$, $I(x, y, t)$, and $C(x, y, t)$ be denoted as $S_1(x, y, t)$, $L_1(x, y, t)$, $I_1(x, y, t)$, and $C_1(x, y, t)$, respectively. To investigate the stability of the system, we linearize Eq (2.5) around the equilibrium point $E^{*}$, using the methodology described in ^[28,29]. The corresponding linearized system can be written as:

To solve the linearized system, a Fourier series approach is employed, as outlined in references ^[28] and ^[29]. The solution for $S_1(x, y, t), L_1(x, y, t), I_1(x, y, t)$ and $C_1(x, y, t)$ can be expressed as:

where $\zeta_i$ (for $i = 1, 2$) are the wave numbers corresponding to the nodes $n_i$, with $\zeta_1 = \frac{n_1 \pi}{2}$ and $\zeta_2 = \frac{n_2 \pi}{2}$. The functions $S_1(x, y, t)$, $L_1(x, y, t)$, $I_1(x, y, t)$, and $C_1(x, y, t)$ are defined over the spatial domain $(x, y) \in \Omega \subset \mathbb{R}^2$ and time domain $t \in [0, T]$, where $\Omega = [X_{\text{min}}, X_{\text{max}}] \times [Y_{\text{min}}, Y_{\text{max}}]$ represents the two-dimensional spatial region of interest. These functions represent perturbations around the equilibrium state and evolve over time under the specified boundary and initial conditions. By substituting the expressions for $S_1(x, y, t)$, $L_1(x, y, t)$, $I_1(x, y, t)$, and $C_1(x, y, t)$ into the system, we obtain a system of equations suitable for further analysis.

The variational matrix $\mathbf{V}$ for (4.3) is

where

To find the eigenvalues of the given matrix $\mathbf{V}$, we reduce the matrix $\mathbf{V}$ to an upper triangular form by performing the following row operations:

To eliminate $a_{21}$, subtract $\frac{a_{21}}{a_{11}} r_1$ from $r_2$. The updated second row becomes:

To eliminate $a_{32}$, subtract $\frac{a_{32}}{a_{22}} r_2$ from $r_3$. The updated third row becomes:

To eliminate $a_{43}$, subtract $\frac{a_{43}}{a_{33}} r_3$ from $r_4$. The updated fourth row becomes:

After performing the row operations, the matrix is transformed into the following upper triangular form:

Thus,

The eigenvalues of the system are:

The three eigenvalues $\lambda_1, \lambda_2, \lambda_3$ are explicitly negative as long as the biological parameters (rates and population sizes) remain positive and satisfy reasonable conditions. $\lambda_4$ depends on the term $\mu_0 + \mu_1 + \gamma_2 - \mu \omega \nu - \frac{q \gamma_1 \sigma}{\mu_0 + \sigma}$, which determines whether it is positive or negative. For stability, $\lambda_4$ must satisfy:

Consider the eigenvalue:

The eigenvalue $\lambda$ is negative ($\lambda < 0$) if and only if:

This implies that the endemic equilibrium is locally stable when the above condition holds.

Conversely, if:

then $\lambda > 0$, indicating that the equilibrium is unstable.

The basic reproduction number $R_0^{HBV}$ is given by:

For $R_0^{HBV} > 1$, the term $\mu \omega \nu - (\mu_0 + \mu_1 + \gamma_2)$ in the denominator must be positive:

This implies that the inequality:

holds in the endemic state ($R_0^{HBV} > 1$). In contrast, when $R_0^{HBV} \leq 1$, the condition flips, and the equilibrium becomes unstable ($\lambda > 0$).

5.   Numerical schemes

The finite difference (FD) schemes are formulated by discretizing the computational domain $[0, L]^2 \times [0, T]$ into a grid comprising $M^2 \times N$ discrete points. The spatial and temporal step sizes are defined as $h = \frac{L}{M}$ and $\tau = \frac{T}{N}$, respectively. The coordinates of the grid points are expressed as:

where $\zeta_1$ and $\zeta_2$ denote spatial indices, and $n$ represents the temporal index. The FD approximations of the variables $S^{n}_{\zeta_1, \zeta_2}$, $L^{n}_{\zeta_1, \zeta_2}$, $I^{n}_{\zeta_1, \zeta_2}$, and $C^{n}_{\zeta_1, \zeta_2}$ are given as $S(\zeta_1h, \zeta_2h, n\tau)$, $L(\zeta_1h, \zeta_2h, n\tau)$, $I(\zeta_1h, \zeta_2h, n\tau)$, and $C(\zeta_1h, \zeta_2h, n\tau)$, respectively.

5.1.   Finite difference method

In this section, we discuss the implementation of the forward Euler finite difference (FD) scheme for solving the two-dimensional reaction-diffusion model describing hepatitis B dynamics. In this method, the time derivative is discretized using a forward difference approach, while the spatial derivatives are handled through a central difference scheme. The forward Euler FD scheme applied to system (2.5) is expressed as follows:

where

5.2.   Crank Nicolson method

In this section, we apply the Crank-Nicolson operator splitting finite difference (OS-FD) scheme to numerically solve the hepatitis B epidemic model. Typically, reaction-diffusion equations are decomposed into two distinct subsystems. The first subsystem addresses the nonlinear reaction terms over a half-time step, while the second subsystem deals with the linear diffusion terms during the subsequent time step. The implementation of the Crank-Nicolson OS-FD scheme begins with the following procedure for the initial time step:

In the second step, the methodology applied for the Crank-Nicolson OS-FD scheme is as follows:

The approach for the third step involves the following process:

The Crank Nicolson OS-FD scheme is unconditionally stable.

5.3.   Unconditionally positivity preserving method

In this section, we design a UPP-FD scheme for the hepatitis B epidemic model in two dimensions. The rules for designing the UPP-FD scheme are based on the rules given by Mickens ^[30]. The UPP-FD scheme for Susceptible in Eq (2.5) is designed as follows:

The UPP-FD scheme for Exposed in Eq (2.5) is designed as follows:

The UPP-FD scheme for Infected in Eq (2.5) is designed as follows:

The UPP-FD scheme for chronic in Eq (2.5) is designed as follows:

Theorem 5.1. The finite difference approximation method UPP-FD, as outlined in Eqs (5.8), (5.10), (5.12), and (5.14), preserves the positivity of the solution under the assumption that the initial conditions are non-negative. Specifically, it holds that:

Proof. We prove positivity preservation by induction, analyzing each equation in the UPP-FD scheme. The proof involves the following steps:

Step 1. Base case:

Assume that at $n = 0$, the initial conditions satisfy:

for all $\zeta_1, \zeta_2$. These initial conditions are biologically realistic, as population densities cannot be negative. Thus, the base case is satisfied.

Step 2. Inductive hypothesis:

Assume that at time step $n$, the positivity condition holds:

for all $\zeta_1, \zeta_2$.

We aim to prove that the positivity condition holds at time step $n+1$:

Step 3. Inductive step:

We prove positivity for each state variable at $n+1$, starting with $S^{n+1}_{\zeta_1, \zeta_2}$.

Positivity of $S^{n+1}_{\zeta_1, \zeta_2}$, from (5.8), we have:

Numerator analysis:

● $S^n_{\zeta_1, \zeta_2} \geq 0$ by the inductive hypothesis.

● $\lambda_1 \left(S^n_{\zeta_1-1, \zeta_2} + S^n_{\zeta_1+1, \zeta_2} + S^n_{\zeta_1, \zeta_2-1} + S^{n}_{\zeta_1, \zeta_2+1}\right) \geq 0$, as $\lambda_1 > 0$ and neighboring terms are non-negative.

● $\tau \mu \omega (1 - \nu C^n_{\zeta_1, \zeta_2}) \geq 0$, since $C^n_{\zeta_1, \zeta_2} \geq 0$ and $\nu < 1$.

Denominator analysis: The denominator $1 + 4\lambda_1 + \tau (\mu_0 + \beta I^n_{\zeta_1, \zeta_2} + \epsilon \beta C^n_{\zeta_1, \zeta_2} + \gamma_3) > 0$, as all parameters are positive. Thus, $S^{n+1}_{\zeta_1, \zeta_2} \geq 0$.

Positivity of $L^{n+1}_{\zeta_1, \zeta_2}$, from (5.10), we have:

Numerator analysis:

● $L^n_{\zeta_1, \zeta_2} \geq 0$ by the inductive hypothesis.

● $\lambda_2 \left(L^n_{\zeta_1-1, \zeta_2} + L^n_{\zeta_1+1, \zeta_2} + L^n_{\zeta_1, \zeta_2-1} + L^{n}_{\zeta_1, \zeta_2+1}\right) \geq 0$.

● $\tau (\beta I^n_{\zeta_1, \zeta_2} + \epsilon \beta C^n_{\zeta_1, \zeta_2}) S^n_{\zeta_1, \zeta_2} \geq 0$.

Denominator analysis: The denominator $1 + 4\lambda_2 + \tau (\mu_0 + \sigma) > 0$. Thus, $L^{n+1}_{\zeta_1, \zeta_2} \geq 0$.

Positivity of $I^{n+1}_{\zeta_1, \zeta_2}$, from (5.12), we have:

Numerator analysis:

● $I^n_{\zeta_1, \zeta_2} \geq 0$.

● $\lambda_3 \left(I^n_{\zeta_1-1, \zeta_2} + I^n_{\zeta_1+1, \zeta_2} + I^n_{\zeta_1, \zeta_2-1} + I^{n}_{\zeta_1, \zeta_2+1}\right) \geq 0$.

● $\tau \sigma L^n_{\zeta_1, \zeta_2} \geq 0$.

Denominator analysis: The denominator $1 + 4\lambda_3 + \tau (\mu_0 + \gamma_1) > 0$. Thus, $I^{n+1}_{\zeta_1, \zeta_2} \geq 0$.

Positivity of $C^{n+1}_{\zeta_1, \zeta_2}$, from (5.14), we have:

Numerator analysis:

● $C^n_{\zeta_1, \zeta_2} \geq 0$.

● $\lambda_4 \left(C^n_{\zeta_1-1, \zeta_2} + C^n_{\zeta_1+1, \zeta_2} + C^n_{\zeta_1, \zeta_2-1} + C^{n}_{\zeta_1, \zeta_2+1}\right) \geq 0$.

● $\tau q \gamma_1 I^n_{\zeta_1, \zeta_2} \geq 0$.

Denominator analysis: The denominator $1 + 4\lambda_4 - \tau \mu \omega \nu + \tau (\mu_0 + \mu_1 + \gamma_2) > 0$. Thus, $C^{n+1}_{\zeta_1, \zeta_2} \geq 0$. By induction, positivity is preserved at all time steps $n+1$, provided the initial conditions are positive. □

Remark 5.1. The Eqs (5.8), (5.10), (5.12) and (5.14) ensure a positive solution due to the non-negativity of all terms on the right-hand side, regardless of the parameters involved in the system.

5.4.   Stability

In this section, we analyze the stability of the finite difference (FD) schemes. We begin by applying the UPP-FD scheme (Eq (5.8)) to the reaction-diffusion equation for $S(x, y, t)$ (Eq (2.5)). By subsequently linearizing this discretized equation and substituting the perturbation $\Phi(t)e^{\iota(\varpi_1 x+\varpi_2 y)}$ for $S^{n}_{\zeta_1, \zeta_2}$, we derive the following stability condition:

Keep in mind that $\Delta x = \Delta y$. Following a similar approach for $L^{n+1}_{\zeta_1, \zeta_2}$, the result is obtained as:

Using a similar process for $I^{n+1}_{\zeta_1, \zeta_2}$, we obtain,

In the same fashion, the procedure for $C^{n+1}_{\zeta_1, \zeta_2}$, we obtain,

The analysis clearly demonstrates that the proposed UPP-FD scheme maintains stability under all conditions.

5.5.   Consistency

The consistency of the UPP-FD scheme is evaluated using the Taylor series expansion. The expressions for $S^{n+1}_{\zeta_1, \zeta_2}$, $S^{n}_{\zeta_1+1, \zeta_2}$, $S^{n}_{\zeta_1-1, \zeta_2}$, $S^{n}_{\zeta_1, \zeta_2+1}$, and $S^{n}_{\zeta_1, \zeta_2-1}$ are derived through their Taylor series expansions.

Considering the UPP-FD scheme for Eq (5.8),

Substituting the values of $S^{n+1}_{\zeta_1, \zeta_2}$, $S^{n}_{\zeta_1+1, \zeta_2}$, $S^{n}_{\zeta_1-1, \zeta_2}$, $S^{n}_{\zeta_1, \zeta_2+1}$, and $S^{n}_{\zeta_1, \zeta_2-1}$ in the above equation and after simplification, we get

replace $\tau = h^3$ and $h\rightarrow 0$, we have

Similarly, the formulas for $L^{n+1}_{\zeta_1, \zeta_2}$, $L^{n}_{\zeta_1+1, \zeta_2}$, $L^{n}_{\zeta_1-1, \zeta_2}$, $L^{n}_{\zeta_1, \zeta_2+1}$, and $L^{n}_{\zeta_1, \zeta_2-1}$ are

Considering the UPP-FD scheme for Eq (5.10),

Substituting the values of $L^{n+1}_{\zeta_1, \zeta_2}$, $L^{n}_{\zeta_1+1, \zeta_2}$, $L^{n}_{\zeta_1-1, \zeta_2}$, $L^{n}_{\zeta_1, \zeta_2+1}$, and $L^{n}_{\zeta_1, \zeta_2-1}$ in the above equation and after simplification, we get

replace $\tau = h^3$ and $h\rightarrow 0$, we have

Similarly, the formulas for $I^{n+1}_{\zeta_1, \zeta_2}$, $I^{n}_{\zeta_1+1, \zeta_2}$, $I^{n}_{\zeta_1-1, \zeta_2}$, $I^{n}_{\zeta_1, \zeta_2+1}$, and $I^{n}_{\zeta_1, \zeta_2-1}$ are

Considering the UPP-FD scheme for Eq (5.12)

Substituting the values of $I^{n+1}_{\zeta_1, \zeta_2}$, $I^{n}_{\zeta_1+1, \zeta_2}$, $I^{n}_{\zeta_1-1, \zeta_2}$, $I^{n}_{\zeta_1, \zeta_2+1}$, and $I^{n}_{\zeta_1, \zeta_2-1}$ in the above equation and after simplification, we get

replace $\tau = h^3$ and $h\rightarrow 0$, we have

Similarly, the formulas for $C^{n+1}_{\zeta_1, \zeta_2}$, $C^{n}_{\zeta_1+1, \zeta_2}$, $C^{n}_{\zeta_1-1, \zeta_2}$, $C^{n}_{\zeta_1, \zeta_2+1}$, and $C^{n}_{\zeta_1, \zeta_2-1}$ are

Considering the UPP-FD scheme for Eq (5.14),

Substituting the values of $C^{n+1}_{\zeta_1, \zeta_2}$, $C^{n}_{\zeta_1+1, \zeta_2}$, $C^{n}_{\zeta_1-1, \zeta_2}$, $C^{n}_{\zeta_1, \zeta_2+1}$, and $C^{n}_{\zeta_1, \zeta_2-1}$ in the above equation and after simplification, we get

replace $\tau = h^3$ and $h\rightarrow 0$, we have

A similar methodology can be utilized to analyze the consistency of the well-established classical forward Euler finite difference scheme.

5.6.   Numerical results

The nonlinearity and spatial variability in model (2.5) make deriving exact analytical solutions under arbitrary initial conditions highly challenging. Consequently, numerical methods are employed to approximate solutions. Various established techniques are commonly used for solving partial differential equations (PDEs) in epidemiological models. These include methods such as the Fourier Spectral Method (FSM), the Non-Standard Finite Difference Method (NSFDM), and the Finite Element Method (FEM), among others. A detailed discussion of these approaches and their applications can be found in related literature, including ^[31]. An ideal numerical method for solving PDEs should strike a balance between accuracy, computational efficiency, adaptability to complex geometries, and ease of implementation. However, no single method excels in all these aspects. For instance, NSFDM provides a higher degree of flexibility and accuracy for certain cases but can introduce complexity and stability challenges, as well as increased computational demands ^[30]. Similarly, FEM is recognized for its adaptability to irregular geometries, but it requires intensive meshing efforts, particularly for intricate domains. Spectral methods, while highly accurate, are constrained by their reliance on periodic boundary conditions and are generally more suitable for problems with simple geometries ^[32]. Considering these trade-offs, we adopt the Crank-Nicolson operator splitting method alongside the Unconditionally Positivity Preserving method to numerically solve the PDEs ^[33,34]. These methods are chosen for their ability to maintain a balance between precision, stability, and computational efficiency.

The Crank-Nicolson strategy is known for its second order accuracy in both instances. By consolidating operator splitting, the strategy decouples the complex PDE framework into less complex subproblems, which are more straightforward to address while keeping up with solidness and precision. This technique can manage a more extensive scope of limit conditions and calculations contrasted with Fourier spectral strategies, which are confined to occasional circumstances. It additionally requires meshing contrasted with FEM, making it computationally more effective in complex geometries. Similarly, one of the vital benefits of the Unconditionally Positivity Preserving strategy is its capacity to save the non-pessimism of the arrangement, which is pivotal in epidemiological models where negative qualities are not truly significant. This technique stays stable no matter what the time step size, taking into account bigger time ventures without forfeiting exactness or presenting hazards. This is a huge improvement over conventional strategies like FDM, which might demand modest moves toward keeping up with solidness. the Unconditionally Positivity Preserving method is simpler to implement, particularly for problems with irregular geometries.

In this section, the CNOS-FD and UPP-FD methods are applied to compute numerical solutions for the model described in Eq (2.5). The numerical simulations were performed using MATLAB R2023a, a popular tool for computational analysis and simulations. The simulations utilized a spatial step size of $h = 0.1$ and a time step size of $dt = 0.005$, ensuring compliance with the Von Neumann stability criterion. The diffusivity constants used in all cases are $d_1 = 0.3$, $d_2 = 0.1$, $d_3 = 0.5$, and $d_4 = 0.01$, where $d_1, d_2, d_3,$ and $d_4$ correspond to the diffusion coefficients for $S(x, y, t)$, $L(x, y, t)$, $I(x, y, t)$, and $C(x, y, t)$, respectively. The model parameters used in the numerical simulations are $q = 0.7$, $\beta = 0.0091$, $\mu = 0.0121$, $\mu_1 = 0.01$, $\mu_0 = 0.0693$, $\omega = 0.85$, $v = 0.46$, $\epsilon = 0.02$, $\gamma_1 = 0.03$, $\gamma_2 = 0.02$, $\gamma_3 = 0.01$, and $\sigma = 0.04$. The spatial and temporal domains are defined as $X_{\text{min}} = 0$, $X_{\text{max}} = 10$, $Y_{\text{min}} = 0$, $Y_{\text{max}} = 10$, and $T_{\text{max}} = 30$. The discretization parameters are given as $h = 0.1$, $N_x = \frac{X_{\text{max}} - X_{\text{min}}}{h} + 1 = 101$, $N_y = \frac{Y_{\text{max}} - Y_{\text{min}}}{h} + 1 = 101$, $\Delta t = 0.005$, and $M = \frac{T_{\text{max}}}{\Delta t} + 1 = 6001$. The spatial grid points are $x = \text{linspace}(X_{\text{min}}, X_{\text{max}}, N_x)$ and $y = \text{linspace}(Y_{\text{min}}, Y_{\text{max}}, N_y)$. These values define the spatial and temporal resolution of the simulation grid, as well as the model parameters used in the reaction-diffusion equations. The initial conditions $S(x, y, 0) = 5 \cdot \left(1 + 0.5 \cdot \sin\left(\frac{\pi x}{5}\right)\right) \cdot \left(1 + 0.5 \cdot \cos\left(\frac{\pi y}{5}\right)\right)$, $L(x, y, 0) = 3 \cdot \left(1 + 0.5 \cdot \cos\left(\frac{\pi x}{5}\right)\right) \cdot \left(1 + 0.5 \cdot \sin\left(\frac{\pi y}{5}\right)\right)$, $I(x, y, 0) = 20 \cdot \sin\left(\frac{\pi x}{10}\right) \cdot \cos\left(\frac{\pi y}{10}\right)$, and $C(x, y, 0) = 0.5 \cdot \cos\left(\frac{\pi x}{10}\right) \cdot \sin\left(\frac{\pi y}{10}\right)$ are considered. Homogeneous Neumann boundary conditions ($\frac{\partial S}{\partial n} = \frac{\partial L}{\partial n} = \frac{\partial I}{\partial n} = \frac{\partial C}{\partial n} = 0$) are applied, ensuring no flux across the boundaries. Simulation results depicting the distribution of acutely infected individuals in one, two, and three spatial dimensions, with and without the incorporation of spatial diffusion, are shown in Figures 1–5.

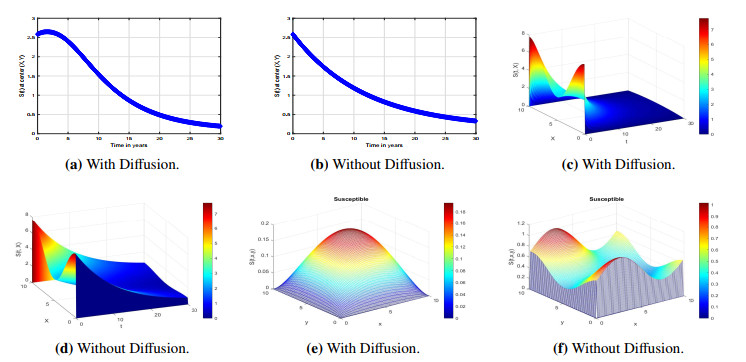
Figure 1 presents the simulation results illustrating the dynamics of the susceptible population in scenarios incorporating spatial diffusion (Figure 1a, c and e) and those without diffusion (Figure 1b, d and f) across one, two, and three spatial dimensions. In the case of diffusion (1a), the susceptible population exhibits a slower decline over time, as diffusion facilitates the spatial redistribution of individuals, resulting in a more gradual exposure to infection based on proximity to infected individuals. Conversely, the absence of diffusion (1b) leads to a faster reduction in the susceptible population, characteristic of a well-mixed population where exposure occurs uniformly. In two dimensions, diffusion (1c) enables a uniform spatial spread of susceptibles, reducing high-density areas and mitigating localized outbreaks through smoother population distribution. Without diffusion (1d), hotspots of high susceptibility persist, highlighting spatial heterogeneity and an increased risk of concentrated outbreaks. Similarly, in three dimensions, diffusion (1e) promotes homogeneity in the distribution of susceptibles, as evidenced by smoother surface plots, while the absence of diffusion (1f) results in pronounced peaks and troughs, indicative of localized population clusters prone to outbreaks. These findings underscore the critical role of diffusion in representing real-world movement, such as migration or urbanization, which mitigates the risk of localized epidemics by evening out infection exposure across regions. In contrast, scenarios without diffusion demonstrate the heightened vulnerability of a static, heterogeneous population to rapid and concentrated outbreaks.

Figure 2 illustrates the spatial and temporal dynamics of the latent population under scenarios with diffusion (Figure 2a, c and e) and without diffusion (Figure 2b, d and f) across one, two, and three spatial dimensions. In the case of diffusion (2a), the latent population exhibits a slower decline over time, as diffusion enables individuals to migrate from high-transmission areas or regions with intense infection pressures, thereby slowing the transition to the infectious stage. In contrast, the absence of diffusion (2b) results in a more rapid reduction of the latent population due to the concentration of individuals in high-risk areas, leading to quicker progression to infection or recovery. In two dimensions, diffusion (2c) enables a smoother spatial distribution of latent individuals, reducing the risk of localized clusters that could exacerbate transmission rates. Without diffusion (2d), hotspots of latent population density emerge, increasing the potential for localized outbreaks and rapid disease progression. Similarly, in three dimensions, diffusion (2e) promotes uniformity in the latent population distribution, reflected by smoother surface plots that highlight reduced spatial gradients. Conversely, the absence of diffusion (2f) leads to pronounced peaks and troughs, representing significant spatial heterogeneity with concentrated latent populations in certain areas. These results emphasize the critical role of diffusion in real-world scenarios, where movement through migration or travel spreads latent carriers more evenly across regions, mitigating localized risks and delaying the progression to acute infection in high-density areas.

Figure 3 illustrates the dynamics of the acutely infected population under conditions with diffusion (Figure 3a, c and e) and without diffusion (Figure 3b, d and f) across one, two, and three spatial dimensions. With diffusion (3a), the acutely infected population exhibits a slower peak and decline, as the spatial redistribution disperses infected individuals across the domain, reducing concentrated hotspots and delaying progression or recovery. In the absence of diffusion (3b), the infected population peaks sharply and declines faster, indicating localized clustering of infected individuals, which intensifies transmission and quickly depletes the compartment as individuals progress or recover. In two dimensions, diffusion (3c) leads to a smoother spatial spread of acutely infected individuals, highlighting the homogenizing effect of movement in reducing sharp variations and hotspots. Without diffusion (3d), high-density clusters emerge, increasing the risk of localized outbreaks and overburdening regional resources. Similarly, in three dimensions, diffusion (3e) ensures a uniform spatial distribution of acutely infected individuals, as reflected in smoother surface plots with smaller peaks, thereby preventing extreme local concentrations. Conversely, the absence of diffusion (3f) results in pronounced peaks and troughs, indicating significant spatial heterogeneity and highly localized infection clusters. These findings emphasize that spatial diffusion, representing real-world movement such as migration or travel, disperses infectious individuals more evenly, reducing localized transmission intensity and delaying the epidemic's progression. Without diffusion, infected individuals remain trapped in high-density regions, amplifying transmission rates, exacerbating localized outbreaks, and straining healthcare resources.

Figure 4 illustrates the dynamics of chronically infected individuals with diffusion (Figure 4a, c and e) and without diffusion (Figure 4b, d and f) across one, two, and three spatial dimensions. When diffusion is included (4a), the chronically infected population shows a gradual rise and fall, indicating slower accumulation and depletion as spatial movement prevents clustering and reduces the intensity of transmission hotspots. In contrast, the absence of diffusion (4b) results in sharper peaks and faster declines, as chronically infected individuals remain concentrated in specific regions, leading to rapid disease progression and higher localized burdens. In two dimensions, diffusion (4c) leads to a smoother and more uniform spatial distribution of chronically infected individuals, mitigating the formation of high-density clusters. Without diffusion (4d), hotspots emerge, with distinct regions of high chronic infection densities that increase the risk of long-term health complications. Similarly, in three dimensions, diffusion (4e) promotes a more balanced spatial distribution, reflected in surface plots with smaller peaks and smoother gradients. Conversely, the absence of diffusion (4f) produces sharp peaks and significant spatial heterogeneity, highlighting areas of concentrated chronic infections and potential localized healthcare burdens. These findings underscore the critical role of diffusion in redistributing chronically infected individuals across the spatial domain, reducing the risk of localized overburdening of healthcare resources and the perpetuation of disease transmission. Without diffusion, chronic cases remain confined to high-density regions, exacerbating long-term health burdens and straining regional healthcare systems. This analysis highlights the importance of incorporating spatial diffusion in models to better understand chronic infection dynamics and inform targeted public health interventions.

6.   Conclusions

The study of traveling wave solutions within the framework of nonlinear reaction-diffusion equations provides valuable insights into the modeling of diverse physical and biological processes. In the context of HBV infection, while the spatial distribution of uninfected host cells and infected hepatocytes remains largely stationary, the diffusion of viral particles and therapeutic agents plays a critical role in disease dynamics. This observation inspired the formulation of a diffusion-based model to better understand the mechanisms governing HBV transmission and its treatment. Through a comprehensive analysis grounded in the theory of monotone dynamical systems, we rigorously investigate the existence of traveling wave fronts in reaction-diffusion systems. Our findings indicate that the traveling wave front in the modeled system, under specific initial conditions, represents the action of therapeutic interventions, culminating in the eventual elimination of HBV. These solutions illustrate a dynamic transition, characterized by specific wave velocities, from a persistent infection state to one of eradication. This transition captures the gradual replacement of infection by therapeutic effects, effectively linking equilibrium states over temporal and spatial domains. The determination of the basic reproduction number through the next-generation matrix method offers a crucial metric for understanding the conditions under which the disease can invade or persist in a population. We identify the disease-free and endemic equilibria, demonstrating their stability under specific parameter conditions. This emphasizes the importance of chronic infections, given their role in severe long-term disabilities, such as cirrhosis and hepatocellular carcinoma, and the associated societal and healthcare burdens. The numerical simulations, performed using advanced techniques like the Crank-Nicolson scheme and positivity-preserving methods, validate the theoretical findings and provide actionable insights. These simulations underscore the importance of spatial considerations and the effectiveness of intervention strategies, such as vaccination and treatment, in curbing HBV transmission. This research not only advances the understanding of HBV dynamics but also serves as a critical tool for public health planning, offering valuable guidance for designing targeted interventions, and optimizing resource allocation. Researchers could expand upon this work by integrating additional real-world complexities, such as heterogeneity in host immunity and varying healthcare access, to further refine the model's applicability and precision.

Author contributions

Kamel Guedri: Writing – original draft, Formal analysis, Data curation; Rahat Zarin: Writing – original draft, Software, Investigation; Ashfaq Khan: Formal analysis, Writing – original draft, Resources; Amir Khan: Conceptualization, Writing – review & editing, Supervision; Basim M. Makhdoum: Funding acquisition, Project administration, Validation; Hatoon A. Niyazi: Writing – review & editing, Methodology, Visualization. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to the King Salman center For Disability Research for funding this work through Research Group no KSRG-2024-200.

Funding

The authors extend their appreciation to the King Salman center For Disability Research for funding this work through Research Group no KSRG-2024-200.

Conflict of interest

All authors declare no conflicts of interest in this paper.