1.
Introduction
In the domain of computational intelligence, researchers have utilized the remarkable capabilities of Artificial Neural Networks ANNs to develop intelligent models capable of learning, reasoning and decision-making. The structure of ANNs is subject to variation, influencing the network's capabilities and efficiency in processing and learning from data [1]. As a flexible mathematical model, ANNs sparked a revolution in diverse fields. This transformative impact has led to significant progress in specific areas including image processing [2], speech recognition [3], time series analysis [4], traffic classification [5] and optimization of wireless networks [6]. Building upon the flexible capabilities of ANNs, one variant of ANNs is Discrete Hopfield Neural Network (DHNN) [7]. This network employed local field equation to update the neuron states, offering a potential solution to optimization problems. DHNN have gained considerable attention due to its straightforward structure, resembling of single-layer feedback neural networks [8]. These single-layer networks typically consist of input and output layers without hidden layers. The synaptic weights represent the connections between the neurons and their ability to learn and store information. Specifically, the simple structure of DHNN has proven effective in tackling various optimization challenges [9,10]. While acknowledging the capabilities and efficiency of DHNN in solving optimization problems, there is a very limited strategy to govern the structure of DHNN, primarily due to the predominant focus on achieving optimal neuron states. This often leaves DHNN functioning as a black box model. The term "black box model" implies that the inner workings of the network are not well-understood. This lack of interpretability can lead researchers into uncertainty, potentially optimizing the wrong aspects or facing challenges in determining what should be optimized. By refining these models, the capacity of the network to effectively store and retrieve patterns can be enhanced.
Abdullah [11] addressed this gap by further advancing the DHNN through the incorporation of the concept of satisfiability (SAT) ensuring proper neuron connectivity without compromising network behavior. This approach utilized the structure of Horn Satisfiability (HornSAT), where each clause has at most one positive literal to represent the neurons in DHNN. This milestone not only established a novel approach to neuron representation but also laid the foundation for the subsequent development of the Wan Abdullah (WA) method. This WA method involves comparing the cost function and Lyapunov energy function to find the synaptic weight values. This innovation sparked a new wave of research perspectives, which led to the recognition of SAT as systematic SAT and non-systematic SAT. Kasihmuddin et al. [12] introduced the incorporation of 2 Satisfiability (2SAT) into DHNN. This implementation resulted in a notable increase in the states that achieve global minima energy.
Moreover, Sathasivam et al. [13] introduced the first non-systematic SAT namely, Random 2 Satisfiability (RAN2SAT), which incorporates both first and second-order logics. The flexibility to represent the number of literals in each clause results in enhanced logical variation during the learning phase. However, in minimizing the cost function, the task of finding a satisfied interpretation becomes increasingly challenging as the number of neurons increases. This is due to the presence of more first order logic, which has a low probability of getting satisfied interpretation thereby contributing to more logical inconsistency. Expanding on this idea, Karim et al. [14] extended RAN2SAT to include third-order logic, known as Random 3 Satisfiability (RAN3SAT). The proposed RAN3SAT comprises three different logical combinations, (k=1,3,k=2,3,andk=1,2,3). The simulation results indicated that the combination of second and third-order logics offers the most promising results such that this combination is more consistent in obtaining lower learning and testing errors. This finding led to the introduction of another new non-systematic logical rule, namely Major 2 Satisfiability (MAJ2SAT) in DHNN [15]. While the (k=2,3) ratio remains consistent in RAN3SAT, the structure of MAJ2SAT diverged by incorporating a bias 2SAT clauses compared to 3SAT clauses. Simulated results demonstrated the successful incorporation of MAJ2SAT into DHNN, as the model exhibited the capability to generate global minima solutions and retrieve the optimal final neuron states. Conversely, Zamri et al. [16] proposed another non-systematic logic that represents a distinct perspective. In this work, Weighted Random k Satisfiability (r2SAT) was proposed with inclusion of a weighted ratio involving negative literals. r2SAT managed to obtain a good performance as compared to existing SAT which indicates that having dynamic distribution of negative literals will facilitate producing global minima solutions with diverse final neuron states.
However, the role of negative literals in systematic SAT remain unclear as current works based on systematic SAT failed to emphasize the influence of negative literals within the clauses. For example, Mansor et al. [17] capitalizes 3 Satisfiability (3SAT) structure to represent the neurons in DHNN. Despite the great performance of higher-order systematic logic, this model neglects the negative links in the neuron connections. The formulation of this logical rule only considers the random distribution of positive and negative literals within e clauses. No attention has been given to investigate the impact of negative synaptic weight distribution on the retrieval of final neuron states with global energy. Negative literals are often neglected due to their association with faults or errors. It is crucial to mention that variations in synaptic weights in terms of magnitude are essential for accurately representing real-life classification problems. Therefore, introducing a systematic SAT that promotes the appearance of negative literals results in diverse final neuron states produced, making DHNN a more effective computational system for any optimization problem.
In enhancing the overall performance of DHNN, various initiatives have been proposed by recent researchers to optimize the learning phase of DHNN [12,15,17,18,19,20]. However, there has been limited attention among researchers towards optimizing the retrieval phase. The most recent work that focused on enhancing the retrieval capabilities of DHNN was proposed by Kasihmuddin et al. [21]. In this work, an Estimation of Distribution Algorithm (EDA) was employed to optimize the retrieval phase. Specifically, a univariate marginal Gaussian distribution probability model was used to introduce minor perturbations to the neurons, which in turns will reduce the possible local minima solutions. However, the diversification of the optimized final neuron states in terms of negativity remains unclear and the proposed model failed to guarantee all the optimized final neuron states attained global minima energy. Additionally, the dissimilarity of the optimized final neuron states, particularly focusing on the negative states, also remains uncertain.
These gaps can be addressed by introducing a new metaheuristic approach to optimize the retrieved final neuron states and tackle the multi-objective functions. In response to this, one simple algorithm that has gained attention from many researchers is known as the Black Hole algorithm (BHA). BHA is a natural phenomenon-based algorithm that draws inspiration from the dynamics of black holes in space. It efficiently solves complex optimization problems by simulating how a black hole attracts nearby stars to find optimal solutions. As introduced by Hatamlou [22], BHA has been successfully applied to data clustering challenges using six different benchmark datasets with varying levels of complexity. When compared to other optimization algorithms, BHA outperformed them by generating high-quality solutions with low standard deviation. This success paves the way for implementing BHA into applications such as machine learning [23], image processing, aircraft systems [24] and network applications [25]. In another development, Pashaei & Aydin [26] introduced the Binary Black Hole Algorithm (BBHA) as a streamlined solution for feature selection problems in biological datasets. BBHA addresses the complexities associated with conventional methods by minimizing parameter requirements, offering remarkable computational speed and straightforward implementation. BBHA was used as part of a method for feature selection. The research discovered that the utilization of the hyperbolic tangent function enabled BBHA to effectively overcome challenges associated with feature selection in text, image and biomedical data. This approach outperformed other algorithms considered in the study.
Despite BHA showing promise in various contexts, the incorporation of BBHA into DHNN for optimization problems remains uncertain. This gap presents an interesting opportunity for further investigation, focusing on examining the effectiveness of incorporating BBHA to optimize the retrieval phase of DHNN. It is worth noting that in terms of solving logic satisfiability in DHNN, this work represents the first attempt to optimize the retrieval phase of DHNN in achieving multi-objective functions, which consequently improves the quality of retrieved final neuron states. Thus, this paper presents a new logical rule referred to as Negative Based Higher Order Systematic logic. This logical rule emphasizes the restriction in the appearance of negative literals within the clauses of 3SAT. By incorporating this new logical rule, we can effectively model the neuron in DHNN, leading to enhanced performance of higher order systematic logic. An effective model will result in a higher satisfied interpretation and ultimately optimize the learning phase. Consequently, an optimal synaptic weight will contribute to an improved retrieval phase. By implementing the Hybrid Binary Black Hole Algorithm during the retrieval phase of DHNN, this study aims to enhance the diversification of the states in terms of negativity while attaining global minima solutions and minimizing the similarity index. Therefore, the contribution of this paper is as follows:
1. To formulate a new higher order systematic logical rule namely Negative Based Higher Order Systematic Logic as a symbolic neuron representation in Discrete Hopfield Neural Network. By incorporating the proposed logical rule, the neuron in Discrete Hopfield Neural Network is effectively modelled leading to improved performance of higher order systematic logic.
2. To propose Hybrid Binary Black Hole Algorithm in the retrieval phase of Discrete Hopfield Neural Network by implementing Election Algorithm as a learning algorithm. In this context, the proposed metaheuristic algorithm will be utilized to optimize the final neuron states, aiming to enhance the diversification of the states in terms of negativity and attain global minima solutions while having lowest similarity index. Thus, implementation of this proposed algorithm will guarantee the optimized final neuron states will be beneficial in the perspective of logic mining.
3. To evaluate the performance of Negative Based Higher Order Systematic Logic in Discrete Hopfield Neural Networks and analyze the effectiveness of Hybrid Binary Black Hole Algorithm in optimizing the final neuron states obtained by the network. The performance analysis will be divided into two parts. First, the performance of the proposed logic with different logical rules will be evaluated using various metrics such as learning error, testing error and similarity analysis. Second, we examine how well Hybrid Black Hole Algorithm performs in optimizing the retrieval capabilities of Discrete Hopfield Neural Network.
To effectively fulfil all the objectives, we begin by discussing its motivation in Section 2. In Section 3, we describe the proposed logical representation and discuss the implementation of the logical structure for DHNN in Section 4. Then, we explain the proposed multi-objective functions in the retrieval phase of DHNN in Section 5. In Section 6, we explain the proposed Hybrid Black Hole Algorithm in achieving the multi-objective functions. Next, the experimental framework will be explained in Section 7, and we focus on the findings and analysis in Section 8. Finally, the conclusions drawn from the study and suggestions for future research exploration are provided in Section 9.
2.
Motivation
2.1. Ineffective structure of logical representation
Logical rule is important to guarantee that the knowledge can be represented effectively without losing any information [27]. Note that each structural component on logical rule must be represented correctly before being encoded as symbolic rules into any computational systems. However, much uncertainty exists about the generalizability characteristics of logical rule formulation to be formed in a specific manner or condition. In the context of systematic Satisfiability (SAT) in the DHNN models, existing works such as 2SAT by Kasihmuddin et al. [12] and 3SAT by Mansor et al. [17] disregarded the distribution of negative literals throughout respective SAT logical rules. This implied that the distribution of negative literals is set randomly. When the SAT model operates with randomized positive and negative activated neuron connections, the interpretability quality of DHNN is questioned. This is because, with no demand and unclearness on the distribution of either negative or positive literals, the SAT model provided unclear information on what logical relations are significant to be directed towards optimal production of the final neuron states. Consequently, the practicality of embedding SAT as logical rules into DHNN declines which depicts the importance for the SAT to have some level of negation control to ensure the direction of the retrieval phase can be strengthened. Unfortunately, little attention was given in the development of formulating logic with specific conditions before being encoded as an actual symbolic language. Therefore, we introduced Negative Based Higher Order Systematic logic or NR3SAT as a logical rule to control the appearance of negative literals within the clauses. Note that this is the first approach on introducing higher-order systematic logical rule that emphasize the restriction on the appearance of negative literals in the formulation of SAT.
2.2. Limited diversification of states concerning negativity
The final neuron states retrieved during the retrieval phase of DHNN are significant as the states represent the network's pattern and act as an indicator of successful pattern retrieval. Evaluating the quality of the retrieved final neuron states often involves assessing the diversity of the solutions. Previous studies in the literature typically assessed solution diversification through similarity index analysis. In this context, a low similarity index indicates high dissimilarity between the retrieved and benchmark states, contributing to diversified solutions. For instance, Karim et al. [14], employed measures such as the Jaccard index, Kulczynski Measure and Ochiai coefficient to evaluate the quality of the retrieved solutions. Additionally, Roslan et al. [28] categorizes a solution as diverse from the benchmark if it surpasses the specified diversity tolerance value told=0.1. Another study by Alway et al. [29] defined diversified solutions in terms of dissimilarity compared to benchmark states, categorizing retrieved final neuron states as diversified if there is at least a 10% dissimilarity to the benchmark states. However, existing works have predominantly overlooked a crucial aspect which is diversification concerning solution string. While each solution string may differ from the benchmark states, the diversification of the solution string in terms of negativity remains uncertain. This oversight can lead to high neuron overfitting due to the low impact of diversity. Therefore, this paper proposes the incorporation of the Hybrid Black Hole Algorithm to optimize the retrieved final neuron states, ensuring that the optimized states achieve the desired proportion of negative states in each solution string while maintaining achieve maximum global solutions.
2.3. Inefficient discrete Hopfield neural network
According to Gharehchopogh et al. [30], optimization refers to the process of determining the most favorable values for decision variables to achieve either the minimum or maximum value of a given objective function. The primary aim of optimization techniques is to thoroughly explore and analyze the search space, ultimately finding an optimal solution for a specific problem [31]. In the context of logic satisfiability within the DHNN framework, current research predominantly directs its efforts toward improving the learning phase of the network. Numerous researchers employ metaheuristic algorithms to bolster the DHNN framework, resulting in optimal synaptic weight being retrieved during the learning phase [18,20,32,33]. If the proposed learning algorithm fails to attain the satisfied interpretation, synaptic weights will be generated randomly. However, despite the achievement of optimal synaptic weights leading to the retrieval of global solutions, uncertainties persist regarding the quality of the retrieved final neuron states, particularly within the solution strings. This can be supported by the work on systematic SAT, which encounters an overfitting issue, even though the solutions obtained are global [34]. In another development, Kasihmuddin et al. [21] utilized an Estimation of Distribution Algorithm (EDA) to optimize the retrieval phase of DHNN but encountered suboptimal results in the learning phase due to relying on Exhaustive Search (ES) as a learning algorithm. Previous studies have focused on improving either the learning or retrieval phases of DHNN individually, but little attention has been given to enhancing both simultaneously. This provides motivation to enhance the efficiency of the DHNN framework by optimizing both learning and retrieval phase. Thus, Election Algorithm inspired by Sathasivam et al. [34] will be employed during the learning phase to enhance the learning capabilities of DHNN in minimizing the cost function. Moreover, Hybrid Black Hole Algorithm will be proposed to optimize the retrieval phase of DHNN in achieving the multi-objectives functions. The aim of introducing these objectives is to ensure the optimized final neurons state are in optimal configurations. The optimization will focus on generating optimal final neuron states by considering the diversification of the solutions string, the attainment of global solutions and the lowest similarity index.
3.
Negative based higher order systematic satisfiability
Negative Based Higher Order Systematic Satisfiability referred to as NR3SAT is a logical representation that consists of higher order logic 3SAT with a restriction on the appearance of negative literals within the clauses. The main features of the proposed NR3SAT are presented as follows:
(a) Set of m variables represent as q1,q2,q3,…,qm, which holds bipolar values of qi∈{1,−1}.
(b) Set of literals, qi∈{qi,¬qi} such that qi and ¬qi represents positive and negative literals, respectively.
(c) Set of n definite third order clauses represent as Q∗1,Q∗2,Q∗3,…,Q∗n such that each clause, Q∗i consists of at least one negative literals in a clause and n∈Z+.
(d) Each clause of Q∗i is restricted to only three literals such that all clauses are connected to logical AND (∧), and literals in each clause are connected to logical OR (∨).
Using the information gathered in (a)–(d), the general formulation of NR3SAT is introduced as follows:
where the possible combination of ℓNR3SAT is defined as in Eq (2) such that:
These combinations of clauses do not consider all positive literals in a clause such that Q∗i∉(qi∨qj∨qk). By considering both Eq (1) and Eq (2), the possible structure of ℓNR3SAT for the minimum number of neurons can be represented as follows:
4.
Negative based higher order systematic satisfiability in discrete Hopfield neural network
Incorporating NR3SAT into the learning phase of DHNN, often denoted as ℓNR3SAT serves as the central objective, aiming to minimize the cost function of the network corresponding to the logic. This minimization of the cost function can be obtained by reducing the logical inconsistency of ℓNR3SAT. Therefore, the cost function, EℓNR3SAT of ℓNR3SAT can be deduced as shown in Eq (4).
Referring to Eq (4), n is the number of clause in ℓNR3SAT and Zij denoted as the inconsistency of ℓNR3SAT. In this context, the inconsistency of ℓNR3SAT can be derived by taking the negation of ℓNR3SAT and then expand it using Eq (5) such that ¬qi is the negation of the literal in ℓNR3SAT. It is also crucial to emphasize that by taking the negation of ℓNR3SAT, the logical AND operation will signify the multiplication of literals within the clauses, while the logical OR operation signifies the addition of clauses to other clauses.
Note that, in reducing the logical inconsistency, the value of EℓNR3SAT reflects the count of unsatisfied clauses. If the number of unsatisfied clauses increases, the value of EℓNR3SAT will also increases. Therefore, the minimization of the cost function only obtained when EℓNR3SAT=0 indicates that all clauses in ℓNR3SAT are satisfied. In this case, Exhaustive Search (ES) will be implemented to find a satisfied interpretation of ℓNR3SAT. ES is often referred to as the trial-and-error approach characterized by its comprehensive exploration of all possible combinations of subsets within a given set. The main motivation behind utilizing ES as a learning algorithm is it is easy to be implemented. Additionally, most researchers in the literature including recent works by [35,36,37] employed ES to assess the capabilities and the stability of newly proposed symbolic rule in DHNN. Thus, this makes ES a valuable and commonly used approach for evaluating and benchmarking the performance of novel symbolic rules in DHNN. Using the concept of generate and validate, this approach enumerates all potential solutions within the search space until it identifies the optimal solution. Therefore, ES will be employed to determine the maximum number of satisfied clauses as described in Eq (6) such that Q∗i referred to the clause of ℓNR3SAT and NC is a total clause. A satisfied interpretation of Q∗i clause can be defined as in Eq (7).
In this context, ES plays a crucial role in locating a satisfied interpretation that optimizes the fitness function in Eq (6) which correspond to the minimization of the cost function. Then, by considering all connection of ℓNR3SAT, the Lyapunov energy function of DHNN can be written as outlined in Eq (8).
Hence, the values of the corresponding synaptic weights Wij, W(2)ij and W(3)ijk can be obtained using the Wan Abdullah (WA) method through a direct comparison between the cost function presented in Eq (4) and the Lyapunov energy function of DHNN, as outlined in Eq (8) [11]. These resultant values can then be stored in a Content-Addressable Memory (CAM). This weight holds the properties of always being symmetrical (Wij=Wji) and there are no self-connections among them. Hence, the anticipated global minimum energy can be achieved by substituting the synaptic weight values stored in CAM into Eq (8), by utilizing a satisfied interpretation. As an illustration, one such satisfied interpretation is provided below:
By considering the neuron states as in Eq (9) into Eq (8), the expected global minimum energy of ℓNR3SAT is HminℓNR3SAT=−0.375. This value is defined as the lowest attainable energy state that the network can reach and will serve as a benchmark to evaluate the final energy value [38]. During the retrieval phase of DHNN, the synaptic weight values are used to update the local field of the network. When dealing with higher order neurons connections, the local field denoted as hi can be defined as in Eq (10).
In this case, optimal synaptic weights acquired during the learning phase play a crucial role in ensuring that the network converges to optimal final neuron states during retrieval phase. Then, Hyperbolic Tangent Activation Function (HTAF), as detailed in Eq (11) serves as a squashing mechanism, transforming the values obtained in Eq (10) into bipolar states, typically either 1 or -1. Thus, the final neuron states, Sfi are updated as demonstrated in Eq (12).
Finally, final energy states were obtained using Eq (8). Then, the difference between the final energy and minimum energy will be evaluated based on Eq (13) as follows:
If the difference between global minimum energy and final energy falls within the range defined by Tol such that Tol=0.001, ℓNR3SAT achieve global minima energy confirming it is successfully be embedded in DHNN. In this case, Tol is set to a specific value as recommended by [35,36,37] to reduce the statistical errors within the solutions. The pseudocode of ℓNR3SAT(ES) is presented in Algorithm 1, and the schematic diagram of DHNN is illustrated as in Figure 1.
5.
Multi-objective functions in the retrieval phase of DHNN
We introduce a set of objective functions designed to ensure that the final neuron states obtained are in their optimal configurations. Therefore, our aim of the first objective is to obtain diversified final neuron states. Now, one may wonder, why is diversity essential? To address this question, the need for diversified final neuron states arises from the necessity to create more dynamic induced logic. This involves introducing variations particularly in terms of negativity to effectively tackle real-life classification problems. Diverse solutions provide a wider range of responses, enhancing adaptability, and robustness in problem-solving scenarios. Second, it is crucial to ensure that all the diversified solutions generated are in a global state.
Achieving global minima solutions signify that the proposed logic and algorithm are successfully implemented into the DHNN framework. Last, the third objective of this phase aims to ensure the lowest similarity index is obtained. Therefore, the novelty of this study lies in optimizing these three objectives: (ⅰ) Diversification in terms of negativity, (ⅱ) attainment of a global minima solutions, and (ⅲ) achieving a low similarity index. Mathematically, the proposed multi-objective functions can be generalized as follows:
such that
To accomplish all these objectives, the implementation of a metaheuristic algorithm in the retrieval phase of DHNN is deemed essential. The upcoming section provides a comprehensive explanation of how the proposed metaheuristic algorithm can successfully fulfil all the objectives outlined in Eqs (15)–(17). This algorithm plays a pivotal role in optimizing final neuron states, ensuring diversified and global solutions with low similarity indices, thus enhancing the overall performance and effectiveness of the DHNN framework.
6.
The proposed hybrid black hole algorithm in optimizing retrieval phase of DHNN
In this section, we provide a comprehensive explanation of the optimization process in the retrieval phase of DHNN. To ensure the optimal utilization of synaptic weights during the retrieval phase, the Election Algorithm (EA) is employed during the learning phase to enhance the process of finding satisfied interpretation and consequently minimizing the cost function. EA is a valuable addition as it guarantees the achievement of optimal synaptic weights. Recent research by Abubakar & Danrimi [39], Roslan et al. [28], and Someetheram et al. [33] have demonstrated the effectiveness of EA as a learning algorithm to minimize the cost function within DHNN. The implementation of EA significantly enhances the convergence of the network towards minimizing the cost function. Then, an enhanced optimization algorithm called Hybrid Black Hole Algorithm (HBHA) will be employed to optimize the final neuron states. The primary goal was to ensure that the optimized final neuron states align with the proposed multi-objective function as discussed in the previous section. The HBHA process begins with the initialization of a population of stars, as outlined in Eq (18) as follows:
Referring to Eq (18), the variable Sfi represent the final neuron states to be optimized where Sfi∈[1,NN] and Stari∈[1,NT]. In this context, NN referred to the total number of neurons defined and NT is referring to the number of trials declared in the process. These final neuron states were obtained by squashing the updated local field, hi values using tangent hyperbolic function. Mathematically, the generalized initial star population, P[Stari(Sfi)] can be derived as in Eq (19).
After establishing the initial population, the HBHA utilizes the first two objective functions defined in Eqs (15) and (16) which involve diversifying the final neuron states in terms of negativity and achieving global minima solutions. In this context, fD refers to the diversity fitness of ℓNR3SAT while fZ denotes the fitness value associated with the attainment of global solutions. The diversification of final neuron states is a critical objective. It involves ensuring that the states of neurons in the network exhibit a wide range of patterns and behaviors rather than being uniform or repetitive. To achieve this objective, diversification is defined as the variation in terms of negativity, primarily derived from clauses. In essence, it focuses on diversifying the states of the literals within the clauses, which is pivotal for enhancing the diversity of the logical rules within the network. This can be done by setting the percentage of negativity, m%, that is needed and HBHA will be implemented to ensure the optimized final neuron states achieved at least m% of the clauses containing at least one negated state for each Stari. Thus, the diversity fitness can be declared as follows:
such that
From the perspective of achieving global solutions, one alternative approach to determine whether the states are global or local is by computing the satisfied interpretation of each Stari. In this context, each Stari is said to be global if the star can attain the maximum satisfied interpretation which is associated with the total number of clauses. The generalization of the fitness value associated with the attainment of a global solution can be defined in Eqs (22) and (23) as follows:
such that
By defining the fitness function within the HBHA, fitness values can be calculated for each Stari in the population. Subsequently, based on these fitness values, the Stari with the highest fitness value which achieve both maximum diversity and global solution is selected as the Black Hole, StarBHi(Sfi), while the remaining Stari will be considered as normal stars. To enhance the exploration of the optimal solution within the search space, a global search operator called Star Replication is proposed in this research. This process draws inspiration from the cloning process in the Clonal Selection Algorithm, which is based on the natural processes of the immune system, explaining how the immune system generates antibodies to combat antigens. In the context of the HBHA, by replicating these stars, a balance is struck between exploring the solution space and exploiting promising solutions, a crucial aspect of effective optimization. The new population of stars after replicating those with the highest fitness can be formulated as follows:
such that
According to Eq (24), the StarBHi(Sfi) will be replicated to enhance the ability of HBHA to efficiently discover optimal solutions. The number of replicated star, n[StarRi(Sfi)] can be determined based on Eq (25) such that β represent the replicating rate defined within the range of 0 and 1. By considering the replicated stars denoted as StarRi(Sfi), the total number of population stars P[Stari(Sfi)] will increase compared to the initial population of stars. In this new population, the StarRi(Sfi) are treated like other normal stars, Stari(Sfi). After establishing the new population of stars, StarNi(Sfi), the strong gravitational pull of StarBHi(Sfi) causes all other stars to gradually move closer to the position of StarBHi(Sfi). Consequently, the positions of the stars are updated using Eq (26) as follows:
Referring to Eq (26), Stari(Sfi(t+1)) represents the updated positions of stars in the next iteration, where θ is a random number defined within the range of 0 and 1. Stari(Sfi) and StarBHi(Sfi) refer to the current positions of the stars and BH respectively. During this phase, the positions of Stari(Sfi(t+1)) exist in continuous form. To convert these continuous values of star positions into bipolar values of 1 and -1, a transfer function is essential. This transfer function will determine the probability of changing the elements of the position. In this context, the Hyperbolic Tangent function is employed to modify the positions of the stars, as described in Eqs (27) and (28). It is worth noting that this function belongs to the group of Ⅴ-shaped transfer functions and has been found to exhibit good performance compared to other transfer functions [40]. This function plays a crucial role in discretizing the positions of the stars, making them compatible with the requirements of the optimization algorithm.
such that
After updating the position of the stars, the fitness values will be computed. If F[Stari(Sfi(t+1))]>F[StarBHi(Sfi)], the Stari(Sfi(t+1)) will be assigned as new StarBHi(Sfi) or else StarBHi(Sfi) remain unchanged. It is essential to highlight that as the stars move towards the BH, there is a possibility of crossing the event horizon. If a star crosses the event horizon, it will be absorbed by the BH and disappears. The radius of the event horizon denoted as R is defined as outlined in Eq (29).
To ascertain whether the stars cross the event horizon or not, the distance between the star and BH denotes as D, is computed as described in Eq (30).
If D<R, it indicates that the stars have crossed the event horizon and will disappear. In this case, new stars will be generated randomly to replace those that have crossed the event horizon. This process involves the exploitation of stars towards optimal solutions while simultaneously ensuring the continuous exploration of the search space, even as some stars may be absorbed by the BH during the optimization process. Then, the process in HBHA will be repeated until it meets the defined stopping criteria. This can be either when the process reaches the maximum specified number of generations or when the star population reaches the maximum fitness, as defined in Eqs (15) and (16). The optimize final neuron states can be generalized as follows:
Next, to fulfil the third objective function as in Eq (17), Rogers and Tanimoto similarity index (RT) will be employed in this phase to measure the similarity of states before (Sfi) and after (Sfai) optimization takes place for each string of Stari. This phase is essential to evaluate how HBHA helps to improve the current final neuron states. If there is high similarity between (Sfi) and (Sfai), the implementation of HBHA in optimizing the retrieval phase of DHNN is considered unsuccessful since the optimized solutions are overfitted. The RT value between the neuron of Stari can be obtained by comparing the states before the optimization took place as in Eq (19) and states after the optimization took place as in Eq (31). By considering τ as the similarity index coefficients for states before and after optimization took place, the formulation of RT can be generalized as in Eqs (32)– (37).
such that
Referring to Eq (33), the lower value of RT indicates high dissimilarity between the states before and after the optimization took place. Therefore, the optimized final neuron states will be considered as new final neuron states (Snfi) of ℓNR3SAT if the states after being optimized can successfully achieve all three multi objectives derived as in Eqs (15)–(17). This can be generalized as follows:
The pseudocode of HBHA is presented in Algorithm 2. Additionally, the flowchart of the proposed HBHA can be summarized as in Figures 2 and Figure 3 illustrated the flowchart of the proposed model in optimizing the learning phase and retrieval phase of DHNN.
7.
Experimental framework
In assessing the effectiveness of the proposed model, this section offers a comprehensive overview and discussion of the experimental setup. The first subsection explained the simulation platform employed in this study, followed by a detailed explanation of the parameter setup utilized in both the learning and retrieval phases of DHNN. Subsequently, an overview of the performance metrics considered throughout this study is presented. The final section outlines the baseline model used in the learning phase and the baseline algorithms employed during the retrieval phase.
7.1. Simulation platform
In this paper, all simulations were executed using the open-source software DEV C++ (version 6.3) with Windows 10 operating system as a platform which equipped with an Intel Core i3 processor and 8GB of RAM. This deliberate choice was made to eliminate potential biases during both code execution and result recording. Consequently, the experiments were consistently performed using the same compiler on the same computing device with identical processing power.
7.2. Data simulation
To assess the effectiveness of this proposed model, the simulated dataset utilized in this study was generated by randomly assigning bipolar values of 1 and -1, adhering to the logical structure of ℓNR3SAT. In this context, employing simulated data is a widespread practice for simulating and evaluating the performance of the proposed model, as demonstrated in the research conducted by [24,46,50,51].
7.3. Parameter setup
The parameter setup employed throughout this study will be explained, focusing on both the learning and retrieval phases of DHNN, as detailed in the upcoming subsections.
7.3.1. Parameter setup in the learning phase
In assessing the efficiency of the proposed Negative Based Higher Order Systematic Logic in the framework of DHNN, the analysis involved conducting simulations using 69 distinct logical combinations (number of clauses) which corresponds to a total of 207 neurons. However, to facilitate comparison with prior research on systematic and non-systematic logic, the number of neurons (NN) will be within a defined range. Table 1 summarizes all the essential parameters for the configuration based on ES as the learning algorithm.
7.3.2. Parameter setup in the retrieval phase
To evaluate the effectiveness of HBHA to optimize the final neuron states retrieved by NR3SAT model, performance analysis will be conducted based on specific parameter setup. The parameters involved in the proposed model for simulated dataset are listed in Table 2. Additionally, detailed description of the parameters used in HBHA is presented in Table 3. Furthermore, Table 4 to Table 11provided an overview of the parameters utilized in 10 baseline algorithms to assess their effectiveness compared to HBHA.
7.4. Performance metrics
The evaluation of the DHNN will concentrate on assessing the effectiveness of the proposed logical rule NR3SAT in comparison to other logical structures. In contrast, evaluating the performance of HBHA will primarily consider the ability of the proposed HBHA in achieving a multi-objective functions, which is generating varied and global solutions with low similarity index. Consequently, we categorize the performance metrics into two parts:
(a) The evaluation of the efficiency of NR3SAT in DHNN will involve analyzing various performance metrics such as learning error, testing error, global minimum ratio, total neuron variation, and Jaccard similarity index.
(b) The performance metrics used to assess the effectiveness of HBHA in optimizing the retrieved final neuron states will focus on achieving an optimal solution string. This will be evaluated in terms of diversified solutions, global minima solutions, string that achieve both diversified and global minima solutions, and similarity index analysis.
7.4.1. Performance metrics in learning and retrieval phase
Performance metrics assume a critical role in evaluating the effectiveness and quality of the network's performance, particularly in relation to the proposed model. In this context, these metrics will be applied to assess the performance of the proposed ℓNR3SAT model, comparing it to the existing models. This extensive evaluation encompasses two crucial phases: The learning phase and the retrieval phase of DHNN. In the learning phase of DHNN, error analysis is conducted using Mean Absolute Percentage Error (MAPE). Inspired by Sathasivam et al. [34], we employ this metric to evaluate the efficiency and learning capabilities of ES in finding a satisfied interpretation of NR3SAT. Eq (39) provide the formulations for MAPE. Based on the Equations, fNC represents the maximum fitness of satisfied clauses associated to NR3SAT and fi represent current fitness obtained. Ideally, all these metrics were employed to assess the efficiency of ES in finding maximum satisfaction of the proposed logical rule.
In the retrieval phase, the performance metric will be employed to assess the quality of the retrieved final neuron states using Eq (40) [14]. Based on Eq (40), i referred to the number of iterations throughout the process. According to Roslan et al. [42], this testing error can be used to evaluate the accuracy of the retrieved final neuron states. In this case, zero testing errors indicate global solutions.
Additionally, drawing inspiration from the work of Kasihmuddin et al. [21] to ensure the stability of the retrieved final neuron states and the minimization of energy achieved, the performance will be assessed using Global Minima Ratio, RG as outlined in Eq (41). Worth mentioning that the optimal value of RG is when RG=1, which indicates that the retrieved states achieved global minima energy at the number of neurons.
To comprehensively assess the quality of the final neuron states retrieved, an analysis of similarity index values and cumulative neuron variation will be conducted. Ideally, the similarity index analysis was used to measure the diversification of the states by comparing the final neuron states retrieved by the network with the benchmark states. In this context, the benchmark neuron state is defined as follows:
Referring to Eq (42), qi and ¬qi defined as positive and negative literal respectively. Drawing inspiration from the work of Alway et al. [15], the Jaccard similarity index as outlined in Eq (43) will be utilized to measure the similarity of the positive value in comparison to the benchmark states, as detailed in Eq (42). Table 12 presented all the parameters utilized in both learning and retrieval phase of DHNN and the list of parameters incorporated within the similarity index is presented in Table 13.
Additionally, cumulative neuron variation often referred to as TV, is employed to assess the model's ability to explore diverse solutions across various regions within the search space. The TV can be formulated as in Eqs (44) and (45) such that v represents the total string of retrieved final neuron states while Ki function as a scoring mechanism to determine the count of distinct neuron states between the benchmark and retrieved final neuron states.
such that
7.4.2. Performance metrics in optimizing the retrieval phase of DHNN
To evaluate the effectiveness of the proposed model, we will analyze how well the model optimizes the retrieval phase of DHNN to meet the objective functions. Our proposed HBHA aims to produce diverse and global solutions with low similarity indices, thereby enhancing overall performance and effectiveness of the DHNN framework. A key focus on implementing EA in the learning phase as EA contributes to achieving an optimal learning phase, which consequently leads to an optimal retrieval phase. By incorporating HBHA into the retrieval phase, we anticipate optimizing the final neuron states retrieved by the network. Therefore, various performance metrics will be introduced to assess the quality of the optimized final neuron states. The evaluation focuses on each string of final neuron states emphasizing the diversification of negativity, the attainment of global minima solutions and solutions with low similarity index. Regarding diversification, we focused on obtaining diversified solutions based on clauses. For instance, when the degree of negativity is set to m%, it signifies that the optimized final neuron states must contain at least m% of the total number of clauses, each having at least one negative literal. In this context, the number of diversified solutions, NDS can be defined using Eq (46) as follows with diversification rate of m%.
In Eq (46), n(NSfiDS) represents the number of solution strings that achieved the maximum predefined diversity rate while α denotes the total number of simulation sets to be executed, α=NT×C. Note that α can also be referred to as the total number of solutions. The optimized final neuron will be evaluated based on each string according to Eq (47).
In the perspective of evaluating the solution string that attain a global solution, the number of solution strings that achieve global solutions, NGS can be determined using Eq (48). The solution string NSfiGS that achieves a global solution is defined in Eq (49), indicating the optimized final neuron states that successfully interprets the logical rule NR3SAT.
such that
By evaluating the solution string that achieved NDS and NGS, we can evaluate the solution string that achieved both maximum NSfiDS∩NSfiGS, which is computed as in Eq (50).
Thus, NDG represents the number of solution strings that have met both objectives. Additionally, the global minimum ratio, NGR for the total number of global solutions obtained by NGS can be evaluated using Eq (51).
In the perspective of attaining low similarity index, taking inspiration by the work of Zamri et al., [16], this paper focusses on Rogers and Tanimoto similarity index, RT to assess the quality of the optimize final neuron states. This is due to the ability of this metric to measure the similarity of the negative cases for each string of solutions between before and after optimization took place. In this context, the benchmark solutions are referring to the retrieved final neuron states before optimization takes place which can be define as in the Eq (52) such that qi and ¬qi referring to the positive and negative literals of NR3SAT. Moreover, the optimize final neurons state can be referred to as Sfai.
Thus, the general comparison between the benchmark states and optimize final neuron states is presented as Eq (53) such that τ is referring to the similarity index coefficients defined as in Table 14. The formulation of RT is given as in Eq (54). It is crucial to emphasize that when evaluating the quality of the optimized final neuron states, the effectiveness of the proposed algorithm is measured by its capability to yield low values of RT. Lower values of RT in each comparison between string indicate that the optimized final neuron states differ from the benchmark states. Table 15 presented the list of symbols utilized in the experimental setup.
7.5. Baseline logical rules
In the learning phase of DHNN, NR3SAT will be compared with several existing baseline models. Each of these baseline models is described as follows:
(a) 3SAT [17]: 3SAT is a SAT formulation within the systematic SAT class, characterized by a restricted number of literals per clause. In this context, each clause consists of 3 literals. As described by Mansor et al. [17], 3SAT exhibits a higher probability of obtaining satisfied interpretation compared to other systematic SAT variants. Consequently, 3SAT has the potential to achieve an optimal learning phase, leading to a greater production of global minima solutions.
(b) RANkSAT [14]: RANkSAT is a SAT formulation belonging to the non-systematic SAT class, which encompasses first order, second order and third order classes. Each class in RANkSAT is designed to have an equal representation. The performance for all logical combinations was evaluated and results showed that RANkSAT with a logical combination of (k=2,3) yield the most promising results compared to other combinations. Notably, the trend of RANkSAT for (k=2,3) is more consistent in obtaining lower learning and testing errors. The finding emphasizes that higher order logical structure contributes to higher probability of achieving global solutions.
(c) MAJ2SAT [15]: MAJ2SAT is another non-systematic SAT class which includes both second order and third order classes. In the study, Alway et al. [15] enhance the structure of the logical rule by introducing a bias of 2SAT clauses compared to 3SAT clauses. Simulated results signified MAJ2SAT successfully embedded in DHNN since the model can generate optimal final neuron states that achieve global minima energy. Notably, MAJ2SAT demonstrated its proficiency in retrieving accurate synaptic weights that play a crucial role in achieving global minima solutions.
(d) GRANkSAT [41]: Gao et al. [41] contribute to explore innovative logical structures by proposing a novel and flexible higher-order logic called G – Type Random k Satisfiability (GRAN3SAT) in DHNN. This newly introduced logic stands out as both systematic and non-systematic structure. GRAN3SAT consists of new random feature of first, second and third order clauses and the performance of GRAN3SAT was evaluated using order clauses, different proportions of positive and negative literals and different number of learning trials. Based on the findings, when considering GRAN3SAT with the highest proportion of 3SAT clauses, the learning process exhibited the lowest Mean Absolute Error (MAE) and Root Mean Square Error (RMSE). This observation supports the idea that implementing third-order clauses into GRAN3SAT decreases the learning errors.
7.6. Baseline algorithms
To evaluate the effectiveness of the proposed algorithm in optimizing the retrieved final neuron states, HBHA will be compared against several baseline algorithms. This includes Genetic Algorithm (GA) [12], Clonal Selection Algorithm (CSA) [47], Differential Evolution Algorithm (DEA) [48], Artificial Bee Colony Algorithm (ABCJ) [49], Artificial Bee Colony Algorithm (ABCK) [19], Artificial Bee Colony Algorithm (ABCS) [35], Election Algorithm (EA) [34], Sine Cosine Algorithm (SCA) [44], Whale Optimization Algorithm (WOA) [50], and Black Hole Algorithm (BHA) [26]. All these baseline algorithms can be categorized into four major categories including Evolutionary-based, Swarm intelligence-based, sociopolitical-based, and Natural phenomena-based, which can be presented in Figure 4. Each of these baseline algorithms is described as follows:
(a) GA [12]: The implementation of the GA in DHNN aims to enhance the learning phase and improve the accuracy of finding correct neuron states that can increase the probability of getting satisfied interpretation of 2SAT logical rule. By combining exploration and exploitation processes of the GA, GA helps in searching for an optimal neuron state with high fitness value. This incorporation reduces hamming distance and achieves a higher global minima ratio as compared to traditional exhaustive search methods. Thus, the performance of 2SAT in DHNN has been improved.
(b) CSA [47]: Incorporating the CSA in this research aims to enhance the learning phase of DHNN. CSA, inspired by the natural immune system improves the learning mechanism of the DHNN through selection, cloning and somatic hypermutation. By implementing CSA into the model, it aims to optimize employee resource application approval processes by efficiently searching for an optimal induced logic.
(c) DEA [48]: DEA involves three operators: mutation, crossover and selection. Mutation explores a wide range of potential solutions in the search space for global search. Crossover refines solutions locally near the target vector to exploit optimal results. The balance between exploration and exploitation is crucial for high-quality solutions in optimization problems. In this research, a novel binary differential evolution algorithm based on Taper-shaped transfer functions is proposed to address binary optimization problems that cannot be solved directly by traditional DE due to its reliance on real number operations for mutations. By employing transfer functions such as S-shaped, U-shaped or Ⅴ-shaped curves, the binary form of DE can be attained efficiently.
(d) ABCJ [49]: Jia et al. [49] introduced a new binary optimization algorithm that is based on the original ABC algorithm. The main process of this algorithm consists of three phases: Employed bees' phase, onlooker bees' phase, and scout bees' phase. Movement in these phases is done using bitwise operators. The proposed bitwise ABC algorithm has been compared to other binary algorithms using various benchmark functions. Additionally, this study also compared the proposed ABC with other variations of both the ABC and GA algorithms. Experimental results demonstrated that the proposed ABC achieves better accuracy in optimization as well as faster convergence speed when compared to other algorithms used in this research.
(e) ABCK [19]: Kasihmuddin et al. [19] implemented a novel bitwise operator in the ABC algorithm to solve the 2SAT. The purpose of this implementation was to improve the learning phase of DHNN. By incorporating ABC as a searching technique with DHNN, they aimed to find a satisfied interpretation of 2SAT logic within an acceptable timeframe. Their goal was to compare the performance of solutions produced by DHNN with ABC, HNN2SAT-ABC against traditional learning algorithms, HNN2SAT-ES. The results show that HNN2SAT-ABC outperforms HNNSAT-ES in terms of global minima ratio, hamming distance and CPU time, suggesting that using ABC is a better alternative method for finding satisfied interpretation of 2SAT.
(f) ABCS [35]: Sidik et al. [35] provided insights into the effectiveness of different bitwise logic gate operators and their compatibility with the ABC algorithm. They focused on controlling the distribution of negative literals by implementing the ABC algorithm in the logic phase. The study compares the performance of different logic gate operators in producing desired logical structures. The results showed that implementing the NAND operator with the ABC algorithm outperforms other operators in terms of generating negative literals. Choosing the correct logic gate operator enhances fitness and improves exploration and exploitation processes for finding optimal solutions. Different operators have varying levels of success depending on specific ratios of negative literals.
(g) EA [34]: Sathasivam et al. [34] investigated the use of EA to enhance the learning phase of a DHNN. The goal is to optimize the learning phase of DHNN by ensuring that the cost function of RAN2SAT converges to zero, indicating a satisfied interpretation of the logical rules. Due to low probability of finding satisfied interpretation for first order clauses, complexity of logic satisfiability increases significantly in DHNN. However, by employing EA, neuron states can be effectively flipped. The results demonstrated the accuracy and effectiveness of EA as a learning algorithm in DHNN for RAN2SAT with varying numbers of neurons compared to other algorithms such as Exhaustive Search and Genetic Algorithm.
(h) SCA [44]: This research proposed two binary SCA, S-shape and Ⅴ-shape, for medical feature selection. These algorithms convert continuous values into binary using transfer functions. The goal is to select effective feature subsets from medical data, improving classification accuracy while reducing the subset length. Experimental results showed that both binary SCAs outperform other algorithms in classifying medical datasets.
(i) WOA [50]: Hussien et al. [50] proposed two binary versions of the WOA called bWOA-S and bWOA-Ⅴ for feature selection problems. These versions use specific transfer functions, either S-shaped or Ⅴ-shaped, to convert continuous search space solutions into binary solutions. The objective of implementing WOA is to deal with feature selection problems by simplifying high-dimensional datasets and improving classification accuracy through selecting relevant features while removing irrelevant and redundant data. Inspired by humpback whales' bubble-net feeding hunting technique, the classical WOA sets the current best candidate solution close to either the optimum or target prey while other whales update their position towards this best solution.
(j) BHA [26]: Pashaei & Aydin [26] used binary version of BHA and decision tree algorithm to solve the feature selection and classification problem in biological data. BHA is an optimization technique inspired by black holes in outer space, where stars simulate their behavior. The best star with the best fitness value acts as the black hole, pulling other stars towards it like gravitational force in real space. The Binary Black Hole Algorithm (BBHA) is an extended version of the BHA that solves discrete problems, such as feature selection. BBHA applied binary structure to indicate which features belong in the final set. BBHA was tested on biological datasets and compared with other methods, showing superior performance in all metrics.
8.
Results and discussion
In this section, we focus on providing a comprehensive analysis of the performance of the proposed DHNN model, considering the selected performance metrics and all the parameters configured in both the learning and retrieval phases of DHNN. The analysis focused on the capabilities and efficiency of the proposed model in comparison to well-established baseline models. To elaborate further, the results and discussions are divided into two main parts. The first part will be focused on evaluating the performance and stability of DHNN in reducing the logical inconsistencies of NR3SAT compared to the existing models. This section focused on the results and discussions pertaining to the use of ES as the learning approach. The subsequent section will shift the focus to the efficiency of the proposed HBHA in optimizing the retrieval phase of DHNN when compared to existing baseline algorithms.
8.1. Performance analysis of ℓNR3SAT in the learning phase
The performance analysis of the proposed NR3SAT logical rule in the framework of DHNN will be discussed based on several metrics. In the first subsection, we focus on the learning errors analysis followed by testing errors analysis and similarity index analysis. In the last subsection, we discuss non-parametric statistical analysis. Moreover, in the second part of this section, we explain the results and findings based on optimizing the retrieval capabilities of DHNN.
8.1.1. Learning error analysis
To provide insight on the performance of DHNN by incorporating NR3SAT logical rule and ES as the learning approach in finding satisfied interpretation, the analysis was carried out using four essential metrics: Learning error, testing error, energy analysis, and similarity index. Table 16 presented the learning errors obtained through MAPElearn which also can be visualized as in Figure 5. In general, the proposed NR3SAT can achieve the smallest learning errors compared to other existing models as observed in Table 16. The smallest errors produced by NR3SAT highlight the superiority of the proposed model in attaining a satisfied interpretation, leading to the minimization of the cost function. Besides this, when ES is used as the learning algorithm and the number of neurons increases, the learning error also tends to increase, as shown in all illustrated figure. These higher values of MAPElearn indicate a high percentage of unsatisfied clauses. When ES fails to find the satisfied clauses, this causes the network to retrieve random synaptic weights to be stored in CAM This, in turn leads to a non-optimal learning phase. This phenomenon occurs because as the number of neurons increases, the probability of finding a satisfied interpretation becomes very low. This is because it becomes more challenging for the neurons to achieve zero-cost function. One of the main reasons contributing to this trend is the nature of ES which relies on a trial-and-error approach to find satisfied interpretation. As the problem complexity increases with a greater number of neurons, ES may struggle to find a satisfied interpretation due to the increase search space. However, NR3SAT consistently maintains the lowest errors when compared to existing logics. The logic that comes closest to achieving the lowest error is 3SAT. Based on the observation between NR3SAT and 3SAT, the restriction feature in NR3SAT with at least one negative literal in each clauses promotes a higher probability of obtaining a satisfied interpretation. Additionally, when comparing the errors obtained using NR3SAT and 3SAT, it becomes evident that the inclusion of all positive literals in 3SAT clauses can disrupt the process of finding satisfied interpretation leading to higher MAPElearn errors.
In comparison with non-systematic logics, it is worth noting that the errors obtained when using non-systematic logics, which involved first order clauses RANkSAT (k=1,3), RANkSAT (k=1,2,3) GRANkSAT (k=1,2,3), and GRANkSAT (k=1,3), were consistently higher than those obtained by systematic logics. Additionally, an observation from Table 16 revealed that as the number of neurons surpasses 90, these non-systematic logics demonstrate suboptimal performance. Notably, no errors are generated beyond a certain threshold of neurons, indicating the inability of non-systematic logics to identify satisfied interpretation. This finding highlighted the instability of these logical rules when compared to the systematic logics. This demonstrated that increasing number of first-order clauses significantly influences the process of finding a satisfied interpretation of the logical rule. This is because there is only one possibility to achieve a satisfied interpretation, which is either 1 or -1 [16]. This contrasts with second and third order clauses which have more combinations to make it satisfied. This observation is further supported by the results obtained using GRANkSAT. As evident in the MAPElearn metric, the learning errors produced by GRANkSAT exhibit inconsistency compared to other logics. This inconsistency can be due to the flexibility of GRANkSAT, which can function as both systematic 3SAT and non-systematic SAT logic. It is noticeable that at certain neuron numbers, such as when NN falls within the range of 45<NN<53 and 81<NN<89, the MAPElearn errors experienced drastic decrease. This decrease in errors align with GRANkSAT transitioning into a 3SAT logic. The lowest errors observed when GRANkSAT behaves as a 3SAT logic indicate that at that point, GRANkSAT easily finds satisfied interpretation leading to lower errors. This observation indicated that higher-order logic increases the probability of achieving a satisfied interpretation. Therefore, it can be summarized that DHNN by incorporating NR3SAT logical rule exhibited the best learning capability across metrics in terms of its learning capability.
8.1.2. Testing errors analysis
During the retrieval phase of DHNN, conducting error analysis is crucial to assess the quality of the retrieved final neuron states. This is particularly important because as pointed out by Zamri et al. [16], DHNN often generates repetitive final neuron states instead of producing new ones. To tackle this challenge, the assessment of the retrieved final neuron states was conducted from three critical perspectives: Testing error evaluation, the generation of global minima solutions, and the quality of the retrieved solution in comparison to benchmark states. Once NR3SAT has successfully found a satisfied interpretation resulting in EℓNR3SAT=0, the optimal synaptic weights are generated. Therefore, the conducted error analyses aim to examine how NR3SAT behaves based on the synaptic weights acquired during the learning phase specifically in terms of generating local or global minima solutions when compared to other existing baseline models. Graphical results of MAPEtest can be observed in Figure 6 with tabulated results as shown in Table 17. Indeed, these errors exhibit a strong correlation with the errors encountered during the learning phase. In simpler terms, when learning error increases due to the challenges in finding satisfied interpretation, this subsequently leads to an increase in MAPEtest. Nonetheless, NR3SAT consistently managed to attain the lowest testing errors among all baseline models. This can be due to its high capability of finding satisfied interpretation in comparison to the other logics. Consequently, this underscores the ability of ℓNR3SAT to generate a higher number of global solutions compared to existing logic models.
Furthermore, a comparison between systematic and non-systematic logics revealed that systematic logics can achieve zero MAPEtest when NN<63. Within this range, both NR3SAT and 3SAT excel in finding satisfied interpretation leading to zero testing errors. On the other side, non-systematic logics with lower-order logic of 1SAT such as RANkSAT (k=1,2,3), RANkSAT (k=1,3), GRANkSAT (k=1,2,3) and GRANkSAT (k=1,3) tend to generate higher MAPEtest compared to MAJ22SAT which does not include 1SAT. This can be due to the lower probability of obtaining satisfied interpretation in lower-order logics during the learning phase of DHNN as indicated by Karim et al. [14]. When dealing with higher-order logics like 2SAT or 3SAT, there are significantly more possible arrangements that can satisfy the clauses. In contrast, 1SAT can only be satisfied by values of 1 or -1. Consequently, when these logics fail to obtain satisfied interpretation, non-optimal synaptic weights are generated resulting in higher errors. From a systematic logic perspective, NR3SAT begins to outperform 3SAT when NN⩾72. The MAPEtest produced in this range are significantly lower when compared with 3SAT, despite both logics being of the same order. This superiority of NR3SAT can be due to its logical structure which incorporates more negative literals in a clause compared to existing 3SAT. The presence of these negativity biased clauses enhanced the process of obtaining satisfied interpretations, resulting in lower errors during the retrieval phase.
As previously discussed, the ability to achieve low error values during the retrieval phase indicates the model's effectiveness in discovering a greater number of global minima solutions, thereby ensuring the convergence property of DHNN. This can be quantified through the retrieved energy represented as the ratio of global minima solutions, RG as depicted in Figure 7 and Table 18. Generally, NR3SAT and baseline models featuring higher-order logics such as 3SAT, RANkSAT (k=2,3), GRANkSAT (k=2,3), and MAJ2SAT (k=2,3), tend to attain their maximum global minima ratios when NN falls within the range of 9 to 18. This range signifies the successful implementation of the proposed SAT into DHNN. From another perspective, it can also be observed that non-systematic models incorporating first order logics such as RANkSAT (k=1,2,3) and RANkSAT (k=1,3) exhibit a notable decrease in their performance values as the number of neurons increases. This decline in performance can be due to the increased number of first-order clauses in these models. Essentially, the increased presence of first order clauses reduces the probability of these models achieving satisfied interpretations. This in turn complicates the process of minimizing logical inconsistencies. Consequently, the cost function minimization becomes unsuccessful, leading to the generation of non-optimal synaptic weights. In simpler terms, the inability to attain satisfied interpretation which leads to a zero-cost function results in incorrect synaptic weights and ultimately affecting the overall quality of the retrieved final neuron states. These findings are further supported by the performance of GRANkSAT (k=1,2,3) and GRANkSAT (k=1,3) in comparison to GRANkSAT (k=2,3). GRANkSAT (k=2,3) significantly outperforms the other two models, as it can achieve high RG approaching 1 when the number of neurons falls within the range of 9 to 62. However, as the number of neurons increases, the inclusion of 1SAT in GRANkSAT (k=1,2,3) and GRANkSAT (k=1,3) disrupts the process of obtaining global solutions. Additionally, the flexibility of these models which can also be systematic 3SAT, demonstrated that when these models transition into systematic 3SAT (without first order logics), the global solution ratio increases dramatically. This results in fluctuations in the performance patterns of these models.
Furthermore, a close comparison between the global minima ratios produced by NR3SAT and 3SAT can be observed in Figure 8. Notably, NR3SAT consistently achieves a maximum ratio of 1 up to NN=80, whereas in the case of 3SAT, the ratio of global minima solutions starts to decrease as NN exceeds 63. The significance of attaining global minima solutions is closely linked to the quality of the retrieved final neuron states which will be further explained in the context of the similarity index perspective. The question is, why is it so important to have global solutions? To address the importance of having global solutions, it is essential to understand that global solutions play a critical role in assessing the quality of the retrieved final neuron states. Without global solutions, the quality of the retrieved final neuron states remains uncertain. This connection between global solutions and the quality of final neuron states is particularly evident when examining the relationship between learning and testing errors. Thus, the quality of the retrieved final neuron states can be effectively evaluated using similarity index.
8.1.3. Similarity index analysis
To assess capability of NR3SAT in producing highly dissimilar states, its performance was analyzed using two key metrics: the Jaccard value and Total Neuron Variation (TV). These metrics are utilized to compare NR3SAT with other baseline models, as illustrated in Figure 9 and Figure 10. Additionally, the tabulated data can also be presented in Table 19 and Table 20. In the context of Jaccard values, smaller values indicated high dissimilarity between the retrieved final neuron states and the benchmark states. Referring to Figure 9 and Table 19, a notable observation is that the majority of the baseline models achieved Jaccard values exceeding 0.550, while NR3SAT consistently obtained relatively low Jaccard values, falling below 0.5. These lower Jaccard values indicate that the final neuron states retrieved by NR3SAT exhibit a high degree of dissimilarity when compared to the benchmark states. This high dissimilarity signifies non-overfitting solutions. In contrast, overfitting occurs when all the retrieved final neuron states match the benchmark states precisely. It is crucial to emphasize that when addressing real-life datasets for classification problems, the presence of overfitting solutions can result in suboptimal logical rules representing the datasets. Consequently, this suboptimal logical rule may fail to precisely extract information and explain the strength of associations between variables. Furthermore, as mentioned by Guo et al. [8], the assessment of similarity index only for those solutions which achieved global solutions. When comparing systematic and non-systematic logics, the non-systematic logics failed to achieve Jaccard values for certain NN. This is because the generated solutions were trapped in local minima due to the non-optimal synaptic weights being used to update the local field. One of the main reasons why this contributes to non-optimal synaptic weights is because of the nature of ES. ES, which operates based on a trial-and-error approach, faces limitations in finding a satisfied interpretation as the number of neurons increases, impacting the minimization of the cost function [33].
Based on systematic logic, both 3SAT and NR3SAT generally obtain better Jaccard values compared to non-systematic logic. However, Table 19 reveals a significant difference in the values obtained, with NR3SAT outperforming 3SAT by consistently achieving lower Jaccard values. Additional feature of including at least one negative literal in NR3SAT has a substantial impact on the quality of the retrieved final neuron states. Consequently, this promotes more diversified final neuron states. Shifting the focus to the possible combination of 3SAT and NR3SAT, it becomes apparent that NR3SAT does not include all positive literals in a clause, such that Q∗i∉(qi∨qj∨qk). This observation highlights the influence of the presence of this combination on the performance of 3SAT. The underlying reason for this is that there is no variation in terms of the individual contribution of synaptic weight for this combination, resulting in repetitive final neuron states. Consequently, these repetitive final neuron states exhibit high similarity with the benchmark states.
On the other side, TV values can be explained in terms of the efficiency of the models in exploring different solutions across various areas within the search space. TV can only be measured if the retrieved final neuron states satisfy Eq (13) [8]. As shown in Figure 10 and Table 20, the non-systematic logics achieved highest TV when the number of neurons falls within the range of 35 to 62. In contrast, 3SAT and NR3SAT consistently achieve higher TV values up to NN<72. However, considering all logics, NR3SAT generates the highest TV compared to all baseline models. This is due to the presence of more global minima solutions in NR3SAT, which indirectly leads to higher TV values. These higher TV demonstrates the effectiveness of the proposed model in exploring different areas in the search space [16].
In conclusion, based on the above analyses, NR3SAT has been successfully integrated into DHNN, resulting in the attainment of global minima solutions with diversified final neuron states. However, it is important to note that the performance of DHNN can be further improved by addressing certain limitations identified in this work. One notable limitation is the utilization of the proposed learning algorithm. It is evident that the trial-and-error approach in ES poses challenges in finding satisfied interpretations, especially as the number of neurons increases. This is because this approach requires trying out all possible solutions in the search space to obtain satisfied interpretations. Moreover, this approach introduces time constraints, leading to suboptimal optimization processes. Ideally, when an algorithm is implemented into DHNN, it should possess the ability to rapidly identify optimal solutions. Therefore, implementation of learning algorithms is crucial to enhance the process of finding satisfied interpretation which led to optimal synaptic weights.
8.1.4. Non-parametric test
A non-parametric test, specifically known as Friedman test was employed in this study to assess the significance of the proposed NR3SAT in comparison to other baseline models. The importance of this test lies in its ability to determine whether there is a statistically significant difference in the performance among the models under consideration. This analysis is crucial for drawing meaningful conclusions about the effectiveness of the proposed NR3SAT in the context of DHNN based on various performance metrics, when compared to other existing models. For clear illustration, the hypothesis can be declared as follows:
H0: There is no significant difference in the performance metrics between the proposed NR3SAT and other baseline models.
H1: There is a significant difference in the performance metrics between the proposed NR3SAT and other baseline models.
In this study, the Statistical Package for the Social Sciences (SPSS) software was employed to conduct the Friedman test, and the results are presented in Table 21. Using a pre-defined significance level of 0.05, the null hypothesis will be rejected if the obtained p-value is less than 0.05. The observations from Table 21 clearly indicated that, for all performance metrics, the associated p-values were below 0.05. Consequently, all the null hypotheses are rejected, leading to the conclusion that a significant difference exists in the performance metrics between the proposed NR3SAT and other baseline models. Additionally, the mean rank of the models based on different performance metrics is provided in Table 22. In the context of learning errors, testing errors, and Jaccard values, lower values indicate good results. As for the global minima ratio and TV values, the maximum values of 1 for global ratio and higher values of TV indicate a positive impact on the overall performance.
Thus, it can be observed that the proposed NR3SAT achieved the lowest mean rank for learning errors, testing errors, and Jaccard values, indicating that this proposed model can generate the lowest errors and has high dissimilarity between the retrieved final neuron states and the benchmark states. On the other hand, the proposed NR3SAT attained the highest mean rank for global ratio and TV, indicating that NR3SAT attained more global solutions, and the model explored different solutions in various areas of the search space compared to other baseline models. Therefore, it can be concluded that the proposed NR3SAT has been successfully integrated into the DHNN framework, enhancing the overall performance of DHNN.
8.2. Performance analysis of optimizing retrieval phase of ℓNR3SAT
In optimizing the retrieval phase of DHNN, it is essential to ensure that all the retrieved final neurons state attained global minima solutions. Therefore, we implemented EA during the learning phase of DHNN to acknowledge all the limitations mentioned in the previous section. Researchers [28,33,39,51] employed EA as the learning algorithm to handle the task of SAT minimization within DHNN. By implementing this optimization algorithm, EA can significantly improve the converge of network towards minimizing the cost function while maintaining a high level of dissimilarity compared to the benchmark states. However, the diversification of the solutions particularly concerning negativity remains uncertain. Therefore, incorporating a degree of negativity in the final neuron states becomes imperative to boost DHNN's performance in classification tasks. To achieve this, HBHA was employed during the retrieval phase of DHNN to optimize the final neuron states. These optimized solutions aim to satisfy the multi-objective function outlined in Eqs (15)–(17), with a specific target of achieving negativity within each solution, Stari:Sf1Sf2Sf3Sf4Sf5…SfNN. This raises the question of to what extent HBHA can maximize negativity while ensuring the attainment of global solutions and maintaining low similarity indices. Therefore, the performance of HBHA in maximizing the degree of negativity within the solution states will be thoroughly evaluated.
Figure 11illustrated the impact of optimizing the retrieval phase of DHNN through HBHA in achieving a degree of negativity in the solution states while preserving the attainment of global solutions in comparison to not optimizing the retrieved final neuron states. Several observations can be drawn from Figure 11. First, it is evident that the implementation of a metaheuristic algorithm significantly enhances the performance of DHNN in achieving maximum diversification while retaining the ability to obtain global solutions. As indicated by the black line representing the state "Before HBHA, " without optimizing the retrieved final neuron states, the solutions obtained fail to achieve maximum diversity. With the implementation of HBHA, optimized final neuron states can achieved maximum diversity and achieve global solutions. Based on the findings presented in Figure 12, it can be concluded that HBHA performs optimally when the degree of negativity in a solution string is set to be at least 60%. However, when the number of neurons exceeds 81, HBHA struggles to ensure all solution strings can achieve maximum diversity and achieve global minima energy. To address this challenge, parameter tuning was conducted by specifically focusing on adjusting the rate of replicating the best solutions. HBHA with at least 60% negativity performs effectively when β=0.7 ensuring that all optimized final neuron states achieve both diversity and global minima energy. Additionally, the performance of HBHA start to drop when degree of negativity is set to be at least 70% because of the limited solution space to obtained optimal solutions. Besides that, although all solution strings can achieve maximum diversity and reach global minima energy when m is in the range of 0.1 to 0.5 as shown in Figure 11, the optimized states encounter overfitting issue. This occurs because when number of percentages is too low, there is a high tendency to obtain repetitive final neuron states due to the lack of variation in terms of negativity.
To assess the effectiveness of HBHA in achieving the desired at least 60% negativity in a solution, the performance of HBHA will be compared with 10 baseline algorithms. The evaluation will focus on achieving high diversity, attaining a high number of global solutions and obtaining solutions that exhibit both diversity and attained global solutions with low similarity indices. A performance comparison between HBHA and 10 other algorithms with a focus on diversity, NDS are provided as in Figure 13 and Table 23. In Figure 13, it is evident that several algorithms including ABCK, GA, ABCJ, ABCS and DEA fail to attain maximum NDS when the negativity variation is set to be at least 60%.
One contributing factor to these findings is the lack of an efficient exploitation process in these algorithms. For example, in the case of GA, the mutation process is designed to enhance exploitation but it only selects one random chromosome out of 100 solution sets to mutate. Regarding the ABC algorithms, all three of them primarily focus on global search by introducing various bitwise operators to update the positions of employed bees. However, they lack an exploitation process to improve neighbourhood solutions, which ultimately results in low NDS being obtained. Another issue related to the lower NDS values for ABCK is the implementation of bitwise operations to update the employed bee solutions. In this scenario, the proposed bitwise operator results in more 1 output compared to -1. This indirectly reduces the efficiency of ABC in producing more negative states compared to positive states. Other than that, an issue can also be observed in the DEA process, where there is an imbalance between the exploration and exploitation processes. The absence of an effective exploitation process in DEA leads to a lower NDS of solutions obtained.
In contrast, several algorithms demonstrated exceptional performance in achieving maximum NDS as shown in Table 23. It is worth noting that SCA, EA, WOA and BHA exhibited an increase in NDS and were able to achieve maximum NDS as the number of neurons increases. However, when considering overall performance, HBHA and CSA stood out as the only algorithms that consistently achieved maximum diversity across all neuron numbers. One shared feature of these two algorithms was their capacity for duplicating solutions to boost the performance of the algorithms. In CSA, a cloning process was employed to clone the best solution using a predefined clone rate 0.5 based on the total number of populations. In the case of HBHA, solution replication was performed based on the top best solution obtained, utilizing a replication rate of 0.7. This highlights the effectiveness of the operator in improving global search capabilities, leading to their remarkable achievement of maximum diversity. From the perspective of global minima solutions, NGR the performance of all algorithms was evaluated to determine whether the solution converge to local or global solution while achieving maximum diversity. The result as presented in Table 24 and Figure 14 reveal a notable trend such that BHA, SCA, WOA and EA experience a significant decline in performance when striving to achieve a maximum global solution. This contrasts with the performance trends depicted in Figure 13. This observation implies that while these algorithms are effective at attaining a high NDS, the solutions they produce may not necessarily be global since it led to unsatisfied interpretation. This is due to the updating rule concept in BHA, SCA and WOA where updates occur for each state of the solutions string. While this process enhances diversity, the alterations in each state disrupt the attainment of a satisfied interpretation, resulting in lower global solutions [26,44,50].
A similar situation arises in EA where at each stage of the algorithm, the random mutation process contributes to an increased chance of achieving the desired negativity rate. However, this also leads to a reduced probability of obtaining a satisfied interpretation, resulting in lower global solutions. In other words, random mutations may introduce alterations to the solution that deviate from the conditions required for a solution to be considered satisfied. Another observation from Table 24 and Figure 14 is the remarkable performance of DEA, ABCJ, ABCK, ABCS, CSA and HBHA in consistently maintaining global solutions across all numbers of neurons. While ABCJ, ABCK, ABCS and DEA may not have excelled in achieving high NDS, it is important to highlight that all the solutions generated by these algorithms consistently exhibited are global. One contributing factor to this finding is the implementation of bitwise operators to update the position of employed bees, facilitating a higher output of 1. This increases the probability of obtaining satisfied interpretation, leading to increase chances of obtaining global minima solutions. In the case of HBHA and CSA, the optimized final neuron states consistently achieved a global ratio of 1. This indicates that the cloning operator in both algorithms which expands the solution space has enhanced the exploration of optimal solutions and has a significant impact on the overall performance of HBHA and CSA.
Figure 15 and Table 25 illustrates the performance of HBHA and other baseline algorithms in achieving both maximum diversity and a maximum global solutions, NDG. As the number of neurons increases, several algorithms including ABCJ, ABCK, EA, WOA, SCA and GA encounter challenges in obtaining NDG. This highlights that, as these algorithms aim to achieve the desired negativity in the solution string, it has an impact on the state of the neurons. Notably, GA exhibits the poorest performance in optimizing the retrieved final neuron states as the algorithm failed to achieve any of the predefined objectives. One significant factor contributing to this outcome is the absence of additional operators in these algorithms to enhance the exploration of global solutions. As highlighted by Karim et al. [51], EA, ABC and GA face limitations in optimizing the learning phase of DHNN to fulfil multi-objective functions due to constraints in improving local solutions. The findings also reveal that only HBHA and CSA possess the capability to achieve NDG. However, the quality of the optimized final neuron states obtained by these algorithms remain uncertain. Figure 16 and Table 26 presents an evaluation of the quality of the optimized final neuron states obtained through various algorithms. During the retrieval phase of DHNN, the evaluation of the retrieved final neuron states involved a comparison with benchmark states.
However, in optimizing the retrieved final neurons state, the assessment focuses on comparing the quality of the optimized final neuron states to their initial, unoptimized counterparts. The low values of RT indicate a significant dissimilarity between the states before and after optimization and the high values of RT indicate high similarity between before and after optimization took place. In this context, RT was chosen to assess the similarity within the solutions strings as this metric able to measure the similarity of negative cases [16]. Based on the results in Figure 16, ABCK demonstrated the worst performance. Regardless of the number of neurons, the similarity index RT consistently achieved the maximum value of 1. This indicates that there was no improvement in the quality of the final neuron states after optimization. The performance patterns of ABCJ and ABCS also show a significant increase in the similarity of the optimized final neuron states as the number of neurons increases. In contrast, when comparing HBHA with all the algorithms, it is evident that HBHA consistently achieved the lowest values of RT for most of the number of neurons, indicating that DHNN produced high-quality final neuron states through the HBHA optimization process. The quantitative performance of the proposed HBHA and other baseline algorithms is presented as in Table 27. Based on the findings, it can be concluded that HBHA was effectively implemented to optimize the retrieval phase of DHNN, successfully achieving all the objectives outlined in Eqs (15)–(17). The Friedman test is used to assess the significant difference between the proposed HBHA and other baseline algorithms in general for a specific metric. For clarity, the null hypothesis and the alternative hypothesis for the Friedman test are outlined as follows:
H0: There is no significant difference in the performance metrics between the proposed HBHA and other baseline algorithms.
H1: There is a significant difference in the performance metrics between the proposed HBHA and other baseline algorithms.
The Friedman test results are presented in Table 28. Based on the results, the p-value for all performance metrics is less than 0.05. Since 0.000<0.05, we can reject the null hypothesis. Thus, it can be concluded that there is a significant difference in the performance metrics between the proposed HBHA and other baseline algorithms. Furthermore, Table 29 presents the mean rank of the algorithms across various performance metrics. In the context of maximizing the diversity and global solutions of the optimized final neuron state, higher values indicate the algorithms' capacity to generate maximum diversity and achieve global solutions. Notably, HBHA and CSA stand out with the highest mean rank in this regard. Given their strong performance in maximizing these metrics, it is evident that both algorithms also exhibit the lowest mean rank in terms of error rate when seeking maximum diversified solutions and maximum attainment of global solutions. However, concerning the similarity index, HBHA secures the lowest rank of 1.17 compared to other baseline algorithms, underscoring its efficiency in producing optimized solutions with high dissimilarity compared to benchmark states.
8.3. Impact analysis of ℓNR3SAT
So far, the sections have demonstrated the overall performance of the proposed model focusing on the implementation of SAT in DHNN and the optimization of the retrieval phase of DHNN. This section discusses the impact of the proposed work on the overall performance of DHNN. Ideally, NR3SAT was formulated to address the limitation exits in the existing 3SAT. Both SAT are focusing on higher order systematic logic. The main difference between the existing 3SAT and the proposed NR3SAT lies in the appearance of negative literals within the clauses. In 3SAT, the appearance of positive and negative literals is random, often resulting in more positive literals compared to negative ones. In fact, this issue was supported by the finding of Abdeen et al. [36] which highlighted that the occurrence of negative literals for SAT is exceptionally infrequent. Neglecting the role of these negative literals not only limits the expressiveness of the logical structure but also inhibits the exploration of undiscovered solutions. Consequently, when this logic is embedded into DHNN, the network tends to produce repetitive final neuron states, leading to overfitting solutions. In other words, there is a high similarity between the retrieved states and the benchmark states. However, controlling the appearance of negative literals within NR3SAT clauses has impacted the overall performance of DHNN. This is supported by the learning errors shown in Figure 5 and Figure 6. Controlling the appearance of negative literals in NR3SAT increases the chances of obtaining satisfied interpretation, resulting in more global solutions. Additionally, NR3SAT produces high dissimilarity between the retrieved states and the benchmark states, as shown in Figure 9. Therefore, the formulation of NR3SAT is significant for enhancing DHNN's performance in obtaining global solutions and avoiding overfitting.
Next, to ensure this intelligent model can classify and extract knowledge, optimizing the retrieval capabilities of DHNN is crucial. One might wonder why it is necessary to propose multi-objective functions in the retrieval phase. The answer lies in the potential use of this model in logic mining. In this context, the final neuron states retrieved will be converted in the form of induced logic [52]. This logic will have the capability to classify and extract knowledge. Unlike other classification approaches that only indicate the model's accuracy, this induced logic can extract patterns and relationships, explaining the reasoning behind the value obtained. Therefore, it is vital to ensure the network can retrieve high-quality induced logic to enhance interpretability in explaining these relationships. It is worth noting that existing works focus solely on obtaining global solutions but there is a high risk of all solutions being global but overfitted. How does this overfitting issue affect induced logic? Overfitting may cause the network to retrieve the same pattern of induced logic. In other words, this will reduce the interpretability issue. Therefore, it is essential to consider these multi-objective functions in the retrieval phase to ensure that the network can retrieve high quality final neuron states which will be beneficial in doing logic mining.
9.
Conclusions
The primary objective of optimizing the DHNN model is to enhance its applicability in solving real-life classification problems. We introduce a new logical rule called NR3SAT to be embedded into the DHNN framework. The motivation behind proposing NR3SAT is to address the limitations of existing 3SAT models. The 3SAT model, which operates with randomized positive and negative activated neuron connections, raises concerns about the interpretability of DHNN. Moreover, the final neuron states retrieved by the 3SAT model tends to be overfitted due to the lack of variations compared to benchmark states in terms of negativity. The implementation of NR3SAT into DHNN results in improved performance. We found that this implementation leads to the lowest learning and testing errors and enables the model to attain more global minima solutions compared to existing baseline models. Additionally, the quality of the retrieved final neuron states is enhanced as evidenced by the lowest Jaccard similarity index values, indicating high dissimilarity compared to benchmark states.
In addressing the variation of negativity in the retrieved final neuron states, the study proposes a multi-objectives function during the optimization of the retrieval phase of DHNN. The goal is to achieve final neurons states with maximum diversity, maximum global solutions and the lowest RT values. To optimize the retrieval phase, the study introduces the Hybrid Black Hole Algorithm (HBHA). The results indicate that HBHA performs optimally when the degree of negativity in a solution is configured to achieve the desired proportion of clauses containing at least one negative state. The results also demonstrate that HBHA achieves maximum diversity for all numbers of neurons with all optimized solutions are global and attain the lowest similarity index.
The study opens opportunities for future research to explore the efficacy of the model in the context of non-systematic logics, involving higher-order logical structures such as RAN3SAT [14], GRAN3SAT [41], and MAJ2SAT [15]. In the context of the proposed structure of SAT, researchers may explore the impact of controlling the appearance of negative literals in a clause without considering all positive literals in perspective of non-systematic logics [8,28]. Additionally, researchers may focus on achieving diversified solutions by considering the overall literals rather than clauses. Besides this, to assess the efficiency of this proposed model, researchers may extend this work from the perspective of logic mining in solving real- life classification problems. This is due to the limitation of the logic mining model, which does not consider on optimizing both learning and retrieval phase in enhancing the performance in addressing classification problems [29,47,53]. Additionally, from another perspective, the success of the proposed Hybrid Black Hole Algorithm in addressing multi-objective functions within the DHNN framework can be extended to other neural networks such as Cohen-Grossberg Neural Networks and to different problems such as parameter estimation within neural networks by making appropriate adjustments and modifications [54,55].
Author contributions
Nur 'Afifah Rusdi: Conceptualization, Project Administration, Writing – Original Draft. Mohd. Asyraf Mansor: Funding Acquisition, Resources. Nur Ezlin Zamri: Visualization, Formal Analysis, Investigation. Mohd Shareduwan Mohd Kasihmuddin: Supervision. Nurul Atiqah Romli: Methodology. Gaeithry Manoharam: Writing – Review & Editing. Suad Abdeen: Validation. All authors have read and approve the final version of the manuscript for publication.
Acknowledgments
This research is financially supported by the Ministry of Higher Education Malaysia for the financial support of the Fundamental Research Grant Scheme (FRGS) with Project Code: FRGS/1/2022/STG06/USM/02/6 and Universiti Sains Malaysia. All the authors gratefully acknowledge the support.
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
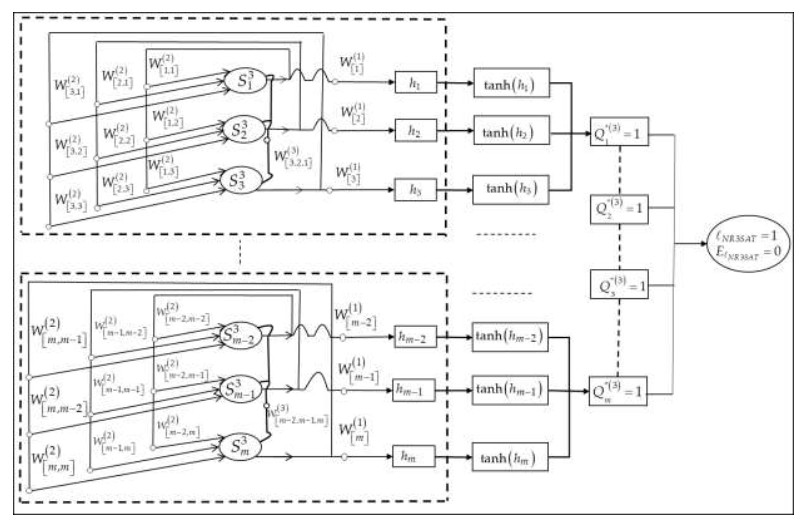









 DownLoad:
DownLoad:


















